Computational Modeling of Flow and Scour around Two Cylinders in Staggered Array
Abstract
:1. Introduction
2. Numerical Model
2.1. Hydrodynamic
2.2. Sediment Transport
2.3. Morphodynamic
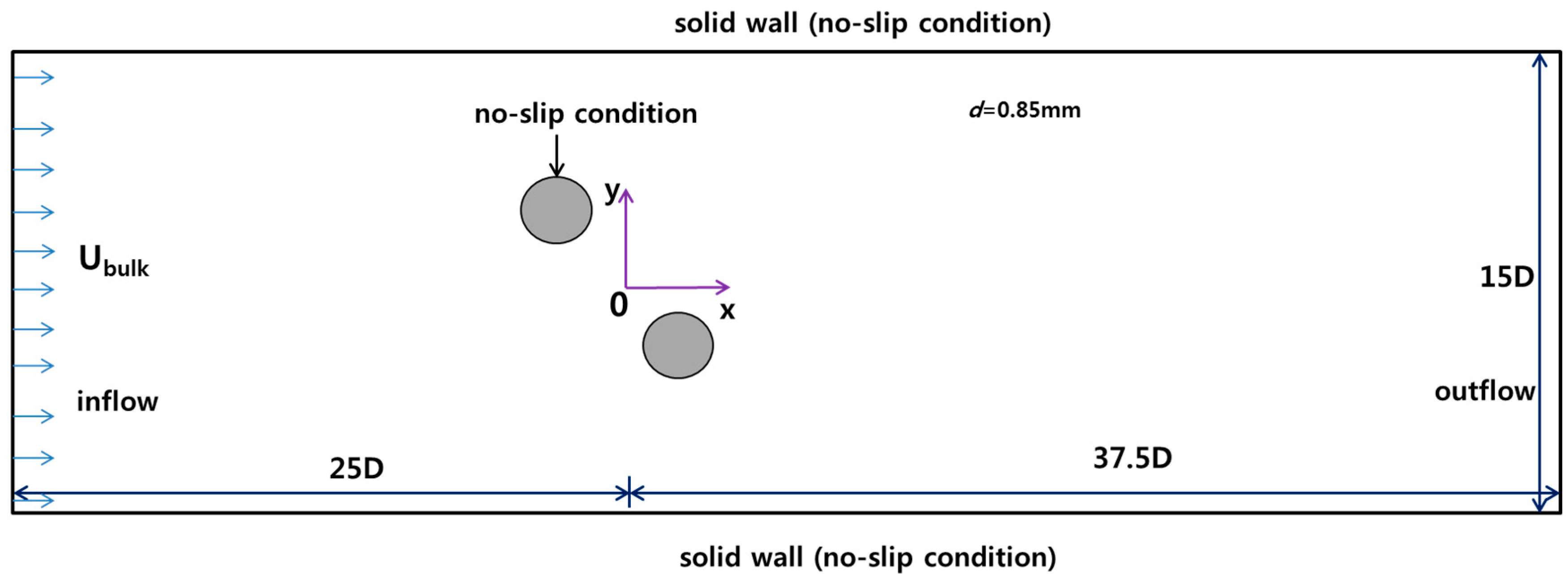
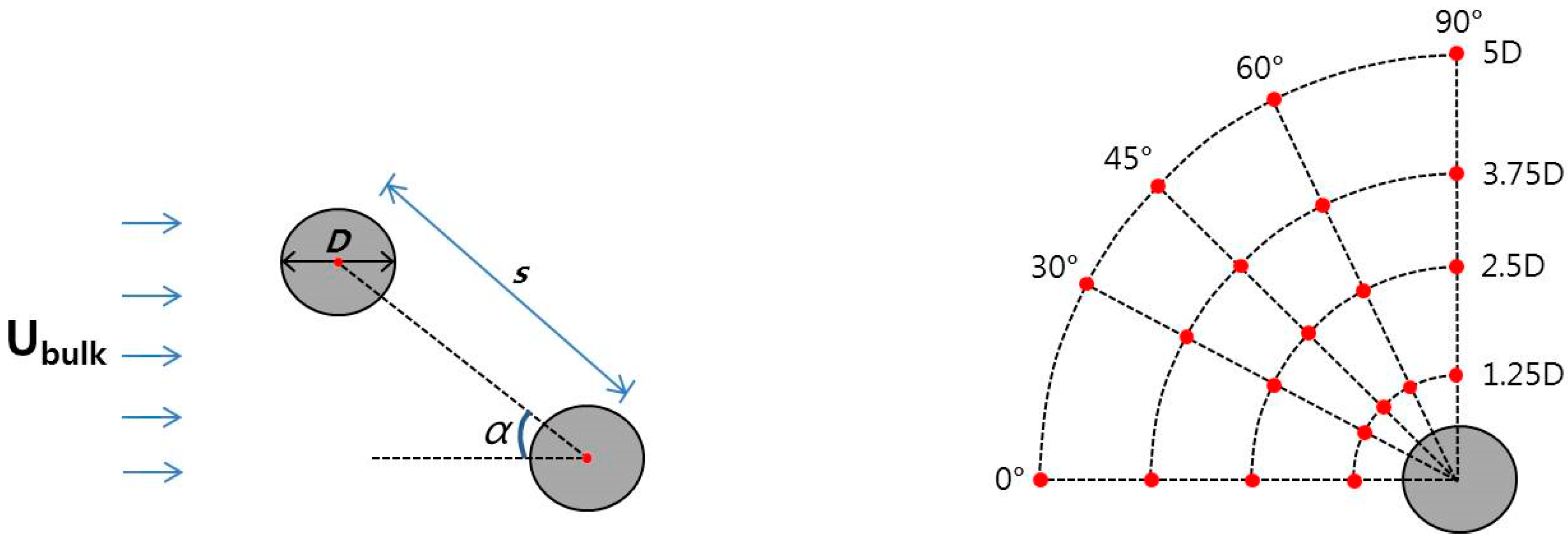
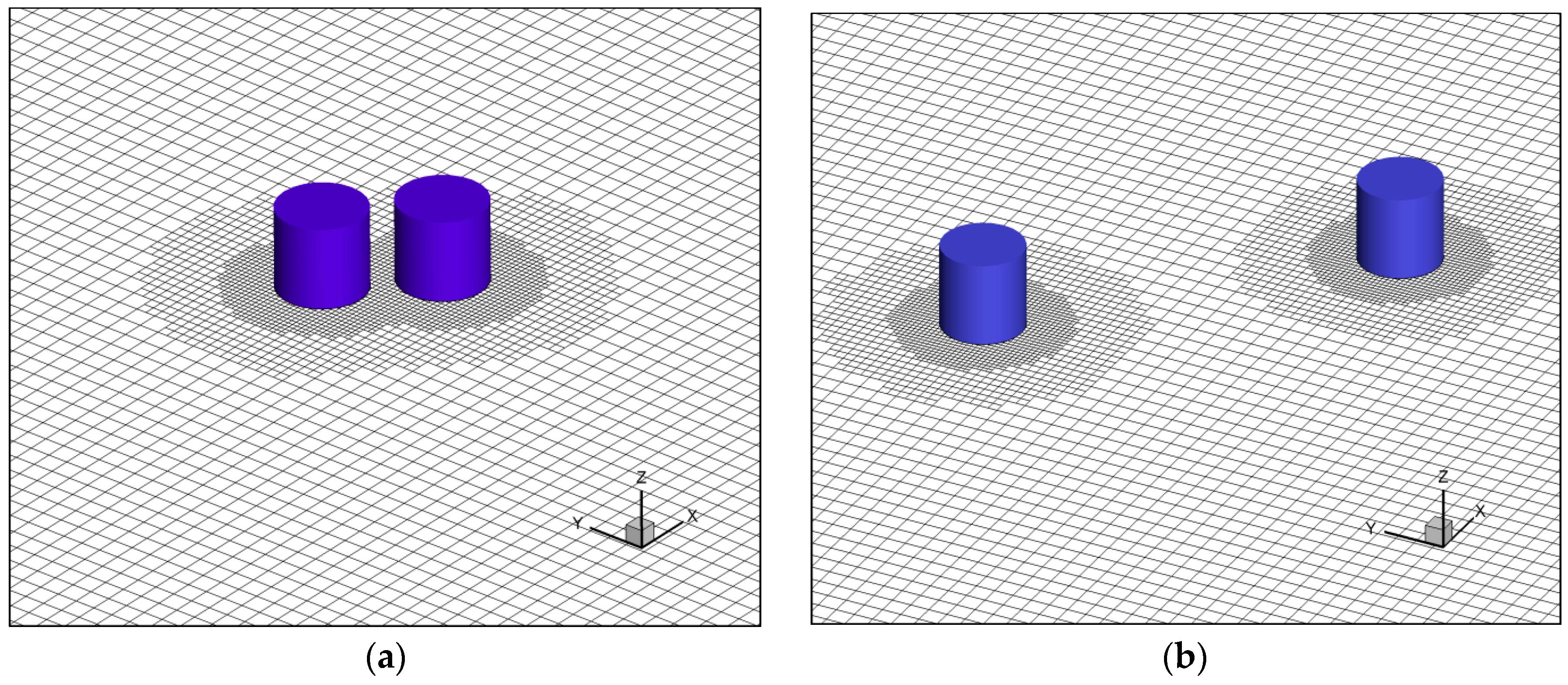
3. Numerical Conditions
4. Numerical Results
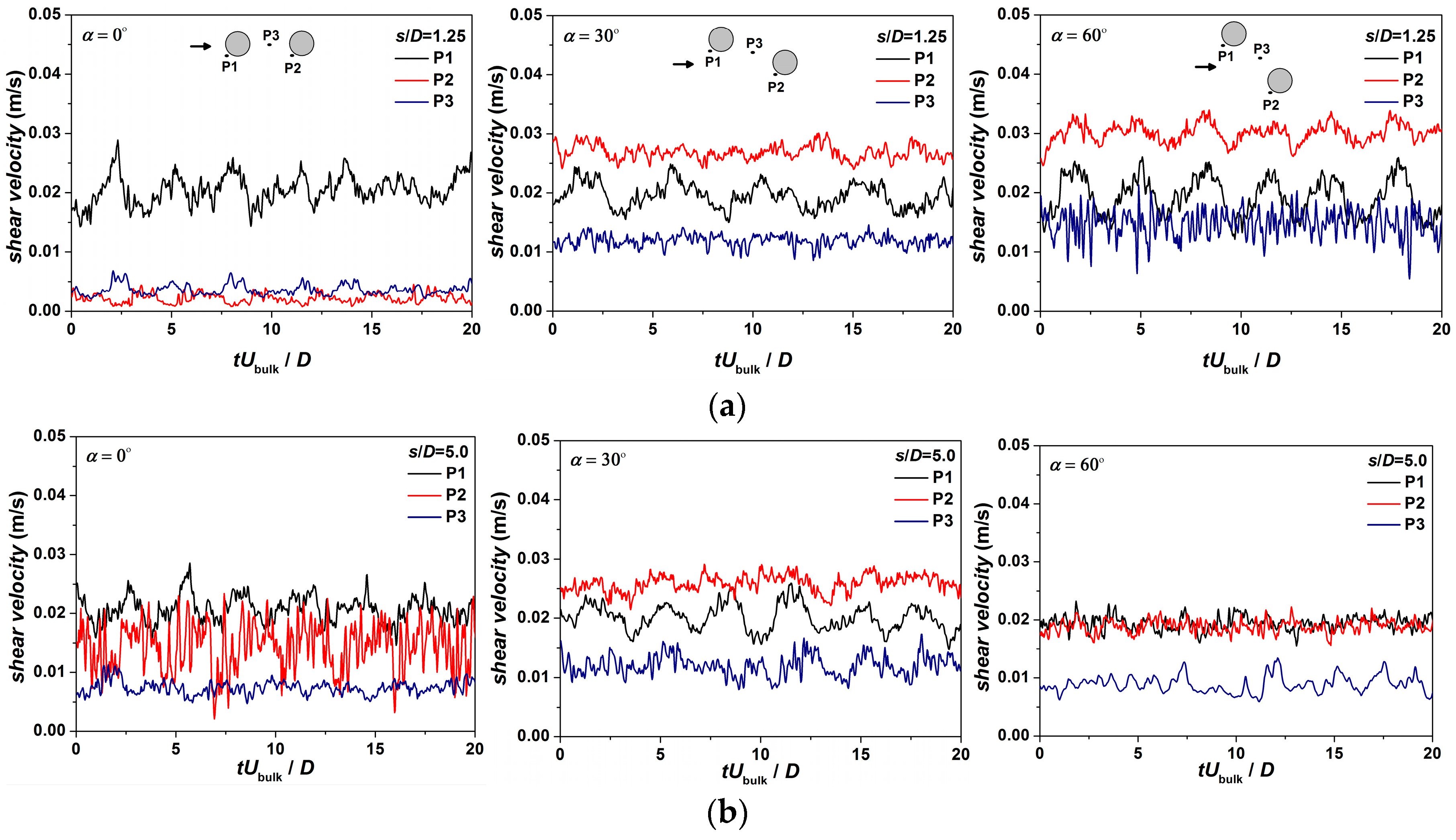
4.1. Flow Field
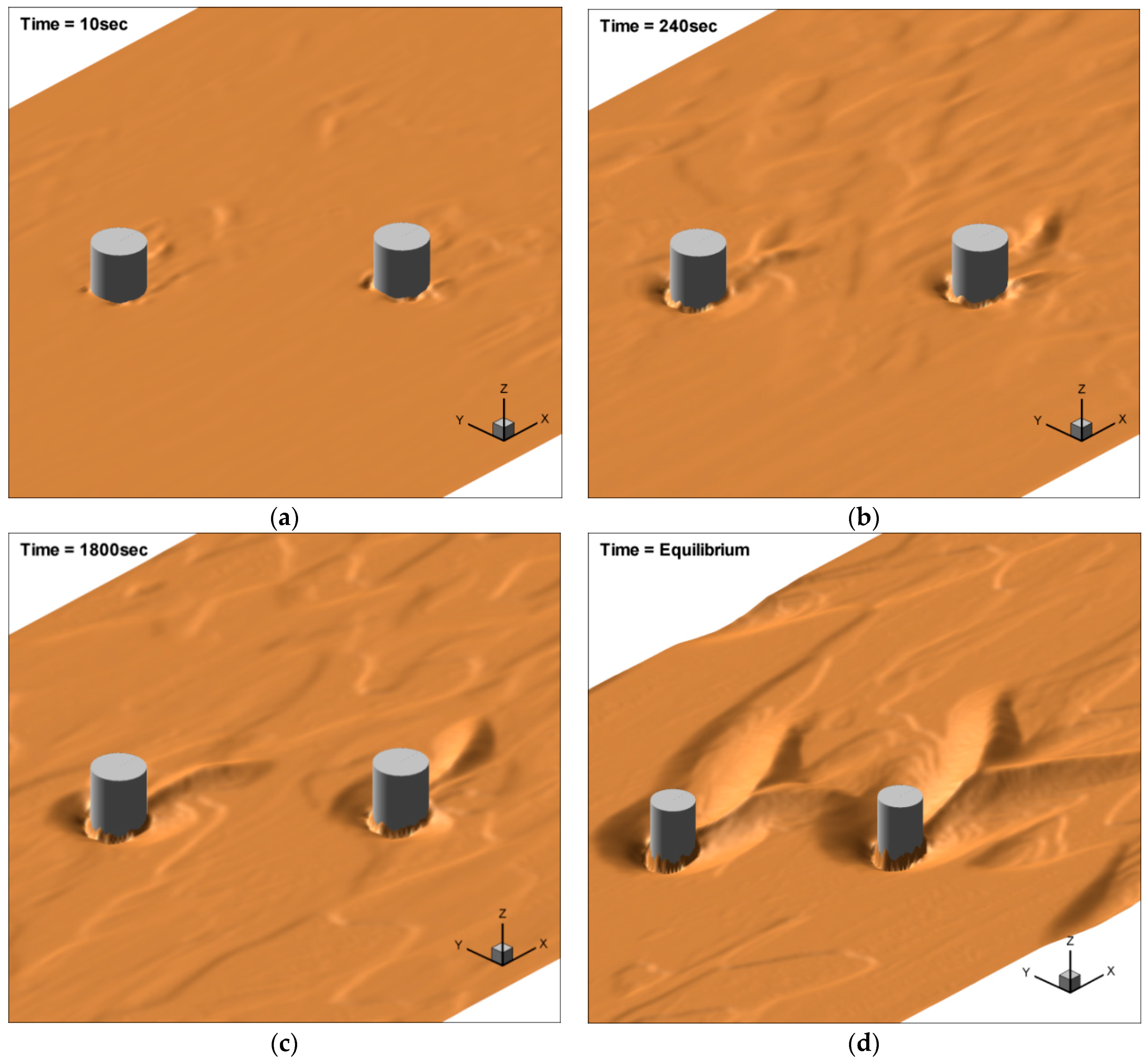
4.2. Scour Process
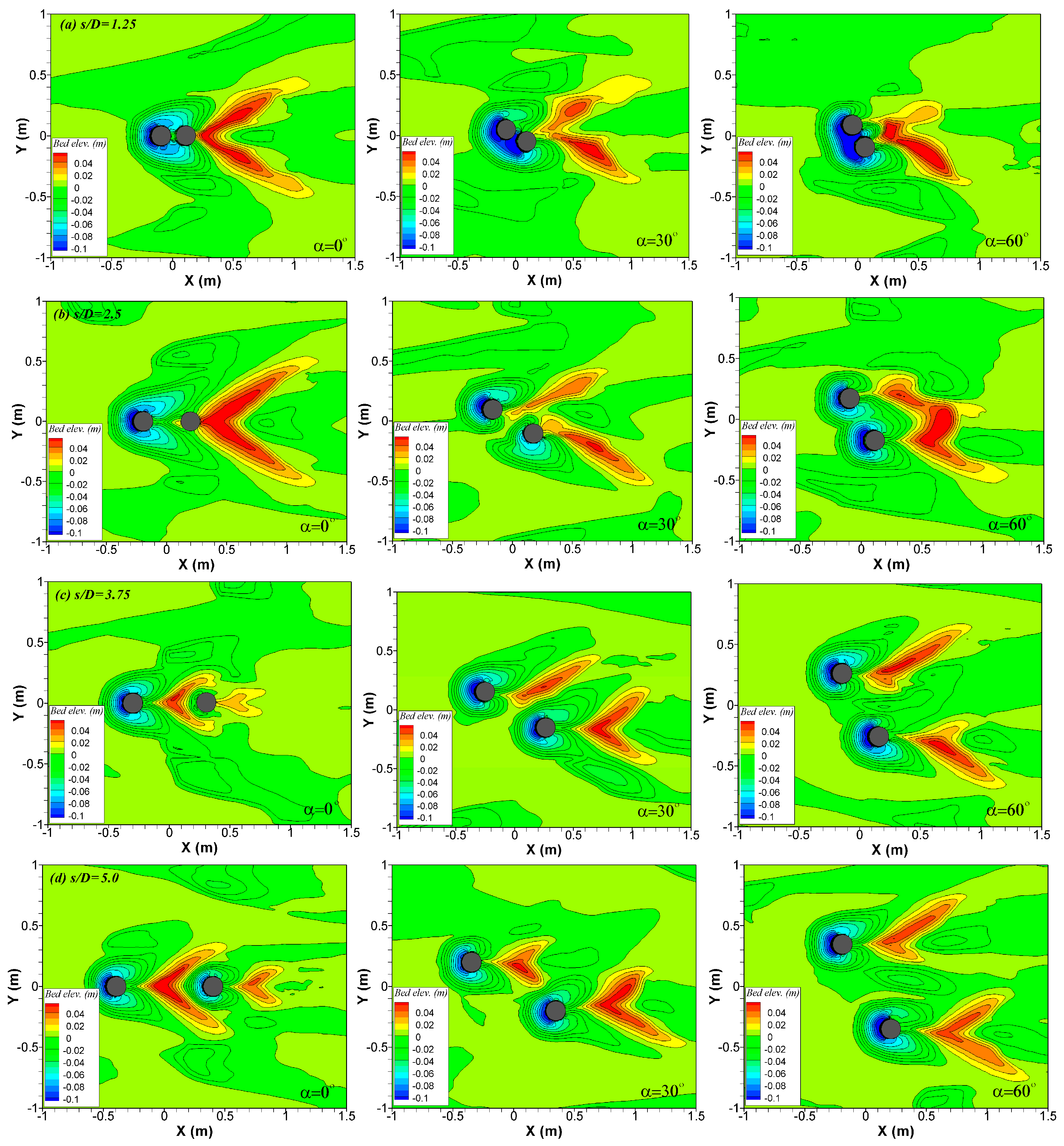
4.3. Equilibrium Bed Topography
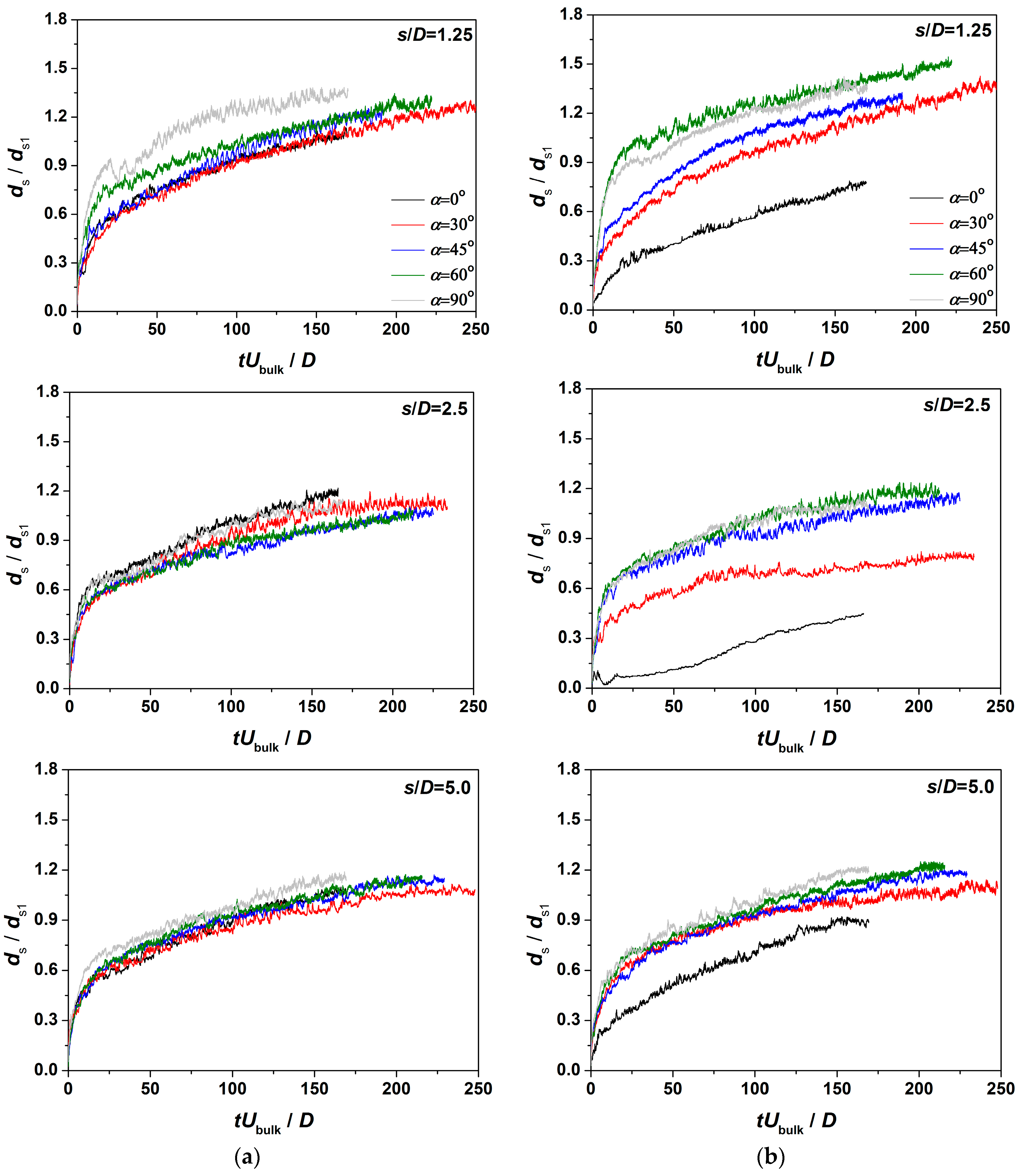
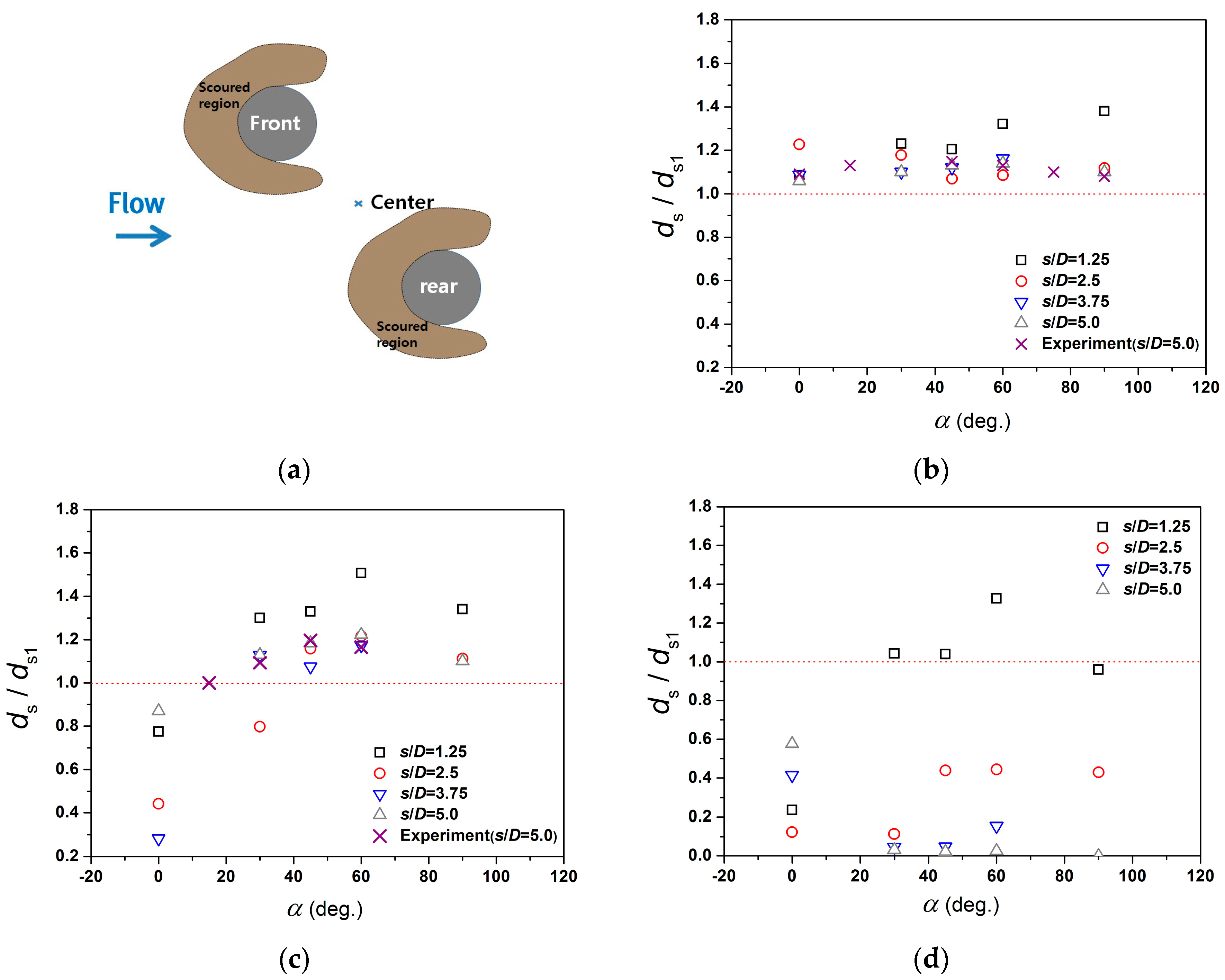
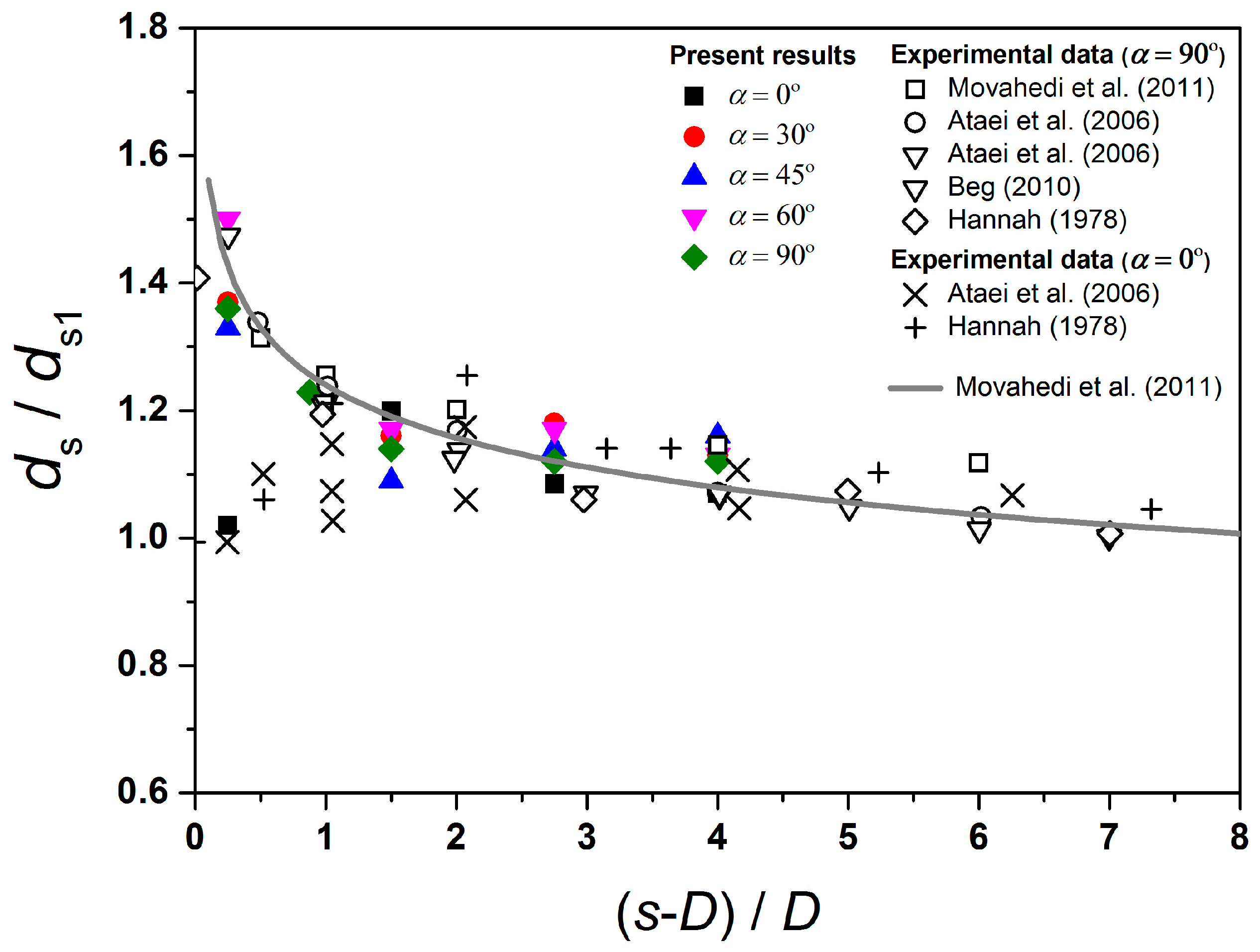
4.4. Scour Depth
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kirkil, G.; Constantinescu, G.; Ettema, R. Coherent structures in the flow field around a circular cylinder with scour hole. J. Hydraul. Eng. 2008, 134, 572–587. [Google Scholar] [CrossRef]
- Igarashi, T. Characteristics of the flow round two circular cylinders arranged in tandem (1st Report). Bull. JSME 1981, 24, 323–331. [Google Scholar] [CrossRef]
- Igarashi, T. Characteristics of the flow round two circular cylinders arranged in tandem (2nd Report). Bull. JSME 1984, 27, 2380–2387. [Google Scholar] [CrossRef]
- Sumner, D. Two circular cylinders in cross-flow: A review. J. Fluid Struct. 2010, 26, 849–899. [Google Scholar] [CrossRef]
- Zu, G.; Zhou, Y. Stroul numbers in the wake of two inline cylinders. Exp. Fluids 2004, 37, 248–256. [Google Scholar]
- Kitagawa, T.; Ohta, H. Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number. J. Fluids Struct. 2008, 24, 680–699. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, C. Large eddy simulations of the flow past two side-by-side circular cylinders. Int. J. Comput. Fluid Dyn. 2008, 22, 393–404. [Google Scholar] [CrossRef]
- Briaud, J.L.; Ting, F.; Chen, H.; Cao, Y.; Gudavalli, R.; Perugu, S. Prediction of scour rate in cohesive soils at bridge piers. J. Geotech. Geoenviron. Eng. 1999, 125, 237–246. [Google Scholar] [CrossRef]
- Hunt, B.E. Monitoring Scour Critical Bridges; Transportation Research Board: Washington, DC, USA, 2009. [Google Scholar]
- Amini, A.; Melville, B.W.; Ali, T.M.; Ghazli, A.H. Clear water local scour around pile groups in shallow-water flow. J. Hydraul. Eng. 2012, 138, 177–185. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Beheshti, A.A. Experimental investigation of clear-water local scour at pile groups. J. Hydraul. Eng. 2006, 132, 1100–1104. [Google Scholar] [CrossRef]
- Beg, M. Characteristics of developing scour holes around two piers placed in transverse arrangement. In Proceedings of the 5th International Conference on Scour and Erosion, San Francisco, CA, USA, 7–10 November 2010. [Google Scholar]
- Lanca, R.; Fael, C.; Maia, R.; Pego, J.P.; Cardoso, A.H. Clear-water scour at pile groups. J. Hydraul. Eng. 2013, 139, 1089–1098. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Gaudio, R.; Calomino, F. Bridge pier scour mitigation under steady and unsteady flow conditions. Acta Geophys. 2012, 60, 1076–1097. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Nazariha, M.; Mashahir, M.B. Reduction of local scour in the vicinity of bridge pier groups using collars and riprap. J. Hydraul. Eng. 2006, 132, 154–162. [Google Scholar] [CrossRef]
- Ettema, R.; Melville, B.W.; Barkdoll, B. Scale effect in pier-scour experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Lee, S.O.; Sturm, T. Scaling issues for laboratory modeling of bridge pier scour. In Proceedings of the 4th International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008. [Google Scholar]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-dimensional numerical model for flow and bed deformation around river hydraulic structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsoe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Zang, Z. Experimental and numerical investigation of local scour around a submerged vertical circular cylinder in steady currents. Coast. Eng. 2010, 27, 709–721. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Initial stages of erosion and bed form development in a turbulent flow around a cylindrical pier. J. Geophys. Res. 2011, 116, F03007. [Google Scholar] [CrossRef]
- Kim, H.S.; Nabi, N.; Kimura, I.; Shimizu, Y. Numerical investigation of local scour at two adjacent cylinders. Adv. Water Resour. 2014, 70, 131–147. [Google Scholar] [CrossRef]
- Nabi, M.; de Vriend, H.J.; Mosselman, E.; Sloff, C.J.; Shimizu, Y. Detailed simulation of morphodynamics: 3. Ripple and dunes. Water Resour. Res. 2013, 49, 5930–5943. [Google Scholar] [CrossRef]
- Nabi, M.; de Vriend, H.J.; Mosselman, E.; Sloff, C.J.; Shimizu, Y. Detailed simulation of morphodynamics: 1. Hydrodynamic model. Water Resour. Res. 2012, 48, W12523. [Google Scholar] [CrossRef]
- Nabi, M.; de Vriend, H.J.; Mosselman, E.; Sloff, C.J.; Shimizu, Y. Detailed simulation of morphodynamics: 2. Sediment pick-up, transport and deposition. Water Resour. Res. 2013, 49, 4775–4791. [Google Scholar] [CrossRef]
- Smagorinsky, J.S. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- McLaughlin, J.B. Inertial migration of a small sphere in linear shear flows. J. Fluid Mech. 1991, 224, 261–274. [Google Scholar] [CrossRef]
- Mei, R. An approximate expression for the shear lift force on a spherical particle at finite Reynolds number. Int. J. Multiph. Flow 1992, 18, 145–147. [Google Scholar] [CrossRef]
- Dodaro, G.; Tafarojnoruz, A.; Stefanucii, F.; Adduce, C.; Calomino, F.; Gaudio, R.; Sciortino, G. An experimental and numerical study on the spatial and temporal evolution of a scour hole downstream of a rigid bed. In Proceedings of the International Conference on Fluvial Hydraulics, River Flow, Lausanne, Switzerland, 3–5 September 2014; pp. 1415–1422. [Google Scholar]
- Dodaro, G.; Tafarojnoruz, A.; Sciortino, G.; Adduce, C.; Calomino, F.; Gaudio, R. Modified Einstein sediment transport method to simulate the local Scour evolution downstream of a rigid bed. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Schmeeckle, M.W.; Nelson, J.M.; Pitlick, J.; Bennett, J.P. Interparticle collision of natural sediment grains in water. Water Resour. Res. 2001, 37, 2377–2391. [Google Scholar] [CrossRef]
- De Ruiter, J.J.C. Incipient Motion and Pick-up of Sediment as Function of Local Variables; Technical Report R 657-XI; Delft Hydraulics Laboratory: Delft, The Netherlands, 1983. [Google Scholar]
- Hannah, C.R. Scour at Pile Groups; Research report No. 28-3; Civil engineering Dept. Univ. of Canterbury: Christchurch, New Zealand, 1978. [Google Scholar]
- Movahedi, N.; Dehahani, A.A.; Aarabi, M.J.; Zahiri, A.R. Temporal evolution of local scour depth around side-by-side piers. JCEU 2013, 3, 82–86. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.S.; Roh, M.; Nabi, M. Computational Modeling of Flow and Scour around Two Cylinders in Staggered Array. Water 2017, 9, 654. https://doi.org/10.3390/w9090654
Kim HS, Roh M, Nabi M. Computational Modeling of Flow and Scour around Two Cylinders in Staggered Array. Water. 2017; 9(9):654. https://doi.org/10.3390/w9090654
Chicago/Turabian StyleKim, Hyung Suk, Min Roh, and Mohamed Nabi. 2017. "Computational Modeling of Flow and Scour around Two Cylinders in Staggered Array" Water 9, no. 9: 654. https://doi.org/10.3390/w9090654
APA StyleKim, H. S., Roh, M., & Nabi, M. (2017). Computational Modeling of Flow and Scour around Two Cylinders in Staggered Array. Water, 9(9), 654. https://doi.org/10.3390/w9090654




