1. Introduction
The field of water and environmental engineering has attracted interest in the last decade for the development and utilization of various evolutionary algorithms (EAs). These algorithms have emphasized their potential as a solution to various water-engineering problems. The popularity of EAs is likely due to their ability to solve nonlinear, nonconvex, continuous and discrete problems that classic optimization techniques have failed to solve [
1]. We recognize the capability of EAs as the applications of environmental and water-resource engineering problems have become complicated in the sense that they are characterized by large decision spaces. Design of water distribution networks (WDNs) with least investment cost satisfying the pressure requirement and reliability is an example of large scale problems in the field of water resources engineering which needs to be dealt with in optimization models such as EAs. In this problem, because of the large number of network pipes, there are a huge number of designs or alternatives in front of engineers, which cannot be evaluated with only simulation models. The network design problem becomes more complicated when there are also other facilities such as pumps, gates, tanks, etc. Due to the large size of the search space and nature of the problem at hand, categorized as a Non-deterministic Polynomial-time hard (NP-hard) problem, EAs are the search algorithms that are best suited to finding optimal design. Besides, in this problem, cost is not the only criterion which should be considered in the network design. Considering other criteria such as network reliability and resiliency in both quantitative and qualitative aspects requires the development of multi criteria decision making approaches in WDN design problems. Development of multi-objective evolutionary algorithms (MOEAs) that can efficiently search solution spaces and provide an appropriate approximation of the actual trade-off among considered criteria is thus important. For this reason, Keedwell and Khu [
2] emphasized the capability of MOEAs for the design of WDNs. In the work of Montalvo et al. [
3], Pareto optimal solutions which represent a compromise among different criteria were obtained. In this direction, the minimized cost and node pressure deficits were used as the main design factors in the multi-objective swarm optimization (MOSO) algorithm [
3]. In designing WDNs, we mostly focused on minimizing cost and maximizing reliability as the essential design criteria.
Todini (2000) introduced a “resilience” index which expresses the hydraulic reliability based on the surplus head of each node. WDNs in general are designed by loop systems to enhance hydraulic reliability of the networks [
4]. The first hydraulic resilience index was improved by Prasad and Park (2004) to consider system-redundancy concept in the loop systems [
5]. They utilized the nondominated sorting genetic algorithm 2 (NSGA2) in multi-objective design of WDNs with minimized total cost and maximized system resilience. As the cost and system resilience were used as the objective functions in WDN design, some researchers compared the performance of optimization algorithms. Farmani et al. [
6,
7] compared NSGA2 and Strength Pareto evolutionary algorithm 2 (SPEA2) for the design of WDNs and concluded that SPEA2 has better performance than NSGA2.
Research work on multi-objective optimization design of WDNs has shifted from simple evolutionary algorithms to advanced methods with strong local and global search capabilities. For instance, some studies developed cross entropy MOEA methods and compared their performances with NSGA2 [
8]. Zheng et al. [
9] developed the graph decomposition approach to solve the design problem of WDN in the multi-objective optimization framework. This approach was applied for the optimization of each sub-network and it achieved the Pareto optimal solutions for each one. Pareto optimal solutions obtained from separate optimization were integrated to obtain the whole Pareto optimal solutions of the WDN design problem. Matos et al. [
10] introduced an evolutionary strategy to obtain efficient and useful decision-making in engineering problems. The characteristics of this method are crossover and mutation operators that are specific to WDN optimization tasks. Bi et al. [
11] developed high-quality initial populations with MOEAs for optimal design of WDNs with least cost and maximum system resilience. They proposed the Multi-Objective Pre-screened Heuristic Sampling Method (MOPHSM) that assigns pipe diameter, depending on the distance between the source and demand nodes.
In addition to improving their own algorithm performance to increase the efficiency of the search ability, many studies have developed methodologies with hybridization of different algorithms [
12,
13,
14,
15,
16,
17,
18]. However, these methods have been rarely used in multi-objective optimization of WDN design. Keedwell and Khu [
2] proposed CAMOGA that is a hybrid multi-objective optimization algorithm combined with cellular automaton and the genetic algorithm for WDN design in order to obtain better designs compared to NSGA2. Vrugt and Robinson [
19] also developed a hybrid algorithm, called A Multi-Algorithm Genetically Adaptive Multi-objective (AMALGAM). The AMALGAM is a hybrid of four algorithms (Adaptive Metropolis Search (AMS), NSGA2, PSO and DE). Verification of the performance of AMALGAM comprised of the exploration of solutions for some mathematical benchmark multi-objective problems. The results showed the proposed algorithm has better performance for solving complex problems with respect to a few other MOEAs. Raad et al. [
20] compared various hybrid optimization algorithms (AMALGAM, NSGA2, NSGA2-JG) for optimal design of WDNs. AMALGAM showed the best results. Zheng et al. [
9] developed SAMODE which is a hybrid of Non-Linear Programming (NLP) and Multi-Objective Differential Evolution. SAMODE outperformed NSGA2 on three benchmark WDN case studies. Wang et al. [
21] investigated and reported the best-known Pareto optimal solutions for the well-known WDN problems. The study compared five MOEAs (i.e., NSGA2, AMALGAM, Borg, ε-MOEA and ε-NSGA2) and the results showed that NSGA2 was outstanding as it generally produced the best solutions to all the problems.
The aim of this research is improving the search capabilities of the harmony search (HS) and differential evolution (DE) to attain better performances of optimization models for design of WDNs. Therefore, this research paper contributes towards the development of a new hybrid algorithm with HS and DE algorithms in a multi-objective framework to solve the WDN design problem. The hybrid approach uses DE for a global search, followed by a hybridization of DE and HS for enhancing local search capabilities, to find the approximate true Pareto fronts. The efficiency and the reliability of the hybrid algorithm were compared with those of NSGA2, SPEA2, MOEA/D and two other MOEAs, based on HS and DE. The differences were instances of the integration of non-dominance criteria and evolutionary search operators of HS and DE developed in this study. There are some reasons for using these MOEAs in our study which are enumerated below:
- (1)
DE and HS show high efficiency in solving numerous single-objective test problems, especially the least-cost design problems involving WDNs. Moreover, since the proposed algorithm is constituted of DE and HS operators, it is advantageous to include source algorithms in the comparison.
- (2)
New versions of DE and HS algorithms for multi-criteria problems [
22,
23] have shown better performances than other well-known algorithms, such as SPEA2 [
21,
24] and MOPSO [
25].
- (3)
NSGA2 and SPEA2 are widely used in representative MOEAs in water resource and environmental engineering. More importantly, NSGA2 was reported to be the superior method relative to several contenders.
- (4)
MOEA/D is a new approach for solving multi-objective optimization problems (Zhang and Li, [
26]), which has a specific characteristic based on the decomposition scheme to separate the original problem into several sub-problems that can be solved collaboratively and simultaneously.
The proposed hybrid algorithm is applied to four well-known benchmark WDN design problems, and four performance metrics (i.e., generational distance (GD), diversity (D), hypervolume (HV) and coverage set (CS)) are measured to evaluate the performance of the proposed method and implemented MOEAs. The best algorithm is identified based on the results obtained.
2. Methods
The non-dominance criterion is used in MOEAs to sort individuals considering objective function values. Usually MOEAs (i.e., PAES, microGA, NPGA, MOPSO, SPEA2 and NSGA2) use the non-dominated sorting approach to generate Pareto fronts. In this study, the concept of non-dominance is combined with HS and DE to explore the ability of these algorithms in solving the optimal design of WDN in a multi-objective framework. The evolutionary algorithm was developed and implemented as illustrated in the subsections that follow.
2.1. Proposed Algorithm, Non-Dominated Sorting Harmony Search Differential Evolution (NSHSDE)
DE generally has strong global search capability. It is expected that if this method is combined with a local search optimizer, the performance of the evolutionary search improves. According to a study by Yazdi et al. [
27], the harmony search performs very well in finding optimal solutions located in certain parts of the search space, but cannot generate adequately diverse Pareto-optimal solutions, thus degrading the overall performance of the search algorithm. To exploit the local search advantages of HS and the exploratory strength of DE, we propose a hybrid HS-DE method here. The hybrid algorithm borrows the mutation operator from the DE algorithm to generate a new solution and uses the pitch adjustment approach of HS to modify the new solution, called “new harmony” in HS terminology. This solution is then used to update the harmony memory, which is a repository of good solutions. The hybrid method also uses the same non-dominance and crowding distance criteria as NSGA2 to generate the Pareto-optimal curve. The main steps of the hybrid algorithm, called NSHSDE are summarized as follows:
Step 1: The initial population of the harmony memory (HM) with a predefined size, called harmony memory size (HMS), is randomly generated and stored in the harmony memory (HM).
Step 2: Some new harmonies (as many as allowed by the repository size, RS) are generated and stored in the repository. It is recommended that RS be equal to HMS.
To generate a new harmony consisting of decision variables: , the following process is carried out:
- (I).
A mutation vector
is computed according to the equation:
where
HC1,
HC2 and
HC3 are three members randomly selected from HM and
F is a scaling factor in (0,1], preferably within the range 0.3–0.7.
- (II).
A pitch adjustment is used to enhance the diversity of the perturbed harmony vector and is considered as new harmony:
where
PAR is the pitch adjusting rate,
j is the variable index in the decision variable vector, 0 ≤
PAR ≤ 1, and Δ is a small change computed by
.
Fw is the fret width (or band width) parameter with a value considered as a small percentage of the range of decision variable
j, and
N(0,1) is a normal random number with mean 0 and variance 1.
ri,j is the decision variable
j of the new harmony,
Ri.
Step 3: A temporary harmony memory is created by mixing the harmonies in HM and the repository.
Step 4: The temporary harmony memory is sorted according to non-domination. In this process, harmonies are allocated to several fronts F1, F2, …, Fl according to their non-domination sort order, where l is the index of the last front. Harmonies in front 1 dominate the harmonies in higher fronts; similarly, harmonies in front 2 dominate the harmonies in fronts 3, 4, …, l, but are dominated by those in front 1, and so on.
Step 5: The harmonies in each front
F1,
F2, …,
Fl are sorted according to the crowding distance [
27].
In order to attain a better diversity in HM, among the harmonies in each front, those with fewer neighbors should have higher chance of selection in generating new harmonies. To achieve this, a greater crowding distance is allocated to the solutions with a smaller number of neighbors. Crowding distance is defined as [
27]:
where
is the crowding distance of harmony
i in front of
f;
and
are the maximum and minimum value of
mth objective function in front
f, respectively;
and
are respectively the value of
mth objective function of the upper and lower harmonies (sorted ascending) relative to harmony
i in front
f and
Fl is the number of non-dominated fronts in the current iteration.
Step 6: The HMS is updated by initially selecting the non-dominated solutions, starting with the first ranked non-dominated front (F1) and proceeding with the subsequently ranked non-dominated fronts (F2, F3, …, Fl) until the size exceeds the full capacity. It is necessary to reject some of the lower-ranked non-dominated solutions to reduce the total number of the non-dominated solutions to render it equal to the HMS. This is done by using the crowding distance comparison operator; using this procedure, the elements in the HM are updated.
Step 7: Steps 2 through 6 are repeated until the termination criterion (e.g., a maximum number of iterations) is satisfied.
It is worth mentioning that in this study, the value of
Fw was adaptively changed during the search, as recommended by Mahdavi, Fesanghary and Damangir [
28] to improve the efficiency of the local search as:
where
G is the generation count, and constant
c for each generation is given by
Fwmin and Fwmax are the minimum and maximum values of “fret width” respectively, and MaxIt is the number of iterations (generations).
2.2. Algorithms Implemented for Comparison
2.2.1. Non-Dominated Sorting Genetic Algorithm 2 (NSGA2)
NSGA2 is a fast and elitist multi-objective genetic algorithm that has been used successfully in many engineering optimization problems and has attained significant popularity in many disciplines. It is arguably the most popular MOEA developed so far. It uses genetic algorithm operators and two population-sorting criteria, non-dominance and crowding distance [
29].
2.2.2. Non-Dominated Sorting Harmony Search (NSHS) Algorithm
Harmony search [
13] is another popular EA that has garnered considerable attention in various engineering disciplines in the last decade. Several applications of this algorithm have been reported in the water engineering literature and a few multi-objective schemes have recently been developed [
27,
30] combining HS operators with non-domination sorting (NS) and crowding distance criteria to generate Pareto-optimal solutions in multi-objective problems. This algorithm called NSHS was compared with the NSGA2 and MOPSO algorithms based on several benchmark problems and a sewer pipe network application and the results showed that the NSHS algorithm outperformed the other two.
In this study, the effectiveness of the NSHS algorithm for WDN design problems is tested and compared against other MOEAs.
2.2.3. Non-Dominated Sorting Differential Evolution (NSDE) Algorithm
Differential Evolution, which is an improved version of the GA [
31] solves global optimization problems. This algorithm has the same operators as the GA, but its performance relies more on an effective mutation operator than crossover [
17]. The application of DE in single-objective designs of WDN has been reported in several studies [
17,
32,
33]. More recently, Zheng et al. [
9] developed a DE for multi-objective WDN problems by hybridizing it with NLP to estimate the Pareto front in three WDN case studies.
In this study, DE is extended to solve multi-objective problems by employing non-dominance and crowding distance criteria, as used in NSGA2, within the DE framework. The performance of the NSDE algorithm is then compared with that of other MOEAs using various design cases.
2.2.4. Improving the Strength Pareto Evolutionary Algorithm (SPEA2)
Zitzler et al. [
24] developed SPEA2. This algorithm is an improved strength Pareto evolutionary algorithm (SPEA) which is maintained as an external population algorithm and updated in each generation by new non-dominated solutions. In comparison with the initial version, SPEA2 adopts a fine-grained fitness assignment strategy that incorporates density information by taking into account the dominance of a number of individuals. It also adopts a nearest neighbor density estimation technique. Finally, the clustering method is replaced by an archive truncation method that guarantees the preservation of boundary solutions. This algorithm is known as a state-of-the-art MOEA used to assess the performance of algorithms.
2.2.5. Multi-Objective Evolutionary Algorithm Based on Decomposition (MOEA/D)
In addition to the aforementioned MOEAs, we implemented MOEA/D algorithm [
26] to solve WDN design problems. This algorithm was rarely used for WDN design [
34]. In comparison to the MOEAs, MOEA/D is a different solving approach in which a multiobjective optimization problem is decomposed into a number of scalar optimization sub-problems that are simultaneously optimized. At each instance of generation, the population is composed of the best solution found thus far for each sub-problem. The neighborhood relations among these sub-problems are defined based on distances between their aggregation coefficient vectors. Each sub-problem (i.e., scalar aggregation function) is optimized in MOEA/D by using information only from its neighboring sub-problems. It was also reported that MOEA/D recorded lower computational complexity at each instance of generation than NSGA2 and yielded better performance on some benchmark optimization tests and real-world optimization problems [
26,
34]. We use the MOEA/D framework with the Tchebycheff approach [
26] to decompose multi-objective optimization problems. More information about decomposition approaches and the MOEA/D method can be found in the work of Zhang and Li [
26].
2.3. Performance Measures
The performance of the implemented algorithms is evaluated by four performance metrics or indices (i.e., generational distance (GD), diversity (D), hypervolume (HV) and coverage set (CS)) which are briefly explained below.
2.3.1. Generational Distance (GD)
This performance metric was introduced by Van Veldhuizen and Lamont [
35] and is used to measure the distance between elements of the set of non-dominated vectors at any given time and those of the global Pareto-optimal set. It is defined as
where
n is the number of vectors in the set of non-dominated solutions and
di is the distance (measured in objective space) between each of these and the nearest member of the global Pareto-optimal set. The parameter
P stands for the
Pth norm of the distance which is assumed equal 2–i.e. Euclidean distance, in this research. An ideal value of
GD = 0 indicates that all elements generated are in the global Pareto-optimal set. Thus, any other value indicates how “far” the generated elements are from the global Pareto front. The lower
GD, the algorithm’s performance better in terms of convergence.
2.3.2. Diversity (D)
This metric assesses the extent of the Pareto front curve and shows the range of diversity of the solutions obtained. It is defined as:
where
j is the index of
jth objective function,
fj is the vector of
jth objective function values of the Pareto front solutions and
n is the number of objective functions. The higher the value of D metric, the better the diversity of MOEA. There is no specific lower and upper bound for this metric and its value is problem-dependent.
2.3.3. Hypervolume (HV)
This metric was proposed by Van Veldhuizen [
35] for calculating the volume covered between the Pareto fronts and a reference point. This evaluates the performance of convergence and diversity. The reference point represents the worst objective function values. This index is calculated as:
where
is the hyper-volume constructed by solution
i and the reference point in the objective function space. It should be emphasized that in this study the normalized version of
HV called the ratio of
HV, of the approximation set to the true Pareto-optimal front (
HVR), was used to reduce the bias arising out of the magnitudes of different objective functions and to evaluate the quality of solutions found by each MOEA.
HVR varies between zero and one with the ideal value of one.
2.3.4. Coverage Set (CS)
This index was proposed by Zitzler et al. [
36] to compare the Pareto fronts through two different simulations. This metric demonstrates both the convergence and diversity abilities of the algorithm. Considering two Pareto optimal solution sets
and each set of non-domination points in
, denoted by
, CS index can be calculated between [0,1] as:
If all points in dominate, or are equal to, all points in , by the definition given above, CS = 1. A value of 0 for the index implies the opposition. Ordinarily, both and need to be considered, as the set intersections are not necessarily empty. The CS metric is used to compare two Pareto sets in relative terms, without the need for the global Pareto solutions.
2.4. Multi-Objective Design of WDNs
2.4.1. Mathematical Formulation
“Network cost” and “reliability” are two major objectives that have been frequently used in the multi-objective design of water distribution systems. The same criteria are taken as the objective functions in this study, with “network resilience” indicator as the reliability measure proposed by Prasad and Park [
5]. The first objective function involves economic considerations and the latter provides a measure to assess both surplus head and reliable loops in networks of varying size. The optimization problem can then be formulated as:
where
C = total cost (monetary units),
np = number of pipes,
Ui = unit cost of pipe
i of diameter
Di,
Li = length of pipe
i,
In = network resilience,
nn = number of demand nodes,
Cj,
Qj,
Hj, and
are uniformity, demand, actual head and minimum required head respectively, of node
j;
nr = number of reservoirs,
Qk and
Hk are discharge and actual head respectively, of reservoir
k,
npu = number of pumps,
Pi = power of pump
i,
γ = specific weight of water,
npj = number of pipes connected to node
j, and
Di = diameter of pipe
i connected to demand node
j. The constraints of the optimization problem are as follows:
(1) Mass conservation constraint
For each junction node, the mass conservation law should be satisfied which can be written as:
where
Qin and
Qout are in-flow and out-flow of the node, respectively, and
Qe is the external flow rate or demand at the node.
(2) Energy conservation constraint
For each loop in the network, the conservation of energy can be written as follows:
where Δ
hk is the head loss in pipe
k and
Nl is the total number of loops in the system. The head loss in each pipe is the difference in head between connected nodes, and is a function of discharge, pipe diameter, and roughness coefficient of the pipe. Head loss is usually calculated using empirical equations, such as the Darcy-Weisbach or the Hazen-Williams equation.
(3) Minimum and maximum pressure constraints
The minimum and maximum pressure constraints on each node in the network are given by the following:
where
Hj is the pressure head at node
j,
is the minimum required pressure head at node
j,
is the maximum allowed pressure head at node
j, and
nn is the number of demand nodes in the network.
(4) Pipe size availability constraint
The diameter of each pipe must belong to a commercial size set,
A:
where
Di is the diameter of pipe
i, {A} denotes the set of commercially available pipe diameters, and
np is the number of pipes.
(5) Minimum and maximum velocity constraints
The minimum and maximum velocity constraints on each pipe in the network are given by the following:
where
vi Is velocity in pipe
i,
and
are the minimum and maximum allowed velocity in pipe
i, respectively.
To solve the optimization problem, the constrained model is converted into an unconstrained one by adding the number of constraint violations to the objective function as penalty. The constraints for the conservation of mass and energy are automatically satisfied using EPANET2.0 hydraulic solver [
37]. The minimum and maximum pressure and velocity constraints, however, need to be included in the penalty functions:
where
P is a penalty multiplier, which was set to 10
6 in this study.
Cp1 is the summation of the penalties of all nodes with pressure violation,
Cp2 is the summation of the penalties of all pipes with velocity violation and
Cp is the total penalty. Therefore, the total cost of the network is the sum of network cost
C and penalty cost
Cp in nodes and pipes with pressure and velocity violation, respectively.
2.4.2. Experimental Tests on WDNs
The validation of the hybrid algorithm to solve WDN design problems requires application of the algorithm to benchmark problems of different sizes which were selected from the literature including the two-loop network (small-sized problem), the Hanoi network (medium-sized), the Fossolo network (intermediate-sized) and the Balerma network (large-sized problem). These four benchmark networks are briefly described below.
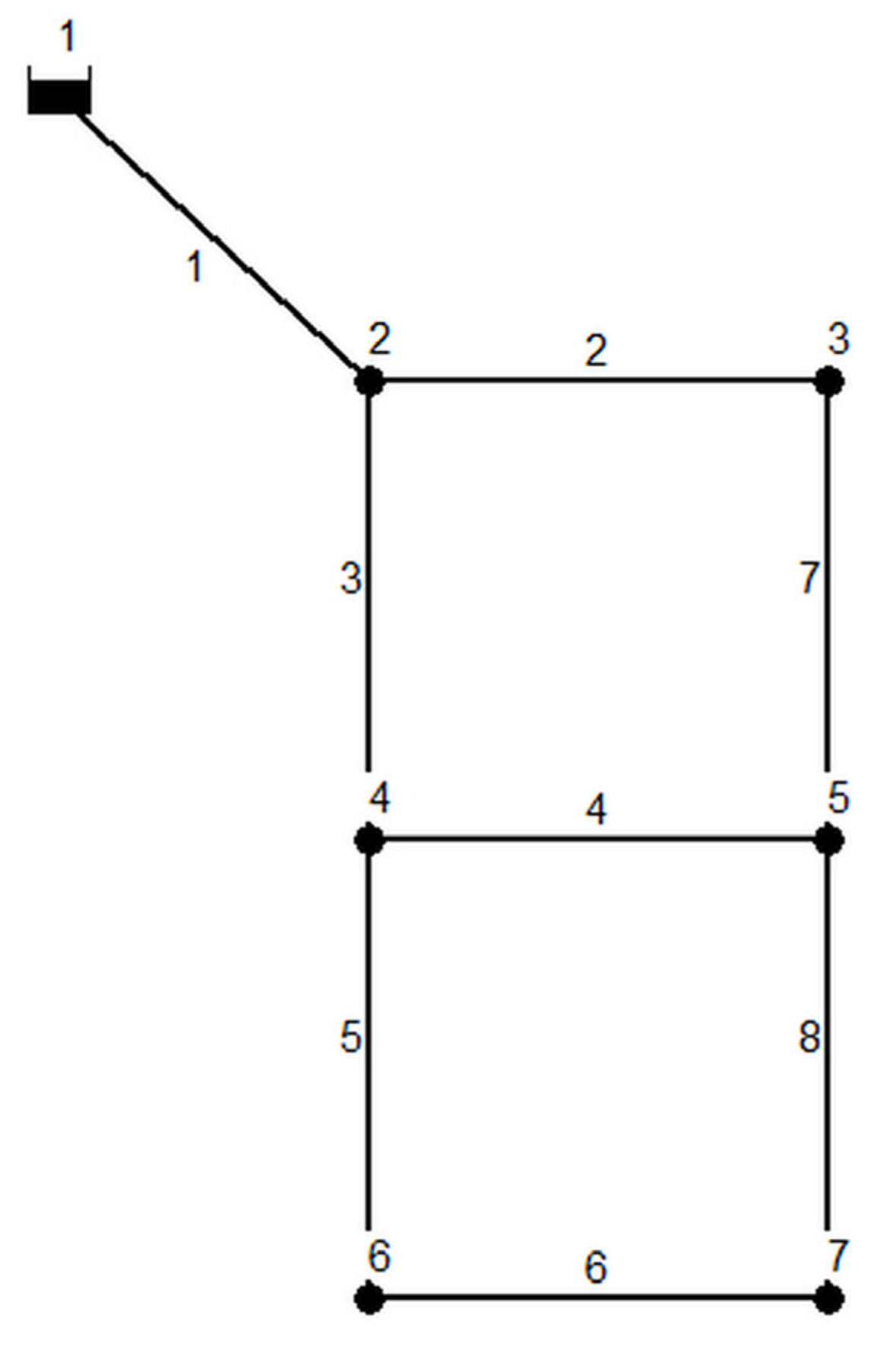
1. Two-loop network (TLN)
The two-loop network (TLN) consists of eight pipes, six demand nodes, and a reservoir. The reservoir had a constant head fixed at 210 m [
21]. As it is a hypothetical network, all pipes had the same length (1000 m) and a Hazen-Williams coefficient of 130. Pressure was set to at least 30.0 m at all demand nodes.
Table 1 shows the commercially available diameters and the corresponding unit costs (1 in. = 0.0254 m) and
Figure 1 depicts the layout of the TLN.
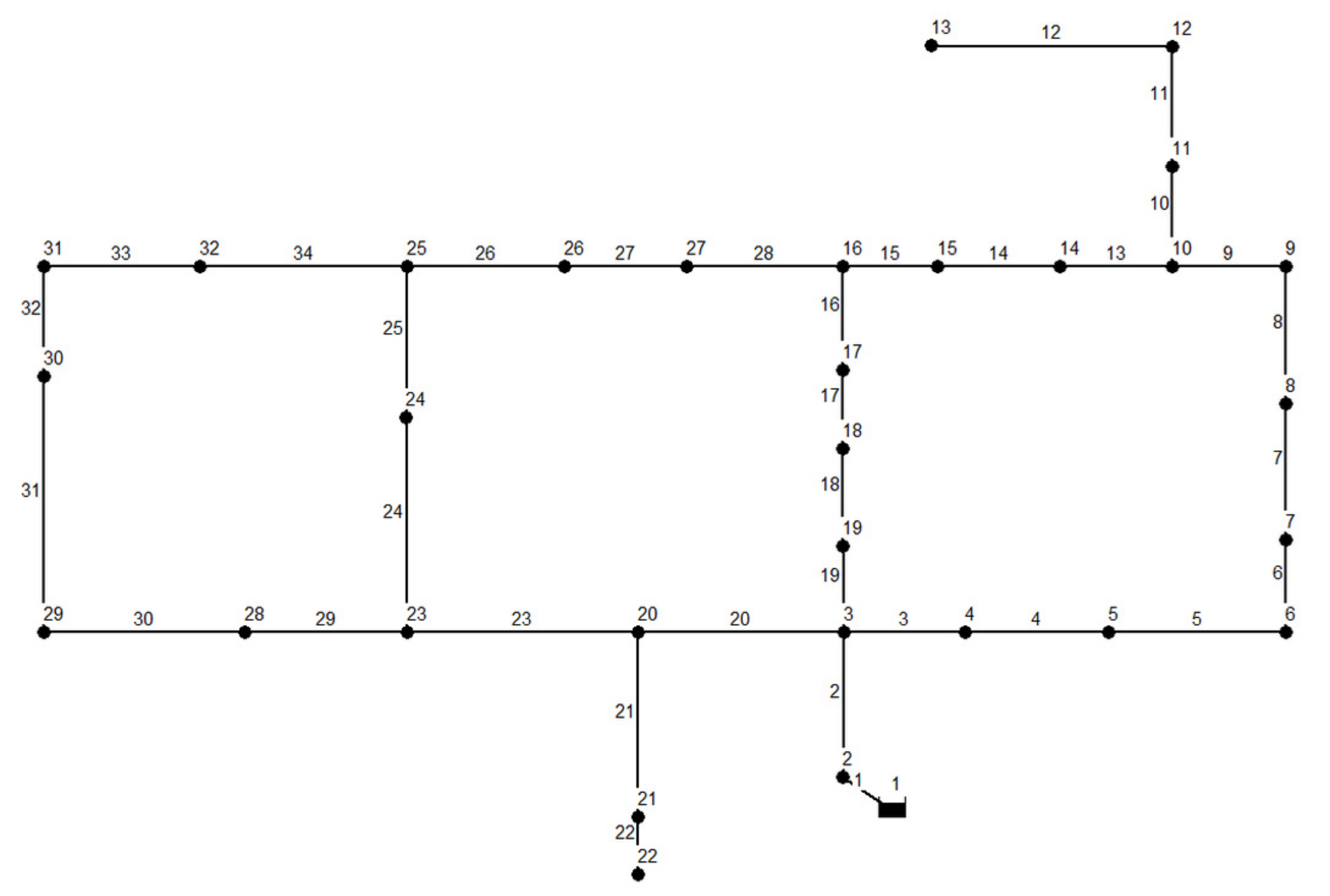
2. Hanoi network (HAN)
The Hanoi network (HAN) consisted of 34 pipes organized into three loops, 31 demand nodes, and a reservoir with a fixed head of 100 m [
21]. The Hazen-Williams roughness coefficient for all pipes was 130. The minimum head above the ground elevation of each node was 30 m. There were six commercially available pipe sizes, ranging from 12 in. to 40 in. (1 in. = 0.0254 m).
Table 2 shows the diameter options and associated unit costs and
Figure 2 depicts the layout of the network.
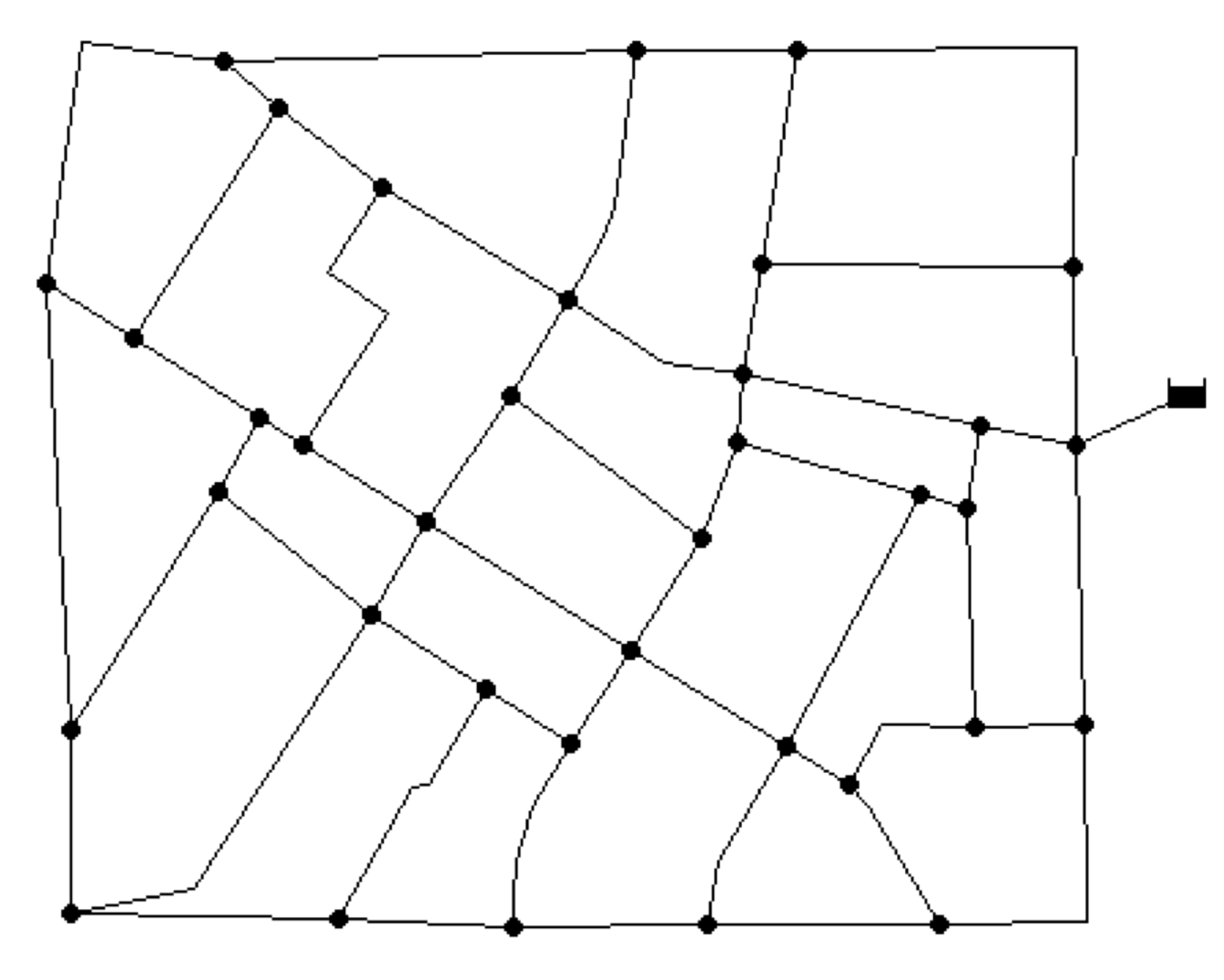
3. Fossolo network (FOS)
The Fossolo network (FOS) consisted of 58 pipes, 36 demand nodes, and a reservoir with a fixed head of 121.00 m [
21]. The material for all pipes was polyethylene. Due to the characteristics of polyethylene, a relatively high Hazen-Williams coefficient of 150 was applied to all pipes. The minimum pressure head of the demand nodes was maintained at 40 m, whereas the maximum pressure head at each node was as specified in
Table 3. Moreover, the flow velocity in each pipe was enforced at less than or equal to 1 m/s.
Table 4 shows the commercially available diameters and the corresponding unit costs.
Figure 3 depicts the layout of the FOS.
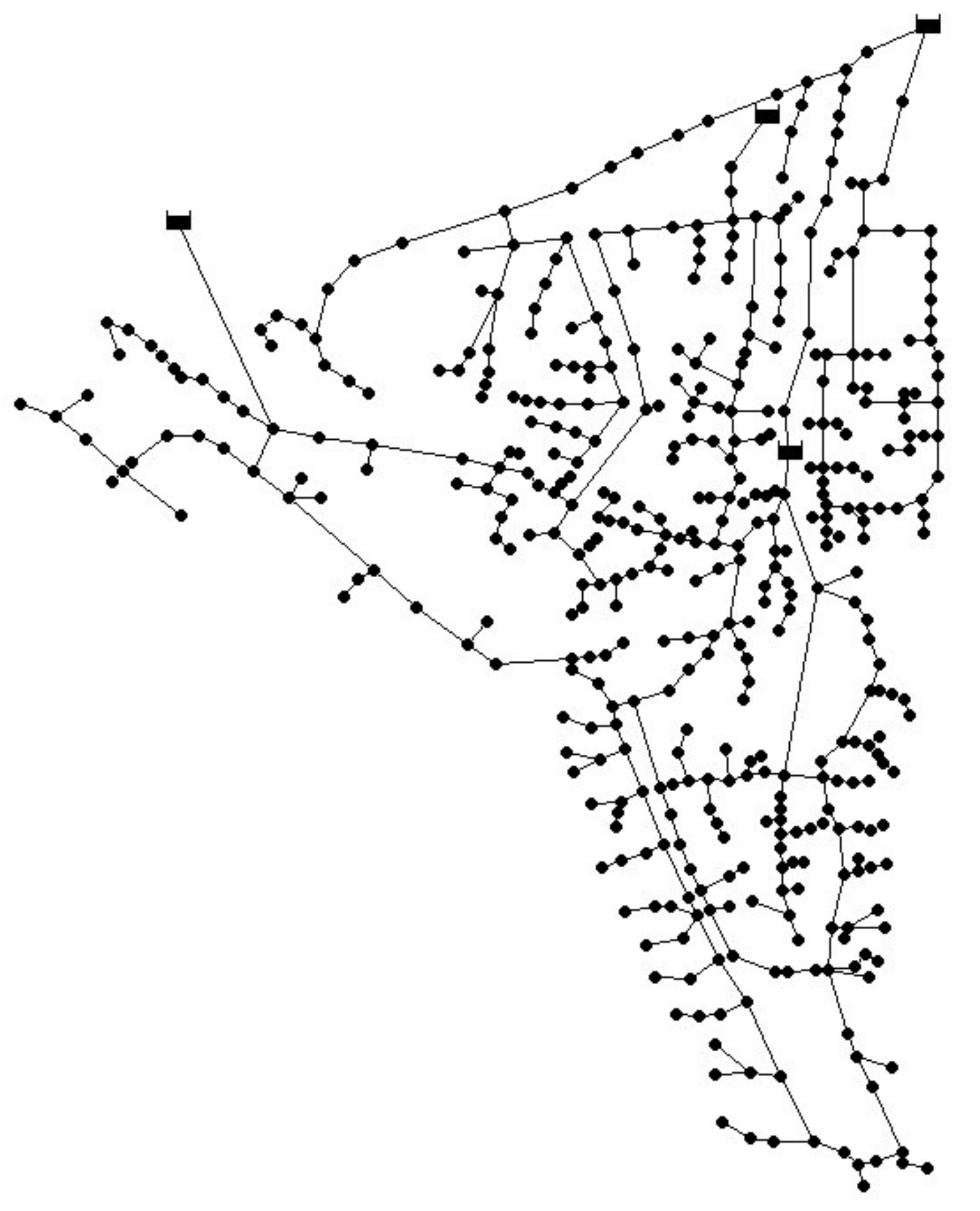
4. Balerma Irrigation Network (BIN)
The Balerma irrigation network (BIN) consisted of 454 polyvinyl chloride (PVC) pipes, 443 demand nodes, and four reservoirs with fixed heads at 112 m, 117 m, 122 m, and 127 m [
21]. The Darcy–Weisbach roughness coefficient of pipes was set at 0.0025 mm for all pipes. The minimum pressure head above ground elevation was 20 m for all the demand nodes. Each pipe was allowed to select a diameter from 10 discrete values.
Table 5 shows the commercially available diameters and the corresponding unit costs.
Figure 4 depicts the layout of the BIN.
3. Results and Discussions
This section presents the results of the computational experiments performed using the selected MOEAs on the four benchmark water distribution networks introduced in the previous section.
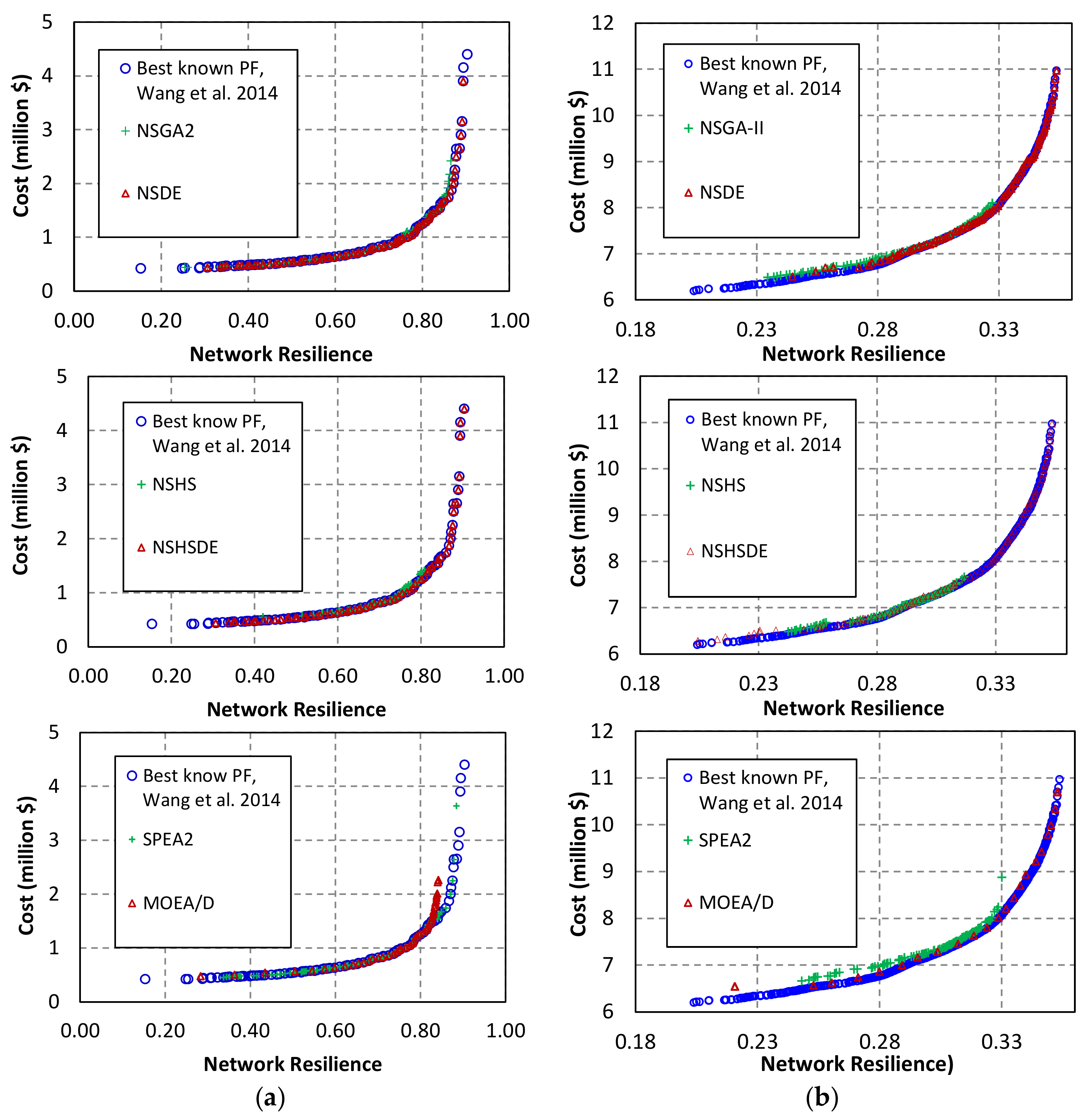
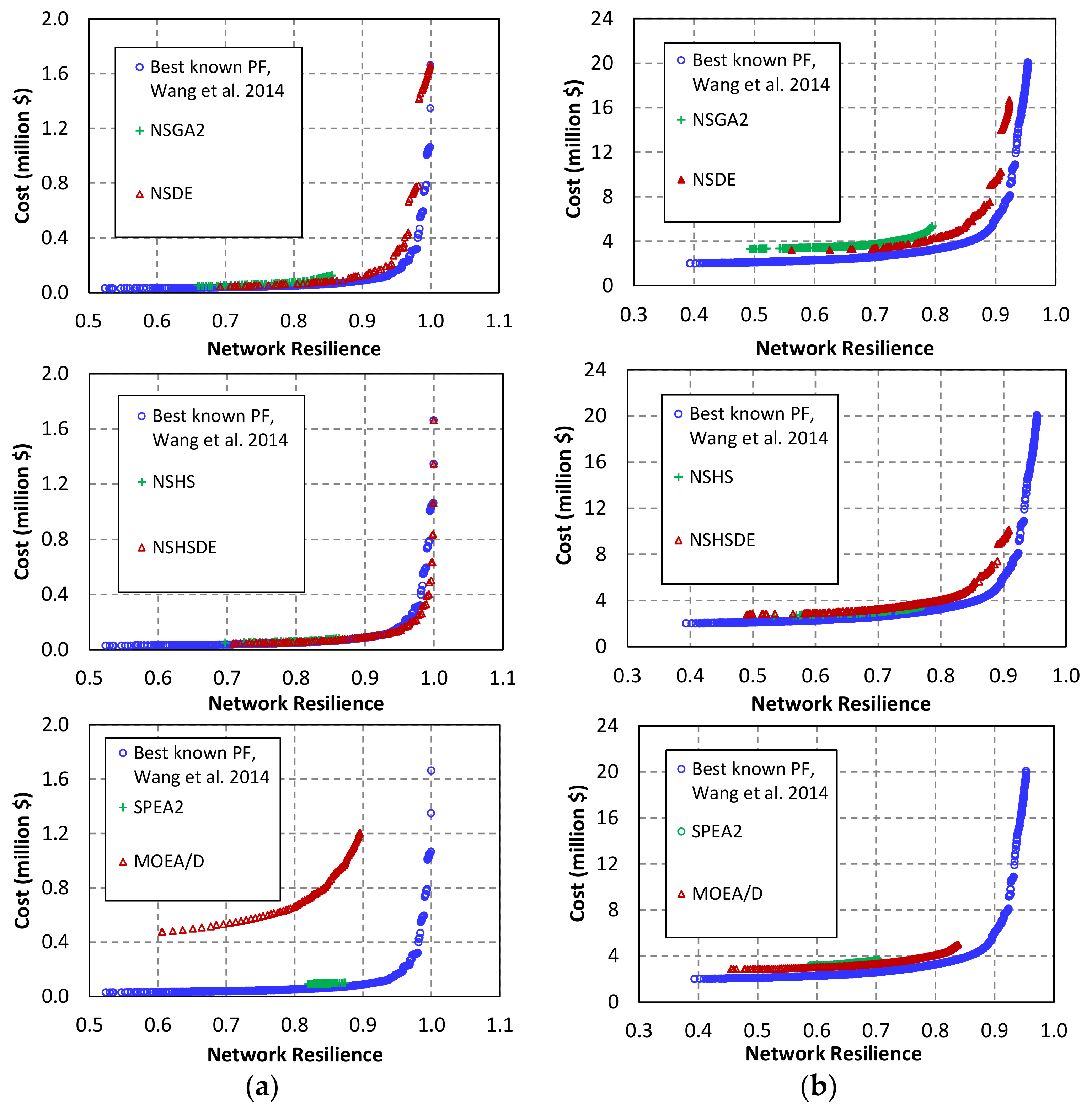
The MOEAs were linked to the EPANET 2.0 hydraulic solver to estimate WDN resilience and assess necessary hydraulic constraints while evaluating different network designs. Shown in
Table 6 are the sizes of the search spaces, the number of decision variables, and population size as well as the computational budget in terms of the number of function evaluations (NFE) and pipe diameter options for each of the four benchmark networks. The parameters of the NSGA2 were set according to widely recommended settings in the literature; for the other algorithms, parameter values were chosen based both on values used in the literature and the results of several trial runs. The final parameters used are presented in
Table 7. Each MOEA was independently run 30 times to solve each problem. The results of a typical run (not average) of each algorithm are shown in
Figure 5 and
Figure 6. As can be seen, the hybrid algorithms namely, NSHSDE and NSDE, generally provided better Pareto fronts than the four other algorithms for all studied networks. The best-known Pareto fronts of the problems reported by Wang et al. [
21] are also shown in the two figures; they were obtained by aggregating the Pareto-optimal solutions of different MOEAs after several executions with different population sizes and very high orders of magnitudes of NFEs.
In order to compare the algorithms more precisely, the performance metrics described in the preceding section were used.
Table 8 shows the average values of the metrics obtained by 30 iterations of each of the algorithms for each benchmark network problem. In this table, the second and third metrics were normalized using those of the best-known Pareto fronts in the literature. The first metric,
GD shows the quality of solutions in terms of non-domination strength. It can be seen that the MOEAs exhibited different behaviors according to this metric. The NSHS outperformed all others for all networks except for the TLN problem, based on the
GD metric. The hybrid method also yielded good values in terms of the
GD metric for two small-sized problems. However, for larger networks, its
GD values were poor, but as explained below, this does not mean the hybrid method is inferior.
The NSDE was inferior to the proposed hybrid method in all four experimental networks in terms of
GD values, and MOEA/D represented the worst results for the TLN, HAN, and FOS networks while its
GD values for the largest network, i.e., the BIN problem, recorded very close to the best value. Two other algorithms, i.e., NSGA2 and SPEA2, represented the median results for the
GD metric. Although the
GD is an indicator of convergence, it is not a good representative of convergence strength. For example, as shown in
Figure 6b, the hybrid method represented high-quality solutions in the same range as found by NSHS. It also yielded other non-dominated solutions not found by NSHS, which were more distant from the best-known Pareto front solutions. As a result, they generated a larger
GD value for the hybrid method than the NSHS, whereas the quality of its solutions was better than those of NSHS in terms of convergence. Therefore, we see that the
GD metric is not an appropriate criterion for measurement of the convergence strength of MOEAs.
According to the second metric—diversity (D)—the hybrid method and NSDE generated wider Pareto fronts and produced more diverse solutions than the other MOEAs, whereas NSHS had the smallest D values, showing that its performance was not global and unable to preserve diversity in the optimal solutions found. This can also be observed in the graphical results presented in
Figure 5 and
Figure 6, where the solutions of the NSDE and NSHSDE algorithms are well spread on both sides of the objective function spaces, while those of the NSHS algorithm (and the other MOEAs) are concentrated in a particular part of the best-known Pareto fronts. The superior diversity of solutions observed in the NSDE and NSHSDE algorithms can be attributed to the efficient mutation operator in the DE for generating new solutions.
It is noteworthy that D metric is also not a perfect comparison measure since it does not consider the non-dominance. The spread Pareto front of an MOEA with long tails may dominated by the small-spread Pareto front of another MOEA and thus, the former would be the inferior, although has a greater D metric. This is the case for NSDE and NSHSDE algorithms and we should see what two other metrics say.
Overall, a comparison between the GD and D values of the hybrid method with those of NSHS and NSDE showed that the proposed hybrid algorithm successfully exploited the mutation operator of differential evolution and the local search capability of harmony search to generate better quality solutions (in terms of convergence) than NSDE and better diversity than NSHS across all experimental networks.
As shown in the last column of
Table 8, NSDE and NSHSDE outperformed the other methods based on the third metric, wherein their HV values were of higher order compared to those achieved from the other MOEAs for all benchmark networks. Although HV measures both convergence and diversity in MOEAs, these values are considered to be more influenced by diversity (see
Table 8); thus, this metric alone could not provide consistent and unbiased evaluation. Another important observation was that, in the case of the third network problem (FOS), NSDE found some undiscovered solutions and NSHSDE found some new optimal solutions that dominated a portion of the best-known Pareto front (PF) in the literature. This was accomplished in both algorithms by incurring lower computational burden (smaller number of function evaluations) than that for the best-known PF. Comparing the coverage set (CS) metric of the best known PF and the two algorithms, NSHSDE and NSDE respectively found on an average 12% and 36% new optimal solutions in each round of execution that were not found in the best PF reported in the literature. NSDE presented more new optimal solutions; however, the analysis of the results showed that most of them are located in small clustered locations at right tail of the Pareto front and other solutions in its Pareto front are dominated by both the best known PF and NSHSDE members. In other words, new optimal solutions in NSDE are in fact undiscovered solutions which come from the strength of diversity in DE, not the strength of convergence. That is to say, they are non-dominated solutions with respect to the best known PF, but they do not dominate solutions of the best known PF. On the other hand, new solutions found by NSHSDE (12% in average) dominate the solutions of the best known PF. This means they are obtained by the strength of convergence in NSHSDE.
These results confirmed the superiority of the proposed hybrid algorithm and the improvement in its search capability. It also showed that the reported Pareto front for this network was not global. In order to complete our analysis, a pairwise comparison among the MOEAs was carried out based on the CS metric for all four experimental networks. The results are demonstrated in
Table 9. CS shows what percentage of the non-dominated solutions are found by each of MOEAs, in a pairwise comparison. The pairwise comparison (diagonal values in the table) shows that NSHSDE outperformed all other MOEAs for all four WDN design problems. The performance of the other algorithms varied for different benchmark network problems; but in general, the NSDE algorithm was second best, and SPEA2 exhibited weak performance compared to the other methods. Since the CS metric is based on the non-dominance strength, unlike the three preceding metrics, CS is an unbiased and perfect convergence measure. By observing the CS values of MOEA/D, it is evident that this algorithm underperformed in the first three networks, but delivered the second best performance in the last network (BIN problem). It is likely that the MOEA/D yields good performance for large-sized problems. Moreover, based on the CS values, NSHS recorded relatively better performance than NSGA2.
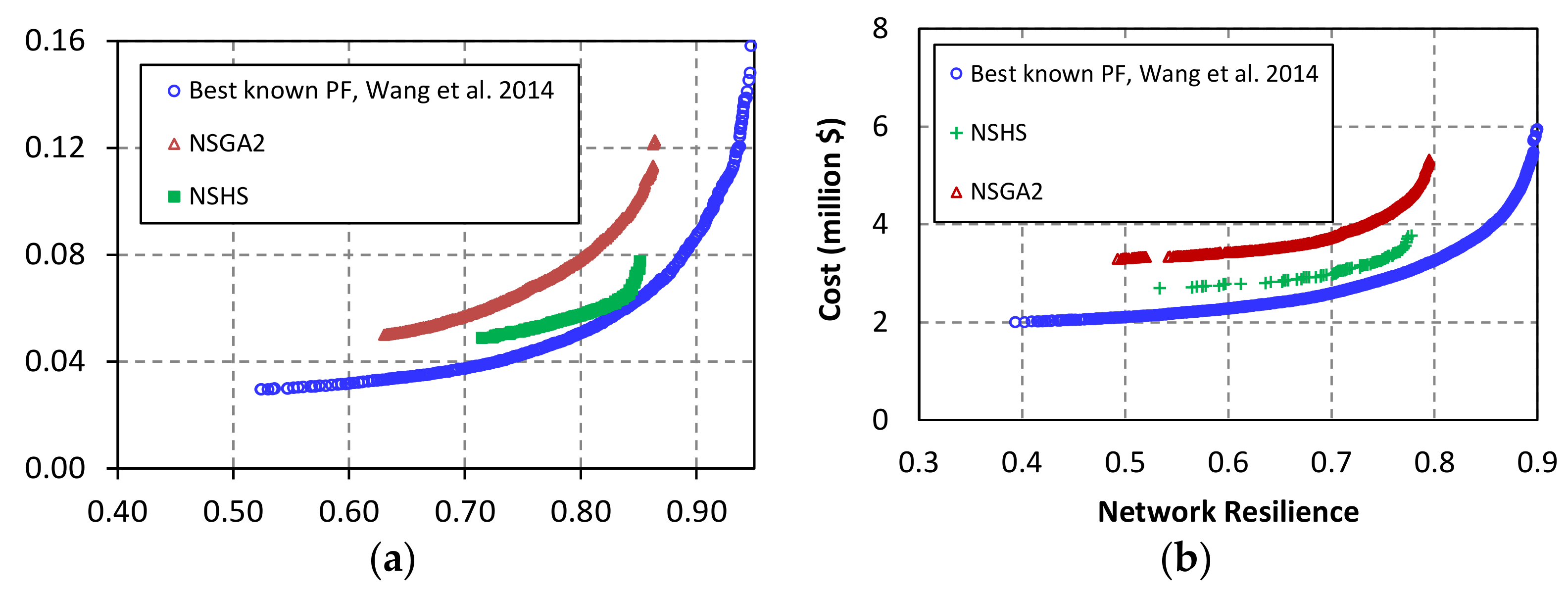
A close-up view of Pareto fronts generated by these algorithms on the FOS and BIN network problems is given in
Figure 7. As shown, the solutions found by NSHS dominated the main part of the NSGA2 solutions. Compared with NSGA2, the harmony search had better local search capability with regard to the quality of solutions. This was also observed in the work of Yazdi et al. [
29] for the sewer pipe network application. This algorithm, however, could not find the tails of the Pareto front, as it suffered from an inability to preserve the diversity of the population during the evolutionary search steps. Hybridizing HS with DE, which has a strong global search feature, provides considerably better performance than the MOEAs considered, as shown in
Figure 5 and
Figure 6 and in
Table 8 and
Table 9.
4. Conclusions
In this research article, a hybrid multi-objective algorithm was proposed by integrating the concepts of HS and DE in a unified framework. The proposed algorithm was compared with well-known methods—NSGA2, SPEA2, MOEA/D—and two other extended versions of harmony search and differential evolution, on multi-objective problems. A quantitative comparison was made (by plotting the Pareto fronts) in terms of the generational distance (GD), diversity (D), hyper-cube volume (HV), and coverage set (CS) metrics. Results demonstrated that GD due to ignoring the cardinality (the number of solutions) of the Pareto front and D metric due to ignoring non-dominance criterion are not suitable comparative measures. While two other metrics measure both convergence and diversity, HV may have biased results because of the scaling effects of different objective functions and being more influenced by diversity. CS, which is directly calculated based on the non-dominance strength, was found to be the best comparative measure. According to HV metric, NSHSDE had the top rank in the first three considered WDN design problems and the second rank in the fourth case. Therefore, it delivered a better overall performance based on HV values. Additionally, evaluation of the NSHSDE Pareto fronts for four WDN design problems showed that the hybrid method is the superior MOEA in terms of CS metric. These results confirm the credibility of the proposed hybrid algorithm.
Of the algorithms considered, the hybrid algorithm provided on average 12% of new optimal solutions for the FOS network problem, dominating the best-known Pareto front in the literature that had been obtained by aggregating the results of several widely used algorithms. This gain, achieved by using a considerably smaller number of function evaluations, is due to the successful exploitation of the global search capability of differential evolution and the local search capability of harmony search operators. Although some limited parameter tuning was done in this work, we believe that if more computational effort is put on parameter settings, even better performance can be achieved by the hybrid method. The results also show that NSDE yielded the second best performance and SPEA2 was generally inferior to all other methods compared. Similarly, MOEA/D showed weak performance on small- and medium-sized problems, but exhibited the second best results on the large-sized Balerma network problem. The median-scoring algorithms were NSHS and NSGA2, where the former provided better local convergence but the latter provided better diversity.
In summary, the overall results of this study show that the proposed hybrid algorithm can be successfully used to solve multi-objective design problems of WDN with better efficiency. More complex networks are being studied to confirm the credibility of the proposed approach and will be reported in the future.