Analyzing the Effect of Ocean Internal Variability on Depth-Integrated Steric Sea-Level Rise Trends Using a Low-Resolution CESM Ensemble
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Rhein, M.; Rintoul, S.R.; Aoki, S.; Campos, E.; Chambers, D.; Feely, R.A.; Gulev, S.; Johnson, G.C.; Josey, S.A.; Kostianoy, A.; et al. Observations: Ocean (Chapter 3). In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 255–315. [Google Scholar] [CrossRef]
- Llovel, W.; Willis, J.K.; Landerer, F.W.; Fukumori, I. Deep-ocean contribution to sea level and energy budget not detectable over the past decade. Nat. Clim. Chang. 2014, 4, 1031–1035. [Google Scholar] [CrossRef]
- Purkey, S.G.; Johnson, G.C. Warming of global abyssal and deep Southern Ocean waters between the 1990s and 2000s: Contributions to global heat and sea level rise budgets. J. Clim. 2010, 23, 6336–6351. [Google Scholar] [CrossRef]
- Koutetsu, S.; Doi, T.; Kawano, T.; Masuna, S.; Sugiura, N.; Sasaki, Y.; Toyoda, T.; Igarashi, H.; Kawai, Y.; Katsumata, K.; et al. Deep ocean heat content changeds estimated from observation and reanalysis product and their influence on sea level change. J. Geophys. Res. 2011, 116, 869–881. [Google Scholar]
- Gille, S.T. Warming of the Southern Ocean since the 1950s. Science 2002, 295, 1275–1277. [Google Scholar] [CrossRef] [PubMed]
- Gille, S.T. Decadal-scale temperature trends in the Southern Hemisphere ocean. J. Clim. 2008, 21, 4749–4765. [Google Scholar] [CrossRef]
- AchutaRao, K.M.; Ishii, M.; Santer, B.D.; Gleckler, P.J.; Taylor, K.E.; Barnett, T.P.; Pierce, D.W.; Stouffer, R.J.; Wigley, T.M.L. Simulated and observed variabilty in ocean temperature and heat content. Proc. Natl. Acad. Sci. USA 2007, 104, 10768–10773. [Google Scholar] [CrossRef] [PubMed]
- Gouretski, V.; Koltermann, K.P. How much is the ocean really warming? Geophys. Res. Lett. 2007, 34, L01610. [Google Scholar] [CrossRef]
- Domingues, C.M.; Church, J.A.; White, N.J.; Gleckler, P.J.; Wijffels, S.E.; Barker, P.M.; Dunn, J.R. Improved estimates of upper-ocean warming and multi-decadal sea-level rise. Nature 2008, 453, 1090–1093. [Google Scholar] [CrossRef] [PubMed]
- Durack, P.J.; Gleckler, P.J.; Landerer, F.W.; Taylor, K.E. Quantifying Underestimates of Long-term Upper-Ocean Warming. Nat. Clim. Chang. 2014, 4, 999–1005. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, J.; Abraham, J. Global Upper Ocean Heat Content Estimation: Recent Progress and the Remaining Challenges. Atmos. Ocean. Sci. Lett. 2015, 8, 333–338. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, J.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Abraham, J. Improved estimates of ocean heat content from 1960 to 2015. Sci. Adv. 2017, 3, e1601545. [Google Scholar] [CrossRef] [PubMed]
- Sriver, R.L.; Urban, N.M.; Olson, R.; Keller, K. Towards a physically plausible upper bound of sea-level rise projections. Clim. Chang. 2012, 115, 893–902. [Google Scholar] [CrossRef]
- Buchanan, M.K.; Kopp, R.E.; Oppenheimer, M.; Tebaldi, C. Allowances for evolving coastal flood risk under certain local sea-level rise. Clim. Chang. 2016, 137. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, B.P.; Kemp, A.C.; Tebaldi, C. Past and future sea-level rise along the coast of North Carolina. Clim. Chang. 2015, 132, 637–707. [Google Scholar] [CrossRef]
- Cazenave, A.; Le Cozannet, G. Sea level rise and its coastal impacts. Earths Future 2014, 2, 15–34. [Google Scholar] [CrossRef]
- Liang, X.; Wunsch, C.; Heimback, P.; Forget, G. Vertical redistrubution of oceanic heat content. J. Clim. 2015, 28, 3821–3833. [Google Scholar] [CrossRef]
- Kuhlbrodt, T.; Gregory, J.M. Ocean heat uptake and its consequences for the magnitude of sea level rise and climate change. Geophys. Res. Lett. 2012, 39, L18608. [Google Scholar] [CrossRef]
- Hu, A.; Deser, C. Uncertainty in future regional sea level rise due to internal climate variability. Geophys. Res. Lett. 2013, 40, 2768–2772. [Google Scholar] [CrossRef]
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Coz, P.; Driouech, F.; Emori, S.; Eyring, C.; et al. Evaluation of Climate Models. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Thompson, D.W.K.; Barnes, E.A.; Deser, C.; Foust, W.E.; Phillips, A.S. Quantifying the role of internal calimte variability in future climate trends. J. Clim. 2015, 28, 6443–6456. [Google Scholar] [CrossRef]
- Sriver, R.L.; Forest, C.E.; Keller, K. Effects of intial conditions uncertainty on regional climate variability: An analysis using a low resolution CESM ensemble. Geophys. Res. Lett. 2015, 42, 5468–5476. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–495. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.; Bourdette, V.; Tend, H. Uncertainty in climate change projections: the role of internal variability. Clim. Dyn. 2012, 38, 527–547. [Google Scholar] [CrossRef]
- Kay, J.; Deser, C.; Phillips, A.; Mai, A.; Hannay, C.; Strand, G.; Arblaster, J.M.; Bates, S.C.; Danabasoglu, G.; Edwards, J.; et al. The Community Earth System Model (CESM) Large Ensemble Project: A community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meteorol. Soc. 2015, 96, 1333–1349. [Google Scholar] [CrossRef]
- Fischer, E.M.; Beyrerle, U.; Knutti, R. Robust spatially aggregated projections of climate extremes. Nat. Clim. Chang. 2013, 3, 1033–1038. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Nerem, R.S. Interannual variability in global mean sea level estimated from the CESM Large and last millennium ensembles. Water 2016, 8, 491. [Google Scholar] [CrossRef]
- Fyfe, J.C.; Gillett, N.P.; Zwiers, F.W. Overestimated global warming over the past 20 years. Nat. Clim. Chang. 2013, 3, 767–769. [Google Scholar] [CrossRef]
- Huang, J.; Xie, Y.; Guan, X.; Li, D.; Ji, F. The dynamic of the warming hiatus over the Northern Hemisphere. Clim. Dyn. 2016, 48, 429–446. [Google Scholar] [CrossRef]
- Easterling, D.R.; Wehner, M.F. Is the climate warming or cooling? Geophys. Res. Lett. 2009, 36, L08706. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Fasullo, J.T.; Hu, A.; Trenberth, K.E. Model-based evidence of deep-ocean heat uptake during surface-termpertaure hiatus periods. Nat. Clim. Chang. 2011. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Fasullo, J.T. An apparent hiatus in global warming? Earths Future 2013, 1, 19–32. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasulo, J.T.; Branstator, G.; Phillips, A.S. Seasonal aspects of the recent pause in surface warming. Nat. Clim. Chang. 2014. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World ocean heat content and thermosteric sea level change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39, L10603. [Google Scholar] [CrossRef]
- Griffies, S.M.; Winton, M.; Anderson, W.G.; Benson, R.; Delworth, T.L.; Dufour, C.O.; Dunne, J.P.; Goddard, P.; Morrison, A.K.; Rosati, A.; et al. Impacts on ocean heat from transient mesoscale eddies in a hierarchy of climate models. J. Clim. 2015, 28, 952–977. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1107. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in projections of regional precipitation change. Clim. Dyn. 2011, 37, 407–418. [Google Scholar] [CrossRef]
- Boyer, T.P.; Antonov, J.I.; Baranova, O.K.; Garcia, H.E.; Johnson, D.R.; Locarnini, R.A.; Mishonov, A.V.; O’Brien, T.D.; Seidov, D.; Smolyar, I.V.; et al. World Ocean Database 2009, Volume 1, Introduction. In NOAA Atlas NESDIS; Levitus, S., Ed.; NOAA: Silver Spring, MD, USA, 2009. [Google Scholar]
- National Centers for Environmental Information, National Oceanic and Atmospheric Administration. Available online: https://www.ncei.noaa.gov/ (accessed on 28 June 2017).
- Shields, C.A.; Bailey, D.A.; Danabasoglu, G.; Kiehl, J.T.; Levis, S.; Jochum, M.; Park, S. The low-resolution CCSM4. J. Clim. 2012, 25, 3993–4014. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Smith, R.D.; Jones, P.; Briegleb, B.; Bryan, F.; Danabasoglu, G.; Dennis, J.; Dukowicz, J.; Eden, C.; Fox-Kemper, B.; Gent, P.; et al. The Parallel Ocean Program (POP) Reference Manual: Ocean Component of the Community Climate System Model (CCSM). LANL Technical Report, LAUR-10-01853. Available online: https://staff.ucar.edu/browse/people/11128/manuscripts%3A825 (accessed on 1 July 2017).
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Bitz, C.M.; Shell, K.M.; Gent, P.R.; Bailey, D.; Danabasoglu, G.; Armour, K.C.; Holland, M.M.; Kiehl, J.T. Climate Sensitivity of the Community Climate System Model Version 4. J. Clim. 2012. [Google Scholar] [CrossRef]
- Chylek, P.; Vogelsang, T.J.; Klett, J.D.; Hengartner, N.; Higdon, D.; Lesins, G.; Dubey, M.K. Indirect aerosol effect increases CMIP5 models’ projected arctic warming. J. Clim. 2016. [Google Scholar] [CrossRef]
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 dataset. J. Geophys. Res. 2012, 117, D08101. [Google Scholar] [CrossRef]
- Yin, J.J.; Schlesinger, M.E.; Stouffer, R.J. Model projections of rapid sea-level rise on the northeast coast of the United States. Nat. Geosci. 2009, 2, 262–266. [Google Scholar] [CrossRef]
- McDougall, T.J.; Jackett, D.R.; Wright, D.G.; Feistel, R. Accurate and computationally efficient algorithms for potential temperature and density of sea water. J. Atmos. Ocean. Tech. 2003, 20, 730–741. [Google Scholar] [CrossRef]
- Gupta, A.S.; Muir, L.C.; Brown, J.N.; Phipps, S.J.; Durack, P.J.; Monselesan, D.; Wijffels, S.E. Climate drift in the CMIP3 models. J. Clim. 2012, 25, 4621–4640. [Google Scholar] [CrossRef]
- Lorbarcher, K.; Nauels, A.; Meinshausen, M. Complementing thermosteric sea level rise estimates. Geosci. Model. Dev. 2015, 8, 2723–2734. [Google Scholar] [CrossRef]
- Bilbao, R.A.F.; Gregory, J.M.; Bouttes, N. Analysis of the regional pattern of sea level change due to ocean dynamics and density change for 1993–2099 in observations and CMIP5 AOGCMs. Clim. Dyn. 2015, 45, 2647–2666. [Google Scholar] [CrossRef]
- Roemmich, D.; Owens, W.B. The Argo Project: Global ocean observations for understanding and prediction of climate variability. Oceanography 2000, 13, 45–50. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Rise, J.C.; Thompson, P.F.; Watkins, M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Leuilette, E.W.; Nerem, R.S.; Mitchum, G.T. Calibration of TOPEX/Posidon and Jason altimeter data to construct a continuous record of mean sea level change. Mar. Geod. 2004, 27, 79–94. [Google Scholar] [CrossRef]
- Dieng, H.B.; Cazenave, A.; von Schuckmann, K.; Albain, M.; Meyssignac, B. Sea level budget over 2005–2013: Missing controbutions and data errors. Ocean Sci. 2015, 12, 701–734. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Sallée, J.B.; Chambers, D.; Le Traon, P.-Y.; Cabanes, C.; Gaillard, F.; Speich, S.; Hamon, M. Consitency of the current global ocean observing systems from an Argo perspective. Ocean Sci. 2014, 10, 547–557. [Google Scholar] [CrossRef]
- Lempert, R.; Sriver, R.L.; Keller, K. Characterizing uncertain sea level rise projections support infrastructure investment decisions. Calif. Energy Comm. 2012. Available online: http://www.energy.ca.gov/2012publications/CEC-500-2012-056/CEC-500-2012-056.pdf (accessed on 1 July 2017).
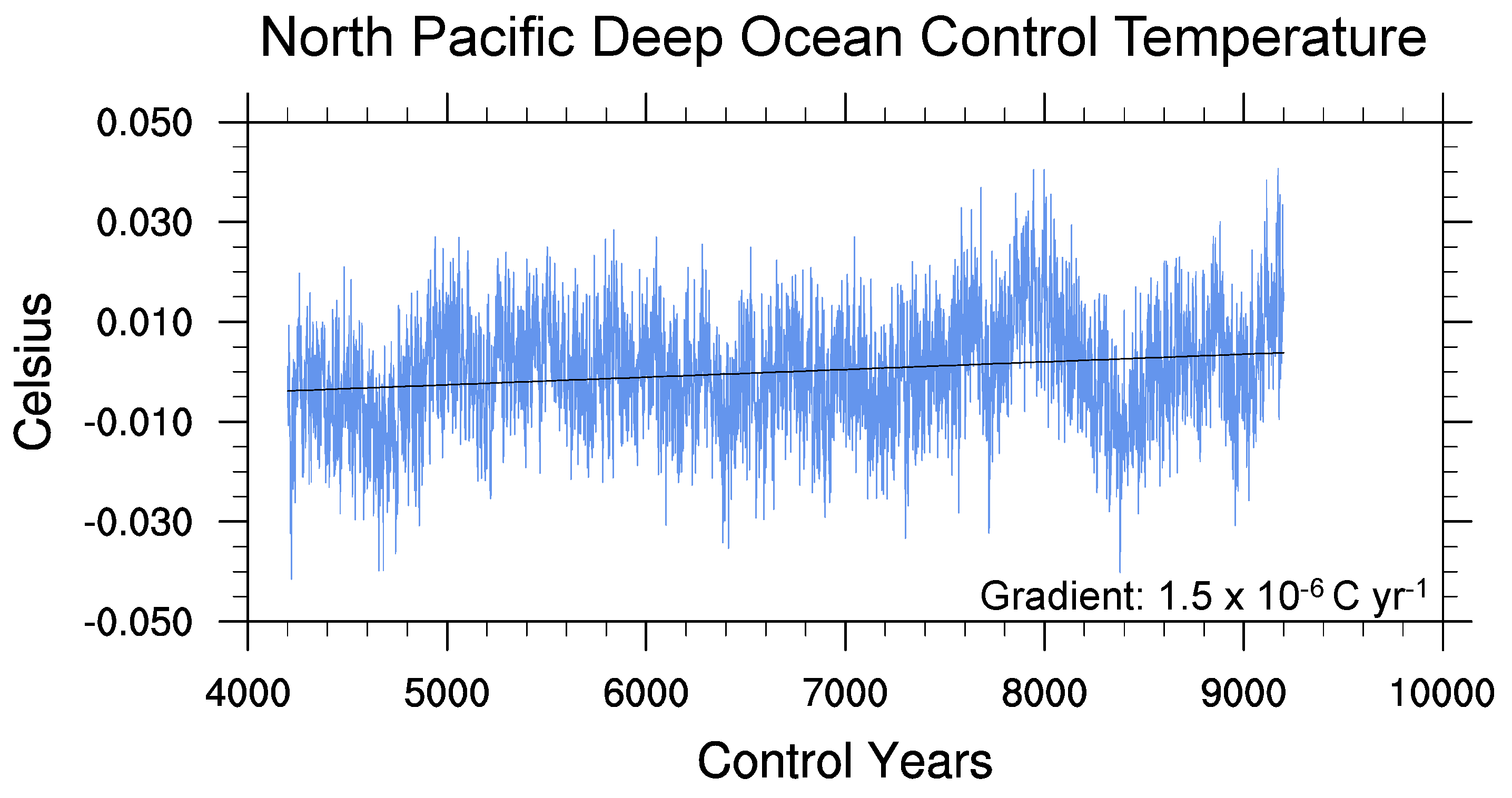
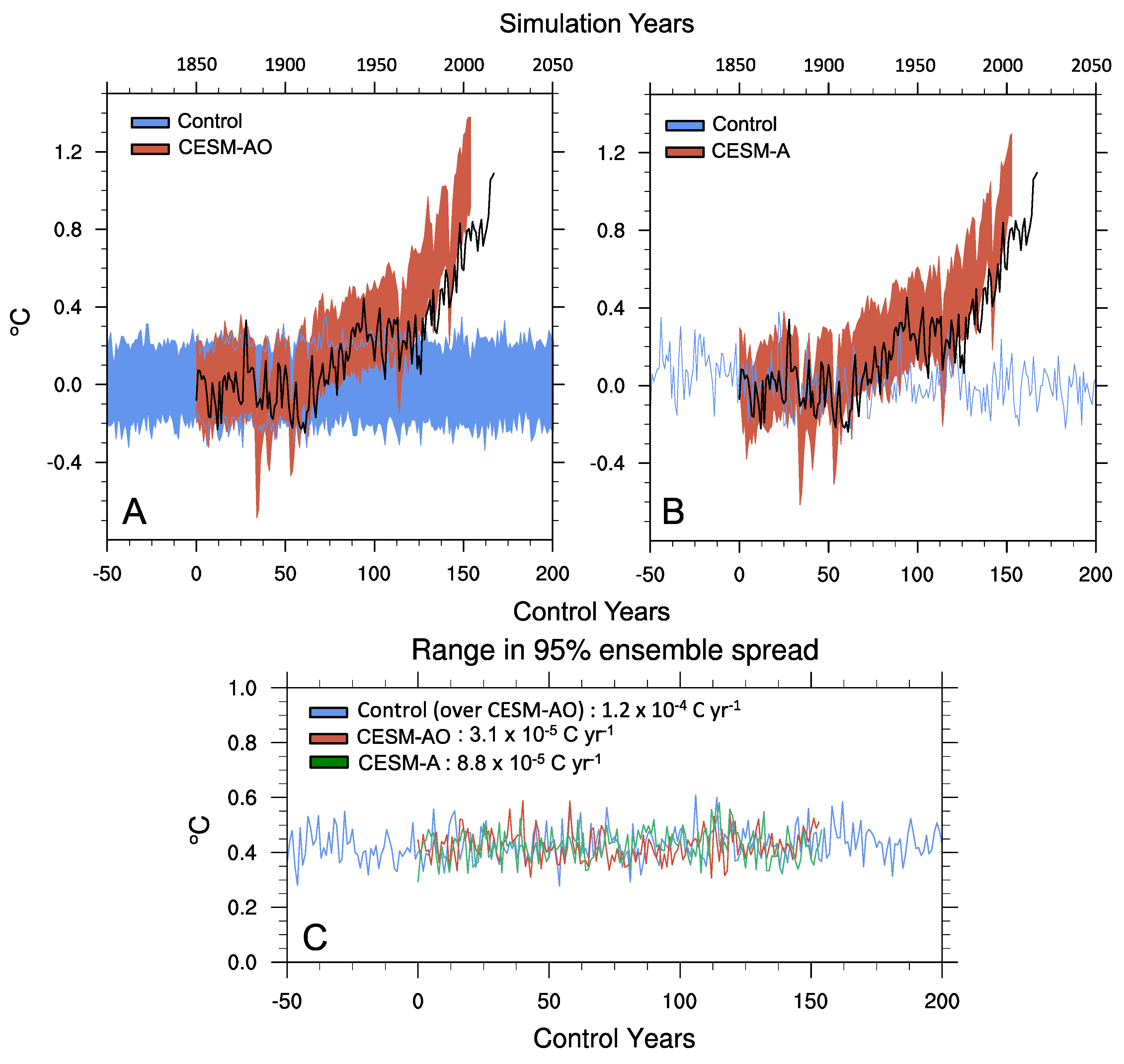
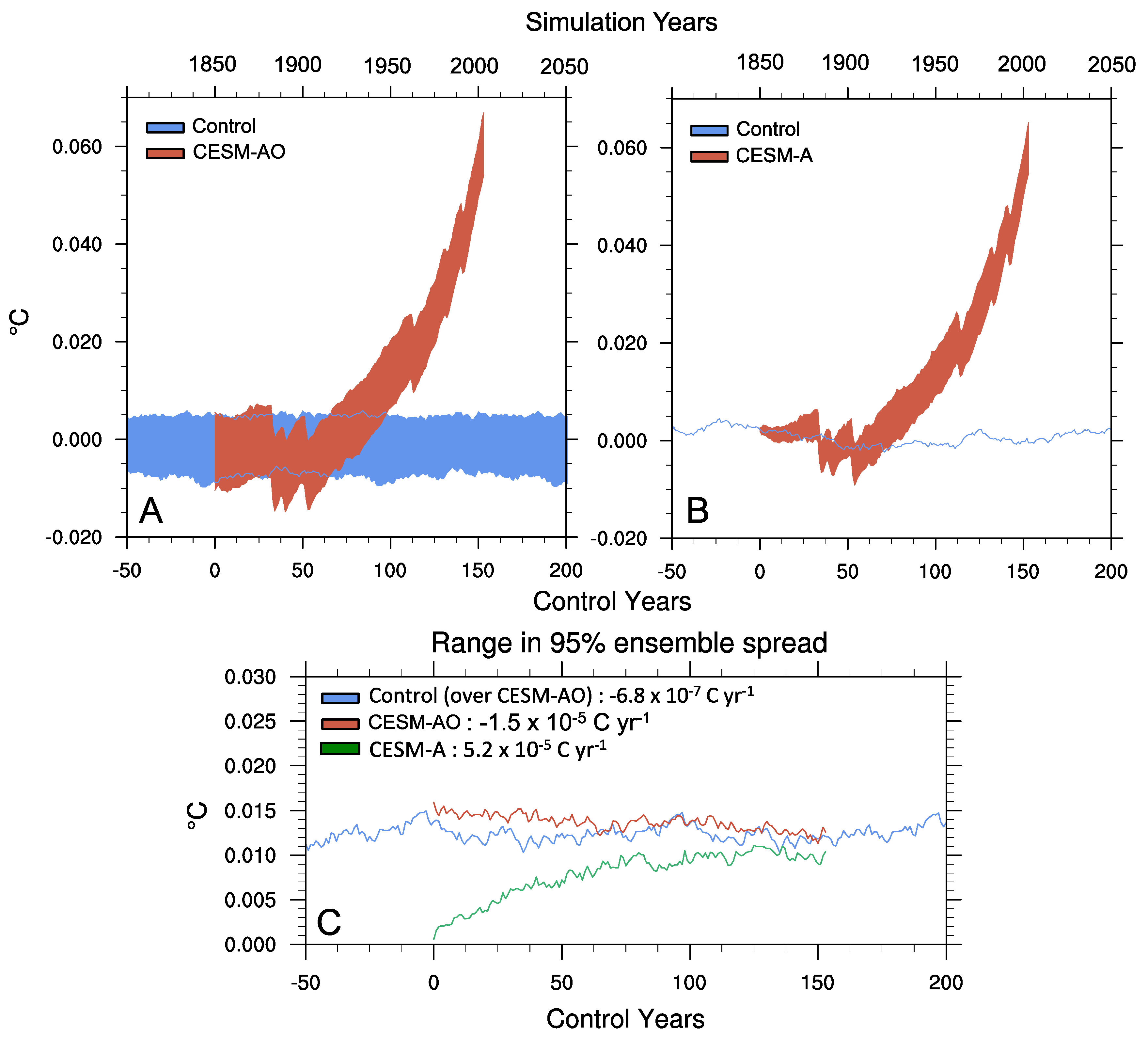
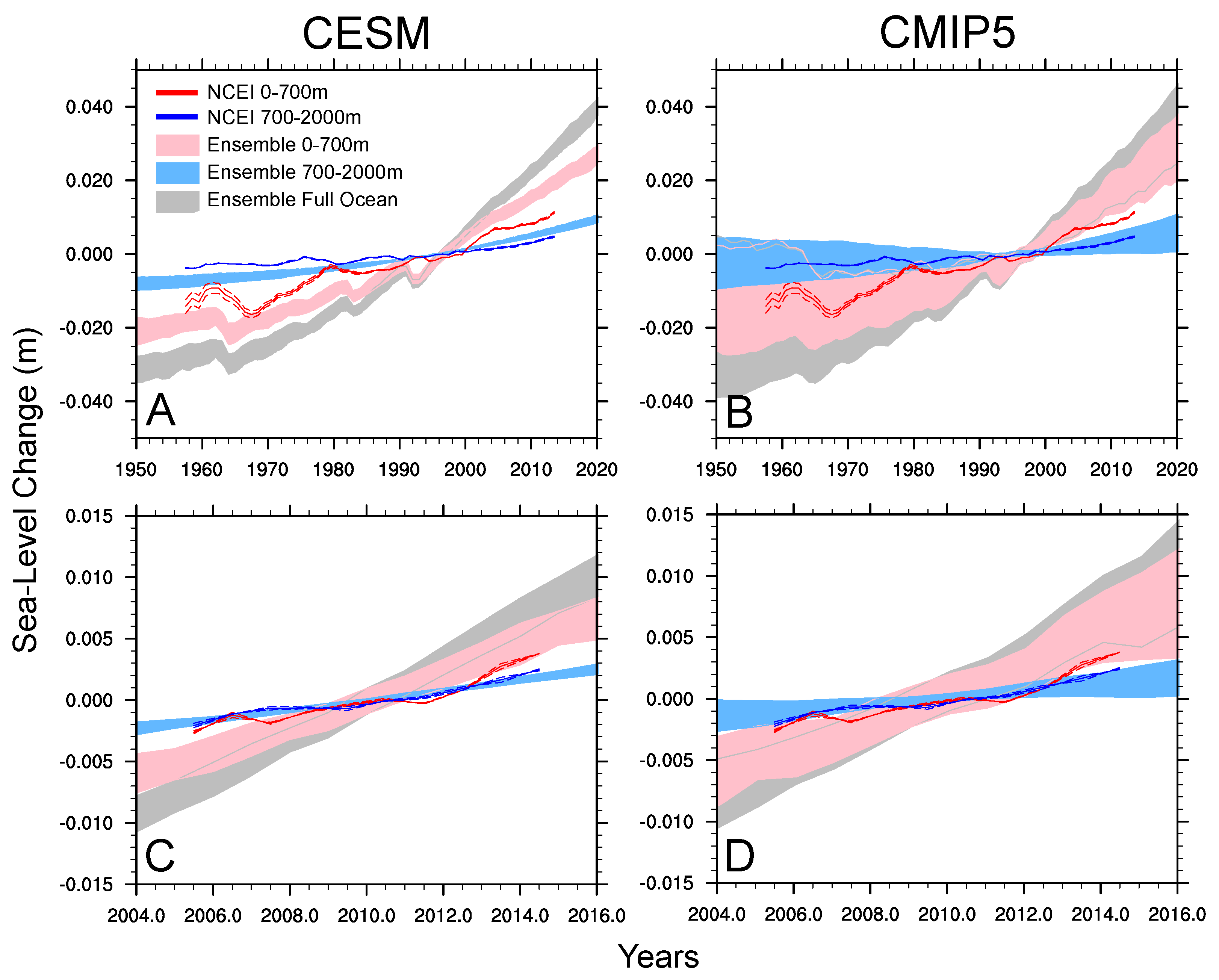
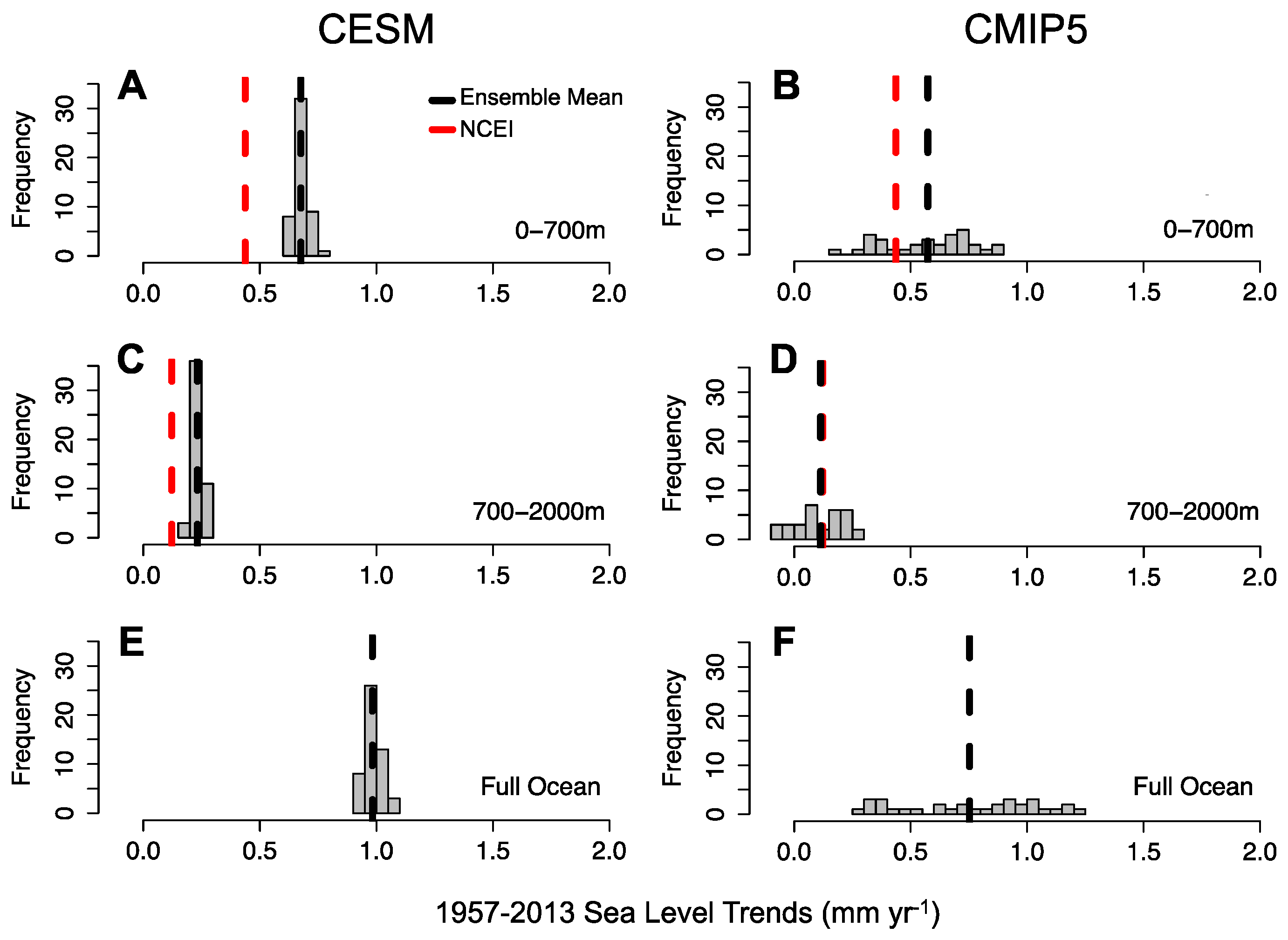
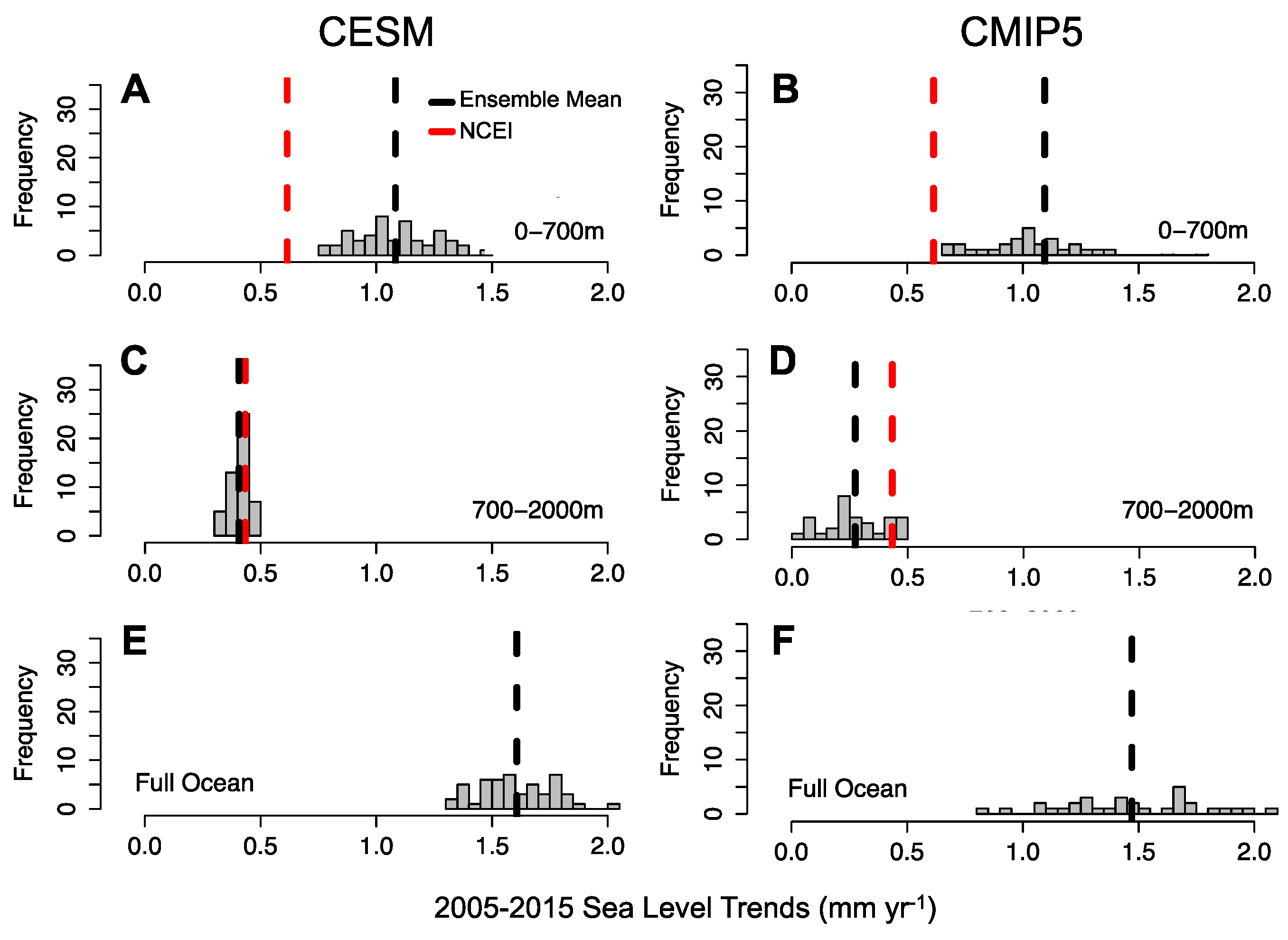
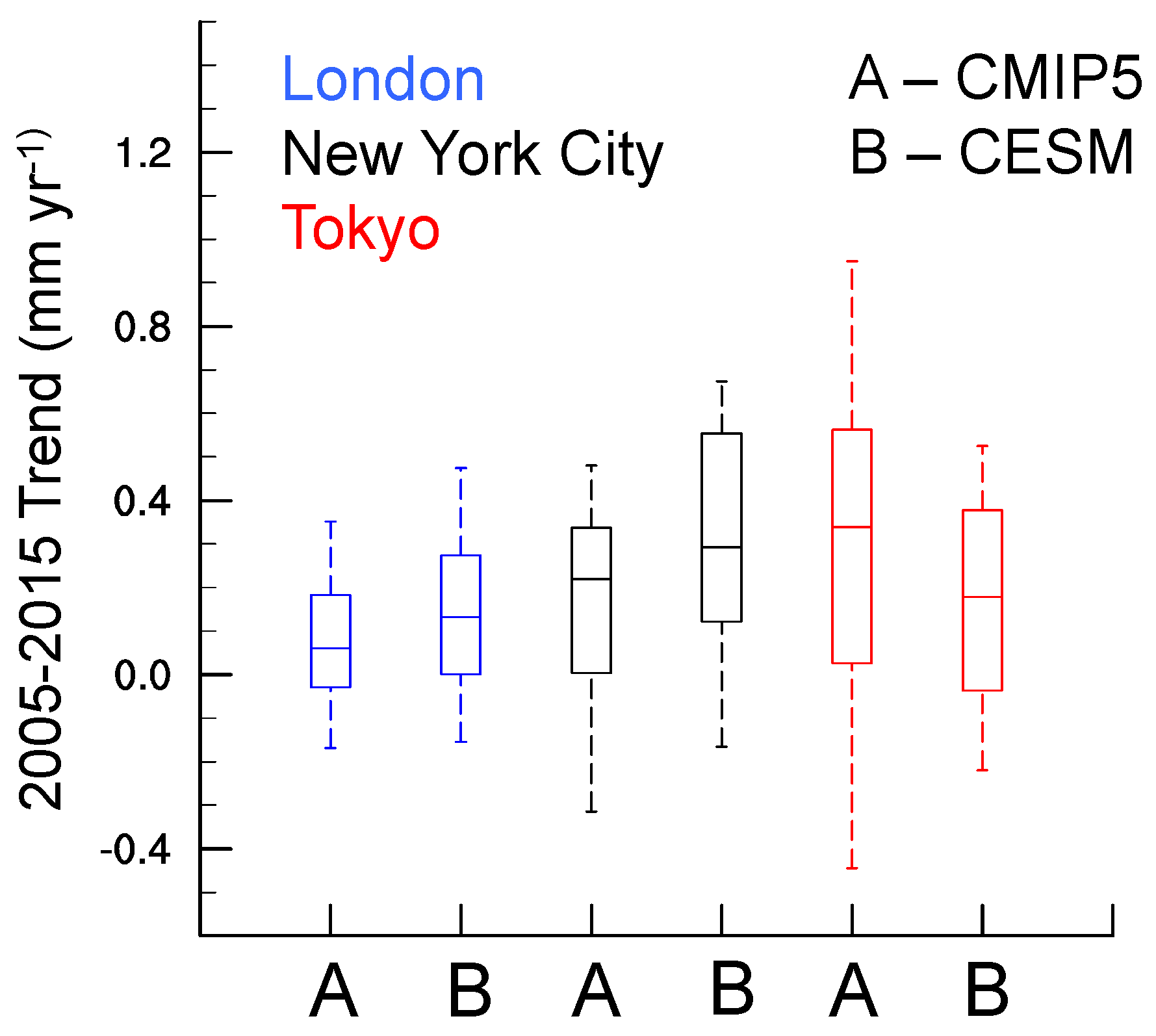
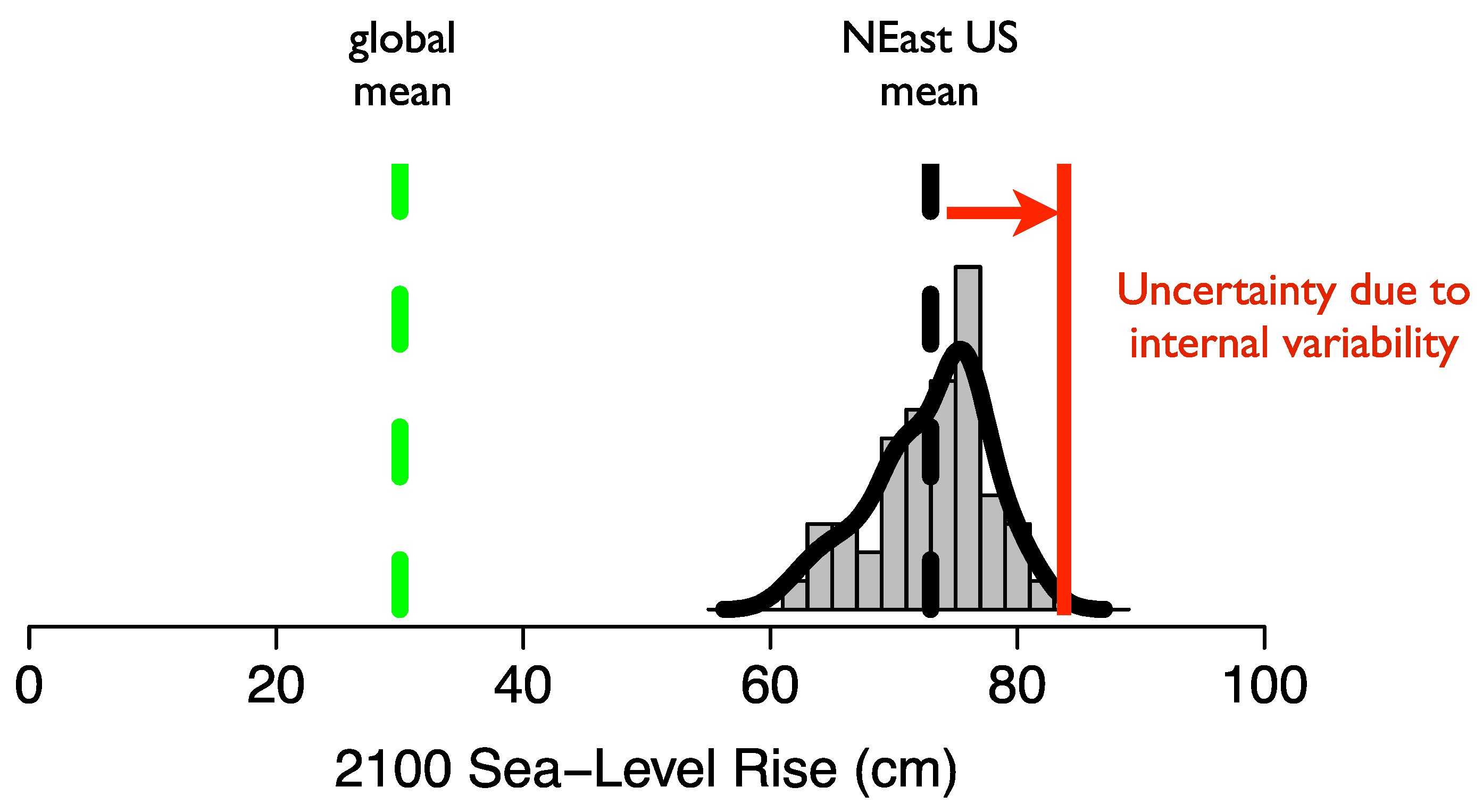
| Mean (mm·year−1) | 1975–2013 | 2005–2015 | ||
|---|---|---|---|---|
| Interactive | Non-Interactive | Interactive | Non-Interactive | |
| 0–700 m | 0.454 | 0.655 | 1.153 | 1.053 |
| 700–2000 m | 0.057 | 0.152 | 0.270 | 0.275 |
| Full Ocean | 0.579 | 0.871 | 1.546 | 1.419 |
| Mean (mm·year−1) | 1975–2013 | 2005–2015 | ||
|---|---|---|---|---|
| CESM | CMIP5 | CESM | CMIP5 | |
| 0–700 m | 0.676 | 0.573 | 1.083 | 1.094 |
| 700–2000 m | 0.232 | 0.113 | 0.407 | 0.273 |
| Full Ocean | 0.983 | 0.753 | 1.607 | 1.470 |
| Mean (mm·year−1) | 1975–2013 | 2005–2015 | ||
|---|---|---|---|---|
| CESM | CMIP5 | CESM | CMIP5 | |
| 0–700 m | 0.117 | 0.597 | 0.573 | 0.993 |
| 700–2000 m | 0.081 | 0.342 | 0.126 | 0.436 |
| Full Ocean | 0.151 | 0.895 | 0.509 | 1.096 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hogan, E.; Sriver, R. Analyzing the Effect of Ocean Internal Variability on Depth-Integrated Steric Sea-Level Rise Trends Using a Low-Resolution CESM Ensemble. Water 2017, 9, 483. https://doi.org/10.3390/w9070483
Hogan E, Sriver R. Analyzing the Effect of Ocean Internal Variability on Depth-Integrated Steric Sea-Level Rise Trends Using a Low-Resolution CESM Ensemble. Water. 2017; 9(7):483. https://doi.org/10.3390/w9070483
Chicago/Turabian StyleHogan, Emily, and Ryan Sriver. 2017. "Analyzing the Effect of Ocean Internal Variability on Depth-Integrated Steric Sea-Level Rise Trends Using a Low-Resolution CESM Ensemble" Water 9, no. 7: 483. https://doi.org/10.3390/w9070483
APA StyleHogan, E., & Sriver, R. (2017). Analyzing the Effect of Ocean Internal Variability on Depth-Integrated Steric Sea-Level Rise Trends Using a Low-Resolution CESM Ensemble. Water, 9(7), 483. https://doi.org/10.3390/w9070483




