3.1. Water Structure
An electric field produces torque on water molecules because of the electric forces acting on the positively charged hydrogen atoms and negatively charged oxygen atom. As a result, the electric field changes the molecular orientation of water (see
Figure 2).
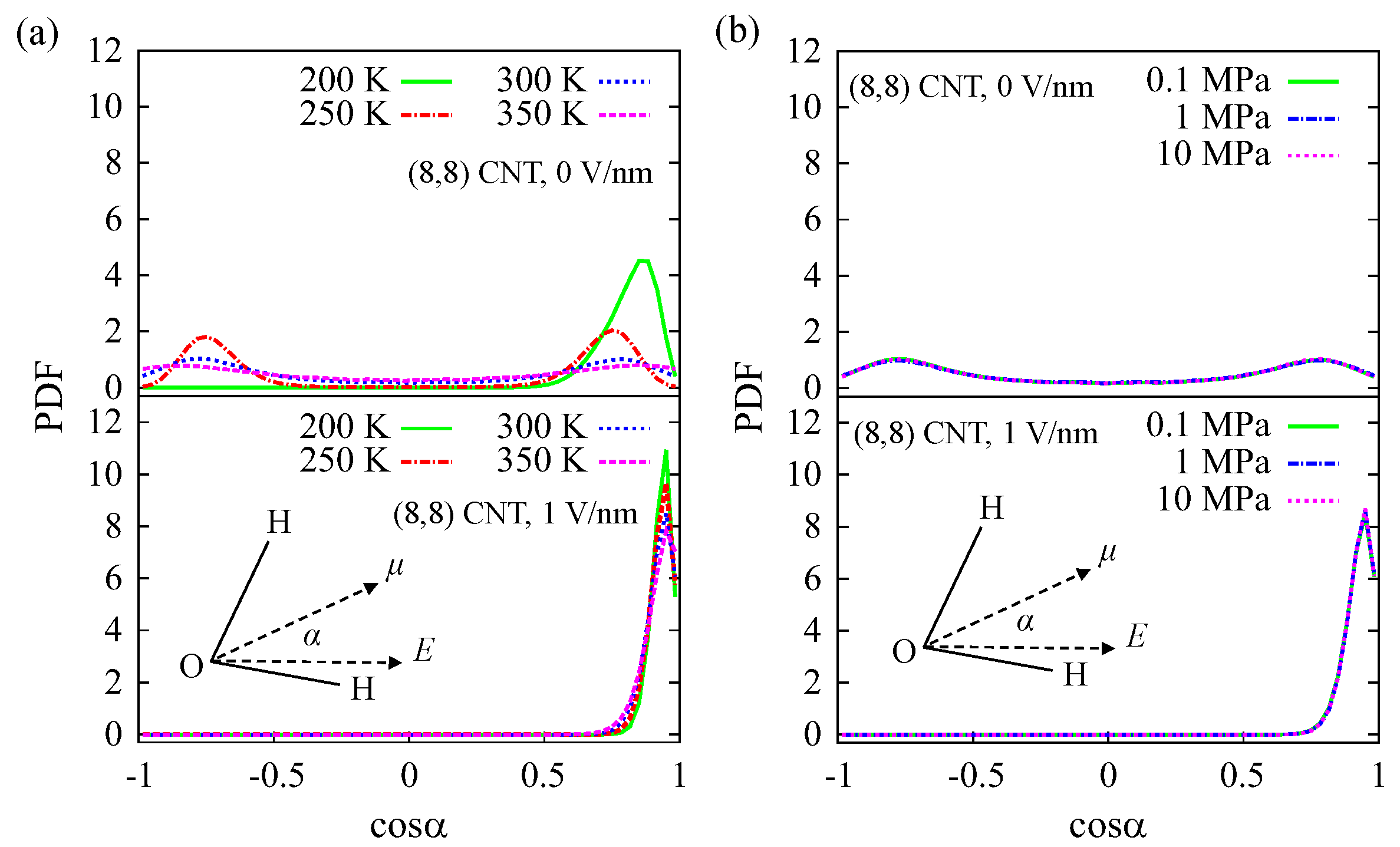
Figure 2a shows the probability distribution functions (PDFs) of water orientation in an
CNT at 200 K to 350 K, ambient pressure of 0.1 MPa, and under electric fields of 0 V/nm and 1 V/nm. The orientation is represented with the angle
between the vectors of the dipole moment and the electric field. At 0 V/nm and 250 K to 350 K, water molecules tend to show two peaks in the PDFs, at
and
. The peaks are higher at the lower temperature of 250 K than those at the higher temperatures of 300 K and 350 K. The two peaks mean at conditions of 0 V/nm and 250 K to 350 K, water in the CNT tends to having two dipole moment orientations, i.e., on the positive
z-axis and the negative
z-axis, which are opposite to each other, as shown in a previous study at 300 K [
47]. When the temperature decreases at 200 K, the distribution consists of a single orientation with one peak at
, instead of the two peaks observed at higher temperature. Water molecules have a uniform orientation in the
CNT at 200 K, i.e., parallel to the CNT axis. Under an applied electric field of 1 V/nm, water molecules in the CNT have a uniform orientation at all simulated temperature conditions. The orientation of the dipole moment of water is restrained parallel to the direction of the electric field.
Figure 2b shows the orientation of water molecules in an
CNT at various pressures of
0.1 MPa to 10 MPa, constant temperature of
300 K, under applied electric fields of 0 V/nm and 1 V/nm. The change in pressure does not affect the orientation of water molecules in the CNT under any of the electric field conditions. Simulations with the TIP4P model show the same results (see
Figure S1 in supporting information). However, the major difference of the TIP4P model from the SPC model is the peak at
at the condition of 200 K and 0 V/nm. The peak at
is significantly lower than that at
. This indicates that the TIP4P water shows as a ferroelectric material in the CNT at low temperatures. This result is the same as that shown with the SPC model.
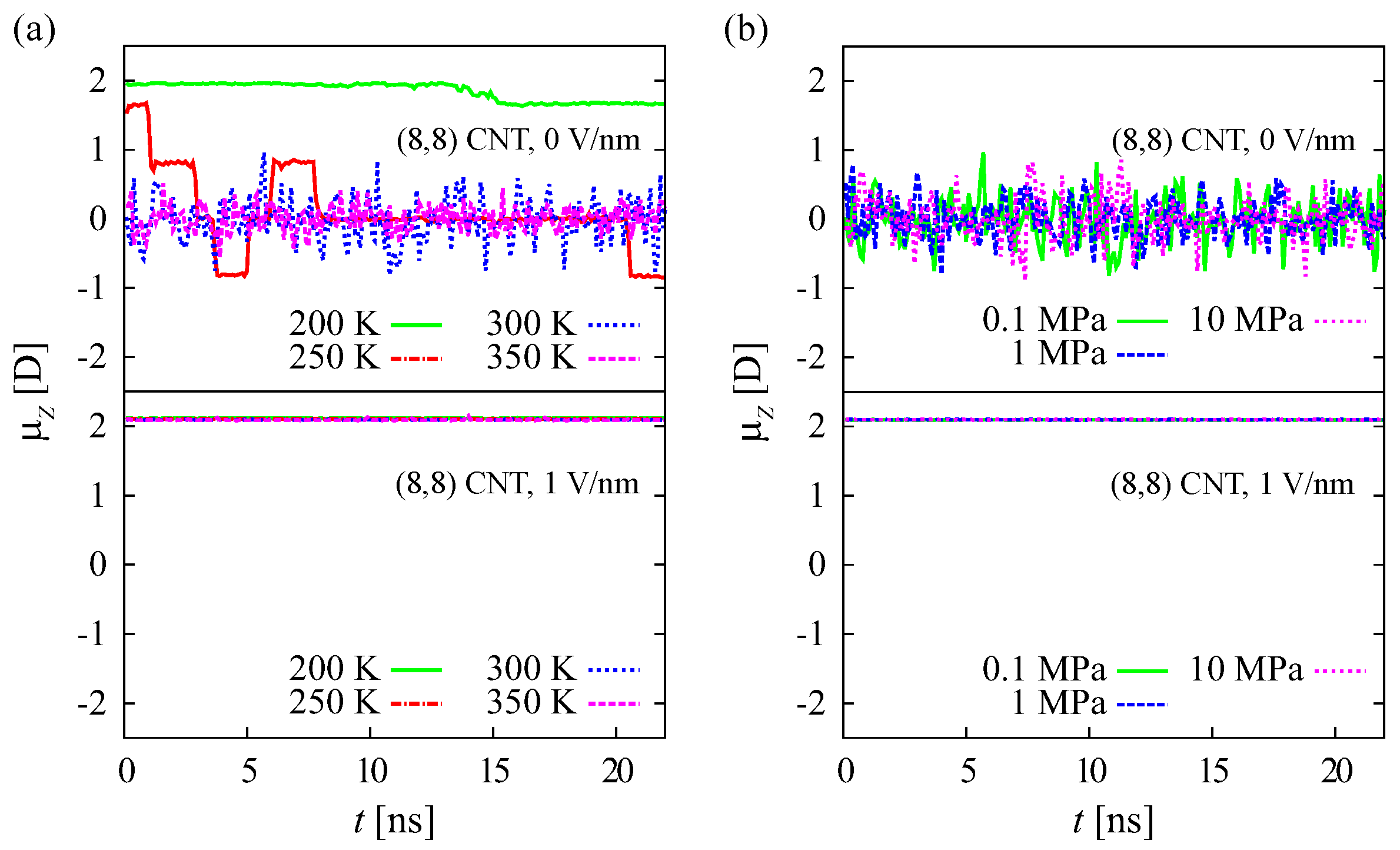
Polarization was determined by calculating the average
z-component of the dipole moment (
) of water molecules in the CNT. The average value was calculated for 0.1 ns (100 frames) from 22 ns of simulation data, and is shown in
Figure 3a,b. At a temperature of 200 K and applied electric field of 0 V/nm, the polarization is
≥ 1.7 Debye (D). This indicates that water in the CNT exhibits ferroelectric behavior at 200 K. This is consistent with the water orientation result shown in
Figure 2a, in which one peak is observed at 200 K. The polarization of water molecules at low temperature has also been reported in previous studies [
48,
49]. However, one of these studies reported that polarization does not occur in a 4-gonal ice-nanotube [
49]. As explained in the next paragraph, the structure of water molecules in the CNT at 200 K observed in the current study is 4-gonal. The previous study [
49] was based on water in an infinite length CNT, rather than a CNT with reservoirs at each end. The dynamics of water molecules in the reservoirs may affect the polarization of water in the CNT at low temperature. At 250 K and 0 V/nm, the direction of polarization changes with time between
D and
D. A similar result was reported for a 5-gonal ice-nanotube structure in a CNT [
48]. At 300 K
fluctuates, and at the higher temperature of 350 K, the amplitude of
decreases. This result is similar to that reported in the previous study [
48]. Under an applied electric field, the orientation of water molecules is uniform (see
Figure 2a,b), so
is positive, i.e., 2.1 D. Changes in pressure up to 10 MPa do not affect the polarization of water in the CNT (see
Figure 3b). Simulations with the TIP4P model show similar results (see
Figure S2). However, at the condition of 300 K and 0 V/nm, the
change with time between
= +0.8 D and
= −0.8 D, which is different from that of the SPC model. As explained in the next paragraph, the structure and dynamics of the TIP4P water is slightly different from those with the SPC model at the condition of 300 K and 0 V/nm. This suggests the melting temperature of the TIP4P model is slightly higher than that of the SPC model.
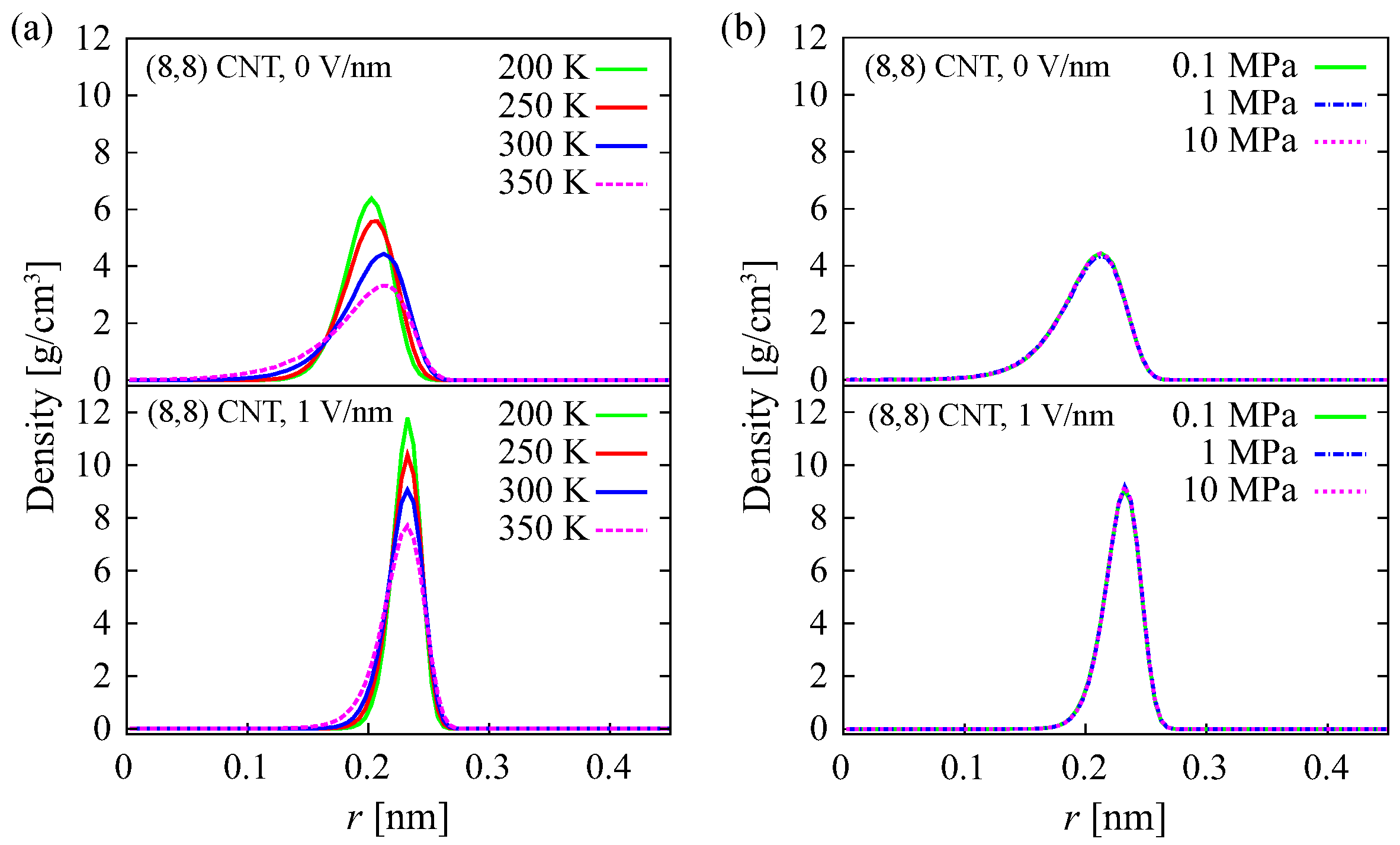
The densities of oxygen atoms in an
CNT in the radial direction at various temperatures and pressures are shown in
Figure 4a,b, respectively. At
E = 1 V/nm, the density distribution is narrower and the peak is higher, compared with at
E = 0 V/nm. This is observed for both various temperatures (
Figure 4a) and pressures (
Figure 4b). This implies that the water structure in an (8, 8) CNT under an electric field differs from that in the absence of an electric field at all simulated temperature and pressure conditions. This is discussed in more detail in the next paragraph. At lower temperatures, the distribution is narrower and consequently the peak is higher, especially at 0 V/nm (
Figure 4a). This indicates that, at
E = 0 V/nm, the water structure changes with increasing temperature. The change in pressure does not change the radial density distribution, either in the presence or absence of an electric field, as shown in
Figure 4b. This suggests that increasing the pressure up to 10 MPa does not change the water structure. A similar result is observed using the TIP4P model (
Figure S3). However, the distribution with the TIP4P model is slightly narrower than that with the SPC model at 300 K and 0 V/nm. It is consistent with the result of polarization in the previous paragraph. Another difference is that the distribution with the TIP4P model is slightly wider than that with the SPC model at 350 K and 1 V/nm. This suggests that, at 350 K and 1 V/nm, both water models have different structures.
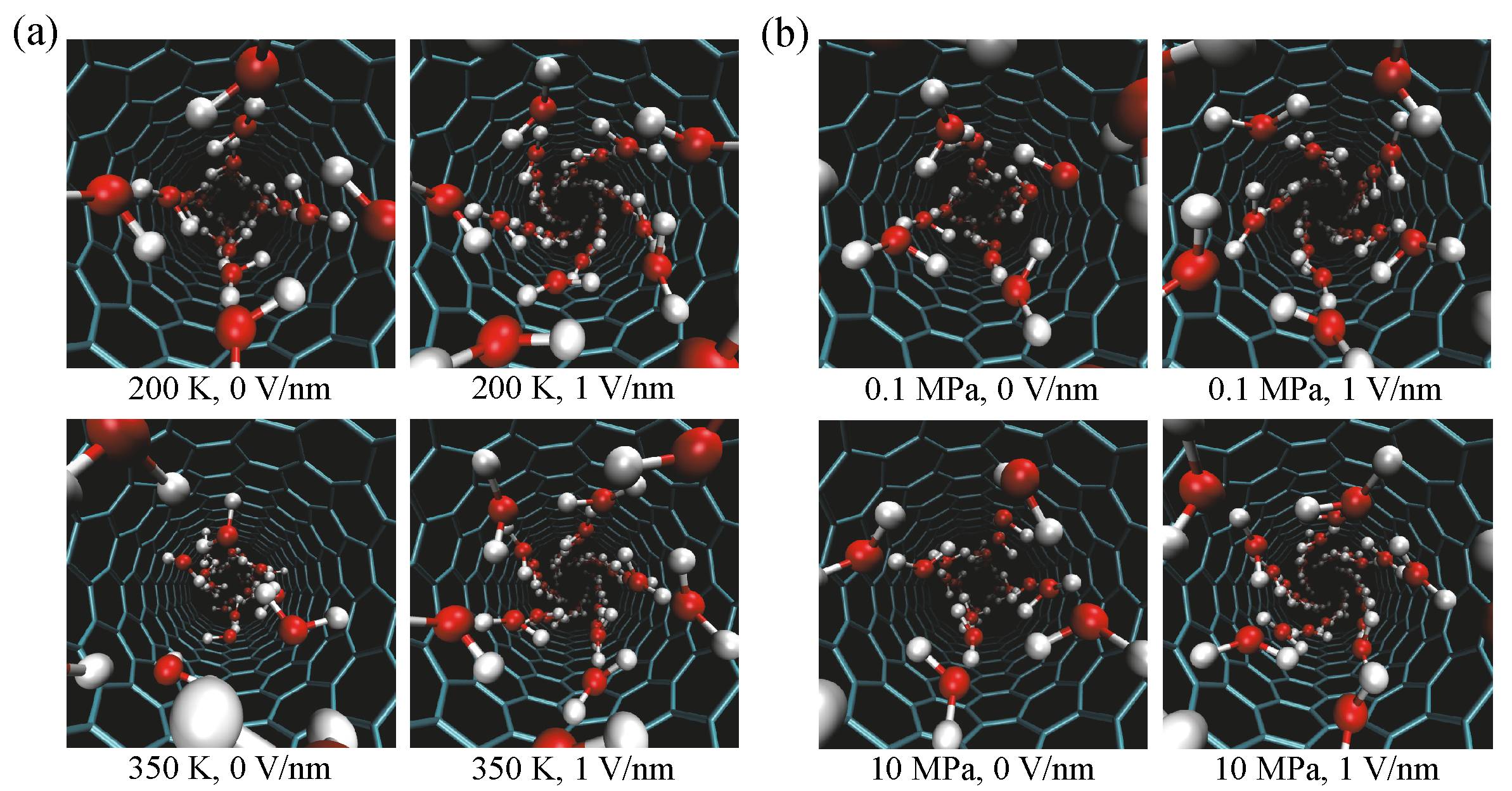
Snapshots of water structures in an (8, 8) CNT at temperatures of 200 K and 350 K and at pressures of 0.1 MPa and 10 MPa are shown in
Figure 5a,b, respectively. Snapshots under applied electric fields of 0 V/nm and 1 V/nm are shown in both cases. The structure of water molecules is helical under an applied electric field of 1 V/nm. Under the applied electric field, the structure is the same at all temperature and pressure conditions. This result differs to that in the absence of an electric field. To better understand the water structure, we unrolled the water structure to obtain a two-dimensional (2D) structure. The radial positions of oxygen atoms in the CNT are averaged to determine the radius of the tube. The unrolled 2D structures are shown in
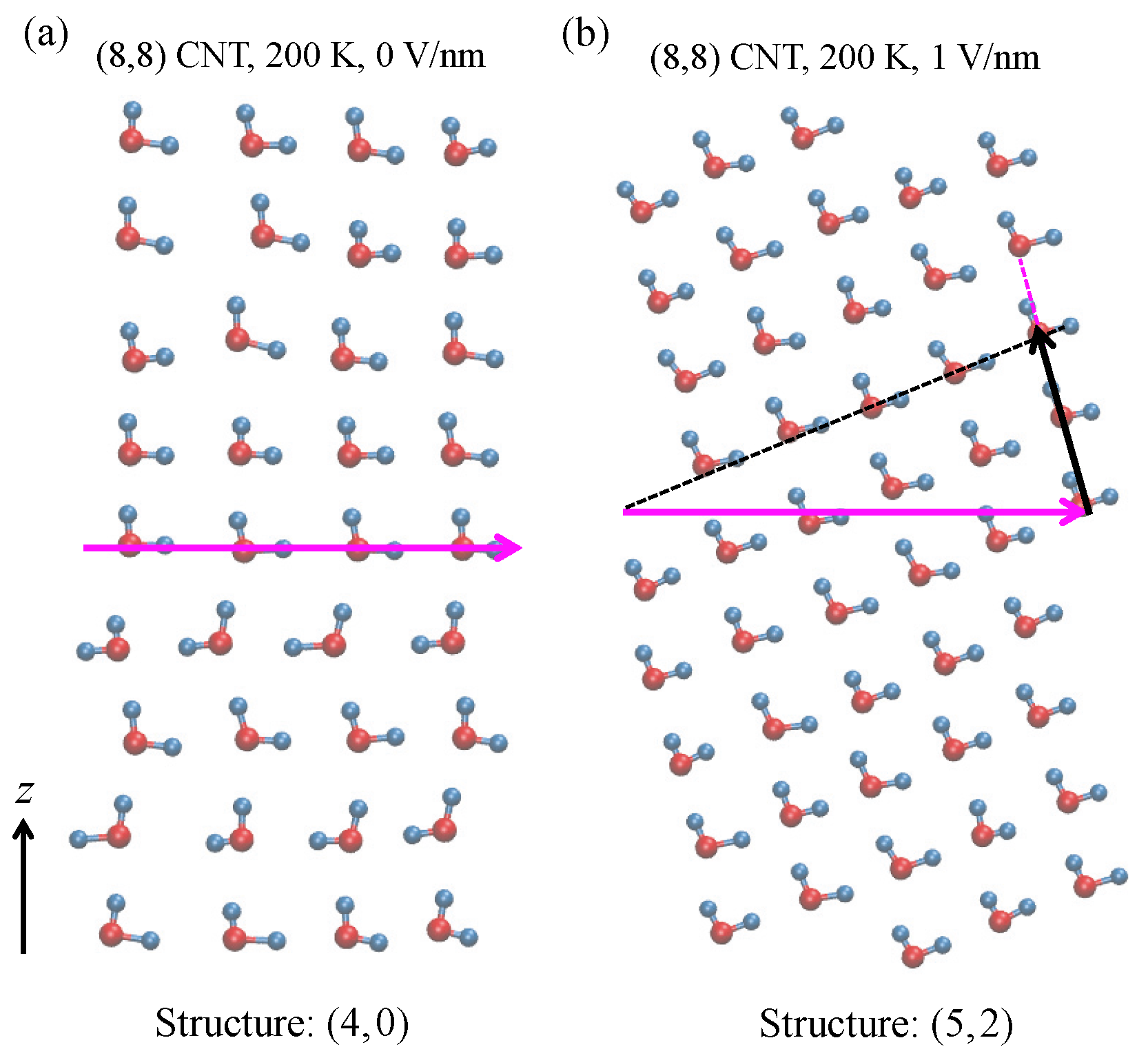
Figure 6a for 200 K, 0.1 MPa, and 0 V/nm, and in
Figure 6b for 200 K, 0.1 MPa, and 1 V/nm. The structure is identified using the
index [
50,
51], as was used in our previous study [
35]. If
m, the structure is helical. If
m = 0, it is an
n-gonal structure [
10,
50,
51]. As an example, water molecules in the structure of
Figure 6b form an orderly arrangement, i.e., in both the column (magenta-dotted line) and row (black-dotted line) directions. The width of the structure is five column units (magenta arrow), and the number of rows corresponding to the five unit width is two units (i.e., the length of black arrow). Thus, it is a
helical structure. In the same manner, the structure shown in
Figure 6a is a
4-gonal structure. The difference in the two ordered structures,
and
, suggests that an electric field induces a phase transition from solid to solid. The snapshot in
Figure 6a also supports our above conclusion that at 200 K and 0 V/nm, the water exhibits ferroelectric behavior. The directions of the dipole moments of all water molecules are on the positive
z-axis.
The water structures at all temperature conditions are summarized in
Table 1. In the absence of an electric field, water has a solid-like structure of
at a low temperature of 200 K and 250 K. At 300 K, the structure of water is
or disordered. This indicates that the ordered structure of
is unstable at these conditions. The solid-like structure of
readily changes to the disordered or liquid-like structure, and vice versa [
35]. This indicates that the thermodynamic conditions of the simulation are near the melting or freezing point. A similar result was reported in a previous study, in which the formation of a 5-gonal ice-nanotube in a CNT of diameter 1.15 nm reportedly occurs at 310 ± 5 K [
48]. The unstable structure at 300 K and 0 V/nm causes oscillation of the dipole orientation because of rearrangement of the water molecules into a tube-like structure (see
Figure 3a). At a higher temperature of 350 K, the structure is completely disordered, and the water behaves as a liquid phase. Interestingly, under an applied electric field of
E = 1 V/nm, the structure of water molecules in the
CNT (diameter 1.08 nm) is
at all temperatures. This structure is different from the
structure at low temperature in the absence of an electric field. Previous studies of water in CNTs of slightly larger diameters under an electric field at ambient pressure showed different results [
24,
38,
39]. In a CNT of diameter 1.2 nm and under a 1 V/nm field, TIP4P water has a solid-like structure at
T < 105 K, and a liquid-like structure at higher temperatures [
38]. In a 1.31 nm diameter CNT under a 1 V/nm field, the solid-like structure of TIP4P water reportedly melts to a liquid phase at
T > 230 K [
39]. These differences may have arisen from the different simulation configurations. In previous studies [
38,
39], the CNTs are immersed in bulk water, i.e., there are water molecules both inside and outside of the CNT wall. The interaction of water inside the CNT with water outside the CNT may result in a different freezing point. Moreover, in a 1.11 nm diameter CNT of infinite length under a 1 V/nm field, the melting point of TIP4P water reportedly occurs at 310 K [
24]. In our system, there is no water outside the CNT wall. The water is instead located in reservoirs at the ends of the CNT. This may result in the different freezing points of water structures within the CNTs. Snapshots of the TIP4P water in the
CNT are shown in
Figures S4 and S5, and the structures at various temperatures are summarized in
Table S1. In general, the structures are similar to those of the SPC. Slight differences are at the conditions of 300 K and 0 V/nm and of 350 K and 1 V/nm. At condition of 300 K and 0 V/nm, the
structure with the TIP4P model is more stable than that with the SPC model. This indicates that the melting point of the TIP4P is slightly higher than that of the SPC. At 350 K and 1 V/nm, the structure with the TIP4P is
instead of
with the SPC. Hydrogen bond dynamics analysis shows that the structure of the TIP4P at this condition is weaker than that of the SPC. This suggests that, under an electric field, the melting point of the TIP4P model is slightly lower than that of the SPC model.
Table 2 summarizes the water structures in an
CNT under various pressure conditions. Under a
E = 0 V/nm field, water forms a
or a disordered structure that is unstable, as explained above. Increasing the pressure up to 10 MPa does not yield a stable
solid-like structure. This implies that the freezing point occurs at a pressure higher than 10 MPa. Under a
E = 1 V/nm field, the structure at all pressure conditions is
. This structure is the same as that at all temperature conditions in
Table 1. An electric field 1 V/nm causes the formation of a
structure at all simulated temperatures and pressures. This differs from the structure in the absence of an electric field. Structures of TIP4P at various pressures are listed in
Table S2. The structures are
and
at 0 V/nm and 1 V/nm, respectively. Pressure up to 10 MPa does not change the structures.
3.2. Hydrogen Bond Dynamics
We calculated the hydrogen bond (HB) autocorrelation function
, to investigate the dynamic behavior of the water structures [
52,
53]:
where
if a pair of water molecules is bonded at time
t, and
if otherwise. The denominator
is for normalization and is the number of hydrogen bonds (HBs) tagged at
. The HBs between water molecules in the CNT are determined by the following geometrical criteria:
< 0.36 nm,
< 0.24 nm, and angle of
[
54,
55].
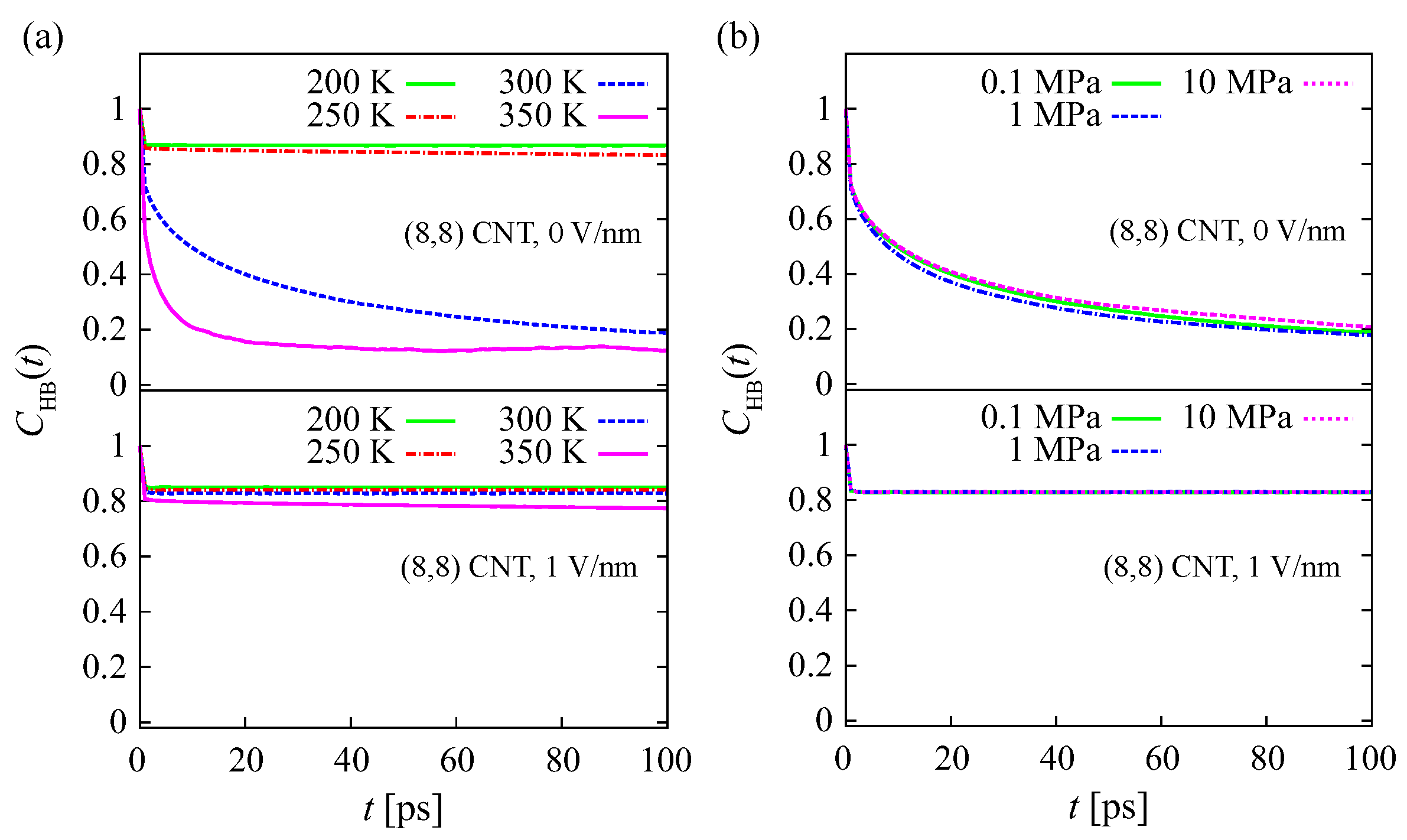
The HB autocorrelation functions
within the water structures at various temperatures and 0 V/nm and 1 V/nm fields are shown in
Figure 7a. At
200 K, 250 K, and 0 V/nm,
decreases slightly and then becomes constant with increasing
t. The value of
is still higher than 0.8 at
t = 100 ps. This indicates that the lifetime of the HBs is long. Similar results are observed for HBs within water structures under a 1 V/nm field at all temperature conditions. This indicates that the solid-like structures in the CNT, i.e., both the
-structure at 0 V/nm, and the
-structure at 1 V/nm, are retained by strong HBs. Different results are observed at temperatures of 300 K and 350 K under a 0 V/nm field, where the
decreases to less than 0.2 at
t = 100 ps. This indicates that more than 80% of HBs within the water structure are broken. Pairs of water molecules in this structure are not maintained by strong HBs. Consequently, pairs are easily broken, and the two molecules diffuse away from each other. As seen in
Table 1, the structure at these temperatures is disordered, i.e., a liquid-like structure. The
within TIP4P structures at various temperatures with 0 V/nm and 1 V/nm are shown in
Figure S6a. The dynamics of HB of TIP4P structures is similar to that of SPC except at 300 K and 0 V/nm. At this condition, the
of the TIP4P is higher than that of the SPC. This implies that HBs within
-structure of the TIP4P is stronger, and the structure is more stable than that of the SPC. Moreover, this denotes that the melting point of the TIP4P is slightly higher than that of the SPC. This result supports the explanation in the previous paragraph. At the condition of 350 K and 1 V/nm, the
of the TIP4P is slightly lower than that of the SPC. The HBs within the TIP4P structure is weaker. This suggests that, under an electric field, the melting point of the TIP4P is lower than that of the SPC.
The effect of pressure on
under 0 V/nm and 1 V/nm fields is shown in
Figure 7b. At
V/nm, the value of
decreases to around 0.2 for all pressure conditions. A pair of water molecules within the disordered (liquid-like) structure will readily diffuse away from each other. Increasing the pressure up to 10 MPa has no significant effect on the HB strength within the structure. Under a 1 V/nm field,
at
. This indicates that the
-structure within the CNT is retained by strong HBs. This supports the notion that the water behaves as a solid phase. Increasing the pressure up to 10 MPa does not change the
within the structure in the CNT under a
V/nm field. The dynamics of HBs in the structures at 200 K and 250 K under 0 V/nm and 1 V/nm fields are similar (
Figure 7a). The lifetimes of HBs within the
-structure (at 0 V/nm) and
-structure (at 1 V/nm) are very long. The
with the TIP4P model at various pressures are presented at
Figure S6b. The pressure up to 10 MPa does not change
.
3.3. Potential Energy
To identify the main driving force for the formation of the
-structure and
-structure within the CNTs, we analyzed the Lennard–Jones (LJ) and Coulomb potential energies of water molecules in the reservoir and in the CNT. In addition, under an external electric field, water has a dipole potential energy
, where
is the vector of the dipole moment, and
is the electric field.
Table 3 shows averages of the LJ potential energy, Coulomb potential energy, and dipole potential energy per water molecule in the reservoirs and in the CNT at 200 K and 250 K.
is the difference between the potential energy in the CNT (
) and that in the reservoir (
),
. Thus,
indicates the effect of the CNT wall on the water molecules in the tube. There is no electrostatic interaction of water molecules with the CNT and graphene walls because the CNT and graphene have no charge, i.e., the Coulomb potential represents only water–water interactions.
In the absence of an electric field, i.e.,
V/nm, the LJ potential energy in the CNT is lower than that in the reservoirs at
K and 250 K. The values of
are
kJ/mol and
kJ/mol at 200 K and 250 K, respectively. The negative value of
indicates that the van der Waals interaction facilitates water molecules to occupy the tube. On the other hand, the Coulomb potential energy in the reservoirs is lower than that in the CNT. The energy differences
are 14.86 kJ/mol and 8.53 kJ/mol at 200 K and 250 K, respectively. This indicates that the electrostatic interaction tends to move the water molecules from the CNT into reservoir. Therefore, at 200 K and 250 K under a 0 V/nm field, the van der Waals interaction is the main driving force maintaining water within the CNT. Similar results are shown by the simulation with the TIP4P water model as presented in
Table S3. The values of
are
kJ/mol and
kJ/mol at 200 K and 250 K, respectively. Meanwhile, the
with the TIP4P are 16.08 kJ/mol and 6.70 kJ/mol at 200 K and 250 K, respectively. To clarify the contribution for the van der Waals interaction, we calculated the LJ potential energy of the water–water interaction (
) and water–CNT interaction (
) in the reservoirs and in the CNT (see
Table 4). The potential energy
does not include any contribution from the graphene sheets. Under a 0 V/nm field,
in the reservoirs and CNT have similar positive values. In contrast,
in the CNT has negative values of
and
kJ/mol at 200 K and 250 K, respectively. This indicates that, in the absence of an electric field, the van der Waals interaction of CNT–water is the main driving force for the formation of the
-structure in the CNT, which facilitates water molecules to occupy the CNT. Simulations with TIP4P model show similar results (
Table S4). The
in the reservoirs and CNT do not have significant different values. On the other hand, the
in the CNT have negative values,
kJ/mol and
kJ/mol at 200 K and 250 K, respectively.
Under an electric field of 1 V/nm, the LJ potential energy difference between the reservoir and CNT is small. The
values are
kJ/mol and 0.13 kJ/mol at 200 K and 250 K, respectively (see
Table 3). The TIP4P water model shows similar results (
Table S3). The values of
are
kJ/mol and
kJ/mol at 200 K and 250 K, respectively. We now consider the contribution of the van der Waals interaction. The
facilitates water molecules to occupy the CNT, while the
tends to remove water from the CNT (see
Table 4). Simulations with the TIP4P model show the same results (
Table S4). In contrast, the Coulomb potential energy in the CNT is significantly lower than that in the reservoirs. The
values are
kJ/mol and
kJ/mol at 200 K and 250 K, respectively (
Table 3). Therefore, under an electric field of 1 V/nm, the electrostatic interaction of water molecules in the CNT is the main driving force for the formation of the
-structure in the CNT, and facilitates water molecules to occupy the CNT. Similarly, the presence of an electric field strengthens the electrostatic interaction within the TIP4P water structure. Coulomb potential energy per TIP4P molecule in the CNT at 1 V/nm is significantly lower than that at 0 V/nm (
Table S3). At 200 K, the
is
kJ/mol, which is still higher than
kJ/mol of
. Therefore, at a low temperature of 200 K, the
is still dominant for facilitating the TIP4P water to occupy in the CNT. However, at higher temperatures of 250 K,
becomes
kJ/mol, which is the main driving energy to facilitate the TIP4P water to fill the CNT. This is due to the Coulomb potential energy of water in reservoirs increasing at a higher temperature. At 300 K and 1 V/nm,
decreases to
kJ/mol.
We now consider the mechanism of phase transition of the water structure from
to
within the CNT under an electric field, using the energy differences (see
Table 3). Under the electric field, the LJ potentials in the CNT increase by 13.27 kJ/mol and 11.47 kJ/mol at 200 K and 250 K, respectively, compared with those in the absence of an electric field. This main contribution to this increase is the water–water interaction (
). In contrast, the Coulomb potentials decrease by
kJ/mol and
kJ/mol at 200 K and 250 K, respectively. These results indicate that the phase transition of the water structure from
to
results from the decrease in Coulomb potential and increase in LJ potential (i.e., mainly water–water interactions). This explanation also applies for the TIP4P model. With 1 V/nm, the LJ potentials in the CNT increase by 9.88 kJ/mol and 10.10 kJ/mol at 200 K and 250 K, respectively, compared with those with 0 V/nm (
Table S3). Contrarily, the Coulomb potentials decrease by
kJ/mol and
kJ/mol at 200 K and 250 K, respectively.
The dipole potential energy will be at a minimum if the direction of the dipole moment is parallel to that of the electric field. However, the direction of the dipole moment is not statically parallel to the electric field, but instead oscillates around it. The presence of the graphene sheet causes polarization in the reservoirs, and induces an internal electric field in the direction opposite to the external electric field [
35]. As a result, the effective electric field in the reservoir is lower than that in the CNT. The orientation of the dipole moment of water in the reservoir therefore oscillates more than that in the CNT. This causes the average dipole potential in the reservoirs to be slightly higher than that in the CNT, so
becomes negative (
Table 3). This means that the dipole potential energy promotes water to fill the CNT. However, the contribution of the dipole energy is minor compared to that of the Coulomb potential energy. This supports the notion above that the electrostatic interaction within the water structure is the main driving force for the transition from the
-structure to
-structure. The
of the TIP4P water is slightly higher than that of the SPC. This is owing to the fact that the dipole moment of the TIP4P is lower than that of the SPC, i.e., 2.18 D and 2.27 D, respectively.
In the absence of an electric field, the LJ potential is the main driving force for the formation of an ordered structure in the CNT. However, the electrostatic interaction within water structure tends to remove water from CNT. At the condition of 300 K and 0 V/nm,
of the SPC is higher than that of the TIP4P, i.e.,
kJ/mol and
kJ/mol, respectively (see
Table S5). This makes the
of the SPC higher than that of the TIP4P, i.e.,
kJ/mol and
kJ/mol, respectively. As the result, at 300 K and 0 V/nm the solid-like structure of the TIP4P in the CNT is more stable, and the melting point is higher than that of the SPC. Conversely, with the presence of an electric field, the electrostatic interaction within water structure is the main driving force for the formation of an ordered structure. At 350 K and 1 V/nm,
of the SPC is lower than that of the TIP4P, i.e.,
kJ/mol and
kJ/mol, respectively (see
Table S6). This makes
of the SPC lower than that of the TIP4P, i.e.,
kJ/mol and
kJ/mol, respectively. This causes the structure of the SPC at a high temperature of 350 K under an electric field to be stronger than that of the TIP4P. This suggests that other water models having higher dipole moments, such as TIP3P and TIP4P/2005, may have higher melting point within CNTs.