Next Article in Journal
Influence of Anionic Surfactant on Saturated Hydraulic Conductivity of Loamy Sand and Sandy Loam Soils
Previous Article in Journal
Nutrients and Phytoplankton in a Shallow, Hypereutrophic Urban Lake: Prospects for Restoration
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 9
Issue 6
10.3390/w9060432
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Two-Dimensional Dam-Break Flood Analysis in Data-Scarce Regions: The Case Study of Chipembe Dam, Mozambique

by
Manuel Álvarez
,
Jerónimo Puertas
,
Enrique Peña
and
María Bermúdez
*
Water and Environmental Engineering Group (GEAMA), Universidade da Coruña, A Coruña 15071, Spain
*
Author to whom correspondence should be addressed.
Water 2017, 9(6), 432; https://doi.org/10.3390/w9060432
Submission received: 15 February 2017 / Revised: 6 June 2017 / Accepted: 8 June 2017 / Published: 14 June 2017
Browse Figures
Versions Notes

Abstract

:
This paper presents the results of a modeling study of the hypothetical dam break of Chipembe dam in Mozambique. The modeling approach is based on the software Iber, a freely available dam break and two-dimensional finite volume shallow water model. The shuttle radar topography mission (SRTM) online digital elevation model (DEM) is used as main source of topographic data. Two different DEMs are considered as input for the hydraulic model: a DEM based on the original SRTM data and a hydrologically-conditioned DEM. A sensitivity analysis on the Manning roughness coefficient is performed. The results demonstrate the relevant impact of the DEM used on the predicted flood wave propagation, and a lower influence of the roughness value. The low cost modeling approach proposed in this paper can be an attractive option for modeling exceptional flood caused by dam break, when limited data and resources are available, as in the presented case. The resulting flood-inundation and hazard maps will enable the Regional Water Management Administration of Mozambique (ARA) to develop early warning systems.

1. Introduction

Dams play an essential role in meeting water supply demands from towns, agriculture, industry or power generation, as well as in managing flood events. However, they also pose a potential risk of failure, which can cause serious material damage and loss of life. Examples of well-known dam failures that caused fatalities are the 1923 collapse of Gleno dam in Italy [1]; the 1928 St. Francis dam disaster in California [2]; the 1959 collapse of Vega de Tera dam in Spain [3]; the 1976 Teton dam break in Idaho [4]; the 1982 Tous dam collapse in Spain [5]; and the 2004 Camará dam failure in Brazil [6]. In the African continent, the failure of the Virginia No. 15 tailing dam in South Africa in 1994 is worth noting [7]. A compilation of historical dam failure events, classified into flood severity categories, is provided by the U.S. Bureau of Reclamation [8].
Dam failure studies and flood inundation mapping are vital to establish emergency plans that enable competent authorities to provide a quick and effective response. Numerical flood models are generally used to assess the consequences of a potential failure and produce flood extent maps. They also provide information on flow depth, velocity and derived parameters such as flow force and intensity that can be used to assess potential damage to structures [9]. In practical applications, the modeling approaches involve using either one-dimensional (1-D) or two-dimensional (2-D) hydrodynamic models based on the unsteady open channel flow equations. The choice of model approach is driven mainly by the physical characteristics of the river channel and floodplain. One-dimensional models such as the US Army Corps of Engineers’ River Analysis System (HEC-RAS) or the US National Weather Service Flood Wave Dynamic Model (NWS-FLDWAV) have been widely used in dam breach modeling [10]. However, flows over extensive flat floodplains or around river confluences can be strongly two-dimensional, and the use of a one-dimensional approach may not be appropriate. Given the limitations of 1-D models and the increase of computational power in recent years, 2-D models that solve the shallow water equations have become a well-established choice [11]. Examples of models based on this approach and used in dam-break studies are MIKE software, FLO-2D, DSS-WISE, TELEMAC or the model Iber [12,13]. It should also be noted that newest release of HEC-RAS (Version 5.0, Hydrologic Engineering Center, US Army Corps of Engineers, Davis, CA, USA) includes two-dimensional unsteady flow modeling capabilities.
The provision of good topographic data is critical to the application of the aforementioned models [14,15,16,17]. In developed countries, elevation data are now routinely collected using LiDAR technology (Light detection and ranging), producing digital elevation models (DEMs) with high horizontal resolution (0.5 m is not uncommon) and a high degree of vertical accuracy (from 0.05 m to 0.2 m) [18,19]. These features make LIDAR DEMs a popular choice for modeling flood inundation [20,21]. However, developing countries often lack this accurate cartography due to budgetary constraints, in which case open access online digital elevation models can constitute a suitable alternative [22]. Within this category, two DEMs have been mainly applied in flood modeling studies: the Shuttle Radar Topography Mission (SRTM) DEM [23,24] and the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEM. In comparative studies, SRTM has emerged as the favored choice for a global source of terrain data for flood modeling due to its greater feature resolution, reduced number of artifacts and lower noise, particularly in the flatter areas of concern to flood modelers [25]. This DEM has a spatial resolution of around 30 m (SRTM-1s) and a vertical accuracy of ~10 m.
The new Dam Safety Regulation in Mozambique includes among its priorities the preparation of contingency plans for large dams considering dam-break and downstream impacts. According to the International Committee on Large Dams (ICOLD), 12 dams are classified as large dams in Mozambique. One of them is Chipembe dam, an embankment dam with a storage capacity of 25 hm3 built in the early 1970s. The dam is now in a state of abandonment and requires urgent rehabilitation. Moreover, it lacks an emergency plan that evaluates the consequences of a hypothetical dam failure and delineates potential flood areas downstream.
This paper presents the results of a numerical modeling study of the hypothetical dam break of Chipembe dam in Mozambique. It is part of the work of the research group GEAMA (Water and Environmental Engineering Group of the University of A Coruña, A Coruña, Spain) on cooperation projects related to water resources and institutional strengthening of the Regional Water Management Administration in Northern Mozambique (ARA-Norte) and the National Directorate of Water (Direcção Nacional de Águas, DNA). The DNA is responsible for policy making, planning and management of water resources in Mozambique. The strategic activities undertaken by DNA are implemented by the regional ARAs. GEAMA has been working in capacity building and identification of key projects in Africa for the last ten years, in collaboration with the responsible institutions in the water sector and other stakeholders (companies, NGOs) in Tanzania, Mali and Mozambique. The work presented in this paper arises from the participation of the group GEAMA in a EuropeAid project which aims to share best practice on flood modeling and support informed policy making on flood risk management in Mozambique.
A 2-D modeling approach was adopted for this study. The software Iber [26], a full two-dimensional shallow water model, was used to simulate the dam-break and the downstream impacts. The results presented in this paper include flood extent and hazard maps, as well as flood wave travel times along a 36 km reach downstream from the dam. The source of topographic data was the online SRTM-1s DEM and the only model parameter was the roughness coefficient. We analyzed how the quality of the SRTM topographic data may affect simulation results by performing a hydrologic reconditioning of the DEM, which enforces the river course into the SRTM data and removes the noise introduced by the riparian vegetation. A sensitivity analysis on the roughness coefficient was conducted, which allows the assessment of the uncertainty in this estimate and provides a range of peak flow and flood wave speed. Model results are compared with real-world dam failure data from Pierce et al. [27], with the aim of assessing whether peak discharge predictions are consistent with available observations. This database [27] comprises hydrologic and geometric variables from 87 dam break case studies and provides regression relations that predict peak discharge for breached embankment dams. The results can enable the Regional Water Administration of Mozambique (ARA-Norte) to develop an early warning system for the area, in collaboration with other related institutions such as the National Meteorological Institute or the National Institute for Disaster Management, engaging in multidisciplinary policy development. The study can also provide guidance in the limitations and application of freely available modeling tools and data to simulate the potential dam failure of other dams in data-scarce regions. As a further goal, the activities on capacity building of the ARA conducted in the framework of this study aim to contribute to the implementation of an effective national flood risk management system.

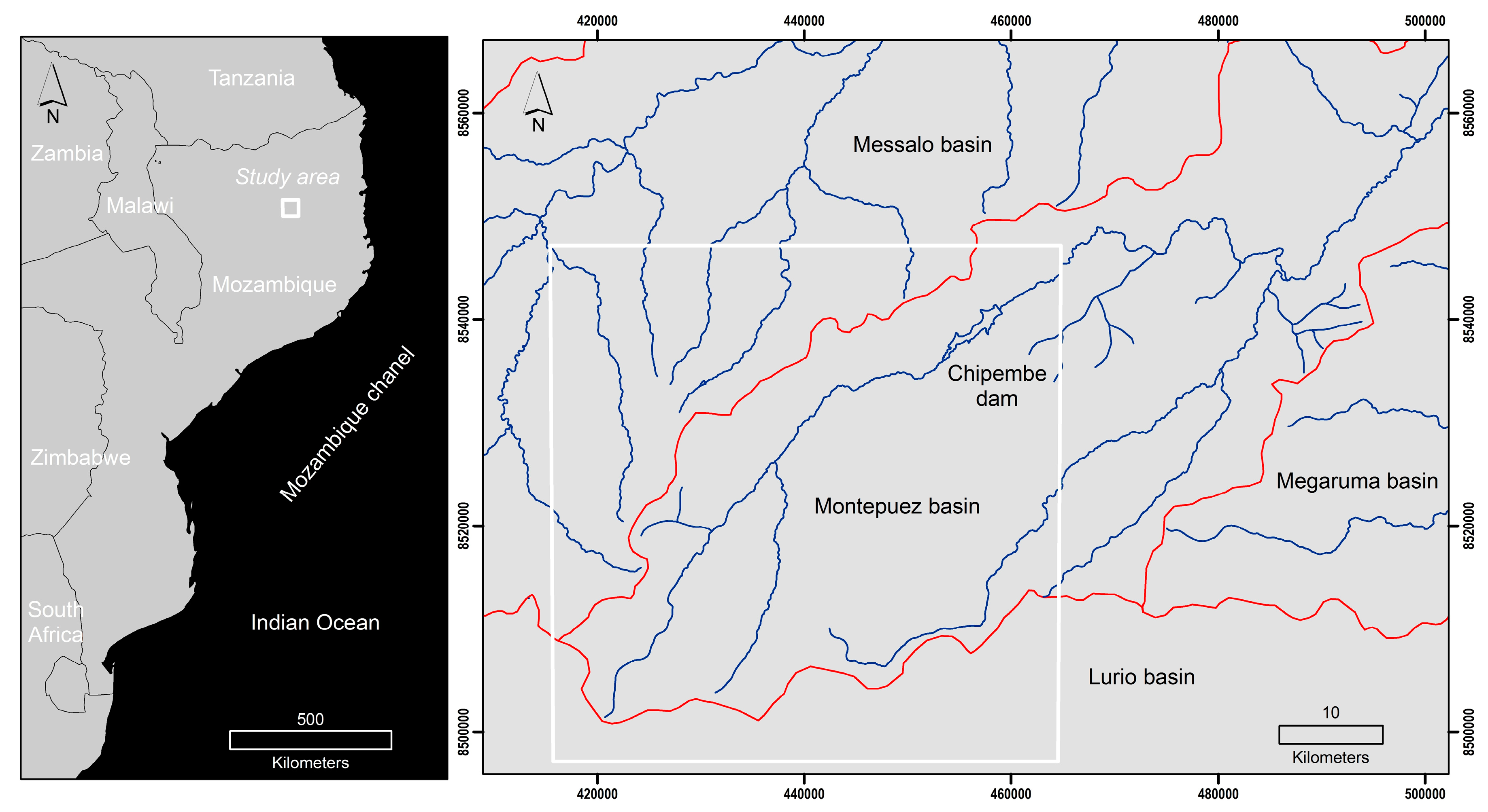
2. Study Site

Chipembe dam is located near Montepuéz city in the province of Cabo Delgado in northern Mozambique. The drainage area above the dam is 946 km2, which accounts for approximately 9.5% of the total drainage area of river Montepuéz (Figure 1). The average height of the basin is 561 m above sea level and the average slope, 1.8%. The mean annual runoff is in the order of 167 hm3 [28,29].
Chipembe dam is a 1220 m long embankment dam, with a maximum height of 12 m and a crest width of ~10 m. It is equipped with a lateral spillway for flood discharge and a water intake for an irrigation system that was never developed. The maximum normal water surface elevation in the reservoir is 503.6 m. Based on the reservoir storage curve, this water level corresponds to a reservoir gross storage of ~24.8 hm3 and a reservoir surface area of 7.1 km2. According to the dam rehabilitation study [30], the maximum safe inflow to the reservoir is 2450 m3/s and the maximum safe outflow is 1051 m3/s.
The dam was built in the 1970s and is now in a state of abandonment. This was verified during the field visit of the authors of this study and the technicians of ARA-Norte in 2013 [28]. The bottom outlet of the dam was found to be blocked and out of operation. Erosion damage was observed at the beginning of the spillway discharge channel. It was further noted that discharges through this spillway during flood events had significantly eroded the downstream face of the dam. At present, Mozambique’s National Directorate of Water (DNA) has launched a project involving an investment of about 50 million USD for the rehabilitation of Chipembe dam. The project will also include the exploitation of a potential irrigable area of around 2200 hectares, located downstream of the dam [30].

3. Materials and Methods

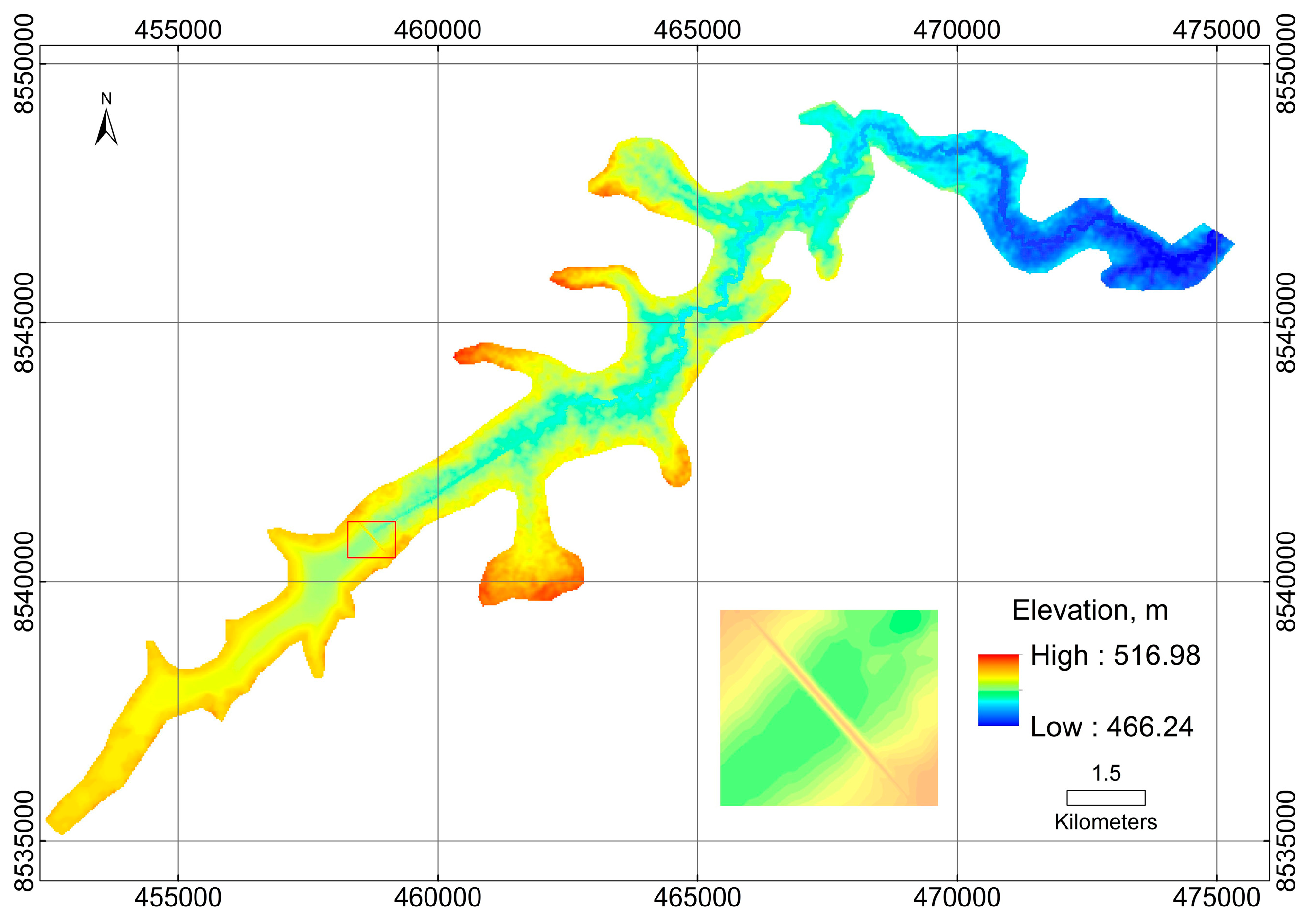
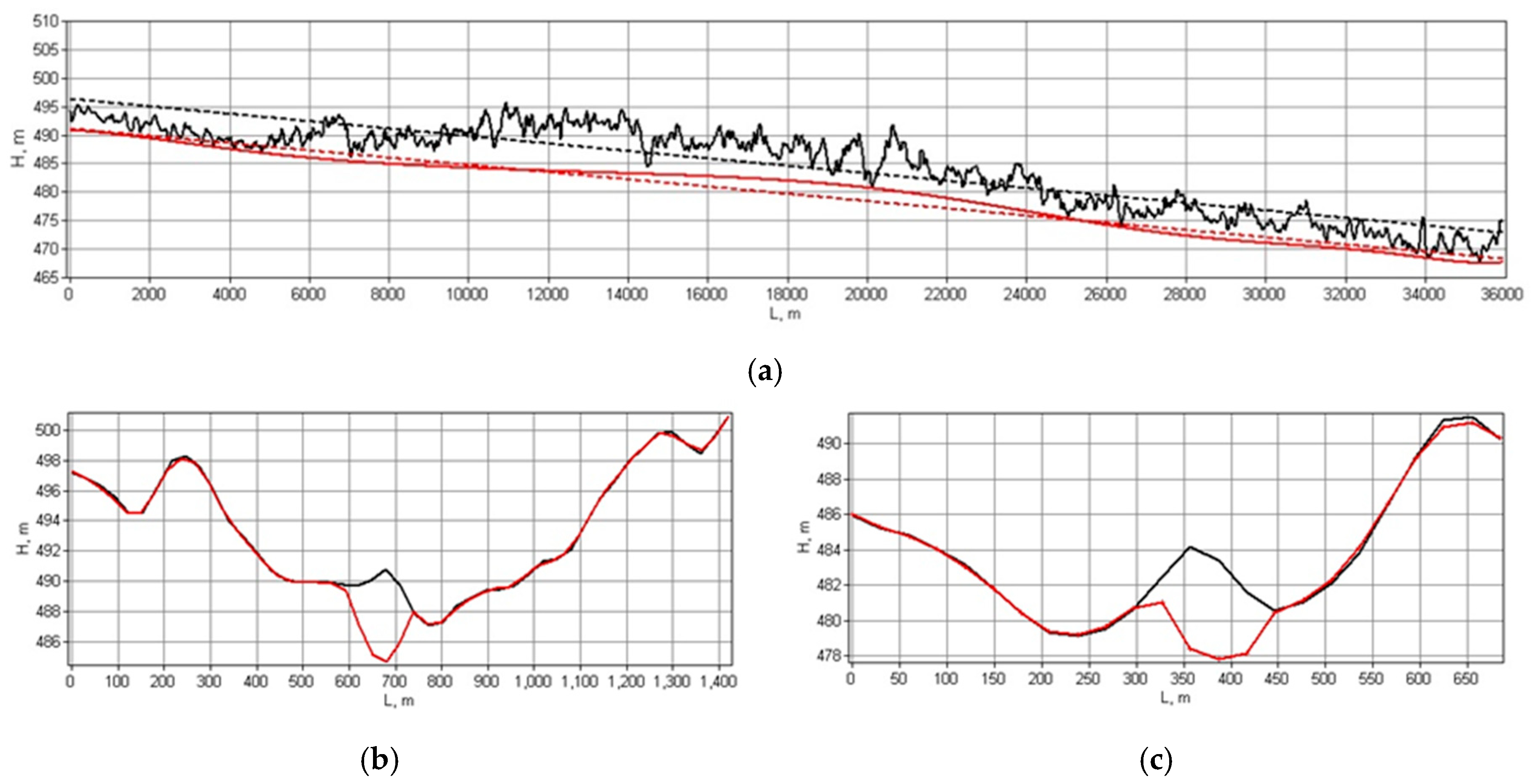
3.1. Cartographic Information

The source of topographic data for this study was the open access SRTM-1s DEM [31]. The SRTM elevations include terrain features (e.g., tree tops and buildings), so that this DEM is not a “bare-earth” digital terrain model (DTM) but a digital surface model (DSM). In this study, DEM refers to grid of elevation, so it is used as a generic term for DSMs and DTMs. SRTM-1s has a ground spatial resolution of 1 arc-seconds, which corresponds to about 30 m grid size at the equator. A correction process was applied to this void filled elevation data to incorporate the topography of the reservoir bed. Historical cartographic information, prior to the dam construction, was used to modify the DEM. It was verified that the storage capacity of the dam was reproduced accurately in the processed DEM. Sub-grid dam elevation data were extracted from the historical cartographic information to define the geometry of the dam. Figure 2 shows the topography of the selected model domain. The model domain includes the reservoir area and a 36 km reach downstream of the dam.
The validation of the SRTM data on continental scales [31] showed an absolute height error of 5.6 m for Africa. However, this vertical accuracy is strongly influenced by terrain relief, and smaller vertical errors can be expected in low altitude and low relief environments [32]. In this case study, the floodplain downstream of the dam has an average height of 491 m a.s.l. with an average slope of 3.2%, which suggests that the elevation errors may be lower than the continental error. A total of 20 ground control points located along both banks of the reservoir were used to assess the elevation errors of the SRTM dataset. These control points were obtained in a real-time kinematic global navigation satellite systems (RTK GNSS) survey. The comparison of the SRTM dataset to the measured elevations revealed an absolute error of 4.53 ± 1.25 m (mean ± standard deviation), which is slightly lower than the error estimated for Africa. These values should nevertheless be taken with caution given the limited number of control points and their distribution within the studied area.
The interferometric synthetic aperture radar signal on which the SRTM dataset is based only penetrates vegetation cover to a certain degree resulting in decreased vertical accuracy. This is especially true for forested areas, and becomes a problem in using these data to support hydraulic modeling, where accurate information on floodplain elevation is essential [33]. The vegetation cover in the floodplain downstream of Chipembe dam is minimal, as can be verified in the global canopy height dataset developed by Simard et al. [34]. The 1-km resolution canopy height raster map shows a value of zero throughout practically the whole of this area, which suggests that vegetation bias in the SRTM DEM might not a be significant issue in this case study. However, the aerial image of the study area (Figure 3) shows riparian vegetation along the reach, which is not reflected in the map of Simard et al. [34]. The presence of vegetation results in significant positive biases in the SRTM ground elevation around the river channel. Besides, given that the width of the river is around 10 m, the river bed topography is not accurately represented in the DEM. Consequently, the location of the thalweg derived from the aerial imagery is significantly different from the flow path derived from the original SRTM data (Figure 3), which might have an impact on the hydraulic model predictions.
A terrain reconditioning procedure was applied to enforce the river course into de SRTM data, following the thalweg derived from the aerial image, and to deepen the channel bed. The resulting digital elevation model is denoted in the following as DEM SRTMTR. The reconditioning process is based on the so-called stream burning procedure, which is used to correct surface drainage patterns derived from DEM [35,36]. The vector river network derived from the aerial image is assumed to be correct, and is converted into a raster river with the same spatial resolution as the DEM (~30 m). This raster river network is burnt into the un-conditioned SRTM DEM, so that the elevation values are artificially lowered at cells that are part of this raster drainage. The burning depth is variable along the longitudinal profile of the river, considering the envelope of the minimum elevations of the original SRTM, as shown in Figure 4a. The red line in Figure 4a is the new bed profile along the thalweg. The average burning depth was 4.8 m (standard deviation of 2.4 m) and the maximum burning depth was 11 m. It was verified that the average slope of the longitudinal profile of the river before and after the hydraulic conditioning process were very similar (0.00065 and 0.00063, respectively). The average slope is represented by a straight line (dotted lines in Figure 4a), which, when superposed on the longitudinal profile of the river, creates a balance between the total areas above and those below the straight line. The changes in a set of representative river cross sections are shown in Figure 4.
The original DEM SRTM and the DEM SRTMTR were used as input for the hydraulic model in this study. When channels are not resolved, as in the original DEM SRTM, models are likely to overestimate flood extent and underestimate flood speeds [22]. However, the value of the friction coefficient could potentially be adjusted in order to achieve more accurate predictions of water depths and velocities. As observed by Neal et al. [37], the loss of cross-sectional area for a given depth of flow can be partially compensated for by a reduction in friction, in the context of parameterizing the sub-grid scale topography of a floodplain. On the other hand, the suitability of a DEM for flood modeling also depends on flood frequency. Dam-break floods in which the channel is completely submerged may not require as fine a resolution DEM compared to studies with shallow flows [22]. The route of flood flow will not be dictated by the river channel, but more by the overall valley topography [38]. Based on the above, this study analyzes the differences in the hydraulic model predictions caused by the choice of DEM (DEM SRTM or DEM SRTMTR), combined with a sensitivity analysis on the roughness coefficient.

3.2. Hydraulic Model Description

The Iber model [26] was used to simulate the dam-break flood of Chipembe dam. It is a freely distributed numerical model for simulating turbulent free surface unsteady flow. It has been successfully used for a wide range of applications, including modeling of river flow and quality [39,40,41], geomorphic impacts of dam failure [12], sedimentation and flushing in reservoirs [42] or check dam hydraulics [43]. For a detailed description of model equations and numerical methods, the reader is referred to [26] and the references therein.
The model solves the 2-D shallow water equations, which assume negligible vertical variations of flow properties and hydrostatic pressure distribution. Models based on this approach are considered appropriate tools to simulate inundation depth and arrival time of dam-break flow [44,45]. These equations are solved with an unstructured finite volume solver explicit in time, which implements the scheme of Roe [46] for the discretization of the inertial terms and an upwind discretization of the bottom source term [47]. This Godunov type scheme is especially suitable for simulating dam-break flows, which often involve flow discontinuities and changes in flow regime. Several RANS type turbulence models are implemented in the model Iber [48]. In this case, the k-ε model from Rastogi and Rodi [49] was chosen.
Embankment dams like Chipembe dam usually fail by progressive erosion and breach parameters are generally obtained from regression equations based on dam and reservoir properties [50]. The simple data requirements of these formulations enable them to be applied when limited data are available, as in this study. The breach formation model implemented in Iber is based on the Guide for dam classification as a function of its potential risk [51]. It applies an empirical formula to estimate the breach characteristics, which has been derived from data of case studies. Breach growth is assumed to be a linear process and the breach shape is trapezoidal with 1H:1V side slopes. The final average width of the breach b (m) and the breach development time T (h) are calculated as follows:
b = 20 ⋅ ( V ⋅ h ) 0.25
T = 4.8 ⋅ V 0.5 h
where V is the storage volume (hm3) and h is the dam height (m). This model is in line with widely-used parametric breach formation models [52,53], which have uncertainties related to the poor documentation of historical failure events, the inherent variation in the erodibility of cohesive materials or the effects of variability of embankment design, among others. However, it is beyond the scope of this work to address the uncertainty in breach parameters and the estimations provided by the above model are thus treated as deterministic.
The hazard criteria implemented in the model Iber considers three different levels of flood hazard (high, medium and low) based on flow conditions [26]. In high hazard zones, one or several of the following hydrodynamic conditions are met: the depth of inundation exceeds 1 m, the velocity is higher than 1 m/s or the product of depth and velocity is greater than 0.5 m2/s. In low hazard areas, the depth is below 0.5 m, the velocity is lower than 0.5 m/s and the product of depth and velocity is below 0.25 m2/s. Between these two levels are the medium hazard conditions. These thresholds are based on the combinations of water depth and flow velocity that can represent danger to human life. They are consistent with the literature on human instability in flowing water [54]. The model incorporates an interface compatible with GIS environments, which allows the obtained flood hazard areas to be displayed directly in any GIS platform.

3.3. Model Setup

The model domain extends up to 36.0 km downstream from the dam. It was discretized into an unstructured computational mesh of approximately 22,000 triangular elements with a variable size (from 5 to 30 m) to ensure a correct definition of the dam geometry. A zero inflow condition was defined at the upstream boundary, whereas a critical flow condition was imposed at the downstream boundary. It was verified that results obtained with a critical outlet condition were very similar to the ones obtained with a subcritical outlet (with a weir of height 0 m, i.e., crest elevation = terrain elevation). Water level corresponding to full reservoir capacity (503.6 m above sea level) was set as initial condition in the reservoir. A dry bed (zero depth) was assumed as initial condition downstream of the dam. The breach was located in the central part of the dam, as illustrated in Figure 5. This model set-up corresponds to a “sunny-day” failure scenario, in which dam failure is solely due to structural causes and water storage conditions in the reservoir [13]. This dam failure scenario is thought to have the greatest potential to cause loss of life due to the surprise factor [55].
A Manning roughness coefficient between 0.03 m−1/3·s and 0.04 m−1/3·s was selected as reference value range or most likely range of values for both the channel and floodplain. This estimated value is based on the field observations and the analysis of the aerial photographs. The river channel has an earth bottom and is generally dry outside the wet season. The floodplain is covered by short grass and small crop areas scattered across the valley, for local community consumption. Open spaces with little or no vegetation are dominant.
As aforementioned, a sensitivity analysis on the roughness coefficient was conducted. Besides the difficulty in choosing a roughness value from the literature, the limitations derived from the spatial resolution of the DEM may also require an adjustment of the Manning’s value. Therefore, an ensemble of simulations with different values for the friction coefficient was run. A range of Manning’s between 0.02 and 0.06 m−1/3·s was examined.
Simulations were run until the hydrograph passes through the lower end of the reach. Depending on the DEM used and Manning’s value, simulations are run up to 25.5 h from breach initiation, with model results being stored every 800 s. A total of 9 control cross-sections were defined along the 36.0 km reach (Figure 4). Section S1 is located immediately downstream of the dam, whereas S9 is located at the end of the studied reach. The spacing between sections is not uniform and is determined by the nature of the watercourse. The average spacing is about 4.5 km (Table 1 and Table 2).

4. Results and Discussion

4.1. Peak Flows and Flood Wave Travel Times

An essential part of any dam failure analysis is the estimation of the hydrograph at the breach and its propagation downstream, in terms of peak flows and travel times. Table 1 and Table 2 list the peak flow of the flood wave (Qp), the time to peak (Tp) and the flood wave arrival time (Ta) at the downstream control sections, using the DEM SRTM (Scenario A) and the DEM SRTMTR (Scenario B), and considering different roughness coefficients in both scenarios. From the point of view of emergency plans and evacuation strategies, the flood wave arrival time (Ta) is more useful than the time to peak (Tp). Ta is the elapsed time between dam failure and initial wetting, thus allowing a margin of time to evacuate the population at risk.
Based on peak flow attenuation and wave travel speed, cross sections can be grouped into an upper reach (S1 to S4) and a lower reach (S5 to S9). In Scenario A, peak flows in the upper reach are within the range of 2748–1450 m3/s, depending on the roughness coefficient and the specific cross section. Further downstream (lower reach) the peak discharge is significantly lower, ranging from 546 m3/s to 66 m3/s. In Scenario B, peak flows in the upper reach are in the range of 2747–1606 m3/s, similar to the values obtained in Scenario A. The differences between the two scenarios become larger in the lower reach, where flows are in the range of 1376–740 m3/s in Scenario B. Peak discharges are up to ~10 times higher at the downstream section in Scenario B. Figure 6 shows the propagation of the flood wave along the reach in both scenarios, considering a roughness coefficient of n = 0.03 m−1/3·s. The attenuation of the peak flow magnitude can be clearly observed as the flood wave moves downstream. The percentages of peak flow attenuation in the upper reach are similar in both scenarios, ranging from 4% (section S2) to 36% (section S4). In the lower reach, attenuation percentages are between 83% (section S5) and 97% (section S9) in Scenario A, and between 56% (section S5) and 65% (section S9) in Scenario B. On average, attenuation decreases in Scenario B by 30 percentage points. A similar behavior of the flood wave is observed if other roughness values are used in the simulations.
Figure 7 shows the predicted water depth, velocity and specific discharge field in a 14 km reach between sections S6 and S8 at selected times with the two DEMs. In order to make them comparable, maps are plotted at the arrival time of the flood wave at section S8, which corresponds to t = 56,000 s in Scenario A and t = 18,000 s in Scenario B. The time mismatch between the two scenarios reflects the influence of the DEM used on the propagation of the flood wave. The differences between the maps calculated with the two DEMs can be clearly seen in Figure 7. The non-physical elevation variations present in the original DEM affect the prediction of flow direction, velocity and depth. The river channel is even dry in some areas, probably due to flow blockages caused by vegetation biases. Predictions for Scenario B are consistent with the configuration of the river channel shown in the aerial image.
Figure 8 shows the time to peak (Tp) and the flood wave arrival time (Ta) as a function of the distance from the dam (L) in Scenarios A and B and for different values of the roughness coefficient. In Scenario A, the peak of the flood hydrograph occurs in the first section (S1) about 2 h after the start of the dam failure, regardless the value of the friction coefficient. This is consistent with the breach development time calculated with Equation (2). Further downstream, in section S4, Ta and Tp values vary within a narrow range, between 2 h (n = 0.02 m−1/3·s) and 2.4 h (n = 0.06 m−1/3·s) and between 2.9 h (n = 0.02 m−1/3·s) and 3.6 h (n = 0.06 m−1/3·s), respectively. Similar results are obtained in Scenario B, being the travel times slightly lower (Table 1 and Table 2). Therefore, in this upper part of the reach, the flood wave travel times show little dependence on the roughness coefficient. Further downstream in Scenario A, the sensitivity of Ta and Tp to the value of the roughness coefficient increases progressively. As the peak flow reduces, bottom friction becomes more important. At the downstream end of the reach (section S9), Ta is between 16 h (n = 0.02 m−1/3·s) and 24 h (n = 0.06 m−1/3·s), that is to say, there is a time difference of 8 h due to the roughness coefficient. Tp ranges between 18.2 h (n = 0.02 m−1/3·s) and 27.8 h (n = 0.06 m−1/3·s). Differences between the two scenarios are larger in this lower reach. In Scenario B, Ta at the downstream section ranges from 5.6 h (n = 0.02 m−1/3·s) to 7.6 h (n = 0.06 m−1/3·s). Compared with Scenario A, these predictions are approximately 3 times lower. A similar decrease is observed for the time to peak values. This can be attributed to the unrealistic flow path derived from the original SRTM data, given the elevation biases in and around the river channel.
The flood wave velocity was calculated from the time to peak at cross-sections S1 and S9. It was estimated to be in the range between 0.62 m/s (n = 0.02 m−1/3·s) and 0.39 m/s (n = 0.06 m−1/3·s) in Scenario A. These values seem unrealistically low when compared with those of Scenario B (between 1.95 m/s and 1.28 m/s, respectively).

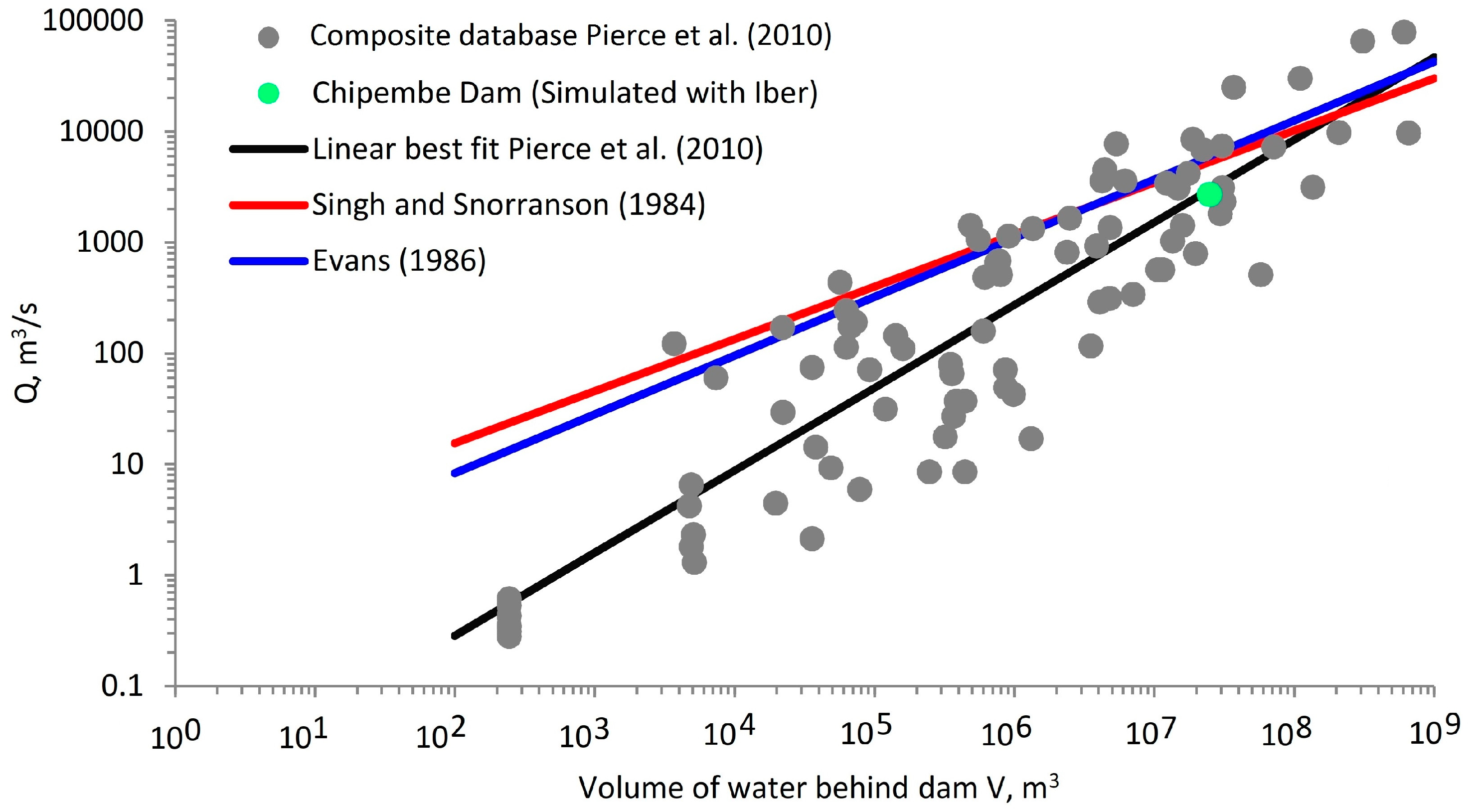
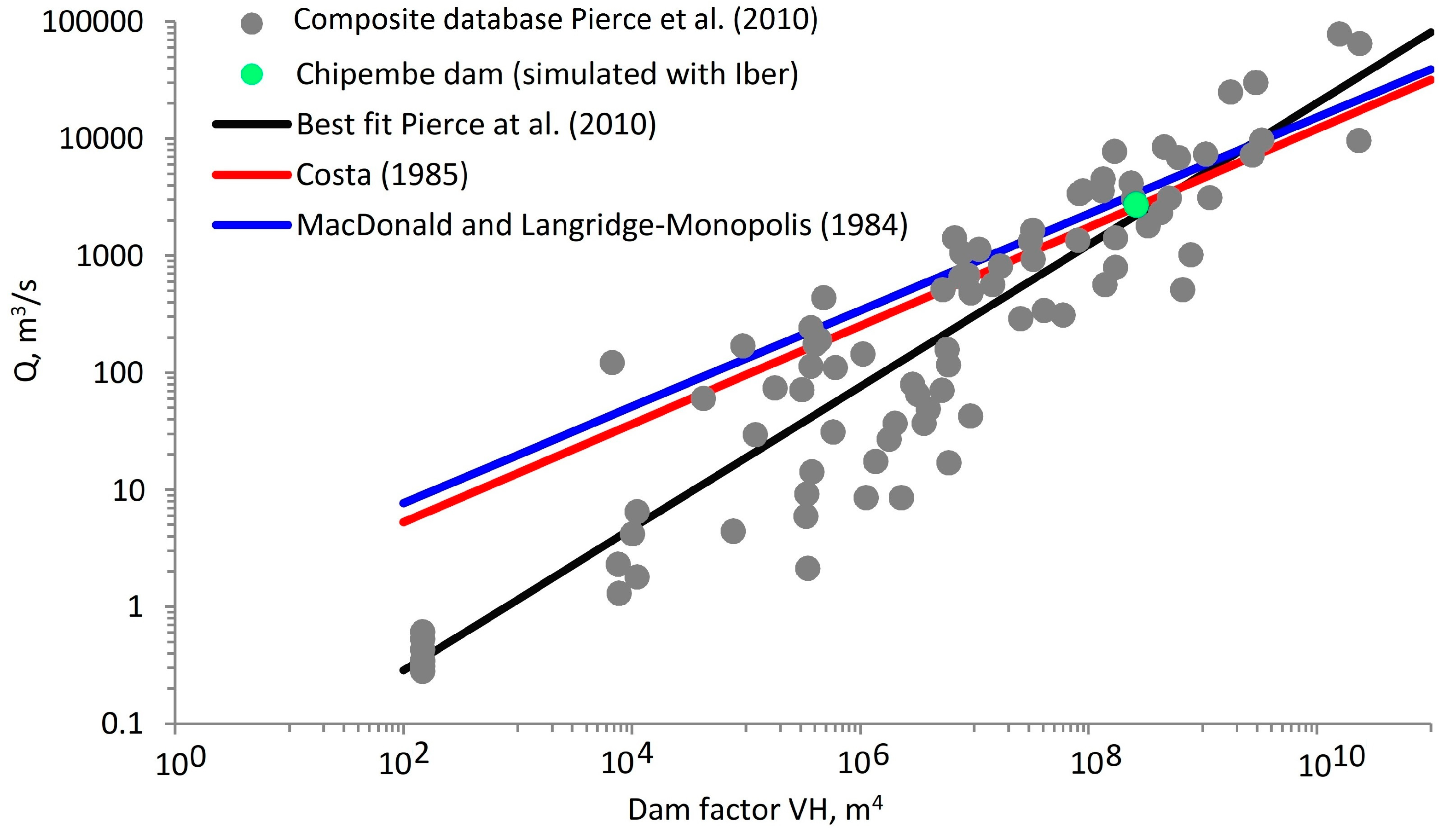
4.2. Comparison with Real Dam Failure Data

The predicted peak outflow rate was compared with real dam failure data from Pierce et al. [27]. Figure 9 shows the best-fit equation between the peak outflow and the volume of water behind the dam obtained by Pierce et al. [27], the expressions of Evans [56] and Singh and Snorrason [57], and the results for Chipembe dam. The last corresponds to the peak flow predicted by the model Iber for n = 0.04 m−1/3·s (2674 m3/s in section S1), although very similar values were obtained for the tested range of Manning coefficients, as can be seen in Table 1. A peak flow of 2966 m3/s is obtained for Chipembe dam with the aforementioned equation of Pierce et al. [27], which has a coefficient of determination R2 of 0.805. This represents around a 10% difference in peak flow with model predictions. The expressions of Singh and Snorrason [57] and Evans [56], which were developed with a more limited case-study data, are more conservative. Using these expressions, a peak flow of 5307 and 5975 m3/s is obtained, respectively.
Pierce et al. [27] also obtained a satisfactory linear relationship (R2 = 0.844) between the peak outflow and the dam factor; the latter defined as the product of the height (H) and the volume of water behind the dam (V). This relationship is plotted in Figure 10, together with the expressions given by MacDonald and Landgridge-Monopolis [58] and Costa [59]. The peak flow predicted by the Iber model for Chipembe dam fits reasonably well with the three historic regression relations. Given the dam factor of Chipembe dam (2.63 × 108 m4), the peak outflow using Pierce et al. [27] equation is 2228 m3, which represents a decrease of 20% in comparison with the numerical model predictions. The expression of Costa [59] results in a peak outflow of 2653 m3/s, whereas a more conservative value of 3397 m3/s is obtained with the equation of MacDonald and Langridge-Monopolis [58]. Peak discharge predictions are consistent with the observations reported in Pierce et al. [27], which are plotted in Figure 9 and Figure 10.

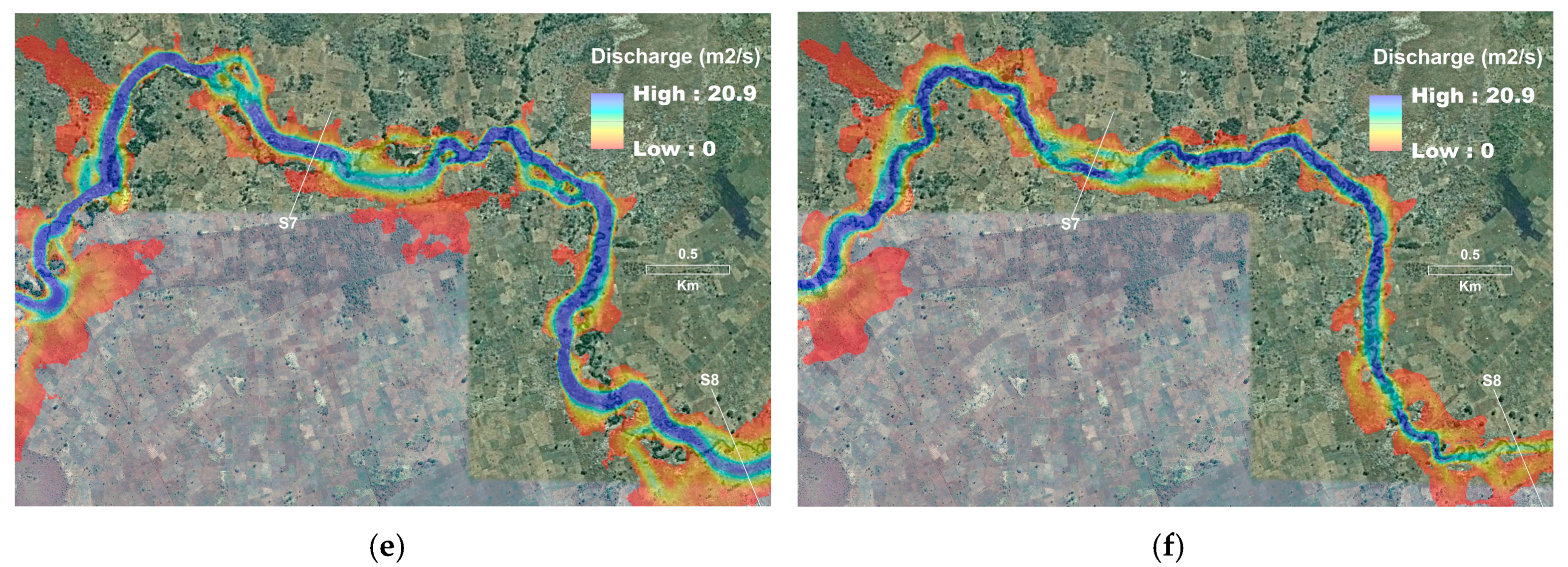
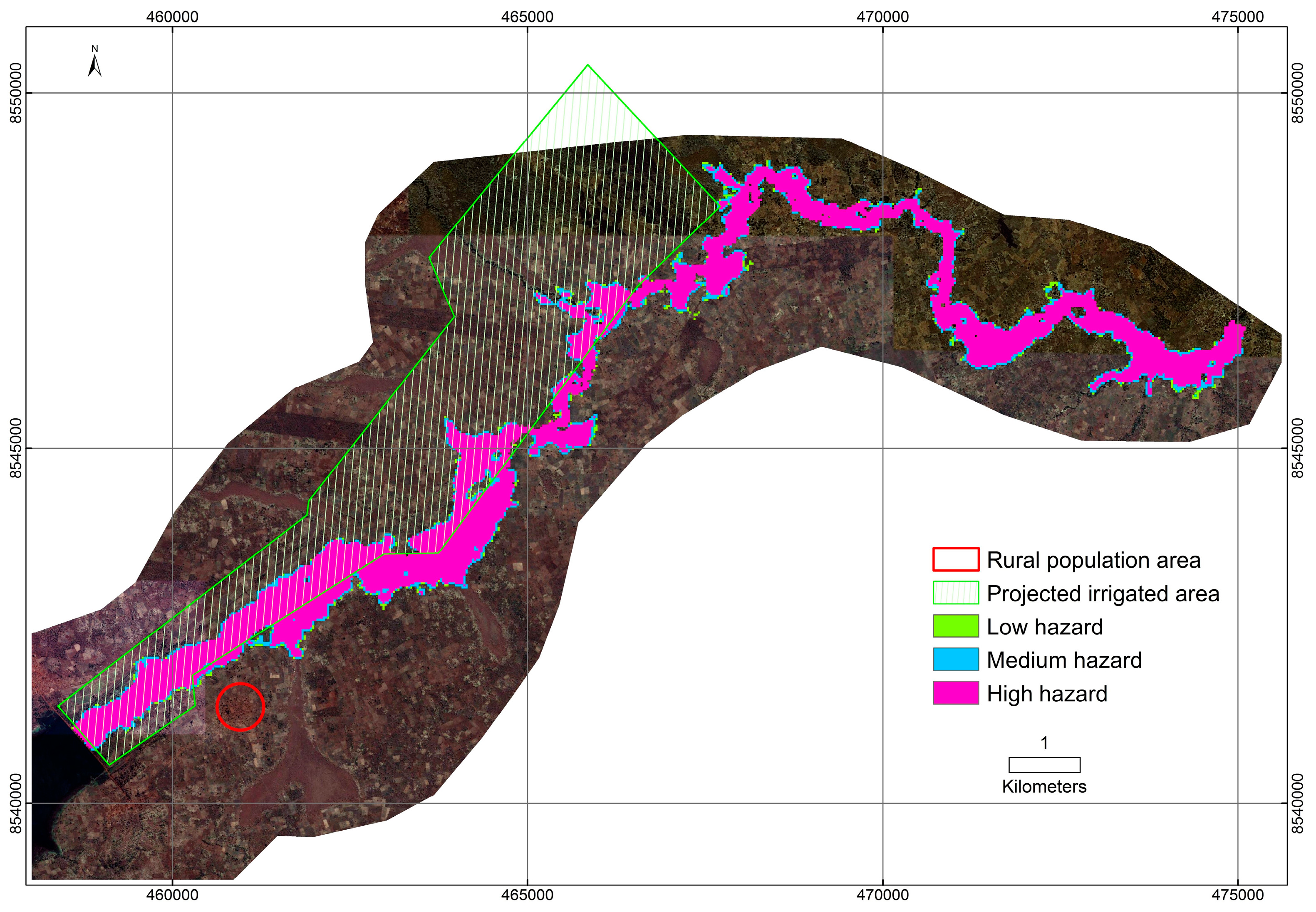
4.3. Flood Extent Delineation

The extent of flooding is basic information for emergency planners. Table 3 compares the computed flooded areas in Scenarios A and B using different roughness coefficients. The average flood width shown in Table 3 is the ratio of the flooded area to the main channel length. The average flood depth is the spatial average of the maximum depth calculated during the flood. In both scenarios, as the roughness increases, so does the flood extent. However, in Scenario A its influence is very limited, the differences in total area being below 2%. The same applies to the average flood width, which increases from 368 m for n = 0.02 m−1/3·s to 373 m for n = 0.06 m−1/3·s. The differences in maximum depth are below 0.04 m. In Scenario B, the influence of the roughness coefficient is larger, with differences in flood extent and average flood width of around 5% and differences in maximum depth of 0.10 m, for the range of Manning’s tested.
The use of the hydrologically-conditioned DEM results in lower flood extent and flood width (~19%), and higher average flood depth (~9%) when compared with the predictions obtained with the original DEM SRTM (Table 3). This is consistent with the observations of Sanders [22] or Yan et al. [60] regarding the use of higher resolution DEMs instead of the SRTM DEM. SRTM topography has been found to yield larger flood inundation extent compared with high precision topography, due to the poorer representation of the small channels. However, this may not always be the case, depending on site specific topography and local uncertainties in the SRTM DEM. Specifically, the positive bias of the SRTM elevation data in heavy vegetated floodplains can lead to underestimation of inundation extent [32]. In this case, the study area is a single channel river system with little vegetation in the floodplain, as was verified during the field visit. Given these characteristics, the flood extent predictions obtained in this work in Scenario A may be considered as conservative. The use of a higher Manning in this case, even if it has a limited influence, will tend toward more conservative results.
The sensitivity analysis on the roughness coefficient proposed in this paper is of course not intended to replace the use of more accurate DEMs, and should be understood in the context of limited data availability. Previous studies that have evaluated different DEM products (different sources and resolutions) for flood modeling have also observed minor differences in flood extent and more relevant differences in terms of travel times in some cases (e.g., St. Francis dam-break flood test case modeled by Sanders [22]). Following this strategy, the worst-case predictions in the flood analysis (larger flood extent and shorter travel times) correspond to: (a) flood extent calculated with the higher range of Manning’s values (n = 0.05–0.06); and (b) travel times calculated with the lower range of Manning’s values (n = 0.02–0.03). The results show that the use of the DEM SRTM combined with a low Manning’s value is insufficient to match the flood wave travel times obtained with the DEM SRTMTR. This confirms the important influence of the topography on the hydraulic model predictions. If only open access online digital elevation models are available, as in the present case, it is suggested to analyze and pre-process the DEM to improve its accuracy and to ensure that it is hydrologically consistent. A sensitivity analysis of the flood model on the Manning’s value can be performed, and the worst-case predictions of flood extent and travel times can be used to support flood management and emergency response planning.

4.4. Flood Hazard Mapping

A rural settlement of around 200 houses is located at the right bank of the river, approximately 1.9 km downstream of the dam. In addition, an irrigation project, covering about 2200 hectares [30], is planned for this area. In terms of exposure to flooding, these are the main people and property at risk within this area, which should be taken into account when assessing dam-break impacts.
A hazard-map was derived from the inundation depth and velocity distributions. In each cell of the mesh, the level of hazard was determined according to the criteria explained in the model description section. Following this criteria, in Scenario A 79.8% of the flooded area (~13.34 × 106 m2) is classified as high hazard zone, 15.4% as medium hazard and 4.8% as low hazard, considering n = 0.04 m−1/3·s (Figure 11). Very similar hazard distributions were obtained for the range of roughness values tested. An increase in the Manning coefficient results in a smaller high hazard zone and a larger medium and low hazard zones. In Scenario B, 84.2% of the flooded area is classified as high hazard zone, which represents a percentage increase from Scenario A. However, in absolute terms, the area classified as high hazard is smaller in Scenario B.
Approximately 21% of the planned irrigation area falls under the high hazard zone. Therefore, flooding could damage this infrastructure and lead to important material and economic losses. Besides, it could constitute a potential risk to the people working in this area, particularly in the upper 5–6 km reach. Nonetheless, average flood wave arrival time increases from 1 h in section S2 (L = 2.5 km) up to 2.2 h in section S4 (L = 8.3 km) in Scenario A, and from 0.9 h to 1.8 h in Scenario B, which allows some time to implement evacuation plans.
Figure 11 shows the perimeter of the rural settlement at the right bank of Montepuéz river. It can be seen that there is a 280 m margin from the boundaries of the flooded areas. According to the DEM, the settlement is at an altitude of 502 m. At the closest cross-section, the water level reached values between 495 m and 496 m at the peak of the flood, which occurred 2 h after the initiation of the breach. This height is significantly below that of the settlement. Therefore, the settlement is located in a no hazard area under the sunny dam-break scenario.

4.5. Model Applicability

The methodology and analysis presented in this paper constitute a best practice case study on risk identification, supported by sophisticated prediction models of dam failure and subsequent flooding. The models have been carefully chosen to ensure that they are applicable under the specific circumstances of the region, such as data availability, physical characteristics of the river systems and previous academic and professional experience of the local technicians. The model Iber is freely available and incorporates an interface to facilitate the setting-up, running and output visualization. The model interface is compatible with GIS environments, so flood hazard areas are incorporated into a GIS-based tool, in which a variety of other geospatial information can be integrated: water infrastructures, water monitoring network, types of land-use, etc. The computational efficiency was also a relevant criterion used to choose the model. In this case, the computation time required for each run is in the order of 6 h on standard computing hardware. Given the limited number of simulations to be performed, it is considered adequate. However, it could be reduced with the aid of high-performance computing for other applications beyond the present case.
The same methodology can be applied and similar results can be expected if other two-dimensional hydrodynamic models, based on the depth-averaged shallow water equations and finite volume methods, are used instead of the model Iber. Several software packages of this nature are mentioned in the introduction section. However, dam-break flows usually involve shockwaves and subcritical, supercritical and transcritical flows. Therefore, the performance of the numerical schemes used to solve the model equations are also worthy of attention. The Godunov type numerical scheme implemented in the model Iber is known to deal well with such complex, mixed flow regimes.

5. Conclusions

This study analyzes the consequences of a potential failure of Chipembe dam (Mozambique) on the 36 km downstream reach. The two-dimensional hydrodynamic model Iber was used to simulate dam failure and propagation of the flood wave for a sunny day scenario. Two different DEMs were considered as input for the hydraulic model: a DEM based on the original SRTM-1s data and a hydrologically-conditioned DEM, in which a stream burning procedure was applied. The differences in the hydraulic model predictions caused by the choice of DEMs were analyzed. A sensitivity analysis on the Manning roughness coefficient was performed, considering values between n = 0.02 and n = 0.06 m−1/3·s.
The results demonstrate the relevant influence of the DEM used on the predicted flood wave propagation and the lower influence of the roughness value. The use of the hydrologically-conditioned DEM, instead of the original SRTM data, results in:
(a)
Higher peak discharges, up to ~10 times at the downstream section;
(b)
Lower peak flow attenuation, from ~90% to ~60% in the lower reach;
(c)
Lower time to peak and flood wave arrival time, reaching a 65% reduction at the downstream section;
(d)
Lower flood extent and flood width (~19%), and higher average flood depth (~9%).
Flood extent and average flood depth are not significantly affected by the choice of Manning’s value. Differences are below 5% and 7%, respectively, with the hydrologically-conditioned DEM, and below 1% and 4% with the original SRTM DEM, for the range of n tested.
The flood inundation and flood hazard maps obtained have uncertainties associated with the accuracy of the DEM, the technical data of the dam and reservoir, and the hydraulic modeling approach. Nevertheless, they can serve as a basis to develop the emergency response plan for the area and show the possibilities for extending the methodology to other dams in Mozambique. The case study exemplifies the importance of a correct representation of the main channel geometry in the DEM. The noise introduced by the riparian vegetation in the SRTM data resulted in a significant underestimation of flood travel times. The low cost modeling approach proposed in this paper is an attractive option for modeling exceptional flood caused by dam break, when limited data and resources are available, as in the presented case.

Acknowledgments

The authors thank the financial support provided by Xunta de Galicia (GRC2014/041). They would like to acknowledge the European Union and the Spanish Regional Government of Galicia (Galician Cooperation Agency and Augas de Galicia) for funding the projects EUROPEAID/129-510/C/ACT/ACPTPS/10EDF_ACP-EU and COOPERACION GALEGA PR815A-2014-11. The EuropeAid project involves the Regional Water Management Administration in Northern Mozambique (ARA-Norte), the National Directorate of Water in Mozambique (Direcção Nacional de Águas, DNA- http://www.dnaguas.gov.mz), the Polytechnic University of Catalonia, the University of A Coruña and the consultancy Amphos21. María Bermúdez gratefully acknowledges financial support from the Spanish Regional Government of Galicia (Postdoctoral grant reference ED481B 2014/156-0). The authors would also like to thank the assistance provided by Carlos Jopela, the director the ARA-Norte, and the technical staff of this institution. The authors are grateful to the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper. The product SRTM-1s for the study area was retrieved from the USGS website: http://earthexplorer.usgs.gov/, courtesy of the NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota.

Author Contributions

The study was designed by Manuel Álvarez, Jerónimo Puertas, Enrique Peña and María Bermúdez. Manuel Álvarez conducted the model setup and performed the simulations. Manuel Álvarez and María Bermúdez performed the data analysis and wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

References

  1. Pilotti, M.; Maranzoni, M.; Tomirotti, M.; Valerio, G. 1923 Gleno dam break: Case study and numerical modeling. J. Hydraul. Eng. 2011, 137, 480–492. [Google Scholar] [CrossRef]
  2. Rogers, D.J. Lessons learned from the St. Francis Dam failure. Geo-Strata 2006, 6, 14–17. [Google Scholar]
  3. Jansen, R.B. Dam and Public Safety; US Department of the Interior, Water and Power Resources Service: Denver, CO, USA, 1980. [Google Scholar]
  4. Arthur, H.G. Teton Dam failure. The Evaluation of Dam Safety. In Proceedings of the Engineering Foundation Conference Proceedings, Pacific Grove, CA, USA, 28 November–3 December 1976; American Society of Civil Engineers: New York, NY, USA, 1977; pp. 61–71. [Google Scholar]
  5. Alcrudo, F.; Mulet, J. Description of the Tous Dam break case study (Spain). J. Hydraul. Res. 2007, 45, 45–57. [Google Scholar] [CrossRef]
  6. Menescal, R.A.; Vieira, V.P.; Oliveira, S.K. Terminologia para análise de risco e segurança de barragens. In A Segurança de Barragens E a Gestão de Recursos Hídricos; Menescal, R.A., Ed.; Ministério da Integração Nacional: Brasília, Brazil, 2005; pp. 31–39. (In Portuguese) [Google Scholar]
  7. Saxena, K.R.; Sharma, V.M. DAMS Incidents and Accidents; A.A. Balkema Publishers: Amsterdam, The Netherlands, 2005. [Google Scholar]
  8. U.S. Department of Interior Bureau of Reclamation (USBR). RCEM—Reclamation Consequence Estimating Methodology. Dam Failure and Flood Event Case History Compilation; U.S. Department of Interior Bureau of Reclamation: Washington, DC, USA, 2015.
  9. Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Structural damage prediction in a high-velocity urban dam-break flood: A field-scale assessment of predictive skill. J. Eng. Mech.-ASCE 2012, 138, 1249–1262. [Google Scholar] [CrossRef]
  10. Gee, D.M.; Brunner, G.W. Dam break flood routing using HEC-RAS and NWS-FLDWAV. In Impacts of Global Climate Change, Proceedings of the World Water and Environmental Resources Congress 2005, Anchorage, AK, USA, 15–19 May 2005; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1–9. [Google Scholar] [CrossRef]
  11. Néelz, S.; Pender, G. Benchmarking the Latest Generation of 2D Hydraulic Modelling Packages; Report No. SC120002; Environment Agency: Bristol, UK, 2013. [Google Scholar]
  12. Soares-Frazão, S.; Canelas, R.; Cao, Z.; Cea, L.; Chaudhry, H.M.; Die Moran, A.; Kadi, K.E.; Ferreira, R.; Cadórniga, I.F.; Gonzalez-Ramirez, N.; et al. Dam-break flows over mobile beds: Experiments and benchmark tests for numerical models. J. Hydraul. Res. 2012, 50, 364–375. [Google Scholar] [CrossRef]
  13. Federal Emergency Management Agency. Federal Guidelines for Inundation Mapping of Flood Risks Associated with Dam Incidents and Failures; Federal Emergency Management Agency P-946; Federal Emergency Management Agency: Washington, DC, USA, 2013. [Google Scholar]
  14. Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Two-dimensional, high-resolution modeling of urban dam-break flooding: A case study of Baldwin Hills, California. Adv. Water Resour. 2009, 32, 1323–1335. [Google Scholar] [CrossRef]
  15. Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
  16. Legleiter, C.J.; Roberts, D.A. A forward image model for passive optical remote sensing of river bathymetry. Remote Sens. Environ. 2009, 113, 1025–1045. [Google Scholar] [CrossRef]
  17. Trigg, M.A.; Wilson, M.D.; Bates, P.D.; Horrit, M.S.; Alsdorf, D.E.; Forsberg, B.R.; Vega, M.C. Amazon flood wave hydraulics. J. Hydrol. 2009, 374, 92–105. [Google Scholar] [CrossRef]
  18. Hodgson, M.E.; Jensen, J.R.; Schmidt, L.; Schill, S.; Davis, B. An evaluation of LIDAR- and IFSAR-derived digital elevation models in leaf-on conditions with USGS Level 1 and Level 2 DEMs. Remote Sens. Environ. 2003, 84, 295–308. [Google Scholar] [CrossRef]
  19. Smith, M.J.; Edwards, E.P.; Priestnall, G.; Bates, P.D. Exploitation of New Data Types to Create Digital Surface Models for flood Inundation Modeling; FRMRC Research Report UR3; FRMRC: University of Manchester, Manchester, UK, 2006. [Google Scholar]
  20. Bates, P.D.; Marks, K.J.; Horritt, M.S. Optimal use of high-resolution topographic data in flood inundation models. Hydrol. Process. 2003, 17, 537–557. [Google Scholar] [CrossRef]
  21. Cobby, D.M.; Mason, D.C.; Horritt, M.S.; Bates, P.D. Two-dimensional hydraulic flood modelling using a finite-element mesh decomposed according to vegetation and topographic features derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1979–2000. [Google Scholar] [CrossRef]
  22. Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
  23. Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
  24. Van Zyl, J.J. The shuttle radar topography mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001, 48, 559–565. [Google Scholar] [CrossRef]
  25. Sampson, C.C.; Smith, A.; Bates, P.D.; Neal, J.C.; Trigg, M.A. Perspectives on open access high resolution digital elevation models to produce global flood hazard layers. Front. Earth Sci. 2016, 3, 1–6. [Google Scholar] [CrossRef]
  26. Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Iber—River modelling simulation tool. Rev. Int. Métodos Numér. Para Cálc. Diseño Ing. 2014, 30, 1–10. (In Spanish) [Google Scholar] [CrossRef]
  27. Pierce, M.W.; Thornton, C.I.; Abt, S.R. Predicting peak outflow from breached embankment dams. J. Hydraul. Eng. 2010, 15, 338–349. [Google Scholar] [CrossRef]
  28. Universidade da Coruña. Manual Técnico de Planificação e Gestão de Infraestructuras Hidráulicas das Bacias Internas de Cabo Delgado; Technical Manual for Planning and Management of Hydraulic Infrastructures in the Interior Catchments of Cabo Delgado; Internal Report; Universidade da Coruña: A Coruña, España, 2014. (In Portuguese) [Google Scholar]
  29. Jones, A.; Breuning-Madsen, H.; Brossard, M.; Dampha, A.; Deckers, J.; Dewitte, O.; Gallali, T.; Hallett, S.; Jones, R.; Kilasara, M.; et al. Soil Atlas of Africa; European Commission, Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
  30. EIA—Avaliação de Impacto Ambiental. Reabilitação da Barragem de Chipembe: Instrução do Processo; Estudo do Impacto Sócio—Ambiental: Pemba, Mozambique, 2013. (In Portuguese) [Google Scholar]
  31. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–43. [Google Scholar] [CrossRef]
  32. Yan, K.; Di Baldassarre, G.; Solomatine, D.P.; Schumann, G.J.P. A review of low-cost space-borne data for flood modelling: Topography, flood extent and water level. Hydrol. Process. 2015, 29, 3368–3387. [Google Scholar] [CrossRef]
  33. Kreiselmeier, J. Development of a Flood Model Based on Globally-Available Satellite Data for the Papaloapan River, Mexico, 2015. (Dissertation). Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-256399 (accessed on 9 June 2017).
  34. Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116, G04021. [Google Scholar] [CrossRef]
  35. Callow, J.N.; van Niel, K.P.; Boggs, G.S. How does modifying a DEM to reflect known hydrology affect subsequent terrain analysis. J. Hydrol. 2007, 332, 30–39. [Google Scholar] [CrossRef]
  36. Lindsay, J. The practice of DEM stream burning revisited. Earth Surf. Process. Landf. 2016, 41, 658–668. [Google Scholar] [CrossRef]
  37. Neal, J.C.; Odoni, N.A.; Trigg, M.A.; Freer, J.E.; Garcia-Pintado, J.; Mason, D.C.; Wood, M.; Bates, P.D. Efficient incorporation of channel cross-section geometry uncertainty into regional and global scale flood inundation models. J. Hydrol. 2015, 529, 169–183. [Google Scholar] [CrossRef]
  38. Morris, M.W. Concerted Action on Dambreak Modelling—CADAM; Final Report SR 571; HR Wallingford Ltd.: Wallingford, UK, 2000. [Google Scholar]
  39. Bladé, E.; Cea, L.; Corestein, C. Modelización numérica de inundaciones fluviales. Ing. Agua 2014, 18, 71–81. [Google Scholar] [CrossRef]
  40. Cea, L.; Bermudez, M.; Puertas, J.; Blade, E.; Corestein, G.; Escolano, E.; Conde, A.; Bockelmann-Evans, B.; Ahmadian, R. IberWQ: New simulation tool for 2D water quality modelling in rivers and shallow estuaries. J. Hydroinform. 2016, 18, 816–830. [Google Scholar] [CrossRef]
  41. González-Aguirre, J.; Vázquez-Cendón, M.E.; Alavez-Ramírez, J. Simulación numérica de inundaciones en Villahermosa México usando el código Iber (Flood modelling in Villahermosa Mexico with the model Iber). Ing. Agua 2016, 20, 201–218. [Google Scholar] [CrossRef]
  42. Castillo, L.; Carrillo, J.; Álvarez, M. Complementary Methods for Determining the Sedimentation and Flushing in a Reservoir. J. Hydraul. Eng. 2015, 141, 5015004. [Google Scholar] [CrossRef]
  43. Castillo, C.; Pérez, R.; Gómez, J. A conceptual model of check dam hydraulics for gully control: Efficiency, optimal spacing and relation with step-pools. Hydrol. Earth Syst. Sci. 2014, 18, 1705–1721. [Google Scholar] [CrossRef]
  44. Cannata, M.; Marzocchi, R. Two-dimensional dam break flooding simulation: A GIS-embedded approach. Nat. Hazards 2012, 61, 1143–1159. [Google Scholar] [CrossRef]
  45. Wang, L.; Liang, Q.; Kesserwani, G.; Hall, J. A 2D shallow flow model for practical dam-break simulations. J. Hydraul. Res. 2011, 49, 307–316. [Google Scholar] [CrossRef]
  46. Roe, P.L. Discrete models for the numerical analysis of time-dependent multi-dimensional gas dynamics. J. Comput. Phys. 1986, 63, 458–476. [Google Scholar] [CrossRef]
  47. Bermúdez, A.; Dervieux, A.; Desideri, J.A.; Vázquez, M.E. Upwind schemes for the two-dimensional shallow water equations with variable depth using unstructured meshes. Comput. Methods Appl. Mech. Eng. 1998, 155, 49–72. [Google Scholar] [CrossRef]
  48. Cea, L.; Puertas, J.; Vázquez-Cendón, M.E. Depth averaged modelling of turbulent shallow water flow with wet-dry fronts. Arch. Comput. Methods Eng. State Art Rev. 2007, 3, 303–341. [Google Scholar] [CrossRef]
  49. Rastogi, A.K.; Rodi, W. Predictions of heat and mass transfer in open channels. J. Hydraul. Div. 1978, 104, 397–420. [Google Scholar]
  50. Wahl, T.L.; Hanson, G.J.; Courivaud, J.; Morris, M.W.; Kahawita, R.; McClenathan, J.T.; Gee, D.M. Development of next-generation embankment dam breach models. In Proceedings of the US Society of Dams Annual Meeting and Conference 2008, Portland, OR, USA, 28 April–2 May 2008. [Google Scholar]
  51. Ministerio del Medio Ambiente. Clasificación de Presas en Función del Riesgo Potencial (Guidelines for Dam Classification According to their Potential Risk of Failure); Dirección General de Obras Hidráulicas y Calidad de las Aguas: Madrid, Spain, 1996; p. 64. (In Spanish)
  52. Wahl, T.L. Uncertainty of predictions of embankment dam breach parameters. J. Hydraul. Eng. 2004, 130, 389–397. [Google Scholar] [CrossRef]
  53. Wu, W.; Altinakar, M.S.; Bradford, S.F.; Chen, Q.J.; Constantinescu, S.G.; Duan, J.G.; Gee, D.M.; Greimann, B.; Hanson, G.; Zhiguo, H.; et al. Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar] [CrossRef]
  54. Jonkman, S.N.; Vrijling, J.K.; Vrouwenvelder, A.C.W.M. Methods for the estimation of loss of life due to floods: A literature review and a proposal for a new method. Nat. Hazards 2008, 46, 353–389. [Google Scholar] [CrossRef]
  55. International Committee on Large Dams (ICOLD). Small Dams Design, Surveillance and Rehabilitation; International Committee on Large Dams: Paris, France, 2011; p. 159. [Google Scholar]
  56. Evans, S.G. The maximum discharge of outburst floods caused by the breaching of man-made and natural dams. Can. Geotech. J. 1986, 23, 385–387. [Google Scholar] [CrossRef]
  57. Singh, K.P.; Snorrason, A. Sensitivity of outflow peaks and flood stages to the selection of dam breach parameters and simulation models. J. Hydrol. 1984, 68, 295–310. [Google Scholar] [CrossRef]
  58. MacDonald, T.; Langridge-Monopolis, J. Breaching charateristics of dam failures. J. Hydraul. Eng. 1984, 110, 567–586. [Google Scholar] [CrossRef]
  59. Costa, J.E. Floods from Dam Failures; Open File Report 85-560; US Geological Survey: Denver, CO, USA, 1985; p. 54.
  60. Yan, K.; Neal, J.C.; Solomatine, D.P.; Di Baldassarre, G. Global and low-cost topographic data to support flood studies. In Hydro-Meteorological Hazards, Risks, and Disaster, 1st ed.; Shroder, J.F., Paron, P., Di Baldassarre, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 105–124. [Google Scholar]
Water 09 00432 g001 550
Figure 1. Study region and location of Chipembe dam.
Figure 1. Study region and location of Chipembe dam.
Water 09 00432 g001
Water 09 00432 g002 550
Figure 2. Subset of the SRTM-1s DEM used for the dam-break simulation.
Figure 2. Subset of the SRTM-1s DEM used for the dam-break simulation.
Water 09 00432 g002
Water 09 00432 g003 550
Figure 3. Location of the thalweg based on the aerial image and the original SRTM data, and the locations of the control cross sections.
Figure 3. Location of the thalweg based on the aerial image and the original SRTM data, and the locations of the control cross sections.
Water 09 00432 g003
Water 09 00432 g004 550
Figure 4. (a) Longitudinal profile along the corrected thalweg with the original digital elevation model (DEM SRTM) (black) and the hydrologically-conditioned digital elevation model (DEM SRTMTR) (red), and average slope calculated by fitting a linear trend to the elevation profiles (dotted lines). Cross section profiles S4 (b) and S7 (c) with the original DEM SRTM (black) and the DEM SRTMTR (red).
Figure 4. (a) Longitudinal profile along the corrected thalweg with the original digital elevation model (DEM SRTM) (black) and the hydrologically-conditioned digital elevation model (DEM SRTMTR) (red), and average slope calculated by fitting a linear trend to the elevation profiles (dotted lines). Cross section profiles S4 (b) and S7 (c) with the original DEM SRTM (black) and the DEM SRTMTR (red).
Water 09 00432 g004
Water 09 00432 g005 550
Figure 5. Position of the breach within the dam (a); initial conditions (b); and developed breach (c).
Figure 5. Position of the breach within the dam (a); initial conditions (b); and developed breach (c).
Water 09 00432 g005
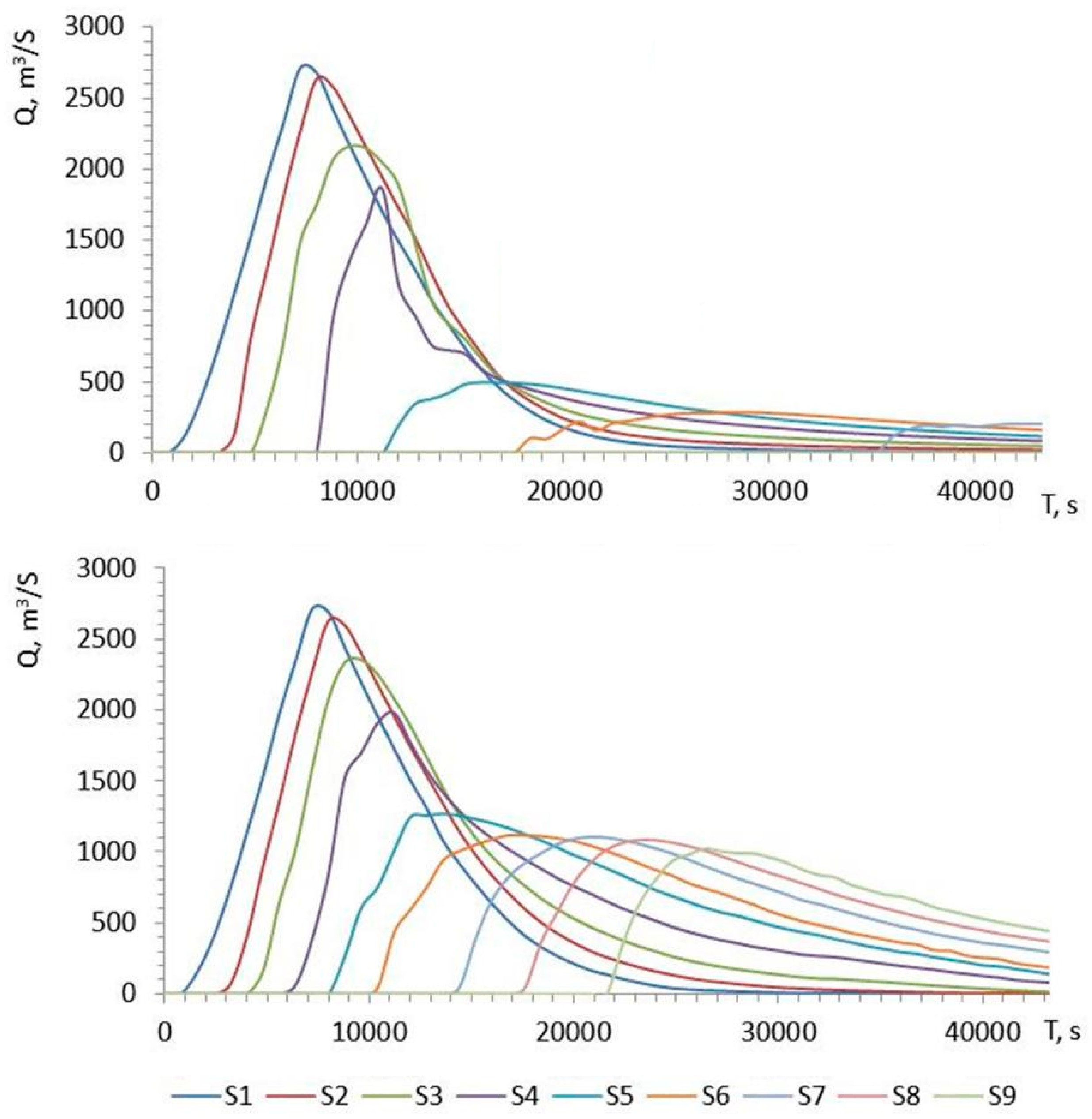
Water 09 00432 g006 550
Figure 6. Attenuation and translation of the flood hydrograph as the flood wave propagates downstream in: Scenario A (top); and Scenario B (bottom). Results for n = 0.03 m−1/3·s.
Figure 6. Attenuation and translation of the flood hydrograph as the flood wave propagates downstream in: Scenario A (top); and Scenario B (bottom). Results for n = 0.03 m−1/3·s.
Water 09 00432 g006
Water 09 00432 g007a 550Water 09 00432 g007b 550
Figure 7. Predicted water depth, velocity and specific discharge maps in the reach between S6 and S8 with the original DEM at t = 56,000 s (left) and with the conditioned DEM at t = 18,000 s (right). Manning’s value of n = 0.03 m−1/3·s: (a) Depth, DEM SRTM; (b) Depth, DEM SRTMTR; (c) Velocity, DEM SRTM; (d) Velocity, DEM SRTMTR; (e) Specific discharge, DEM SRTM; and (f) Specific discharge, DEM SRTMTR.
Figure 7. Predicted water depth, velocity and specific discharge maps in the reach between S6 and S8 with the original DEM at t = 56,000 s (left) and with the conditioned DEM at t = 18,000 s (right). Manning’s value of n = 0.03 m−1/3·s: (a) Depth, DEM SRTM; (b) Depth, DEM SRTMTR; (c) Velocity, DEM SRTM; (d) Velocity, DEM SRTMTR; (e) Specific discharge, DEM SRTM; and (f) Specific discharge, DEM SRTMTR.
Water 09 00432 g007aWater 09 00432 g007b
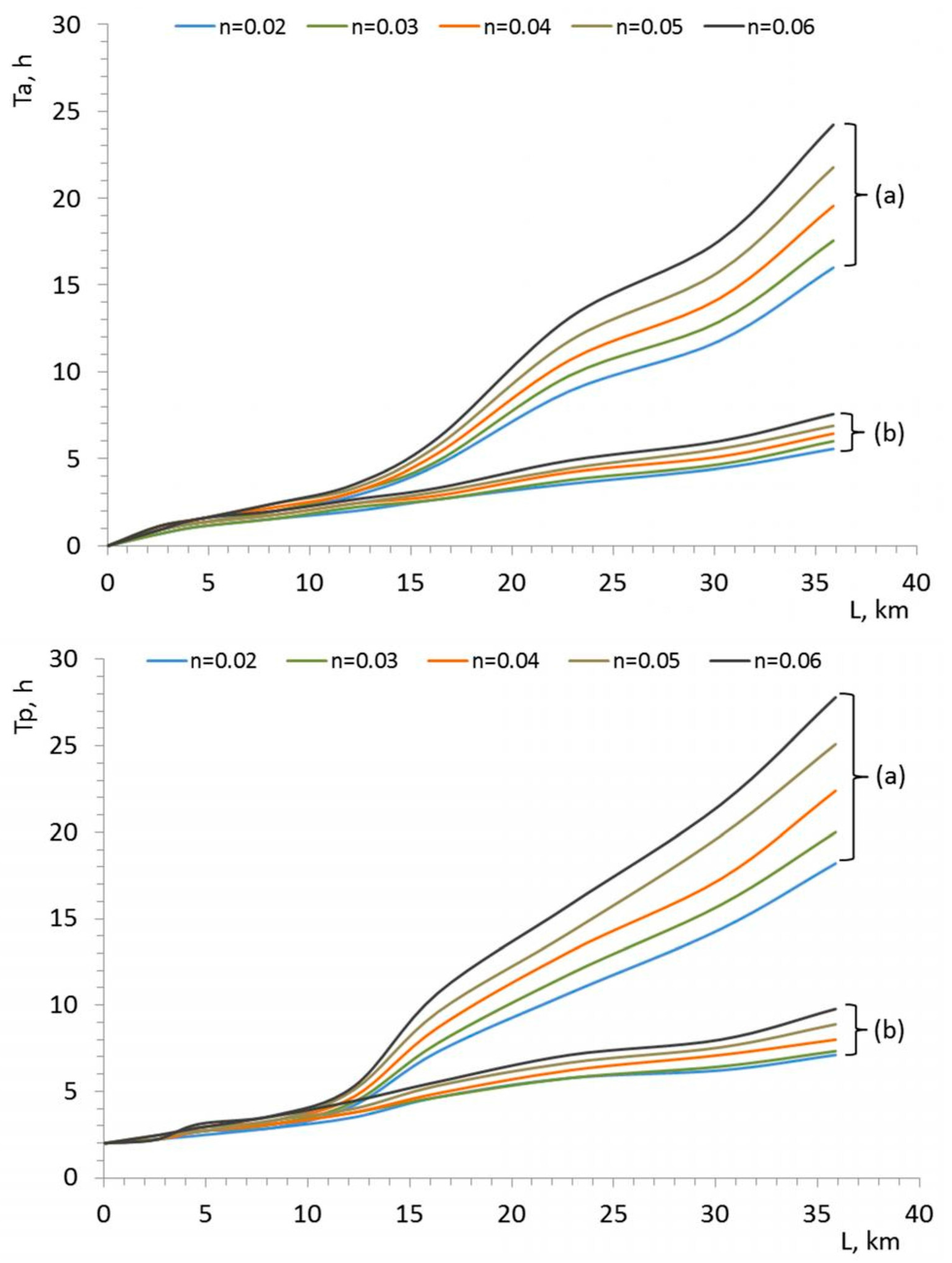
Water 09 00432 g008 550
Figure 8. Flood wave arrival time (Ta) (top); and time to peak (Tp) (bottom) versus distance from the dam (L), with the: DEM SRTM (a); and the DEM SRTMTR (b) for different values of the roughness coefficient.
Figure 8. Flood wave arrival time (Ta) (top); and time to peak (Tp) (bottom) versus distance from the dam (L), with the: DEM SRTM (a); and the DEM SRTMTR (b) for different values of the roughness coefficient.
Water 09 00432 g008
Water 09 00432 g009 550
Figure 9. Comparison of the linear best-fit equations of Sing and Snorrason [57], Evans [56], Pierce et al. [27] and the peak flow predicted by the Iber model in Chipembe dam.
Figure 9. Comparison of the linear best-fit equations of Sing and Snorrason [57], Evans [56], Pierce et al. [27] and the peak flow predicted by the Iber model in Chipembe dam.
Water 09 00432 g009
Water 09 00432 g010 550
Figure 10. Comparison of the best-fit equations of MacDonald and Landgridge-Monopolis [58], Costa [59], Pierce et al. [27], and the peak flow predicted by the Iber model in Chipembe dam.
Figure 10. Comparison of the best-fit equations of MacDonald and Landgridge-Monopolis [58], Costa [59], Pierce et al. [27], and the peak flow predicted by the Iber model in Chipembe dam.
Water 09 00432 g010
Water 09 00432 g011 550
Figure 11. Hazard map derived from the inundation depth and velocity distributions. Predictions using the DEM SRTMTR and n = 0.04 m−1/3·s.
Figure 11. Hazard map derived from the inundation depth and velocity distributions. Predictions using the DEM SRTMTR and n = 0.04 m−1/3·s.
Water 09 00432 g011
Table
Table 1. Peak flow (Qp), arrival time (Ta) and peak time (Tp) of the flood wave at downstream sections in Scenario A (DEM SRTM) considering different roughness coefficients (n).
Table 1. Peak flow (Qp), arrival time (Ta) and peak time (Tp) of the flood wave at downstream sections in Scenario A (DEM SRTM) considering different roughness coefficients (n).
SectionL (km)Qp (m3/s)Ta (h)Tp (h)Qp (m3/s)Ta (h)Tp (h)Qp (m3/s)Ta (h)Tp (h)
n = 0.02 m−1/3·sn = 0.03 m−1/3·sn = 0.04 m−1/3·s
S10.12747.6-22702.9-2.02673.9-2.0
S22.52716.80.92.22637.31.12.22527.71.12.2
S34.62271.81.32.72160.11.32.72053.11.62.9
S48.31901.52.02.91863.72.03.11711.22.23.3
S512.3546.62.94.2497.43.14.4442.43.14.7
S616.4326.34.77.3287.14.97.8253.15.38.7
S722.8232.98.910.7204.39.811.8181.110.713.1
S830.3162.611.814.4143.412.915.8125.814.217.3
S935.9109.316.018.295.517.620.084.119.622.4
n = 0.05 m−1/3·sn = 0.06 m−1/3·s-
S10.12619.8-2.02556.4-2.0---
S22.52451.31.12.22350.91.12.2---
S34.61938.81.62.91801.81.63.1---
S48.31557.92.43.31449.52.43.6---
S512.3390.53.35.1346.63.65.3---
S616.4221.65.89.6195.36.210.7---
S722.8160.211.814.2141.613.115.8---
S830.3111.615.819.899.117.621.6---
S935.976.221.825.166.024.227.8---
Table
Table 2. Peak flow (Qp), arrival time (Ta) and peak time (Tp) of the flood wave at downstream sections in Scenario B (DEM SRTMTR) considering different roughness coefficients (n).
Table 2. Peak flow (Qp), arrival time (Ta) and peak time (Tp) of the flood wave at downstream sections in Scenario B (DEM SRTMTR) considering different roughness coefficients (n).
SectionL (km)Qp (m3/s)Ta (h)Tp (h)Qp (m3/s)Ta (h)Tp (h)Qp (m3/s)Ta (h)Tp (h)
n = 0.02 m−1/3·sn = 0.03 m−1/3·sn = 0.04 m−1/3·s
S10.12746.5-2.02710.0-2.02664.5-2.0
S22.52722.90.72.22629.50.72.22523.10.892.4
S34.62450.41.12.42354.01.12.72240.81.332.7
S48.32094.11.62.91981.91.63.11831.21.783.1
S512.31376.12.03.51268.92.23.81162.32.443.8
S616.41185.42.74.71117.82.74.71027.12.894.9
S722.81181.03.65.81104.83.85.81002.54.226.2
S830.31159.94.46.21083.64.76.4978.15.117.1
S935.91106.75.67.11021.06.07.3901.06.448.0
n = 0.05 m−1/3·sn = 0.06 m−1/3·s-
S10.12587.1-2.02532.9-2.0---
S22.52441.80.92.42348.50.92.4---
S34.62115.91.32.72005.51.62.9---
S48.31723.51.83.31605.72.03.6---
S512.31076.12.44.0990.12.74.4---
S616.4939.93.15.3855.13.35.6---
S722.8911.34.46.7827.74.97.1---
S830.3885.45.67.6801.96.08.0---
S935.9824.26.98.9739.67.69.8---
Table
Table 3. Inundation depth and flood extent in Scenarios A and B with different roughness coefficients.
Table 3. Inundation depth and flood extent in Scenarios A and B with different roughness coefficients.
n (m−1/3·s)Flooded Area (×106 m2)Average Flood Depth (m)Maximum Depth (m)Average Flood Width (m)
ABABABAB
0.0213.2810.982.722.949.588.67368305
0.0313.3011.062.753.029.618.69369307
0.0413.3411.222.783.069.618.73370312
0.0513.3911.352.803.129.628.76372315
0.0613.4511.492.823.159.628.77373319

Share and Cite

MDPI and ACS Style

Álvarez, M.; Puertas, J.; Peña, E.; Bermúdez, M. Two-Dimensional Dam-Break Flood Analysis in Data-Scarce Regions: The Case Study of Chipembe Dam, Mozambique. Water 2017, 9, 432. https://doi.org/10.3390/w9060432

AMA Style

Álvarez M, Puertas J, Peña E, Bermúdez M. Two-Dimensional Dam-Break Flood Analysis in Data-Scarce Regions: The Case Study of Chipembe Dam, Mozambique. Water. 2017; 9(6):432. https://doi.org/10.3390/w9060432

Chicago/Turabian Style

Álvarez, Manuel, Jerónimo Puertas, Enrique Peña, and María Bermúdez. 2017. "Two-Dimensional Dam-Break Flood Analysis in Data-Scarce Regions: The Case Study of Chipembe Dam, Mozambique" Water 9, no. 6: 432. https://doi.org/10.3390/w9060432

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop