4.1. Glacier Evolution and Runoff Contribution
The results of glacier changes in the Gunt River Basin (
Figure 2) show that the southern Pamirs are not part of the “Pamir-Karakoram Anomaly”, as originally assumed by Gardelle et al. [
13]. A retreat of glacier areas in the Gunt River Basin by 14% (96 km
2) took place between 1998 and 2011 (
Table 1). Glacier retreat rates doubled in comparison to the period 1969–2002 [
17]. The “accelerated retreat” reported for parts of the Rushan and Shugnan Pamir (No. 6 in
Figure 1; [
17]) can be extended to the entire southern Pamirs (No. 13 in
Figure 1). This region of recent and intense glacier retreat can be classified into a larger scale of glacier retreat documented in the literature, including the Hindu Kush (Nos. 8 and 9 in
Figure 1; [
6,
19]) and the Wakhan Pamir (No. 7 in
Figure 1; [
18]). If at all, a “Pamir Anomaly” of glaciers gaining mass can therefore only be existent in parts of the Northern Pamirs (No. 1 in
Figure 1; [
13]) and in the Chinese Pamirs (No. 5 in
Figure 1; [
4,
5,
20]). The findings of mass gaining glaciers in the Northern Pamirs can only be true for the late 20th and the early 21st century because studies regarding longer time periods identified volume losses (No. 3 in
Figure 1; [
14]) or area retreat (No. 4 in
Figure 1; [
16]) there. Nevertheless, long-term mass losses of the Fedchenko glacier are one order of magnitude smaller than, e.g., at Abramov glacier (
Table 1; [
37]) or than recent losses in the Southern Pamirs (
Table 1 and
Table 3).
In total, glaciers lost 5.3 ± 0.8 km
3 of ice volume between 1998 and 2011 (12%), based on the GlabTop approach. Average thinning rates of glaciers were 0.53 m·y
−1 (
Table 3). These results are in line with the results of Kääb et al. [
20], who estimated thinning rates between 0.3 and 0.8 m·y
−1 for the Southern Pamirs (mean 0.55 m·y
−1;
Table 3), using ICESat laser altimetry data. Glacier wastage estimated with GRACE and a mass balance model ([
26]; expressed as m of water column) is 15% larger (
Table 3), but still within the range of the parameter uncertainty of the GlabTop results (
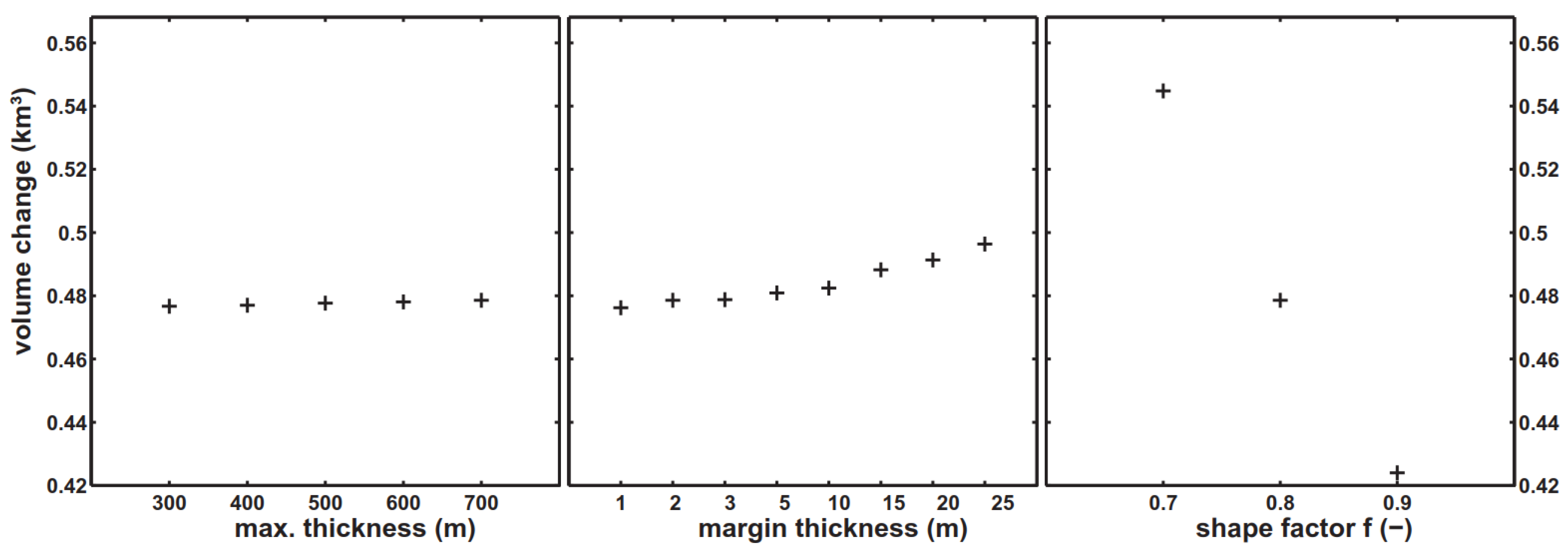
Appendix A.1).
Ice thickness distribution models, therefore, appear to be an efficient option to estimate glacier volume change on the catchment scale. They are process based [
58] and are independent from uncertain precipitation records. Their spatial resolution is higher than that of large-scale satellite approaches, and the combination of both seems beneficial. Exemplary, we validated such a model successfully on a large scale (entire river basin) by reviewing corresponding satellite-based approaches. The spatial resolution allows exploiting the model results on the subbasin scale, subsequently (
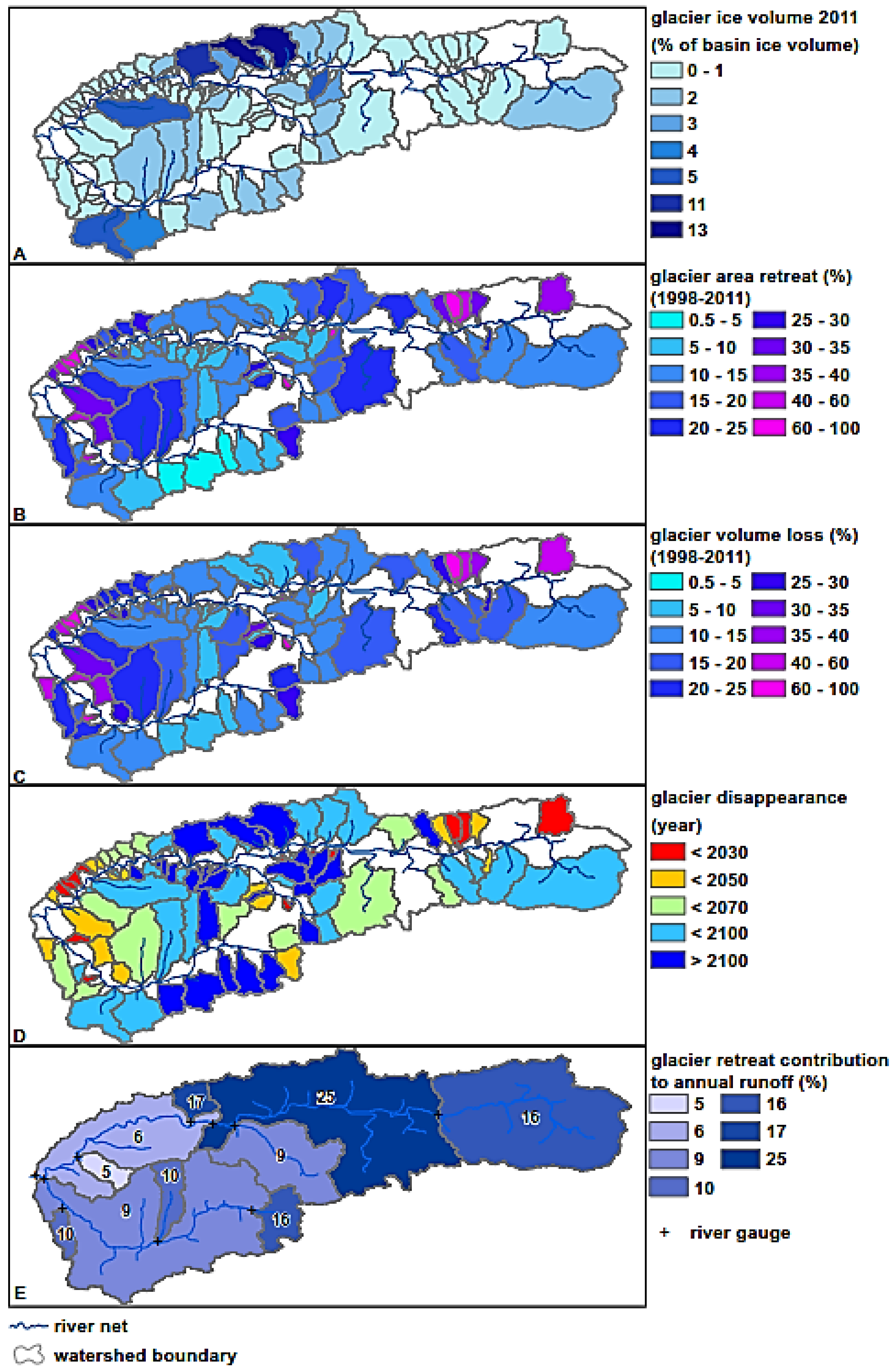
Figure 2).
Glacier retreat in the Gunt River Basin takes place in all sub-basins without exception, but the magnitude of glacier area and volume retreat in the Gunt Basin is spatially heterogeneous (
Figure 2B,C). The largest glacier wastage takes place at small glaciers in the western part of the catchment and at south-facing subbasins in the north-east parts of the catchment (Northern Alichur Range). The smallest glacier retreat takes place in the north-facing subbasins surrounding the highest mountains (Peak Karl Marx, Peak Engels). Subbasins storing the largest ice volumes (
Figure 2A) show retreat rates of five to 15% (area and volume;
Figure 2B,C) between 1998 and 2011.
Here, we assume linearly continuing retreat rates as a conservative (minimal) scenario of glacier retreat, based on the projections of Lutz et al. [
65] and Pohl et al. [
26]. In the subbasins of the western and north-eastern Gunt catchment, glacier coverage is expected to completely disappear already until 2030 (
Figure 2D). Most other subbasins might be deglaciated until the year 2100 with potentially large impacts on the local fresh-water supply and traditional irrigation agriculture in the late ablation period (August, September). Nevertheless, subbasins storing the largest amounts of total basin-wide ice volumes, in the north-central and south-west catchment (
Figure 2A), might still be glaciated for centuries, even if glacier retreat does not slow down due to potentially smaller retreat rates in higher elevations. This means that runoff rates of the Gunt River can still benefit from glacier melt for decades or even centuries, which is important for hydropower production and drinking water availability. However, local communities receive their fresh-water directly from tributaries, where irrigation ditches transport meltwater to gardens and settlements at the hillslopes. This water supply is endangered by the absence of glacier meltwater during the ablation period, which is the main growing season. In August and September, the basin hardly receives any rainfall, and snow cover has already disappeared (Pohl et al. [
32,
43]).
The contribution of glacier retreat to river runoff is relatively smaller in western subbasins (
Figure 2E). Subbasins with smaller precipitation rates receive up to 25% of annual runoff from glacier retreat (
Figure 2E). This means complete disappearance of glaciers will severely affect total river runoff in the more arid parts of the Pamirs (towards the east), which nowadays receive proportionally more meltwater from retreating glaciers. Regions of higher precipitation rates are less affected, and strengthening westerly precipitation [
45,
46] might potentially compensate for decreasing glacier meltwater. However, deglaciation most likely will leave a gap in river runoff amounts during summer months, because in the Western Pamirs, precipitation almost exclusively falls in winter and spring (see below).
On average, glacier retreat contributes 10% to the annual Gunt River runoff between 1998 and 2011, estimated based on two independent methods (
Table 3). This robust estimation has recently been assimilated into a glacio-hydrological model by Tarasova et al. [
33], who modeled melt rates of snow-free glacier ice to amount to 10% ± 4% of annual runoff.
Applying the mass balance results from Pohl et al. [
26] (
Table 3) to the classified glacier area of 707 km
2 [
23] fractionizes their results into 13% runoff contribution from glacier retreat and 6% runoff contribution from perennial snow cover (
Table 3). The glacier retreat contribution to annual runoff is in line with the results of the other two studies. Nevertheless, they modeled total glacier melt to contribute 30% of annual runoff (in the same basin) [
26,
32], but with a different hydrological model, which defines glacier melt as the meltwater of glacier ice plus snowmelt from glacier surfaces. The substantial difference to Tarasova et al. [
33] can further be explained by the treatment of permanent snow and ice cover as “glaciers”, based on the application of gridded land cover data (MODIS MCD12Q1 dataset).
Runoff contribution from perennial snow cover seems to be rather large, especially under consideration that “glaciers” in the hydrological model are treated as infinite reservoirs (which is typical for conceptual models). The definition of “glacier retreat contribution to runoff” (also used in
Figure 2E) quantifies the gap that will occur in river runoff, when glaciers will have completely disappeared. Snowmelt from glacier surfaces will still be present after glacier disappearance, but probably with a shift in runoff timing. The example shows that divergent definitions of which runoff fractions are incorporated into the term “glacier melt” can lead to larger uncertainties than those arising from glacio-hydrological modeling itself. A clear definition of runoff fractions is essential, when model results are to be used in water supply planning for communities that will be impacted by hydrologic change.
4.2. Runoff and Climate Trends versus Glacier Evolution
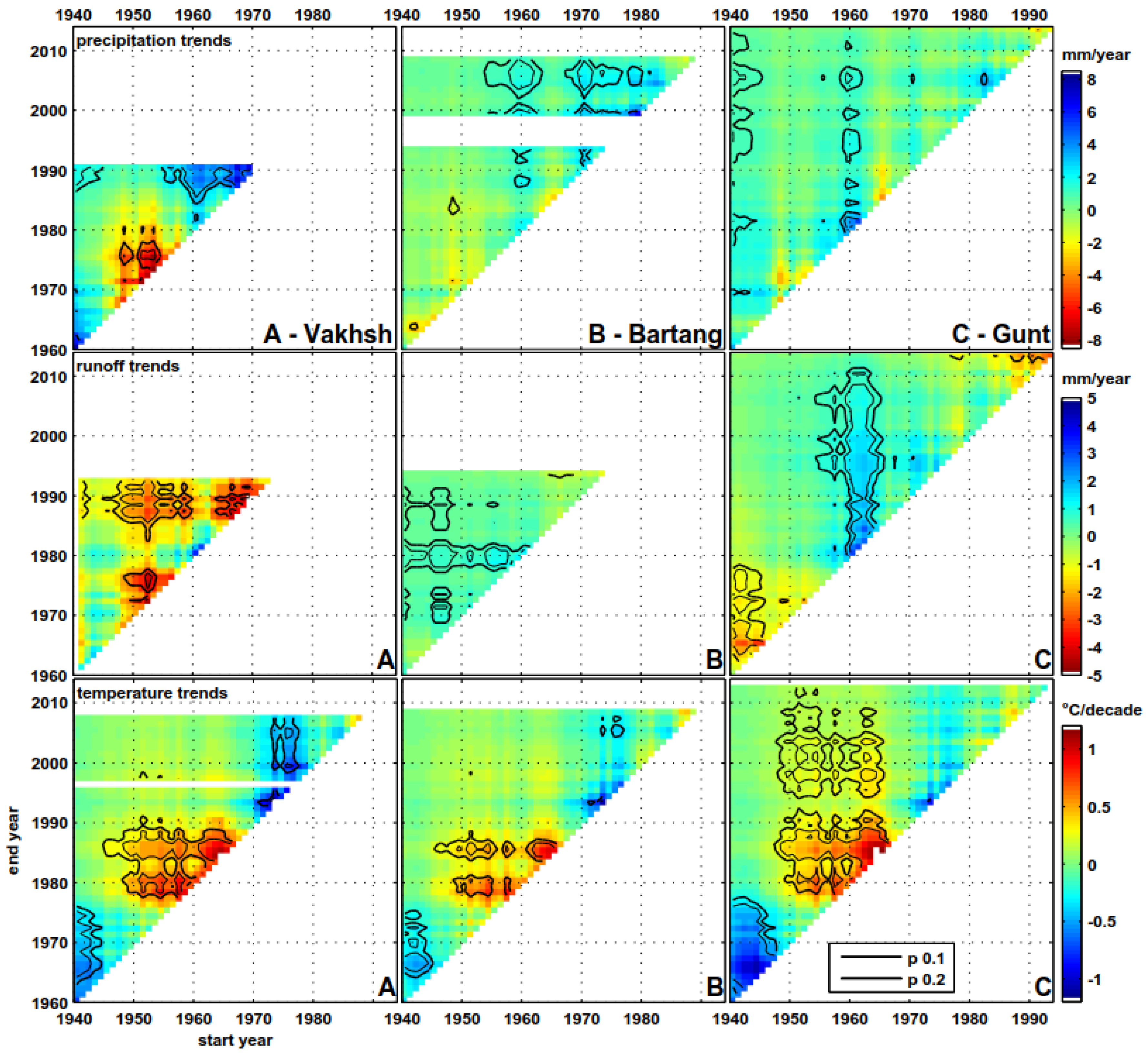
Trends in river runoff for the three river basins for different time periods are shown in
Figure 3. River runoff in the Vakhsh Basin (North Pamirs) declines over large periods between 1940 and 1990 (
Figure 3A, center row) with a magnitude of up to five millimeters per year. In contrast, river runoff in the Gunt Basin (South Pamirs) increases between 1955 and 2010 by up to 5 mm·y
−1 (
Figure 3C, center row). Both trends are statistically significant at the 10% level. The Bartang River in the Central Pamirs shows stable runoff trends over decades (
Figure 3B, center row).
Figure 3 allows a direct comparison of runoff trends (center row) with precipitation trends (top row) and temperature trends (bottom row). The River Gunt (
Figure 3C) shows a statistically significant runoff decline between 1940 and the end of the 1970s, where the temperature trend shows intense cooling. Starting 1960, temperatures show a strong warming trend. Along with an increase in precipitation, runoff trends become positive for decades until recent times.
In the Vakhsh Basin (
Figure 3A), river runoff declined in a statistically significant manner between 1950 and ca. 1980, although temperature shows a strong warming in that time, which is assumed to increase the meltwater contribution of glaciers. In the same time, precipitation trends show a strong decline of up to 8 mm·y
−1. This strong precipitation decline, which is obviously not observed in the South and Central Pamirs, probably caused the first period of negative runoff trends in the Vakhsh River basin, although the temperature was rising. A second period of runoff decline followed one decade later and lasted at least until 1994 (where the time series ends). Parallel to this runoff decline, precipitation rates increased significantly. This is surprising and might be explained by a statistically significant cooling of partly up to 1 °C per decade in July and August, between 1970 and 2010 (
Figure 3A, bottom row). We suppose that increasing precipitation along with cooling temperatures caused higher glacier accumulation rates in the Vakhsh Basin in the late 20th and the beginning of the 21st century. This might explain the findings of balanced glacier mass budgets in the North-West Pamirs [
13].
Similar characteristics were found in parts of the Upper Indus Basin: Fowler and Archer [
64] explain the decline in river runoff in the Hunza Basin (Karakoram) by a decline of mean summer temperatures by 1 °C since 1961, causing glacier mass gain. Here, also a significant precipitation increase was detected [
66]. Kapnick et al. [
37] deduced a “prevailing hypothesis” from the literature for the Karakoram: increasing glacier accumulation occurs due to decreasing warm-season temperatures along with increasing precipitation rates.
We find a decline in summer temperatures (July, August) in all depicted climate stations used for the trend statistics after 1970 (
Figure 3 bottom row). In the Northern Pamirs, this trend is persistent and statistically significant. In the Southern Pamirs (
Figure 3C), the trend is statistically not significant, less pronounced and not persistent. Much more, a warming trend of ca. 0.2 °C per decade is statistically significant from 1950–2010. Assuming that the applied climate data are also representative for glaciated elevations, this could partly explain the largely divergent pattern of glacier evolution between the North and South Pamirs (
Figure 1;
Table 1).
On the other hand, the temporal patterns of temperature trends look quite similar in the North, Central and South Pamirs (
Figure 3, bottom row) and seem to be similar to trends in the Karakoram and Hindu Kush [
64]. Diverging patterns of glacier evolution might be driven by other (stronger) forces. When the cooling trend after 1970 is responsible for glacial mass gain in the Northern Pamirs and Karakoram, why not in the Southern Pamirs and Hindu Kush? The elevation effect and precipitation characteristics seem to be stronger proxies for diverging patterns of glacial evolution.
The impact of glacier evolution on river discharge in the Pamirs follows a distinct spatial pattern: the Gunt River recently receives 10% ± 4% of the annual river discharge from glacier retreat [
33], while the runoff trend is significantly rising since the end of the 1950s. This is comparable to those tributaries of the Upper Indus, which drain the Hindu Kush. There, glacier retreat causes rising river flows [
67,
68]. In contrast, the Vakhsh River basin shows decreasing runoff trends along with glacier mass gain or moderate glacier mass losses. This is comparable to the Hunza Catchment draining the Northern Karakoram [
68].
Therefore, runoff trends in the Pamir-Hindu Kush-Karakoram region show the same spatial pattern as glacier evolution does (
Figure 1), an anomaly in the North-West Pamirs and North Karakoram versus a distinct glacier and hydrological change in the South Pamirs and Hindu Kush. Meanwhile, the Bartang River (Central Pamirs) shows almost no significant runoff trend over several decades (
Figure 3C, center row), which outlines a stable runoff regime, potentially because the two runoff extremes cancel each other out between North and South Pamir.
4.3. Precipitation Pattern versus Glacier Evolution
We believe that the cooling of summer temperatures since the 1970s plays a crucial role in glacier mass gain in the Northern Pamirs and Karakoram. However, the cooling trend cannot explain why glaciers in the Southern Pamirs and Hindu Kush are retreating rapidly. Therefore, precipitation characteristics require a more detailed investigation.
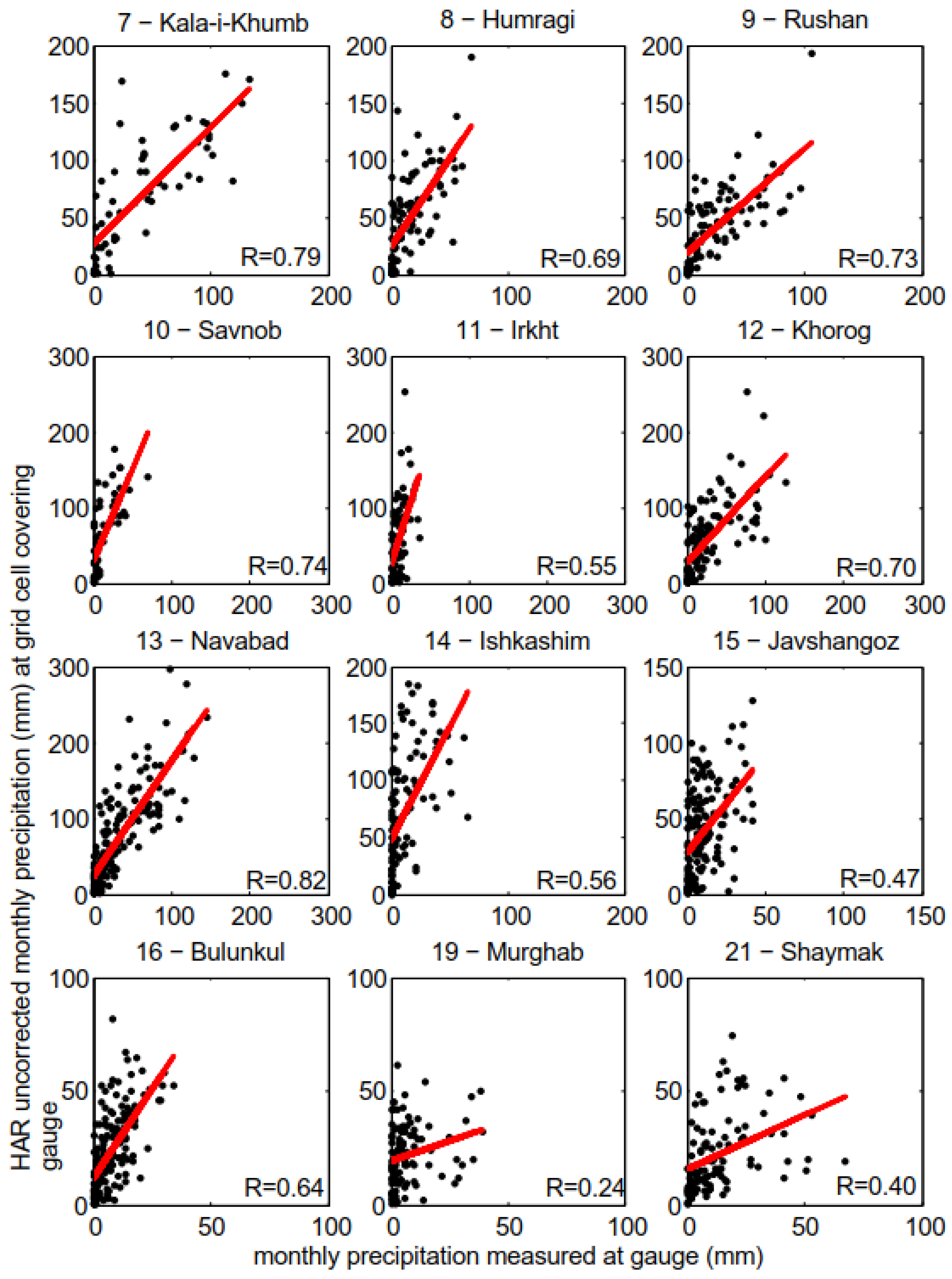
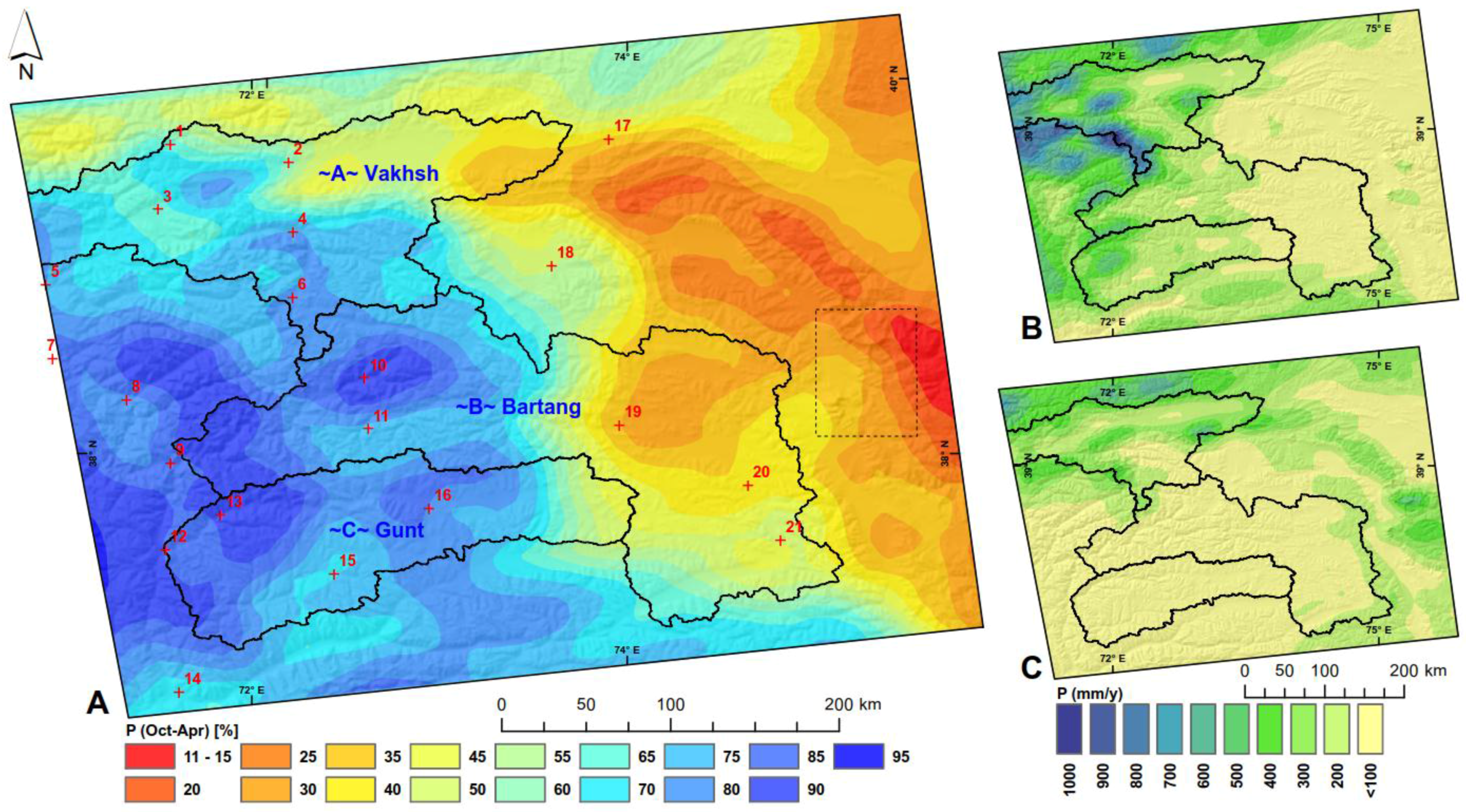
Generally, assumptions on precipitation characteristics have to be seen in the light of the uncertainties depicted in the Methods section. We figured out that high-resolution data of the High Asia Refined analysis (HAR; [
39]) provides reliable information on winter precipitation rates (
Figure 4A), stemming from westerly wind systems. In the opposite way, convective summer precipitation in the Eastern Pamirs is less well reflected by the HAR dataset. Absolute magnitudes of precipitation had to be bias-adjusted (
Figure A2).
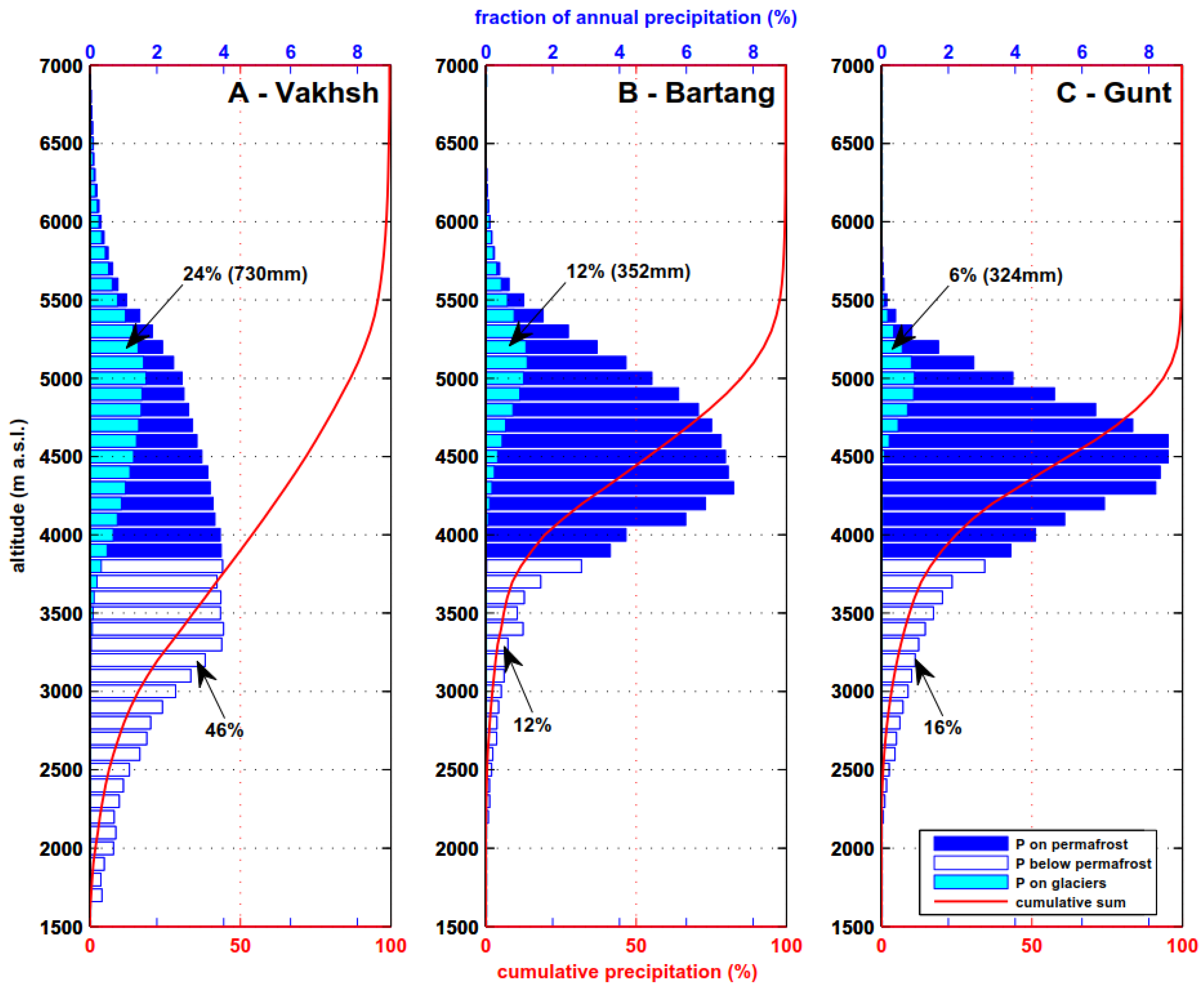
Bias-corrected HAR precipitation data from 2001 to 2011 imply that the contrasting glacier evolution in the North and South Pamirs can potentially be explained by the distribution of basin-wide precipitation. In the Vakhsh Basin, 24% of basin-wide precipitation falls directly on glaciated areas which cover 17% of the basin area (
Figure 5A). In the Gunt Basin, it is only 6% of annual basin-wide precipitation that directly falls on glaciers covering only 5% of the basin area (
Figure 5C;
Table 2). We assume that the “unique water cycle” of the Karakoram [
37] is also present in the nival regime of the Western, Central and Southern Pamirs, where up to 95% of precipitation falls in winter (
Figure 4). This means that in the North Pamirs, at least 24% of annual precipitation (
Figure 5A) contributes to glacier accumulation. In contrast, up to 94% of annual precipitation in the South Pamirs is preset to melt within the seasonal water cycle (
Figure 5C). Further, the ratio of precipitation on glaciers to glacier area shows that glacier areas in the Vakhsh basin receive proportionally more precipitation than glacier areas in the South Pamirs (
Figure 5).
Higher accumulation rates in the north can partly explain why runoff trends tend to be negative there and vice versa. Rising runoff trends in the South Pamirs are likely to be caused by increasing westerly precipitation (
Figure 3C, top row) in addition to warming-induced glacier retreat (
Figure 3C, bottom row). Thus, an increase in westerly precipitation [
45,
46] in both regions causes glacier mass gain in the Northern Pamirs and rising river flows in the Southern Pamirs.
Altitudinal precipitation distribution (
Figure 5) further shows that in the Vakhsh Basin, 46% of annual precipitation falls below the permafrost boundary (ca. 3800 m a.s.l.; [
17]). At altitudes below permafrost, meltwater can better infiltrate into soils, where it is prone to evaporation and transpiration by plants (“green water” [
69]). In the Gunt River Basin, 86% of annual precipitation falls on potential permafrost sites, which allow less infiltration into the ground and cause higher fractions of surface runoff.
A plausible scenario is that precipitation increase (
Figure 3, top row; [
45,
46]) causes higher rates of green water losses and glacier accumulation rates in the Vakhsh Basin, and therefore, runoff declines (
Figure 3A, center row). In contrast, increasing precipitation in the Gunt Basin is followed by a more or less direct increase in river runoff (
Figure 3C, center row) due to limited glacier accumulation and limited meltwater infiltration (
Figure 5C). The winter precipitation regime itself, as proposed by Kapnick et al. [
37] for the Karakoram, cannot explain diverging trends of glacial evolution in the Pamirs, because also shrinking glaciers in the Southern Pamirs receive almost exclusively winter precipitation (
Figure 4A).
The “elevation effect” [
12,
36] seems to advantage some glaciated regions in the Pamirs, because the smallest rates of glacier retreat occur around the highest peaks: locally around Peak Karl Marx (6723 m) in the South Pamirs (
Figure 2B), more regionally in the Fedchenko area (up to 7495 m) in the North Pamirs and in the Muztaq Ata region (>7500 m) in the East Pamirs. Associated glacier systems might benefit from those “water towers” and yearlong temperatures below the freezing point. Nevertheless,
Figure 4 illustrates that highest precipitation rates of up to 1400 mm·y
−1 are much more a regional feature than an altitudinal effect (
Figure 5). Thus, glaciers in the Northern Pamirs are supposed to simply benefit from their position towards the westerly wind systems and declining temperatures (see
Section 4.2). In this context, the hypothesis of Cannon et al. [
46], saying the Karakoram Ranges might be more prone to orographic blocking due to intensification and a northward shift of westerly wind systems, might also be meaningful for the high Pamirs.
Further influences on the relationship between glaciers and runoff, such as debris cover and (scale-dependent) aspect-distributions of glaciers, have not been investigated in this study, e.g., debris cover may have an additional impact on glaciers’ response to climate change [
70].