Author Contributions
Cuilin Pan performed the experiments, processed the data, analyzed the results, and wrote the manuscript; Xianwei Wang designed experiments, analyzed the results, and wrote and revised the manuscript; Lin Liu, Huabing Huang, and Dashan Wang contributed to obtaining the in situ measurements, set up the SWMM model, improved the experiments, and revised the manuscript.
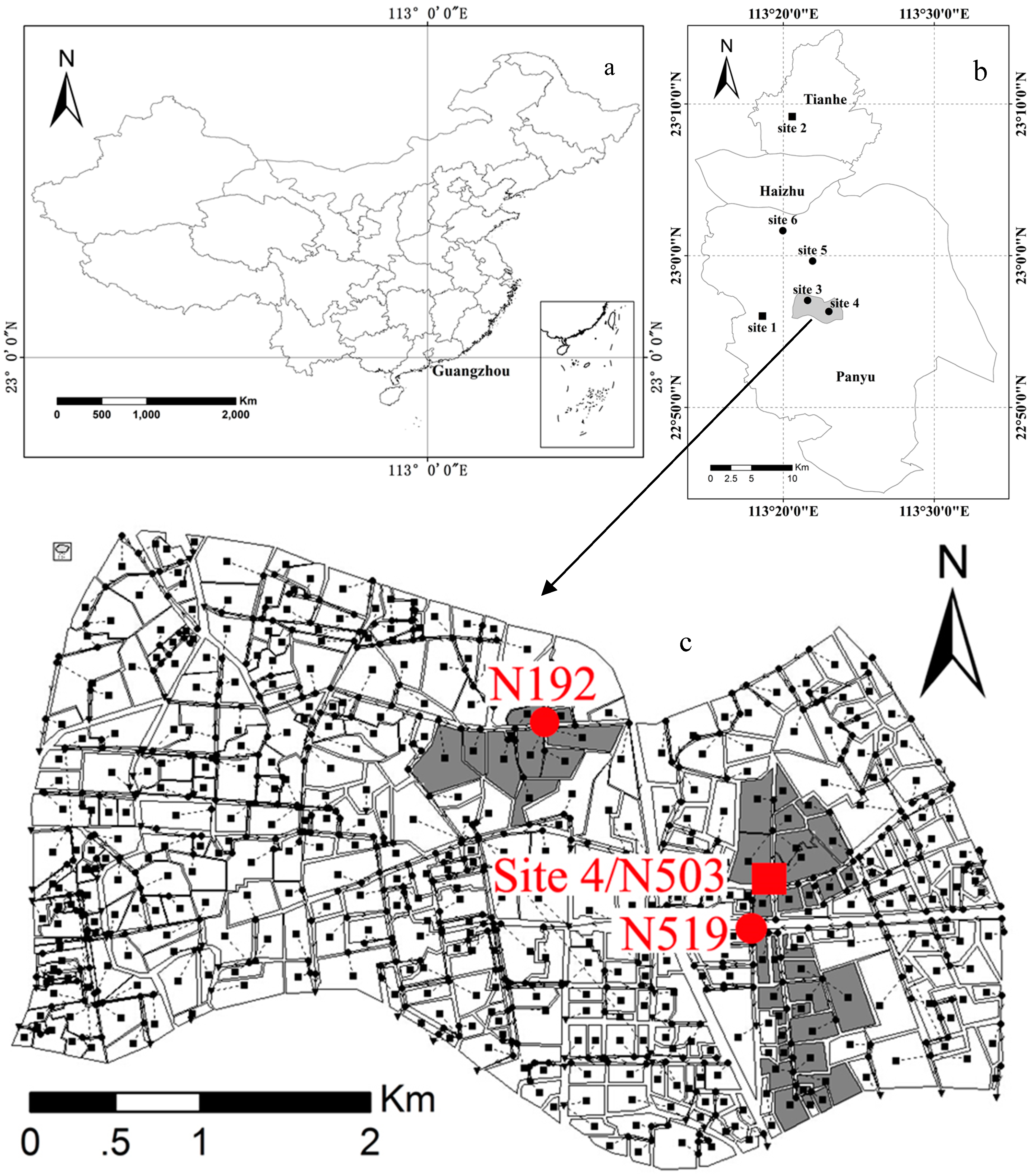
Figure 1.
The locations of Guangzhou (a); meteorological sites (b); and the three selected nodes and their catchment area/ modeling areas by SWMM in Panyu District (c). Street flooding water depth is recorded near Site 4/Node 503 by a wireless electronic water depth meter.
Figure 1.
The locations of Guangzhou (a); meteorological sites (b); and the three selected nodes and their catchment area/ modeling areas by SWMM in Panyu District (c). Street flooding water depth is recorded near Site 4/Node 503 by a wireless electronic water depth meter.
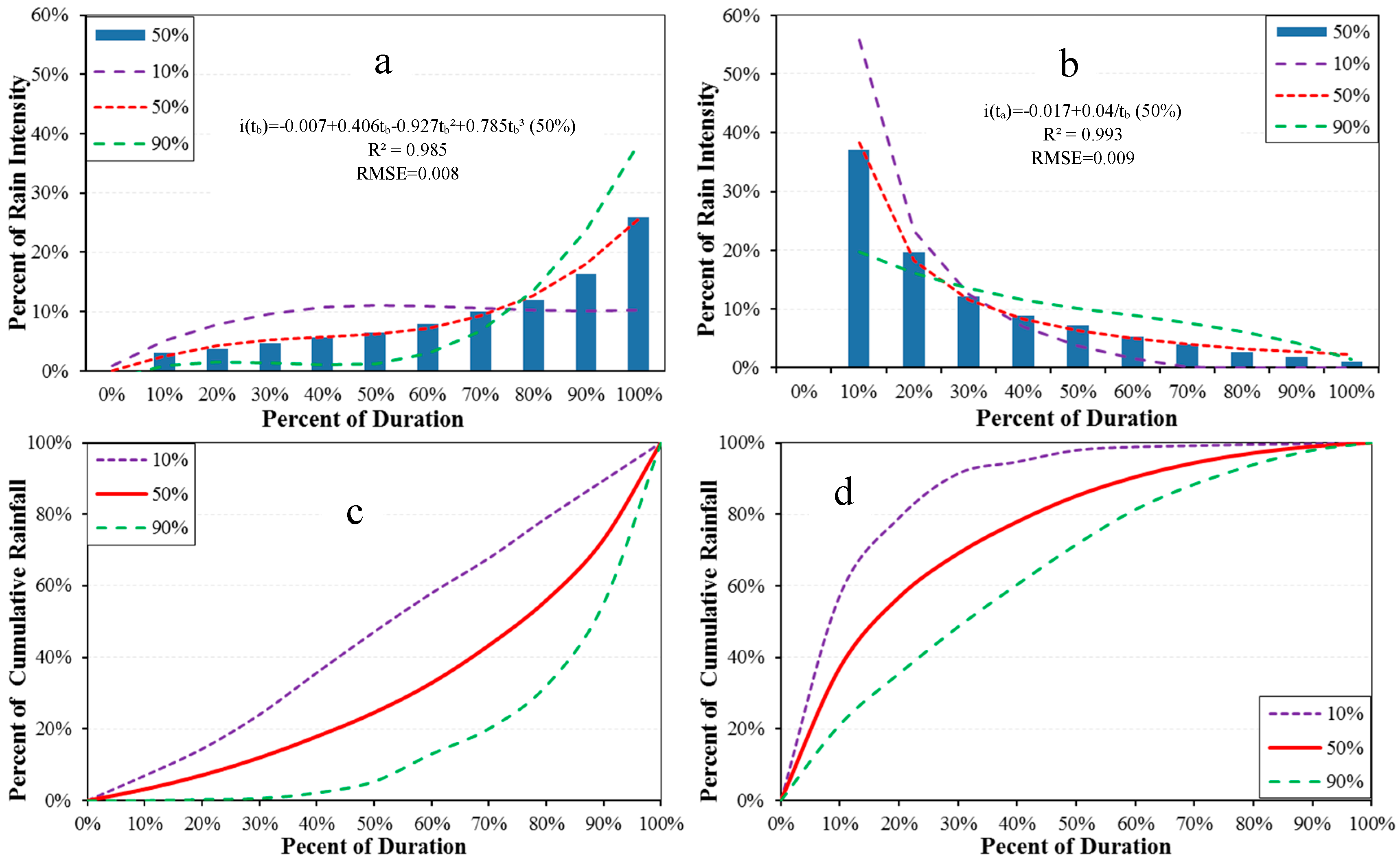
Figure 2.
Comparisons of rainfall intensity and cumulative rainfall percent derived by the Improved Huff curve at three probabilities (10%, 50%, and 90%) for the rising limb (a,c), and the falling limb (b,d), which are separated by the time of peak rainfall (33%) at Site 2.
Figure 2.
Comparisons of rainfall intensity and cumulative rainfall percent derived by the Improved Huff curve at three probabilities (10%, 50%, and 90%) for the rising limb (a,c), and the falling limb (b,d), which are separated by the time of peak rainfall (33%) at Site 2.
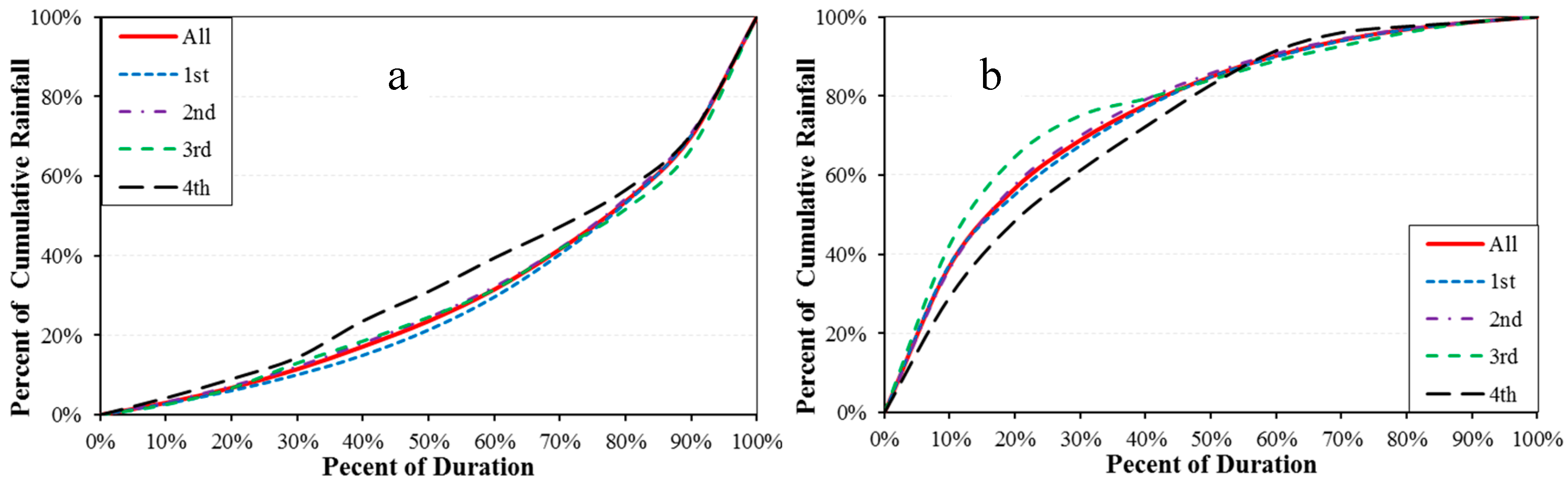
Figure 3.
The Huff curves for the rising (a) and falling (b) limbs at a probability of 50% by all storm events and by those within the four quartiles at Site 2.
Figure 3.
The Huff curves for the rising (a) and falling (b) limbs at a probability of 50% by all storm events and by those within the four quartiles at Site 2.
Figure 4.
Comparisons of cumulative rainfall between ground observations and the design storms for the storm events at Site 3 on 21 September 2015 (a); at Site 4 on 25 May 2015 (b); at Site 5 on 3 October 2015 (c); and at Site 6 on 21 July 2015 (d).
Figure 4.
Comparisons of cumulative rainfall between ground observations and the design storms for the storm events at Site 3 on 21 September 2015 (a); at Site 4 on 25 May 2015 (b); at Site 5 on 3 October 2015 (c); and at Site 6 on 21 July 2015 (d).
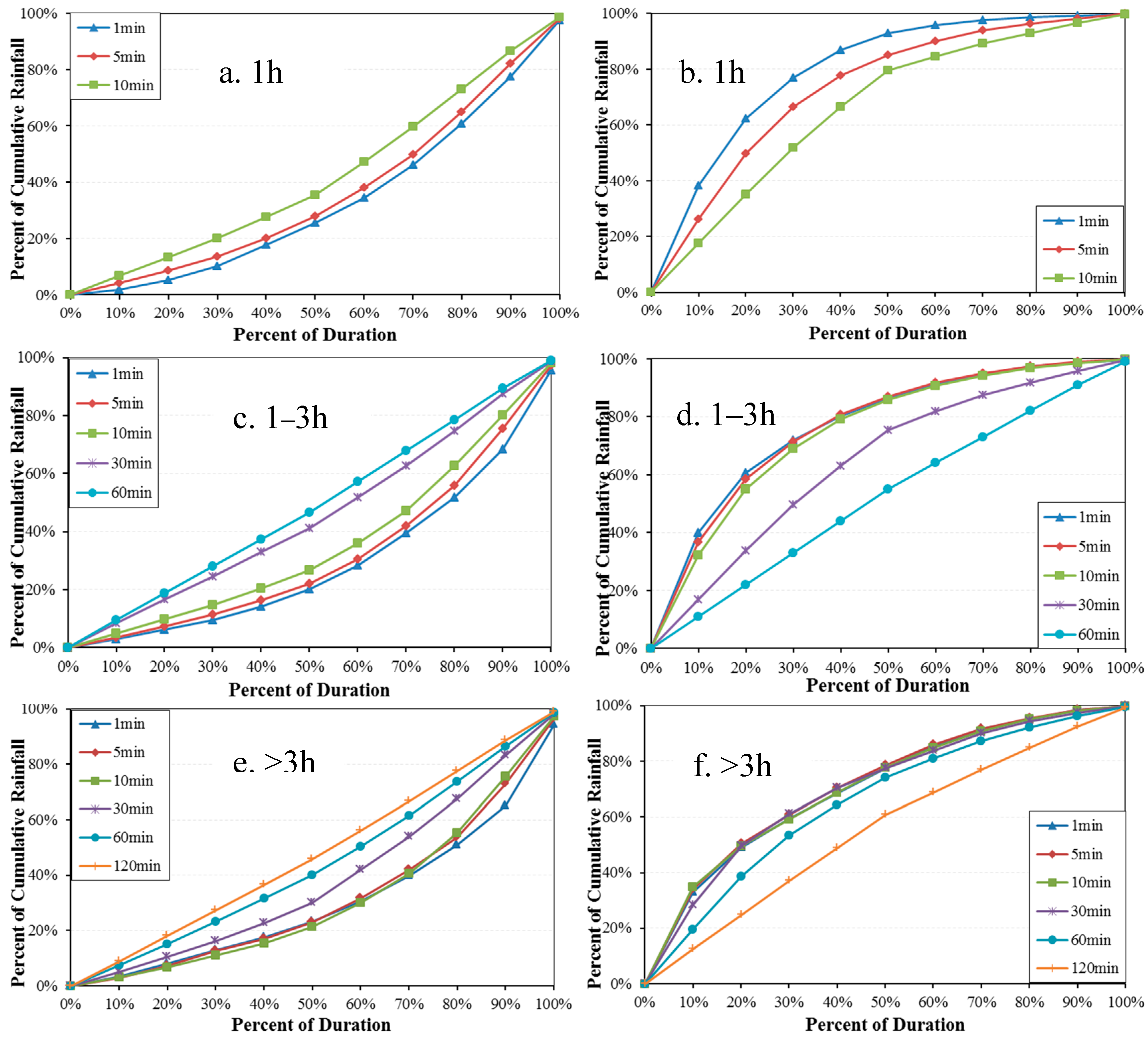
Figure 5.
Percent of cumulative rainfall depth derived by the Improved Huff curves (probability 50%) using different time intervals for three groups (rainfall duration: 1 h, 1–3 h, and >3 h) of storms from 2008 to 2012 at Site 2. Plots (a,c,e) are for the rising limb, and plots (b,d,f) are for the falling limb.
Figure 5.
Percent of cumulative rainfall depth derived by the Improved Huff curves (probability 50%) using different time intervals for three groups (rainfall duration: 1 h, 1–3 h, and >3 h) of storms from 2008 to 2012 at Site 2. Plots (a,c,e) are for the rising limb, and plots (b,d,f) are for the falling limb.
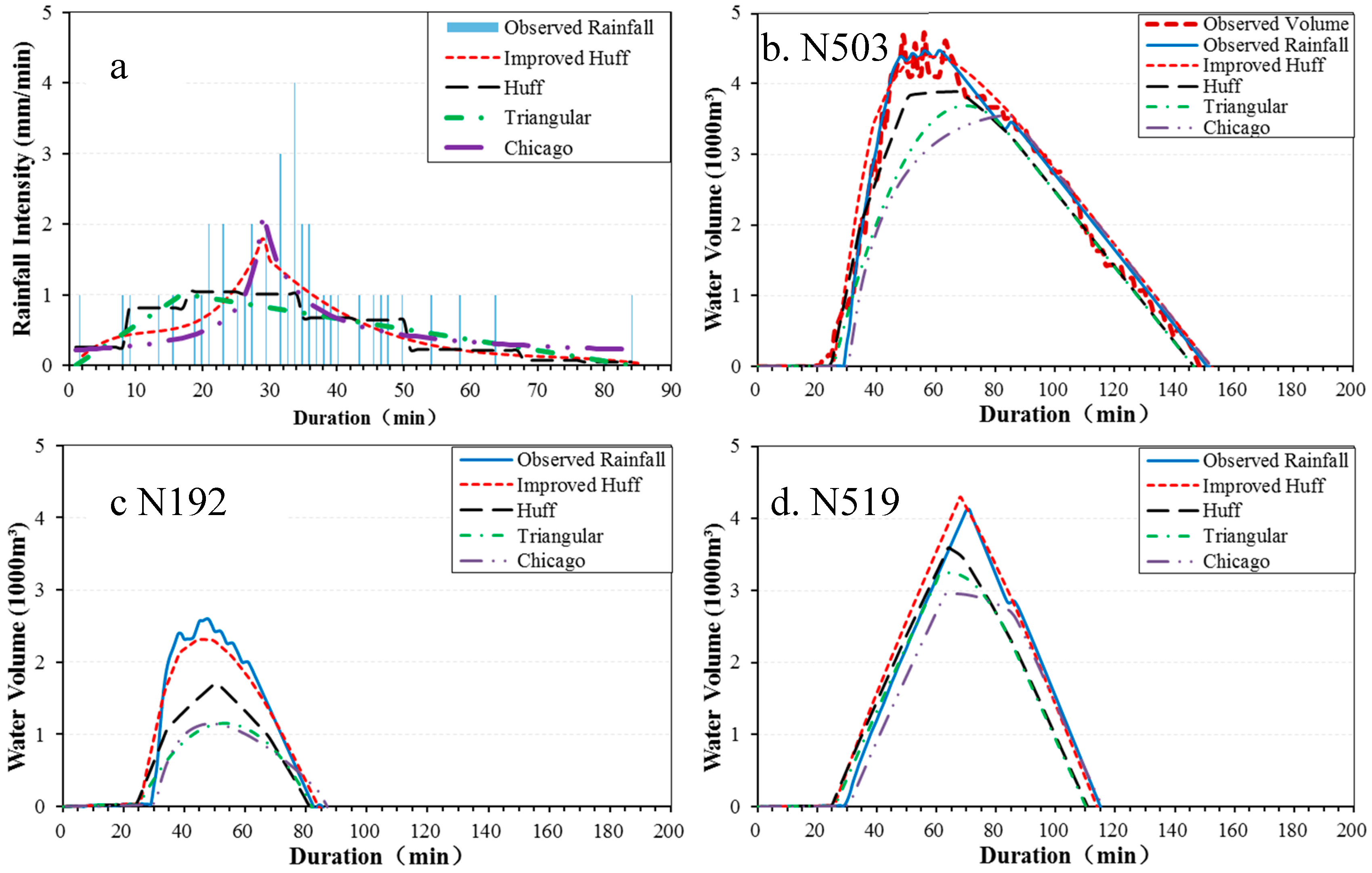
Figure 6.
Comparisons of hyetographs (a) and the according ground measured and simulated flooding volume by SWMM using different hyetographs at Node 503 (b), Node 192 (c) and Node 519 (d) for the storm event recorded at Site 4 on 2 August 2014, with total rainfall of 42 mm and duration of 84 min.
Figure 6.
Comparisons of hyetographs (a) and the according ground measured and simulated flooding volume by SWMM using different hyetographs at Node 503 (b), Node 192 (c) and Node 519 (d) for the storm event recorded at Site 4 on 2 August 2014, with total rainfall of 42 mm and duration of 84 min.
Table 1.
The number of storms in different durations at two sites for the period 2008–2012.
Table 1.
The number of storms in different durations at two sites for the period 2008–2012.
| Rain Gauges | Duration (h) |
|---|
| <1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | >6 | Total |
|---|
| Site 1 (Sub-urban) | 12 | 27 | 15 | 3 | 6 | 5 | 3 | 71 |
| Site 2 (Urban) | 25 | 37 | 16 | 11 | 6 | 5 | 4 | 104 |
| Total | 37(21%) | 64(36%) | 31(18%) | 14(8%) | 12(7%) | 10(6%) | 7(4%) | 175 |
Table 2.
The number of storms in each quartile defined according to the occurrence of peak rainfall considering a normalized time at two sites for the period 2008–2012.
Table 2.
The number of storms in each quartile defined according to the occurrence of peak rainfall considering a normalized time at two sites for the period 2008–2012.
| Quartiles | 1st | 2nd | 3rd | 4th | Total |
|---|
| Site 1 | 31(44%) | 27(38%) | 9(13%) | 4(6%) | 71 |
| Site 2 | 33(32%) | 56(54%) | 8(8%) | 7(7%) | 104 |
| Total | 64(37%) | 83(47%) | 17(10%) | 11(6%) | 175 |
Table 3.
Statistics of the rising and falling limbs for storm events at Sites 1 and 2 from 2008 to 2012.
Table 3.
Statistics of the rising and falling limbs for storm events at Sites 1 and 2 from 2008 to 2012.
| Title | Rainfall Depth (%) | Rainfall Duration (%) | Intensity (mm/min) |
|---|
| Rising | Falling | Rising | Falling | Rising | Falling |
|---|
| Site 1 | 45 ± 5% | 55 ± 5% | 33 ± 5% | 67 ± 5% | 0.66 ± 0.26 | 0.36 ± 0.03 |
| Site 2 | 41 ± 4% | 59 ± 4% | 33 ± 5% | 67 ± 5% | 0.62 ± 0.23 | 0.32 ± 0.07 |
| Mean | 43 ± 5% | 57 ± 5% | 33 ± 5% | 67 ± 5% | 0.64 ± 0.24 | 0.34 ± 0.05 |
Table 4.
Direct Catchment Area (DCA), Upstream Catchment Area (UCA), Total Catchment Area (TCA), and Drainage Capacity (DC) of the three selected nodes.
Table 4.
Direct Catchment Area (DCA), Upstream Catchment Area (UCA), Total Catchment Area (TCA), and Drainage Capacity (DC) of the three selected nodes.
| Node | DCA (ha) | UCA (ha) | TCA (ha) | DC (m3/s) |
|---|
| 503 | 8.8 | 26.2 | 35.0 | 0.88 |
| 192 | 10.1 | 27.3 | 37.4 | 1.76 |
| 519 | 2.4 | 40.5 | 43.0 | 1.69 |
Table 5.
RMSE and NSE values computed between design storms and observed rainfall at Sites 3-6, where the observed storm data are not used to develop design storms. Both the Improved Huff and original Huff curves represent those at a probability of 50%.
Table 5.
RMSE and NSE values computed between design storms and observed rainfall at Sites 3-6, where the observed storm data are not used to develop design storms. Both the Improved Huff and original Huff curves represent those at a probability of 50%.
| Site | Date | Rainfall Depth (mm) | Duration (min) | Intensity (mm/h) | Index | Improved Huff | Huff | Triangular | Chicago |
|---|
| 3 | 19 August 2014 | 40 | 28 | 86 | RMSE | 1.08 | 1.22 | 4.91 | 4.33 |
| NSE | 0.99 | 0.99 | 0.87 | 0.88 |
| 21 September 2015 | 95 | 175 | 33 | RMSE | 6.92 | 16.43 | 10.79 | 9.75 |
| NSE | 0.94 | 0.65 | 0.85 | 0.88 |
| 03 October 2015 | 55 | 136 | 24 | RMSE | 3.70 | 9.34 | 3.56 | 4.09 |
| NSE | 0.96 | 0.75 | 0.96 | 0.95 |
| 4 | 02 August 2014 | 42 | 84 | 30 | RMSE | 2.75 | 3.53 | 5.39 | 4.90 |
| NSE | 0.97 | 0.94 | 0.88 | 0.90 |
| 11 May 2015 | 78 | 97 | 48 | RMSE | 5.58 | 8.54 | 14.25 | 12.25 |
| NSE | 0.95 | 0.87 | 0.65 | 0.74 |
| 25 May 2015 | 53 | 66 | 48 | RMSE | 2.74 | 3.91 | 4.60 | 3.87 |
| NSE | 0.97 | 0.94 | 0.91 | 0.93 |
| 5 | 16 May 2015 | 27 | 65 | 25 | RMSE | 1.74 | 2.80 | 2.05 | 1.22 |
| NSE | 0.94 | 0.83 | 0.91 | 0.97 |
| 21 July 2015 | 22 | 59 | 22 | RMSE | 2.56 | 2.89 | 2.99 | 2.64 |
| NSE | 0.82 | 0.76 | 0.75 | 0.80 |
| 03 October 2015 | 26 | 49 | 32 | RMSE | 0.85 | 1.53 | 3.56 | 3.36 |
| NSE | 0.99 | 0.96 | 0.81 | 0.83 |
| 6 | 21 June 2014 | 30 | 105 | 17 | RMSE | 1.32 | 1.62 | 3.87 | 3.63 |
| NSE | 0.95 | 0.94 | 0.55 | 0.61 |
| 20 August 2014 | 34 | 125 | 16 | RMSE | 1.28 | 3.38 | 2.88 | 1.81 |
| NSE | 0.99 | 0.92 | 0.94 | 0.98 |
| 21 July 2015 | 35 | 148 | 15 | RMSE | 1.17 | 2.95 | 2.84 | 1.78 |
| NSE | 0.99 | 0.93 | 0.94 | 0.97 |
Table 6.
Mean RMSE and NSE values between the 71 observed hyetographs at Site 1 and their design storms, and the mean relative difference of the simulated peak flooding volume (PV) and time (PT) at the three nodes by the design storms against those simulated by the 71 observed storms at Site 1. All design storms are computed using the parameters derived from the 104 storms at Site 2, together with the total rainfall depth and duration for each storm at Site 1.
Table 6.
Mean RMSE and NSE values between the 71 observed hyetographs at Site 1 and their design storms, and the mean relative difference of the simulated peak flooding volume (PV) and time (PT) at the three nodes by the design storms against those simulated by the 71 observed storms at Site 1. All design storms are computed using the parameters derived from the 104 storms at Site 2, together with the total rainfall depth and duration for each storm at Site 1.
| Index | Improved Huff | Huff | Triangular | Chicago |
|---|
| RMSE | 6.43 | 6.62 | 7.38 | 7.57 |
| NSE | 0.66 | 0.63 | 0.55 | 0.54 |
| N503 | PV(%) | 2 | −12 | −22 | −17 |
| PT(%) | 19 | 24 | 45 | 41 |
| N192 | PV(%) | −6 | −43 | −62 | −19 |
| PT(%) | 17 | 19 | 15 | 24 |
| N519 | PV(%) | 8 | −16 | −38 | −21 |
| PT(%) | 8 | 8 | 9 | 10 |
Table 7.
NSE, RMSE, (mm) and Relative Difference (RD) values between design storms derived by the Improved Huff curves (probability 50%) using different time intervals and observed rainfall depth for all storms at Site 2 from 2008 to 2012.
Table 7.
NSE, RMSE, (mm) and Relative Difference (RD) values between design storms derived by the Improved Huff curves (probability 50%) using different time intervals and observed rainfall depth for all storms at Site 2 from 2008 to 2012.
| Duration (h) | Title | Time Interval (min) |
|---|
| 1 | 5 | 10 | 30 | 60 | 120 |
|---|
| 1 | NSE | 0.97 | 0.94 | 0.81 | | | |
| RMSE | 1.32 | 2.12 | 3.80 | | | |
| RD (%) | 2 | −5 | 13 | | | |
| 1–3 | NSE | 0.94 | 0.94 | 0.94 | 0.89 | 0.75 | |
| RMSE | 2.22 | 2.24 | 2.36 | 3.61 | 5.27 | |
| RD (%) | −2 | −3 | −3 | −5 | −13 | |
| >3 | NSE | 0.92 | 0.92 | 0.92 | 0.92 | 0.90 | 0.82 |
| RMSE | 5.81 | 5.85 | 5.87 | 5.94 | 5.99 | 8.00 |
| RD (%) | 2 | −3 | −3 | −4 | −4 | −10 |
Table 8.
Peak flooding volume, time, and NSE simulated by SWMM using rainfall depths from gauge observations at Sites 4 and the considered design storms. The last four columns are the difference in the simulated peak flooding volume and time using design storms (DS) against those by gauge (G) rainfall depth. The water volume at Node 503 is computed according to the DEM and water depth recorded at Site 4/Node 503, while that at Node 192 and 519 is simulated by SWMM using gauge rainfall depth data at Site 4.
Table 8.
Peak flooding volume, time, and NSE simulated by SWMM using rainfall depths from gauge observations at Sites 4 and the considered design storms. The last four columns are the difference in the simulated peak flooding volume and time using design storms (DS) against those by gauge (G) rainfall depth. The water volume at Node 503 is computed according to the DEM and water depth recorded at Site 4/Node 503, while that at Node 192 and 519 is simulated by SWMM using gauge rainfall depth data at Site 4.
| Date Total P & T | Node | Flooding Volume & Time by Gauge Rain | Difference of Flooding Volume and Time (DS-G) |
|---|
| Improved Huff | Huff | Triangular | Chicago |
|---|
| | | 4733 m3 | −342 | −844 | −1044 | −1173 |
| | 503 | 57 min | 0 | 10 | 14 | 27 |
| | | NSE | 0.97 | 0.93 | 0.90 | 0.86 |
| 2 August 2014 | | 2596 | −281 | −703 | −1313 | −1319 |
| 42 mm | 192 | 46 | −1 | 3 | 7 | 2 |
| 84 min | | NSE | 0.97 | 0.71 | 0.38 | 0.39 |
| | | 4126 | 173 | −532 | −879 | −1171 |
| | 519 | 70 | −2 | −7 | −6 | −5 |
| | | NSE | 0.98 | 0.92 | 0.93 | 0.92 |