Next Article in Journal / Special Issue
Interannual and Decadal Variability in Tropical Pacific Sea Level
Previous Article in Journal
Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme
Previous Article in Special Issue
Global Sea Surface Temperature and Sea Level Rise Estimation with Optimal Historical Time Lag Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 9
Issue 6
10.3390/w9060401
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Role of Perturbing Ocean Initial Condition in Simulated Regional Sea Level Change

by
Aixue Hu
1,*,
Gerald A. Meehl
1,
Detlef Stammer
2,
Weiqing Han
3 and
Warren G. Strand
1
1
Climate and Global Dynamics Laboratory, National Center for Atmospheric Research, Boulder, CO 80303, USA
2
Centrum für Erdsystemforschng und Nachhaltigkeit (CEN), Universität Hamburg, 20146 Hamburg, Germany
3
Department of Atmospheric and Oceanic Sciences, University of Colorado, Boulder, CO 80309, USA
*
Author to whom correspondence should be addressed.
Water 2017, 9(6), 401; https://doi.org/10.3390/w9060401
Submission received: 28 April 2017 / Revised: 27 May 2017 / Accepted: 31 May 2017 / Published: 5 June 2017
(This article belongs to the Special Issue Sea Level Changes)
Browse Figures
Versions Notes

Abstract

:
Multiple lines of observational evidence indicate that the global climate has been getting warmer since the early 20th century. This warmer climate has led to a global mean sea level rise of about 18 cm during the 20th century, and over 6 cm for the first 15 years of the 21st century. Regionally the sea level rise is not uniform due in large part to internal climate variability. To better serve the community, the uncertainties of predicting/projecting regional sea level changes associated with internal climate variability need to be quantified. Previous research on this topic has used single-model large ensembles with perturbed atmospheric initial conditions (ICs). Here we compare uncertainties associated with perturbing ICs in just the atmosphere and just the ocean using a state-of-the-art coupled climate model. We find that by perturbing the oceanic ICs, the uncertainties in regional sea level changes increase compared to those with perturbed atmospheric ICs. Thus, in order for us to better assess the full spectrum of the impacts of such internal climate variability on regional and global sea level rise, approaches that involve perturbing both atmospheric and oceanic initial conditions are necessary.

1. Introduction

Observations indicate that since the mid-20th century, ocean heat content is increasing [1,2], ice caps and mountain glaciers are retreating [3,4,5], and the Greenland and Antarctic ice sheets are losing mass [6,7,8,9,10,11,12]. As the ocean becomes warmer, seawater expands, leading to a thermal steric sea level rise. The changes of the air-sea interaction in terms of evaporation and precipitation over the ocean and the changes of ocean circulation can also affect the local and global sea level through the changes in ocean salinity (halosteric sea level change). The retreat of land based ice (glaciers and ice sheets), on the other hand, resulting in more water discharged from land to sea, leads to an ocean mass increase and thus to a eustatic sea level rise. During the 20th century, the observed global mean sea level increased by 18 cm (e.g., Refs. [7,13]), and another 6 cm during the first 15 years of the 21st century [14]. Studies also suggest that the rates of sea level change may have accelerated in the 21st century (e.g., Refs. [10,15]). Rising sea levels could potentially pose significant threats to coastal and island communities (e.g., Refs. [7,13,16,17,18,19,20]). Moreover, multiple studies have indicated that regional sea level rise (SLR) is not uniform, and could be significantly different from the global mean and among different regions because of the internal climate processes (e.g., Refs. [13,21,22,23,24,25,26,27,28]). To successfully predict future regional SLR in order to benefit human society, it becomes necessary to better assess the SLR uncertainties associated with these internal climate processes, such as examining ocean dynamics.
Ocean dynamics are affected by exchanges of momentum, heat and freshwater between air and sea. Modulations in these exchanges due to internal climate processes or external forcing will affect both the wind-driven gyre circulation and the thermohaline-driven overturning circulation in the ocean (see Ref. [29] for details). As a result, there will be either redistribution of heat and salt in the ocean if there are no changes in external forcing, or a net gain or loss of heat and salt if there are changes in external forcing. This redistribution or net gain/loss of heat and/or of salt in the ocean will change the local seawater density and lead to subsequent changes in regional and/or global sea level through thermosteric and halosteric effects. Previous studies have used multi-model ensembles (such as simulations from the Coupled Model Intercomparison Project Phase 5 (CMIP5) models) or single-model perturbed initial-condition ensembles (such as simulations with the Community Climate System Model version 3: CCSM3) to assess the influence of internal climate processes on SLR and associated uncertainties in their prediction/projection [22,24,30]. In CCSM3, while global mean SLR is not appreciably altered by internal climate processes among different ensemble members, regional SLR can differ significantly from one ensemble member to another [24]. The degree to which this spread in regional SLR among different ensemble members depends on the details of how the ensemble members are initialized (e.g., whether just in the atmosphere as in CCSM3, or also in the ocean) remains to be investigated.
In the multi-model ensemble such as CMIP5, both regional and global mean SLR projections can be significantly different from one model to another under the same external forcing conditions [13,22,31]. This suggests that differences in model physics and possibly also in model horizontal and vertical resolutions may have affected regional and global SLR projections. These differences may also imply that the ocean state in each model and the method by which it is initialized could play a role in determining future projected SLR. Thus, understanding the impact of the details of the ensemble initialization procedure may inform the interpretation of model spread in SLR in multi-model archives such as CMIP5.
Conventionally, a large ensemble of simulations with a given coupled climate model is generated by adding small random perturbations to the atmospheric initial states, keeping initial conditions in the other model components and in the radiative forcing the same. For example, the CCSM3 40-member ensemble uses different days in a given year for the atmospheric initial conditions in each simulation, but with identical ocean, sea ice, and land initial states [32,33,34,35]. In the Community Earth System Model version 1 (CESM1) large ensemble, a round-off level perturbation is added in the atmospheric initial temperature field [36]. Since the CMIP5 multi-model ensemble shows wide spread of projected global mean SLR under the same external forcing which may have hinted at an important role for the oceanic initial state, here we assess how perturbing the oceanic initial state will affect simulated regional and global mean SLR in comparison with perturbing just the initial atmospheric state using a single model—CCSM version 4 (CCSM4). The time frame we are interested in here is decadal to multi-decadal.
The remainder of the study is structured as follows. Section 2 details the CCSM4 model and the experimental design; Section 3 contains the results and Section 4 summarizes the findings in this paper.

2. Model and Experiments

The model used here is the National Center for Atmospheric Research Community Climate System Model version 4 (CCSM4), which is a fully coupled climate model and is developed by collaboration between NCAR scientists, scientists from US Department of Energy laboratories, and university scientists [37]. This model contains the Community Atmospheric Model version 4 (CAM4) with 26 vertical levels and a horizontal resolution of 1 degree, the Parallel Ocean Program (POP) version 2 with 60 levels vertically and nominal 1 degree resolution horizontally, the Community Land Model version 4 (CLM4), and the Community Ice Code version 4 (CICE4). The equilibrium climate sensitivity of this model to a CO2 doubling is 3.2 °C and the transient climate response from a 1% CO2 simulation around the time of CO2 doubling is 1.73 °C, near the median values among the CMIP5 models [38].
Three sets of experiments are used here. The first set is a 30-member ensemble of simulations in which a random round-off level (10−14 K) perturbation is introduced into the initial atmospheric temperature field and the initial conditions (ICs) from all other atmospheric fields and other model components (land, sea ice, and ocean) are kept identical. These ensemble simulations are branched (on 1 January 1970) from the same 20th century simulation forced by time-evolving “all-known” external forcings, such as CO2, methane, volcanic and anthropogenic aerosols, and solar forcing, and are run from 1 January 1970 to 31 December 2005. Hereafter, we call the atmospheric and oceanic ICs (the latter are identical for all members) used in this ensemble simulation as ATM1 and OCN1, and refer to this ensemble as “ATM small” (small perturbation in the initial atmospheric condition).
The second and third sets of ensemble simulations are run with much larger perturbations in the initial atmospheric or oceanic conditions (hereafter referred to as “ATM large” and “OCN large”). To form these ensembles, we make use of the ocean and atmospheric states on 1 January 1970 from six different 20th-century all-forcing simulations of CCSM4. These states are used as initial conditions of atmosphere or ocean for our additional experiments, and are hereafter referred to as ATM1–6 and OCN1–6, respectively (e.g., ATM2 refers to the atmospheric state on 1 January 1970 from the second 20th century all-forcing simulation, ATM3 from the third 20th century simulation, and so on). Note that the six 20th century simulations differ in terms of when they were branched from the 1850 pre-industrial control simulation (see Table 1). Fifteen additional simulations covering the period 1 January 1970 to 31 December 2000 using various combinations of the six atmospheric and oceanic ICs (e.g., ATM 1–6 and OCN 1–6) were performed as follows. Five simulations were carried out using initial conditions ATM1 (sub-ensemble ATM1), four simulations using ATM2 (sub-ensemble ATM2), four simulations using ATM5 (sub-ensemble ATM5), and two simulations using ATM3 (sub-ensemble ATM3) (see Figure 1a). By adding the unperturbed original six CCSM4 20th century simulations using each of the ATM1–6, respectively, the total number of the simulations in this ensemble is 21. For these simulations, the ICs in the other model components other than the ocean were taken from the same simulation as the ATM, but the ICs for ocean model is either from the same simulation as the ATM (unperturbed original simulations) or from the ocean ICs other than that one which is consistent with the ATM ICs (Figure 1a). Another way to look at these simulations is to sort these simulations based on the same ocean ICs. For each of the oceanic initial conditions OCN2 to OCN6, 4 simulations were carried out (Figure 1b). For these simulations, the ICs in the other three model components including the atmosphere were randomly chosen from ATM1 to ATM6 (Table 1 provides salient details of each simulation).
We then use these additional experiments in various combinations to form “ATM large” and “OCN large” as follows. To form ATM large, we sort them based on the same oceanic initial condition, but different atmospheric initial conditions. To form OCN large, we sort them based on the same atmospheric initial condition, but different ocean initial conditions. As outlined in the previous paragraph, these simulations are initialized differently from the ensemble simulations of CCSM3, CESM1 and ATM small which is essentially initialized from the same oceanic IC with small perturbations in atmospheric ICs. The ICs of both atmosphere and ocean in these latter simulations are significantly altered. To construct ATM large (OCN large), we have to remove the sub-ensemble mean SLR with the same ocean (atmospheric) IC first, then the ensemble mean SLR from the 20-member (21-member) ensemble is added back to each of the 20 (21) ensemble members. For example, in the sub-ensemble of ATM1, there are six ensemble members. The ensemble mean of this sub-ensemble is removed first before the full ensemble of ATM large is constructed (see Figure 1). This is equivalent to removing the dependence of the SLR variation on the unperturbed different ocean (atmosphere) ICs. What we will discuss later is the variance of the SLR due to the perturbation of the ocean or atmospheric ICs, which are at least partially independent of the differences among the unperturbed ocean or atmospheric ICs. Note that we have used six different ocean or atmospheric ICs for these simulations.
The ocean component (POP) of CCSM4 uses the Boussinesq approximation that requires conservation of the total ocean volume. Therefore POP can only simulate the dynamic component of SLR associated with the redistribution of heat and salt (this term has a global mean of zero) which is related to ocean circulation changes caused by variations of the momentum, heat and freshwater exchanges between air and ocean. The SLR due to a net gain or loss of heat and salt (steric components of SLR) is diagnosed off-line based on Greatbatch [39] in CCSM4 [24]. Currently, the influence of net freshwater gain due to land-based ice melt, human water management (eustatic) and local vertical land movement (e.g., Refs. [13,29,40]) on SLR is not incorporated in CCSM4 and most other climate models participating CMIP5. Efforts to count this effect offline have been made in recent years (e.g., Refs. [41,42,43]). The Intergovenmental Panel on Climate Change (IPCC) 5th Assessment Report (AR5) is the first IPCC assessment report that combined the effect of anthropogenic forcings, glacial isostatic adjustment, melting of glaciers, and icesheet surface mass balance on regional relative sea level by simply assuming that these terms can add up linearly [13]. It is still a research question about how these processes will interact and feedback to each other and whether the effects of these processes on SLR can be linearly added. Therefore, here we focus only on the contribution of the dynamic and diagnosed thermosteric components of SLR, and refer to their sum as the total SLR, and assess how a perturbed ocean and/or atmospheric initial condition(s) will affect regional and global SLR.

3. Results

Figure 2a shows time series of simulated global mean sea level for each of the six 20th century simulations (colored curves) superimposed upon a 500-year segment (years 800–1299) of the pre-industrial (1850) control run (gray curve) from which they were branched. Figure 2b is the same as Figure 2a except that the linear trend in the control run (based on years 800–1299) has been removed from all curves. Note that the colored curves span a 155-year period (corresponding to the years 1850–2005). In the control run, the almost linear decrease of global mean sea level suggests that the ocean is losing heat at nearly a constant rate, and the resulting rate of sea level fall is about 0.16 cm/decade (8 cm in 500 years). As can be seen, the time evolution of SLR is nearly the same in each of the six 20th century simulations, with only minor differences. The short-lived downward spikes in sea level in each simulation are associated with volcanic eruptions [44]. From Figure 2, it is also clear that the time evolution of global mean SLR with the same ocean initial condition is nearly the same regardless whether the control run SLR trend is removed or is not. The spread for each of the six different initial ocean states is very small, as indicated by the nearly invisible shading which shows the individual members of the ensemble simulations. For example, the left-most one represents the first ensemble—the ATM small. From this point on, we shall only discuss results based on removing the control run trend from each of the 20th century simulations and each of the perturbed initial condition simulations.
The top panel of Figure 3 summarizes the amount of global mean SLR averaged over the period 1996–2005 (the last decade of the simulations) relative to the mean of 1970–1979, while bottom panel of Figure 3 shows the overall rate of SLR expressed as a linear trend during 1970–2005. In both cases, the results are stratified by type of initial condition uncertainty (e.g., ATM small, ATM large, and OCN large). After the removal of the control run trend, the global mean SLR with different ocean initial conditions is a bit larger than that with the same ocean initial conditions, implying that the oceanic initial state may affect the total amount of heat absorbed by the ocean under greenhouse gas forcing (Table 1, Figure 3). Both metrics show similar results. In particular, the ensemble-mean values are approximately 3% smaller for ATM small compared to ATM large and OCN large, while the spread across ensemble members (measured by their standard deviation) is relatively small (order less than 5% of the mean value) for all three ensembles. Therefore, these small differences in global mean SLR among different ensembles and within the same ensemble suggest that internal climate processes do not significantly alter the rate of total additional heat absorption by the ocean induced by changes in external forcing on time scale longer than a decade, agreeing well with previous studies (e.g., Ref. [24]). However, the external forcing and internal variability do affect the temporal evolution of the global mean SLR ash shown in Figure 2 (e.g., Refs. [24,25]).
Regionally, the influence of perturbing the oceanic or atmospheric initial conditions can be much larger than for the global mean. Figure 4 shows the geographic locations of selected coastal cities whose SLR we examine next. Figure 5 shows the 1996–2005 mean SLR anomaly relative to the mean of 1970–1979 while Figure 6 shows the linear trend in SLR over the period 1970–2005 for these cities. In all three ensembles, the decadal mean SLR anomalies and the decadal trends are, in general, higher than the global mean for east coast cities, but lower than the global mean for west coast cities, agreeing with previous studies [24,25,26,27,28]. The variability of the SLR decadal mean anomalies and the decadal trends for these selected cities is much larger than the global mean regardless of initial-condition type. For example, the standard deviation of the decadal mean SLR anomaly across ensemble members for New York is 1.3–2.2 cm (22–40% of the ensemble mean SLR anomaly) vs. 0.11–0.12 cm (–3% of the ensemble mean SLR anomaly) for the global mean, and for decadal trends for New York it is 0.45–0.77 cm/decade (21–35% of the ensemble mean SLR trend) vs. 0.04–0.05 cm/decade (–3% of the ensemble mean SLR trend) for the global mean. In both OCN large and ATM large, more cities show greater ensemble spread compared to ATM small for both decadal mean anomalies and decadal trends (red triangles in Figure 5 and Figure 6). It is also apparent that the ensemble spread of both the decadal mean SLR anomalies and the decadal trends at most cities is larger (red circles) for OCN large than ATM large. These results indicate that by perturbing the ocean initial condition, larger variability in regional SLR is introduced compared to simulations with only the atmospheric initial condition being perturbed.
To quantify differences in the SLR variability at each selected city among different ensembles further, the ratio of the standard deviation for the decadal mean SLR anomalies and the SLR decadal trends is calculated. As shown in Figure 7, in comparison to the ATM small, the variabilities of the SLR decadal mean anomalies and decadal trends are close to 30% smaller for most of the cities in the ATM large ensemble, however these variabilities are more than 30% larger for many cities in the OCN large ensemble. Moreover, the comparison between the OCN large and ATM large ensembles indicates that these variabilities are more than 30% larger in over 50% of the cities, and in some cities, these variabilities are nearly doubled in the OCN large ensemble than in the ATM large ensemble, such as Dar es Salaam, on the east coast of Africa. This result further suggests that the perturbation of the ocean initial conditions is capable of generating larger SLR variability than perturbing the atmospheric initial condition alone at least in some of these coastal cities.
Next, the regional SLR decadal mean anomalies and decadal trends and their variabilities on the globe are shown in Figure 8 and Figure 9. In general, the patterns of the SLR decadal mean anomalies are similar among all three ensembles, such as a larger SLR anomaly in the Southern Oceans, subpolar North Atlantic, and a smaller SLR anomaly in most parts of eastern Pacific and subtropical Atlantic. The variabilities of the SLR decadal mean anomalies are greater in the Pacific except the equatorial and eastern Pacific, the subpolar North Atlantic, Southern Oceans, and western Indian Ocean, smaller in the equatorial and subtropical Atlantic, Northern and eastern Indian Ocean. The SLR decadal trend and variability patterns are very similar to those of the SLR decadal mean anomalies.
The variability patterns in the Pacific are similar to the Interdecadal Pacific Oscillation (IPO)—a major mode of Pacific internal variability on a multi-decadal timescale [45,46]. Both observational and modeling studies show that the SLR variability in the Pacific can be significantly affected by IPO (e.g., Refs. [46,47,48,49,50,51] and see Ref. [52] for more detailed review). In the negative phase of the IPO, the eastern equatorial Pacific is cooler than normal, the easterlies are stronger than normal, leading to a stronger than normal equatorial Ekman divergence and the subtropical Ekman convergence. As a result, the equatorial upwelling and subtropical downwelling are both stronger than normal. This will reduce the heat content in the equatorial Pacific and increase it in the subtropics [53], thus, a higher sea level rise in the western Pacific, a lower one in the eastern Pacific as shown by recent observational based studies (e.g., Refs. [48,50,54]). Moreover, studies show that IPO is an internal climate variability and the IPO phases are not significantly influenced by changes of the external forcings. The phases of the IPO from different ensemble members are not consistent, thus lead to different variability among different ensemble members [55]. Therefore, the resulting SLR variability is also larger, especially in the subtropical western Pacific.
In the subpolar North Atlantic, the SLR variability is mostly affected by the North Atlantic Oscillation (NAO)—a mode of variability that is possibly intrinsic to the atmosphere or is a coupled variability between the air and sea (e.g., Refs. [56,57,58,59,60]). Previous studies suggest that the decadal timescale NAO variability can significantly affect the wind and buoyancy forcing in the subpolar North Atlantic, and modulate the strength of the deep convection there, and subsequently the strength of the Atlantic meridional overturning circulation (AMOC) [61,62,63]. AMOC is a global scale ocean circulation that transports warm salty water to the subpolar North Atlantic, where this water losses heat to the atmosphere and sinks to depth, and then flows southward and upwells elsewhere in the global ocean. The heat transported by this circulation can affect the sea level changes in the Atlantic basin [24,30,51,62,64]. The changes of the AMOC and the upper ocean stratification affect the upper ocean circulation and the regional SLR. As indicated by Ref. [51], NAO can affect the variability of SLR in the subpolar North Atlantic, but due to its lack of a longterm trend, the NAO does not significantly affect the SLR long term trend. Therefore, the high SLR variability in the subpolar North Atlantic in all ensemble simulations is associated with the NAO variability and its modulation of the AMOC.
In the Southern oceans, the large SLR variability is associated with the changes of Southern Ocean winds, possibly caused by the variability of the Southern Annular Mode (SAM)—another atmospheric mode [65]. The differences across ensemble member in the phases and amplitudes of the SAM can induce different strength in westerly wind around the southern oceans, altering the Antarctic circumpolar oceanic currents (ACC) and the regional sea level [51]. The higher SLR away from Antarctic and lower SLR near the Antarctic continent is related to the strengthening of the westerly wind and a faster ACC. As a result, the ocean tilts higher north of the ACC and lower south of the ACC.
To demonstrate further the importance of perturbing the ocean initial condition, the ratio of the standard deviation for SLR decadal mean and decadal trend among different ensembles is calculated and shown in Figure 10. In general, these standard deviation ratio patterns of the SLR decadal mean among different ensembles are similar to those of the SLR decadal trend. However, the ratio of the former is a bit smaller than the latter, suggesting that the SLR decadal trend is affected by the initial conditions more than the SLR decadal mean. In comparisons between the ATM large and ATM small ensembles, there are many places where the SLR decadal mean (trend) variability is larger in the former than the latter, but there are also many places where the SLR decadal mean (trend) variability is less in the former than the latter. This result may suggest that the larger or smaller perturbation of the atmospheric fields may not make a significant difference on the regional sea level change. However, in comparing the OCN large and ATM small ensembles, it is clear that the variability of the SLR decadal mean (trend) in the OCN large ensemble is much bigger than that in ATM small in most of regions, except portions of the Pacific and parts of North Atlantic. Moreover, when OCN large and ATM large ensembles are compared, the larger variability of the SLR decadal mean (trend) across ensemble members in the former becomes even more obvious in most regions. In some regions, such as part of Southern Ocean, south of Australia, South Atlantic, and Indian Ocean, the SLR decadal mean (trend) variability in OCN large ensemble is twice as large as that in ATM large. Therefore, perturbing the oceanic initial condition can indeed produce larger internal climate processes induced variance than perturbing the atmospheric initial condition. This may be a key to understanding why both global mean SLR and regional SLR differ from one model to another under the same external forcing. 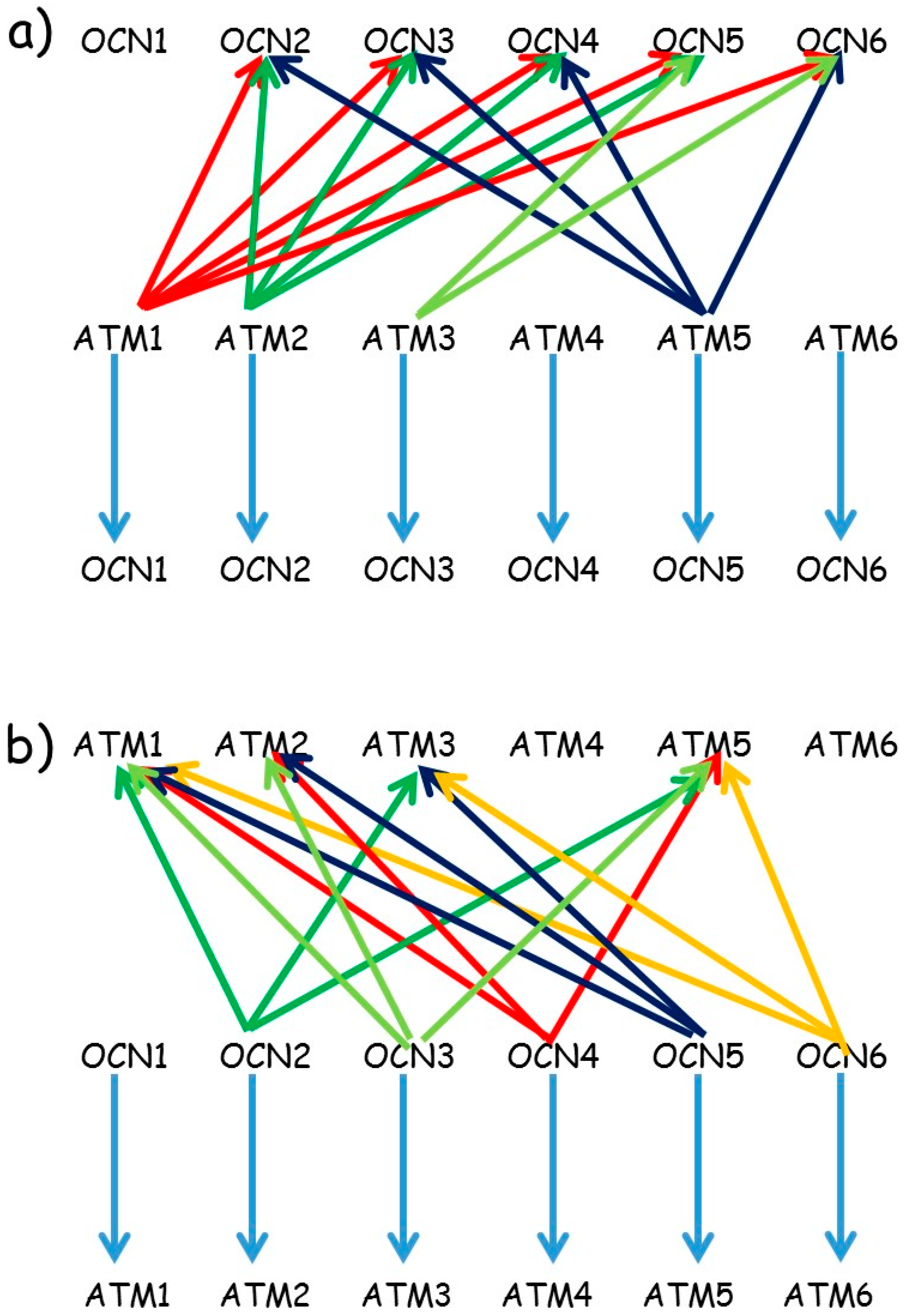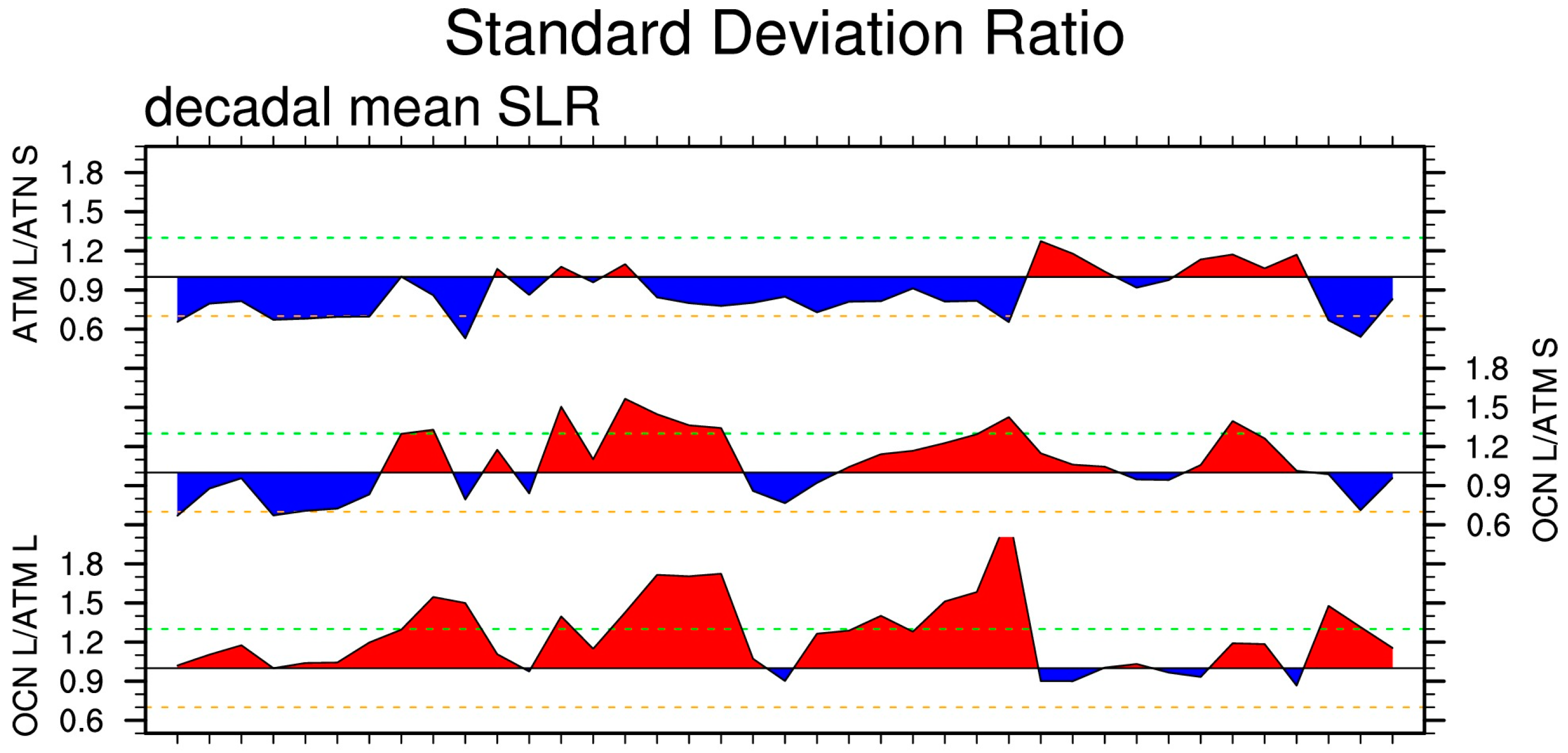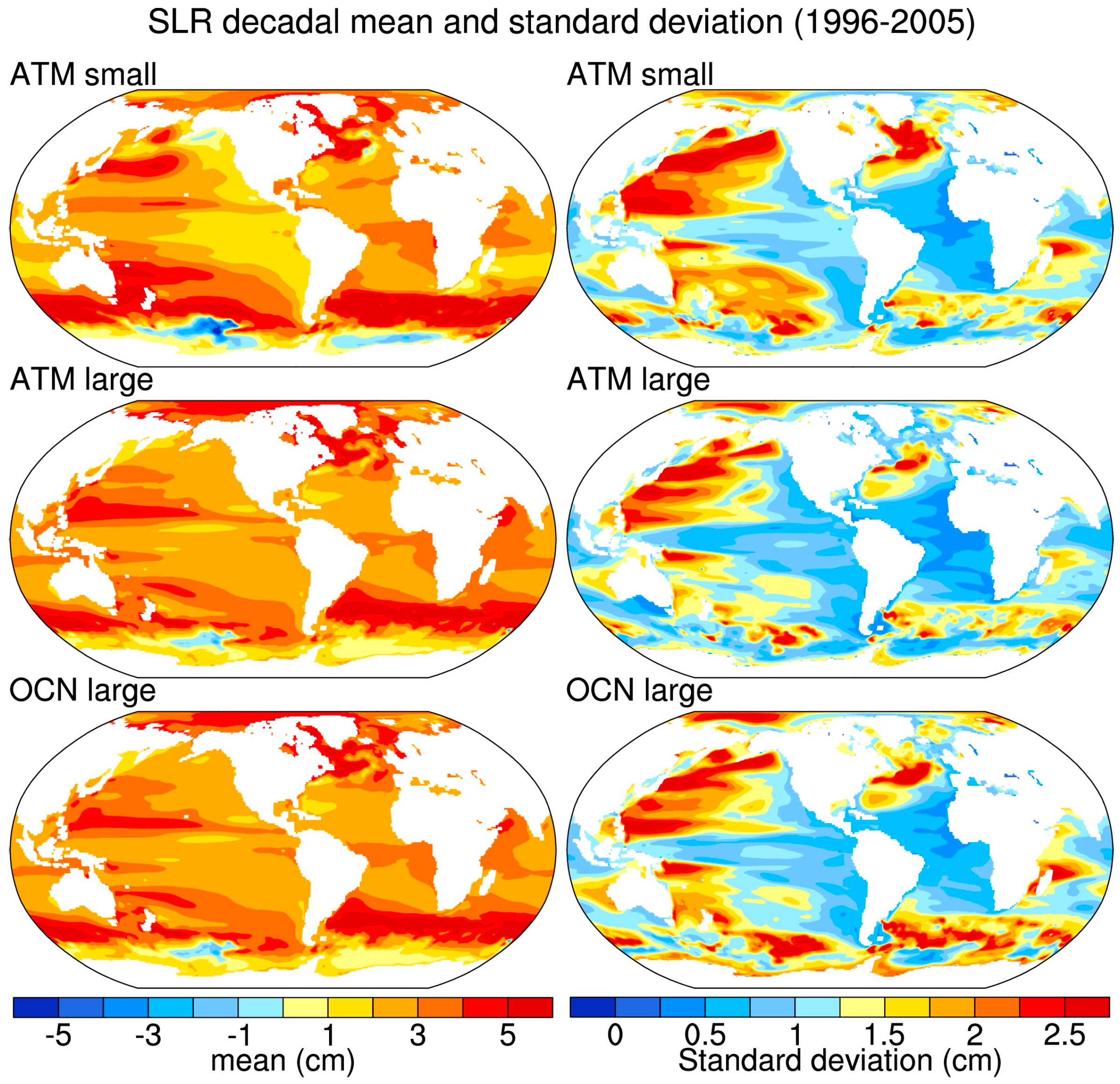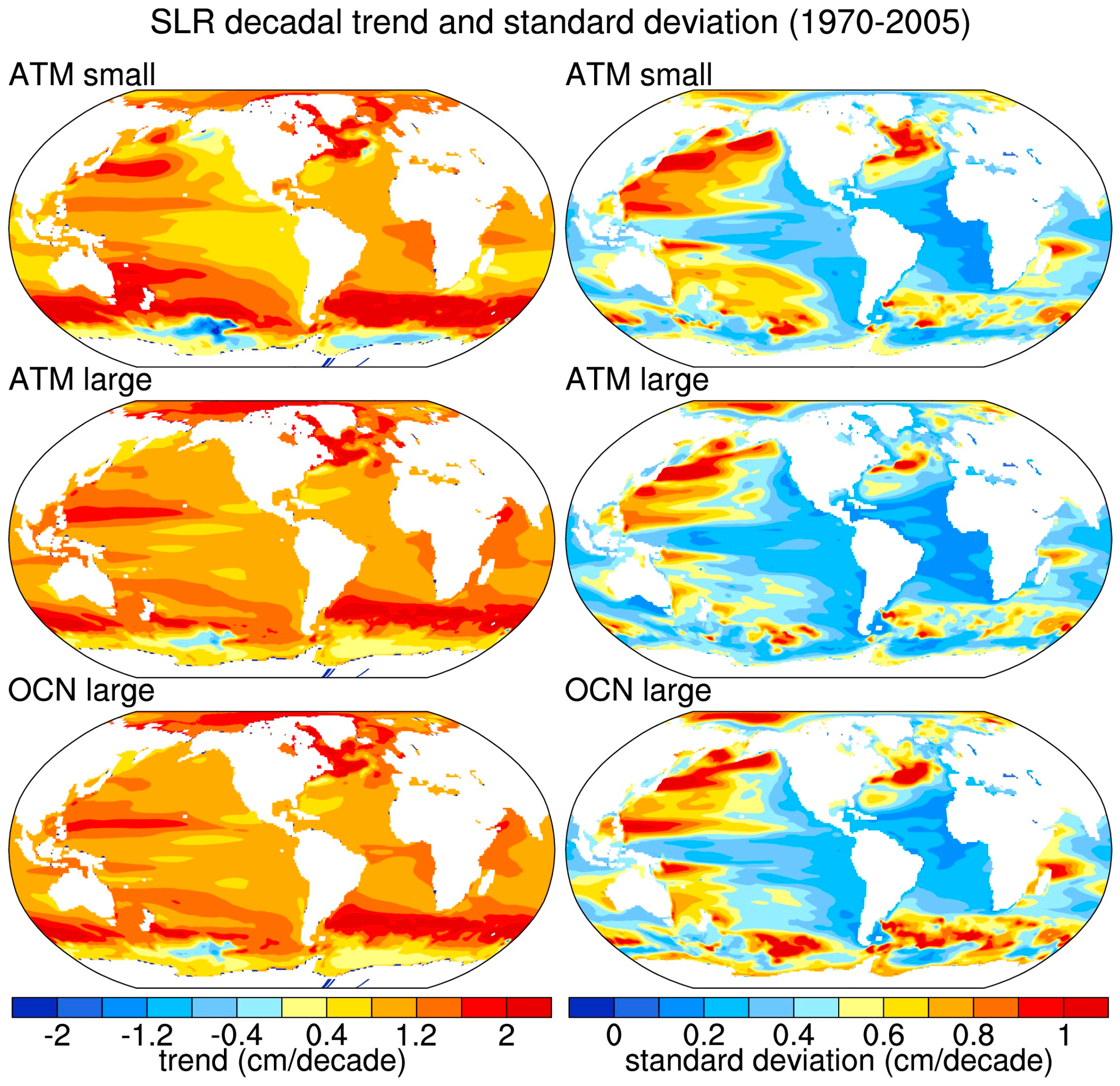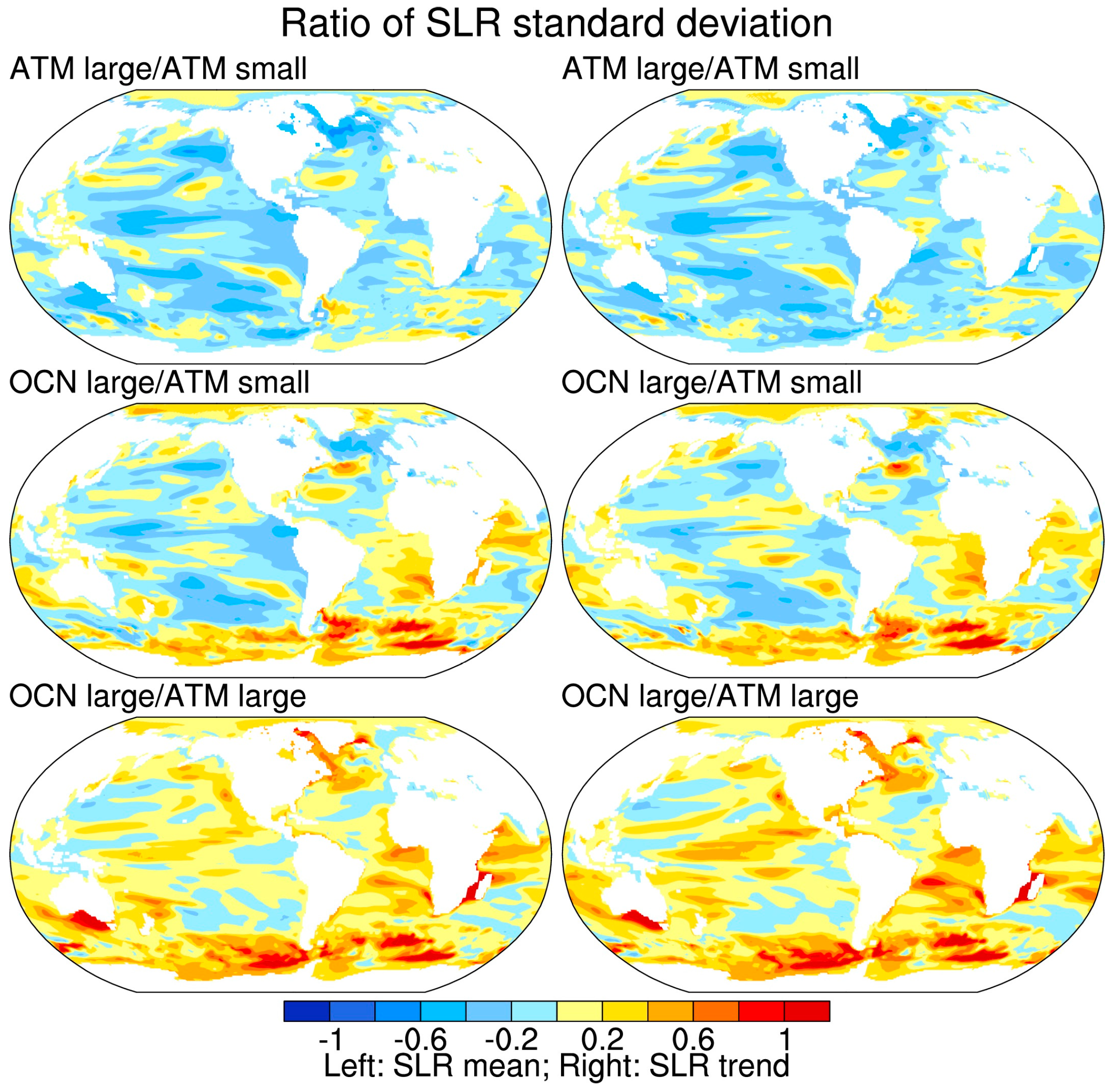From our analysis, this is at least partly due to the different ocean states in each model other than just due to the different details of the model physics.

4. Conclusions

In this study, we investigated the influence of perturbing ocean initial conditions vs. perturbing atmospheric initial conditions on projected/predicted regional and global SLR through analyzing three sets of ensemble simulations using a coupled climate model—CCSM4. Our results show that perturbing the ocean initial conditions in general can produce larger variance on regional sea level change than perturbing the atmospheric initial conditions, on a multi-decadal timescale. The intra-ensemble variance for regional SLR in the ensemble with perturbed ocean initial conditions is much larger than the intra-ensemble variance in the ensemble with only perturbed atmospheric initial conditions. As a result, the inter-ensemble variance for regional SLR is larger in the ensemble with perturbed ocean initial conditions than in the ensemble with perturbed atmospheric initial conditions. To a lesser degree, this is also true for the global mean SLR. Therefore, our results suggest that the inter-model spread of the projected SLR in CMIP5 models for both global mean and regional SLR may at least partially be associated to the different ocean states although the different model physics and model horizontal and vertical resolutions may still play a more dominant role. This is consistent with Ref. [5] showing that individual CMIP5 models have substantially different climate sensitivity, in part due to different vertical stratifications of the ocean and thus different capacities to take up anthropogenic heat anomalies (among other parameters), furthering differences in global mean SLR.
In this study, the ensemble simulations were run for only 36 years, and the ensemble size may not be large enough to conclusively determine the importance of the perturbing ocean initial conditions on projected/predicted regional and global SLR, especially on a centennial timescale. Longer simulations and increasing the number of ensemble members are needed to address these issues in future studies. Nevertheless, our research sheds more light on the potential impact of the intrinsic variabilities of the climate system on the projected SLR regional spread and to certain extent uncertainties in SLR. For future ensemble simulations, especially a set from a single model, perturbing both ocean and atmospheric initial conditions is necessary to sample the uncertainties of the regional SLR or other climate variables due to the intrinsic climate variability in our Earth system.
Finally, we would like to mention a caveat on the model biases in simulating the observed ocean properties, specifically for CCSM4. These model biases have been documented in much detail in Refs. [66,67,68], such as the deep convection sites in the subpolar North Atlantic, the ENSO variability etc. These biases have been improved in this version of the CCSM in comparison to the previous version of the CCSM. For our study, since we are using the same model, the biases exist in all simulations. Therefore, when we compare the anomalies of the sea level changes, these biases would be removed and would not affect our results much.

Acknowledgments

Authors want to express sincere appreciation for many suggestions from Clara Deser. A portion of this study was supported by the Regional and Global Climate Modeling Program (RGCM) of the U.S. Department of Energy’s Office of Science (BER), Cooperative Agreement No. DE-FC02-97ER62402. This research used computing resources of the Climate Simulation Laboratory at the National Center for Atmospheric Research (NCAR), which is sponsored by the National Science Foundation. The National Center for Atmospheric Research is sponsored by the National Science Foundation.

Author Contributions

A.H. conceived, designed and performed the experiments; A.H., G.M., D.S., W.H. and W.S. are all analyzed the data; and all authors actively wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

References

  1. Antonov, J.I.; Levitus, S.; Boyer, T.P. Steric sea level variations during 1957–1994: Importance of salinity. J. Geophys. Res. 2002, 107, 8013. [Google Scholar] [CrossRef]
  2. Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Regan, J.R.; Seidov, D.; Yarosh, E.S. World Ocean heat content and thermosteric sea level change (0–2000 m) 1955–2010. Geophys. Res. Lett. 2012, 39, L10603. [Google Scholar] [CrossRef]
  3. Crowley, T.J. Causes of Climate Change Over the Past 1000 Years. Science 2000, 289, 270–277. [Google Scholar] [CrossRef] [PubMed]
  4. Gregory, J.M.; Huybrechts, P. Ice-sheet contributions to future sea-level change. Philos. R. Soc. Lond. A 2006, 364, 1709–1731. [Google Scholar] [CrossRef] [PubMed]
  5. Gregory, J.M.; White, N.J.; Churcg, J.A.; Bierkens, M.F.P.; Box, J.E.; vanden Broeke, M.R.; Cogley, J.G.; Fettweis, X.; Hanna, E.; Huybrechts, P.; et al. Twentieth-century global-mean sea level rise: Is the whole greater than the sum of the parts? J. Clim. 2013, 26, 4476–4499. [Google Scholar] [CrossRef]
  6. Rignot, E.; Velicogna, I.; van den Broeke, M.R.; Monaghan, A.; Lenaerts, J. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 2011, 38, L05503. [Google Scholar] [CrossRef]
  7. Church, J.A.; White, N.J.; Konikow, L.F.; Domingues, C.M.; Cogley, J.G.; Rignot, E.; Gregory, J.M.; van den Broeke, M.R.; Monaghan, A.J.; Velicogna, I. Revisiting the Earth’s sea-level and energy budgets from 1961 to 2008. Geophys. Res. Lett. 2011, 38, L18601. [Google Scholar] [CrossRef]
  8. Jacob, T.; Wahr, J.; Tad Pfeffer, W.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
  9. Bamber, J.; van den Broeke, M.; Ettema, J.; Lenaerts, J.; Rignot, E. Recent large increases in freshwater fluxes from Greenland into the North Atlantic. Geophys. Res. Lett. 2012, 39, L19501. [Google Scholar] [CrossRef]
  10. Vaughan, D.G.; Comiso, J.C.; Alison, I.; Carrasco, J.; Kaser, G.; Kwok, R.; Mote, P.; Myrray, T.; Paul, F.; Ren, J.; et al. Observations: Cryosphere. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., et al., Eds.; Cambridge Univ. Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
  11. Van Angelen, J.H.; van den Broeke, M.R.; Wouters, B.; Lenaerts, J.M.T. Contemporary (1960–2012) evolution of the climate and surface mass balance of the Greenland ice sheet. Surv. Geophys. 2014, 35, 1155–1174. [Google Scholar] [CrossRef]
  12. Kahn, S.A.; Aschwanden, A.; Bjørk, A.; Wahr, J.; Kjeldsen, K.K.; Kjaer, K.H. Greenland ice sheet mass balance: A review. Rep. Prog. Phys. 2015, 78, 046801. [Google Scholar] [CrossRef] [PubMed]
  13. Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermenn, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., et al., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
  14. Beckley, B.D.; Zelensky, N.P.; Holmes, S.A.; Lemoine, F.G.; Ray, R.D.; Mitchum, G.T.; Desai, S.; Brown, S.T. Assessment of the Jason-2 Extension to the TOPEX/Poseidon, Jason-1 Sea-Surface Height Time Series for Global Mean Sea Level Monitoring. Mar. Geod. 2010, 33, 447–471. [Google Scholar] [CrossRef]
  15. Fasullo, J.T.; Nerem, R.S.; Hamlington, B. Is the detection of accelerated sea level rise imminent? Sci. Rep. 2016, 6, 6. [Google Scholar] [CrossRef] [PubMed]
  16. Milne, G.A.; Gehrels, W.R.; Hughes, C.W.; Tamisiea, M.E. Identifying the causes of sea-level change. Nat. Geosci. 2009, 2, 471–478. [Google Scholar] [CrossRef]
  17. National Research Council. Sea-Level Rise for the Coasts of California, Oregon, and Washington: Past, Present, and Future; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
  18. Tebaldi, T.; Strauss, B.H.; Zervas, C.E. Modelling sea level rise impacts on storm surges along US coasts. Environ. Res. Lett. 2012, 7, 014032. [Google Scholar] [CrossRef]
  19. Sallenger, A.H., Jr.; Doran, K.S.; Howd, P.A. Hotspot of accelerated sea-level rise on the Atlantic coast of North America. Nat. Clim. Chang. 2012, 2, 884–888. [Google Scholar] [CrossRef]
  20. Goddard, P.B.; Yin, J.; Griffies, S.M.; Zhang, S. An extreme event of sea-level rise along the Northeast coast of North America in 2009–2010. Nat. Commun. 2015, 6, 6346. [Google Scholar] [CrossRef] [PubMed]
  21. Han, W.; Meehl, G.A.; Rajagopalan, B.; Fasullo, J.T.; Hu, A.; Lin, J.; Large, W.G.; Wang, J.; Quan, X.-W.; Trenary, L.L. Patterns of Indian Ocean sea-level change in a warming climate. Nat. Geosci. 2010, 3, 546–550. [Google Scholar] [CrossRef]
  22. Yin, J.; Griffies, S.M.; Stouffer, R.J. Spatial variability of sea level rise in twenty-first century projections. J. Clim. 2010, 23, 4585–4607. [Google Scholar] [CrossRef]
  23. Merrifield, M.A.; Thompson, P.R.; Lander, M. Multidecadal sea level anomalies and trends in the western tropical Pacific. Geophys. Res. Lett. 2012, 39, L13602. [Google Scholar] [CrossRef]
  24. Hu, A.; Deser, C. Uncertainty in future regional sea level rise due to internal climate variability. Geophys. Res. Lett. 2013, 40, 2768–2772. [Google Scholar] [CrossRef]
  25. Häkkinen, S.; Rhines, P.B.; Worthen, D.L. Warming of the Global Ocean: Spatial Structure and Water-Mass Trends. J. Clim. 2016, 29, 4949–4963. [Google Scholar] [CrossRef]
  26. Seidov, D.; Mishonov, A.; Reagan, J.; Parsons, R. Multidecadal variability and climate shift in the North Atlantic Ocean. Geophys. Res. Lett. 2017. [Google Scholar] [CrossRef]
  27. Häkkinen, S.; Rhines, P.B.; Worthen, D.L. Heat content variability in the North Atlantic Ocean in ocean reanalyses. Geophys. Res. Lett. 2015, 42, 2901–2909. [Google Scholar] [CrossRef] [PubMed]
  28. Lozier, M.S.; Leadbetter, S.; Williams, R.G.; Roussenov, V.; Reed, M.S.C.; Moore, N.J. The Spatial Pattern and Mechanisms of Heat-Content Change in the North Atlantic. Science 2008, 319, 800–803. [Google Scholar] [CrossRef] [PubMed]
  29. Stammer, D.; Cazenave, A.; Ponte, R.M.; Tamisiea, M.E. Causes for contemporary regional sea level changes. Annu. Rev. Mar. Sci. 2013, 5, 21–46. [Google Scholar] [CrossRef] [PubMed]
  30. Yin, J.; Schlesinger, M.E.; Stouffer, R.J. Model projections of rapid sea level rise on the mortheast coast of the United States. Nat. Geosci. 2009, 2, 262–266. [Google Scholar] [CrossRef]
  31. Slangen, A.B.A.; Church, J.A.; Zhang, X.; Monselesan, D. Detection and attribution of global mean thermosteric sea level change. Geophys. Res. Lett. 2014, 41, 5951–5959. [Google Scholar] [CrossRef]
  32. Deser, C.; Alexander, M.A.; Xie, S.P.; Phillips, A.S. Sea surface temperature variability: Patterns and mechanisms. Ann. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed]
  33. Deser, C.; Phillips, A.S.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: The role of internal variability. Clim. Dyn. 2012, 38, 527–546. [Google Scholar] [CrossRef]
  34. Deser, C.; Knutti, R.; Solomon, S.; Phillips, A.S. Communication of the role of natural variability in future North American climate. Nat. Clim. Chang. 2012, 2, 775–779. [Google Scholar] [CrossRef]
  35. Branstator, G.; Teng, H. Two limits of initial-value decadal predictability in a CGCM. J. Clim. 2010, 23, 6292–6311. [Google Scholar] [CrossRef]
  36. Kay, J.E.; Deser, C.; Phiillips, A.; Mai, A.; Hannay, C.; Strand, G.; Arblaster, J.M.; Bates, S.C.; Danabasoglu, G.; Edwards, J. The Community Earth System Model (CESM) Large Ensemble Project: A community resource for studying climate change in the presence of internal climate variability. Bull. Am. Met. Soc. 2015, 96, 1333–1349. [Google Scholar] [CrossRef]
  37. Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M. The community climate system model version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
  38. Meehl, G.A.; Washington, W.M.; Arblaster, J.M.; Hu, A.; Teng, H.; Tebaldi, C.; Strand, W.G.; White, J.B., III. Climate system response to external forcings and climate change projections in CCSM4. J. Clim. 2012, 25, 3661–3683. [Google Scholar] [CrossRef]
  39. Greatbatch, R.J. A note on the representation of steric sea level in models that conserve volume rather than mass. J. Geophys. Res. 1994, 99, 12767–12771. [Google Scholar] [CrossRef]
  40. Kopp, R.E.; Hay, C.C.; Little, C.M.; Mitrovica, J.X. Geographic variability of sea-level change. Curr. Clim. Chang. Rep. 2015, 1, 192–204. [Google Scholar] [CrossRef]
  41. Mitrovica, J.X.; Gomez, N.; Clark, P.U. The sea level fingerprint of West Antarctic collapse. Science 2009, 232, 753. [Google Scholar] [CrossRef] [PubMed]
  42. Kopp, R.E.; Mitrovica, J.X.; Griffies, S.M.; Yin, J.; Hay, C.C.; Stouffer, R.J. The impact of Greenland melt on regional sea level: A partially coupled analysis of dynamic and static equilibrium effects in idealized water-hosing experiments. Clim. Chang. 2010, 103, 619–625. [Google Scholar] [CrossRef]
  43. Spada, G.; Bamber, J.L.; Hurkmans, R.T.W.L. The gravitationally consistent sea-level fingerprint of future terrestrial ice loss. Geophys. Res. Lett. 2013, 40, 482–486. [Google Scholar] [CrossRef]
  44. Meehl, G.A.; Washington, W.M.; Collins, W.D.; Arblaster, J.M.; Hu, A.; Buja, L.E.; Strand, W.G.; Teng, H. How much more global warming and sea level rise. Science 2005, 307, 1769–1772. [Google Scholar] [CrossRef] [PubMed]
  45. Power, S.; Casey, T.; Folland, C.; Colman, A.; Mehta, V. Interdecadal modulation of the impact of ENSO on Australia. Clim. Dyn. 1999, 15, 319–324. [Google Scholar] [CrossRef]
  46. Meehl, G.A.; Hu, A. Megadroughts in the Indian monsoon and southwest North America and a mechanism for associated multi-decadal Pacific sea surface temperature anomalies. J. Clim. 2006, 19, 1605–1623. [Google Scholar] [CrossRef]
  47. Miller, L.; Douglas, B.C. Gyre-scale atmospheric pressure variations and their relation to 19th and 20th century sea level rise. Geophys. Res. Lett. 2007, 34, L16602. [Google Scholar] [CrossRef]
  48. Hamlington, B.D.; Leben, R.; Nerem, R.S.; Han, W.; Kim, K.Y. Reconstructing sea level using cyclostationary empirical orthogonal functions. J. Geophys. Res. 2011, 116, C12015. [Google Scholar] [CrossRef]
  49. Zhang, X.; Church, J.A. Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 2012, 39, L21701. [Google Scholar] [CrossRef]
  50. Hamlington, B.D.; Leben, R.; Strassburg, M.W.; Nerem, R.S.; Kim, K.Y. Contribution of the Pacific decadal oscillation to global mean sea level trends. Geophys. Res. Lett. 2013, 40, 5171–5175. [Google Scholar] [CrossRef]
  51. Hu, A.; Bates, S. Influence of internal climate variability on mitigating the projected future regional sea level rise. Nat. Commun. 2017. under revision. [Google Scholar]
  52. Han, W.; Meehl, G.A.; Stammer, D.; Hu, A.; Hamlington, B.; Kenigson, J.; Palanisamy, H.; Thompson, P. Spatial Patterns of Sea Level Variability Associated with Natural Internal Climate Modes. Serv. Geophys. 2017, 38, 217–250. [Google Scholar] [CrossRef]
  53. Hu, Z.; Hu, A.; Hu, Y. Impacts of Interdecadal Pacific Oscillation and Atlantic Multidecadal Oscillation on Global Ocean Heat Content Distribution. J. Clim. 2017. under revision. [Google Scholar]
  54. Hamlington, B.D.; Strassburg, M.W.; Leben, R.; Han, W.; Nerem, R.S.; Kim, K.Y. Uncovering the anthropogenic warming-induced sea level rise signal in the Pacific Ocean. Nat. Clim. Chang. 2014, 4, 782–785. [Google Scholar] [CrossRef]
  55. Si, D.; Hu, A. Internally generated and externally forced multidecadal oceanic modes and their influence on the summer rainfall over East Asia. J. Clim. 2017. under revision. [Google Scholar]
  56. Hurrell, J.W. Decadal trends in the North Atlantic Oscillation regional temperatures and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
  57. Hurrell, J.W.; van Loon, H. Decadal variations in climate associated with the North Atlantic oscillation. Clim. Chang. 1997, 36, 301–326. [Google Scholar] [CrossRef]
  58. Jones, P.D.; Jonsson, T.; Wheeler, D. Extension of the North Atlantic Oscillation using early instrumental pressure observations from Gibraltar and south-west Iceland. Int. J. Climatol. 1997, 17, 1433–1450. [Google Scholar] [CrossRef]
  59. Barsugli, J.J.; Battisti, D.S. The basic effects of atmosphere-ocean internal coupling on midlatitude variability. J. Atmos. Sci. 1998, 55, 477–493. [Google Scholar] [CrossRef]
  60. Saravanan, R.; McWilliams, J.C. Advective ocean-atmosphere interaction: An analytical stochastic model with implications for decadal variability. J. Clim. 1998, 11, 165–188. [Google Scholar] [CrossRef]
  61. Hu, A. Changes in the Arctic and Their Impact on the Oceanic Meridional Overturning Circulation. Ph.D. Dissertation, University of Miami, Coral Gables, FL, USA, 2001; 171p. [Google Scholar]
  62. Hu, A.; Meehl, G.A.; Han, W.; Yin, J. Transient Response of the MOC and Climate to Potential Melting of the Greenland Ice Sheet in the 21st Century. Geophys. Res. Lett. 2009, 36, L10707. [Google Scholar] [CrossRef]
  63. Hu, A.; Meehl, G.A.; Han, W.; Timmermann, A.; Otto-Bliesner, B.; Liu, Z.; Washington, W.M.; Large, W.; Abe-Ouchi, A.; Kimoto, M.; et al. Role of the Bering Strait on the hysteresis of the ocean conveyor belt circulation and glacial climate stability. Proc. Natl. Acad. Sci. USA 2012, 109, 6421–6422. [Google Scholar] [CrossRef] [PubMed]
  64. Hu, A.; Meehl, G.A.; Han, W.; Yin, J. Effect of the potential melting of the Greenland Ice Sheet on the Meridional Overturning Circulation and global climate in the future. Deep-Sea Res. II 2011, 58, 1914–1926. [Google Scholar] [CrossRef]
  65. Thompson, D.W.J.; Wallace, J.M. Annular modes in the extratropical circulation. Part I: Month-to-month variability. J. Clim. 2000, 13, 1000–1016. [Google Scholar] [CrossRef]
  66. Danabasoglu, G.; Yeager, S.G.; Kwon, Y.-O.; Tribbia, J.J.; Phillps, A.S.; Hurrell, J.W. Variability of the Atlantic Meridional Overturning circulation in CCSM4. J. Clim. 2012, 25, 5153–5172. [Google Scholar] [CrossRef]
  67. Deser, C.; Phillips, A.S.; Tomas, R.A.; Okumura, Y.M.; Alexander, M.A.; Capotondi, A.; Scott, J.D.; Kwon, Y.-O.; Ohba, M. ENSO and Pacific Decadal variability in the community climate system model version 4. J. Clim. 2012, 25, 2622–2651. [Google Scholar] [CrossRef]
  68. Yeager, S.; Karspeck, A.; Danabasoglu, G.; Tribbia, J.; Teng, H. A decadal prediction case study: Late twentieth-century North Atlantic ocean heat content. J. Clim. 2012, 25, 5173–5189. [Google Scholar] [CrossRef]
Water 09 00401 g001 550
Figure 1. Schematic plot for the atmospheric (ATM) large and ocean (OCN) large simulations: the arrows point from atmospheric initial condition to the oceanic initial condition for panel (a) and from oceanic initial condition to atmospheric initial condition for panel (b). Blue arrows represent the original six 20th century all forcing simulations; other color arrows represent the sub-ensemble simulations from a common atmospheric or oceanic initial conditions with different oceanic or atmospheric initial conditions respectively.
Figure 1. Schematic plot for the atmospheric (ATM) large and ocean (OCN) large simulations: the arrows point from atmospheric initial condition to the oceanic initial condition for panel (a) and from oceanic initial condition to atmospheric initial condition for panel (b). Blue arrows represent the original six 20th century all forcing simulations; other color arrows represent the sub-ensemble simulations from a common atmospheric or oceanic initial conditions with different oceanic or atmospheric initial conditions respectively.
Water 09 00401 g001
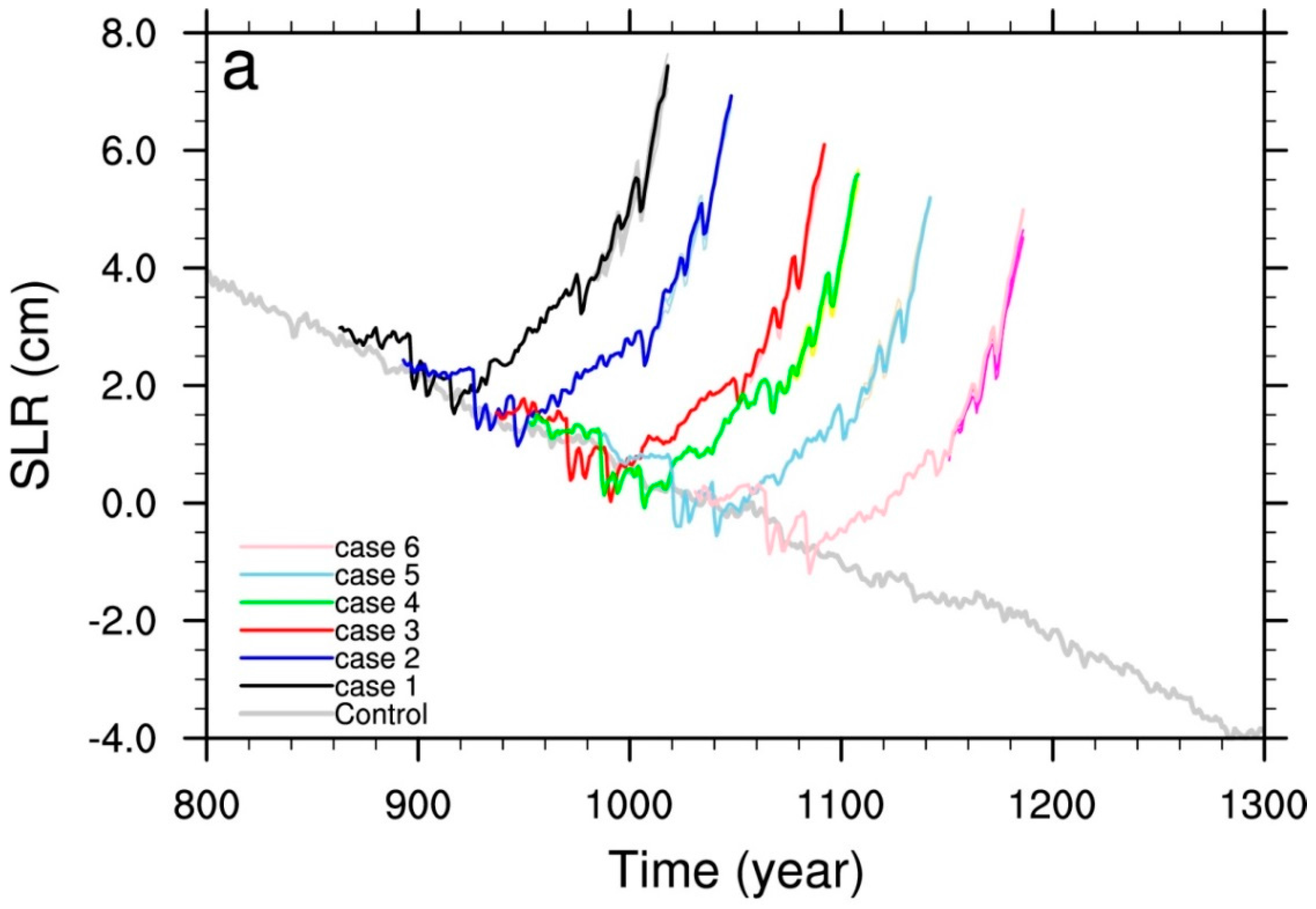
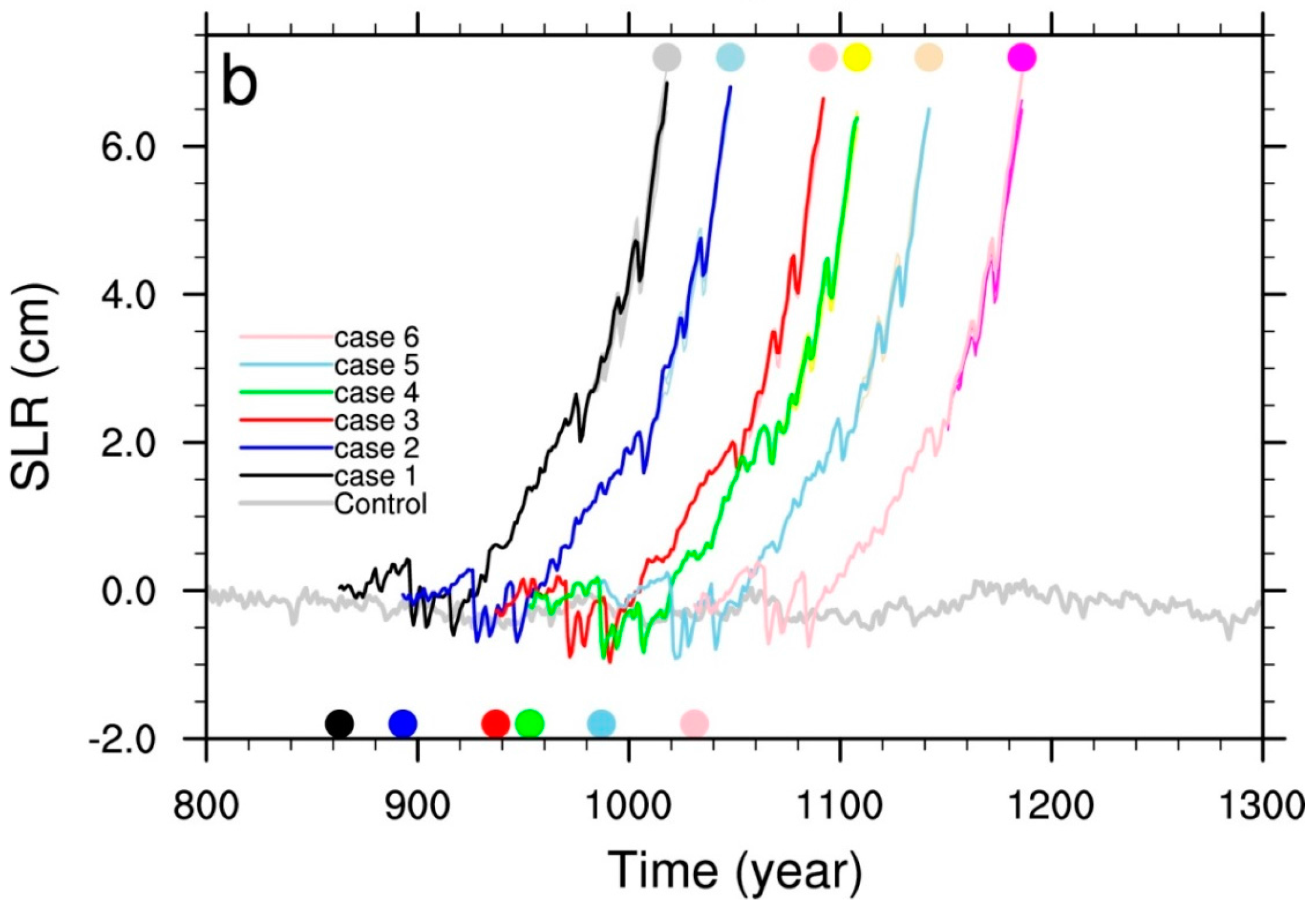
Water 09 00401 g002a 550Water 09 00401 g002b 550
Figure 2. Time evolution of the global mean sea level for the control and six historical runs with (a) or without (b) the control run trend. The shadings are each individual member from each of the six different ocean initial states. The dots at the bottom of panel (b) indicate when the 20th century simulations are branched from the 1850 control run. The dots on the top show the ending year of each individual 20th century runs (year 2005).
Figure 2. Time evolution of the global mean sea level for the control and six historical runs with (a) or without (b) the control run trend. The shadings are each individual member from each of the six different ocean initial states. The dots at the bottom of panel (b) indicate when the 20th century simulations are branched from the 1850 control run. The dots on the top show the ending year of each individual 20th century runs (year 2005).
Water 09 00401 g002aWater 09 00401 g002b
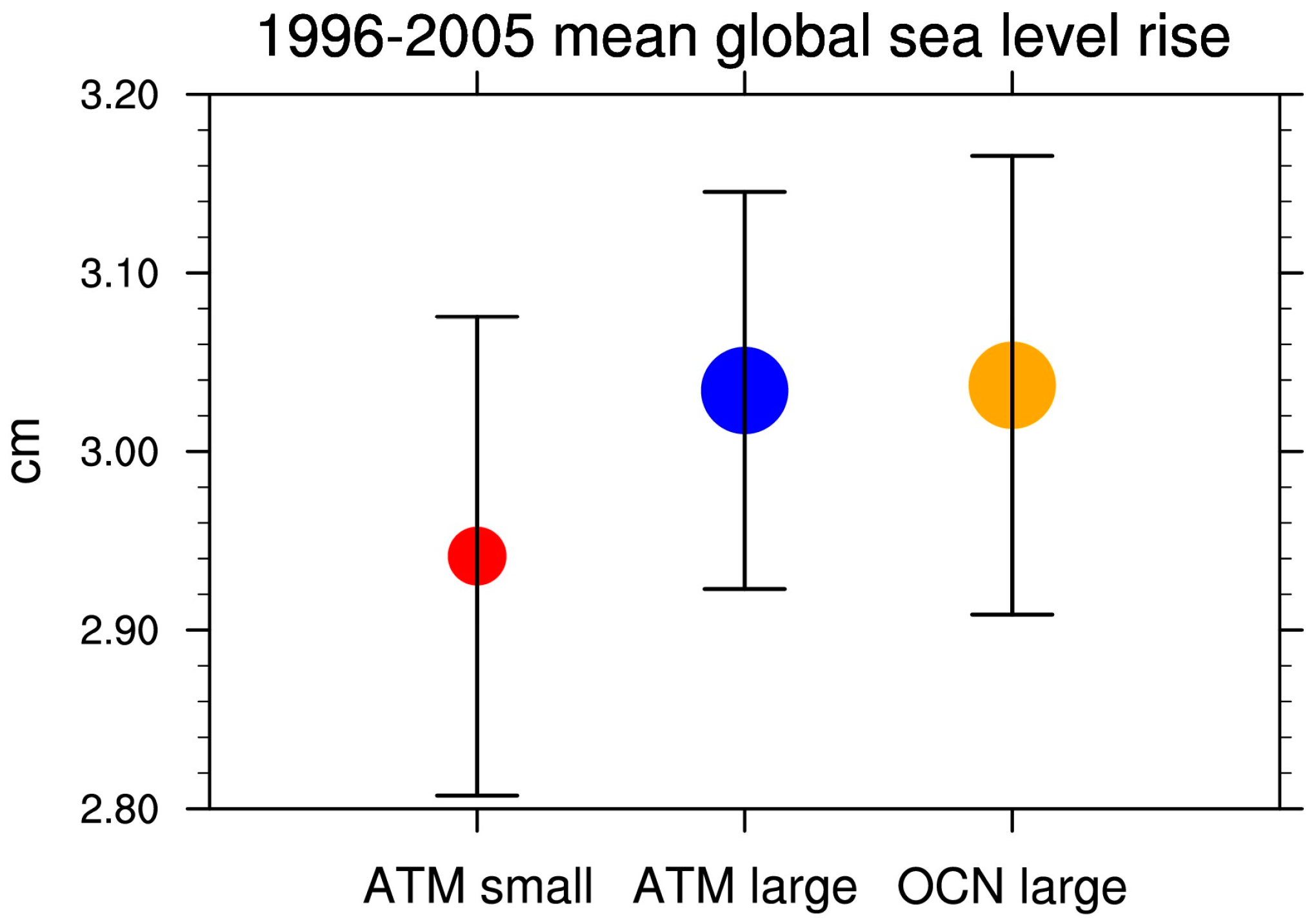
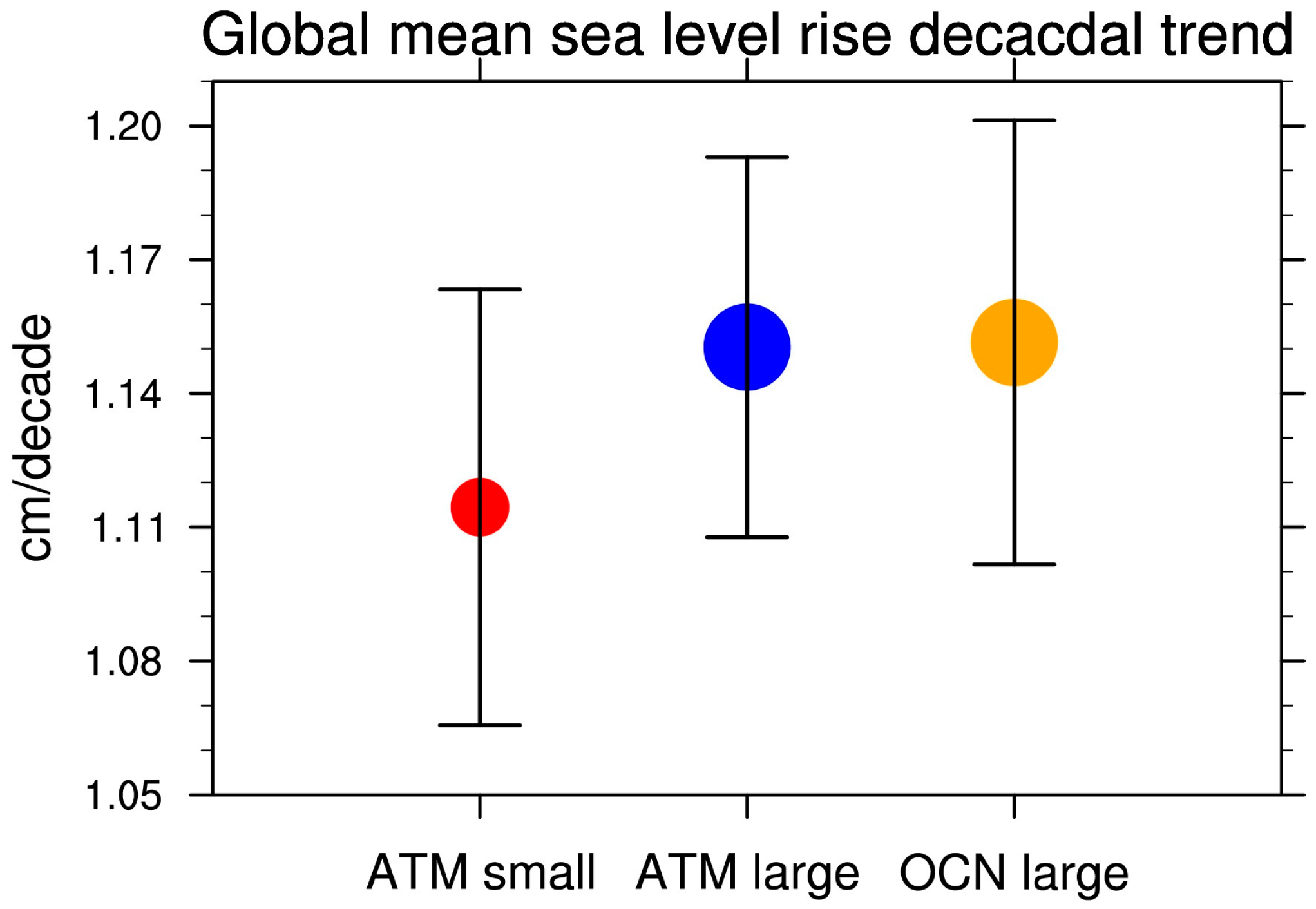
Water 09 00401 g003a 550Water 09 00401 g003b 550
Figure 3. The global mean decadal sea level rise averaged over 1996–2005 relative to the mean sea level in 1970–1979 (top), and the decadal trend of the global mean sea level rise (1970–2005) (bottom). The bars show the ± SD. The dot sizes indicate the relative side of the perturbation in the initial conditions.
Figure 3. The global mean decadal sea level rise averaged over 1996–2005 relative to the mean sea level in 1970–1979 (top), and the decadal trend of the global mean sea level rise (1970–2005) (bottom). The bars show the ± SD. The dot sizes indicate the relative side of the perturbation in the initial conditions.
Water 09 00401 g003aWater 09 00401 g003b
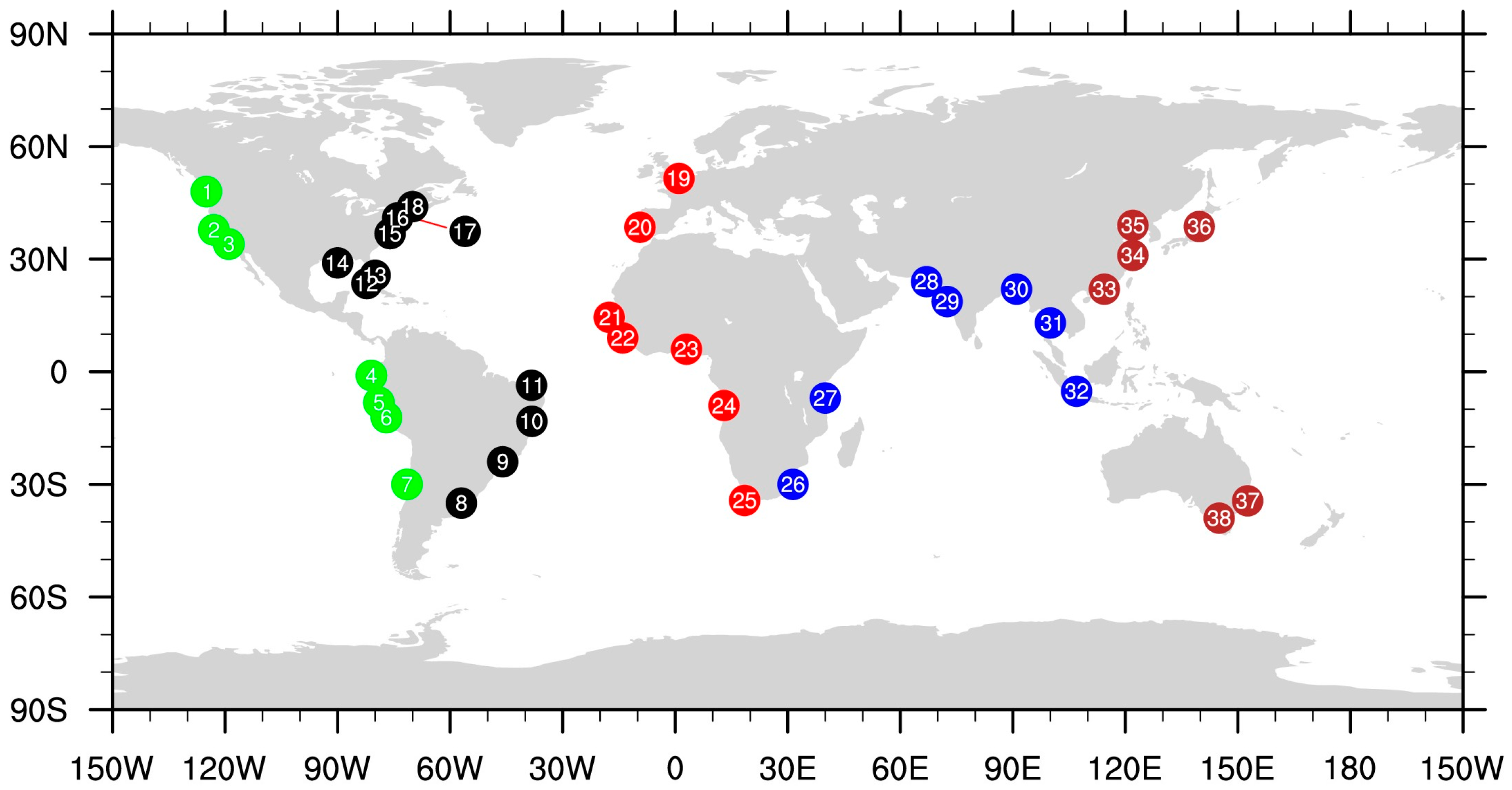
Water 09 00401 g004 550
Figure 4. Geographic locations of the selected cities, color-coded by region.
Figure 4. Geographic locations of the selected cities, color-coded by region.
Water 09 00401 g004
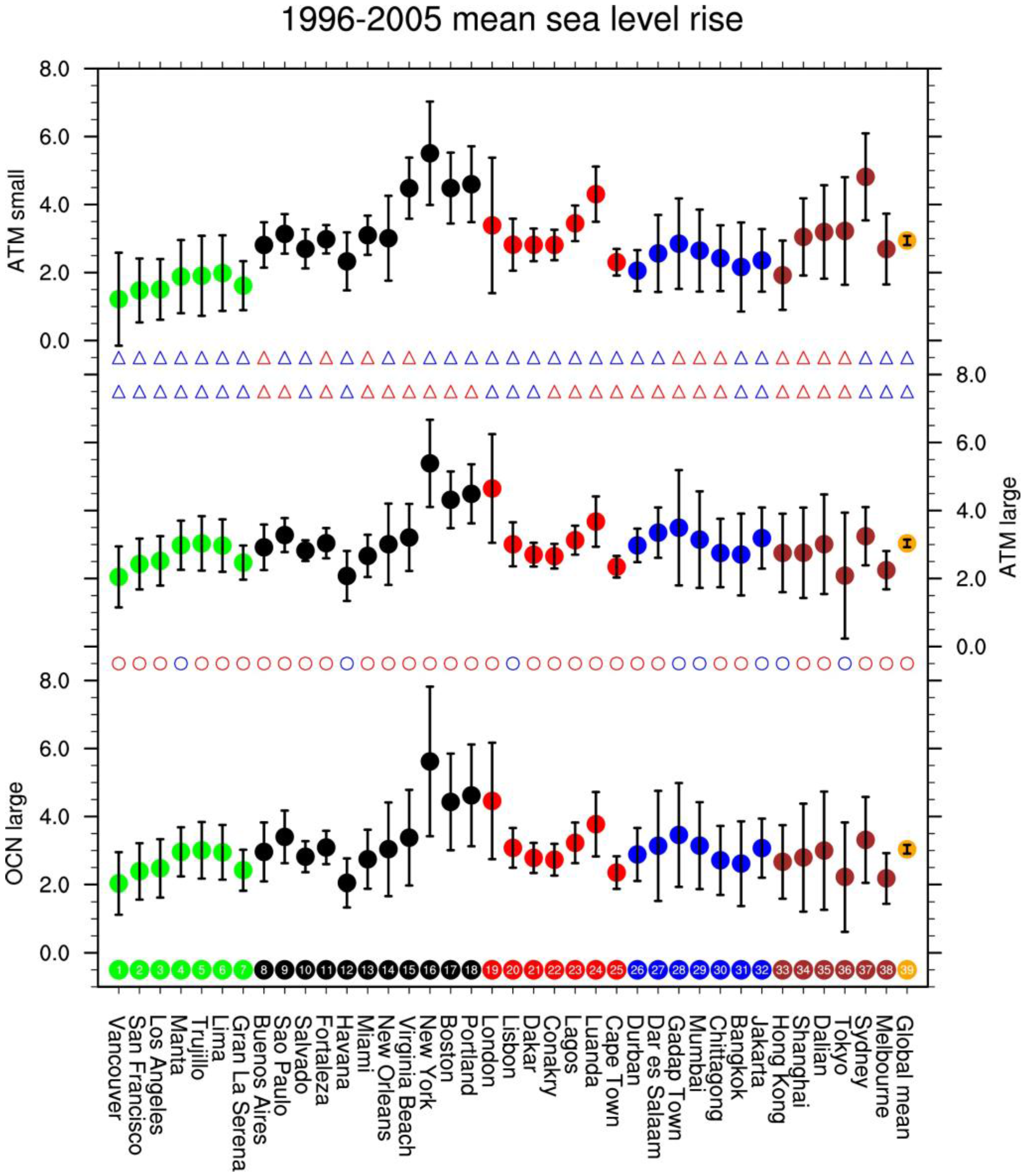
Water 09 00401 g005 550
Figure 5. Decadal mean sea level rise for selected cities in the three ensemble simulations (1996–2005 relative to 1970–1979). Unit is cm. The triangles represent the ratio of the decadal mean SLR standard deviation across ensemble member between ATM large and ATM small (top), between OCN large and ATM small (bottom); and open circles represent the ratio between OCN large and ATM large. Red/blue color indicates the ratio is greater (less) than 1.
Figure 5. Decadal mean sea level rise for selected cities in the three ensemble simulations (1996–2005 relative to 1970–1979). Unit is cm. The triangles represent the ratio of the decadal mean SLR standard deviation across ensemble member between ATM large and ATM small (top), between OCN large and ATM small (bottom); and open circles represent the ratio between OCN large and ATM large. Red/blue color indicates the ratio is greater (less) than 1.
Water 09 00401 g005
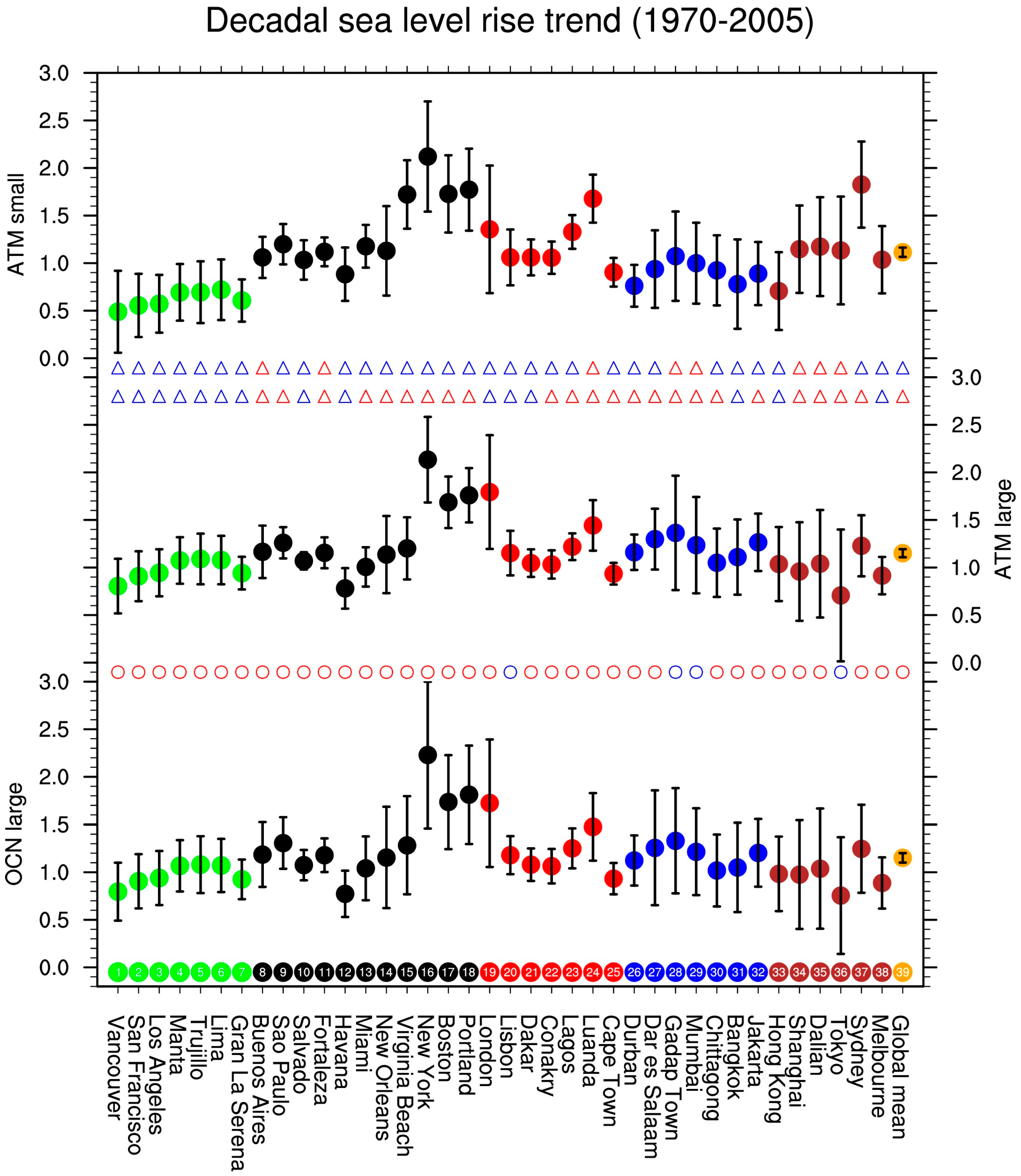
Water 09 00401 g006 550
Figure 6. Decadal trend of sea level rise for selected cities (1970–2005). Unit is cm/decade.
Figure 6. Decadal trend of sea level rise for selected cities (1970–2005). Unit is cm/decade.
Water 09 00401 g006
Water 09 00401 g007a 550Water 09 00401 g007b 550
Figure 7. Ratio of the standard deviation for the decadal mean SLR (1996–2005 relative to 1970–1979) and the SLR decadal trend (1970–2005) for the selected cities and global mean. ATM S is ATM small, ATM L is ATM large and OCN L is OCN large. Red represents a ratio greater than 1, and blue less than 1. The green/orange dashed lines represent 30% above and 30% below 1.
Figure 7. Ratio of the standard deviation for the decadal mean SLR (1996–2005 relative to 1970–1979) and the SLR decadal trend (1970–2005) for the selected cities and global mean. ATM S is ATM small, ATM L is ATM large and OCN L is OCN large. Red represents a ratio greater than 1, and blue less than 1. The green/orange dashed lines represent 30% above and 30% below 1.
Water 09 00401 g007aWater 09 00401 g007b
Water 09 00401 g008 550
Figure 8. Regional decadal mean sea level rise (left) and its standard deviation (right) for 1996–2005 relative to 1970. The contour interval for left panels is 0.8 cm, and for the right panels is 0.25 cm.
Figure 8. Regional decadal mean sea level rise (left) and its standard deviation (right) for 1996–2005 relative to 1970. The contour interval for left panels is 0.8 cm, and for the right panels is 0.25 cm.
Water 09 00401 g008
Water 09 00401 g009 550
Figure 9. Regional decadal sea level rise trend (left) and its standard deviation (right) for period 1970–2005. The contour interval for left panels is 0.4 cm/decade, and for the right panels is 0.1 cm/decade.
Figure 9. Regional decadal sea level rise trend (left) and its standard deviation (right) for period 1970–2005. The contour interval for left panels is 0.4 cm/decade, and for the right panels is 0.1 cm/decade.
Water 09 00401 g009
Water 09 00401 g010 550
Figure 10. Ratio of the SLR decadal mean and trend standard deviation. The ratio is calculated as the standard deviation of OCN large minus that of ATM small and this difference is divided by the standard deviation of ATM small.
Figure 10. Ratio of the SLR decadal mean and trend standard deviation. The ratio is calculated as the standard deviation of OCN large minus that of ATM small and this difference is divided by the standard deviation of ATM small.
Water 09 00401 g010
Table
Table 1. Global mean sea level. 1
Table 1. Global mean sea level. 1
CasesBranch Year1850 Sea Level (cm)1970 Δsea Level (cm)Number of Ensemble Members2005 Δsea Level (cm)
OCN1/ATM small8632.842.79304.09 ± 0.11
OCN28932.342.4844.43 ± 0.10
OCN39371.422.5744.38 ± 0.05
OCN49531.232.4844.25 ± 0.06
OCN59870.952.3344.25 ± 0.23
OCN610310.052.6144.37 ± 0.09
ATM large--2.49204.34 ± 0.10
OCN large--2.49214.35 ± 0.11
1 There are six CCSM4 historical all forcing simulations from 1850 to 2005. The year for each of the historical simulations branched from the 1850 pre-industrial control simulation is listed in the second column of the table. The global mean sea level relative to control run mean (800–1299) for each historical run at year 1850 is listed in the third column. The sea level change relative to 1850 for 1970 is listed in the fourth column. Column 5 is the number of ensemble for each of the six ocean initial states. Column 6 is the sea level change relative to 1970 at 2005. The unit for sea level rise is cm.

Share and Cite

MDPI and ACS Style

Hu, A.; Meehl, G.A.; Stammer, D.; Han, W.; Strand, W.G. Role of Perturbing Ocean Initial Condition in Simulated Regional Sea Level Change. Water 2017, 9, 401. https://doi.org/10.3390/w9060401

AMA Style

Hu A, Meehl GA, Stammer D, Han W, Strand WG. Role of Perturbing Ocean Initial Condition in Simulated Regional Sea Level Change. Water. 2017; 9(6):401. https://doi.org/10.3390/w9060401

Chicago/Turabian Style

Hu, Aixue, Gerald A. Meehl, Detlef Stammer, Weiqing Han, and Warren G. Strand. 2017. "Role of Perturbing Ocean Initial Condition in Simulated Regional Sea Level Change" Water 9, no. 6: 401. https://doi.org/10.3390/w9060401

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop