Abstract
Prediction of global temperatures and sea level rise (SLR) is important for sustainable development planning of coastal regions of the world and the health and safety of communities living in these regions. In this study, climate change effects on sea level rise is investigated using a dynamic system model (DSM) with time lag on historical input data. A time-invariant (TI-DSM) and time-variant dynamic system model (TV-DSM) with time lag is developed to predict global temperatures and SLR in the 21st century. The proposed model is an extension of the DSM developed by the authors. The proposed model includes the effect of temperature and sea level states of several previous years on the current temperature and sea level over stationary and also moving scale time periods. The optimal time lag period used in the model is determined by minimizing a synthetic performance index comprised of the root mean square error and coefficient of determination which is a measure for the reliability of the predictions. Historical records of global temperature and sea level from 1880 to 2001 are used to calibrate the model. The optimal time lag is determined to be eight years, based on the performance measures. The calibrated model was then used to predict the global temperature and sea levels in the 21st century using a fixed time lag period and moving scale time lag periods. To evaluate the adverse effect of greenhouse gas emissions on SLR, the proposed model was also uncoupled to project the SLR based on global temperatures that are obtained from the Intergovernmental Panel on Climate Change (IPCC) emission scenarios. The projected SLR estimates for the 21st century are presented comparatively with the predictions made in previous studies.
1. Introduction
Analysis of environmental and human impact of global warming is an important challenge which is studied in the literature, considering several different problems and approaches. One of the potential consequences of global warming is sea level rise (SLR) that may threaten the coastal regions of the world and impact human life. Based on historical records, global sea surface temperatures (SST) have increased by about 0.8 °C over the past 100 years, with seventy five percent of the increase occurring since 1980 [1]. According to the projection of IPCC greenhouse emission scenarios, the global SST is likely to rise further within the range 1.1–6.4 °C depending on the emission scenarios hypothesized to occur during the 21st century [2,3,4]. Due to global warming, the global mean sea level has been observed to rise about 15–20 cm in the past century [5,6], and it is predicted that this rise will continue in the 21st century [4,7]. Thus, it is important to predict the global SST change and SLR in the future for sustainable development planning of coastal regions of the world.
The inherent relationship between global SST and SLR is complicated. In recent studies, in an effort to simplify this relationship, empirical and semi-empirical models were proposed to predict global SLR based on temperature change data [8,9,10,11,12,13,14,15]. These are primarily unidirectional models that use the temperature series data simulated from IPCC greenhouse gas emission scenarios as known inputs to project SLR, although there are some variations to this approach that are reported in the literature [9,12,15]. Based on the predictions of these models, the SLR in the 21st century is estimated to be in the range 0.5–2.0 m relative to 1990 levels, which are much higher than IPCC estimates [4].
As an extension of these approaches, a dynamic system model (DSM) was proposed to predict future SST change and SLR simultaneously [16]. In DSM, the behavior of SST and SLR was described by a pair of coupled ordinary differential equations with two state variables: the sea surface temperature and the sea level. Thus, in the dynamic approach, the sea level change and sea surface temperatures are not independent but they are correlated. This underlying hypothesis is distinctly different from all other empirical models that are used in the literature and explained in more detail in [16]. Later on, a vector-autoregressive (VAR) model that employs the same mathematical form of the discrete DSM approach was also developed in [17] that uses a stochastic cointegration method to describe the relationship between SST and SLR. This model has the same structure as the DSM model used in [16]. Their results also confirm the hypothesis underlying the DSM approach [16]. As stated in [17], the sea surface air temperatures will adjust to the average temperatures of the upper ocean due to the larger heat capacity of oceans relative to the atmosphere. As a result of this difference in heat capacities, SLR will directly affect the SST. Further, it is also well known that temperature change will affect SLR due to ice sheet melting, steric effects and other hydrologic phenomena. The information on both state variables is already imbedded in the historical data on SST and SLR which can be used to calibrate DSM. In both of these studies, the earth is considered to be a system and the behavior of the system is developed in terms of the two state variables of the system, i.e., SST and sea level. In this approach, the evolution of both states depends on the current state of both states and also on the behavior of the evolution of the system states over time. The resulting model, when calibrated using the historical data, showed that the rate of SLR is proportional to SST and this rise is also a function of the temporal state of the sea level. Similarly, the rate of SST change is a function of the temporal state of the SST and is also affected by the SLR. Unlike previous models, after calibration using the historical data, this model can be used to simultaneously predict both SST and SLR for the next century, which is one of the distinct difference between the DSM model and the previous models used in the literature. Applying this model [16], the authors have predicted the global SST and SLR in the 21st century. Relative to 1990, the results show an increase in SST of about 1.3 °C with a 90% confidence interval [1.1, 1.5] °C and a SLR of about 42.4 cm with a 90% confidence interval [40.0, 44.8] cm. These predictions are based on the assumption that the system operates under the historical pattern drawn from historical records [16]. The DSM model was later extended to include greenhouse emissions as an external forcing function in the model [18] and a spatial SLR analysis version of the DSM model was also introduced in subsequent studies [19,20]. In these studies authors argued that this concept is more meaningful than earlier semi-empirical studies since this approach incorporates the inherent two-way interaction that exists between SST and SLR into the model and its predictions.
These empirical models may provide an alternative approach to predict global warming and SLR in the 21st century over physically based models [4,20]. However, one may notice that the earlier DSM models do not include the time lag impacts of temperature and sea level status on future SLR which is important. In the earlier DSM model and its various applications [16,18,19,20], a one year time lag was used, whereas environmental systems may respond to changes imposed on them over a time lag period. To address the time lag effect between temperature increase and SLR, a time lag coefficient was introduced to the earlier semi-empirical models as well [9,12]. This approach overlooks the impact of a series of temperature and sea level status over the previous years on the current temperature and sea level. In this study, we have noticed that, if the impact of SST and sea level status of a series of previous years are considered, the results obtained would be more accurate based on the evaluation of the performance measures that are discussed in this paper. Using this approach, the warming trend and SLR that is predicted with the DSM analysis would be different.
In this study, a time-invariant (TI-DSM) and time-variant (TV-DSM) optimal DSM approach is proposed based on the earlier model proposed in [16]. The model will include the impact of SST and sea levels in previous years on current temperature and SLR. The optimal time lag is determined using the root mean square errors and the coefficients of determination measures for both state variables. The optimal model is used to predict the temperature change and SLR in the 21st century. In order to evaluate the adverse effect of greenhouse gas emissions, a decoupled model is also used and the temperature series data from the six IPCC emission scenarios are used as the model input for temperature and the SLR is predicted based on these scenarios for the 21st century. The results obtained for this case are presented comparatively with earlier results which can be used in inundation studies of coastal regions [19].
2. Dynamic Systems Model with Time Lag
In an earlier study, the discrete solution of the DSM was presented using only the previous time values of SST and sea level [16]. In this study, we extend this approach assuming that global SST change and SLR in the future depends on the status of global SST and sea level of several of the previous years. Introducing the time lag concept the DSM can be given as,
where t is time, T(t) is the SST at t, and H(t) is the sea level at t, n is the number of time lags, is the ith time lag where , is the time interval and is set as one year for the prediction of yearly SST and sea levels, aj,t, bj,t and cj are time lag coefficients which are time lag period dependent. In this model, SST and sea level are the state variables of the system. The discrete solution of this model can be represented as,
where k is the index of years, n is the specified maximum time lag, T(k) is the global SST in year k, H(k) is the global sea level in year k, aj,k−i is the coefficient associated with global SST at previous year(s) i and reflects the impact of global SST in previous year(s) i on current global SST and sea level, bj,k−i is the coefficient associated with global sea level at previous year(s) i and reflects the impact of the global sea level in previous year(s) i on the current global SST and sea level, cj is a constant and j = 1, 2. In Equation (2), n prior years is considered to give the equation in a general form. In application, fifteen years are considered and the optimum value of eight years is predicted to give the best results in an optimum sense. We define
and obtain the matrix form of Equation (2) expressed as,
where X(k) is the state vector in year k, Ak−i is a (2 × 2) matrix for i = 1, …, n, C is a (2 × 1) vector. In this model, the system behavior depends on interaction of global SST and sea level in previous n years. This model is an extension of the DSM that was proposed earlier, or the original DSM is a special case of Equation (4) where n = 1 [16].
3. Calibration of DSM with Time Lag
We assume that time series historical data of yearly global SST and sea levels are available and this is denoted as,
where N is the total number of years. In the DSM analysis [16], the available N-year time series data were used to identify the system coefficients. For that case, the coefficients identified would reflect the dynamic properties of the system on average for the complete dataset. However, it is expected that the SST and sea level predicted in the next year should be associated with the values of the state variables of several previous years. Assuming that the data at previous n years have the most impact on the SST and sea level during the next year, we can use the N-year data to identify the system coefficients for a fixed period time lag analysis, resulting in a time-invariant dynamic system (TI-DSM). The other option can be the following. When new data is added to the historical dataset, we may move the time lag data window forward a year as we drop the data for the first year of the historical time lag data set used earlier and use the new sub-dataset which still includes an N-year time lag data set to identify the new system coefficients for the period of n time lags. In this approach, the time lag period will also be moving forward. In this manner, as time moves forward, we can dynamically identify the new system coefficients, resulting in a time-variant dynamic system (TV-DSM). For generality, assuming that we need to predict the SST and sea level at year k + 1, based on the data from the previous n years, we define,
where Y is a 2 × (N − n) matrix, B is a (N − n) × (2n + 1) matrix, P is 2 × (2n + 1) matrix. Applying least squares method, we can identify the parameters of the n time lag matrix coefficients as,
where the symbol ^ indicates the estimates of the corresponding coefficients. Once the system matrices are recognized, we can use Equation (4) to predict the global SST change and SLR using previous n year data as the initial condition (TI-DSM).
As time elapses, new data obtained from measurements will increase. One can utilize this new data to improve system matrices. Assuming that the length of data series used to recognize the system matrices is initially N, we define the length of the complete data window as N. When a new pair of yearly data is collected, we add the new data into the historical series and move the N-year time lag data window forward a year and then repeat the least squares method described above to recognize new system matrices. The system coefficients recognized using this procedure are time dependent, and we identify this system as the time-variant dynamic system (TV-DSM), expressed as,
where Ak−i (k) and C(k) are matrices for i = 1, …, n and vector for year k. It is important to notice that as we conduct this analysis in the year 2013; currently, there is no new data added to the dataset for 2014 and beyond. Thus, to demonstrate this approach, we will use a synthetic data generation process and add the data predicted for year (k + 1) into our dataset to form the new dataset and move on with our computation sequence as described above. We recognize that, in this case, the predicted data we have added to the dataset is not a measured data and will include modeling errors. Thus, the reader needs to recognize that the results obtained for this case will include the propagation of modeling errors over time which will render the one hundred year predictions less reliable. The synthetic data generation process is included here to demonstrate the time-variant modeling approach that is described in this study.
In order to incorporate the modeling and measurement errors, confidence interval theory can be used for reliability analysis [21]. For a given confidence level α, 100 (1 − α) confidence intervals for global SST and SLR for dynamic prediction can be estimated by,
where and represent the 100 (1 − α) confidence intervals of global SST and SLR at the kth year, denotes the t-distribution, is the value of for m degree of freedom and α confidence level, N is the number of historical data used for system recognition, n is the time lag, and are the standard deviations for global SST and SLR, which are estimated in the model calibration, ep is the term accounting for the error propagation in dynamic prediction, given by
Xp(i) is a (2n + 1) vector used in prediction, given by,
4. Determination of Optimal Time Lag
In Equation (2), the maximum time lag n is a variable parameter that needs to be determined by optimization. In building the model, the performance of the proposed model is evaluated using two indexes: the root mean square error (RMSE) and the coefficient of determination (R2). We may combine both performance indexes to determine the optimal maximum time lag. The RMSE is a measure of the differences between values predicted by the model and the actual observations [22]. It is defined as,
where RMSET and RMSEH are the root mean square errors for temperature and SLR, and T(k) and H(k) are the historical measurements of temperature and SLR at time step k. The coefficient of determination R2 is a measure of how well future outcomes are likely to be predicted by the model [23]. The R2 is defined as,
where are the coefficients of determination for SST and SLR, and are the average values of the observations of temperature and SLR, defined as . In statistical definitions, the smaller the RMSE, the better the goodness of fit, while the closer the value of R2 is to one, the better the linear regression fits the data in comparison to the simple average. In model predictions, one wants the proposed model to generate a smaller RMSE but a larger R2.
Optimal maximum time lag n should have the root mean square errors minimized and the coefficients of determination maximized simultaneously. Considering that the magnitudes of SST and SLR are not in the same scale, the following procedure is proposed to determine the optimal time lag n. For a given maximum time lag n, the system matrix can be identified for each time lag and is used to predict the global SST and SLR, and then the RMSE and R2 for SST and SLR can be calculated. The RMSE and R2 for each time lag are divided by their maximum values to transfer all RMSE and R2 to an interval [0, 1], and the optimal maximum time lag n should have a minimum value for the performance index given by
where is the optimal performance index for the optimal maximum time lag , , , and are the maximum values of RMSE and R2 for global SST and SLR, respectively. Equation (16) is a synthetic performance index that reflects the requirements for optimal maximum time lag. In this sense, the model with optimal maximum time lag is identified as the optimal dynamic system time lag model.
5. Numerical Results and Discussion
In this study, we apply the historical observations on SST and sea level data that was used in [16] to demonstrate the application of the model proposed above. The dataset includes yearly time series data of global mean surface SST and sea levels from 1880 to 2001. We use this dataset to calibrate the system coefficients for fixed period time lag (TI-DSM) and moving period time lag (TV-DSM) approaches introduced above. The calibrated model for both cases is then used to predict global SST and SLR in the 21st century where the synthetic data generation process is used for the TV-DSM approach as discussed above.
5.1. Time-Invariant DSM (TI-DSM) Application
The system calibration is based on the historical data on global SST and sea levels relative to 1990. For a given maximum time lag of 15 years, the system matrices for each time lag (1–15) are identified and the resulting model is used to reconstruct the global SST and SLR. Based on the reconstructed results, the RMSE and R2 are calculated and optimal maximum time lag is determined using Equation (16). This analysis resulted in an optimal time lag of eight years, n* = 8. The coefficients for the corresponding system are given in Table 1 for this case. Since none of these coefficients is zero, the results show that the future global SST and sea levels not only depend on their states in the last year, but also are affected by SST and sea level states in previous 8 years.

Table 1.
TI-DSM system matrices and vector recognized for the optimal time lag = 8.
After calibrating the proposed model, we applied Equation (4) using the recognized matrices to reconstruct global SST and sea levels from 1880 to 2001. In the reconstruction, the eight pairs of historical data before 1888 were used as the initial condition, and the reconstructed results are shown in Figure 1. In this figure, it is shown that the historical data have a good fit. The 90% confidence intervals for global SST and SLR were estimated from Equation (11) for , , , , , and , and these results are shown as dashed lines in Figure 1. It can be seen that most of the historical data falls within the 90% confidence interval bands. In this calibration, RMSEs are 0.11 and 0.80, and R2s are 0.71 and 0.98 for global SST and SLR respectively. In comparison to the results obtained in [16], the reconstruction accuracy using this model has been improved. The R2s obtained for the reconstruction period, in particular, show a significant increase. This implies that the future predictions for global SST and SLR obtained from this model are likely to have higher accuracy.
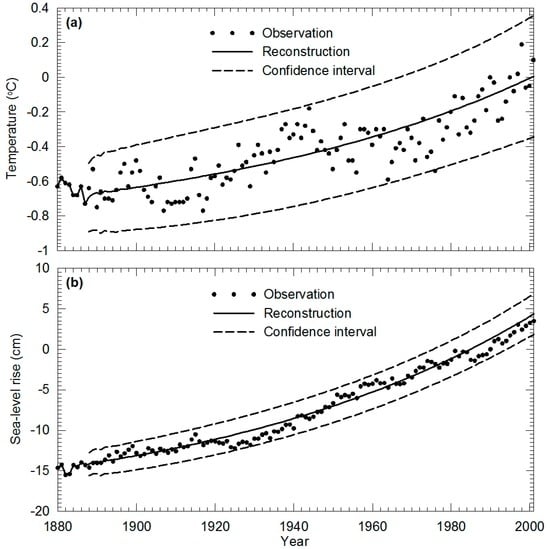
Figure 1.
Reconstructed numerical results using the TI-DSM with the optimal time lag of 8 years. (a) Global temperature; (b) Sea level rise.
In order to validate the performance of the model, a 10-fold cross-validation technique is applied to the measured dataset of SST and SLR from 1880 to 2001 [24]. In this cross-validation technique, the dataset is randomly divided into 10 equal subgroups. Of the 10 subgroups, a single subgroup is retained as the validation data for testing the model while the remaining nine subgroups are used to identify the model. This process is repeated 10 times and the resultant parameters of the model are averaged to produce a single estimation. The resulting matrices are given in Table 2. When compared with Table 1, the values of the corresponding coefficients are very close to those presented in Table 1. When we used these matrices to reconstruct the SST and sea levels from 1880 to 2001 relative to 1990 levels, the resulting RMSEs were 0.1118 and 0.7828, and the R2 was 0.7148 and 0.9773 for SST and SLR, respectively. These values are almost identical to the results obtained from the model identified using the complete dataset from 1880 to 2001.

Table 2.
System matrices and vector obtained from 10-fold validation for the optimal time lag = 8.
The system identified (Table 1), is used to predict global SST change and SLR in the 21st century relative to 1990 levels. In this prediction, eight pairs of the SST and sea levels from previous years relative to 1990 are taken as the fixed initial condition, and the predicted results over the next millennium are shown in Figure 2. The SST and sea levels obtained are monotonically rising if the greenhouse gases emissions to the atmosphere follow the pattern observed in the 20th century. According to this scenario, by the end of the 21st century, the SST will reach 1.9 °C with a 90% confidence interval [0.6, 3.2] °C while the sea level will rise to 56.1 cm with a 90% confidence interval [46.9, 65.2] cm. According to IPCC reports, the global SST rise in the year 2100 spans from 1.23 to 5.55 °C relative to 1990 levels [2,3]. The SST change by the end of 2100, predicted using this model, is close to the best estimate in Scenario B1, in which SST increases about 2 °C with the interval [1.1, 2.9] °C [2,3]. According to the IPCC Third Assessment Report, over the course of this century, the SLR is predicted to be in the range of 90 mm to 880 mm with a central value of 480 mm [3]. The predicted SLR is within this range and very close to this central value. The 90% confidence intervals estimated from Equation (11) are shown as dashed lines in Figure 2. It can be seen that the confidence intervals gradually widen as the prediction time moves forward. This reflects the dynamic error propagation in the system and there is more uncertainty in temperature predictions.
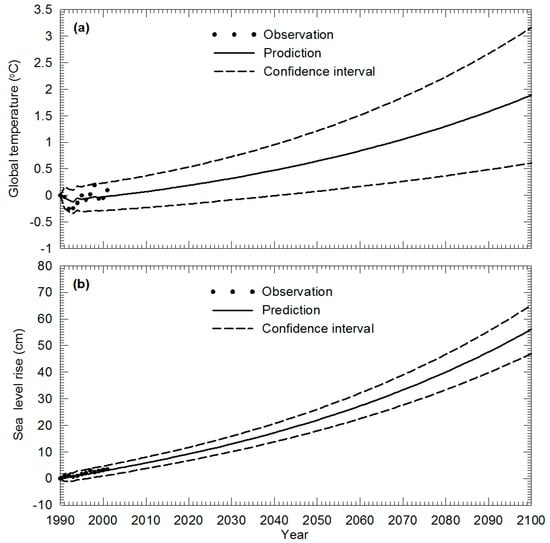
Figure 2.
Predicted numerical results for the 21st century using the TI-DSM with the optimal time lag of 8 years. (a) Global temperature; (b) Sea level rise.
5.2. Time-Variant DSM (TV-DSM) Application
Using the historical and the predicted results as the synthetic data, a time-variant dynamic system model with optimal eight time lag periods (TV-DSM) was also developed. In this approach, during the system calibration, the length of the original data series selected is 122. Thus, the length of the fixed data window will be chosen as 122. We note here that this is not a necessary condition for the proposed approach. The data window used in the calibration of the system may also be increased as the new data arrives over the years. The fixed data window approach is used here for computational convenience. The matrices Ak−i (k) and C(k) at k with years before 2002 are the same as those in the time-invariant DSM as given in Table 1. These matrices are then recalculated year by year from year 2002 forward using the moving data window as described above to form a time-variant dynamic system (TV-DSM). The global SST change and SLR in 21st century using the TV-DSM are shown in Figure 3a,b. The results show that by the end of the 21st century, the SST will reach 2.0 °C with a 90% confidence interval [1.5, 2.5] °C while the sea level will rise to 66.6 cm with a 90% confidence interval [63.2, 69.9] cm. These predictions are much closer to the projections of Scenario B1 [3]. The 90% confidence intervals estimated by Equation (11) are shown as dashed lines in Figure 3. This is similar to the case of the TI-DSM where the widths of the confidence intervals gradually increase as prediction time moves forward. When comparing the results shown in Figure 2 and Figure 3, we may observe two points: (i) the predicted results using the TV-DSM are higher than those obtained using the TI-DSM; and, (ii) the confidence intervals using the TV-DSM are narrower than those obtained using the TI-DSM. These observations indicate that using the TV-DSM and thus new information in system recognition, may improve the prediction reliability although it is synthetic in this application. We must re-emphasize here that the predictions made for this case are based on the synthetic data generation process described earlier.
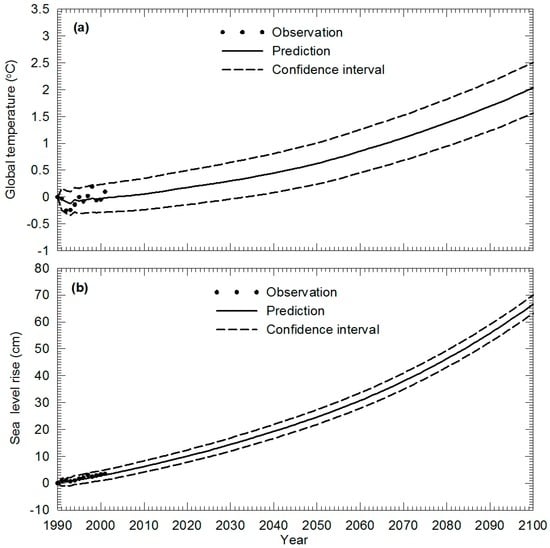
Figure 3.
Predicted numerical results for the 21st century using the TV-DSM with the optimal time lag of 8 years. (a) Global temperature; (b) Sea level rise.
5.3. Applications Using IPCC Scenarios
The SLR in the 21st century depends on natural and anthropogenic radiative forcing generated by greenhouse gases such as carbon dioxide (CO2) [2]. In order to assess the impact of greenhouse gas emissions on global warming, IPCC have developed six emissions scenarios based on different patterns of economic development, industrial development, and population growth in the future and modeled physical processes [2,3]. These emission scenarios are labeled A1FI, A1B, A1T, A2, B1 and B2 [2]. Among these scenarios, A1FI and A2 represent the highest emission of greenhouse gases into the atmosphere, A1T and B1 represent the least emissions, and A1B and B2 represent moderate emissions. The IPCC projected the global mean surface temperature dynamic processes from 1990 to 2100 for the six scenarios using the climate models (IPCC, 2007), which are shown in Figure 4. Accordingly, the temperature increase at the end of the 21st century spans from 2 to 4.5 °C depending on which scenario occurs.
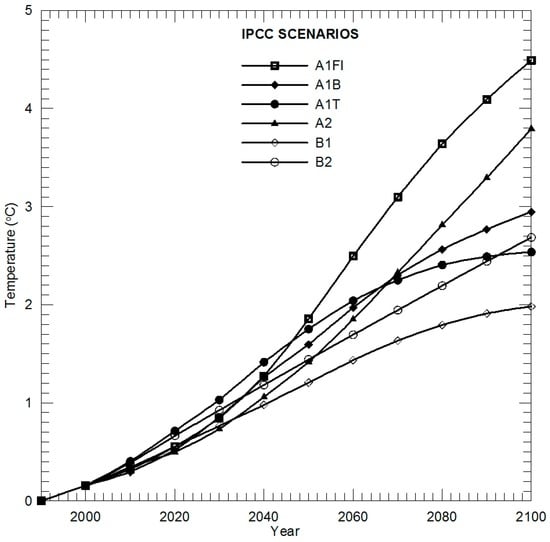
Figure 4.
Temperature change processes simulated by IPCC, based on six greenhouse gas emission scenarios [2].
The model given in Equation (2) is proposed to predict global SST change and SLR simultaneously. This model can also be decoupled and used to predict SLR if the global SST rise is known. In order to assess the adverse effect of greenhouse gas emissions on SLR, the global SST rise scenarios of IPCC, as shown in Figure 4, are chosen as known input data for the temperature and the SLR is predicted using the second equation of Equation (2) as the decoupled model. The predicted results are shown in Figure 5. For comparison purposes, the projections from the semi-empirical model [10] are also shown as dashed lines in Figure 5. It may be seen that both predicted results have similar increasing patterns but the SLR predicted using the TI-DSM is higher than the projections obtained from the semi-empirical model for all scenarios [10]. This reflects the effect of global SST and sea levels for the previous eight years on the current SLR. The 90% confidence intervals estimated from Equation (11) are also shown in Figure 5. The confidence intervals contain the predictions from the TI-DSM and the semi-empirical model [10].

Figure 5.
SLR obtained from the TI-DSM with an 8 year time lag based on IPCC scenarios.
For this case, the predicted SLR at the end of 2100 and the 90% confidence intervals are given in Table 3. Among the IPCC Scenarios, A1FI and A2 show the highest amount of greenhouse gas emissions, resulting in sea levels of 110.2 cm and 92.6 cm on average with 90% confidence intervals of [88.7, 131.7] cm and [75.9, 109.3] cm. B1 is the most environment-friendly scenario, in which greenhouse gas emissions are close to 1990 levels. Even if this scenario occurs in the 21st century, the temperature would increase by 1.8 °C [2]. As a consequence, the sea level would rise 60.6 cm, to 85.8 cm at the end of 2100 relative to 1990 as predicted in this study. These results further illustrate that reducing greenhouse gas emissions is an extremely urgent task for the world. Table 1 also lists the results from the semi-empirical model [10]. The relative differences for best estimates between the current model and the semi-empirical model are 7.9%, 6.5%, 6.4%, 6.2%, 4.6% and 5.3% for Scenarios A1FI, A1B, A1T, A2, B1 and B2, respectively. The SLR predictions by 2100, using the TI-DSM, range between 60 and 132 cm while the projection of the IPCC is between 18 and 59 cm by 2100 [3]. The projections of the IPCC are widely considered to be an underestimation in the literature [10]. The subsequent studies show that the SLR by 2100 ranges between 50 and 140 cm [10], 75 and 190 cm [12], 80 and 200 cm [25], 80 and 130 cm [13] and 59 and 180 cm [15]. In comparison with these results, the predictions obtained from the TI-DSM are consistent but higher than the results projected from the earlier semi-empirical model studies.

Table 3.
SLR at the end of the 21st century predicted by the TI-DSM for IPCC scenarios.
Similar analysis may also be performed using the TV-DSM model. For this case, the predicted SLR at the end of 2100 and the 90% confidence intervals are given in Table 4 and the predicted results for this case are shown in Figure 6. In this case, when the predicted results are used as the synthetic future data, the predictions for SLR are higher than the TI-DSM results.

Table 4.
SLR at the end of the 21st century predicted by the TV-DSM for IPCC scenarios.
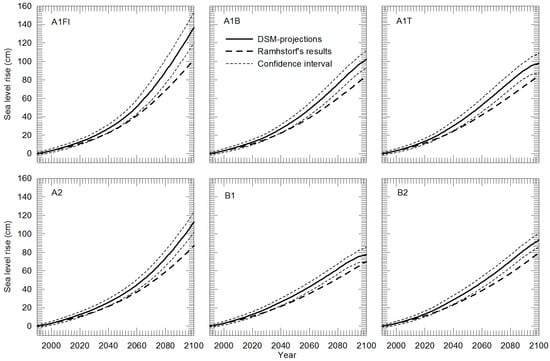
Figure 6.
SLR obtained from TV-DSM with an 8 year time lag based on IPCC scenarios [2,3].
6. Conclusions
In this study, a DSM approach with time lag is developed to predict global SST change and SLR. In comparison with the empirical or semi-empirical models used in previous studies, this model accounts for the impact of global SST and sea level status from several previous years on the current SST and sea level. The optimal time lag to be used in this analysis is determined using an optimization analysis based on the accuracy of predictions among several time lags. The analysis is presented for constant period time lag and variable period time lag analysis. The resulting DSM obtained reveals the inherent historical relationship between global warming and SLR. This analysis is an extension of the DSM proposed by [16] and provides a simpler but effective alternative to predict global warming and SLR in the 21st century simultaneously. This approach also represents a generalized model for previous semi-empirical models. If one of two state variables is known, the model can be uncoupled to predict the dynamic process of other state variables, as the known state variable is chosen as the input. In this manner, the second equation in the DSM, Equations (1) and (2), can be used to predict SLR when the global temperature is obtained from other approaches, such as the AOGCM models of IPCC studies [3].
The optimal DSM was calibrated using the historical dataset on SST and sea level from 1880 to 2001 as used in [16]. Considering that the model includes the effect of SST and sea levels in previous years, in model calibration we used the original historical records instead of the 2-year moving averaged data which were used in [16]. The results show that the optimal DSM is the one with the maximum time lag n* = 8. The model predictions yielded RMSEs of 0.11 and 0.80, and R2s of 0.71 and 0.98 for global SST and SLR, respectively, in calibration, which shows an improvement when compared with [16]. The optimal DSM was applied to predict global SST and SLR in the 21st century, and the results show that the global SST will reach 1.9 °C with a 90% confidence interval [0.6, 3.2] °C and the sea level will rise to 56.1 cm with a 90% confidence interval [46.9, 65.2] cm by the end of the 21st century relative to 1990. In order to assess the impact of greenhouse gas emissions on SLR, the second equation of the optimal model was used to project the SLR in the 21st century while the temperature rise of six emission scenarios, simulated by IPCC (2001), is used as the model input. For these cases, the resulting SLR at the end of the 21st century ranges from 61 to 132 cm. The prediction is consistent but higher than the predictions made in previous studies [10,12,13,15,25,26]. The analysis was performed using both TI-DSM and TV-DSM approaches with similar results obtained for each case with the TV-DSM outcome showing higher estimates. Inundation analysis of coastal regions can be evaluated based on the outcome of these predictions as demonstrated in [20].
Author Contributions
Both authors have contributed to the development of methodology and the analysis of the numerical results discussed in this study. In addition to this joint effort, Jiabao Guan’s contribution was on the computational methods development and the development of the numerical solution. Mustafa M. Aral’s contribution was in the development of DSM and DSM time lag concept and its principles.
Conflicts of Interest
The authors declare no conflict of interest.
References
- National Research Council. America’s Climate Choices; The National Academies Press: Washington, DC, USA, 2011; p. 135. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Intergovernmental Panel on Climate Change. Summary for Policymakers. Available online: http://www.ipcc.ch/report/ar5/wg1/ (accessed on 26 November 2013).
- Douglas, B.C. Global sea rise: A redetermination. Surv. Geophys. 1997, 18, 279–292. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33, L01602. [Google Scholar] [CrossRef]
- Meehl, G.A.; Stocker, T.F.; Friedlingstein, W.D.; Collins, P.; Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Projections of global average sea level change for the 21st century. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Etkins, R.; Epstein, E.S. The rise of global mean sea-level as an indication of climate change. Science 1982, 215, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Gornitz, V.L.; Lebedeff, S.; Hansen, J. Global sea-level trend in the past century. Science 1982, 215, 1611–1614. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S. A semi-empirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Holgate, S.; Jevrejeva, S.; Woodworth, P.; Brewer, S. Comment on “A semi-emprical approach to projecting future sea-level rise”. Science 2007, 317, 1866. [Google Scholar] [CrossRef] [PubMed]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef] [PubMed]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Reconstructing sea level from paleo and projected temperatures 200 to 2100 AD. Clim. Dyn. 2010, 34, 461–472. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Grinsted, A.; Moore, J.C. Anthropogenic forcing dominates sea level rise since 1850. Geophys. Res. Lett. 2009, 36, L20706. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. How will sea level response to changes in natural and anthropogenic forcings by 2100? Geophy. Res. Lett. 2010, 37, L07703. [Google Scholar]
- Aral, M.M.; Guan, J.; Chang, B. A dynamic system model to predict global sea-level rise and temperature change. J. Hydrol. Eng. 2012, 17, 237–242. [Google Scholar] [CrossRef]
- Schmith, T.; Johansen, S.; Thejll, P. Statistical analysis of global surface temperature and sea level using cointegration methods. J. Clim. 2012, 25, 7822–7833. [Google Scholar] [CrossRef]
- Guan, J.; Chang, B.; Aral, M.M. A Dynamic Control System Model for Global Temperature Change and Sea level Rise in Response to CO2 Emissions. Clim. Res. 2013, 58, 55–66. [Google Scholar] [CrossRef]
- Chang, B.; Guan, J.; Aral, M.M. Modeling spatial variations of sea level rise and corresponding inundation impacts: A case study for Florida, USA. J. Water Qual. Expo. Health 2013, 6, 39–51. [Google Scholar] [CrossRef]
- Chang, B.; Guan, J.; Aral, M.M. A scientific discourse: Climate change and sea-level rise. ASCE J. Hydrol. Eng. 2013, 20. [Google Scholar] [CrossRef]
- Wadsworth, H.M. Handbook of Statistical Methods for Engineers and Scientists, 2nd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. For. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied regression analysis. In Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- McLachlan, G.J.; Do, K.-A.; Ambroise, C. Analyzing Microarray Gene Expression Data; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Pfeffer, W.T.; Harper, J.T.; O’Neel, S. Kinematic constraints on glacier contributions to 21st-century sea-level rise. Science 2008, 321, 1340–1343. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S. A new view on sea level rise. Nat. Rep. Clim. Chang. 2010, 4, 44–45. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).