1. Introduction
In this paper, by resorting to recent results obtained in Refs. [
1,
2], we study the fundamental role of water dipole dynamics bridging the interaction between DNA and enzymatic proteins so as to allow polymerase chain reaction (PCR) processes to occur. Some of us have previously reported [
3,
4,
5,
6] the in vitro transduction of bacterial DNA sequences in water and in tumor cells. In water, the DNA was detected by PCR using the
Taq polymerase from the heat-tolerant strain
T. aquaticus. This phenomenon raises several important questions from the theoretical point of view: how is it that a bacterial DNA polymerase (
Taq) can “read” water nanostructures imprinted by bacterial DNA sequences? If so, is there a more general mechanism operating in living cells? The present article offers an explanation by using the formalism of the gauge theory paradigm of quantum fields along the research lines developed in Refs. [
1,
5,
6,
7,
8,
9,
10,
11].
In Ref. [
2], London dispersion forces between DNA base pairs and the dynamics of delocalized electrons are shown to be responsible for the formation of molecular dipole structure. Fine tuning of collective dynamic modes and synchronization of dipole vibrational modes between spatially separated nucleotides and enzymatic molecular subunits have been theorized to promote and sustain the catalytic activity of classes of enzymes which interact with DNA. Long-range molecular correlations in the chemistry of DNA-enzyme interactions, discussed in Ref. [
1], appear to play a key role in understanding how to reconcile the high efficiency and precise targeting of enzymatic catalytic activity with the intrinsically stochastic kinematics of a large number of molecular components [
12,
13,
14]. The highly ordered pattern in the spatial molecular arrangements and the time ordered sequence of steps characterizing the catalytic activity indicate that biochemical methods and the traditional study of the dipole and multipole dynamic structure of the electronic quantum conformations, out of which the chemical properties of interacting molecules emerge, need to be supplemented by results in quantum field theory (QFT). These indeed account for the collective molecular long-range correlations, which are responsible for the highly synchronized, fine-tuned DNA-enzyme interaction.
Thus, in the framework of spontaneously broken gauge symmetry theories, which has proven itself to be the most reliable theoretical scheme able to predict the wide array of experimental observations ranging from condensed matter to elementary particle physics, it has been derived in [
1] a generalized model of the radiative dipole wave field mediating the molecular interactions between DNA and enzyme in water and governing the dynamics of
Taq DNA polymerase in PCR processes.
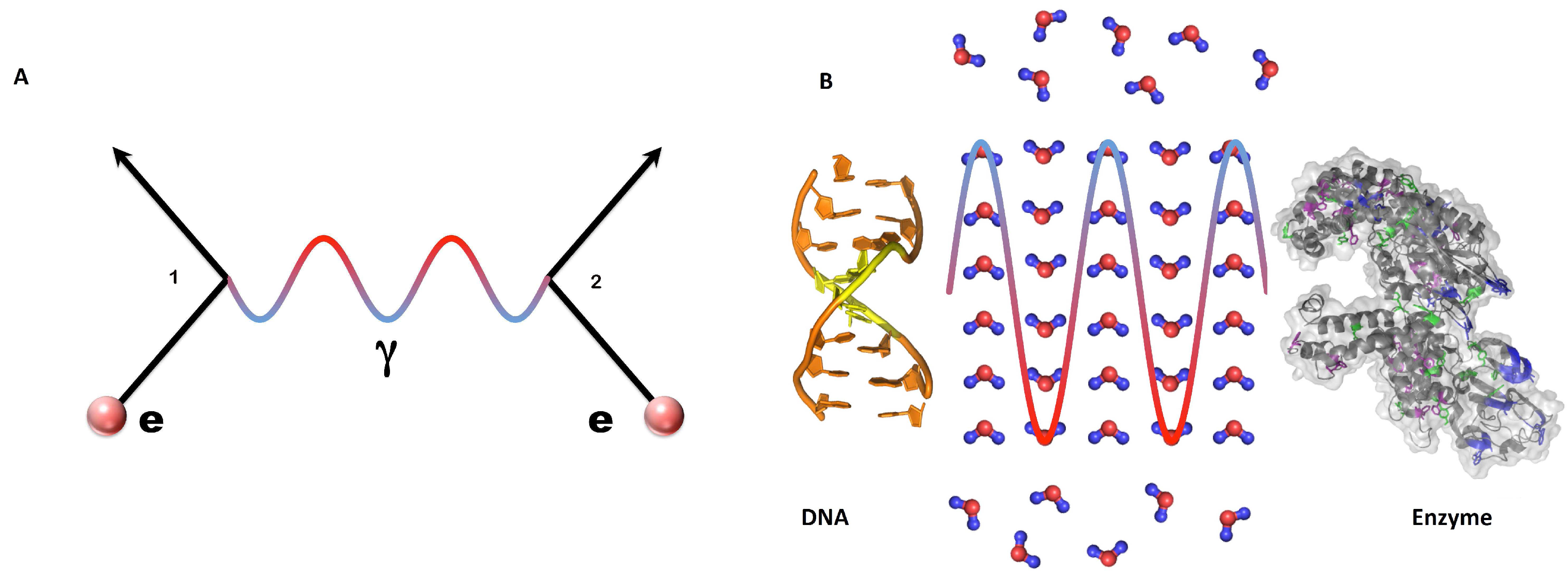
The model is based on the QFT interaction paradigm, which describes the interaction between two systems by the mutual exchange of a mediating wave field or quantum, in analogy with the photon exchanged by two electric charges in quantum electrodynamics [
15,
16] (
Figure 1). The basic constraint in the model construction comes of course from the physical characterization of the system under study. In our case, we have the macromolecules of DNA and enzyme and the water molecules, whose number under standard biological conditions constitutes the supermajority of the system molecules. DNA, enzyme, and water molecules are endowed, as their distinctive physical property in this model, with configurations of electric dipoles. Our modeling is thus focused in a natural way on the radiative dipole interaction.
The wave field mediating DNA-enzyme interactions, of which
Taq amplifying DNA sequence in PCR represents one specific case, are proposed to be governed by the dipole wave field propagating through the water matrix in which DNA and enzymes are embedded (
Figure 1). The mathematical formalism and the results of such a study are reported in [
1]. In the present paper our aim is to discuss developments in the applications to DNA-enzyme interactions with particular attention paid to the
Taq DNA polymerase in PCR processes, providing an understanding based on dynamical field-theoretic grounds, thus supplementing more standard presentations of PCR modeling based on kinetic and stoichiometric methods [
12,
13,
14].
The result of our analysis is that in PCR amplification processes, and more generally in DNA-enzyme interactions, the spatial and temporal distributions of charges [
1,
2,
17], interaction couplings, frequencies, amplitudes, and phase modulations [
1,
2] form a pattern of fields, that constitutes the electromagnetic (em) image of the DNA, in such a way that what the enzyme “sees”, at the level of molecular biology, is such an em image of DNA in the surrounding water. The DNA and the enzyme “see” each other’s em images by exchanging quanta of the radiative dipole waves induced by their presence in the water molecular matrix, which thus acts effectively as a
bridge between the two (of course, until they are sufficiently close for water exclusion and direct binding to occur).
The structure of the paper is as follows. The
Taq-DNA interaction in PCR processes, and DNA transduction in water are discussed in
Section 2. The formalism developed in [
1] is summarized in
Section 3. The description of PCR processes in terms of the gauge theory paradigm of quantum fields is presented in
Section 4.
Section 5 is devoted to further discussions and conclusions. Details of the protocol for DNA transduction in water are reported in
Appendix A; some data on the dipole molecular structure of DNA and
Taq in
Appendix B and some mathematical details on the water dipole field in
Appendix C.
2. The Taq-DNA Interaction and Open Questions
The enzymatic synthesis of DNA is a major subject of molecular biology, to which a large number of studies have been devoted. The elucidations of the double-helix structure of DNA and its scaffolding by water and the hydrogen bonding of its bases in a planar configuration, directly opened the way to understanding DNA duplication. It is generally accepted that in the conditions existing in living cells, DNA polymerases can operate on short, open, single stranded regions at optimal temperatures lower than 40 C, i.e., much lower than the temperature required to melt the DNA double helix in water solutions. A peculiar exception is that of DNA replication in thermophilic bacteria of hot springs and in organisms living under high pressure around hot chimneys close to submarine volcanoes.
The DNA polymerases of thermophilic bacteria have evolved to keep their structure and functionality after being exposed to heating at temperatures close to the boiling point of water. Kary Mullis used the polymerase (Taq) of T. aquaticus to alternate the cycles of heating at 95 C and of cooling at temperatures to allow some specific oligonucleotide primers to recognize sequences of DNA and thus amplify that DNA in a quasi-exponential manner (polymerase chain reaction or PCR) in 30 to 40 cycles.
There remains an open question: How are primers and
Taq able to locate from large cellular distances and recognize short, specific DNA sequences among millions of base pairs of genomic DNA, which is a requirement to initiate DNA polymerization in PCR? The classical explanation that Brownian motion will permit the synchronized meeting of the appropriate molecules is not tenable. The highly efficient coordination of DNA-enzyme processes has been shown to confound the explanatory reach of statistical methods used to describe average regularities in biological matter [
18]. As Schrödinger observed for living matter in general (and his remarks apply equally well to the case of PCR processes), the attempt to explain the high efficiency in terms of ordering generated by “statistical mechanisms” ([
18] (p. 47)) would be “the classical physicist’s expectation that far from being trivial, is wrong” ([
18] (p. 19)), and “it needs no poetical imagination but only clear and sober scientific reflection to recognize that we are here obviously faced with events whose regular and lawful unfolding is guided by a mechanism entirely different from the probability mechanism of physics” ([
18] (p. 79)). We propose in this paper and in [
5,
6] that a third party intervenes in the DNA-enzyme interaction processes, which is organized (coherent) water, and we show how this fits well with the general gauge theory paradigm of quantum fields [
15,
16] (see also [
7,
8,
9,
10,
11]).
Our standpoint is consistent with previous experimental work [
3,
4,
5,
6] that has shown that some DNAs in water dilutions emit electromagnetic waves of low frequency (from hundreds to ≈3 kHz) which could be triggered, as in a resonance phenomenon, by an outside excitation, such as the Schumann waves [
19]. Experimental peaks of Schumann waves are at 7.83, 14.3, 20.8, 27.3, and 33.8 Hz; the peak near 7 Hz is the one found to be minimally active in the case discussed here (for further details see [
3,
4,
5,
6]). The electromagnetic signals (EMS) can be amplified and recorded as a digital form. In
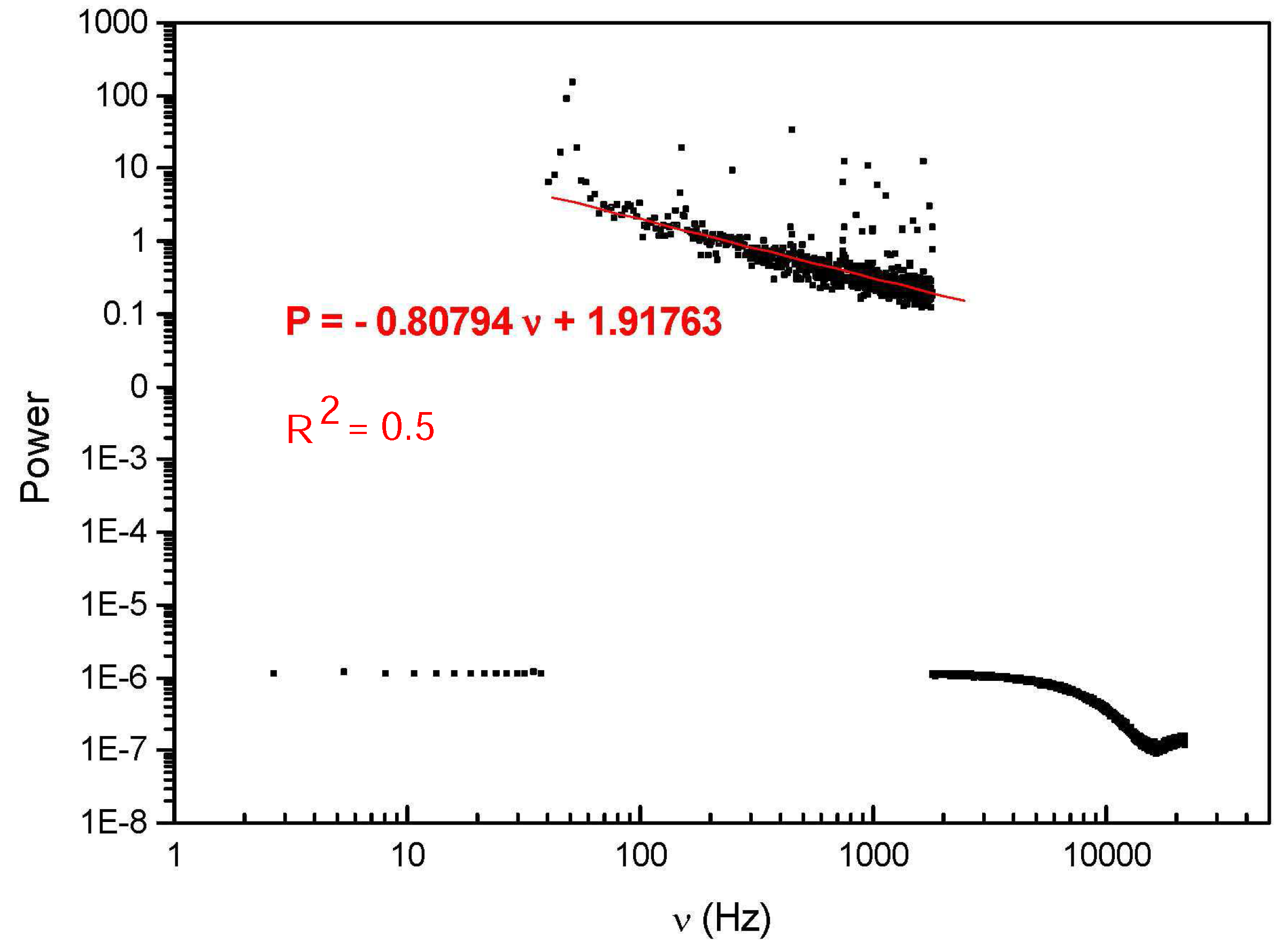
Figure 2 the log-log plot of the EMS from the water solution of a DNA HIV-1 fragment (LTR, 194 bp) (cf.
Appendix A) is reported. The decimal dilutions of original concentration of 2 ng/mL HIV-1 emitting EMS are between
and
(the first of the serial dilutions do not emit detectable signals) [
3,
4,
5,
6]. In the range between about 100 and 2000 Hz the signal shows fluctuations densely distributed around the linear fit with negative slope coefficient d = 0.80794, thus exhibiting scale-free, self-similar behavior in that frequency range with self-similarity (fractal) dimension d. It is known [
20,
21,
22,
23] that such a fractal-like self-similarity structure is the manifestation of coherent dynamics active at a microscopic level, as we indeed find in the following sections.
This first step can be followed in different conditions of space and time by a second step, consisting in transformation of the signal into an analog form and sending its electric vector to a solenoid which will generate a magnetic field in a test tube of water. Specific water nanostructures (domains of coherently oscillating molecular dipoles) will be formed (“signalized” water). Then the electromagnetic image of the initial DNA is “read” by the Taq polymerase in the presence of primers and nucleotide triphosphates, generating and amplifying DNA molecules identical to the initial DNA from Borrelia burgdorferi or the LTR of HIV-1.
An interesting variation of the second step is to replace the test tube of water by a flask of living cultured cells. If the cells were originated from malignant tumor or isolated in vitro as continuous “immortalized” cell lines, after several days of exposure to EMS of a foreign bacterial DNA amplicon (i.e., a fragment of DNA or RNA that is source and/or product of amplification or replication event), they synthesize that DNA which can be detected by usual PCR. At the same time the growth of the exposed cells is inhibited and finally they die.
One interpretation of this surprising result is that such cells possess an enzymatic system analogous to the
Taq polymerase, i.e., able to read the DNA information contained by the nanostructures induced in the water of the cells. This enzymatic system analogous to the
Taq polymerase synthesizes the bacterial DNA in the presence of a pool of nucleotide triphosphates, but without the need of specific primers. This pool in multiplying cells may be smaller than the one artificially provided in water. This difference may explain the delayed effect of EMS carrying the bacterial DNA in living cells. No effect was observed if the exposure to EMS was restricted to one or two days. The origin and location of the cellular enzymatic system has not been determined, although it is sensitive to inhibitors of mitochondria. This enzymatic system may be a modified cellular polymerase or an enzyme of bacterial origin close to it. It should be noted that the reconstruction of foreign bacterial DNA either by the water of a test tube or in the interior of cells has been attained only if this DNA was extracted from pathogenic bacteria or virus and emitted recordable EMS [
3,
4,
5,
6]. The details of this anti-tumor effect of EMS of bacterial origin will be the object of another paper.
These previous results fit very well with the two vertices hypothesis developed below. If we generalize it to the PCR working on any cellular DNA, we have then to make the assumption that the EMS are too weak to be detected and amplified under natural conditions, but are still sufficient to trigger a coherent dynamics in the water. In the following we schematize the two-vertex interaction according to the analysis we present in
Section 4 (see
Appendix A for the operative protocol for DNA transduction in water):
First vertex: DNA-water interaction vertex:
The DNA-water EMS is detected, amplified and digitized → computer recording.
→ The recorded EMS is used for the
Second vertex: {signalized water}-Taq interaction vertex:
The EMS is converted to analog EMS
→ played in water where the initial DNA-water em image is reproduced
(signalized water, coherent nanostructures) → {signalized water}-Taq interaction vertex
→ 40 cycles of PCR → DNA amplification.
When the analog EMS is played in cells → nanostructures in cells
→ DNA → cell death
See Refs. [
3,
4,
5,
6] for more details on the detection of EMS from DNA water solutions and DNA transduction in water and in cells. In
Section 5 we discuss a few characterizing properties of the interactions at the two vertices on the basis of results presented in
Section 3 and
Section 4.
3. Collective Dipole Behavior in DNA and Enzyme Molecules
The electromagnetic radiative properties of DNA and enzyme macromolecules depend on the characterization of their electric dipoles. Therefore we first consider these molecular dipole configurations, summarizing the analysis presented in Refs. [
1,
2].
The molecular structure of DNA base pairs and enzyme amino acids, as well as many other biomolecules, presents aromatic rings containing conjugate planar systems with
electrons delocalized across the structure. A typical example of such rings is benzene. Such an electronic configuration is at the origin of the formation of dipolar arrangements, which in turn can produce non-trivial electromagnetic couplings among biomolecules [
24]. It is also at the origin of the stability and low reactivity in aromatic compounds.
In the DNA a special role is played by the symmetry of the molecular distribution about its helical axis. The dipole-dipole interaction is given by
with
connecting the centers of nearest-neighbor base-pair dipoles
and
. Anisotropies are accounted for by the numerical tensor elements (cf.
Table A1 in
Appendix B)
, which are generally determined to within five percent agreement from perturbation theory [
25], simulation [
26], and experiment [
27].
By following the analysis presented in [
2], one may introduce the normal-mode lowering operator
and its conjugate raising operator
for the
normal mode of the collective electronic oscillations, with
,
(see
Appendix B for their explicit expressions). The system Hamiltonian takes then the standard diagonalized form
The eigenstates of
are given by
. In particular we examine the so-called “zero-point” modes, on which the number operator
in Equation (
2) acts to produce a zero eigenvalue, because these are most easily excited by the free energy changes due to enzyme clamping. They are collective normal modes of the DNA system considered in our model framework. Because these zero-point oscillations are normal modes, a four-base-pair sequence will produce four frequencies of coherent (phase-synchronized) oscillation in the longitudinal direction (see
Appendix B for
in the four-bp case when DNA sequence homogeneity is assumed).
It is noteworthy that in order to break a single phosphodiester bond in the DNA helix backbone, the required energy in vivo is
eV [
28], which is less than two percent of the energy required to ionize the hydrogen atom, but about ten times the physiological thermal energy (
), and comparable with the quantum of biological energy released during nucleotide triphosphate (e.g., ATP) hydrolysis. The meaning of this is that the bonds of the DNA backbone are not so tight as to be unmodifiable, but they are strong enough to resist thermal degradation. As shown in Ref. [
2], at the standard inter-base-pair spacing of
Å, the ground state longitudinal oscillation (a zero-point mode) for a six-bp DNA sequence is calculated to within
of
, the energy required for double-strand breakage.
Taq represents a broad class of enzymes, called DNA polymerases, which replicate DNA strands with high efficiency. It does not recognize specific sequences, but it uses a DNA clamp, which is an accessory multimeric protein encircling the DNA double helix as the polymerase adds nucleotides to the growing strand. The clamp increases the number of nucleotides the polymerase can add to the growing strand per binding event, up to 1000-fold, aided by a layer of water molecules in the central pore of the clamp between the DNA and the protein surface. Due to the toroidal shape of the assembled multimer, the clamp cannot dissociate from the template strand without also dissociating into monomers.
Amino acids are the building blocks of protein and enzyme systems. The most polarizable amino acids are termed aromatic, and as with DNA base pairs, they induce dipole interactions between their constituent ring structures. The most aromatic amino acids (tryptophan, tyrosine, and phenylalanine) are also the most hydrophobic. It has been argued that London force dipoles in such intra-protein hydrophobic pockets could couple together and oscillate coherently, thus generating a radiative field.
In regards to the spacing between aromatic amino acids in protein, when considering tryptophan, tyrosine, and phenylalanine, the spacings are as close as 5 Å in the enzymes of interest, comparable to the inter-dipole spacing of DNA (3.4 Å). We consider the pairwise interaction potential
between each amino acid electric dipole in the enzyme’s aromatic network.
has a similar expression to the one for DNA considered above (cf. Equation (
1)), but without helical symmetry and including pairwise, not just nearest-neighbor, aromatic dipole couplings. The enzyme collective modes, like the DNA modes, are dipole fluctuation modes and can be used to construct the creation and annihilation operators for the radiative electromagnetic field quanta acting on the water molecules. Collective modes for
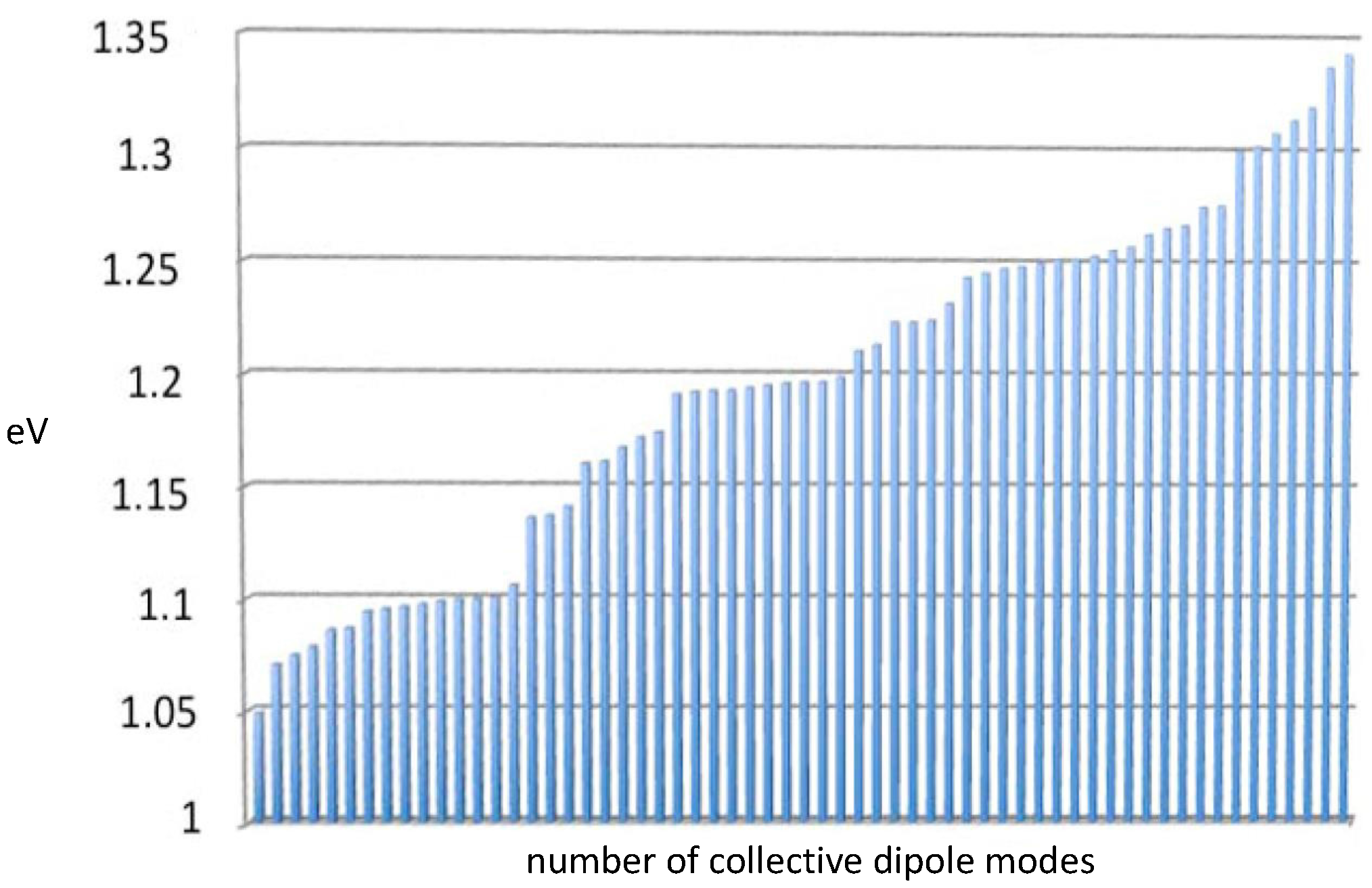
Taq are presented in
Figure 3. The average energy for these
Taq modes is 1.2 eV.
Though the aromatic amino acids of proteins typically absorb in the UV, around 4–5 eV, this observation does not discount coherent oscillations of induced dipoles at longer wavelengths in protein aromatic networks due to the dipolar correlations described in Refs. [
1,
2]. It is quite remarkable that the enzyme collective dipole modes displayed in
Figure 3 fall within the spectrum of DNA collective modes described in full detail in Ref. [
2].
We now turn to study the coupling between the dipole field of the molecular water bath and the radiative dipole fields of the DNA and Taq enzyme. The biochemical activity between DNA and enzyme in PCR is conditioned and thus established by these long-range correlations.
4. DNA and Taq Coupling to the Water Dipole Field
In this section we show that the electromagnetic pattern of the radiative dipole fields generated by DNA and enzyme induces in the water environment dipole wave fields which mediate the DNA-enzyme interaction. We study the DNA-water interaction “vertex”, and the enzyme-water interaction “vertex” (
Figure 1). Our analysis applies to the PCR processes where the DNA template is used and to PCR processes where signalization of the water replaces the use of the DNA template as described in
Section 2 (and in
Appendix A). We will neglect the static dipole-dipole interactions between DNA and water dipoles and between enzyme and water dipoles, focusing our attention instead on the radiative dipole field.
Consider a spatially uniform distribution of
N molecules of liquid water in a volume
V of linear size
ℓ at a non-vanishing temperature
T. In the notation of Refs. [
1,
7], denote the water molecule dipole vector by
, with magnitude
,
Å [
29] and
e the electron charge. We will use natural units, where
. In the absence of DNA and enzyme molecules, the electric dipoles of water molecules are arbitrarily oriented and there is no preferred orientation direction; this is expressed by saying that the system of water molecules is invariant under dipole rotations. Such a dipole rotational symmetry is broken by the interaction with the dipole radiative fields of DNA and enzyme molecules. Our aim is to study the collective rotational transitions in the water dipole field induced by such radiative interactions [
8,
30,
31,
32,
33].
Let
be the complex dipole wave field collectively describing the system of
N water molecules in the unit volume
V (cf.
Appendix C). In the absence of DNA and enzyme, the assumption that molecule density is spatially uniform implies that the only relevant variables are the angular ones. Therefore
may be expanded in terms of spherical harmonics on the unit sphere as
.
For our purposes it is enough [
1,
7] to consider the expansion in the four lowest-energy levels
and
for
, effectively setting
for
. At thermal equilibrium, the populations of these levels are given by
and follow the Boltzmann distribution. We will show that the populations of the
and
levels change once we consider the presence of DNA and enzyme in water.
It is useful to introduce the notations
,
,
, and
are real quantities and
(in natural units). We adopt the value
g·cm
as the average moment of inertia of the water molecule (
Appendix C);
is the eigenvalue of
on the state
, with
denoting the total angular momentum for the molecule. Indeed,
. We restrict our discussion to the resonant radiative em modes, i.e., those for which
, and we use the dipole approximation, where
, since we are interested in the collective behavior of the system of
N molecules. The system linear size
ℓ is then constrained to be
;
thus provides a relevant scale for the system. For water,
cm (in
units).
The dipole rotational invariance implies that the amplitude of
does not depend on
m, or, stated in different words, the three levels
for
are in the average equally populated under normal conditions, thus
, with
for any
. Dipole rotational invariance also implies that the time average of the polarization
along any direction
vanishes. In fact, considering a vector
parallel to the
axis in an arbitrary reference frame, one can show that the time average of
is zero, as it must be:
where
. In such a general setting, the initial conditions at
can be written as
by excluding of course the values of
corresponding to the completely filled state (0,0) (
,
n integer) or completely empty (
,
n integer), which are in fact physically unrealistic states. Interestingly, one finds that the dynamics imposes in a self-consistent way the lower bound for the parameter
. Also note that the equipartition of the field modes among the four levels
and
given by the Boltzmann distribution for
, with
the Boltzmann constant and
the energy of the field modes, corresponds to
.
Let us now consider how the above scenario changes when the DNA-water interaction is present. We need to consider the effects due to the electromagnetic field generated by the dipole vibrational modes of the DNA, discussed in
Section 3, and of the water molecules. Let us denote it by
, with
and
real quantities. One can show [
7,
8,
33] that the amplitude and the phases do not depend on
m, so that we may write
,
,
. We consider the coupling of
with water molecules in the transition
.
The field equations for a water molecule in the field
, for which it is assumed the transversality condition
, with
the polarization vector of the em mode, are given in Refs. [
34,
35] and for brevity we do not report them here (see Refs. [
1,
8]). An inspection of these equations shows that the strength of the coupling between the em modes and the molecular levels is given by
. Under standard conditions, for pure water,
. The coupling
scales with the density
and thus varies with temperature and pressure. The initial conditions (
5) imply that at
we have
.
We remark that the analysis of the field equations shows that
, for any
t, is an instability point so that the system spontaneously runs away from
(which also justifies and is consistent with our assumption made on physical grounds (see the comments following Equation (
5)). It can be shown [
7,
8] that the spontaneous breakdown of the phase symmetry implies that the system runs away from the state with
for any
t, which excludes the values
. Dynamical consistency then requires that
, with
, which is time-independent. The motion equations also lead to
where
. From these equations we see that a time-independent amplitude
exists, i.e.,
, if and only if the phase-locking relation
is satisfied. Equation (
8) gives
with
introduced in Equation (
4). This dynamical regime is the so-called “limit cycle”. By using the normalization condition and the constants of motion, one can obtain
to be compared with
at thermal equilibrium in the absence of collective dynamics. The spontaneous breakdown of the phase symmetry produces as a dynamical effect a coherent em field pattern (“limit cycle” state): the interaction of the em field with the molecular water dipoles is characterized by the “in-phase” (coherent) dynamics expressed by the phase-locking Equation (
8). Equation (
9) means that any change in time of the difference between the phases of the amplitudes
and
is compensated by the change of phase of the em field. The coherence between the matter field and the em radiative dipole field guarantees the gauge invariance of the theory. The formal expression of the collective dynamics is thus expressed by Equations (
8) and (
9). In summary, the combined system of DNA and water’s radiative em field evolves away from the initial symmetric ground state to the asymmetric ground state
.
We consider now the enzyme radiative dipole field interacting with the em field pattern generated by the DNA-water interaction. We add to the system energy the interaction term
, with
the electric dipole moment for water, and
, assumed parallel to the
axis, is the enzyme radiative electric field. The Hamiltonian
can be written in the form of a Jaynes-Cummings-like Hamiltonian for large
N [
34]:
In Equation (
11)
is the coupling constant proportional to the matrix element of the molecular dipole moment and to the inverse of the volume square root
;
and
a are the creation and annihilation operators for the electric field
,
denote the creation and annihilation operators of the dipole wave modes of the field pattern imaging the DNA-water interaction.
One can show that, by using the expansion of in terms of spherical harmonics, induces the mixing: and , with
The polarization
becomes now
where
and
has the limit cycle non-zero value (cf. Equation (
10)). The time averaged polarization is
. It is non-vanishing provided that
and that
. The former condition (
) is realized due to the enzyme electric dipole field, as we have seen above. The latter condition (
) is realized in the water coherent domains imaging the DNA em radiative field.
therefore depends on both the DNA radiative field and the enzyme field, and it is zero if one or both fields are absent. It represents their long-range dipole wave correlation.
The physical meaning of the anthropomorphic expression “the enzyme sees the DNA” is that the enzyme couples to the collective wave mode generated by the radiative em dipole interaction between DNA and water. Such a wave mode accounts for local dependence and space-time distributions of couplings, amplitudes, and frequencies along the DNA molecular chain. The resulting wave mode envelope describes the em dynamical image of the DNA in the surrounding water environment. This water-mediated DNA em image is what the enzyme actually “sees”. The converse can be said from the standpoint of the DNA, which sees the enzyme em image. The action of reciprocal “seeing” is described by the exchange of the dipole wave quanta of the collective dynamics induced by DNA and enzyme in the surrounding water dipole field, as derived above. This suggests that in widely used PCR processes for the amplification of DNA sequences, what is really crucial for their successful occurrence is the formation of the DNA em image in the water and the possibility for Taq DNA polymerase to recognize such an image by dipole wave quanta exchange as described above. This may be helpful in setting the stoichiometric parameters in the PCR preparation, and a study in this direction is in our plans. Our analysis is also consistent with the observation that PCR amplification of DNA is possible through the production of an em image of DNA in pure water by its exposure to the recorded dipole wave radiation emitted by the DNA-water interaction vertex.
5. Discussion and Concluding Remarks
In this paper we have studied the role played by the water radiative dipole wave bridging the interaction between DNA and enzyme macromolecules in the process of PCR. The bridge is realized by the collective long-range correlation triggered in the water by the presence of the dipole structures of DNA, on the one hand, and the enzyme macromolecule, on the other. These two “interaction vertices” have been studied in the frame of the conventional gauge field theory paradigm, stating that any interaction between two systems is mediated by the propagation of a correlation field or quantum, such as, for instance, the photon exchanged between interacting electric charges in quantum electrodynamics.
As far as we know, our study provides the first dynamical description of the conventional PCR process, which is traditionally analyzed in the literature by means of stoichiometric and thermodynamics-based methods. Our study does not contradict or substitute traditional biochemical studies. Their description of average regularities in biological systems in terms of purely statistical methods remains valid. What our study provides is the dynamical description of the long-range em correlation modes orchestrating the PCR process, thus accounting for its remarkable efficiency, space-time ordering, and diverse time scales that would be unattainable by otherwise fully stochastic molecular activities. As observed in the previous section, our discussion shows that in PCR processes what is essential for successful DNA amplification is the formation of a coherent dipole wave pattern representing the em image of DNA in water and the capability of Taq DNA polymerase to recognize such an image. The general process is described by the analysis of two interaction “vertices”: the interaction vertex DNA-{water dipole wave}, on the one hand, and the interaction vertex {water dipole wave}-Taq, on the other.
In the standard DNA-
Taq interaction, this image recognition would aid in the location of the DNA substrate by the polymerase, resulting finally in conformational changes, exclusion of water molecules, and direct polymerase binding. Direct binding would alter
Taq’s conformational and vibrational state, effectively “reading” the DNA and catalyzing chemical reactions to add appropriate nucleotides complementary to the template sequence. Thus, the radiation field from the DNA vertex induces conformational change in the
Taq polymerase at the other vertex, just like in the conventional description where the chemical DNA template induces direct polymerase binding. What
Taq really recognizes and “reads” is the em image of DNA, more specifically the em signals emerging from the collective molecular electrodynamics of the DNA template’s constituent charges. It is consistent with our analysis that the em image of DNA may be thus produced by “signalizing” pure water through the coherent dipole wave “signals” emitted from the interaction vertex DNA-{water dipole wave}, according to the protocol reported in
Appendix A.
Of course, a crucial role is played by the distributions of charges and dipoles, and any other conformational and dynamical details of the DNA and
Taq molecular structures. Moreover, a fundamental role is played by the (fractal-like) self-similarity (
Figure 2) of the EMS emitted by the DNA-{water dipole wave} interaction vertex, which has been shown [
20,
21,
22,
23] to be the manifestation of coherent microscopic dynamics, as indeed our discussion in this paper has suggested. These (fractal-like) self-similarity properties of the EMS in turn induce self-similar organization in the irradiated water. This is often overlooked in chemical spectral analysis. Not only is the spectral composition of the EMS important, but much more relevant to our purposes are these self-similarity (coherence) properties. In some sense, by reverting the argument, one might also say that the observed amplification of DNA in PCR processes appears to provide a “measurement device” for these self-similar structures produced in signalized water.
In order to further analyze the physical properties of the two interaction vertices considered above, we observe that the characteristic time scales of the process are controlled by the radiative dipole field amplitude and, remarkably, they are much shorter than the ones of thermal noise. As a consequence, the collective dynamics is protected by an energy gap. This is better clarified by observing that the factor
multiplying the coupling
(cf. Equation (
11)) implies that for large
N the collective interaction energy scale is larger by the factor
than the microscopic energy fluctuations of short-range molecular interactions, thus providing a protective gap against thermalization for the long-range quantum correlations. Conversely, the collective interaction time scale is shorter by the factor
than the time scale of the short-range interactions among the molecules. In a similar way, the multiplying factor
produces the enhancement of the coupling
G (cf. Equation (
5)). These remarks may account for the stability and efficiency of the PCR process against the high temperatures (up to 95
C) of the various thermal cycles, otherwise inexplicable in a purely statistical approach based on molecular kinematics. These kinds of enhancement phenomena for the coupling constants are well known to occur in superradiance and cooperative two-level systems [
36,
37]. As a result, the macroscopic stability of the system follows since it is protected against quantum fluctuations in the microscopic short-range dynamics, and, for sufficiently large
N, against thermal fluctuations, unless
is of the same order or larger than the height of the protective energy gap.
We have seen that the spontaneous breakdown of the phase symmetry produces as a dynamical effect a coherent em field pattern whose interaction with the molecular water dipoles is characterized by the phase-locking of Equations (
8) and (
9) (“in-phase" (coherent) dynamics). One can show (see, e.g.,
Appendix C in Ref. [
1,
7]) that the system ground state is a coherent condensate of the quanta of the long-range dipole waves (the Nambu-Goldstone boson quanta). In the QFT formalism, gauge invariance requires fixing the phase of the matter field and a specific gauge function has to be selected. One thus introduces the covariant derivative
and the variations in the phase of the matter field lead to the pure gauge
. Since partial derivatives with respect to time and space coordinates can be interchanged for regular (continuous and differentiable) functions, when
is a regular function, then we obtain vanishing electric and magnetic fields,
, and
. This means that in order to obtain non-vanishing values for the fields
E and
B in a coherent region,
must exhibit a divergence or topological singularity within that region [
9,
10,
11]. This is indeed observed in condensed matter physics. For example, in type II superconductors, a vortex core is penetrated by the lines of a quantized magnetic flux. Such a result is particularly relevant in our analysis, since it describes the dynamic formation of observed topologically non-trivial conformations of DNA-enzyme “clamping”: in the
DNA clamp, a protein multimeric structure encircles the DNA double helix, like encircling the core of a vortex, formed indeed by a layer of water molecules in the central pore of the clamp between the DNA and the protein surface. A similar “clamping” is observed in the DNA endonuclease catalytic activity of the
EcoRI enzyme [
1,
2].
Let us close by observing that our analysis may contribute toward answering the question of why divalent cations like Mg
play such a relevant role in the precise control of enzyme behavior for optimum biological functions, which is actually an unsolved problem in biology. We observe that the strict dependence on the pH and Mg
concentration in enzyme catalytic activity suggests that these variations propagating through the buffer solution may produce local perturbations in the electromagnetic environment. In PCR this may produce deformation of the electromagnetic image of DNA to the point that it is no more recognizable by the polymerase. This might thus account for the fact that
Taq is extremely dependent on hydrogen and magnesium ion concentration, and that the success of the PCR depends critically on these concentrations. Divalent cations, in particular, may therefore enhance or maintain or critically deform the long-range dipole wave fields in water solution. This is supported by recent experimental work that shows that ions can influence up to
water molecules, which extend roughly 5 nm from the ion radially [
17].
In conclusion, the interaction between DNA and enzyme is realized through water bridging the dynamics, and is more fully explained within the paradigm of gauge field theory: the interacting systems “see” each other by exchanging a mediating correlation dipole wave emerging from the em field pattern of the aromatic networks of DNA and enzyme molecules in their water environment. The experimental realization of DNA amplification in the PCR process described in
Section 2 using signalized water (according to the protocol reported in
Appendix A) may seem unconventional, though it is not altogether surprising given the complex molecular electrodynamics undergirding all of biochemistry. Thus, it is possible to envision that the chemical DNA template can be replaced by electromagnetic signals that register the collective dynamics of the DNA template’s constituent charges and dipoles. We are aware that there are many open questions and problems to be solved in this arena. As such, detailed studies are warranted to further investigate the implications and theoretical underpinnings of these phenomena. Our results presented here on water mediating the dynamics of PCR, however, suggest the general applicability of the gauge theory paradigm of quantum fields to this area of inquiry.