Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection
Abstract
:1. Introduction
- completely data-driven; it considers as input only historical water demand data;
- completely independent of the data source and therefore directly applicable to urban water demand (SCADA data) as well as individual customer consumption (AMR data);
- based on two-stage learning: (i) identifying and characterizing typical daily consumption patterns and (ii) dynamically generating a set of forecasting models for each typical pattern identified in the previous stage. This approach deals with the nonlinear variability of water demand at different levels, automatically characterizing periodicity (e.g., seasonality) and behaviour-related differences of different types of days and hours of the day;
- able to provide reliable forecasts of the urban water demand (SCADA data) in the short term in order to support optimization of operations, in particular pump schedule optimization;
- able to detect possible anomalies in typical water consumption behaviour at the individual customer level (AMR data) associated with metering faults, possible frauds and cyber-physical threats.
State of the Art of Water Demand Forecasting
2. Materials and Methods
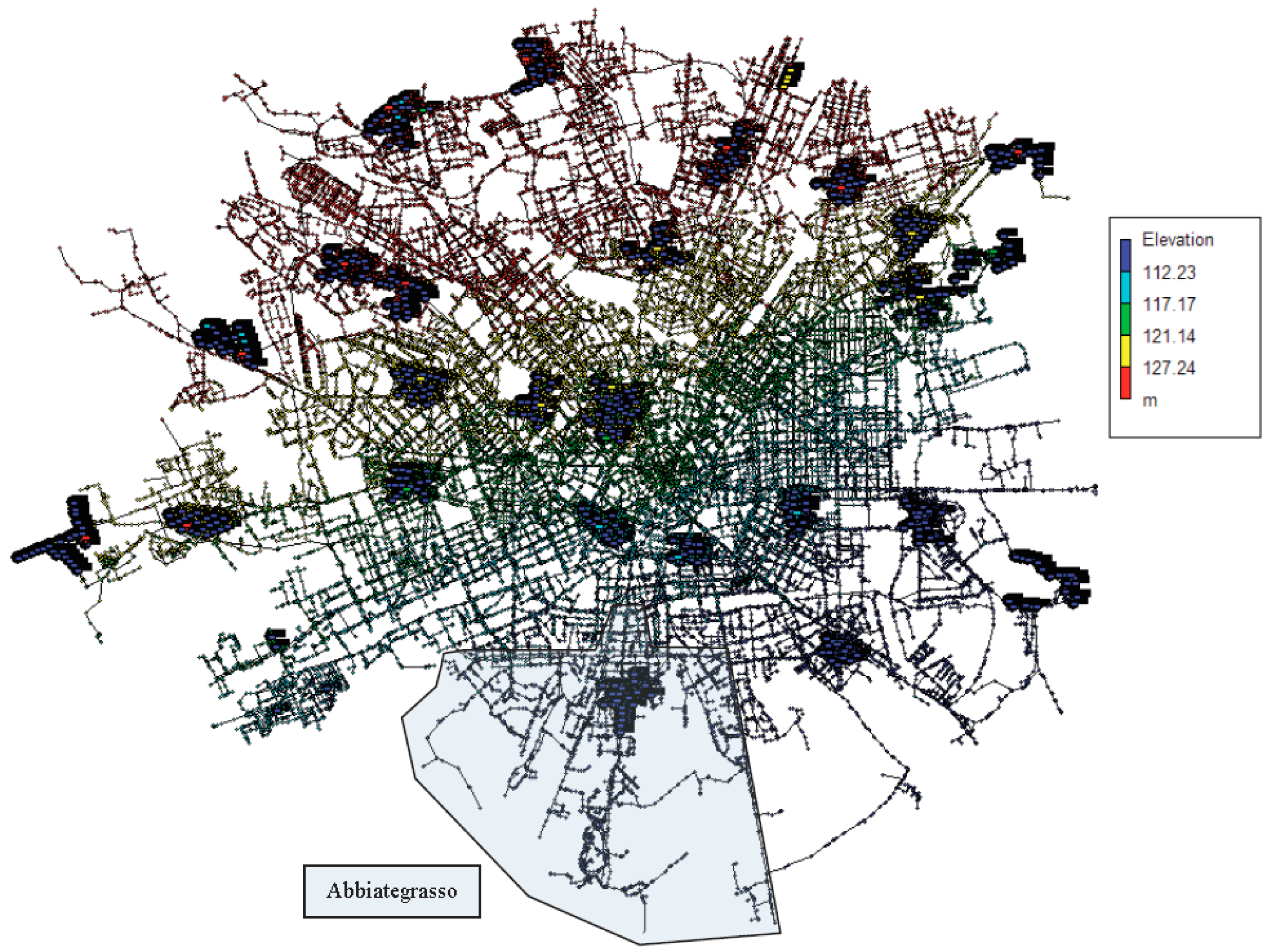
2.1. SCADA Data
- 149,639 junctions
- 118,950 pipes
- 26 pumping stations
- 501 wells and well pumps
- 33 storage tanks
- 95 booster pumps
- 36,295 valves
- 602 check valves
- total base demand 7.5 ± 4.2 m3/s.
2.2. AMR Data
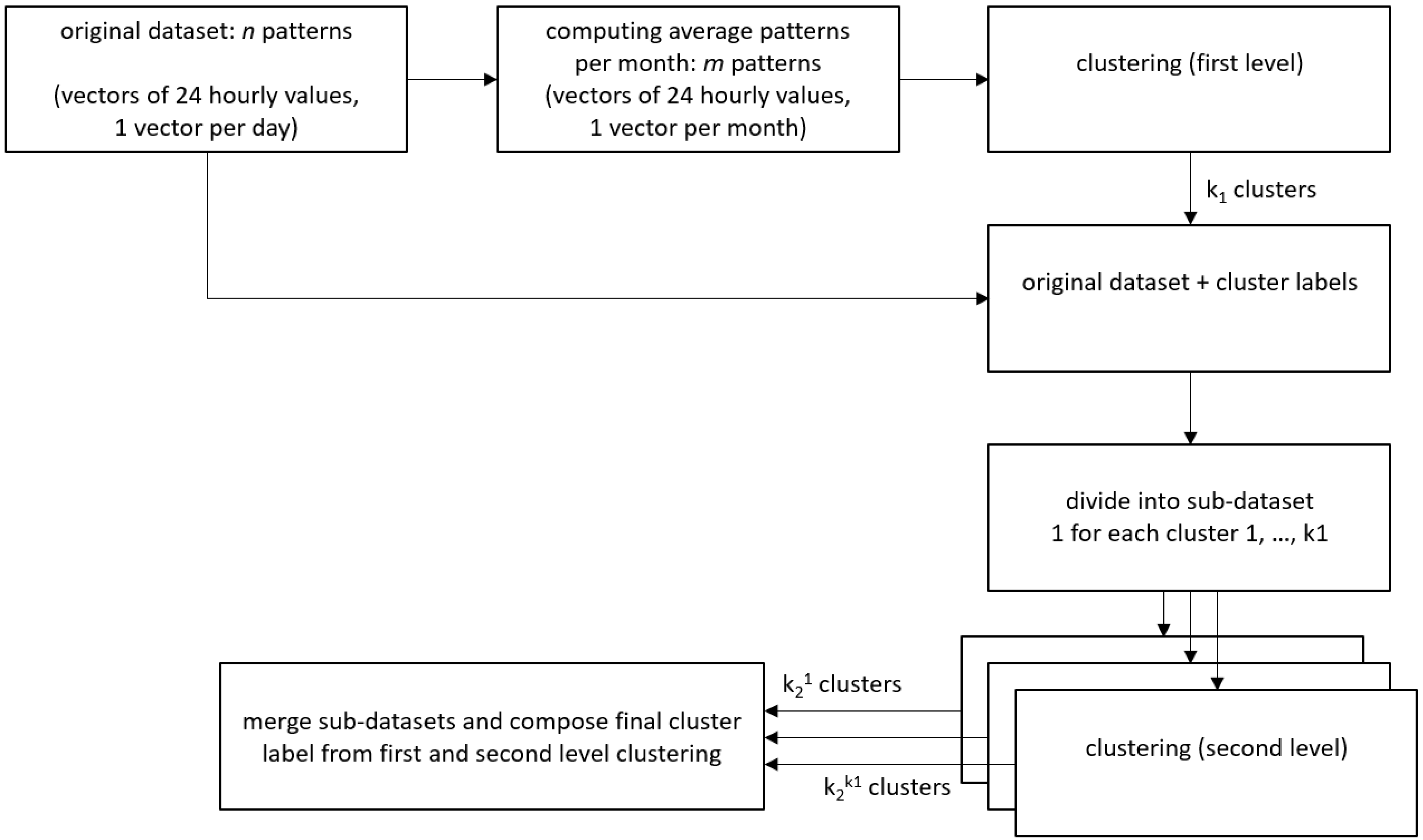
2.3. Time Series Clustering
- Type 1: similarity in time. The goal is to cluster together series that vary in a similar way at each time step. In this case, time series can be clustered by capturing repetitive behaviours occurring always at the same time step or in the same time window (e.g., peak/burst hours).
- Type 2: similarity in shape. The goal is to cluster together time series having common shape features e.g., common trends occurring at different times or similar sub-patterns.
- Type 3: similarity in change. The goal is to cluster together time series that vary similarly from time step to time step. In this case, the data are clustered with respect to the variations between two successive time stamps.
- is the centroid of the k-th cluster.
- is the mean vector of the whole dataset.
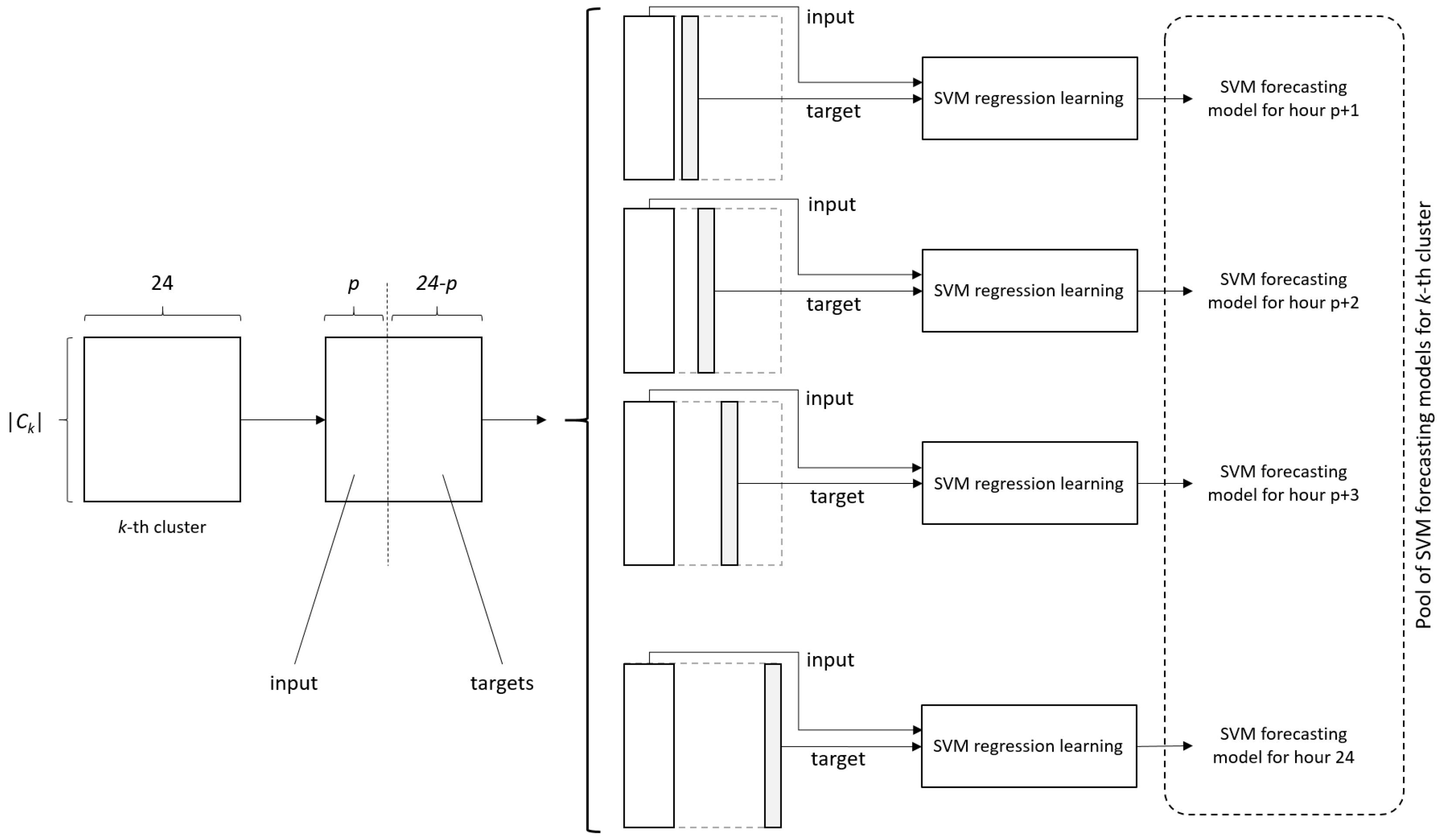
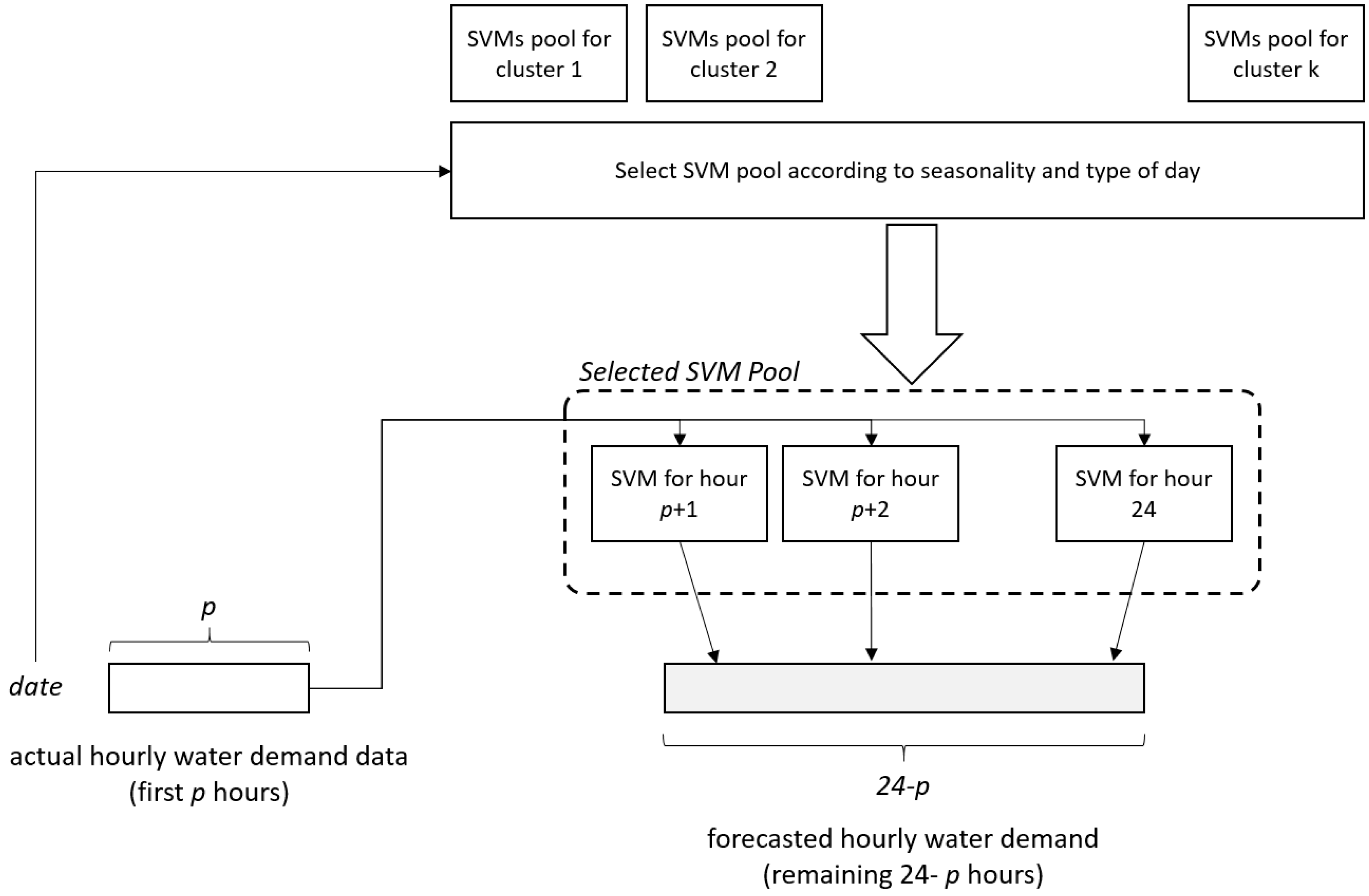
2.4. Support Vector Regression Based Demand Forecasting
- Y—time-series of observed water demand (at any forecast periodicity),
- Yt—water demand observed at the time t,
- Ŷ—time-series of forecasted water demand (at any forecast periodicity),
- Ŷt—water demand forecasted at the time t, and
- N—time-series length;
3. Results and Discussion
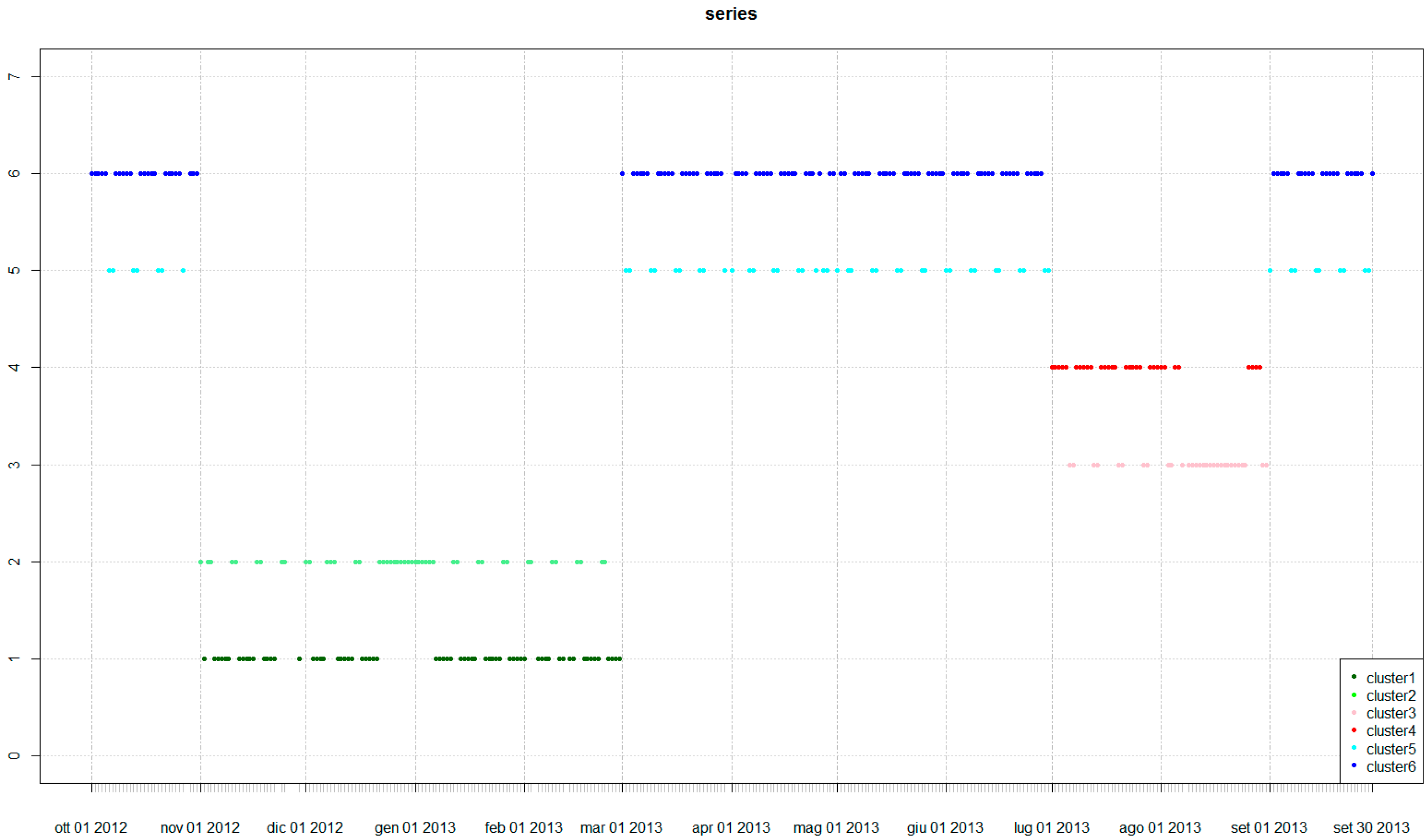
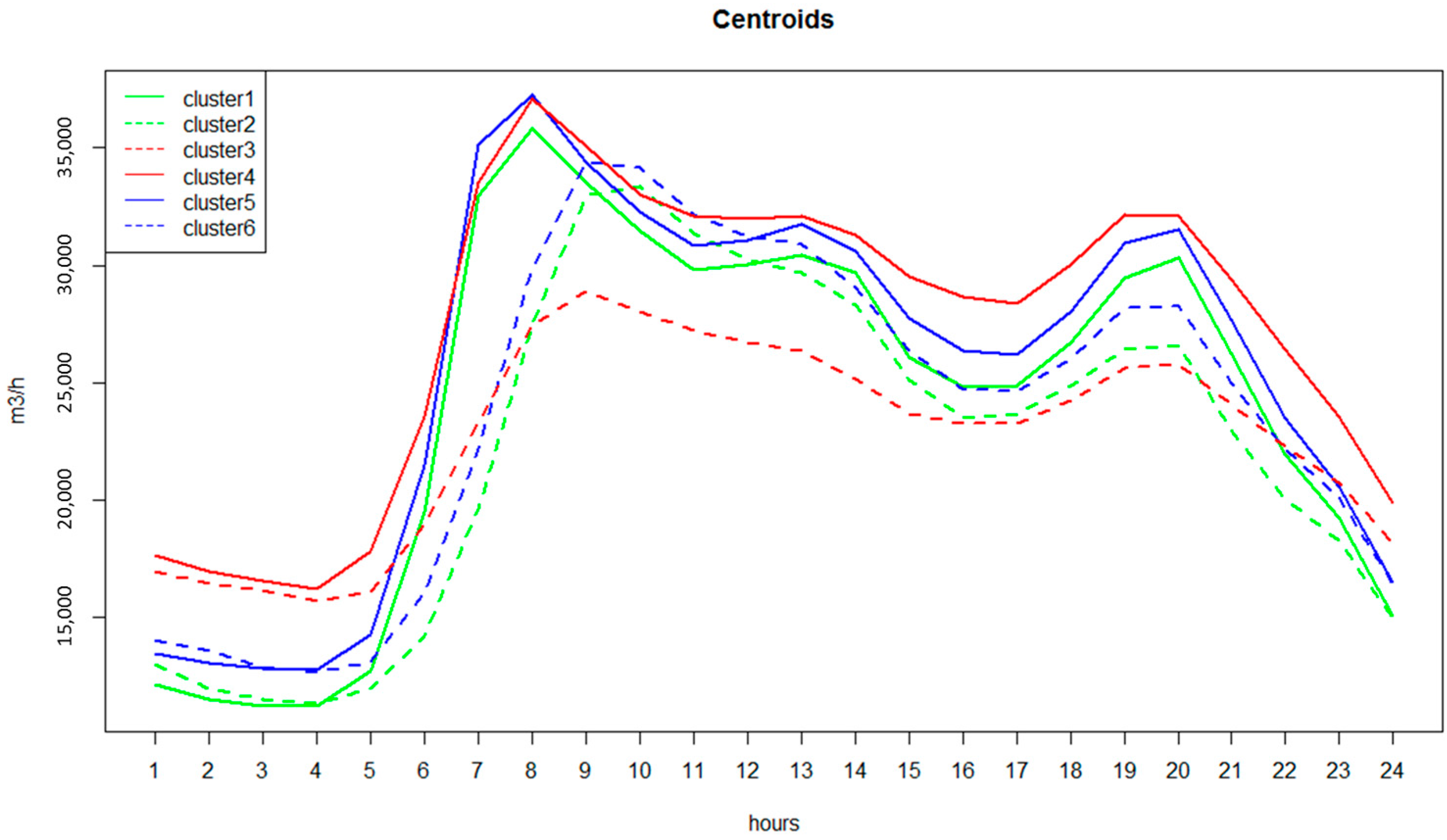
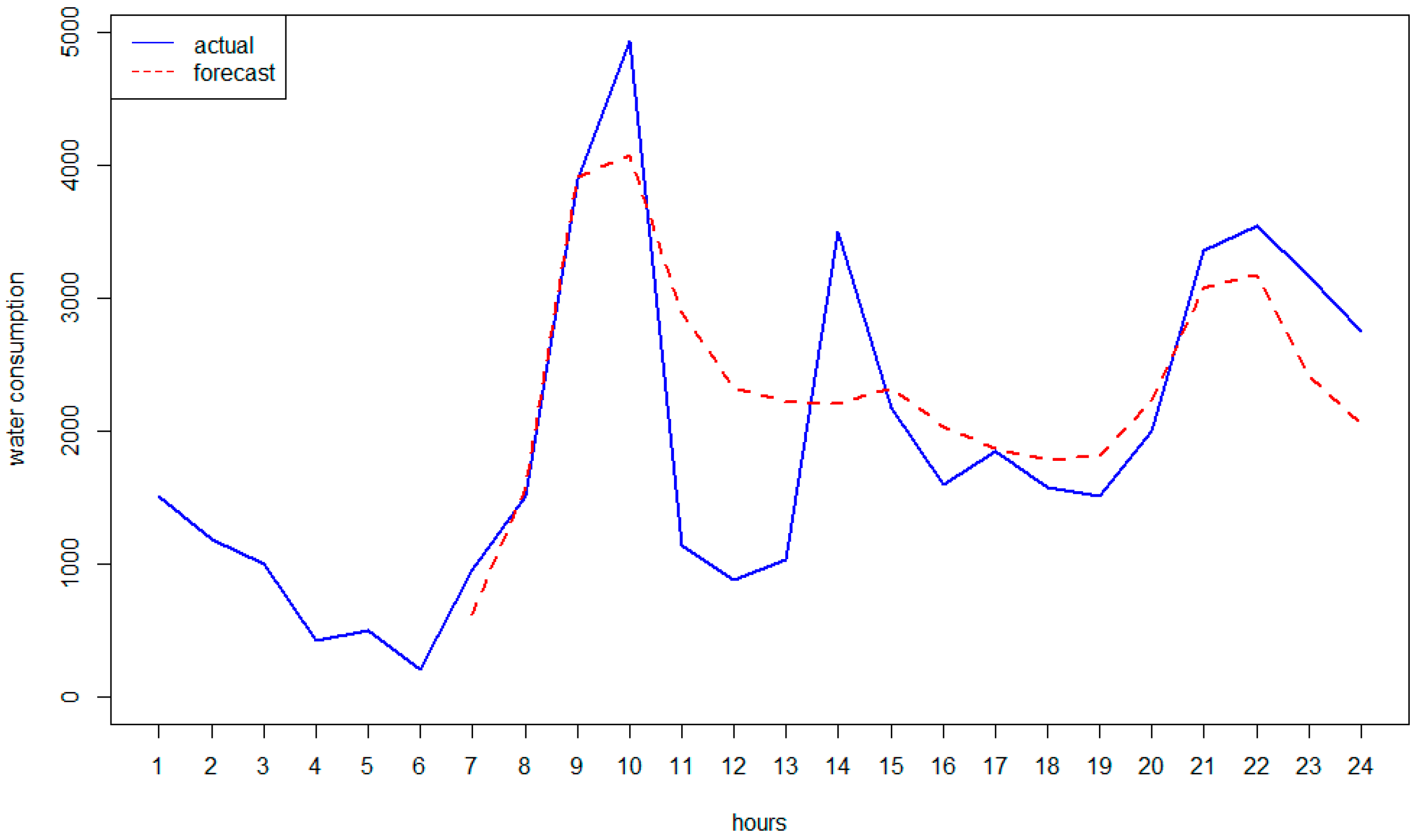
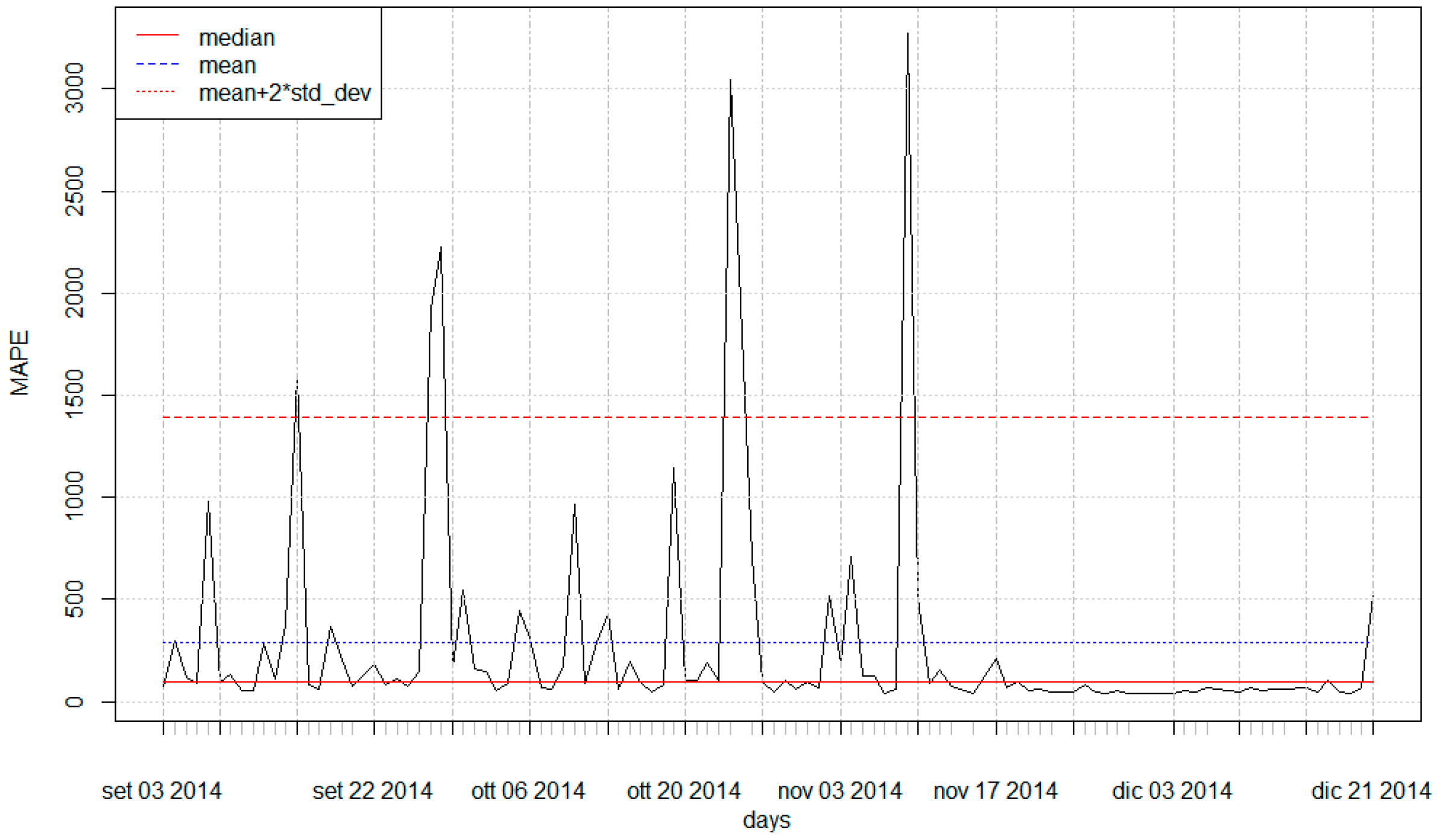
3.1. SCADA Data and Urban Demand Forecasting
- “Fall-Winter”: from November to March
- “Spring-Summer”: from April to June and from September to October
- “Summer break”: July and August
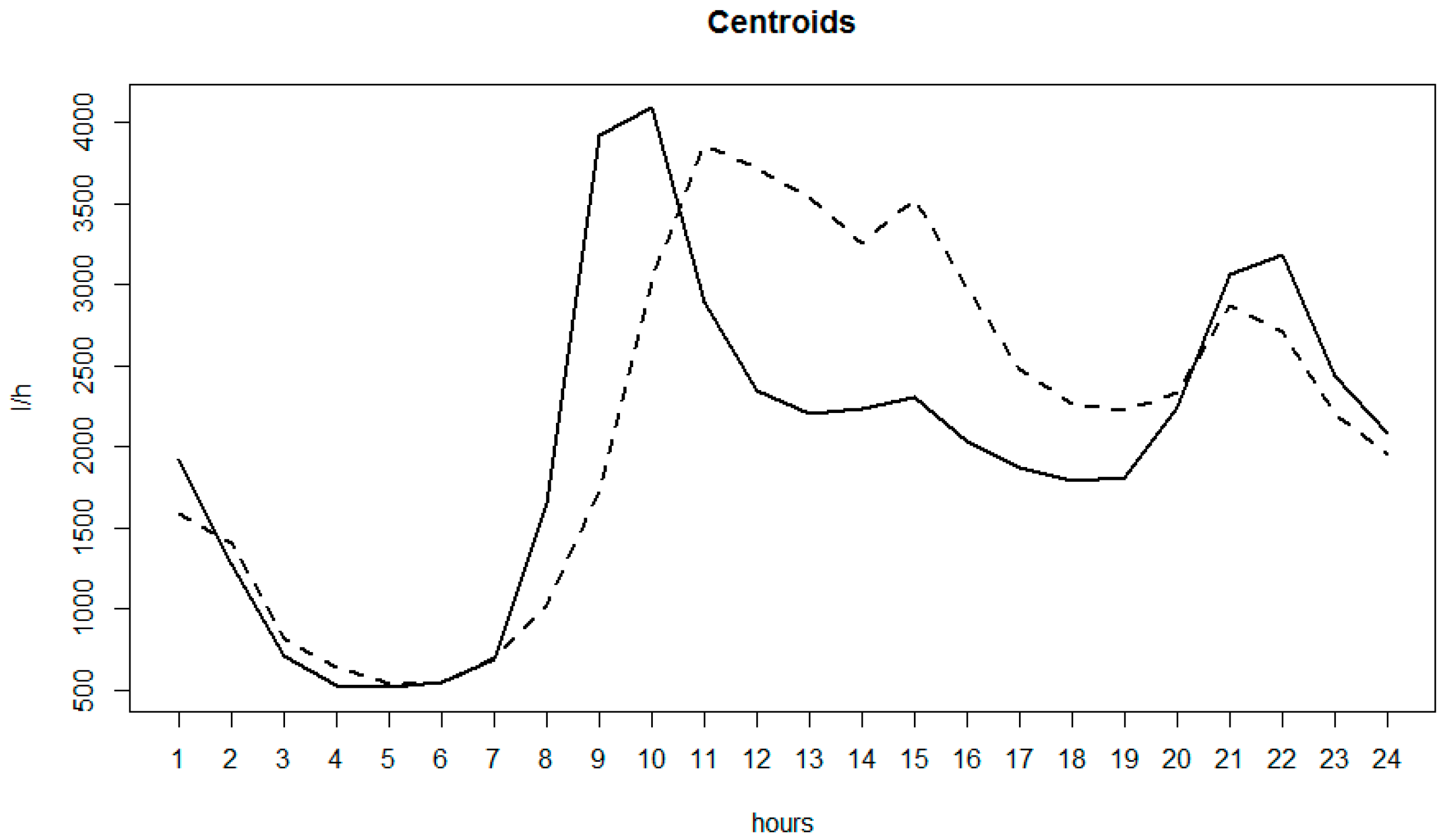
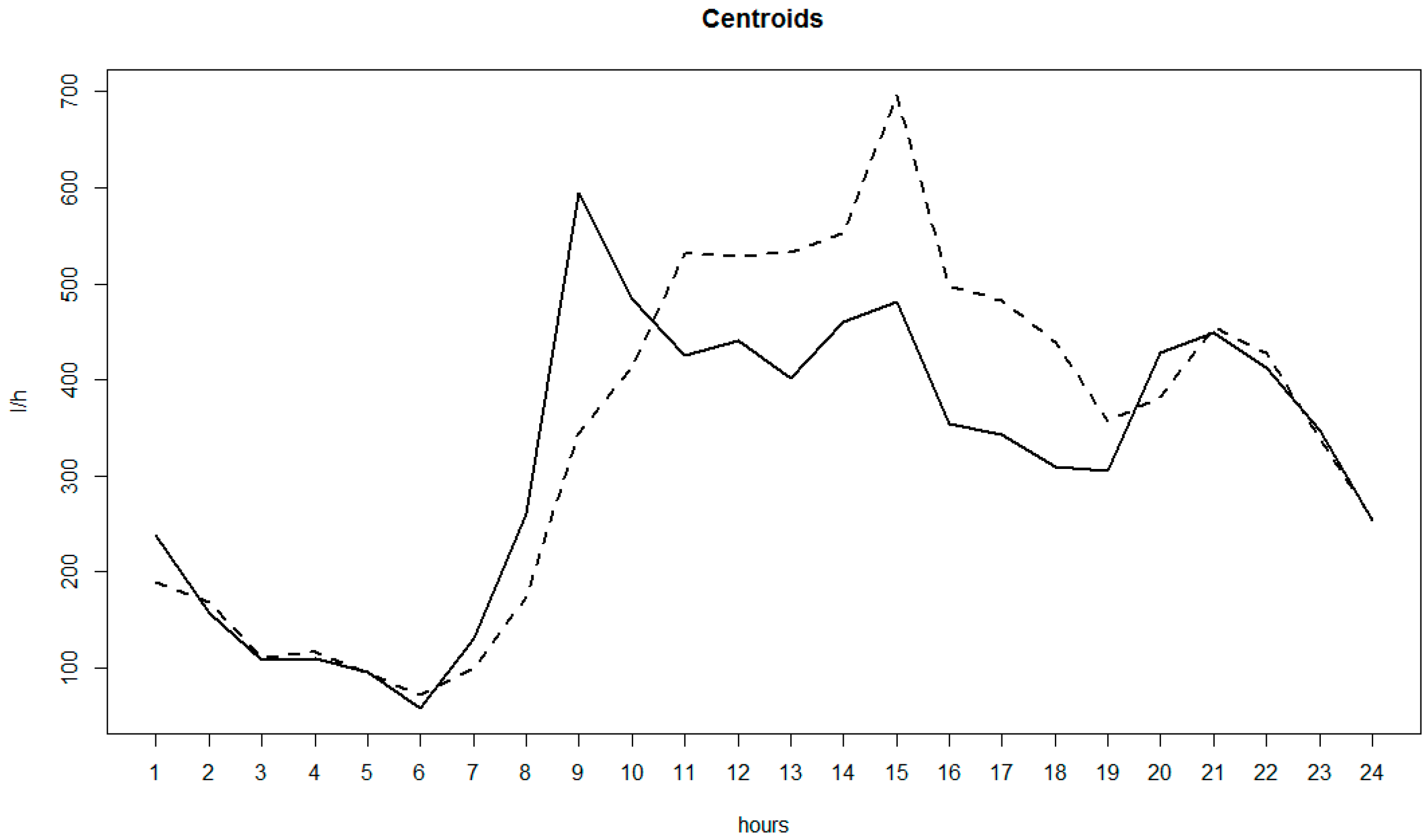
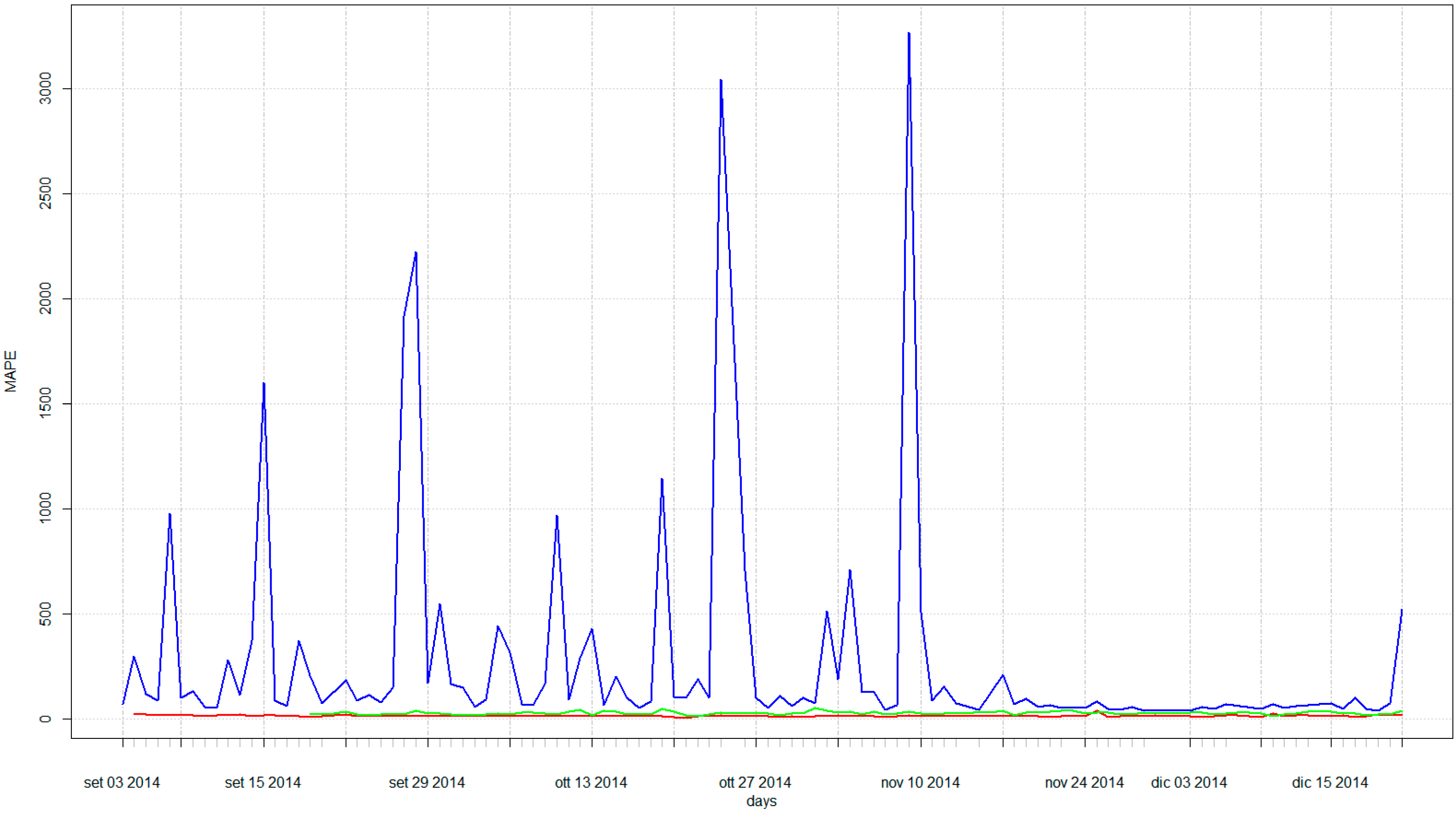
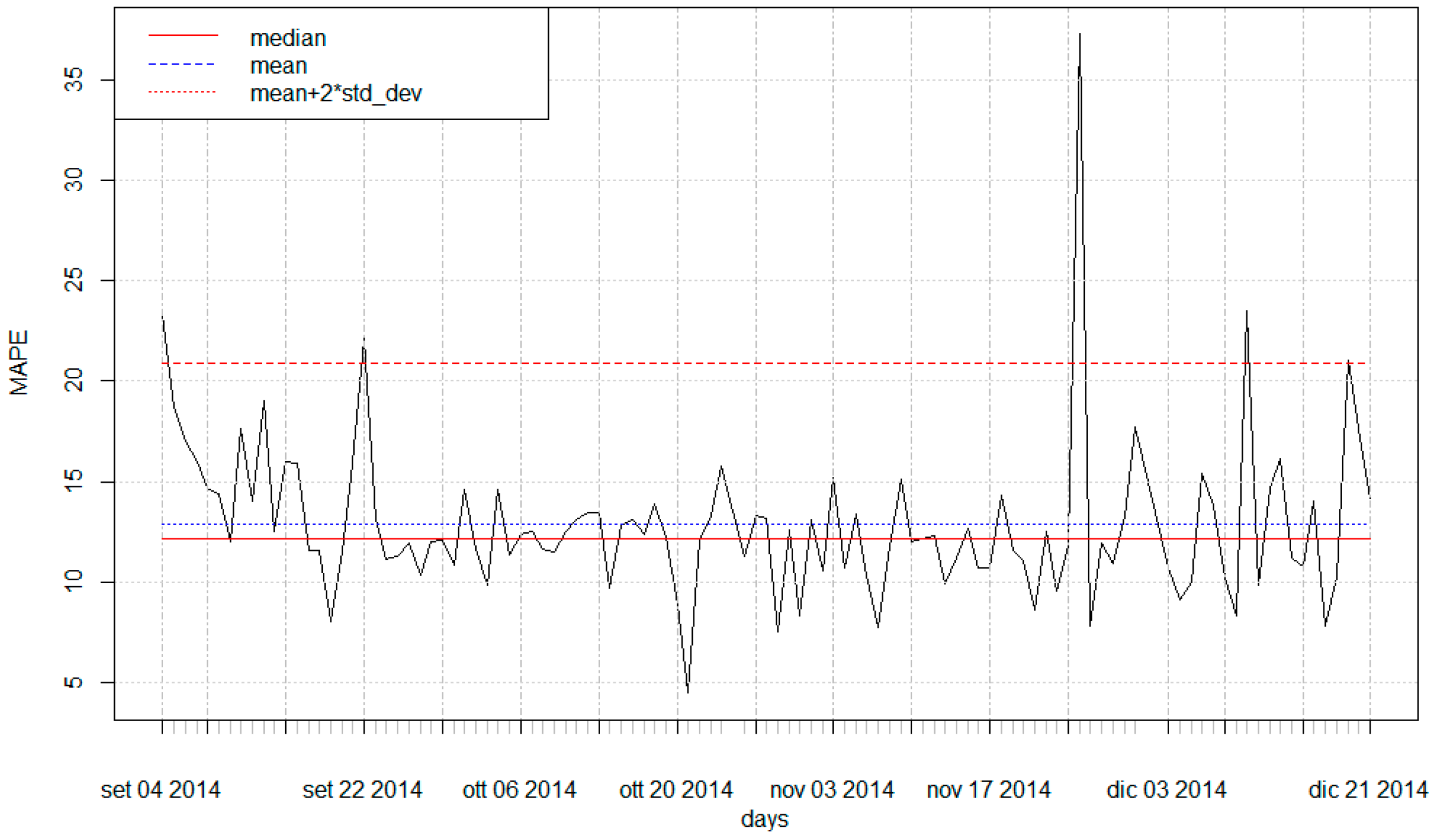
3.2. AMR Data and Anomaly Detection
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mamo, T.G.; Juran, I.; Shahrour, I. Urban water demand forecasting using the stochastic nature of short term historical water demand and supply pattern. J. Water Resour. Hydraul. Eng. 2013, 2, 92–103. [Google Scholar]
- Bakker, M.; van Duist, H.; van Schagen, K.; Vreeburg, J.; Rietveld, L. Improving the performance of water demand forecasting models by using weather input. Proced. Eng. 2014, 70, 93–102. [Google Scholar] [CrossRef]
- New York City Environment Protection. Available online: http://www.nyc.gov/html/dep/html/press_releases/10-78pr.shtml#.WHUdDVPhCUk (accessed on 16 January 2017).
- Bakker, M.; Vreeburg, J.H.G.; Palmen, L.J.; Sperber, V.; Bakker, G.; Rietveld, L.C. Better water quality and higher energy efficiency by using model predictive flow control at water supply systems. J. Water Supply: Res. Technol. AQUA 2013, 62, 1–13. [Google Scholar] [CrossRef]
- Sebri, M. Forecasting urban water demand: A meta-regression analysis. J. Environ. Manag. 2016, 183, 777–785. [Google Scholar] [CrossRef] [PubMed]
- Donkor, E.A.; Mazzucchi, T.A.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Romano, M.; Kapelan, Z. Adaptive water demand forecasting for near real-time management of smart water distribution systems. Environ. Model. Softw. 2014, 60, 265–276. [Google Scholar] [CrossRef]
- Know, H.; So, B.; Kim, S.; Kim, B. Development of ensemble model based water demand forecasting model. EGU Gen. Assem. Conf. Abstr. 2014, 16, 3711. [Google Scholar]
- Gargano, R.; Tricarico, C.; Del Giudice, G.; Granata, F. A stochastic model for daily residential water demand. Water Science and Technology: Water Supply 2016, 16, 1753–1767. [Google Scholar] [CrossRef]
- Magini, R.; Pallavicini, I.; Guercio, R. Spatial and temporal scaling properties of water demand. J. Water Resour. Plann. Manage. 2008, 134, 276–284. [Google Scholar] [CrossRef]
- Alcocer-Yamanaka, V.H.; Tzatchkov, V.G.; Arreguin-Cortes, F.I. Modeling of drinking water distribution networks using stochastic demand. Water Resour. Manage. 2012, 26, 1779–1792. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Vreeburg, J.H.G.; van Dijk, J.C. Simulating residential water demand with a stochastic end-use model. J. Water Resour. Plann. Manage. 2010, 136, 19–26. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Wu, L. A model for instantaneous residential water demands. J. Hydraul. Eng. 1995, 121, 232–246. [Google Scholar] [CrossRef]
- Gargano, R.; Di Palma, F.; de Marinis, G.; Granata, F.; Greco, R. A stochastic approach for the water demand of residential end users. Urban. Water J. 2016, 13, 569–582. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; de Marinis, G. Machine Learning Algorithms for the Forecasting of Wastewater Quality Indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Wu, M.C.; Lin, G.F. An Hourly Streamflow Forecasting Model Coupled with an Enforced Learning Strategy. Water 2015, 7, 5876–5895. [Google Scholar] [CrossRef]
- Adamowski, J.; Karapataki, C. Comparison of multivariate regression and artificial neural networks for peak urban water-demand forecasting: evaluation of different ann learning algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef]
- Cutore, P.; Campisano, A.; Kapelan, Z.; Modica, C.; Savic, D. Probabilistic prediction of urban water consumption using the scem-ua algorithm. Urb. Water J. 2008, 5, 125–132. [Google Scholar] [CrossRef]
- Firat, M.; Yurdusev, M.A.; Turan, M.E. Evaluation of artificial neural network techniques for municipal water consumption modeling. Water Resour. Manag. 2009, 23, 617–632. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. Eng. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Ghiassi, M.; Zimbra, D.; Saidane, H. Urban water demand forecasting with a dynamic artificial neural network model. J. Water Resour. Plan. Manag. 2008, 134, 138–146. [Google Scholar] [CrossRef]
- Herrera, M.; Izquierdo, J.; Pérez-Garćıa, R.; Ayala-Cabrera, D. On-line learning of predictive kernel models for urban water demand in a smart city. Proced. Eng. 2014, 70, 791–799. [Google Scholar] [CrossRef]
- Ji, G.; Wang, J.; Ge, Y.; Liu, H. Urban Water Demand Forecasting by LS-SVM with Tuning Based on Elitist Teaching-Learning-Based Optimization. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 3997–4002.
- Sampathirao, A.K.; Grosso, J.M.; Sopasakis, P.; Ocampo-Martinez, C.; Bemporad, A.; Puig, V. Water Demand Forecasting for the Optimal Operation of Large-Scale Drinking Water Networks: The Barcelona Case Study. In Proceedings of the 19th International Federation of Automatic Control (IFAC) World Congress, Cape Town, South Africa, 2014; pp. 10457–10462.
- Brentan, B.; Luvizotto, E.; Herrera, M.; Izquierdo, J.; Perez-Garcia, R. Real-time water demand forecasting using support vector machine and adaptive fourier series. In Modelling for Engineering and Human Behaviour; Jodar, L., Acedo, L., Cortes, J.C., Eds.; IMM-Universitat Politecnica de Valencia: Valencia, Spain, 2015; pp. 178–182. [Google Scholar]
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. Dynamic forecast of daily urban water consumption using a variable-structure support vector regression model. J. Water Resour. Plan. Manag. 2015, 141, 04014058. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Shabani, S.; Yousefi, P.; Adamowski, J.; Naser, G. Intelligent soft computing models in water demand forecasting. In Water Stress in Plants; Rahman, M.I.M., Begum, Z.A., Hasegawa, H., Eds.; Intech: Rijeka, Croatia, 2016; Chapter 6; pp. 100–117. [Google Scholar]
- Martìnez-Alvarez, F.; Troncoso, A.; Riquelme, J.C.; Aguilar-Ruiz, J.S. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Bokde, N.; Asencio-Cortés, G.; Martínez-Álvarez, F.; Kulat, K. Psf: Introduction to r package for pattern sequence based forecasting algorithm. arXiv:1606.05492v2 [stat.ML] 25 Aug 2016.
- Candelieri, A.; Soldi, D.; Archetti, F. Short-term forecasting of hourly water consumption by using automatic metering readers data. Proced. Eng. 2015, 119, 844–853. [Google Scholar] [CrossRef]
- Candelieri, A.; Archetti, F. Identifying typical urban water demand patterns for a reliable short-term forecasting – the icewater project approach. Proced. Eng. 2014, 89, 1004–1012. [Google Scholar] [CrossRef]
- Liao, T.W. Clustering of time series data—a survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Kavitha, V.; Punithavalli, M. Clustering time series data stream-a literature survey. J.Comput. Sci. Inf. Secur. 2010, 8. [Google Scholar]
- Zhang, X.; Liu, J.; Du, Y.; Lv, T. A novel clustering method on time series data. Expert Syst. Appl. 2011, 38, 11891–11900. [Google Scholar] [CrossRef]
- Maitra, R.; Ramler, I.P. A k-mean-directions algorithm for fast clustering of data on the sphere. J. Comput. Gr. Stat. 2010, 19, 377–396. [Google Scholar] [CrossRef]
- Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; Pérez, J.M.; Perona, I. An extensive comparative study of cluster validity indices. Pattern Recognit. 2013, 46, 243–256. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support. Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]

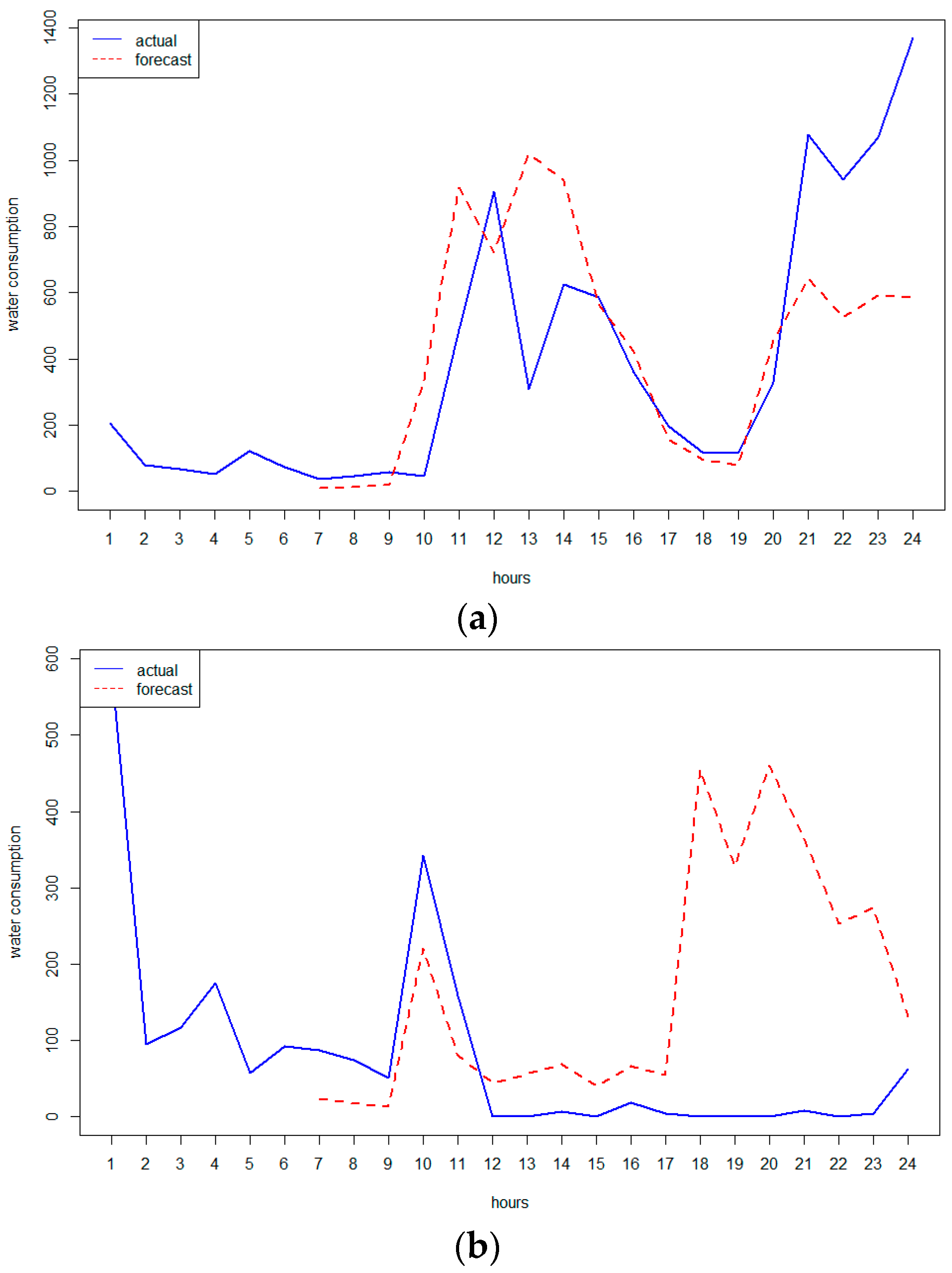
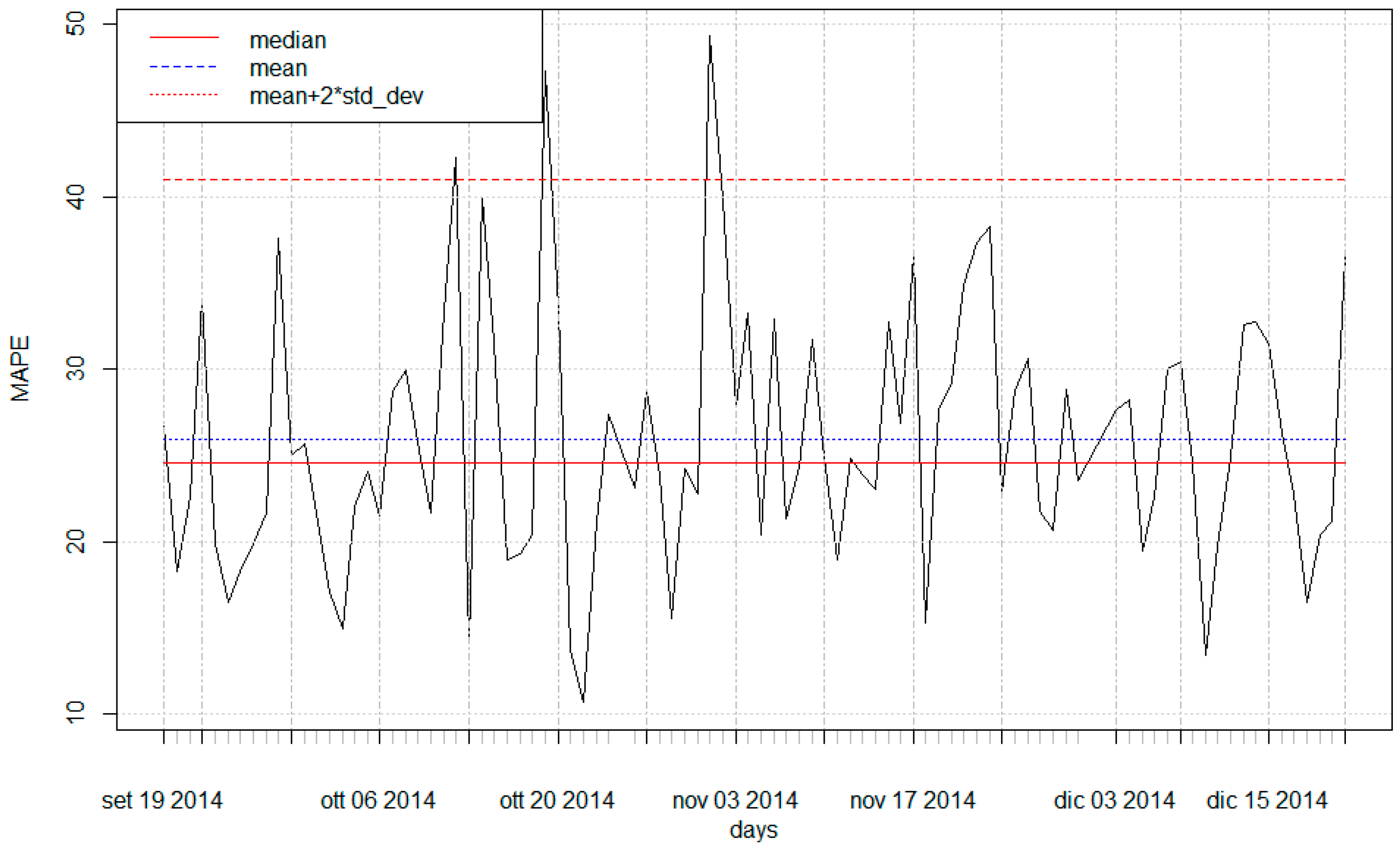
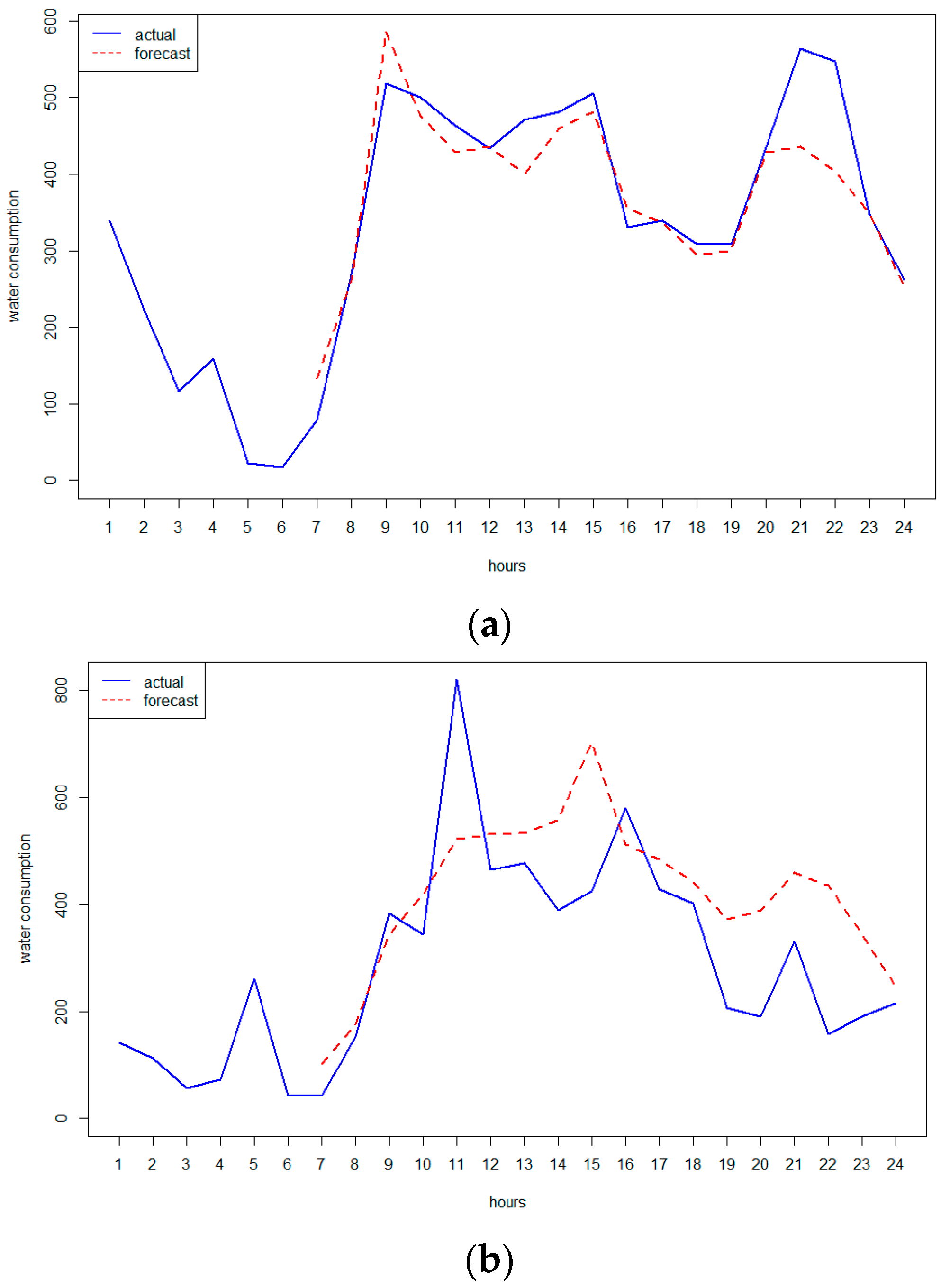
| k1 | Silhouette | Calinski-Harabasz |
|---|---|---|
| 2 | 0.51 | 2.96 |
| 3 | 0.74 | 3.15 |
| 4 | 0.49 | 2.12 |
| k2 | Silhouette | Calinski-Harabasz |
|---|---|---|
| 2 | 0.70 | 192.78 |
| 3 | 0.62 | 54.35 |
| 4 | 0.50 | 36.68 |
| Size | Best | Worst | |
|---|---|---|---|
| Cluster 1 | 67 | 0.79% ± 0.59% | 6.11% ± 2.95% |
| Cluster 2 | 46 | 1.57% ± 1.18% | 14.33% ± 11.68% |
| Cluster 3 | 30 | 0.84% ± 0.66% | 8.48% ± 3.53% |
| Cluster 4 | 31 | 1.71% ± 2.56% | 12.84% ± 7.53% |
| Cluster 5 | 54 | 1.31% ± 0.93% | 7.85% ± 13.26% |
| Cluster 6 | 127 | 1.10% ± 0.85% | 6.54% ± 3.46% |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Candelieri, A. Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water 2017, 9, 224. https://doi.org/10.3390/w9030224
Candelieri A. Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water. 2017; 9(3):224. https://doi.org/10.3390/w9030224
Chicago/Turabian StyleCandelieri, Antonio. 2017. "Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection" Water 9, no. 3: 224. https://doi.org/10.3390/w9030224
APA StyleCandelieri, A. (2017). Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water, 9(3), 224. https://doi.org/10.3390/w9030224





