1. Introduction
Regional climate models (RCMs) that have been used to reproduce past and recent climate features are expected to provide credible predictions of future climate changes and impacts at regional or local scales. For the predictability of RCMs, the coupled models need more realistic and accurate calculations for interactions between the land surface and the atmosphere [
1]. The Intergovernmental Panel on Climate Change (IPCC) also addressed the need for improvements to terrestrial land surface parameterizations in land surface models (LSMs) coupled to RCMs [
2]. As the climate and hydrology modeling studies have developed toward physical sophistication and high resolution, LSMs coupled to RCMs have improved land surface parameterization schemes by incorporating sophisticated process interactions in the terrestrial hydrologic cycle [
3,
4,
5,
6,
7,
8,
9,
10]. However, some unrealistic parameterizations for terrestrial hydrologic schemes in LSMs have a direct or indirect influence on the complex and dynamic responses of land surface processes, which may cause serious errors in both terrestrial water and energy predictions.
The fact that most land surface parameterizations are currently limited to vertical fluxes in each single grid column may negatively affect the model’s predictions for terrestrial water and energy processes, especially because the existing terrestrial hydrologic schemes in most LSMs are incapable of representing the lateral water movement induced by topographic features. As incoming precipitation is divided into evapotranspiration, soil moisture, surface and subsurface runoff by land surface processes in LSMs, runoff plays an important part in the terrestrial water budget. However, runoff is estimated just by the soil water budget without topographically controlled surface and subsurface flow schemes in most LSMs. Moreover, surface runoff used for neither soil moisture nor subsurface runoff calculation as the boundary condition results in a mass balance error in the terrestrial water cycle. The infiltration rate calculations do not take into consideration the role of surface flow depth, which can cause errors in both infiltration and surface flow calculations [
11,
12,
13]. Such unrealistic and simplified parameterizations in the terrestrial hydrologic scheme may affect other key components in land surface water and energy cycles, limiting the predictability of LSMs.
The Common Land Model (CoLM), a Soil–Vegetation–Atmosphere Transfer (SVAT) model [
14], already coupled to the mesoscale Climate–Weather Research and Forecasting model (CWRF), has been developed and updated for sophisticated land surface processes. The CWRF has built-in modules for realistic Surface Boundary Conditions (SBCs) and is the most comprehensive of the weather and climate models [
15,
16,
17]. The CWRF’s responses to various subgrid topographic representations and parameter selections were examined [
18,
19]. A scalable soil moisture transport scheme was developed for representing subgrid topographic control in land–atmosphere interactions of the CWRF [
20,
21]. The CWRF simulations were evaluated based on a continuous integration for the period 1979–2009 using a 30-km grid spacing over the North American domain [
22]. The model improvement and performance of the CWRF were evaluated especially for possible impacts of precipitation, temperature, radiation, and extreme events’ occurrence and magnitude to help with future climate projection [
23]. Also, many studies [
6,
7,
8,
9,
14,
24,
25,
26,
27,
28] have evaluated the performance of the CoLM simulations in a standalone mode by the observational forcing data. Nonetheless, the mesoscale simulations of the CoLM at the 30-km resolution are found to still have problems in the terrestrial hydrologic scheme, especially streamflow runoff predictions. Choi et al. [
10] have therefore developed a conjunctive surface-subsurface flow (CSSF) model based on a one-dimensional (1D) diffusion wave model for the surface flow routing scheme coupled with the 3D volume averaged soil-moisture transport (VAST) model for water flux in unsaturated soils [
21]. However, the CSSF model cannot be widely implemented yet for watersheds all around the world because the VAST model requires closure parameterizations by regional estimates of subgrid and lateral soil moisture fluxes for each local watershed.
Based on an assumption that the lateral soil moisture movement may not be a major water flux in large spatial scale simulations, this study has focused on incorporating a routed surface flow scheme and an unrouted subsurface lateral runoff scheme into the existing 1D soil moisture transport formulation to evaluate the influence of a lateral flow scheme on runoff predictions in the CoLM. A new version of the CoLM, named CoLM+LF, is proposed in this study as it can explicitly route surface runoff from excess water of both infiltration and saturation, and estimate subsurface runoff induced by topographic controls. This study has implemented both the baseline CoLM and the new CoLM+LF at the CWRF 30-km grid resolution, focusing on surface and subsurface runoff predictions because the terrestrial hydrologic parameterizations including the runoff scheme must be tested and evaluated at the same resolution as the coupled climate models.
The principal aim of this study is to assess the improvement to runoff predictions from the new CoLM+LF with a lateral flow scheme using the best Earth observation data possible for model predictability. For evaluating the performance of runoff results simulated from both the baseline CoLM and the new CoLM+LF, this study has selected a watershed under study, the Nakdong River Watershed in Korea. All the CoLM and the CoLM+LF schemes were implemented at 30-km grid points in this study watershed without any downscaling and upscaling schemes for exchanges between the atmosphere and the land surface. For such direct applications of both the CoLM and the CoLM+LF, this study has constructed a set of realistic SBCs and meteorological forcing data based on high-quality Earth observations at the finest possible resolution from multifarious sources such as remote sensing products (see
Section 3.2 for details), photography images, in situ observations, scanned and digitized maps, etc. for the study domain at 30-km (0.25°) resolution on the geographic coordinate system following Choi [
29,
30]. The raw data at finer resolutions were transformed into SBCs on the 30-km spacing grids in the study domain mainly by geoprocessing tools in a Geographic Information System (GIS), ArcGIS (ESRI, Redlands, CA, USA). Most meteorological forcing data to drive both the CoLM and the CoLM+LF simulations in a standalone mode were spatially interpolated onto the 30-km computational grids by the Inverse Distance Weighting (IDW) method in ArcGIS from observations at 19 gauge stations managed by the Korea Meteorological Administration (KMA) around the study watershed. For the performance assessment of the terrestrial hydrologic schemes in predicting runoff by the goodness-of-fit test, the results from both the CoLM and the CoLM+LF simulations through the sensitivity analysis of key parameters for runoff variables were compared with daily streamflow discharges during a year of 2009 observed at the Jindong stream gauge station managed by the Ministry of Land, Infrastructure, and Transport (MOLIT) near the drainage outlet of the Nakdong River Watershed, Korea. It is expected that the proposed CoLM+LF with a lateral flow scheme using realistic Earth observations can more effectively generate daily streamflow variations compared with the baseline CoLM runoff results from the local net excess water flux in each grid when ignoring the role of surface flow depth over the watershed, as most current LSMs do.
3. Model Implementation
The new CoLM+LF model has incorporated a set of topographically controlled surface and subsurface flow schemes into the existing terrestrial hydrologic representation in the baseline CoLM. The performance of both the baseline CoLM and the new CoLM+LF in predicting runoff was evaluated over the second-largest watershed on complex terrain in Korea to study the impact of lateral flow induced by topography using the 30-km computational grid mesh targeted for regional applications. The model experiments were performed in a standalone mode for which both the CoLM and the CoLM+LF were driven by the realistic SBCs and meteorological forcing data at the 30-km grid scale, constructed by applications of Earth observation data and GIS in this study.
3.1. Study Watershed
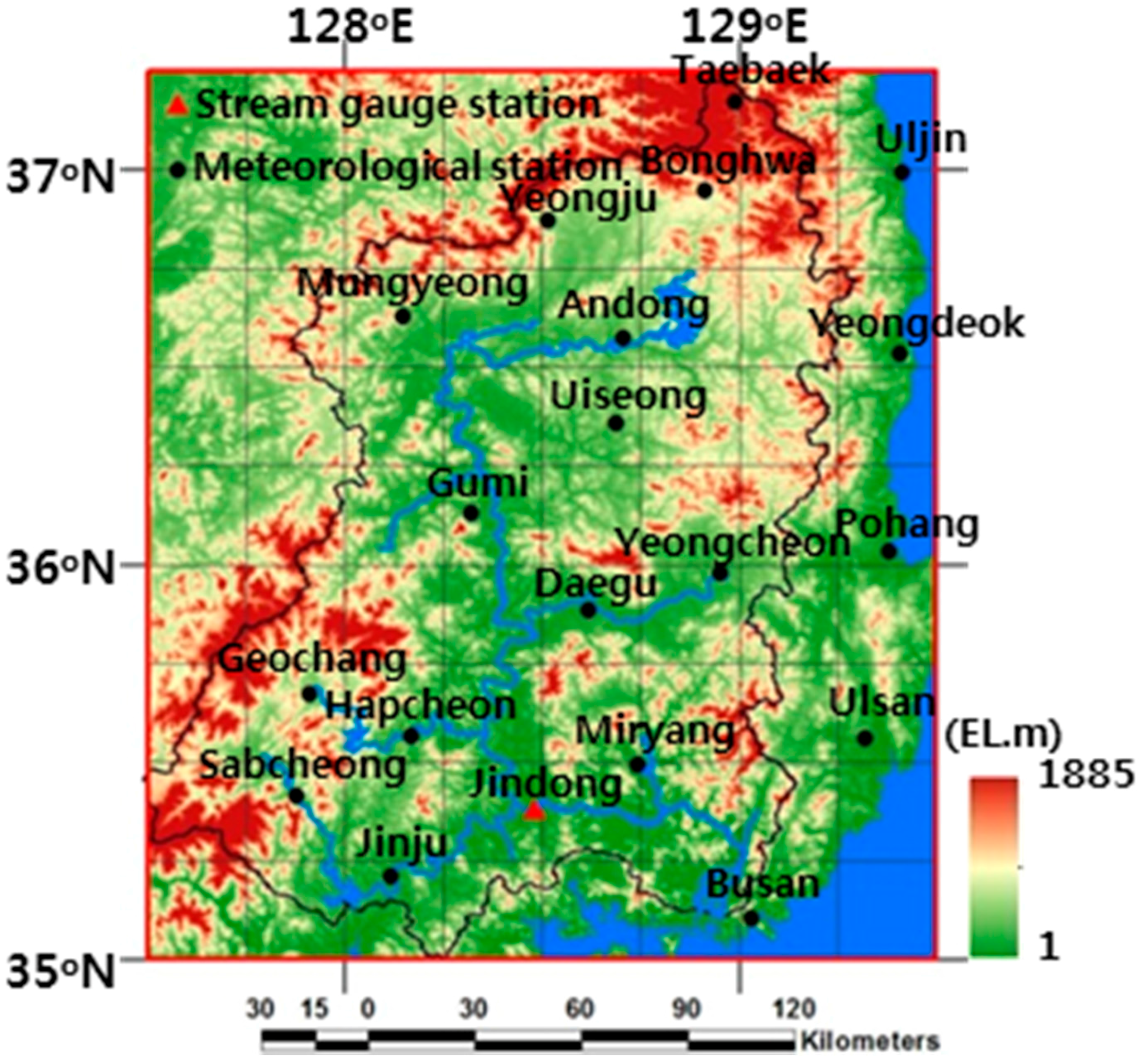
The Nakdong River Watershed with high topographic heterogeneity in Korea was selected under study to evaluate the performance of the baseline runoff simulation in the CoLM and the lateral flow adopted runoff simulation in the CoLM+LF at the 30-km resolution.
Figure 1 shows the study domain comprising 72 (8 × 9) computational grid cells at 30-km (0.25°) horizontal spacing overlaid with the main streamline and the watershed boundary of the Nakdong River on the geographic coordinate system. The Nakdong River Watershed is located between 127°29′~129°18′ E and 35°03′~37°13′ N with the size of 23,384.21 km
2 and the main channel length of 510.36 km. The Nakdong River flows from the Taebaek Mountains over the north region to the South Sea. The terrain elevation ranges from 1 to 1885 EL.m over the watershed, and the width of the river ranges from only a few meters in its upper reaches to several hundred meters towards its estuary. Major land cover types are comprised of irrigated cropland/pasture, cropland/woodland mosaic, savanna, and mixed forest in the USGS land cover classification. A stream gauge station is located at the Jindong Bridge where daily streamflow discharges were measured in 2009 by the MOLIT. There are 19 meteorological gauge stations managed by the KMA around the study watershed for hourly or daily observations. See
Section 3.3 for details on observations and meteorological forcing data in the study domain.
3.2. Surface Boundary Conditions
This study has constructed a set of primary SBCs from high-quality and -resolution observational data over the Nakdong River Watershed. The primary SBCs required for the CoLM and the CoLM+LF implementations comprise three groups of SBC datasets related to vegetation, terrain, and flow direction features on the 30-km spacing grids transformed from various Earth observations at the finest resolution possible for the study domain.
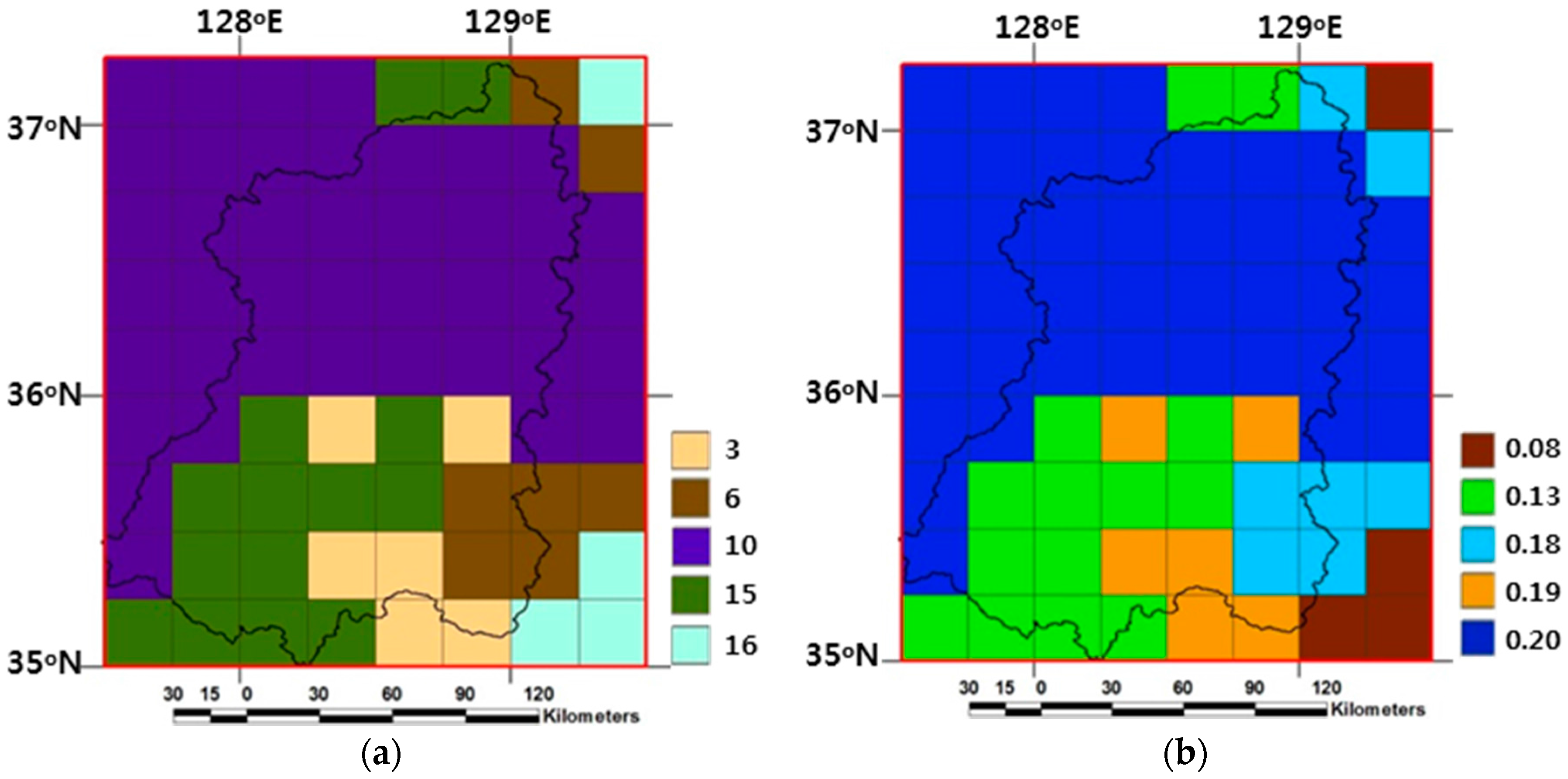
The vegetative SBCs include land cover category, albedo, fractional vegetation cover, and monthly leaf area index in 2009. First of all, the raw data at much finer than the 30-km resolution on various data format and map projections were converted into ArcGIS raster data, and then the representative (majority or average) values were computed for each 30-km computational grid. The 30-km land cover category data was made from the 1-km USGS land cover classification with 24 categories [
36], developed from the Advanced Very High Resolution Radiometer (AVHRR) satellite-derived Normalized Difference Vegetation Index (NDVI) composites. The one of the USGS 24 land cover types constituting the largest fraction is selected as the representative value for each 30-km grid. Provided that category 16 (water bodies) with the largest fraction is not the absolute majority in a grid, this grid’s land cover type is not the water body but belongs in the category that constitutes the second largest fraction. As shown in
Figure 2a, the study watershed consists of the USGS land cover categories 3 (irrigated cropland and pasture), 6 (cropland/woodland mosaic), 10 (savanna), and 15 (mixed forest) at the 30-km scale. The three water body (category 16) grids in the study domain were used as the standard identification for consistency of water bodies in all datasets of SBCs. Following Yucel [
37], the 30-km albedo values were assigned with respect to the 30-km USGS land cover categories, distributed from 0.13 to 0.20 for the study watershed and given to 0.08 for water bodies as shown in
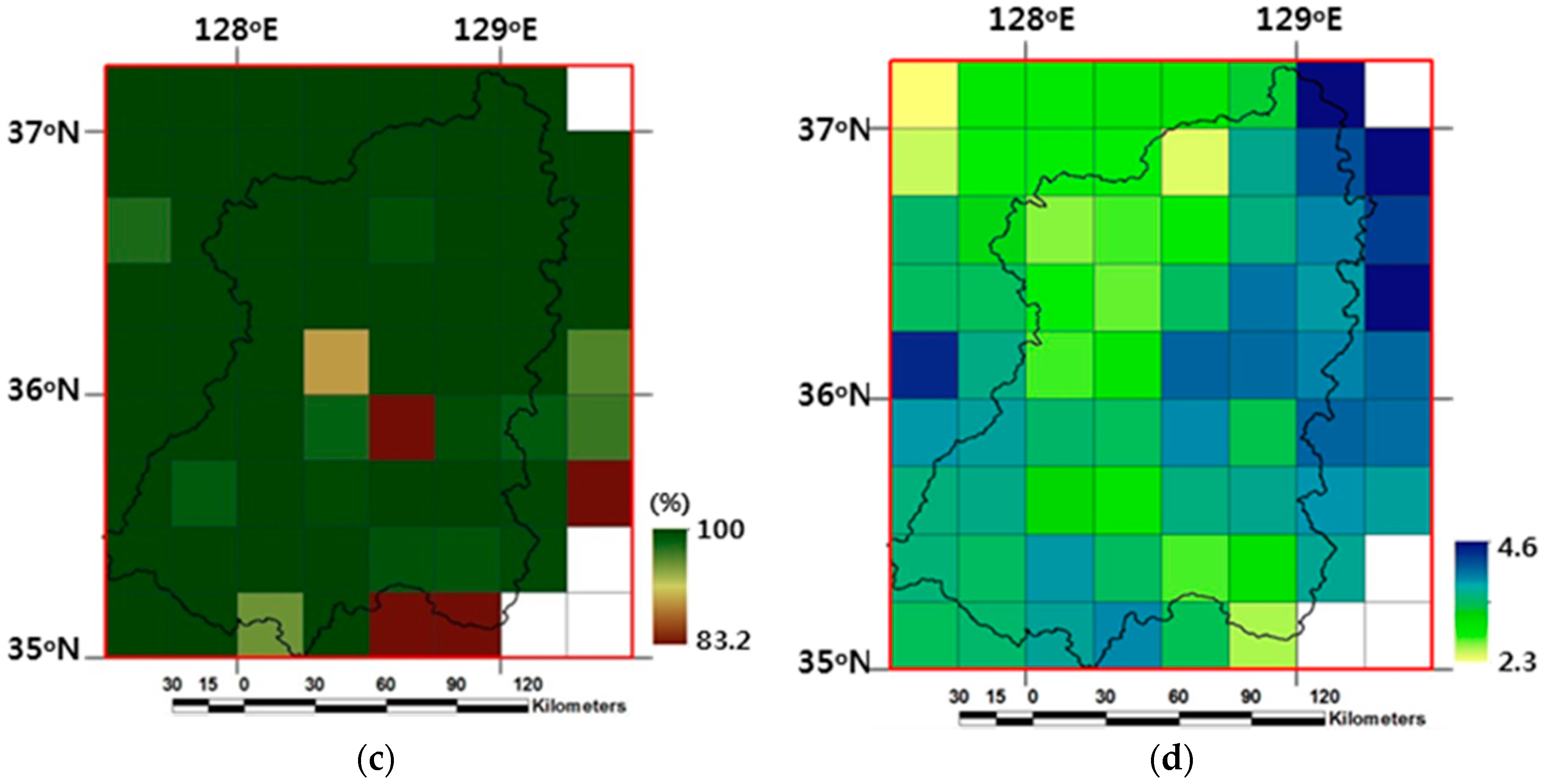
Figure 2b. The high-resolution fractional vegetation cover was computed following Zeng et al. [
38,
39] from the 1-km NDVI data in the Système Pour l’Observation de la Terre-VEGETATION (SPOT-VGT) satellite products [
40].
Figure 2c denotes spatial distributions of the 30-km fractional vegetation cover values ranging from 83.2% to 100%, calculated by averaging all 1-km values within each 30-km grid using a zonal statistic function, ZONALMEAN in ArcGIS geoprocessing tools. The raw leaf area index data is provided from the 1-km MOD 15 LAI data [
41] by Moderate Resolution Imaging Spectroradiometer (MODIS) from the Terra (EOS AM) and Aqua (EOS PM) satellites. After abnormal values were removed by a smoothing filter method by Liang et al. [
16] and then missing values were filled using an interpolation method by Choi [
29], the monthly leaf area index data were calculated following Zeng et al. [
39] for each 30-km grid by the ZONEALMEAN function in ArcGIS.
Figure 2d denotes leaf area index values in a range of 2.3 to 4.6 for the study domain in July 2009.
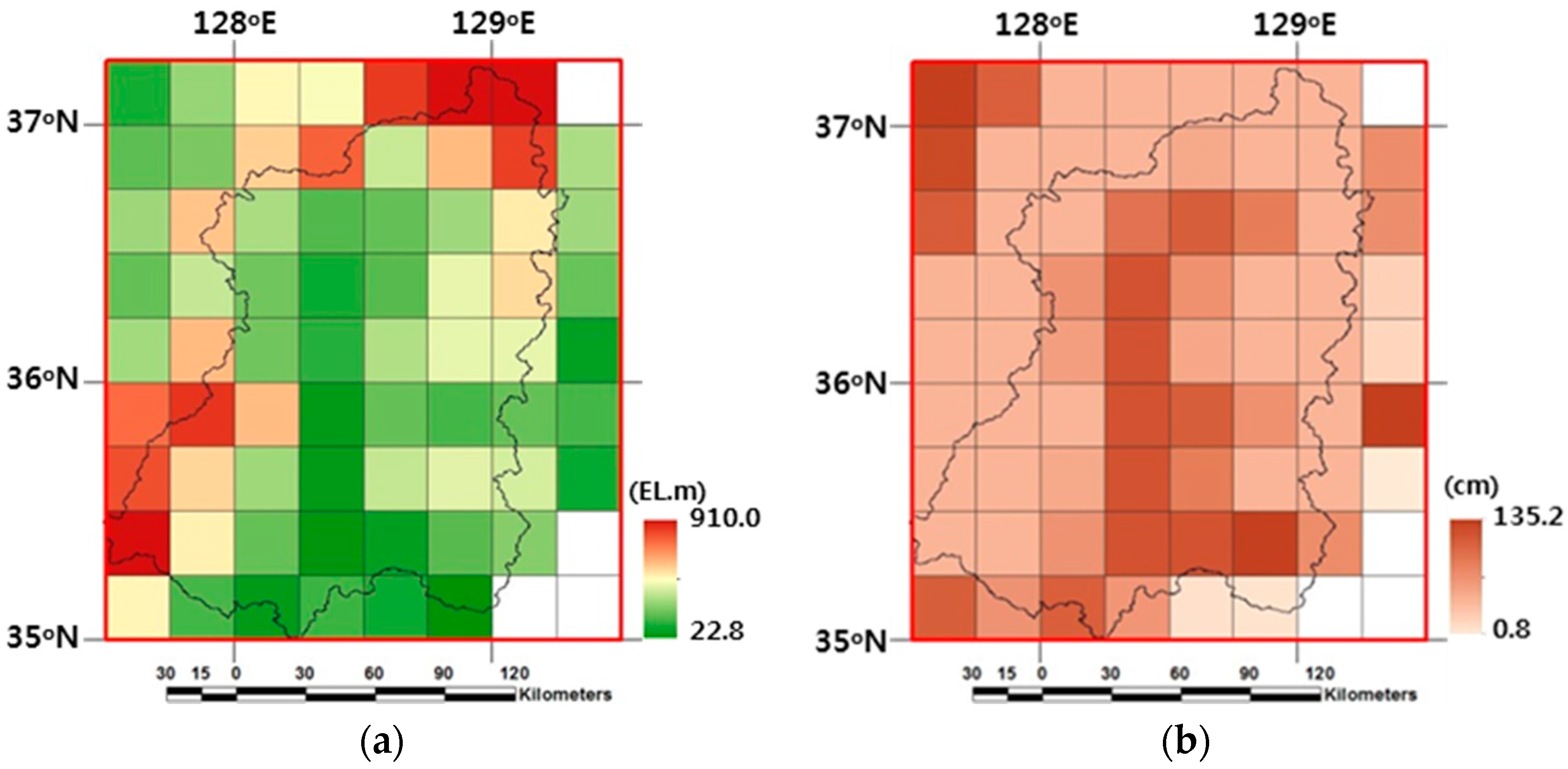
The terrain SBCs comprise surface elevation, bedrock depth, and soil sand/clay fraction profiles over the 11 soil layers at the 30-km resolution. After higher resolution raw data on various data formats and map projections were converted into ArcGIS raster data, the average of all raster values within each 30-km grid was calculated by the ZONALMEAN function in ArcGIS. The surface elevation data was constructed from the 90-m (3 arc-second) DEM provided by the National Aeronautics and Space Administration (NASA) Shuttle Radar Topographic Mission (SRTM) DEM dataset [
42]. The 30-km surface elevation data ranges from 22.8 to 910.0 EL.m for the study domain as shown in
Figure 3a. The bedrock depth and soil sand/clay fraction profiles were constructed by the Harmonized World Soil Database (HWSD) [
43], developed by the Land Use Change (LUC) project of International Institute for Applied Systems Analysis (IIASA) and the Food and Agriculture Organization of the United Nations (FAO). The spatial distribution of the bedrock depth is in the range from 0.8 to 135.2 cm below the surface ground as shown in
Figure 3b.
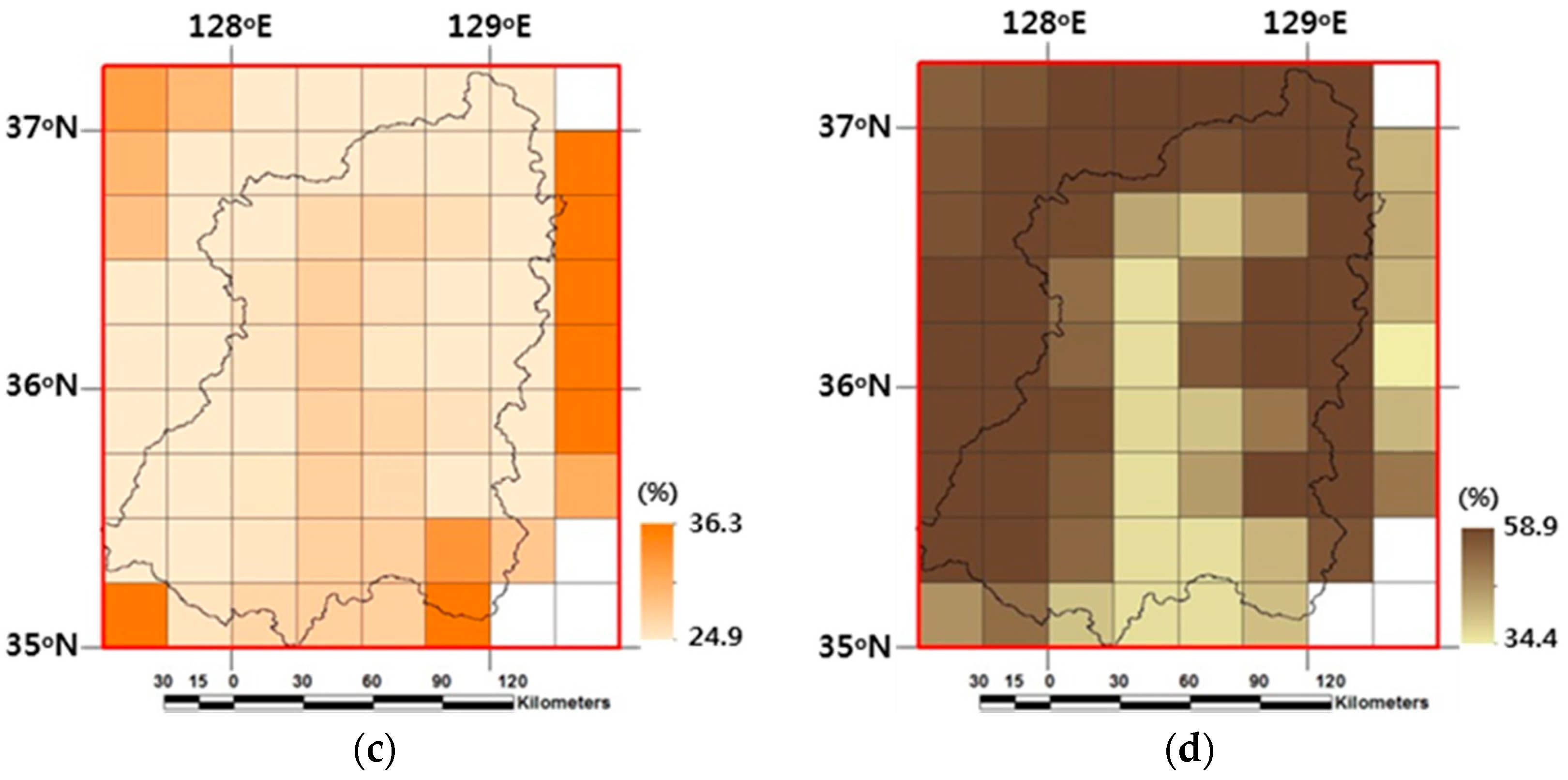
Figure 3c,d denote the 30-km soil composition fraction results for the first soil model layer, ranging between 24.9% and 36.3% for sand, and between 34.4% and 58.9% for clay.
The new CoLM+LF requires additional SBCs on the lateral flow information such as flow direction and accumulation data for each 30-km grid to perform the topographically controlled surface and subsurface flow computations. These fields were constructed by our own upscaling method using the reference flow information data at finer resolution possible, the 90-m (3 arc-second) terrain and drainage data provided by the Hydrological data and maps based on SHuttle Elevation Derivatives at multiple Scales (HydroSHEDS) [
44], derived from the NASA SRTM DEM. The HydroSHEDS geospatial dataset is known to provide the realistic stream flow direction data through a sequence of algorithms such as void-filling, filtering, hydrologic conditioning, stream burning, manual corrections, and upscaling techniques on the original SRTM DEM for improvements to data information accuracy suitable for hydrologic study applications.
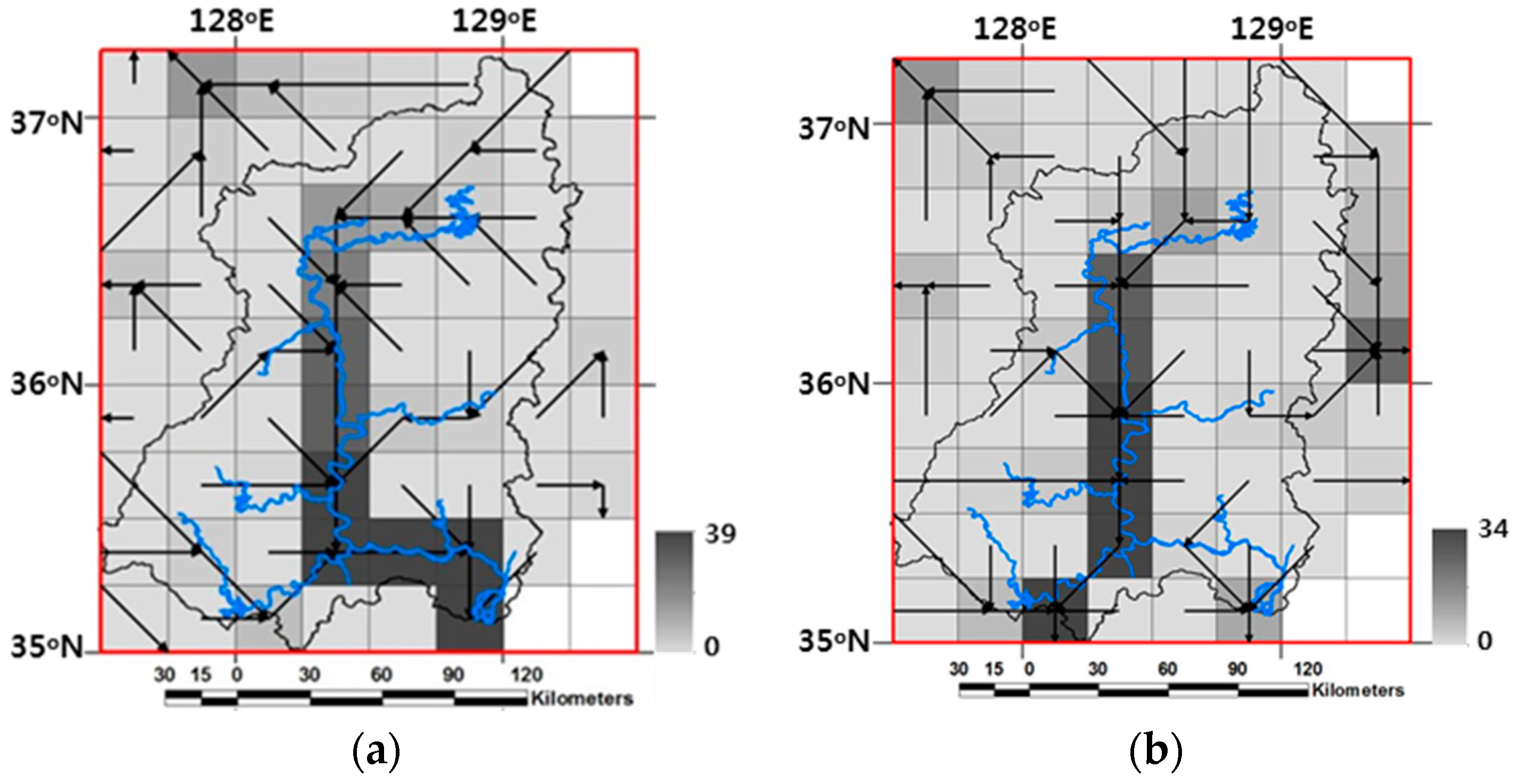
Figure 4 compares the difference between the 30-km flow information datasets derived from our own upscaling method using the 90-m HydroSHEDS data and from the eight direction flow model using the 30-km SBC of surface elevation in ArcGIS. The 30-km flow information result upscaled by our own method properly represents and is much closer to the main streamline of the Nakdong River in the study domain. The 30-km lateral flow SBCs have a significant influence on the lateral surface and subsurface flow computation as well as the drainage area delineation.
To prevent any inconsistency over all the 30-km SBCs due to different sources of the raw data, all constructed SBCs were adjusted by the 30-km land cover category as the standard identification for land and water body grids.
3.3. Meteorological Forcing Data
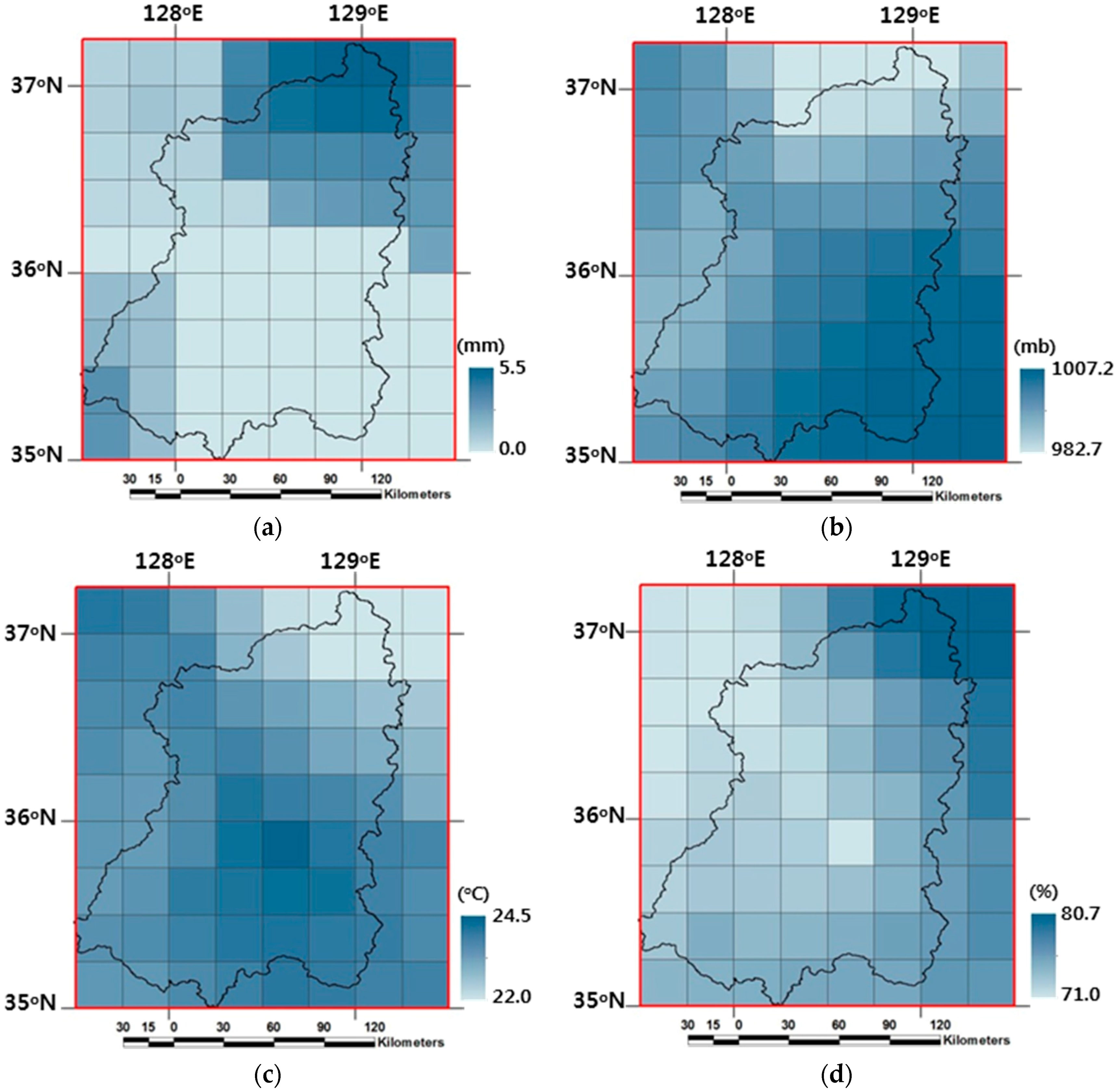
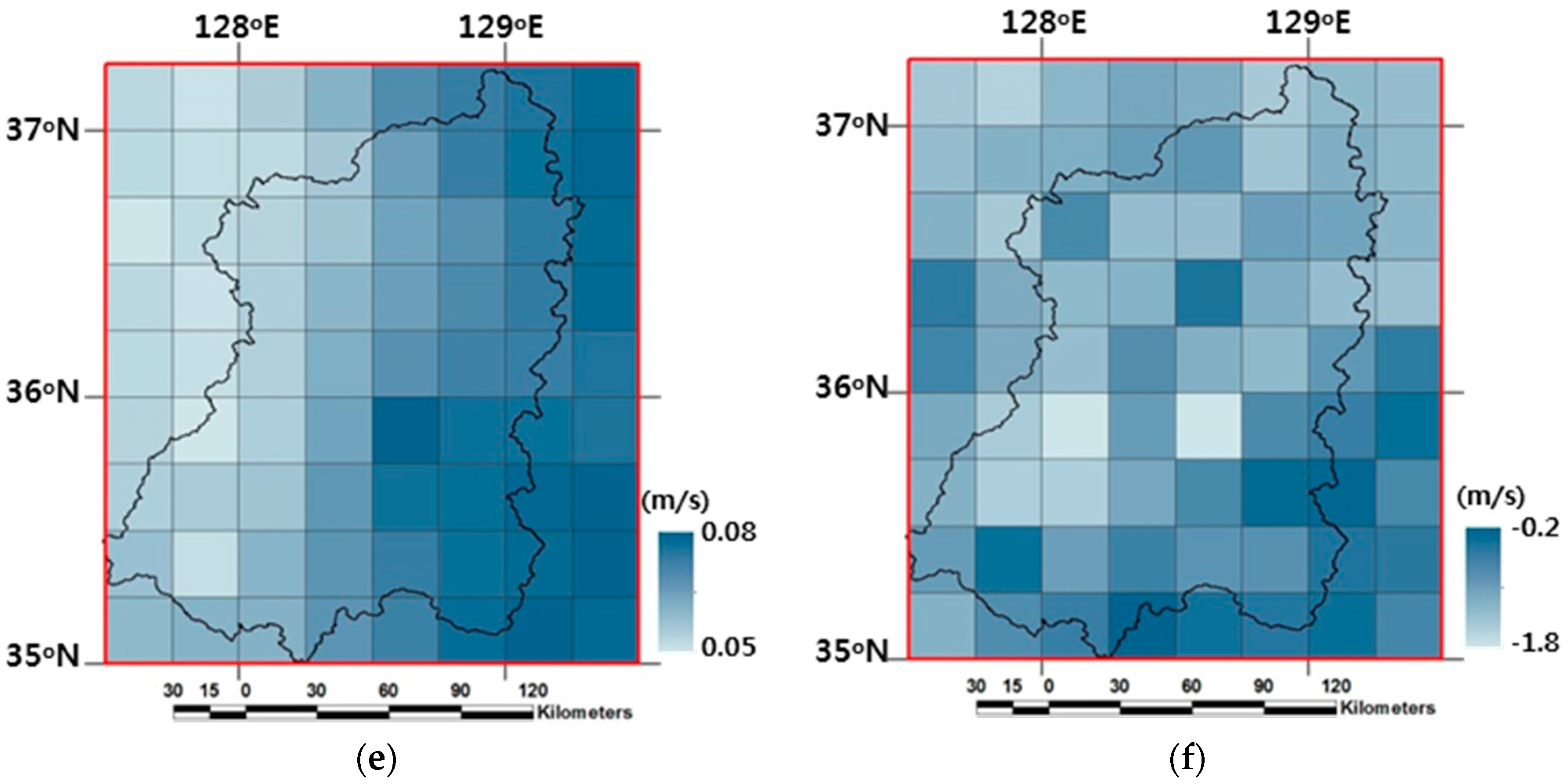
The meteorological forcing variables are required for both the CoLM and the CoLM+LF simulations in the offline mode. Most meteorological forcing data to drive both model simulations during the year of 2009 were also constructed onto the 30-km computational grids by the ZONALMEAN function in ArcGIS after in situ observations at 19 KMA meteorological gauge stations around the study watershed were spatially interpolated onto the study domain with average values weighted by the inverse of the distance from the gauge point. The 30-km daily meteorological forcing data constructed in this study are precipitation (mm), snow (cm), air pressure (hPa), vapor pressure (hPa), air temperature (°C), specific humidity (%), zonal and meridional wind speeds (m/s), and downward short wave radiation (MJ/m2). The daily meteorological forcing data were linearly interpolated for the computational time step of 600 seconds in the both models.
Figure 5 denote spatial distributions of selective meteorological forcing data for the study domain on 5 July, one day of precipitation events in 2009.
3.4. Initial Conditions
To resolve uncertainty in the initial conditions, both CoLM and CoLM+LF under the assumed initial conditions on 1 January 2009 were run six times repeatedly without interruption for the whole of 2009. The sixth set of results from CoLM and CoLM+LF was saved for analysis and interpretation.
5. Discussion
Like most existing LSMs, the baseline CoLM predicts runoff from local net excess water flux after excluding surface evapotranspiration and soil moisture flux from precipitation. A disregard for the role of lateral surface and subsurface runoff in the terrestrial hydrologic cycle may make significant errors in the baseline CoLM simulations. This study has therefore introduced a new model, the CoLM+LF that incorporates the 1D diffusion wave surface flow model and the 1D topographically controlled baseflow scheme into the existing formulations for the terrestrial hydrologic cycle in the baseline CoLM. The baseline CoLM and the new CoLM+LF were implemented for the Nakdong River Watershed in Korea in a standalone mode by the realistic SBCs and meteorological forcings on the 30-km grid mesh for mesoscale applications by direct interactions between hydrological and atmospheric components. This study has collected high quality observational data mainly by multispectral remote sensing products and in situ observations from finer possible spatial data. The various raw data were spatially transformed into the proper representative values on the 30-km spacing grids in the study domain by our own program codes and geoprocessing tools in ArcGIS. The new CoLM+LF simulations need the additional SBCs such as the 30-km flow direction and accumulation data to implement an explicit lateral flow scheme. Since it is problematic to directly use the eight direction flow model provided by ArcGIS on the 30-km resolution grids, our own upscaling method properly generated the 30-km flow direction result, which coincides better with the Nakdong River stream network, compared with the result from ArcGIS. This study has successfully provided a primary set of SBCs and daily meteorological forcing data during the year 2009 for the study domain, including the entire Nakdong River Watershed from the comprehensive Earth observations.
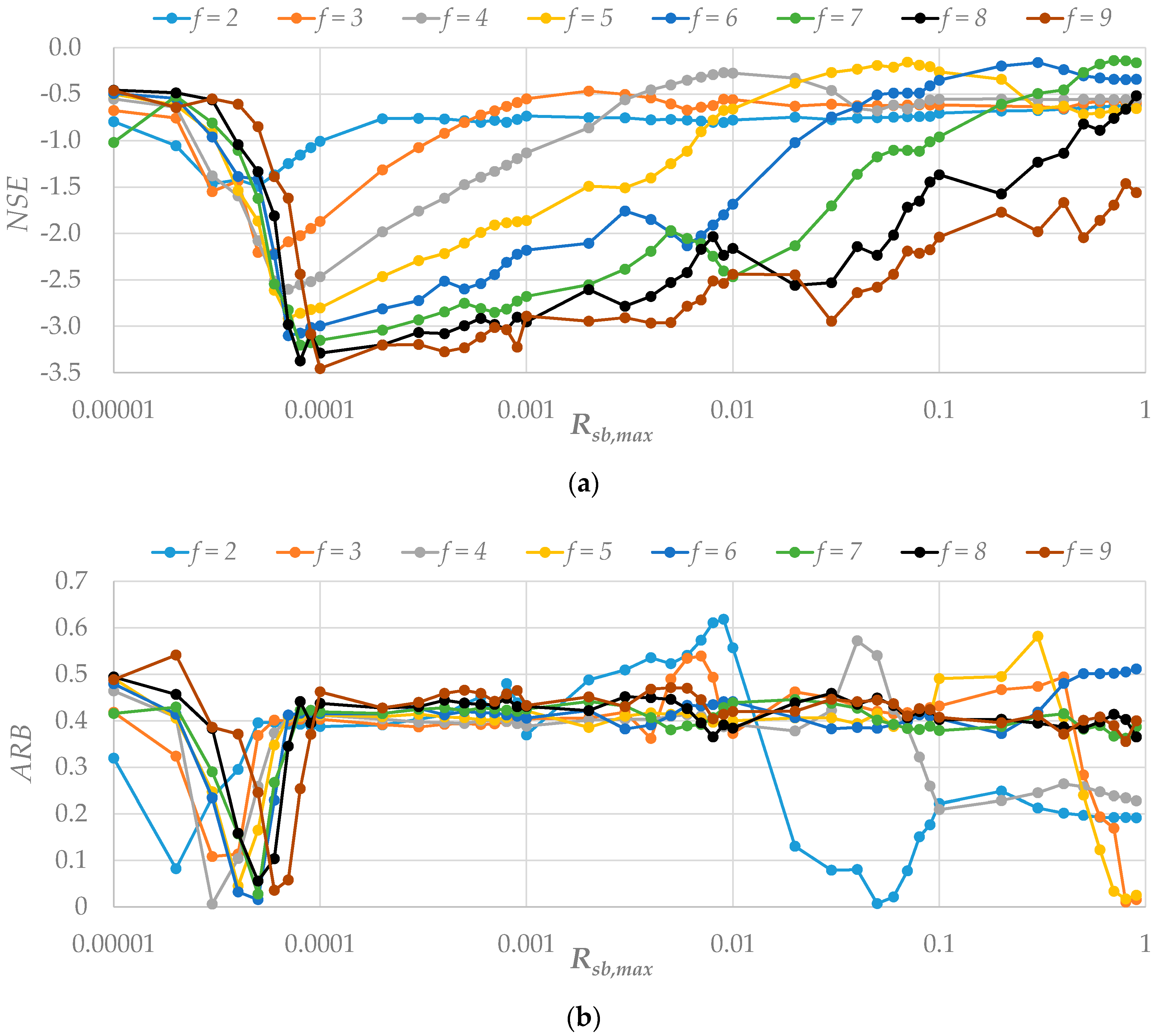
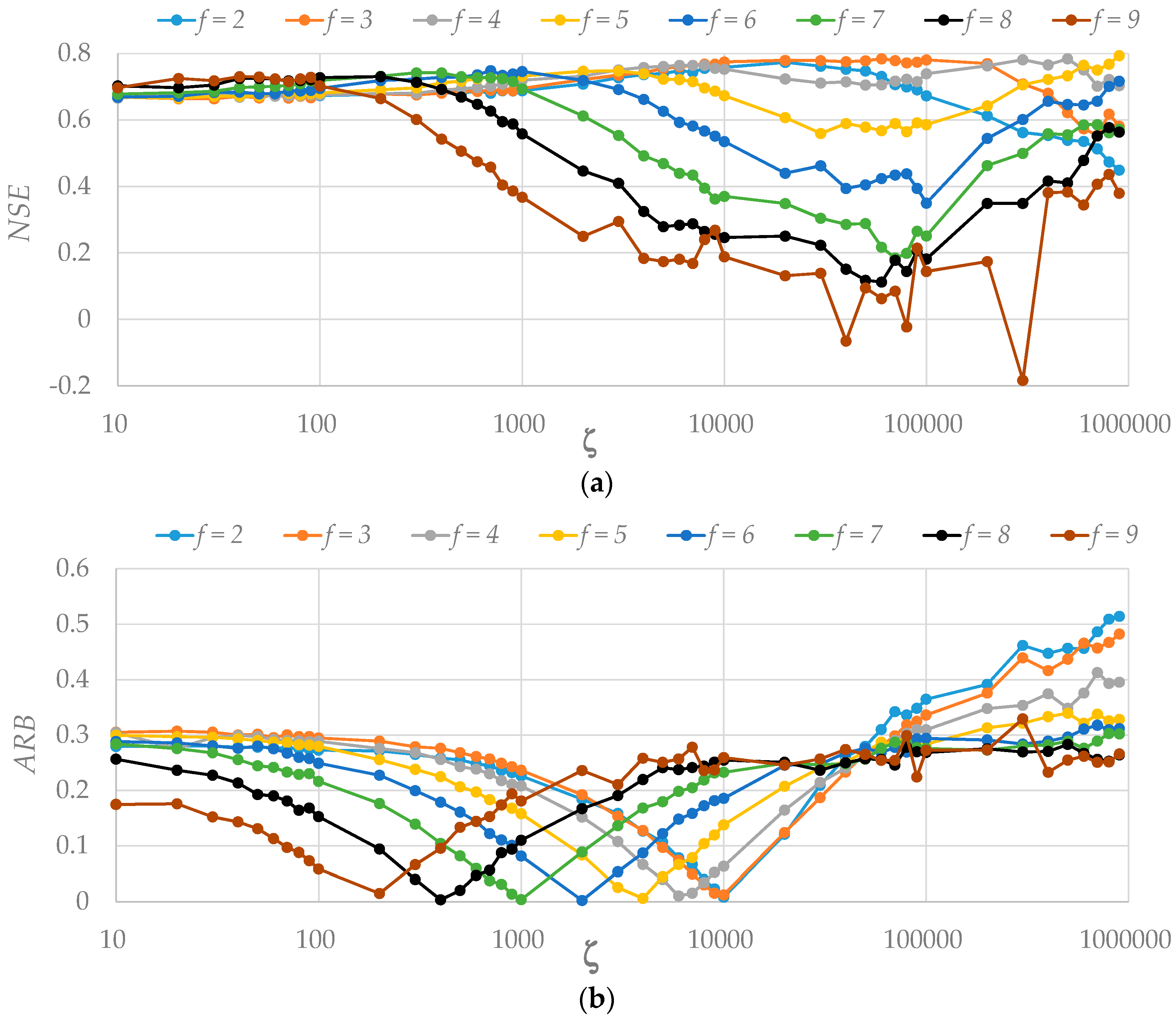
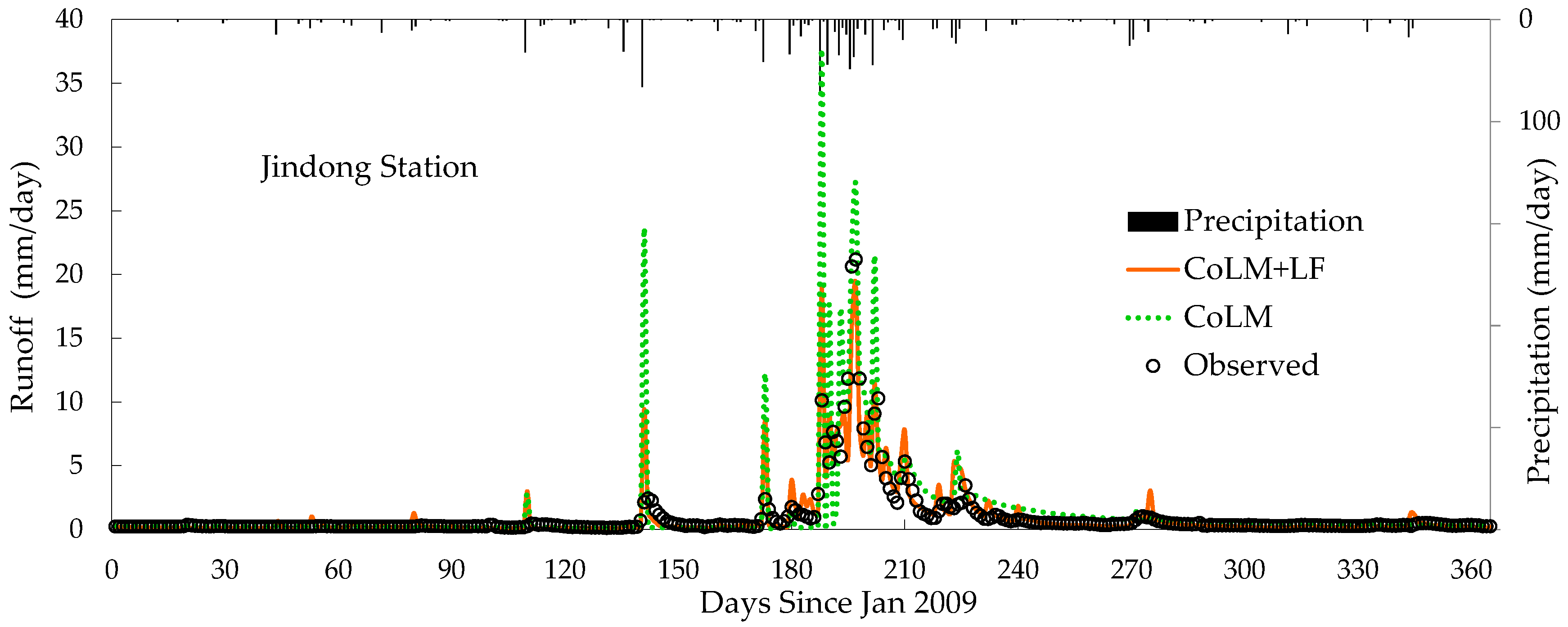
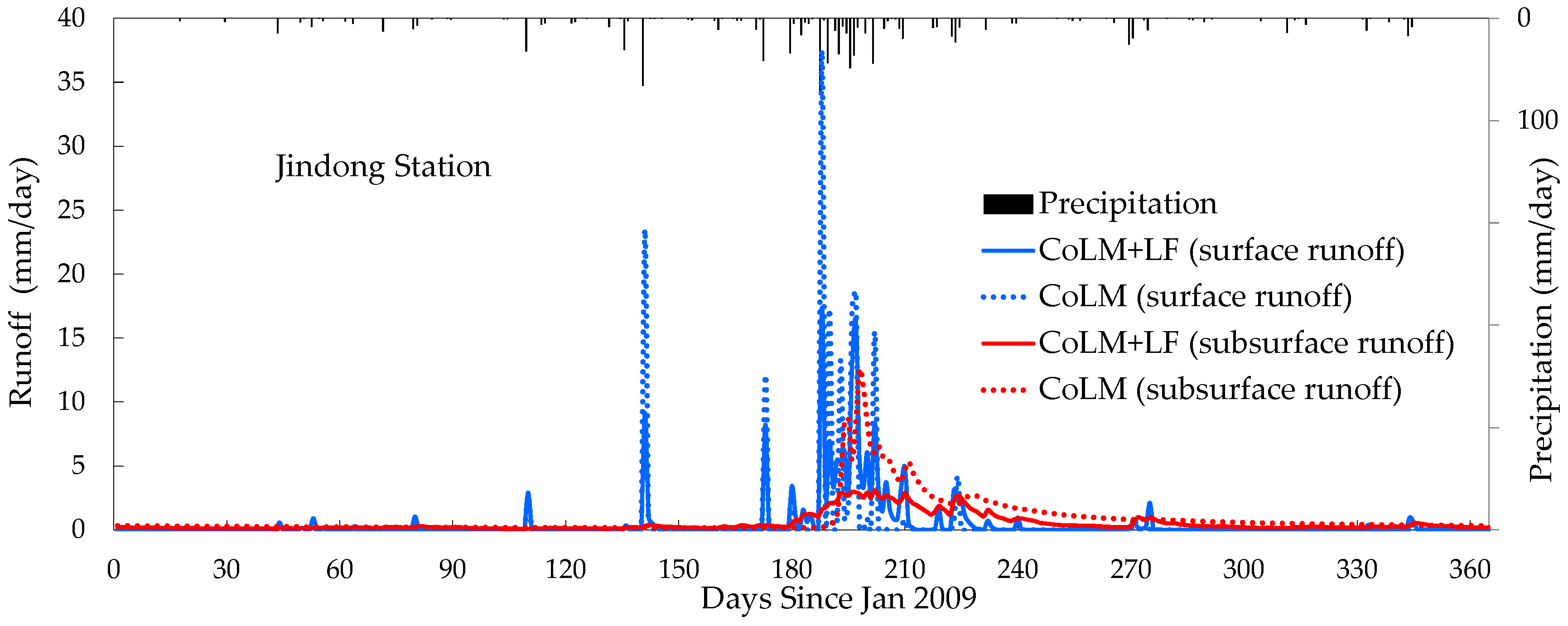
This study has evaluated the performance of the CoLM and the CoLM+LF in offline simulations of daily runoff through the sensitivity analysis of key parameters for runoff variables at a watershed scale by comparison of the simulated results with observations at the Jindong gauge station in the study watershed. Surface runoff generated simply from the local net excess water in each grid disappears at the next computational time step in the baseline CoLM. Since surface runoff calculated at every time step irrespective of the remaining surface runoff at the previous time step makes no contribution to infiltration, larger values of the two calibration parameters (decay factor
f and the maximum baseflow coefficient
) were estimated for the baseline CoLM to enhance both infiltration and baseflow generation. As the baseflow equation in the baseline CoLM is apt to underestimate baseflow, as demonstrated in Choi and Liang [
9], runoff recession curves observed at the Jindong gauge station cannot be captured by runoff results generated with
values in the order of 10
−4 mm/s used in previous studies [
6,
7,
9,
25]. Accordingly, the baseline CoLM simulations that predict sharp and steep peaks in surface runoff were tuned by larger values for
f of 7 m
−1 and
of 7 × 10
−1 mm/s to enhance baseflow generation. Such simplistic assumptions and crude parameterizations for the lateral surface and subsurface runoff processes in the baseline CoLM may cause significant model errors and consequently unrealistic model parameters by calibration. On the other hand, the new CoLM+LF incorporating an explicit surface flow routing scheme can facilitate infiltration by the surface flow depth contribution, leading to the enhanced baseflow generation as well. Moreover, baseflow can be effectually generated in the new CoLM+LF by a new formulation for baseflow controlled by topography which can also depict the effects of surface macropores and vertical hydraulic conductivity changes. In the new CoLM+LF with a set of the lateral surface and subsurface runoff schemes, lower peaks and smoother recession curves of surface runoff were generated under relatively smaller value for
f of 3 m
−1 due to the surface flow routing effect, and the baseflow were successfully generated by the surface flow depth contribution to infiltration and topographically controlled baseflow scheme with the hydraulic conductivity anisotropic ratio
of 10
4.
This study has demonstrated that the CoLM+LF incorporating the topographically controlled surface and subsurface flow computations realistically can predict the temporal variation of the spatial distribution of streamflow runoff at a watershed scale, while the baseline CoLM may generate unrealistic surface runoff and infiltration results, which are important components for terrestrial water distribution and movement. The new CoLM+LF provides improved runoff modeling capability to the baseline CoLM for better streamflow predictions affecting the terrestrial hydrologic cycle crucial to climate variability and change studies. The new CoLM+LF is expected to be a helpful and essential tool for water resource management and hydrological impact assessment, particularly in regions with complex topography. This proposed CoLM+LF targeted for mesoscale climate application and watershed scale hydrologic analysis at relatively large spatial scales needs to be implemented for comprehensive terrestrial hydrologic simulations with long-term observations after climatological data are constructed over various watersheds including this study domain. The next study is planning to perform an analysis on uncertainties in the SBCs constructed from various remote sensing products and examine the sensitivity of model predictability to the spatial and temporal resolutions of input data. The next model also needs to include aquifer recharge, deep aquifer groundwater, channel flow routing, and regulation storage for further investigation.