Modeling Glacier Mass Balance and Runoff in the Koxkar River Basin on the South Slope of the Tianshan Mountains, China, from 1959 to 2009
Abstract
:1. Introduction
2. Study Area and Data Collection
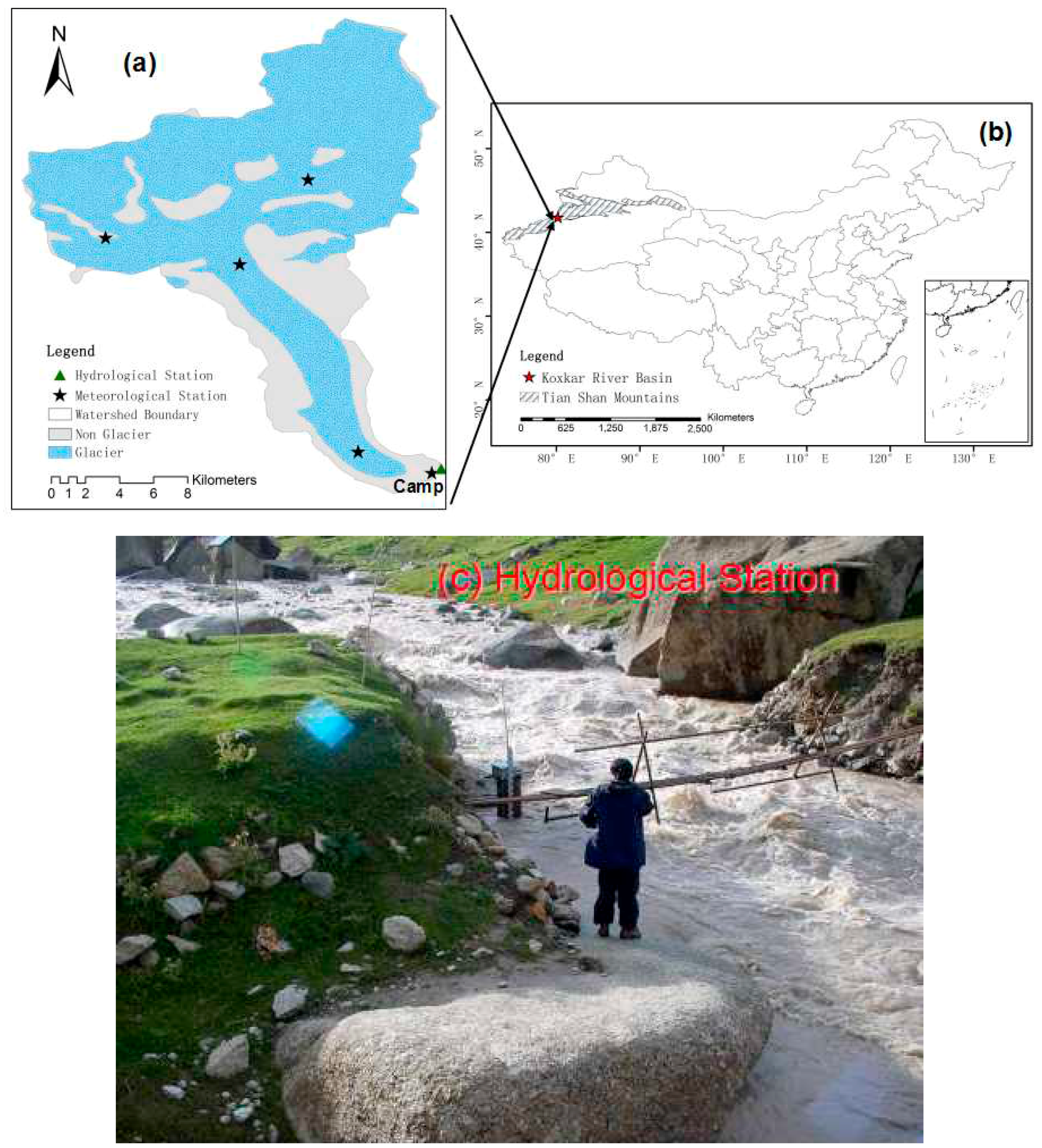
2.1. Study Area
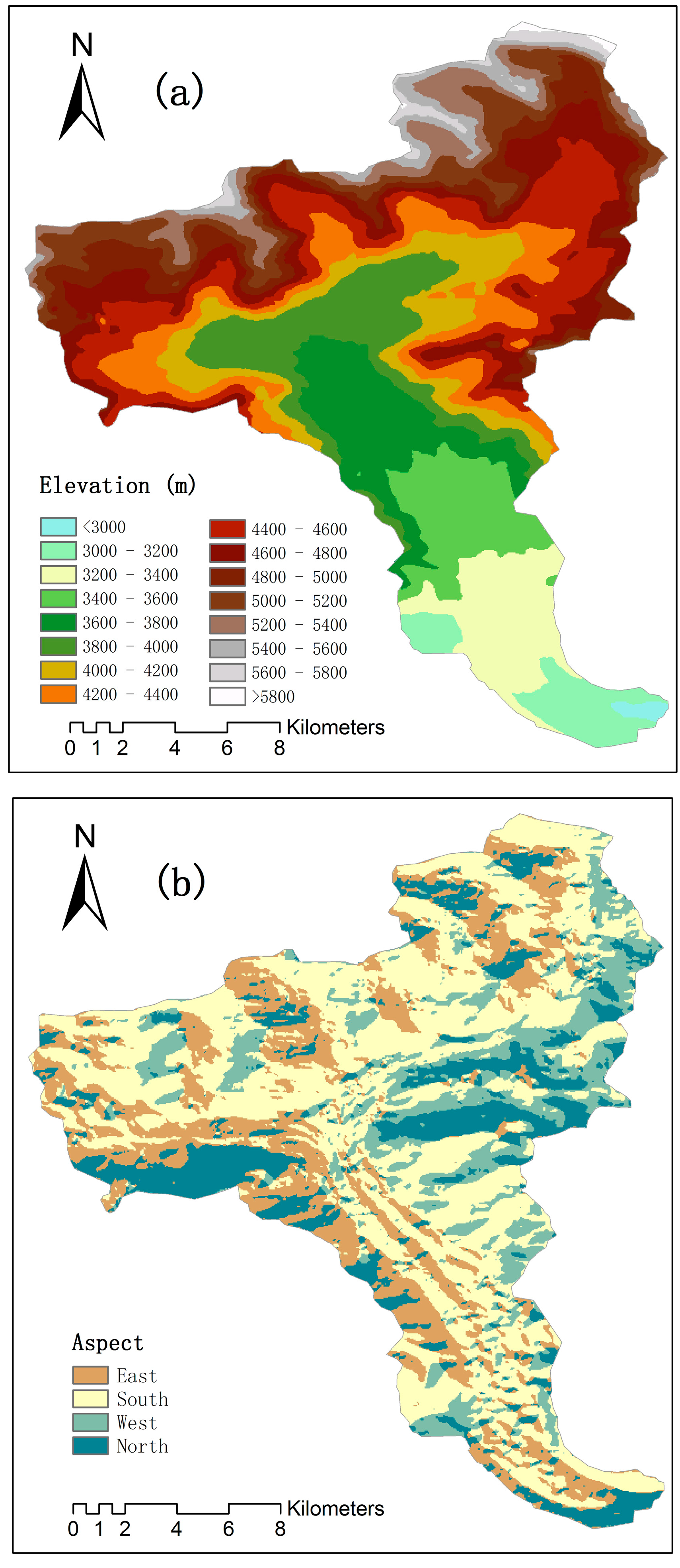
2.2. Geographical Data
2.3. Observations and Meteorological Data
2.4. Hydrological and Glacial Data
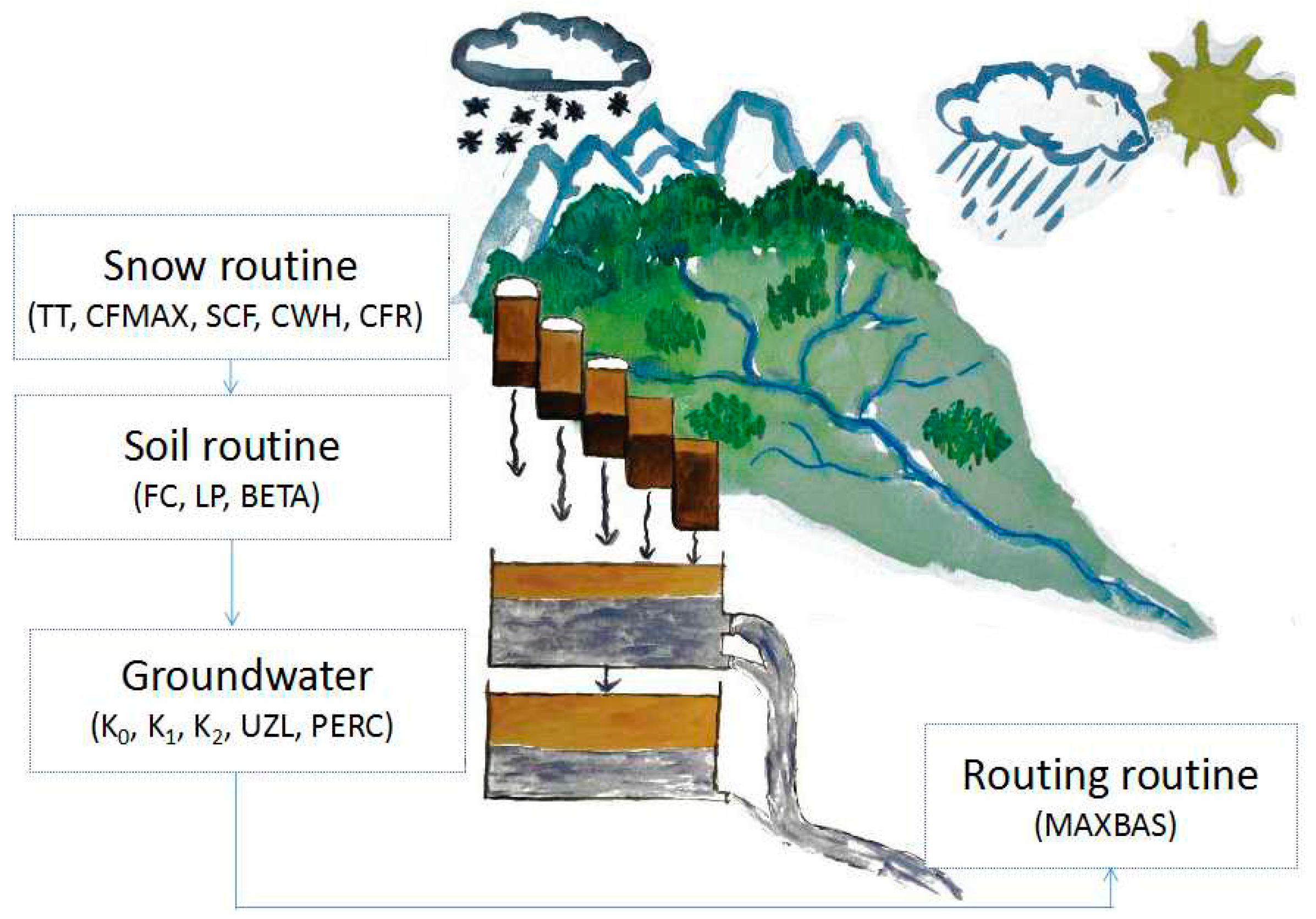
3. Hydrologiska Byrans Vattenavdelning (HBV) Model
4. Reconstruction of Temperature and Precipitation Data
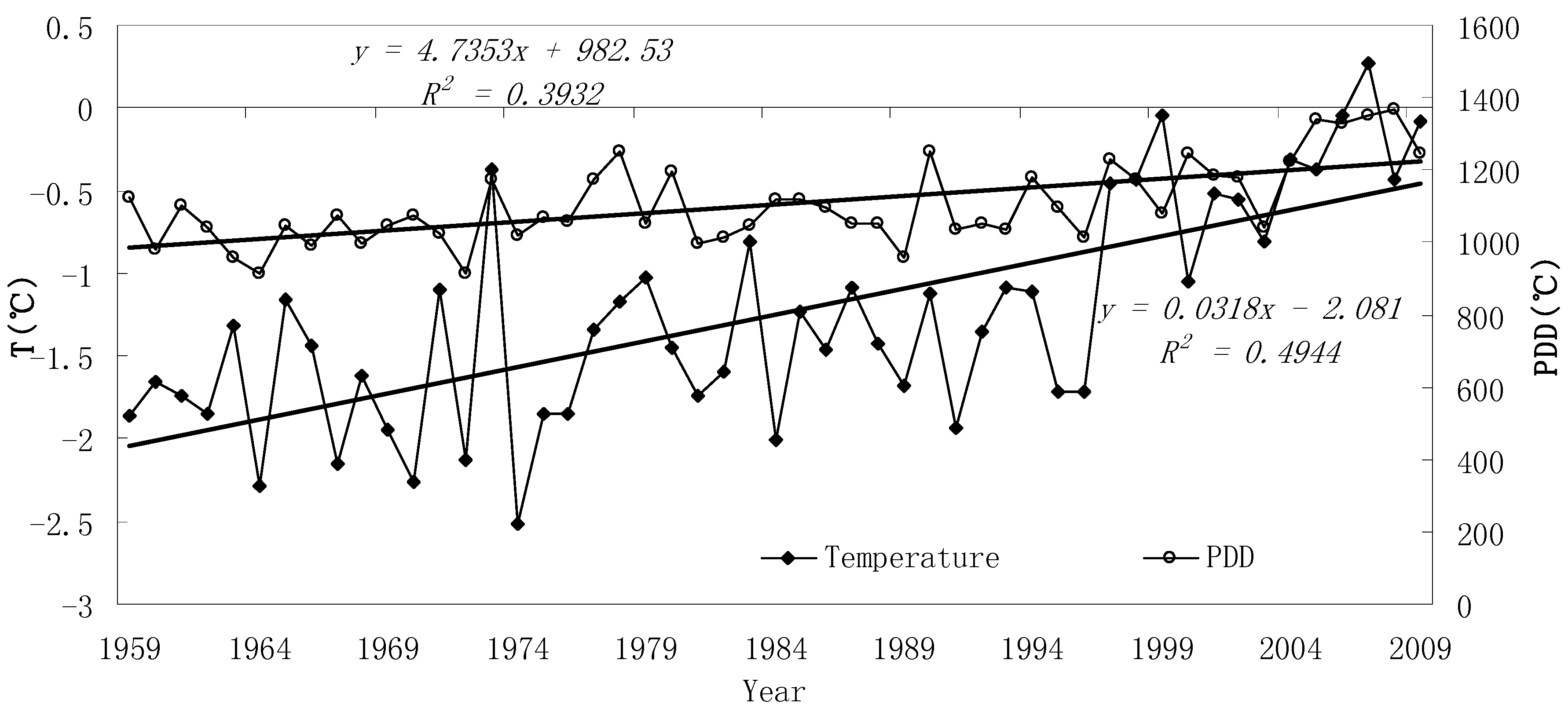
4.1. Reconstruction of Temperature
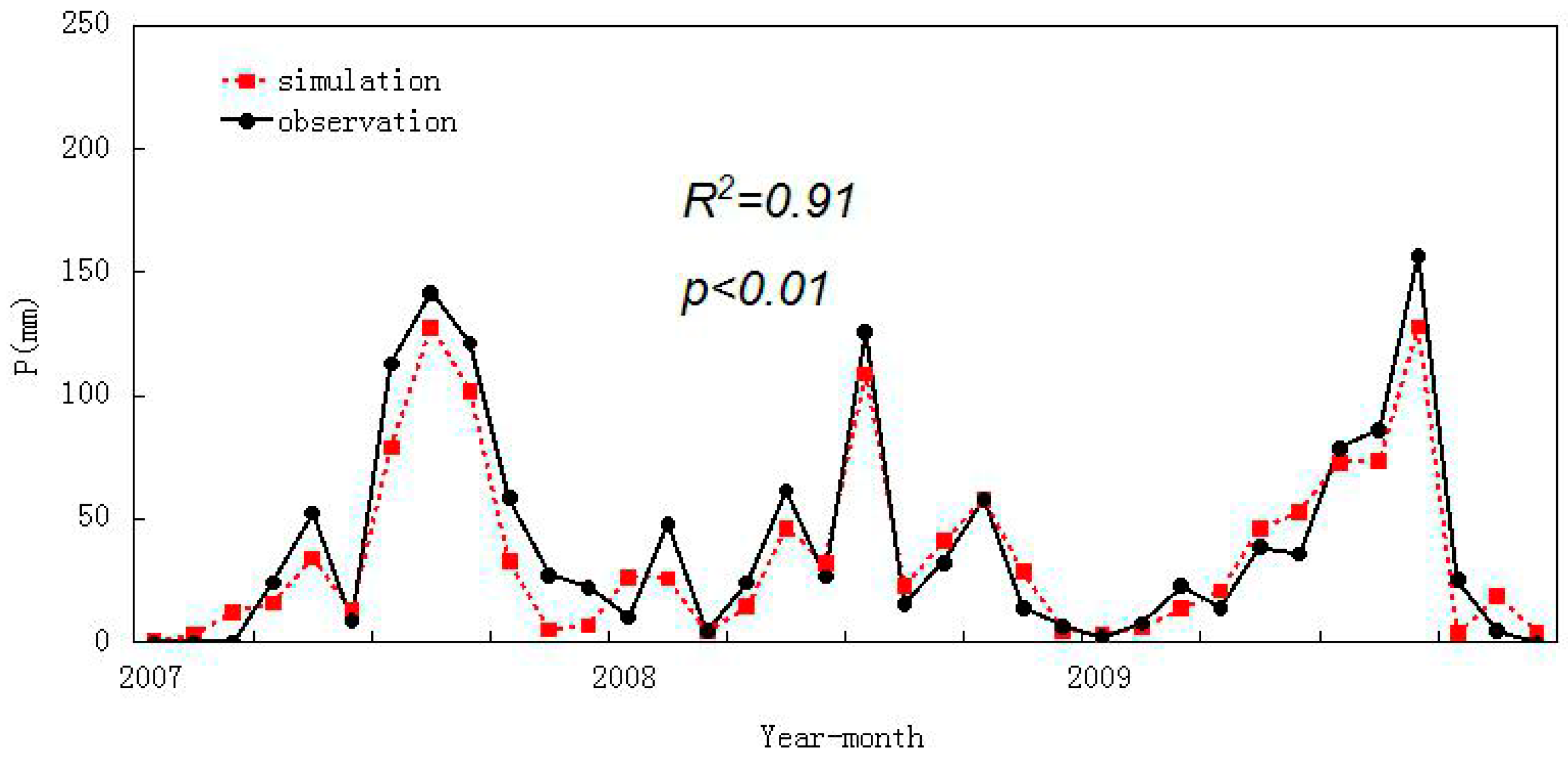
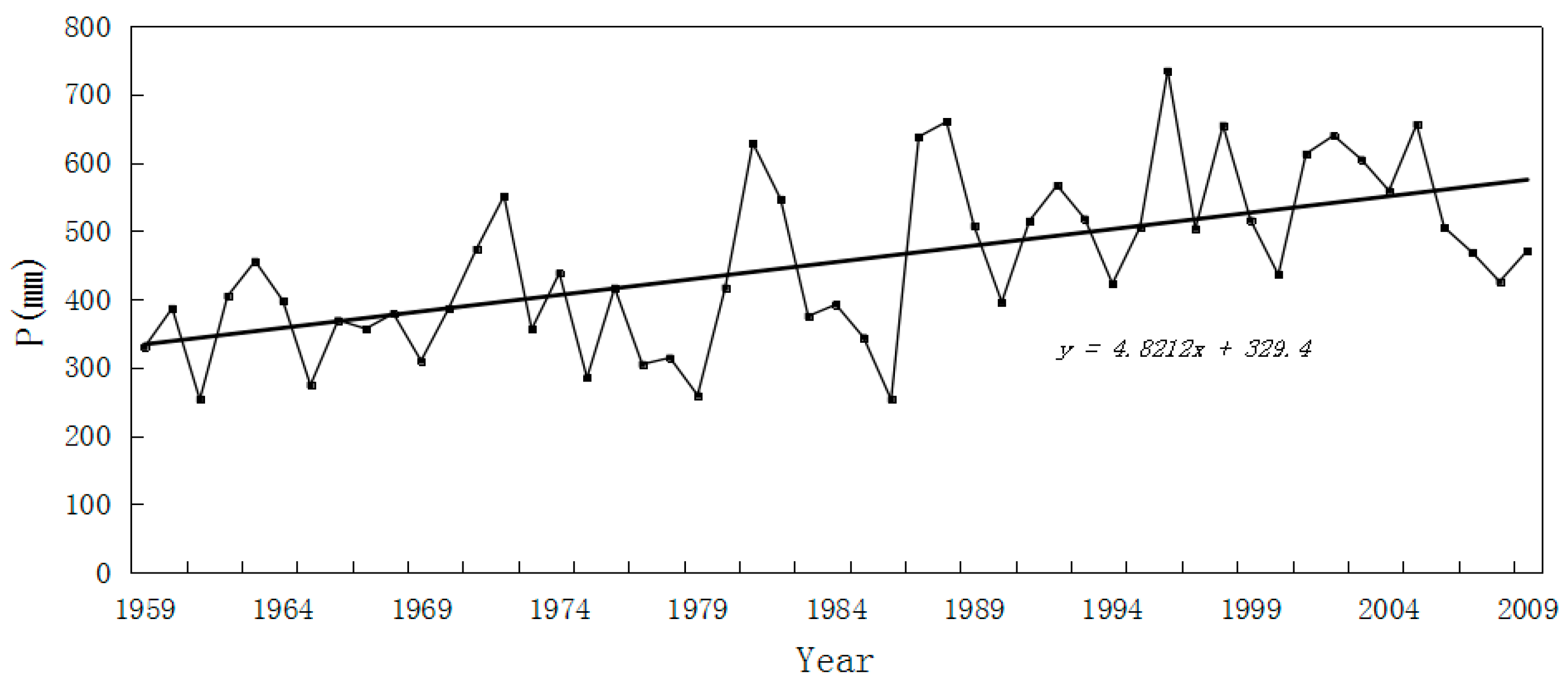
4.2. Reconstruction of Precipitation
5. Results and Discussion
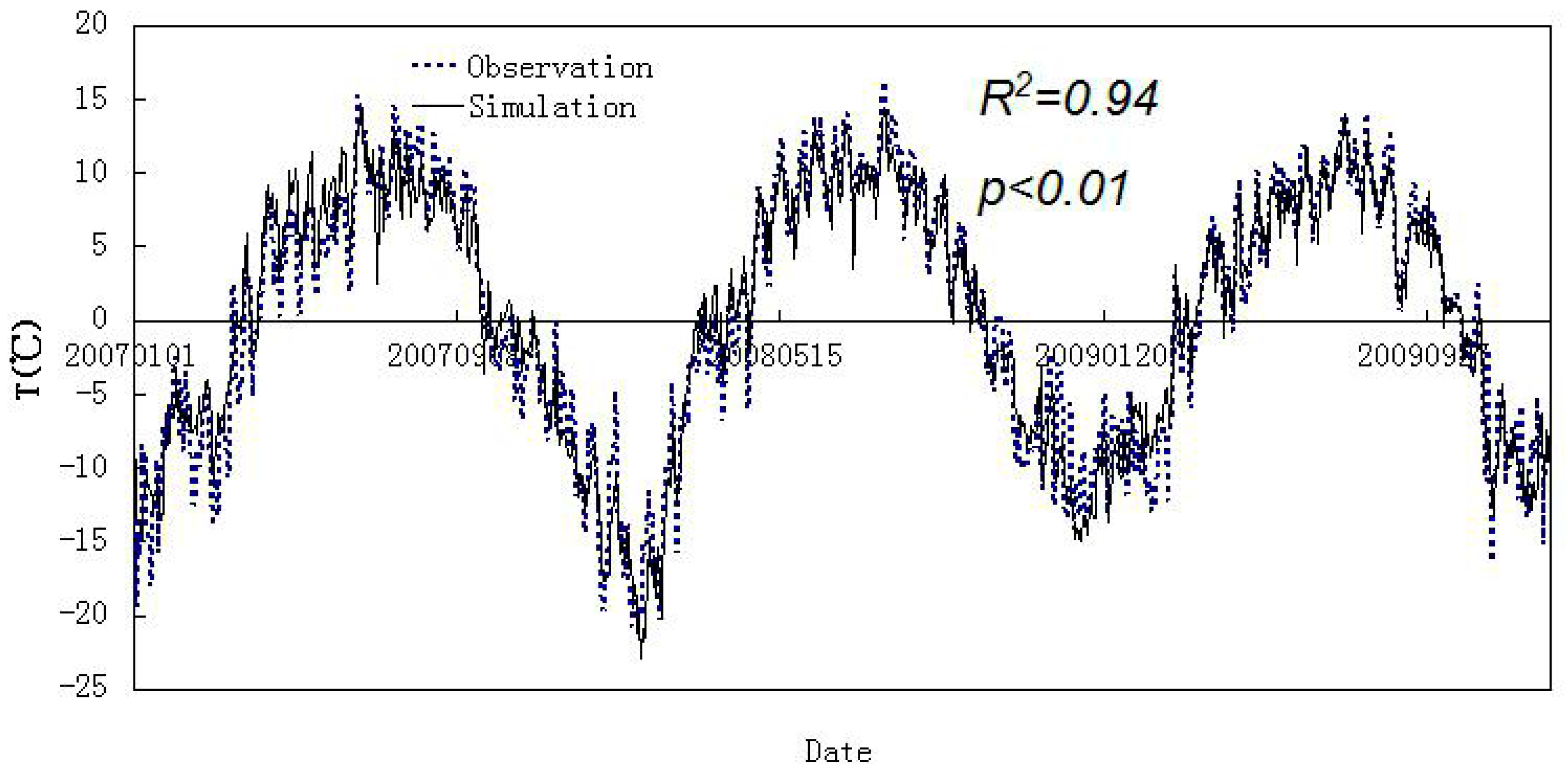
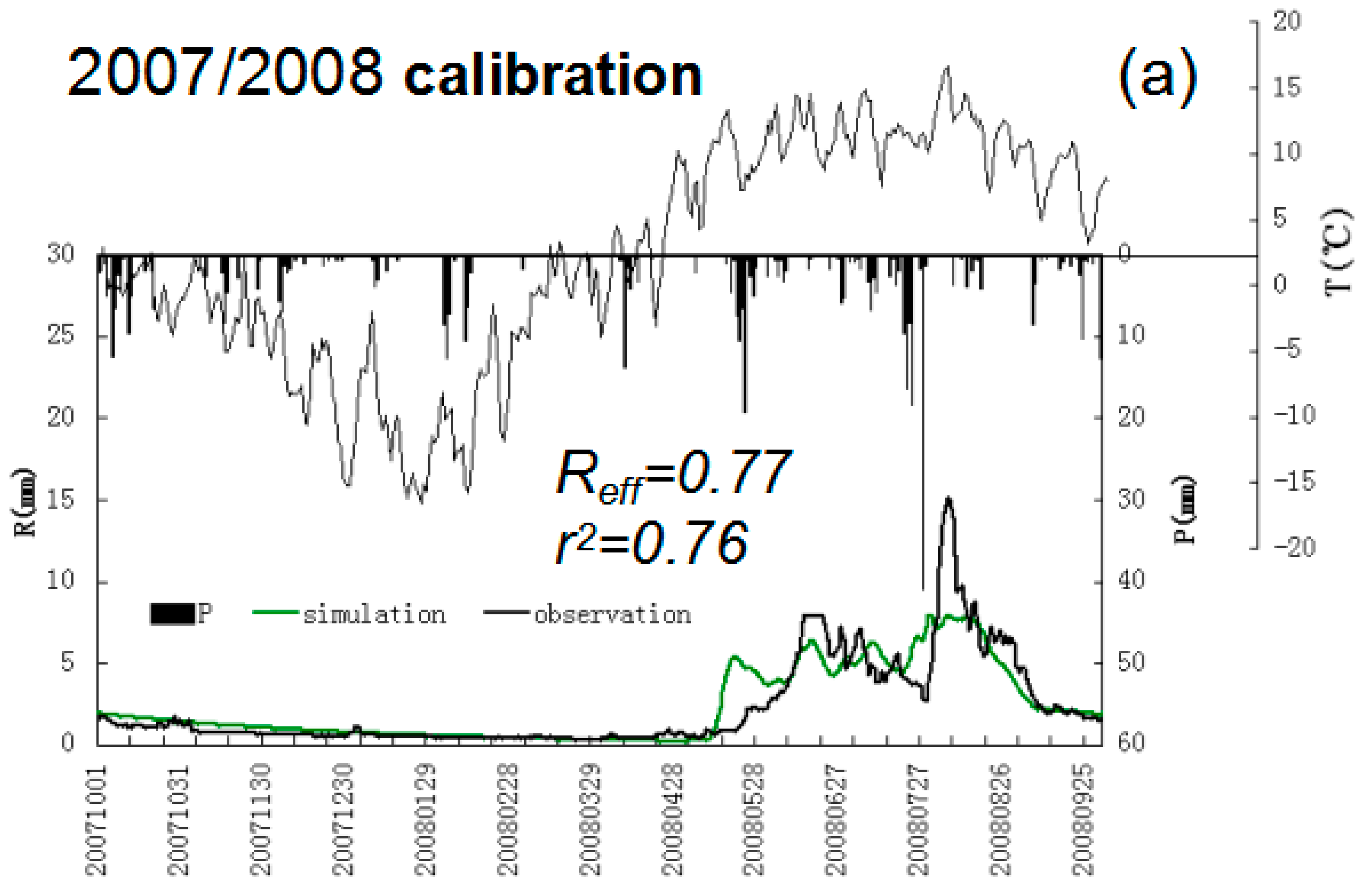
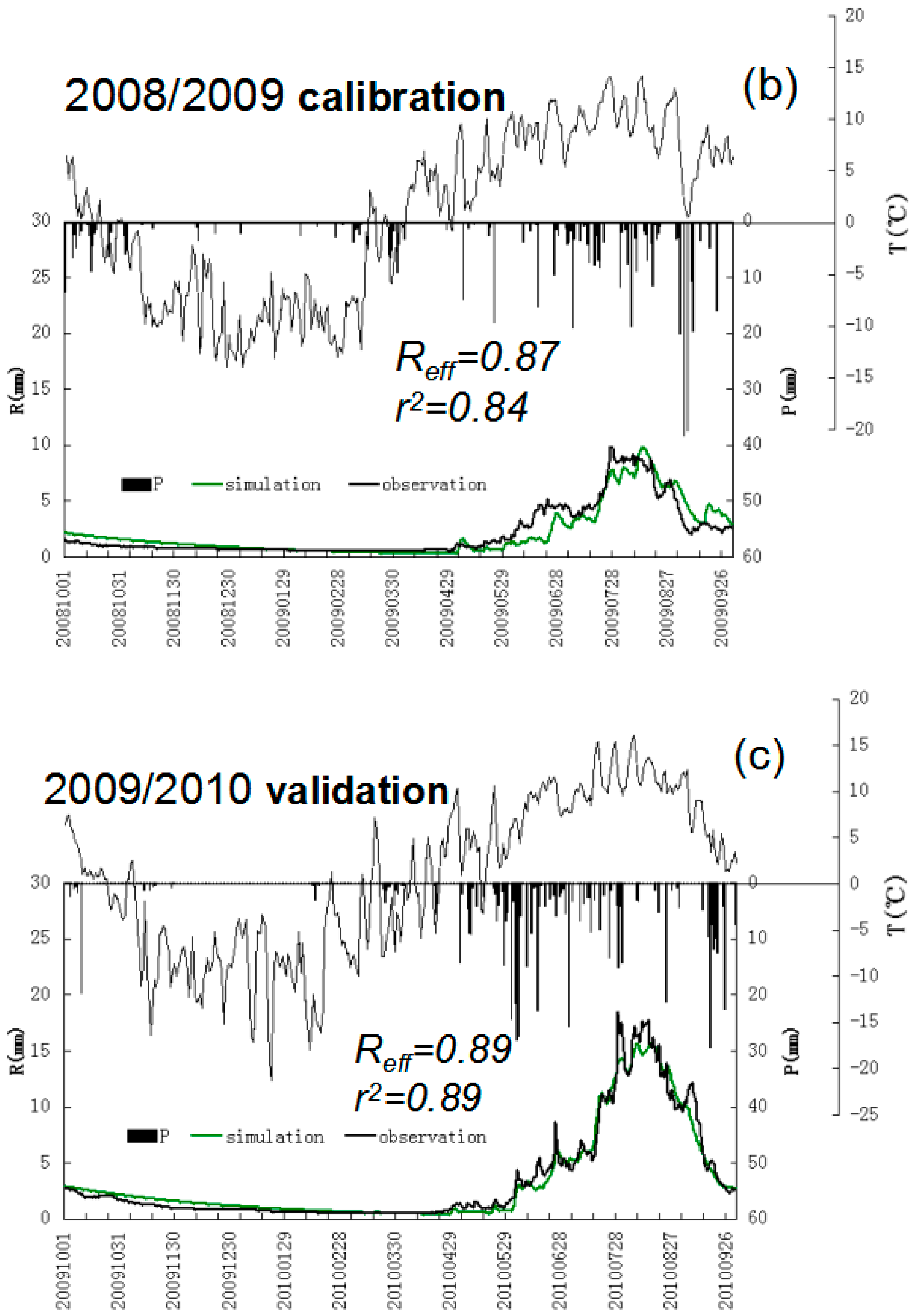
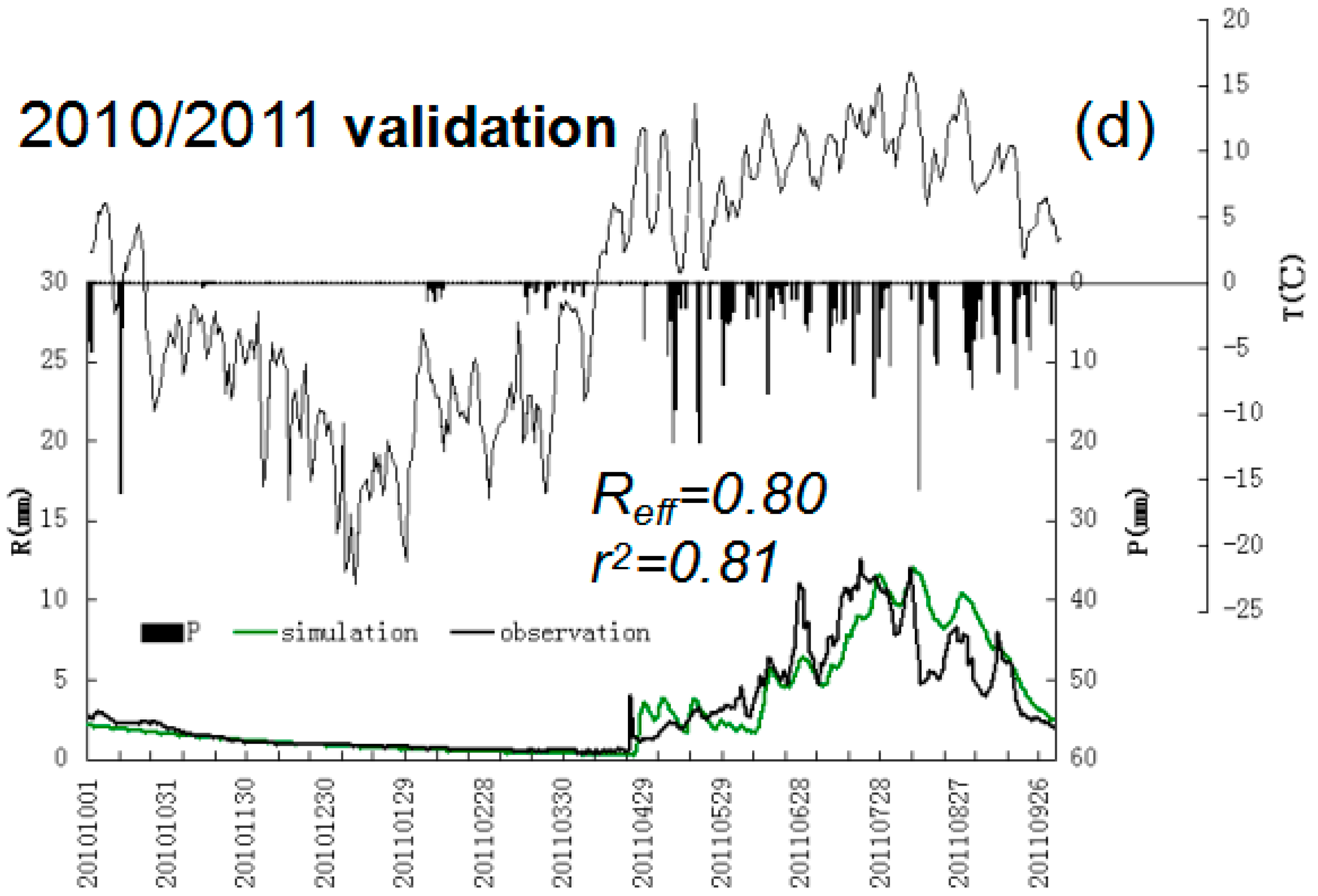
5.1. Model Calibration and Validation
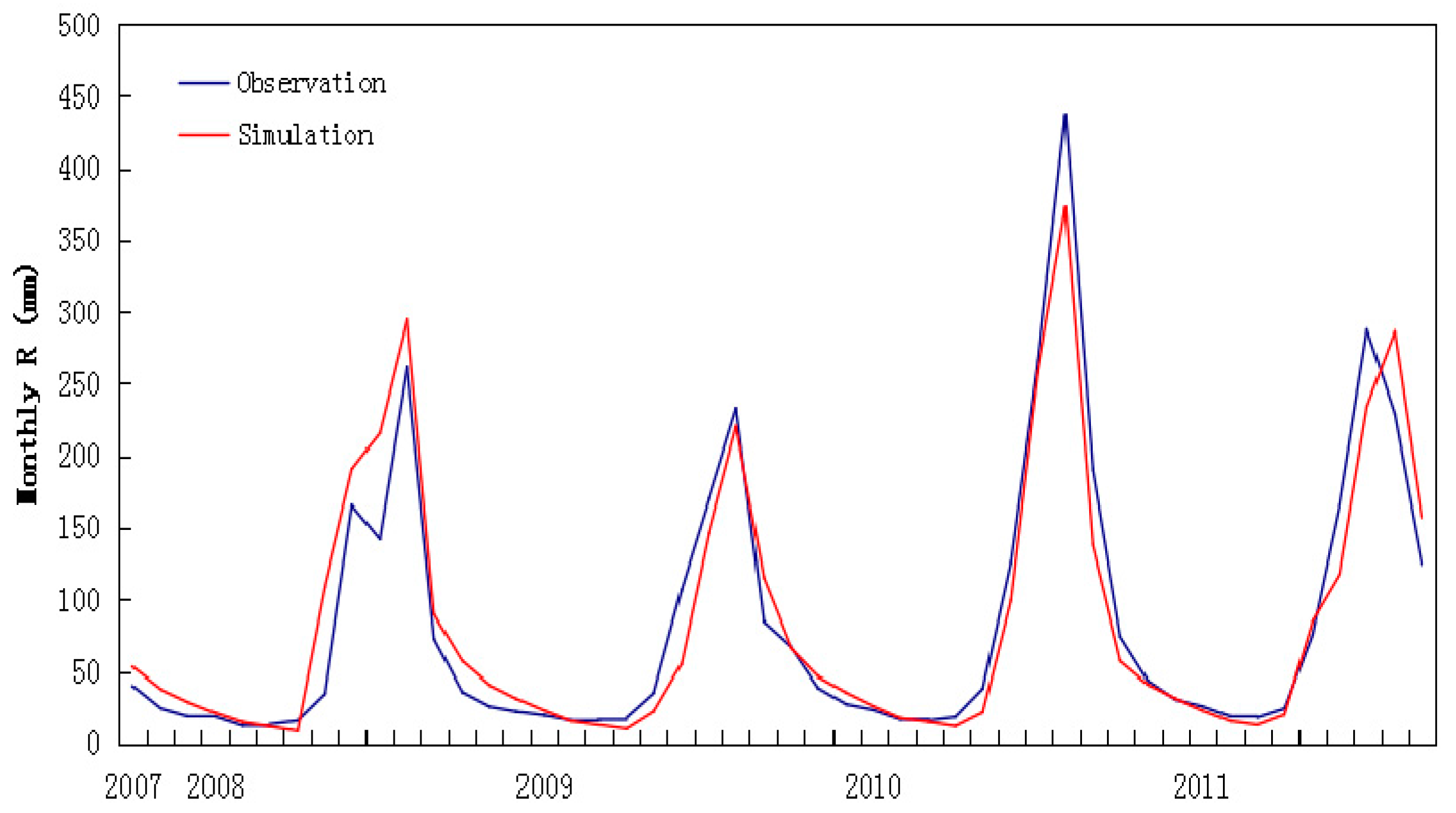
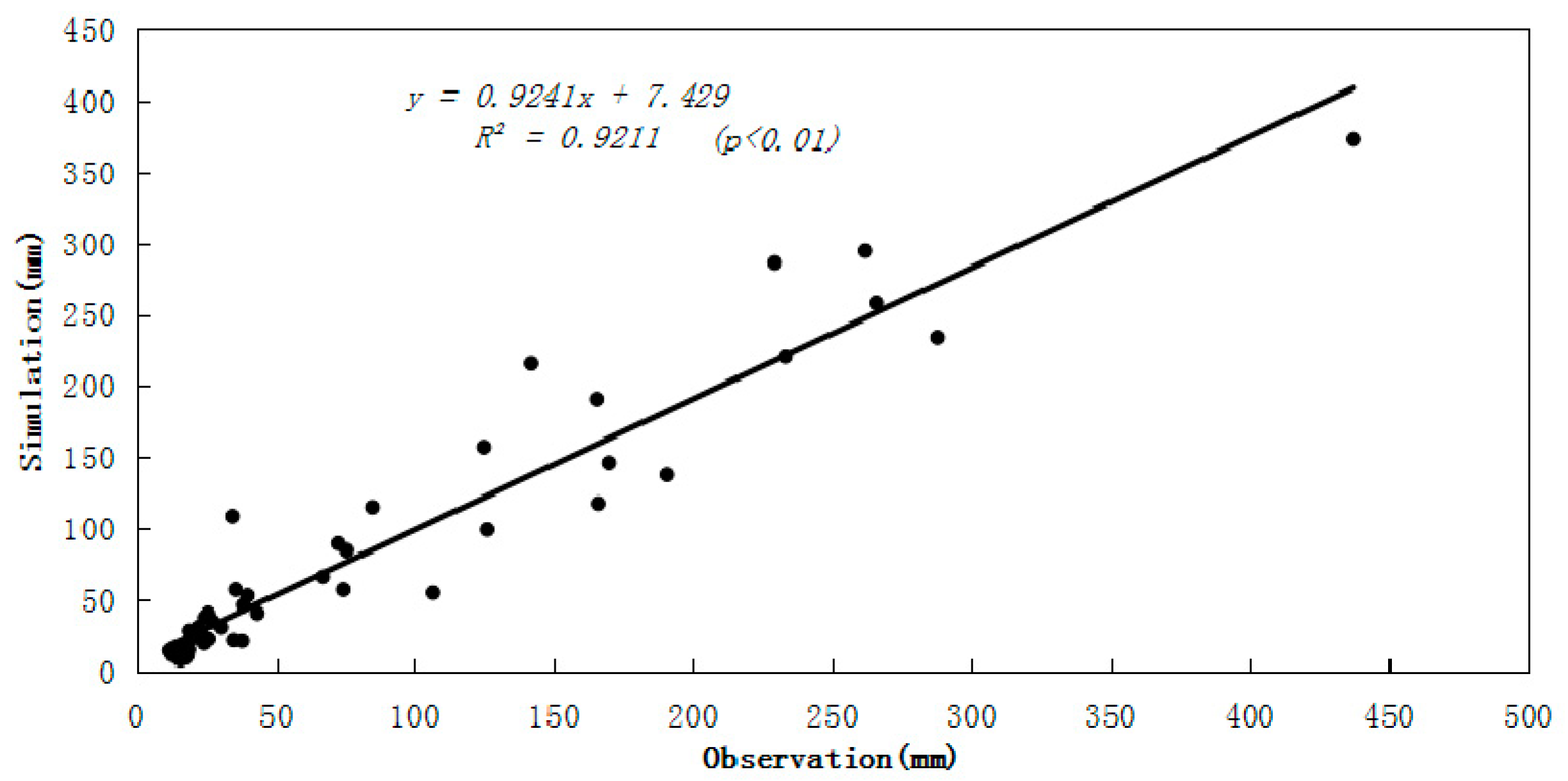
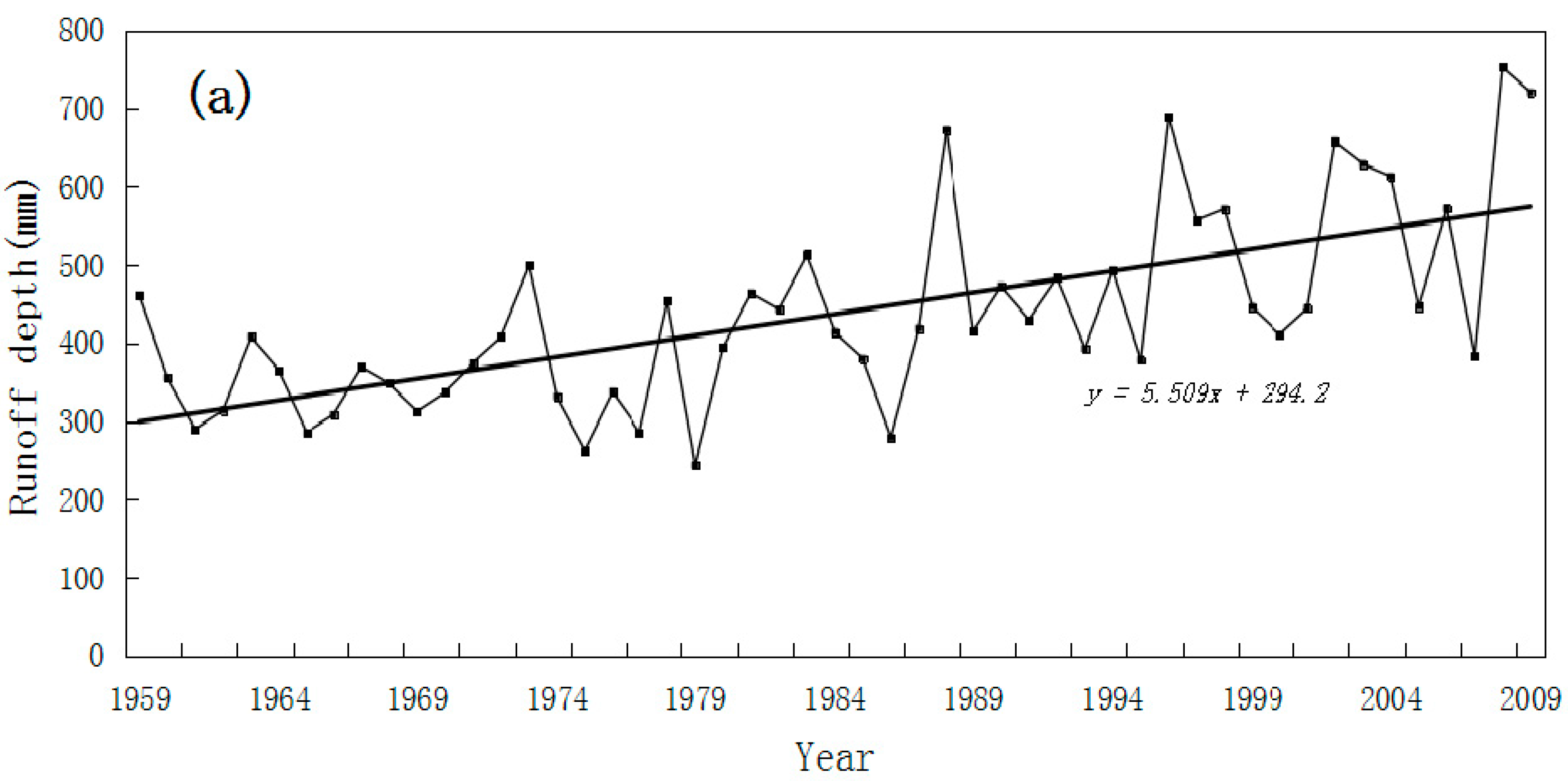
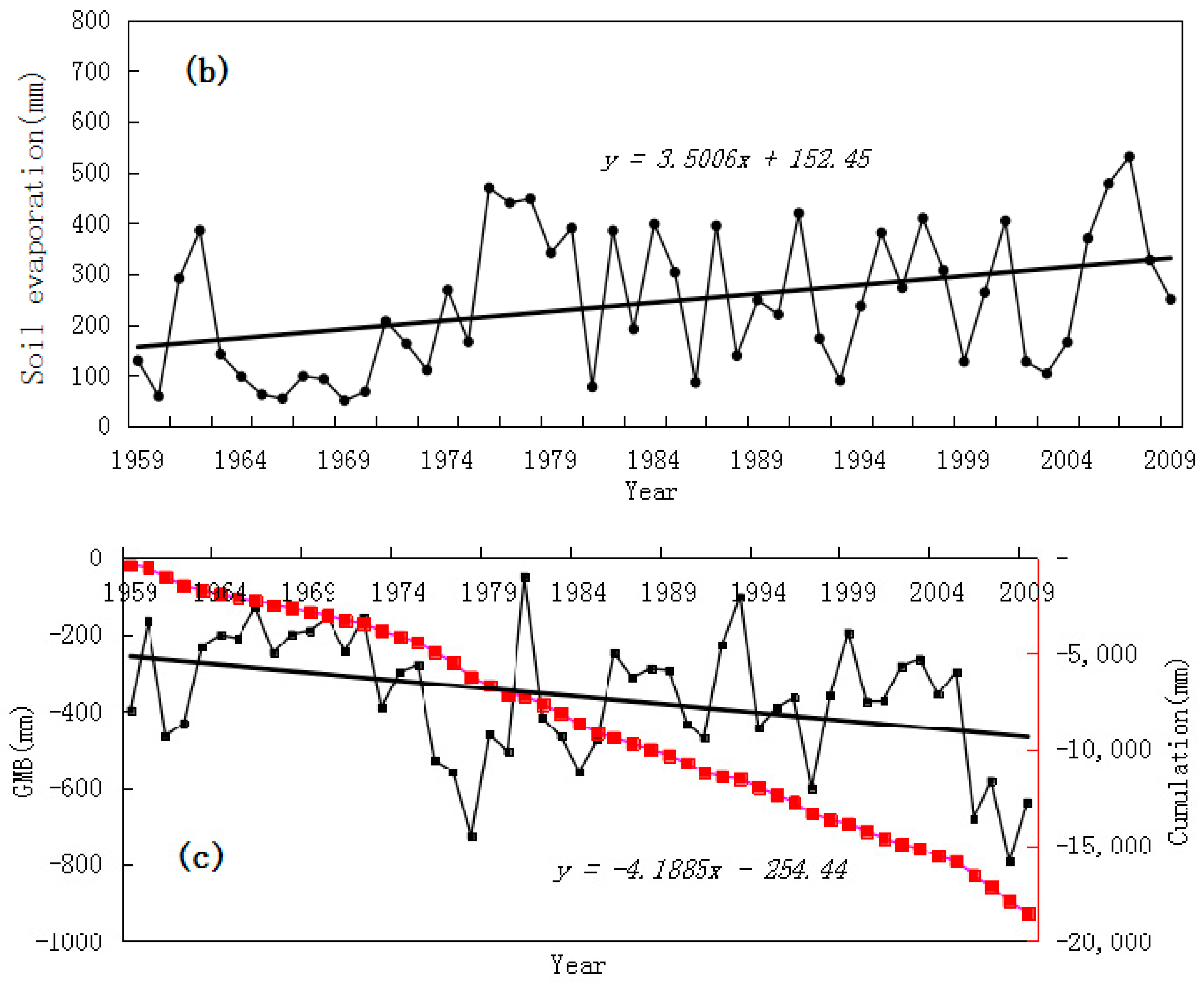
5.2. Simulation of Runoff and GMB for 1959–2009
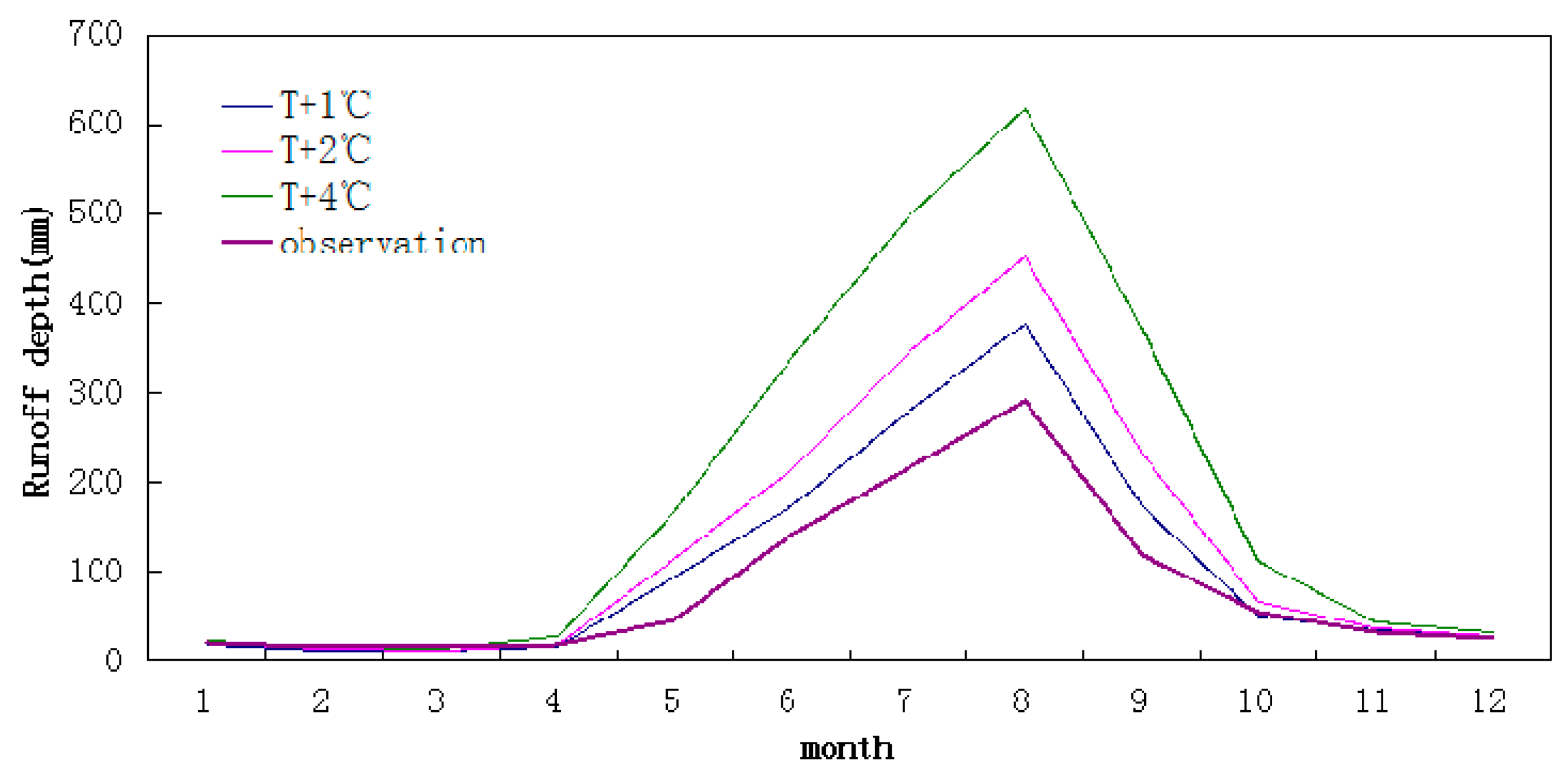
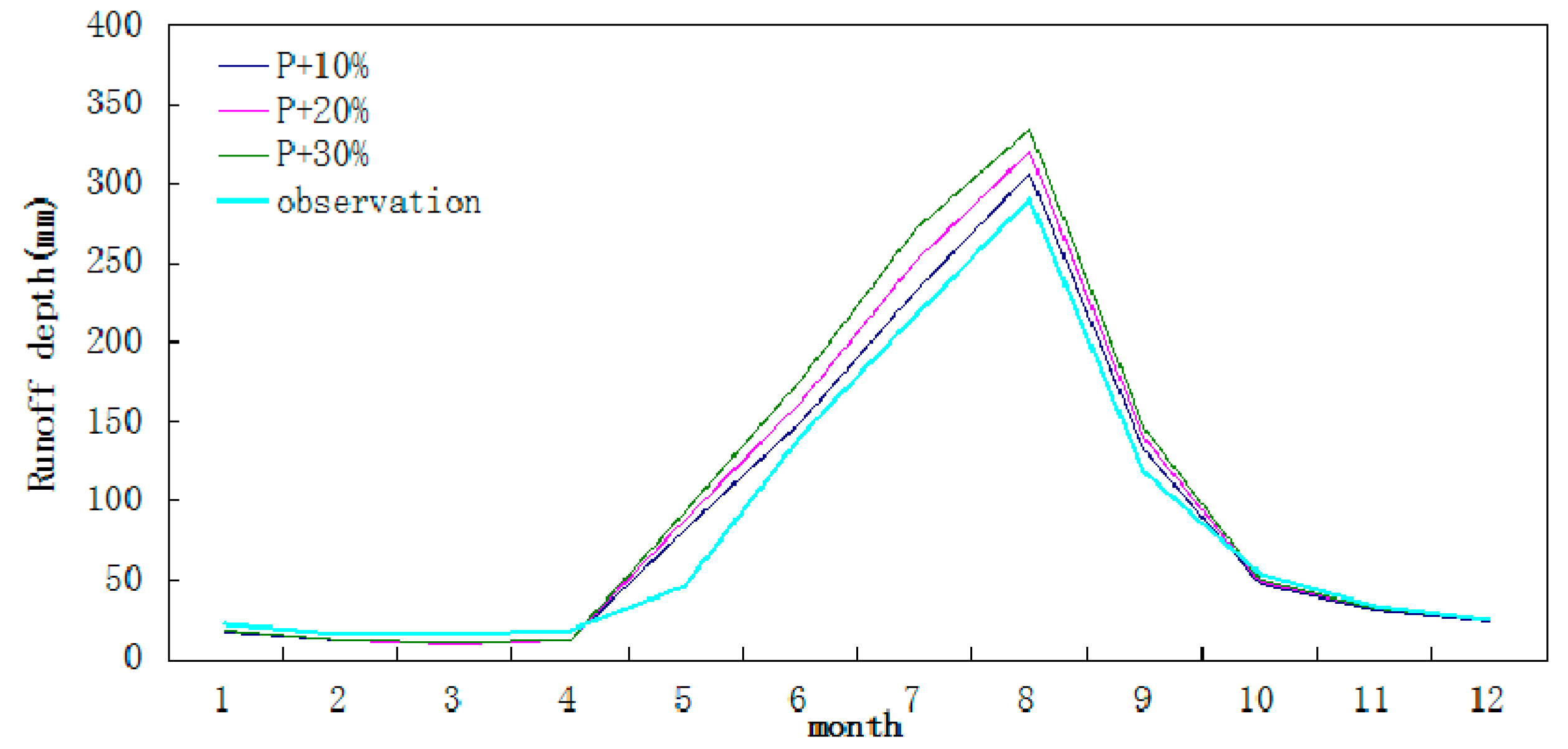
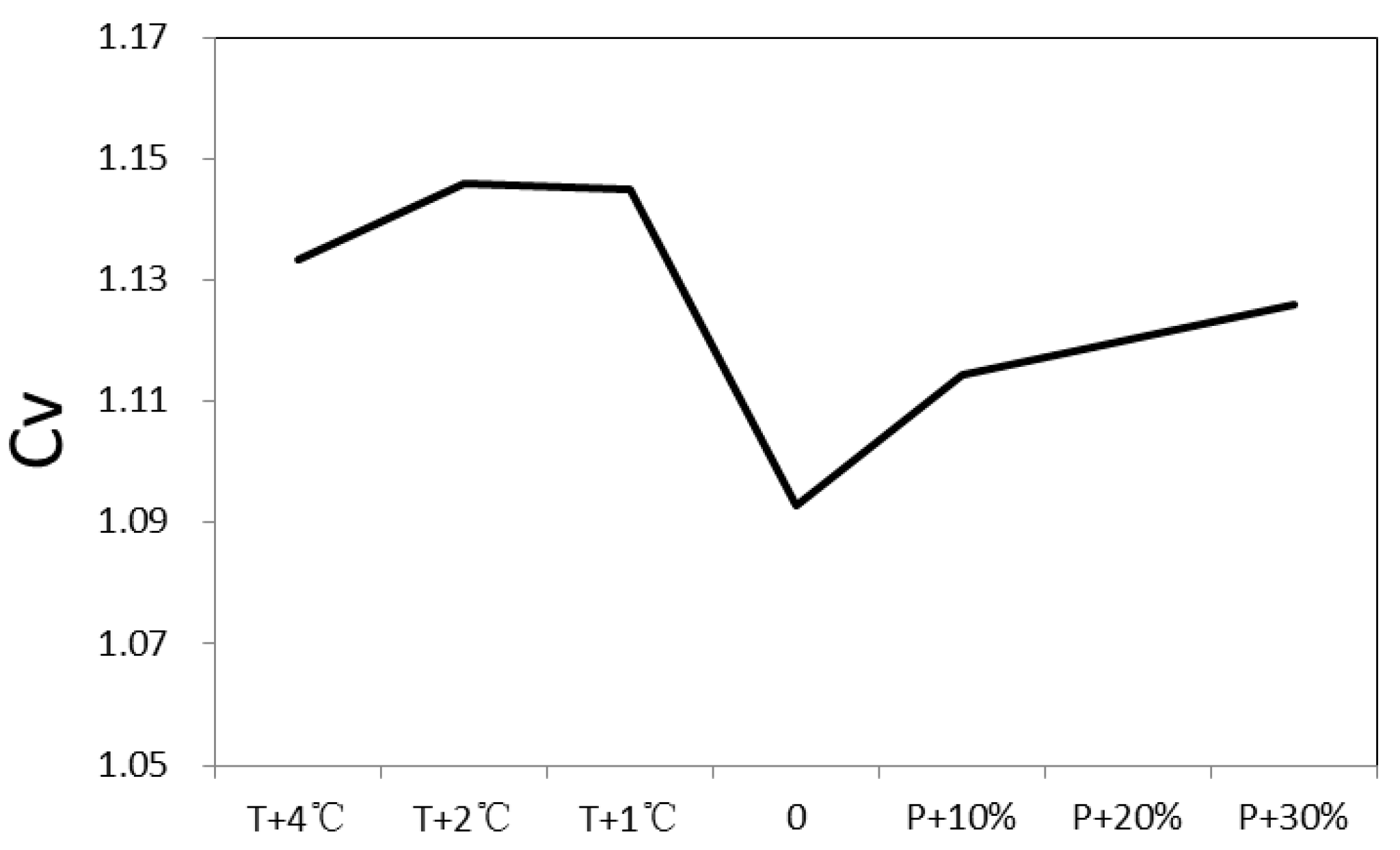
5.3. Sensitivity Analysis of Runoff
5.4. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jansson, P.; Hock, R.; Schneider, T. The concept of glacier storage: A review. J. Hydrol. 2003, 282, 116–129. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.; Bierkens, M.F. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, S.; Han, H.; Zhang, Y.; Wang, J.; Wei, J. Evaluation of runoff from Koxkar Glacier Basin, Tianshan Mountains, China. Prog. Inquis. Demutat. Clim. 2012, 8, 357–363. [Google Scholar]
- Giovanni, R.; Secondo, B.; Alessio, S.; Alfonso, S.; Marco, M. An integrated hydrological model for assessing climate change impacts on water resources of the Upper Po River Basin. Water Resour. Manag. 2015, 29, 1193–1215. [Google Scholar]
- Yang, Z. The Chinese Glacier Water Resource; Gansu Science and Technology Press: Lanzhou, China, 1991; pp. 137–148. [Google Scholar]
- Li, K.; Li, Z.; Gao, W.; Wang, L. Recent East Tianshan Glacier retreat and its impact on water resources. Chin. Sci. Bull. 2011, 56, 2708–2716. [Google Scholar]
- Dombrowsky, I.; Hagemann, N.; Houdret, A. The river basin as a new scale for water governance in transition countries? A comparative study of Mongolia and Ukraine. Environ. Earth Sci. 2014, 72, 4705–4726. [Google Scholar] [CrossRef]
- Li, X. Study on Parameter Calibration and Uncertainty Assessment of Hydrologic Model. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2005. [Google Scholar]
- Lindstrom, G.; Harlin, J. Spill way design floods In Sweden—Applications and sensitivity analysis. Hydrol. Sci. J. 1992, 37, 521–539. [Google Scholar] [CrossRef]
- Liden, R.; Harlin, J. Analysis of conceptual rainfall-runoff modelling performance in different climates. J. Hydrol. 2000, 238, 231–247. [Google Scholar] [CrossRef]
- Gardelin, M.; Bergstrom, S.; Carlsson, B.; Graham, L.P.; Lindström, G. Climate change and water resources in Sweden—Analysis of uncertainties. In Climatic Change: Implications for the Hydrological Cycle and for Water Management; Springer: Dordrecht, The Netherlands, 2006; Volume 10, pp. 189–207. [Google Scholar]
- Menzel, L.; Burger, G. Climate change scenarios and runoff response in the Mulde catchment (Southern Elbe, Germany). J. Hydrol. 2002, 267, 53–64. [Google Scholar] [CrossRef]
- Hundecha, Y.; Bardossy, A. Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model. J. Hydrol. 2004, 292, 281–295. [Google Scholar] [CrossRef]
- Konz, M.; Uhlenbrook, S.; Braun, L.; Shrestha, A.; Demuth, S. Implementation of a process-based catchment model in a poorly gauged, highly glacierized Himalayan headwater. Hydrol. Earth Syst. Sci. 2007, 11, 1323–1339. [Google Scholar] [CrossRef]
- Bergström, S.; Forsman, A. Development of a conceptual deterministic rainfall-runoff model. Nord. Hydrol. 1997, 3, 147–170. [Google Scholar]
- Kang, E.; Cheng, G.; Lan, Y.; Zhang, J. Application of a conceptual hydrological model in the forecast of a mountain watershed. Adv. Earth Sci. 2002, 17, 18–26. [Google Scholar]
- Gao, H.; He, X.; Ye, B.; Pu, J. Modeling the runoff and glacier mass balance in a small watershed on the Central Tibetan Plateau, China, from 1955 to 2008. Hydrol. Process. 2012, 26, 1593–1603. [Google Scholar] [CrossRef]
- Xie, C.; Ding, Y.; Liu, S.; Han, H. Analysis on the glacial hydrological features of the glaciers on the south slope of Mt. Tuomuer and the effects on runoff. Arid Land Geogr. 2004, 27, 251–255. [Google Scholar]
- Zhang, Y.; Liu, S.; Shangguan, D.; Xie, C.; Han, H.; Wang, J. Study of the positive degree-day factors on the Koxkar Baqi Glacier on the south slope of Tianshan Mountains. J. Glaciol. Geocryol. 2005, 27, 335–343. [Google Scholar]
- Han, H.; Shao, J.; Lin, F.; Wang, J. Modeling the sensitivity of meltwater runoff of Tuomuer-type glacier to climate changes. Prog. Inquis. Demutat. Clim. 2012, 8, 357–363. [Google Scholar]
- Wu, L.Z.; Li, X. Dataset of the First Glacier Inventory in China; Cold and Arid Regions Science Data Center: Lanzhou, China, 2004. [Google Scholar]
- Seibert, J.; Vis, M.J.P. Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrol. Earth. Syst. Sci. 2012, 16, 3315–3325. [Google Scholar] [CrossRef]
- Bergström, S.; Lindström, G.; Pettersson, A. Multi-variable parameter estimation to increase confidence in hydrological modelling. Hydrol. Process. 2002, 16, 413–421. [Google Scholar] [CrossRef]
- Lang, H.; Musy, A. Hydrology in Mountainous Regions; IAHS Publ.: Wallingford, CT, USA, 1990; pp. 99–106. [Google Scholar]
- Young, G.J. Snow and glacier hydrology. In Proceedings of the Kathmandu of an International Symposium, Kathmandu, Nepal, 16–21 November 1992.
- Seibert, J. HBV Light User’ Manual; Stockholm University: Stockholm, Sweden, 2005; pp. 1–32. [Google Scholar]
- Braithwaite, R.J.; Olesen, O.B. Ice ablation in West Greenland in relation to air temperature. Zeitschrift fuer Gletscherkunde und Glazialgeologie 1984, 20, 155–168. [Google Scholar]
- Fountain, A.G.; Tangborn, W.V. The effect of glaciers on streamflow variations. Water Resour. Manag. 1985, 21, 579–586. [Google Scholar] [CrossRef]
- Fujita, K.; Seko, K.; Ageta, Y.; Pu, J.C.; Yao, T.D. Superimposed ice in glacier mass balance on the Tibetan Plateau. J. Glaciol. 1996, 42, 454–460. [Google Scholar] [CrossRef]
- Fujita, K.; Ohta, T.; Ageta, Y. Characteristics and climatic sensitivities of runoff from a cold-type glacier on the Tibetan Plateau. Hydrol. Process. 2007, 21, 2882–2891. [Google Scholar] [CrossRef]
- Bergström, S. The HBV-Model—Its Structure and Applications. SMHI Rep. Hydrol. 1992, 4, 32. [Google Scholar]
- Seibert, J.; Mcdonnell, J.J. Land-cover impacts on streamflow: A change-detection modeling approach that incorporates parameter uncertainty. Hydrol. Sci. J. 2010, 55, 316–332. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I—A discussion of principles. J. Hydrol. 1997, 10, 282–290. [Google Scholar] [CrossRef]
- Zhao, G.; Yang, T.; Tian, H. Response of glacier area variation to climate change in southern Tianshan Mountains during 1990–2011. Res. Soil Water Conserv. 2014, 21, 257–268. [Google Scholar]
- Hornberger, G.M.; Cosby, B.J.; Galloway, J.N. Modelling the effect of acid deposition: Uncertainty and spatial variability in estimation of long-term sulphate dynamics in a region. Water Resour. Manag. 1986, 22, 1293–1302. [Google Scholar] [CrossRef]
- Seibert, J. Estimation of parameter uncertainty in the HBV Model. Hydrol. Res. 1997, 28, 247–262. [Google Scholar]
- Uhlenbrook, S.; Seibert, J.; Leibundgut, C.; Rodhe, A. Prediction uncertainty of conceptual rainfall-runoff models caused by problems in identifying model parameters and structure. Hydrol. Sci. J. 1999, 44, 779–797. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Sun, M.; Li, Z.; Yao, X.; Zhang, M. Analysis on runoff variation of Glacier No. 1 at the headwaters of the Urumqi River from 1959 to 2008. J. Nat. Resour. 2012, 27, 650–660. [Google Scholar]
- Zhang, Y.S. Hydrological processes and their features. In Dynamic Features of Cryosphere in the Middle of Qinghai-Tibet Plateau; Geological Press: Beijing, China, 2002; pp. 199–206. [Google Scholar]
- Zhang, Y.; Yao, T.; Pu, J. The features of hydrological processes in the Dongkemadi River Basin, Tanggula Pass, Tibetan Plateau. J. Glaciol. Geocryol. 1997, 18, 214–222. [Google Scholar]
- Zhang, X.; Yang, Z. The primary analysis of water-balance in Binggou Basin of Qilian Mountains. J. Glaciol. Geocryol. 1991, 13, 35–42. [Google Scholar]
- Rolland, C. Spatial and seasonal variations of air temperature lapse rates in Alpine regions. J. Clim. 2003, 16, 1032–1046. [Google Scholar] [CrossRef]
- Wang, N.; He, J.; Jiang, X.; Song, G.; Pu, J.; Wu, X.; Chen, L. Study on the zone of maximum precipitation in the north slope of the central Qilian Mountains. J. Glaciol. Geocryol. 2009, 31, 395–403. [Google Scholar]
- Mu, Z.; Jiang, H. The vertical distribution law of precipitation in the western Tianshan Mountain based on TRMM/TMI. J. Arid Land Resour. Environ. 2010, 24, 66–71. [Google Scholar]
- Shi, Y. Glaciers and Related Environments in China; Science Press: Beijing, China, 2000; pp. 80–86. [Google Scholar]
- Xin, H.; He, Y.; Li, Z.; Wang, S.; Du, J.; Wang, C.; Pu, T.; Zhang, W. Inter-annual variation of temperature and precipitation gradient at the eastern slope of Yulong Snow Mountain. Earth Sci. J. China Univ. Geosci. 2012, 37, 188–194. [Google Scholar]
- Liu, J.; Cheng, R.; Qin, W.; Yang, Y. Study on the vertical distribution of precipitation in mountainous regions using TRMM data. Adv. Water Sci. 2011, 22, 447–454. [Google Scholar]
- Braithwaite, R.J.; Zhang, Y. Sensitivity of mass balance of five Swiss glaciers to temperature changes assessed by tuning a degree-day model. J. Glaciol. 2000, 152, 7–14. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N.; Arora, M. Degree-day factors for snow and ice for Dokriani Glacier, Garhwal Himalayas. J. Hydrol. 2000, 235, 1–11. [Google Scholar] [CrossRef]
- Qiao, C.; He, X.; Ye, B. Study of the degree-day factors for snow and ice on the Dongkemadi Glacier, Tanggula Range. J. Glaciol. Geocryol. 2010, 32, 257–264. [Google Scholar]
- Wu, Q.; Kang, S.; Gao, T.; Zhang, Y. The characteristics of the positive degree-day factors of the Zhadang Glacier on the Nyainqentanglha Range of Tibet Plateau, and its application. J. Glaciol. Geocryol. 2010, 32, 257–264. [Google Scholar]
- Rangecroft, S.; Suggitt, A.J.; Anderson, K.; Harrison, S. Future climate warming and changes to mountain permafrost in the Bolivian Andes. Clim. Chang. 2016, 137, 231–243. [Google Scholar] [CrossRef]
- Rangecroft, S.; Harrison, S.; Anderson, K. Rock glaciers as water stores in the Bolivian Andes: An assessment of their hydrological importance. Arct. Antarct. Alp. Res. 2015, 47, 89–98. [Google Scholar] [CrossRef]
- Sorg, A.; Bolch, T.; Stoffel, M.; Solomina, O.; Beniston, M. Climate change impacts on glaciers and runoff in Tien Shan (Central Asia). Nat. Clim. Chang. 2012, 2, 725–731. [Google Scholar] [CrossRef]
| Cover Type | Area (km2) | Proportion |
|---|---|---|
| Bare Land | 9.3 | 8.0% |
| Shrub | 1.8 | 1.5% |
| Grassland | 6.15 | 5.3% |
| Snow Cover | 6.9 | 5.9% |
| Glacier | 89.6 | 76.9% |
| Water | 2.7 | 2.32% |
| Station | Longitude (°E) | Latitude (°N) | Altitude (m) | Years |
|---|---|---|---|---|
| Akesu | 80.233 | 41.167 | 1103 | 1959–2009 |
| Baichen | 81.900 | 41.783 | 1229 | 1959–2009 |
| Aheqi | 78.450 | 40.930 | 1985 | 1959–2009 |
| Zhaosu | 81.133 | 43.150 | 1851 | 1959–2009 |
| Koxkar | 80.167 | 41.700 | 2974 | 2007–2009 |
| Parameter | Description | Unit | Range | Value | Method of Estimation |
|---|---|---|---|---|---|
| Meteorological data | |||||
| PCalt | Gradient of precipitation | %/100 m | 4.6 | 4.6 | Observation |
| TCalt | Gradient of temperature | °C/100 m | 0.66 | 0.66 | Observation |
| Snow and glacier routine | |||||
| TT | Threshold temperature | °C | −1–2.7 | 2.7 | [20] |
| DDF | Degree-day factor of snow | mm·°C−1·day−1 | 9.5 | 9.5 | Observation |
| CFR | Refreezing coefficient | - | 0.2 | 0.2 | [19] and calibration |
| SFCF | Snowfall correction factor | 0–1 | 0.05 | ||
| Cg | Factor for increased melt of ice | - | 1.3 | 1.3 | [30] and calibration |
| Ca | Factor for increased melt of south slope to north slope | - | 1.1–2 | 1.1 | Calibration |
| Soil routine | |||||
| FC | Maximum soil box (SM) | mm | 100–450 | 300 | [36] and calibration |
| LP | SM threshold for reduction of evaporation | - | 0.3–1 | 0.9 | [36] and calibration |
| BETA | Shape coefficient | - | 1–5 | 1.5 | [36] and calibration |
| Response routine | |||||
| K1 | Recession coefficient | day−1 | 0.01–0.2 | 0.01 | [36] and calibration |
| K2 | Recession coefficient | day−1 | 0.001–0.1 | 0.05 | [36] and calibration |
| PERC | Maximal flow from upper to lower GW-box | mm·day−1 | 0–6 | 2 | [36] and calibration |
| Routing routine | |||||
| MAXBAS | Routing, length of weighting function | day | 1–5 | 1.9 | [36] and calibration |
| Glacier | Koxkar (Simulation) | No. 1 Glacier (Observation) | Tuyuksu Glacier (Observation) |
|---|---|---|---|
| 1959–2009 glacier mass balance accumulation | −18,530 mm | −15,200 mm | −20,384 mm |
| T + 1 °C | T + 2 °C | T + 4 °C | |
|---|---|---|---|
| Changes of runoff (%) | 27.4 | 56.2 | 127.2 |
| P + 10% | P + 20% | P + 30% | |
|---|---|---|---|
| Change of runoff (%) | 6.1 | 11.3 | 19.8 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Han, H.; Kang, S. Modeling Glacier Mass Balance and Runoff in the Koxkar River Basin on the South Slope of the Tianshan Mountains, China, from 1959 to 2009. Water 2017, 9, 100. https://doi.org/10.3390/w9020100
Xu M, Han H, Kang S. Modeling Glacier Mass Balance and Runoff in the Koxkar River Basin on the South Slope of the Tianshan Mountains, China, from 1959 to 2009. Water. 2017; 9(2):100. https://doi.org/10.3390/w9020100
Chicago/Turabian StyleXu, Min, Haidong Han, and Shichang Kang. 2017. "Modeling Glacier Mass Balance and Runoff in the Koxkar River Basin on the South Slope of the Tianshan Mountains, China, from 1959 to 2009" Water 9, no. 2: 100. https://doi.org/10.3390/w9020100
APA StyleXu, M., Han, H., & Kang, S. (2017). Modeling Glacier Mass Balance and Runoff in the Koxkar River Basin on the South Slope of the Tianshan Mountains, China, from 1959 to 2009. Water, 9(2), 100. https://doi.org/10.3390/w9020100





