1. Introduction
Sediment is a primary pollutant to surface water and a leading cause of water quality impairment [
1]. Though erosion is a natural and even necessary process [
2], the rate of erosion has been accelerated due to human activities such as farming and urbanization. In some watersheds, streambank erosion is the main source of sediment to rivers and streams [
3]. The excess sediment affects the water chemistry, aquatic organisms, and the water clarity in our streams and reservoirs. Excess sediment is aesthetically displeasing, increases the cost of treating drinking water, decreases water clarity, and has an overall negative impact on the aquatic ecosystem [
4,
5,
6,
7,
8]. The increased turbidity not only affects the water aesthetics but also reduces photosynthesis and organisms’ visibility. Siltation alters flow in streams and decreases the storage volume in our reservoirs, which in turn affects flooding, drinking water, and recreation.
Alluvial channels continue to adjust, change, and sometimes shift their location [
9]. In some eroding stream reaches, the streambanks are stabilized using conventional or modified stabilization techniques. Such stabilization structures are typically implemented in an effort to lock the stream channel into a relatively fixed location and condition [
9]. The channel bank infrastructure then alters the geomorphic processes and can lead to more erosion at the stabilized site as well as at locations upstream and downstream [
10,
11]. When these channel migration processes are ignored, the erosion-control structures may become ineffective over time, causing failure during large flow events [
2,
9,
10]. Rosgen [
12] has restored and monitored over 48 km of rivers and has monitored various structures’ performance following major floods. The results contradicted the expected pattern, as many structures caused river instability.
The cost of stream restoration continues to increase, yet few resources are being allocated to evaluate and monitor the restoration practices [
13]. Annually, the USA spends
$1 billion on stream restoration, the efforts of which are intended to improve the environmental health of a stream or river, generally by restoring a dynamically stable dimension, pattern, and profile [
14,
15]. One component of stream restoration is streambank stabilization, which is generally intended to maintain a stable channel dimension at the stabilization site. Although post-installation monitoring yields important information on the effectiveness of a stabilization practice, less than 10% of the projects include any assessment of outcomes [
13]. Possible reasons include lack of funds (project ended) and poor project documentation. Even when monitoring occurs, inconsistencies in collection methods and limited reporting are common [
16]. There is an urgent need to use evaluation data to update design and implementation methods to improve restoration approaches and increase the likelihood of success of the thousands of projects currently being planned and implemented [
17].
Though several research papers have been written about monitoring stabilized streambanks, scant long-term monitoring of stabilized streambanks is relayed in the literature. In general, most previous research discusses the effectiveness of stabilization practices based on qualitative analysis or prediction-based models. Daly et al. [
18] used BSTEM to estimate the streambank retreat rate over a seven-year (2003–2010) study period at 10 sites on Barren Fork Creek, Oklahoma. Protected sites had less streambank retreat, ranging from 4.1 to 74.8 m per year, while unprotected sites had an estimated average streambank retreat of 49.2 m per year. Simon et al. [
19] also used a BSTEM model to analyze reduction in streambank sediment loads and bank failures at the Big Sioux River, Lower Tombigbee River and Lake Tahoe Basin. The average annual streambank erosion in the Big Sioux River was reduced by 51% (503,000 m
3 to 243,000 m
3) after toe protection was added, while overall volume of eroded bank material was reduced by 87–100% [
19]. Similarly, in the Lake Tahoe Basin, total streambank erosion was reduced by about 89%. In the lower Tombigbee River, the amount of lateral retreat and volume of failed material reduced by about 500% (from 55,000 m
3 to 9500 m
3) [
14].
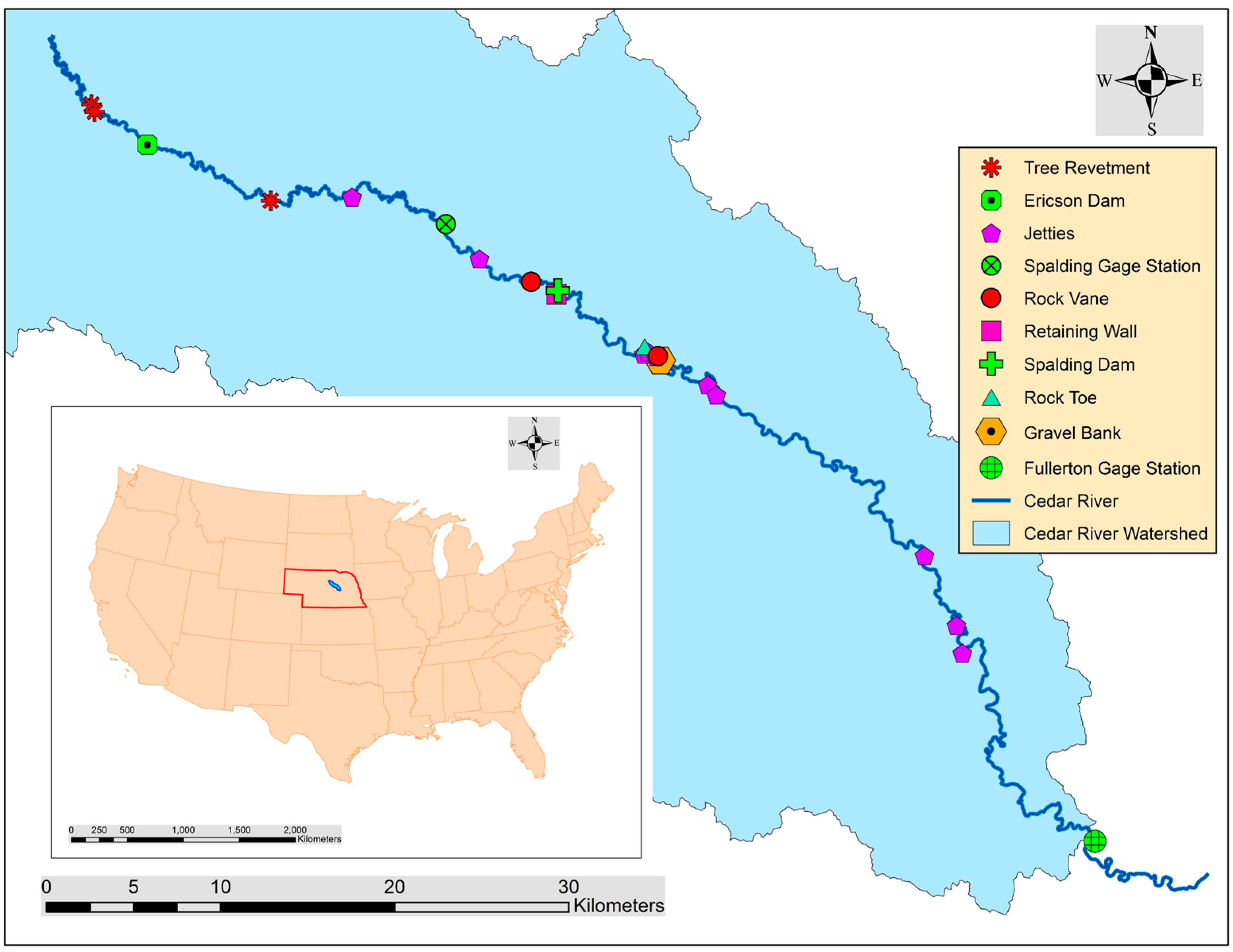
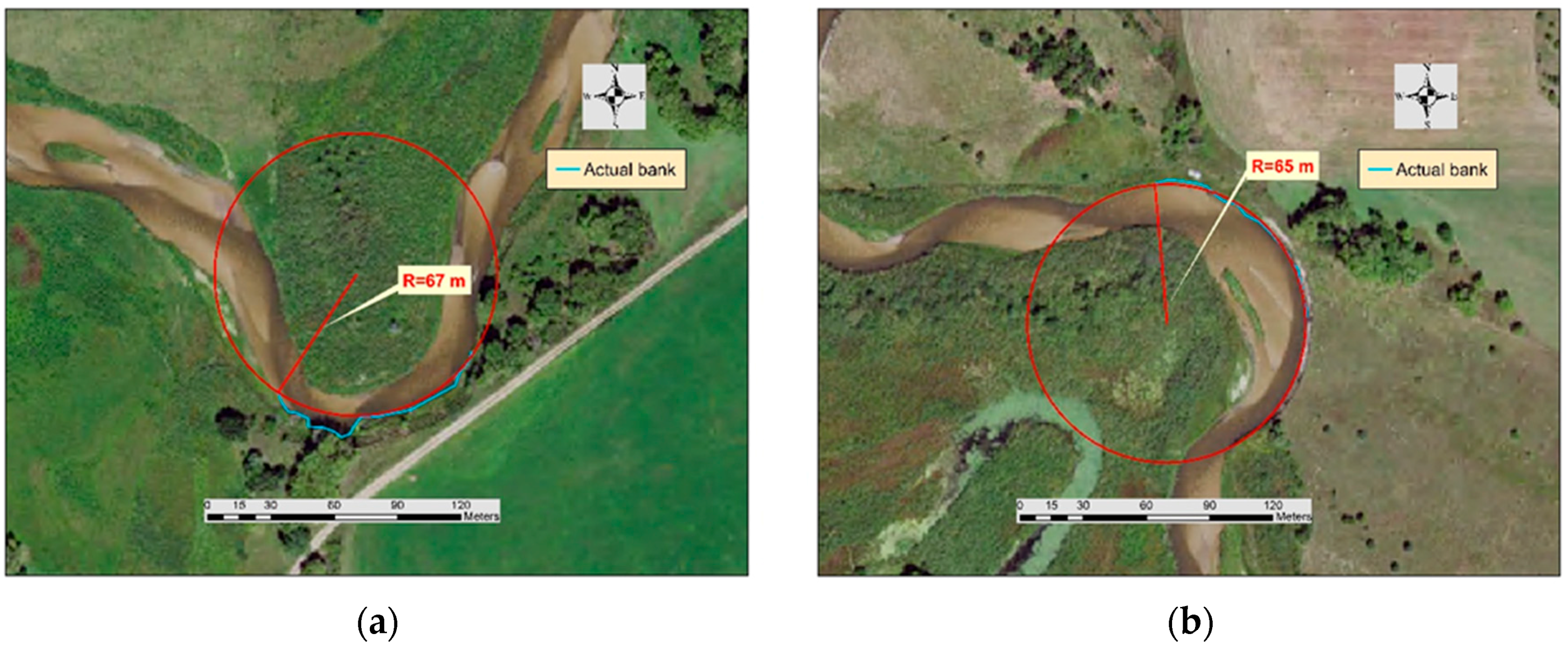
Some project reports exist for stream assessment, but they consider general health of streams and measure sediment loads or fish habitat. Most techniques involve research on riparian vegetation or stream stabilization conducted using bioengineering techniques. No previous study has specifically focused on quantification of streambank erosion for monitoring of stabilization practices. This study evaluated 17 sites stabilized from 2000 to 2005 and one stabilized in 1950 on the Cedar River in Nebraska. These sites were stabilized to reduce surface-water degradation and sedimentation loading of the river system, improve the aquatic habitat through riparian buffers and increased vegetation, and reverse the loss of prime cropland and rangeland. No post-construction monitoring has been conducted for these sites to evaluate the effectiveness or the stability of the practices in mitigating the effects of erosion. For the 18 stabilized streambanks and 40 identified control streambanks, the objectives of this study were to (1) quantify streambank erosion from 1993–2016; (2) evaluate the impact of an extreme flood in 2010; and (3) determine the most cost-efficient technique.
3. Results and Discussion
To determine the success of the implemented practices, the streambank erosion was calculated for 18 stabilized banks and 40 control streambanks. The objectives of this study were to (1) quantify streambank erosion rates from 1993 to 2016; (2) evaluate the impact of the flood in 2010; and (3) determine the most cost-efficient practice.
3.1. Prestabilization and Poststabilization
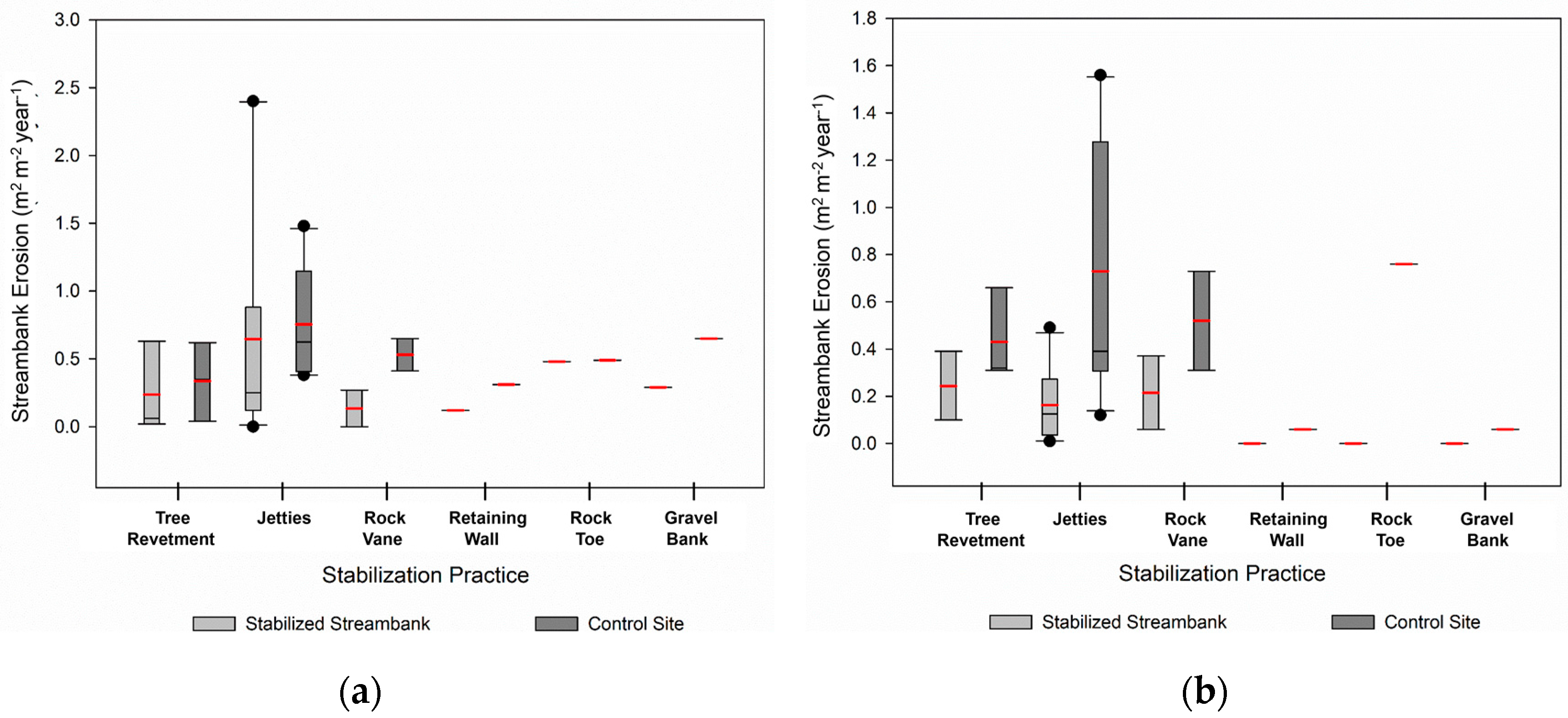
The average streambank erosion rate for the 18 stabilized streambanks before (1993–1999/2003) and after stabilization (1999/2003–2009) was 0.45 m2 m−1 year−1 and 0.16 m2 m−1 year−1, respectively. Assuming an average bank height of 2.1 m, the average total volume is 0.95 m3 m−1 year−1 and 0.34 m3 m−1 year−1. Since the data were not normally distributed, a nonparametric test was used to determine if the pre-stabilization and post-stabilization medians were significantly different. With a p-value of 0.34, the medians (0.22 m2 m−1 year−1 and 0.13 m2 m−1 year−1) were not significantly different. This may be attributed to the difference in streamflow between the two time periods; however, this supposition could not be tested since streamflow data prior to 2006 was not available from either gage station.
The average streambank erosion rate for the jetties was 0.65 m
2 m
−1 year
−1 pre-stabilization and was significantly different from post-stabilization (0.16 m
2 m
−1 year
−1). The streambank erosion rate for the retaining wall, rock toe, and gravel bank was zero following streambank stabilization (
Figure 6). The tree revetments and rock vanes were less successful, with a small amount of erosion occurring. Similar to what we discovered, Brown [
30] found that 27% of the banks protected with rootwad revetment (similar to cedar tree revetment) partially or fully failed to protect the streambank and that outflanking occurred at 25% of the rock vanes assessed. He also found that riprap (similar to the rock toe and gravel bank) fully protected the streambanks. Two years after installation, Buchanan et al. [
13] found that 28% of the bank vanes (which are vanes that do not go across the entire river width but protect only the bank at the desired location) failed and that 36% were impaired. One limitation to comparing differences in streambank erosion rates among the practices observed within the present study is the limited number of observations for several of the practices.
To distinguish the impact of varied streamflow between the pre-stabilization and post-stabilization periods, the streambank erosion rate was compared with the 40 control sites (
Table 2). Although we intended to identify control sites that mimicked our study sites, the median streambank erosion was significantly greater for the control sites (0.55 m
2 m
−1 year
−1) than the stabilized streambanks (0.22 m
2 m
−1 year
−1) during the pre-stabilization period with a
p-value of 0.0042. The average streambank erosion rate pre-stabilization for the stabilized streambanks was 0.45 m
2 m
−1 year
−1 with a range of 0–2.4 m
2 m
−1 year
−1 compared with 0.63 m
2 m
−1 year
−1 and a range of 0.04–1.5 m
2 m
−1 year
−1 for the control sites. The median streambank erosion rate during the post-stabilization period between the stabilized and control streambanks were significantly different (a
p-value of 0.0002) with median streambank erosion rates of 0.13 m
2 m
−1 year
−1 and 0.38 m
2 m
−1 year
−1 for the stabilized and control sites, respectively. The jetties were successful with the median erosion for the stabilized streambanks and controls sites, being 0.13 m
2 m
−1 year
−1 and 0.39 m
2 m
−1 year
−1, respectively. The erosion was significantly different with a
p-value of 0.0036. The more expensive practices (rock toe, retaining wall, and gravel bank) were all successful and completely stabilized the streambanks.
3.2. Flood Impact
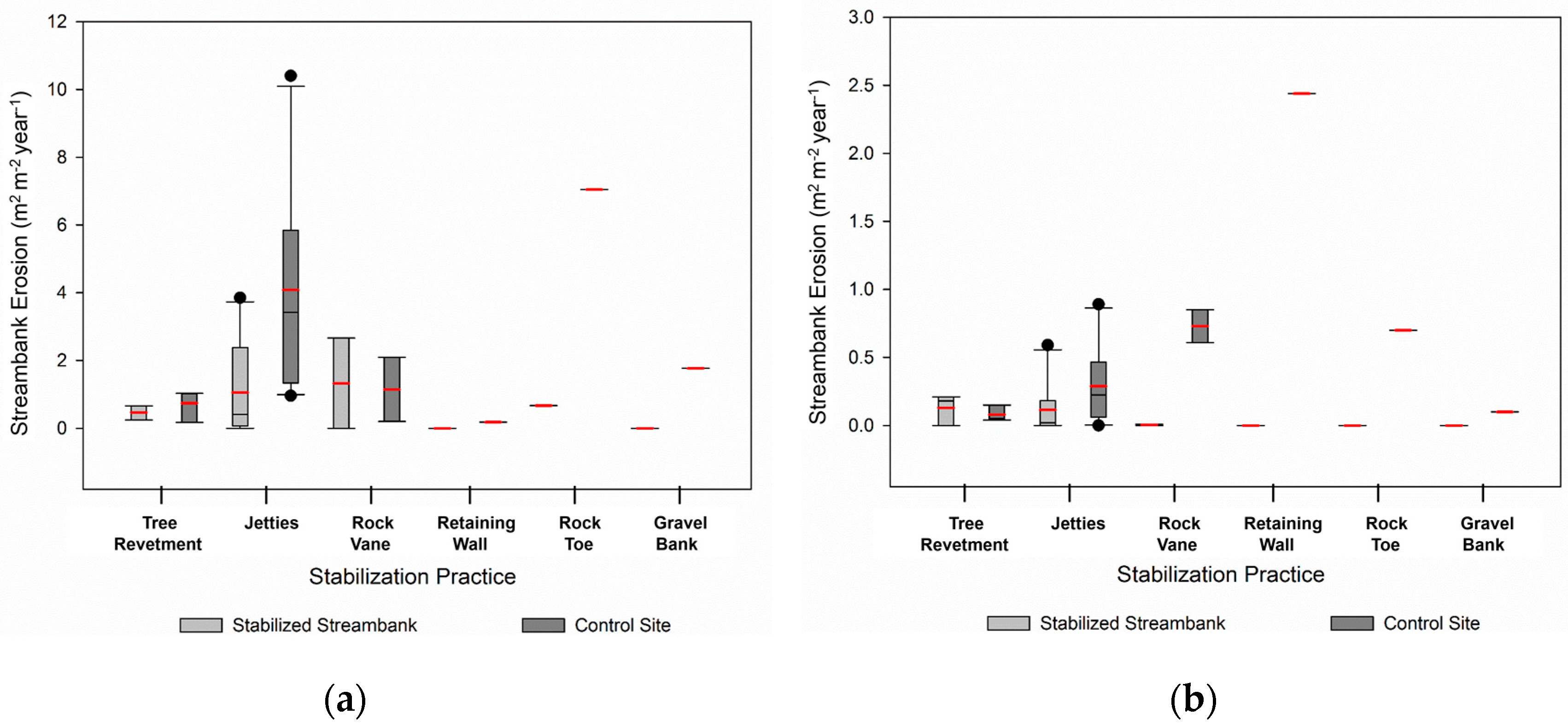
The flood in 2010 caused a significant quantity of erosion, especially at the control sites (
Figure 7). The average erosion rate during the flood was 0.74 m
2 m
−1 and 3.1 m
2 m
−1 for the stabilized streambanks and control sites, respectively. The medians, 0.40 m
2 m
−1 and 1.93 m
2 m
−1, were significantly different with a
p-value of 0.0013. Four sites downstream of Spalding failed because their structure lost functionality during the flood: Sites 10, 16, and 18, which have jetties, and Site 12, which has a rock vane. Even with some of the jetties failing at Sites 10, 16, and 18 (
Figure 3), the average streambank erosion rates for jetties for the stabilized streambanks and the control sites were significantly different (0.007) with a median erosion of 0.41 m
2 m
−1 and 3.42 m
2 m
−1, respectively. Minimal erosion occurred at the top of the streambank at Site 9 (rock toe). No erosion occurred on the streambanks stabilized with the retaining wall and gravel bank. For comparison, Miller and Kochel [
31] conducted an assessment of 26 stream restoration projects across North Carolina and almost 30% of the structures underwent partial or total damage and lost their functionality. Though these were stream restoration projects, calculated results mainly represented the erosion control practices. Spatially, the damage was done at 10 out 16 sites and amongst those sites, cross vanes and double wings exhibited the greatest damage out of six different types of practices: cross vanes, rock vanes, j-hook, double wings, log vanes, and rootwads [
31].
Previously, Dragićević et al. [
32] evaluated flood erosion rates using aerial photography on the Kolubara River, which experienced a flood wave in May 2014, and found that the land loss in 2014 was three times larger than in 2013. Comparable to that study, the average erosion rate for the control sites was five times larger during the flood in 2010 (3.05 m
2 m
−1 year
−1) compared to the time period 2001–2009 (0.57 m
2 m
−1 year
−1).
We also compared the erosion upstream of Ericson Dam (2 sites) to the 4 sites downstream of the breached dam and to the 10 sites downstream of Spalding Dam. For the stabilized streambanks, the medians were not significantly different from the upstream sites (0.45 m2 m−1 year−1), those downstream of the Ericson Dam (0.55 m2 m−1 year−1), or those downstream of Lake Spalding (0.21 m2 m−1 year−1). Since the lack of a significant difference may be attributed to the types of practices installed at the three locations, we evaluated the erosion at the control sites. The median streambank erosion rate was 0.60 m2 m−1 year−1, 1.56 m2 m−1 year−1, and 3.42 m2 m−1 year−1 upstream of Lake Ericson, downstream of Lake Ericson, and downstream of Lake Spalding, respectively. The erosion immediately downstream of the breached dam at the control sites was surprisingly less than the erosion below Spalding Dam. This may be a function of a larger number of control sites or possibly the differences in streambank and channel characteristics. Comparing the stabilized streambanks and the control sites, the median streambank erosion downstream of Lake Ericson was not significantly different, with a p-value of 0.19, but was significantly different downstream of Spalding Dam (a p-value of 0.0029).
3.3. Post-Flood Impact
The flood influenced the stabilized streambanks in an unexpected manner. We expected more erosion during the post-flood period than the pre-flood period (post-stabilization) due to the disturbance caused by the extreme flow event. For this project, however, excluding Sites 10, 14, and 15 (all jetties), the post-flood erosion was much lower than the pre-flood erosion. The median post-flood streambank erosion rate was 0.0 m2 m−1 year−1 for the stabilized streambanks and 0.17 m2 m−1 year−1 for the control sites, significantly different with a p-value of 0.001. The average erosion rate was 0.08 m2 m−1 year−1 and 0.41 m2 m−1 year−1, respectively. The median pre-flood (0.13 m2 m−1 year−1) and post-flood (0.0 m2 m−1 year−1) streambank erosion rate was significantly different for the stabilized streambanks, with a p-value of 0.03. The same was true for the control sites with median pre-flood and post-flood erosion of 0.38 m2 m−1 year−1 and 0.18 m2 m−1 year−1 (a p-value of 0.026). Part of this may be explained by the difference in flow. At the Spalding gage station, the average flow pre-flood (2006–2010) and post-flood (2010–2016) were both 5.5 m3 s−1, although the standard deviation and maximum flow were higher in the pre-flood period (2.97 m3 s−1 and 40.9 m3 s−1) than the post-flood period (2.11 m3 s−1 and 26.0 m3 s−1).
3.4. Deposition
The average deposition for the stabilized streambanks and control sites for the pre-stabilization period was 0.15 m2 m−1 year−1 and 0.14 m2 m−1 year−1, respectively. During the post-stabilization period, the average deposition was 0.24 m2 m−1 year−1 and 0.09 m2 m−1 year−1 for the stabilized streambanks and control sites, respectively. Based on a Mann–Whitney test, the medians (0.14 m2 m−1 year−1 and 0.05 m2 m−1 year−1) were not significantly different, with a p-value of 0.07. For post-stabilization, the deposition for the jetties was significantly different (a p-value of 0.007) with a median deposition of 0.19 m2 m−1 year−1 and 0.03 m2 m−1 year−1 for the stabilized and control sites, respectively. This is not surprising since a function of jetties is to increase the sediment deposition upstream of each jetty.
The control site for jetties had less accumulation (0.51 m
2 m
−1 year
−1) than the stabilized banks (0.99 m
2 m
−1 year
−1) during the flood, which shows a very efficient sediment capture. However, it is believed that excessive sediment deposition causes failure of some structures because it leads to a loss of channel capacity and subsequent change in the stable dimension, pattern and profile of the river [
7].
Not surprisingly, during the flood, the high deposition rates were upstream of the breached dam and downstream of Lake Spalding. Between Lake Ericson and Lake Spalding, there was very little deposition. The average deposition at Sites 3 to 6 downstream of Lake Ericson was 0.23 m2 m−1 year−1 and 0.34 m2 m−1 year−1 for the stabilized and control sites, respectively. Downstream of Lake Spalding, the deposition was much higher, 0.83 m2 m−1 year−1 and 1.23 m2 m−1 year−1 for the stabilized and control sites, respectively.
3.5. Cost-Effectiveness
Although a limitation of the cost-efficiency analysis is the number of sites for some of the practices, the analysis still provides insight into the efficiency of the various practices. Though the exact installation cost per site is unknown, the approximate cost per meter of installation are as follows: jetties:
$26; cedar tree revetments:
$72; rock vanes:
$205; rock toe:
$179; retaining wall:
$625; and gravel bank:
$600 (
Table 3). Cost efficiency is calculated as the reduction in streambank erosion per dollar spent; hence, the larger reduction per dollar spent, the higher the efficiency. To calculate the efficiency, we compared the streambank erosion rate for the post-stabilization period from 1999/2003 to 2009 and 1999/2003 to 2016 for jetties, rock vanes, tree revetments, rock toe, and the retaining wall/gravel bank to the control sites using the following equation:
where CS is the average streambank erosion at the control sites, and SB is the average streambank erosion at the stabilized streambanks.
This comparison assumes that the streambank erosion rate would have been the same at the study sites as the control sites if the streambanks were not stabilized. The number of sites stabilized by each practice is not the same, and some practices, like rock vanes, have very few sites. Hence, to overcome the limitations of our data set, calculations were conducted using the average reduction in erosion per meter per dollar spent. The calculations showed jetties to be the most cost-efficient technique, with reductions of 2.99% and 2.86% per dollar spent per meter for the periods of 1999/2003 to 2009 and 1999/2003 to 2016, respectively. Other than the two expensive stabilization practices, rock vanes were the least cost-efficient, with reductions of 0.23% and 0.32% for the two periods. Rock toe and tree revetments were similar in cost-efficiency, averaging 0.50% (tree revetments) and 0.55% (rock toe) for the two periods. Reductions per dollar spent for the retaining wall/gravel bank were 0.16% and 0.17% for the two periods. With the retaining wall/gravel bank costing around $600 per meter of stabilized streambank, one needs to ask if the cost is justified. The jetties, at a cost of only $26 per foot, reduced the streambank erosion rates significantly compared with the control sites, though 3 of the 10 failed. Based on these results, jetties are successful at stabilizing the streambank at minimal cost, though at some risk, and thus should be installed if some risk can be taken. If it is imperative that the streambank not fail (to protect infrastructure, for example), a retaining wall or gravel bank should be used since their likeliness to fail is minimal.
4. Conclusions
Streambank erosion has increased due to land use change and urbanization. Multiple practices are used to stabilize streambanks, but there is a need to find the most efficient. In 1950 and from 2000 to 2004, 18 streambanks were stabilized on the Cedar River using six techniques: jetties (10), rock-toe protection (1), slope reduction/gravel bank (1), retaining wall (1), rock vanes (2) and tree revetment (3). Using historical aerial images, we documented the streambank erosion and deposition for 18 stabilized streambanks and 40 control points for four periods of time: pre-stabilization, post-stabilization, flood, and post-flood. We found that stabilized banks were more efficient than similar control sites at controlling erosion. Comparing the six erosion-control practices to one another allowed us to identify which was the most efficient and cost-effective. We found that the structurally designed stabilization practices, such as the retaining wall and gravel bank, demonstrated immovability even during the flood in 2010 but required a large investment ($600 per meter). Other practices such as jetties, rock toe, and tree revetments require negligible capital investments but have higher rates of failure. We also found that rock vanes were the least effective, failing during the flood. Although rock vanes were the least effective, our study had a small sample size (two) with which to compare. As mentioned previously, the limitation of this study was the small number of sites for several of the stabilization practices.
For this project, 3 out of 10 sites stabilized with jetties failed during the flood; however, that equates to a 70% success rate at a minimal cost ($26 per meter). In terms of cost efficiency, jetties should be preferred since their cost is much lower, materials are easily available, and they are most efficient at capturing sediment. In conclusion, jetties were the most cost-efficient technique on the Cedar River and should be used if minimal failure of risk is acceptable. The jetty installed in 1950 demonstrates that jetties can endure and be successful for extended periods of time. Our study indicated that structurally designed practices such as retaining walls might be worth the investment only if failure cannot be risked. Because of the ease of installation, affordability, and stability, agricultural producers and others may prefer using jetties.