1. Introduction
Seasonal hydrological forecasts can provide reliable and timely information of land surface hydrologic conditions several months in advance. Early evidence has demonstrated the potential economic benefits of accurate hydrologic predictions, not only in years with hydrological extremes (e.g., drought/flood), but also in years without hydrological extremes [
1,
2]. To facilitate seasonal hydrological forecasts, physical hydrological models are typically initialized with refined initial conditions (ICs) (i.e., antecedent hydrologic states) and then fed with seasonal climate forecasts (CFs) [
3,
4]. Depending on how CFs are generated, the model-based seasonal hydrological forecast is generally grouped into two categories: (1) the Ensemble Streamflow Prediction (ESP) method [
5] which employs the climate sequences resampled from history as the model forcings; and (2) the climate forecast model-based approach fed with downscaled climate forecast fields [
6]. Therefore, seasonal hydrological forecast skill is attributed to the prior knowledge of ICs (primarily snowpack, soil moisture, surface water, and groundwater) on the forecast start date and the posterior information of CFs during the forecast period. Identifying which of these two factors dominates the forecast skill has great implications for the target efforts towards substantially improving the forecast level.
There have been considerable efforts devoted to investigating sources of seasonal hydrological predictability. One common approach is utilizing statistical methods to examine the linkage between indicator variables (including initial moisture states and climate precursors) and the target predictand (e.g., streamflow, soil moisture) [
7,
8]. Alternatively, a few studies have attempted to assess the role of climate forecasts by comparing the climate model-based hydrological forecasts with the parallel ensemble streamflow prediction (ESP), which utilizes the daily climate traces from history as model forcings [
9,
10,
11,
12,
13], or to quantify the contributions (isolated and combined) of soil moisture and snowpack initialization to predictive skill by conducting a set of numerical modeling experiments [
14,
15]. In contrast with these model-based analyses, Wood and Lettenmaier [
16] proposed a theoretical ESP/reverse-ESP (
revESP) framework to partition the relative roles of ICs and CFs in streamflow forecasts over two basins in western U.S. [
16], mainly by comparing two sets of artificial experiments: (1) the ESP forecasts with assumed realistic estimates of initial moisture conditions but random climate forcings; and (2) the parallel
revESP with prescribed observed climate forcings but random estimates of initial moisture conditions. Thereafter, this artificial diagnosis approach was extended to eastern U.S. river basins [
17] and across the total U.S. domain [
18], respectively. These studies consistently reported that the strong influence of ICs on runoff and soil moisture forecasts is expected to last for one month across most of the U.S., and even for up to five months during the wet-to-dry transition period; while the role of CFs starts to become important with the increases in forecast lead, especially during the reverse transition period (i.e., dry-to-wet) and over southeastern and northeastern U.S. To date, given the effectiveness of such an ESP/
revESP scheme, numerous studies have employed it to determine the primary contributor to seasonal hydrological skill or uncertainties over many major river basins globally [
19,
20,
21,
22,
23,
24].
Over the past few decades, China has suffered from several frequent and severe droughts [
25,
26] and floods [
27]. The reported annual economic losses from droughts and floods account for more than half (60%) of the total losses induced by all natural disasters in China [
28]. One possible reason for such huge losses is the lack of prompt response and mitigation strategies to hydrologic extremes due to the absence of the timely and accurate prediction of their evolutions [
29]. To implement an effective operational hydrological prediction over China, a key premise is to provide a comprehensive understanding of the dominant skill contributor for multiple forecast initial dates, varying forecast leads, and different sub-regions across the nation. In reality, China is characterized by many types of hydro-climatic regimes, illustrating that the dominant factor controlling seasonal hydrological forecast skill is related to obvious space-time heterogeneity. To date, limited studies have been pursued to investigate this, e.g., over the Three Gorges Dam [
30], the Hanjiang River basin [
23], the Yellow River basin [
24], and Southwest China [
13]. However, these studies were either conducted by different methods or issued at some specific basins, leaving it hard to draw a consistent conclusion under the same diagnosis framework across the whole country.
To fill this knowledge gap, we systematically investigate the relative roles of ICs and CFs in cumulative runoff (CR) and soil moisture (SM) forecasts under a consistent ESP/
revESP framework, and explore their dependences on the forecast start date (the first day of each calendar month) and forecast lead (one to six months) over 17 hydro-climatic regions of China [
31] (see
Figure 1). Since this study focus on the six-month seasonal hydrological prediction, all the following analyses are based on the monthly aggregated values. Specifically, we aim to answer the following scientific questions: (1) when and where do the initial hydrologic conditions exert the strongest influence on CR and SM forecasts; and (2) how long is such a dominance of ICs expected to last for? The answers to these two questions will provide us valuable insights on the spatial heterogeneity and temporal variations of the key factor affecting seasonal hydrological forecasts over China, consequently enabling us to identify the regions (forecast periods) where (when) improving one of these two factors can significantly enhance the forecast skill. This paper is structured as follows.
Section 2 introduces the data and methodology, including the model description, experiment design, and forecast assessment approach;
Section 3 and
Section 4 present the results and the relevant discussions, respectively; and the conclusions are summarized in the last section.
2. Materials and Methods
2.1. Model Description
The Variable Infiltration Capacity (VIC) hydrologic model [
32] is employed in this study. The VIC model is a macro-scale land surface hydrologic model, which solves both the water and surface energy balance in each grid cell and at each simulation time step. In this model, the saturation- and infiltration-excess runoff generation processes are both dynamically represented through the statistical parameterization of sub-grid spatial heterogeneity (e.g., land cover/vegetation types, soil water storage capacities) within each grid cell. In addition, the VIC is also prominent in depicting the nonlinear recession of baseflow through the ARNO model [
33]. Similar to most land surface models (LSMs), the VIC model has to be coupled with an independent routing model [
34] for the streamflow simulations at any specific location in the channel network. Since its development, this model has been well applied across a number of large river basins worldwide [
35,
36,
37].
The VIC model used in this study was effectively calibrated and validated against observations in China at a spatial resolution of 0.25° [
38], which has been well used in hydroclimatological studies [
39,
40,
41] and climate impact assessments over China [
42,
43]. Specifically, we firstly derived a set of 61-year (1952–2012) daily gridded (0.25° × 0.25°) meteorological data by interpolating ground station observations from the China Meteorological Administration (CMA) [hereafter referred to as the Institute of Geographic Science and Natural Resources Research (IGSNRR) data]. Driven with this high-quality IGSNRR data, VIC was run and calibrated against 20-year monthly observed streamflow records at 15 gauging stations over 11 major river basins of China. The Nash-Sutcliffe efficiency (
Ef) of VIC predictions and observations is above 0.65 and the relative errors (
Er) are less than 25% at all the 15 stations, except for two stations in the Tibetan Plateau. In addition, the simulated soil moisture was compared with observations at eight in-situ sites lying in Northeastern China (NE), central China (CENT), and northwestern China (NW), respectively. The comparison results show that the simulated soil moisture generally presents a compatible seasonal cycle and persistence with observations in NE and CENT, while in NW, the simulation performance is not satisfactory. These assessments suggest that the calibrated VIC model can overall successfully reproduce the observed hydrographs and provide reasonable estimates of land surface hydrological conditions. However, caution should be taken when using the results in western China where the hydrological simulations are subject to large uncertainties due to the sparse gauging network. More specific details of the model setup can be referred to in our previous study [
38].
2.2. Experimental Design
In this study, the ESP/
revESP diagnosis framework [
16] was adopted to partition the relative roles of ICs and CFs. Here, the six-month ESP and
revESP hindcasts are conducted, respectively, for each calendar month of 1980–2010. These two experiments are implemented at a daily time step over 15,775 grid cells with a spatial resolution of 0.25° over China. Specifically, three types of VIC-based numerical experiments are conducted.
Experiment 1 is a retrospective control simulation (CTRL), driven by daily IGSNRR meteorological forcing for 1952–2010. The simulated runoff and SM for the period of 1980–2010 are selected and treated as surrogate observations to assess the performance of ESP and revESP, respectively.
Experiment 2 is the six-month ESP hindcasts starting on the first day of each calendar month for each year from 1980 to 2010. Specifically, for each calendar month j (j = 1, 2,…, 11, 12) of the target year i (i = 1980, 1981,…, 2009, 2010), the VIC model is initialized at the beginning of month j with realistic initial hydrologic conditions produced by experiment 1 (CTRL), but forced by 30-member daily climate ensembles taken from 1980 to 2010 (with the target year i eliminated) for six-month forecasts. For instance, for the ESP hindcasts starting in April 1985, the forecast initial states on April 1 of 1985 are the same as those in experiment 1, while the 30-member daily climate sequences are those used in experiment 1 from April 1 to September 30 for each year of 1980–2010 (except for the target year 1985). Hence, this experiment includes 31 (years; 1980–2010) × 12 (months; January–December) = 372 sets of six-month ESP simulations, wherein each ESP implementation consists of 30 (ensembles; 1980–2010 without the target year) × 6 (months; forecast lead time) = 180 months of daily VIC runs. In sum, there are 31 × 12 × 30 × 6 = 66,960 months of model runs for each 0.25° × 0.25°grid cell across China.
Experiment 3 is the six-month revESP hindcasts parallel to experiment 2. For each calendar month j (j = 1, 2,…, 11, 12) of the target year i (i = 1980, 1981,…, 2009, 2010), this experiment is initialized on the first day of month j with 30-member (1980–2010 without the target year i) estimates of initial moisture conditions produced by experiment 1 on the same calendar date, but fed with six-month (from forecast start date out to six months) daily climate forcings of the target year i taken from experiment 1. For example, to implement the revESP simulation starting in April 1985, the initial hydrologic conditions estimated from experiment 1 on 1 April of each year during 1980–2010 (without the target year 1985) consist of the 30-member ensemble, and the April-September daily climate data in 1985 are directly taken from experiment 1 to serve as model forcings. Overall, the number of VIC runs in experiment 3 is identical to that in experiment 2, including 31 (years; 1980–2010) × 12 (months; January–December) × 30 (ensembles; 1980–2010 without the target year) × 6 months (forecast lead time) = 66,960 months of daily VIC simulations for each grid cell across China.
Here, the first two experiments (i.e., CTRL and ESP) share the same ICs on the forecast start date, while experiments 1 (CTRL) and 3 (revESP) share the same CFs during the forecast period. In this study, given our focus on six-month seasonal hydrological forecasts, the daily sequencing of events is considered less important than the aggregate quantities. Thus, the daily runoff and SM simulations are aggregated at a monthly scale for each experiment. Furthermore, for regional-scale analysis, the monthly cumulative runoff (CR) and SM are spatially averaged over 17 hydro-climatic homogeneous regions of China.
2.3. Forecast Assessment
In this study, we employed three skill metrics to separately assess and compare the deterministic and probabilistic quality of ESP and revESP forecasts against the corresponding observations.
2.3.1. Deterministic Metrics
The root mean square error (RMSE) of ESP and
revESP relative to the CTRL simulation is calculated, respectively, over the hindcast period (1980–2010). Specifically, for each calendar month
j (
j = 1, 2,…, 11, 12), their (i.e., ESP and
revESP) RMSE values with
t (
t = 1, 2,…, 5, 6) month lead are calculated as follows:
where
Y is the number of target years (i.e., 31; 1980–2010);
N is the number of ESP (or
revESP) ensemble members during 1980–2010 with the target year excluded (i.e., 30);
Fij(
t) is the CR (or SM) at lead time
t obtained from the ESP experiment with ICs of the target year
i and CFs of year
j, while
RFij(
t) is the CR (or SM) at lead time
t estimated from
revESP experiment with CFs of the target year
i and ICs of year
j; and
Oi(
t) represents the CR (or SM) generated by the CTRL experiment at lead time
t for the year
i.
The RMSE ratio, defined as RMSEESP/RMSErevESP, is calculated to quantify the relative influence of ICs and CFs for each grid cell and each of the 17 hydro-climatic regions. If the RMSE ratio is less than 1, then the knowledge of ICs dominates; while the signal of CFs is more important if the ratio value is larger than 1.
In addition, a non-dimensional parameter
κ [
15] is used to evaluate the influence of ICs variability on forecast skill. The
κ parameter is defined as the ratio of the standard deviation (SD) of ICs (i.e., the sum of SM and snow water equivalent (SWE)) at the forecast initialization date (
σic) divided by the SD of the cumulative precipitation during the entire forecast period (
σp). The
κ value is calculated based on the 31-year (1980–2010) off-line simulation (i.e., CTRL experiment) with a one- to six-month lead for each calendar month throughout the year (January–December). A
κ value greater than 1 indicates that the influence of ICs variability is stronger than precipitation, and vice versa.
2.3.2. Probabilistic Metric
A probabilistic metric Ranked Probability Score (RPS) [
44], defined as the sum of squared differences of the cumulative probability distribution between forecast members and observations, is employed to compare the probabilistic performance of ESP and
revESP forecasts. In this study, to calculate the RPS, we classify the CR and SM into three categories: low (<33rd percentile), normal, and high (>67th percentile), based on the climatological distributions for each calendar month from the gauge-based off-line simulations (i.e., Experiment 1). The RSP is given in Equation (3):
where
J is the number of categories (here
J = 3); and
y,
m, and
t indicate the calendar year (1980–2010), month (one–12), and forecast lead (one to six months), respectively.
Fj refers to the relative occurrence frequency of ensemble members in the corresponding category
j (
j = 1, 2, 3), defined as the number of forecast members falling into the
jth category divided by the total number (i.e., 30; 1980–2010 without the target year).
Oj represents the observation probability in the category
j, wherein
Oj equals one if the observed data fall into the
jth category and zero otherwise.
Furthermore, we derived the mean RPS over the hindcast period with Equation (4):
where
N is the number of calendar years during the hindcast period (
N = 31). The meanings of
m and
t are the same as in Equation (3).
On this basis, the mean RPS ratio, defined as , is introduced to compare the probabilistic quality of ESP against the revESP for each calendar month and forecast lead. An RPS ratio of less than 1 indicates that ESP is more skillful than revESP, while the superiority of revESP (relative to ESP) is represented by an RPS ratio above 1. If the ratio equals 1, it indicates that these two experiments (ESP and revESP) are comparable.
3. Results
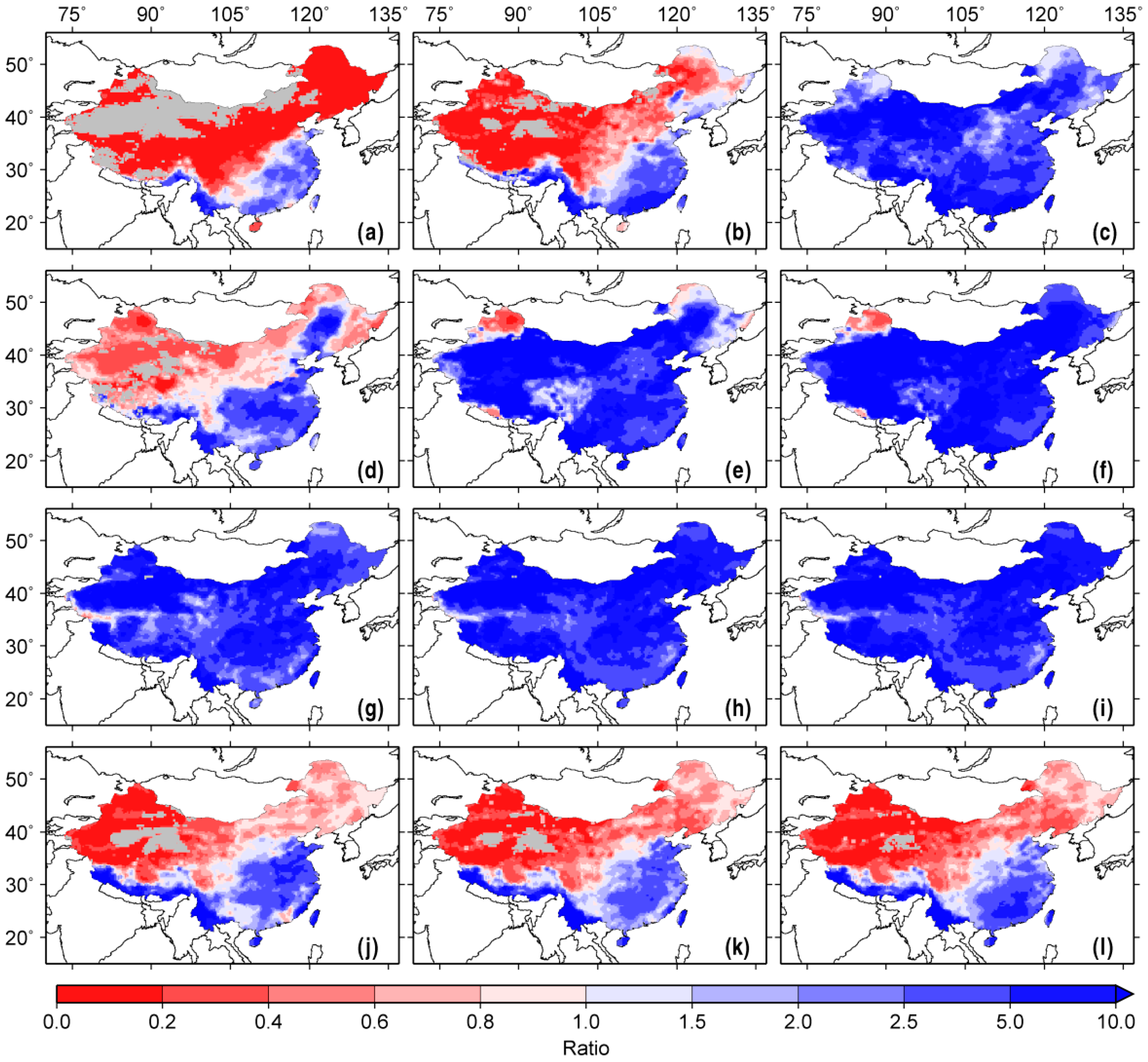
Figure 2 shows the spatial distribution of the RMSE ratio for CR forecasts staring in January, April, July, and October with a one-, three-, and six-month lead. Here, these four initial forecast months fall into dry, dry-to-wet, wet, and wet-to-dry periods, respectively. The result shows the metric scores are characterized with clear spatiotemporal variability. Specifically, the RMSE ratio for January forecasts is less than 1 over northern and western inland China at both one- and three-month leads, suggesting that the first three months (January–March) of CR forecasts are primarily controlled by the antecedent hydrological state in arid and semi-arid regions. As the lead time extends to six months, the climate information during the following forecast period becomes more important (RMSE ratio > 1) across the total domain of China. For the forecasts starting in April, the strong influence of initial moisture storage primarily lies in the first month (April) forecasts over the western inland regions; thereafter, such influence gradually weakens over most of the country except for some snow-dominant regions lying in part of Northwest and Northeast China. This implies that the snowpack could affect the generation of streamflow for up to three to six months over those snow-covered mountainous regions during the melting season. As the initial month entering into summer (July), the ratio increases to >5 over the whole country, regardless of lead times, suggesting that the rainy season CR forecasts mostly rely on the quality of the future climate information. When it comes to October, the initial moisture storage is implied as the dominant source of CR predictability for most of northern China, but the predictive skill over the southeastern part of China primarily comes from the climate forecasts. Overall, the ICs are expected to have the strongest influence on one-month CR forecasts for a dry climate regime which mainly covers the northern portion of China (particularly the western inland regions). Such effects are especially evident during the transition from wet to dry or over the snow-covered regions with three-month or even six-month persistence.
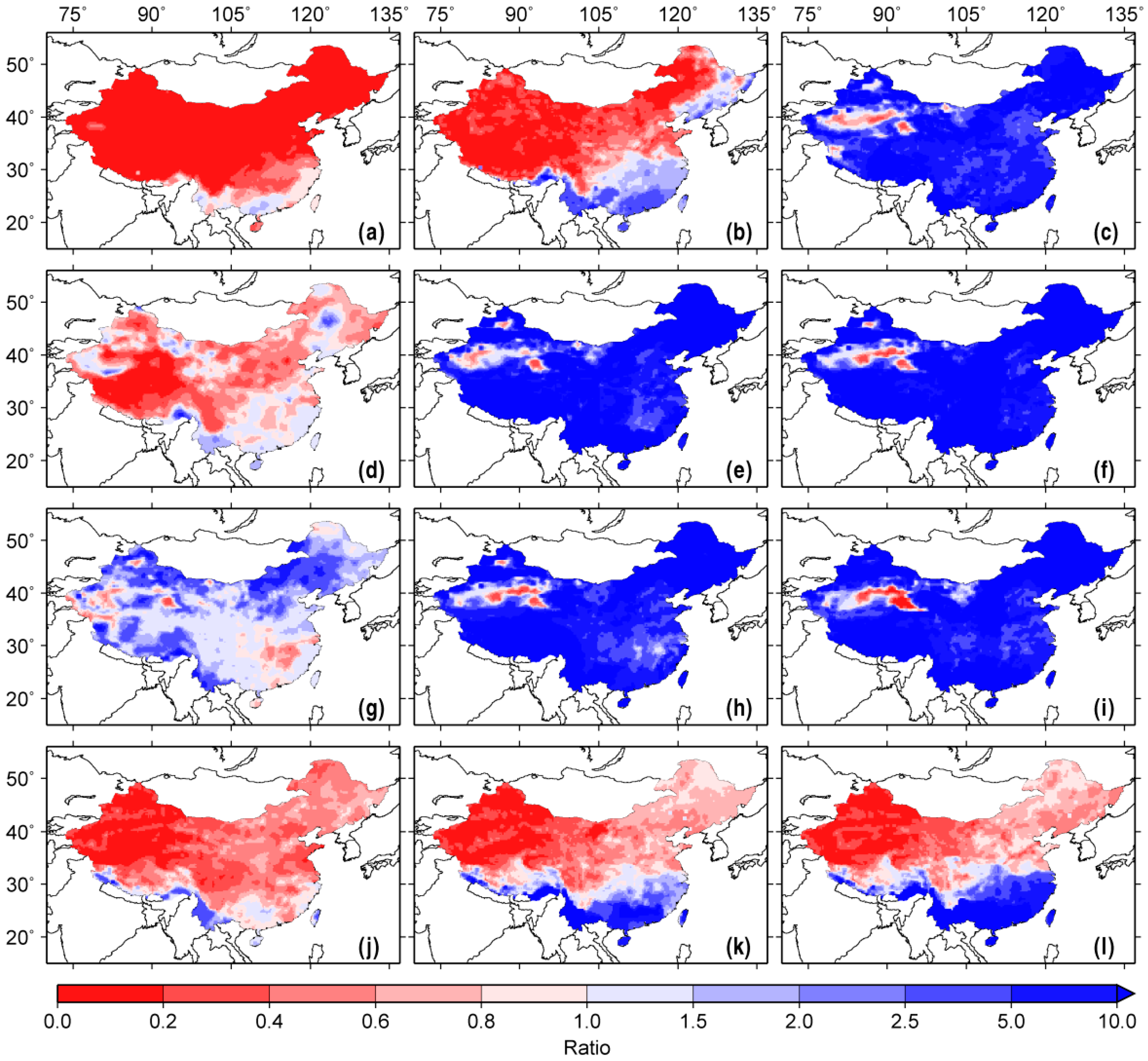
Figure 3 shows the spatial distribution of the RMSE ratio for SM forecasts. Generally, the SM forecasts initialized on the first day of January show RMSE ratios of less than 0.2 over the whole country in January and over most of the northern regions during January-March, indicating the dominance of the initial moisture storage on the January SM forecast for the first month over China and even for up to the first three months over the arid and semi-arid regions. In contrast, the unknown future climate mostly determines July forecasts (RMSE ratio > 1) over most of the country. That is, skillful forecasts of future climate are more crucial for reliable SM predictions during the rainy summer season. Notably, there is a clear difference between the SM forecasts starting in April (dry-to-wet transition) and October (wet-to-dry transition). In April, only the one-month forecasts have a stronger influence of initial hydrologic states over the northern half (North China and western inland China), whereas over the dry regions, the dominance of initial hydrologic conditions can last for up to six months (October–March) during the reverse (from wet to dry) transition (October). Moreover, given the inherent memory of SM, the influence of ICs on SM forecasts seems to cover larger domains and last for longer lead times than on CR forecasts.
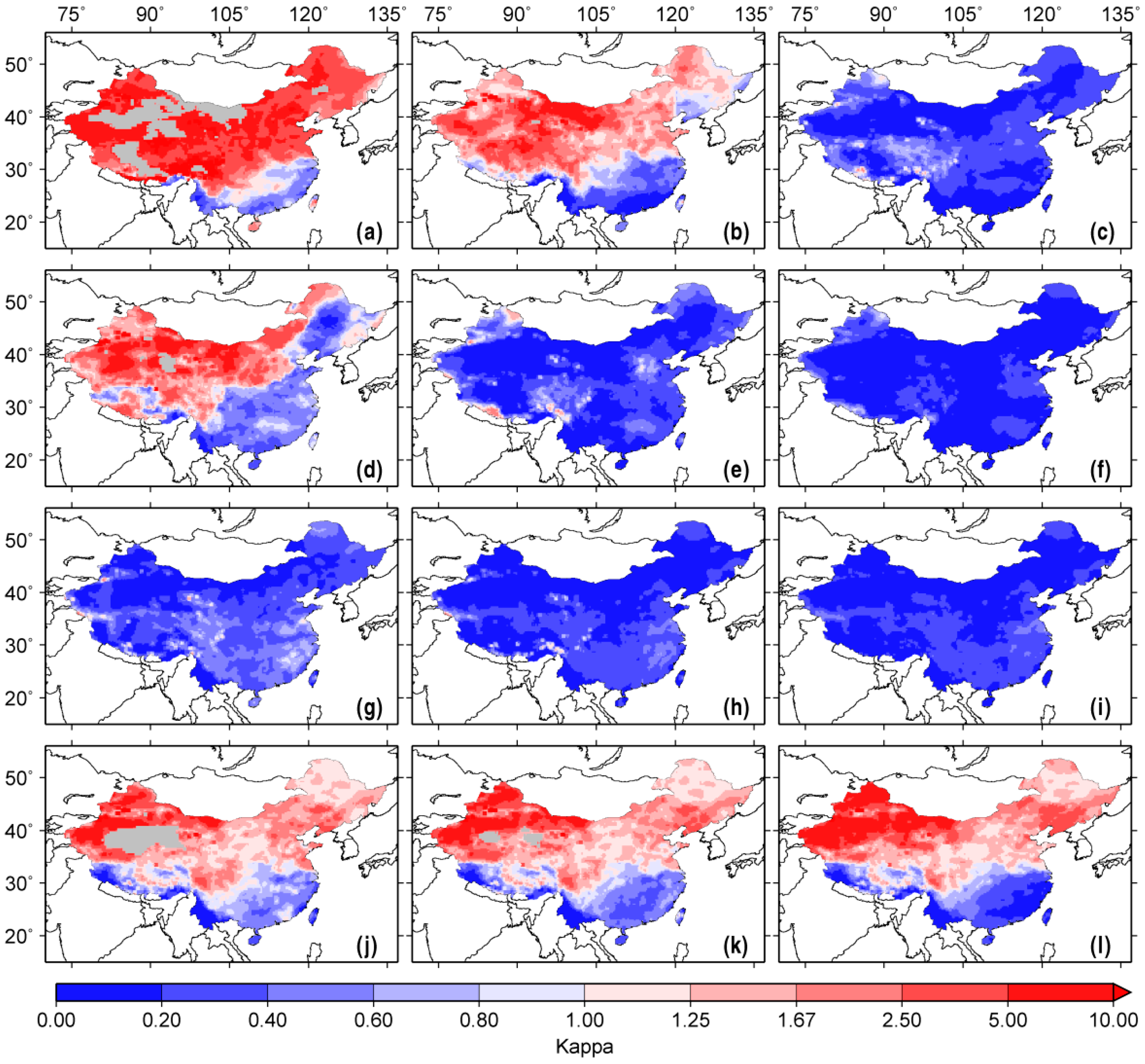
Figure 4 shows the spatial variability of the kappa parameter (
κ) at a one-, three-, and six-month lead for the forecasts starting in January, April, July, and October, respectively. The variability of total moisture storage (the sum of SM and SWE) is generally higher than precipitation variability (
κ > 1) over a large portion of China for the first three months (January–March) in January and for up to six months (October–March) in October. Also, a
κ value greater than 1 is found in April but only for the first month (April) in Northwest China. Aside from these regions and months, the variability in precipitation appears to prevail over the initial moisture variability. For example, the
κ value falls into the <0.6 category at all lead times for July forecasts. Comparing
Figure 2 (or
Figure 3) with
Figure 4 indicates that the spatial pattern of
κ bears an overall resemblance to the inverse RMSE ratio, which is in line with previous findings in the U.S. [
18].
From a regional perspective, we calculated the RMSE ratio as a function of lead time (one to six months) and calendar month (January–December) for each of the 17 hydro-climatic regions (see
Figure 5). As expected, the magnitude of the RMSE ratio varies significantly among these regions and exhibits a strong dependence on the forecast periods. Specifically, the RMSE is found to be less than 1 over 10 regions (i.e., regions 1–10 in
Figure 5) for one-month forecasts starting in late fall to early summer months (October–April), suggesting the ICs exhibit a larger contribution to CR forecast skill than CFs over these dry regions and during the dry season. For those months (October–February) followed by a dry period, the knowledge of initial hydrologic conditions accumulated from the precedent wet season (summer and early fall) will propagate and significantly control the forecast skill for up to three to six months, suggesting that the evolution of drought occurring in this period can be predicted through the ESP approach. Notably, the RMSE of ESP simulations is larger than that of
revESP simulations (i.e., RMSE ratio > 1) for summer months (June–September), implying that the runoff generation mainly depends on the precipitation during wet seasons. Another interesting point is that the RMSE ratios derived from dry ICs during winter and spring are sensitive to lead times of interest and such sensitivity is higher than that initialized from wet ICs in summer months. For the remaining seven regions with either a humid continental climate (Huai River, Southwest River I) or humid subtropical climate (Southwest River II, Middle Yangtze River, Lower Yangtze River, Pearl River, and Southeast River), a ubiquitous RMSE ratio beyond 1 is found for all calendar months, suggesting that the impact of initial moisture storage on CR forecasts is negligible over the humid regions throughout the year. Overall, the above analyses imply that the first one- or three-month CR forecasts substantially benefit from the refined ICs over the arid and semi-arid regions (northern and western inland portions of China) during the dry season, while improving climate forecast models is the most efficient way to boost CR forecast skill during wet seasons or over those humid regions in South China.
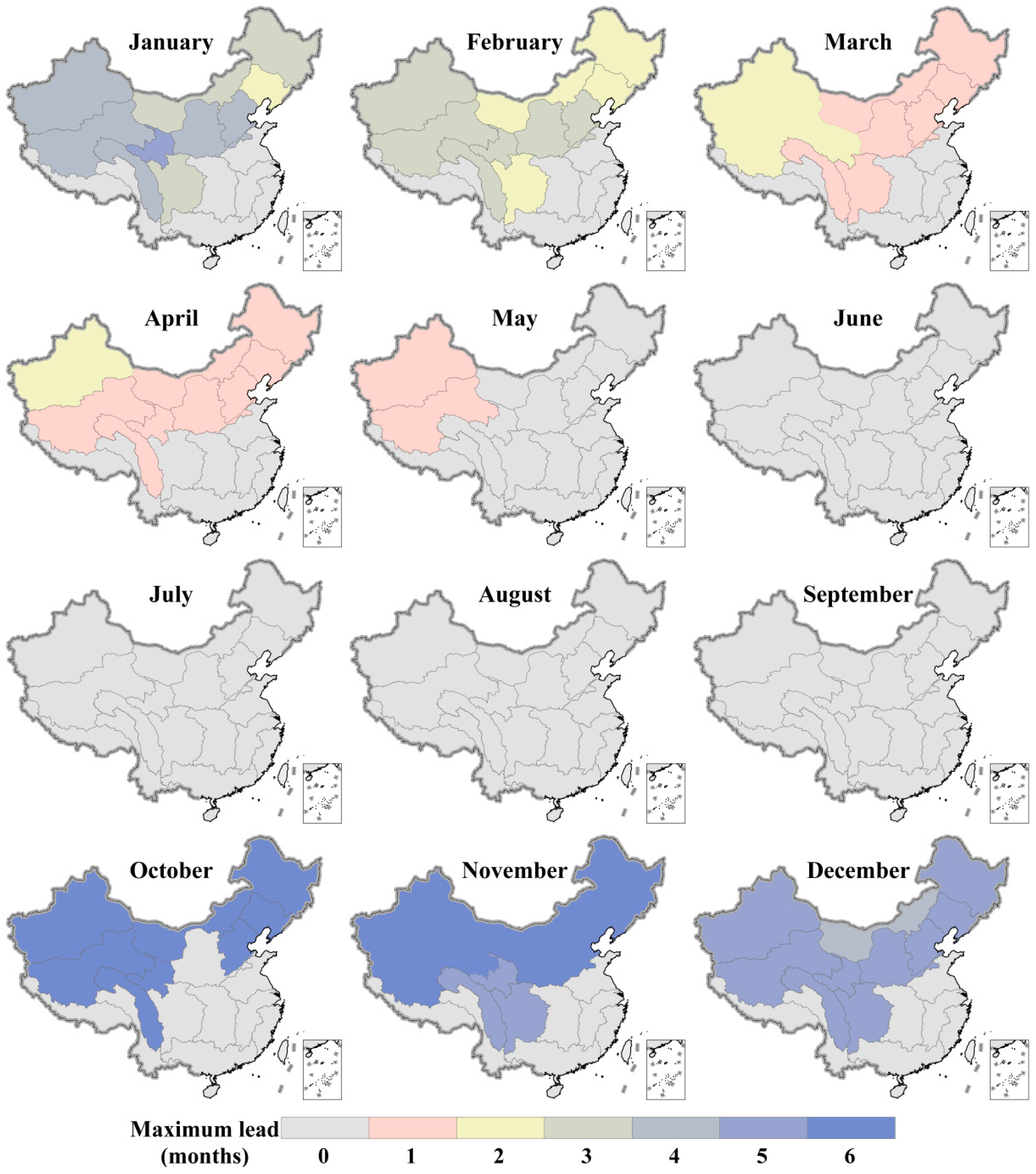
Figure 6 shows the maximum lead time (MLT; months) when the RMSE ratio is less than 1 over the 17 hydro-climatic regions. Obviously, the magnitude of MLT shows a strong dependence on calendar months and study regions. A positive MLT is found in northern and western inland regions during the dry period (October–May). Specifically, the MLT is around four to six months for October–January, decreases to around two to three months for February, and subsequently drops to one month for the spring months (March–May). In general, the MLT over the northwestern mountainous region (i.e., Inland River III) is one-month longer than other regions during the spring months (two-month versus one-month for March–April, and one-month versus zero-month for May). As for the summer initial months (June–September), zero MLT is observed for CR forecasts across all hydro-climatic regions in China. This suggests that the quality of external climate forcings predominantly determines the forecast performance, independent of regions and forecast periods.
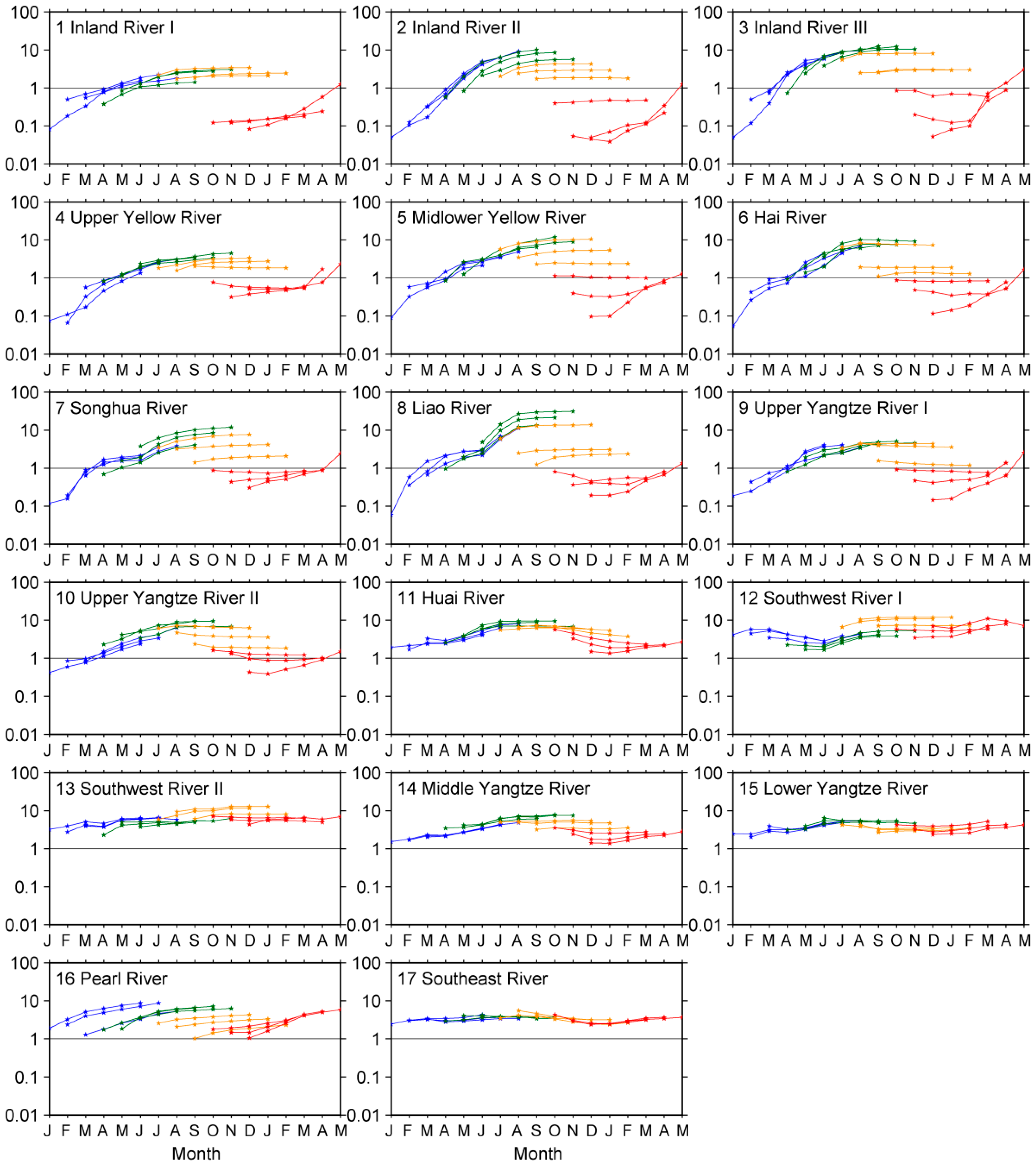
Figure 7 shows the RMSE ratio of SM forecasts with a one- to six-month lead for each calendar month and each hydro-climatic region in China. Generally, the SM forecasts present an RMSE ratio below or near the critical value (i.e., 1) at a one-month lead for almost all calendar months, suggesting that the prior moisture storage contributes most to the one-month SM forecast skill over the whole country, while beyond one month such, the dominant contribution dramatically decays over the humid regions of southern and southeastern China. However, over the northern and northwestern dry regions, the initial hydrologic conditions are expected to still strongly impact SM forecasts for longer lead times (three-month), particularly when the forecasts are initialized in dry (November–March) or wet-to-dry transition (October) months. In addition, in line with the previous findings [
24], the summer RMSE ratio (June–August; orange lines) tends to converge at a specific value with increased lead times over the regions with strong seasonality in hydro-climate. This suggests that wet ICs will largely benefit the prediction of drought development and duration occurring at the end of the wet season.
Figure 8 shows the basin-scale MLT during which the RMSE ratio is less than 1 for monthly SM forecasts. The MLT is found with one-month for almost all hydro-climatic regions and all seasons except for summer. For those SM forecasts starting in summer months (June–August), there are only two regions in the Yangtze River basin (i.e., Middle Yangtze River and Lower Yangtze River) exhibiting a positive (one-month) MLT. Overall, the SM forecasts present a general correspondence with CR forecasts with respect to the spatiotemporal variability of MLT. For instance, they (SM and CR forecasts) both show that antecedent moisture storage significantly controls SM prediction skill for up to three months over the northern and western inland regions during the climatologically dry period (October–January).
In addition to the deterministic metric RMSE, we also introduce a probabilistic metric RPS ratio to evaluate and compare the probabilistic quality of ESP and
revESP.
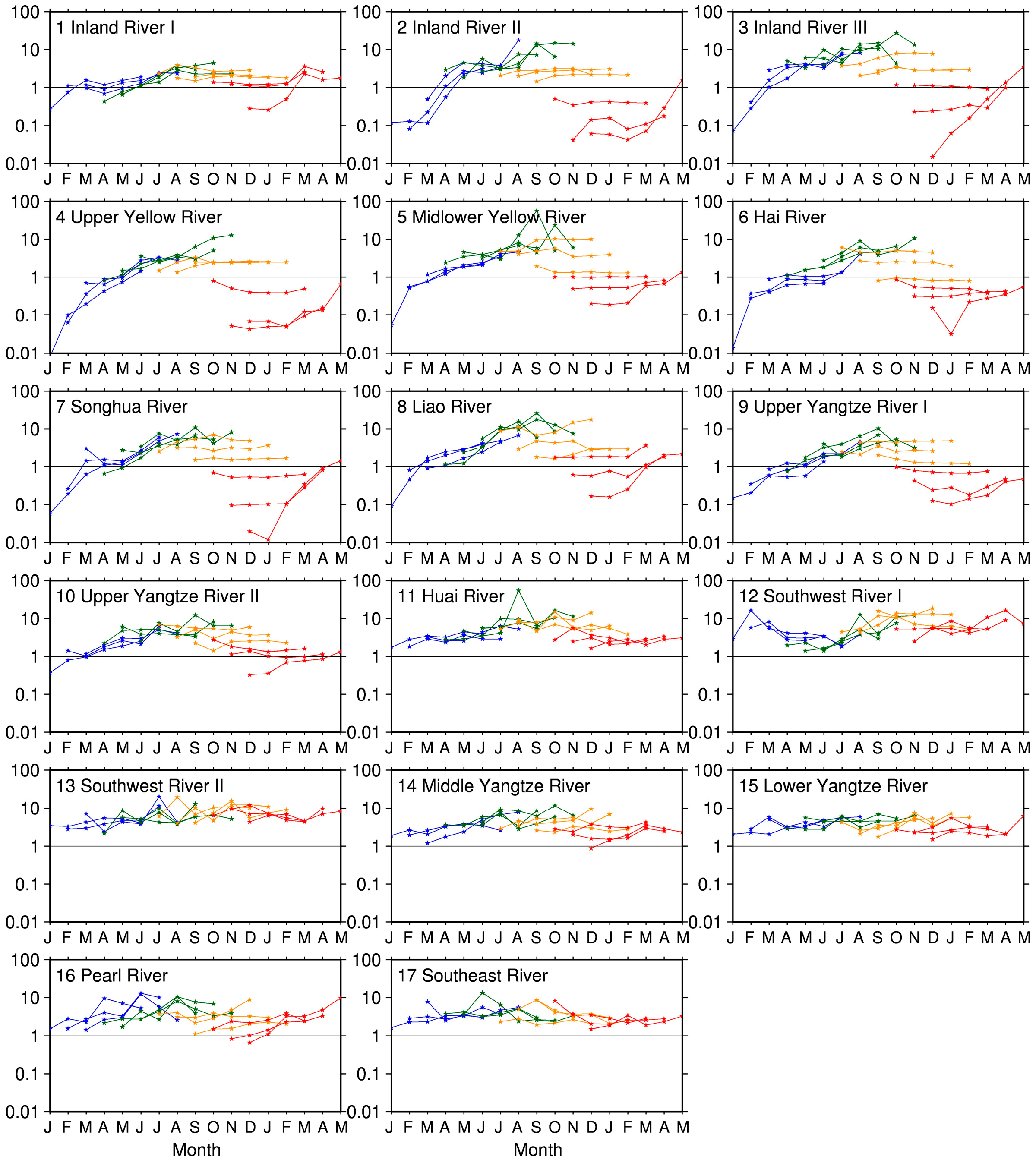
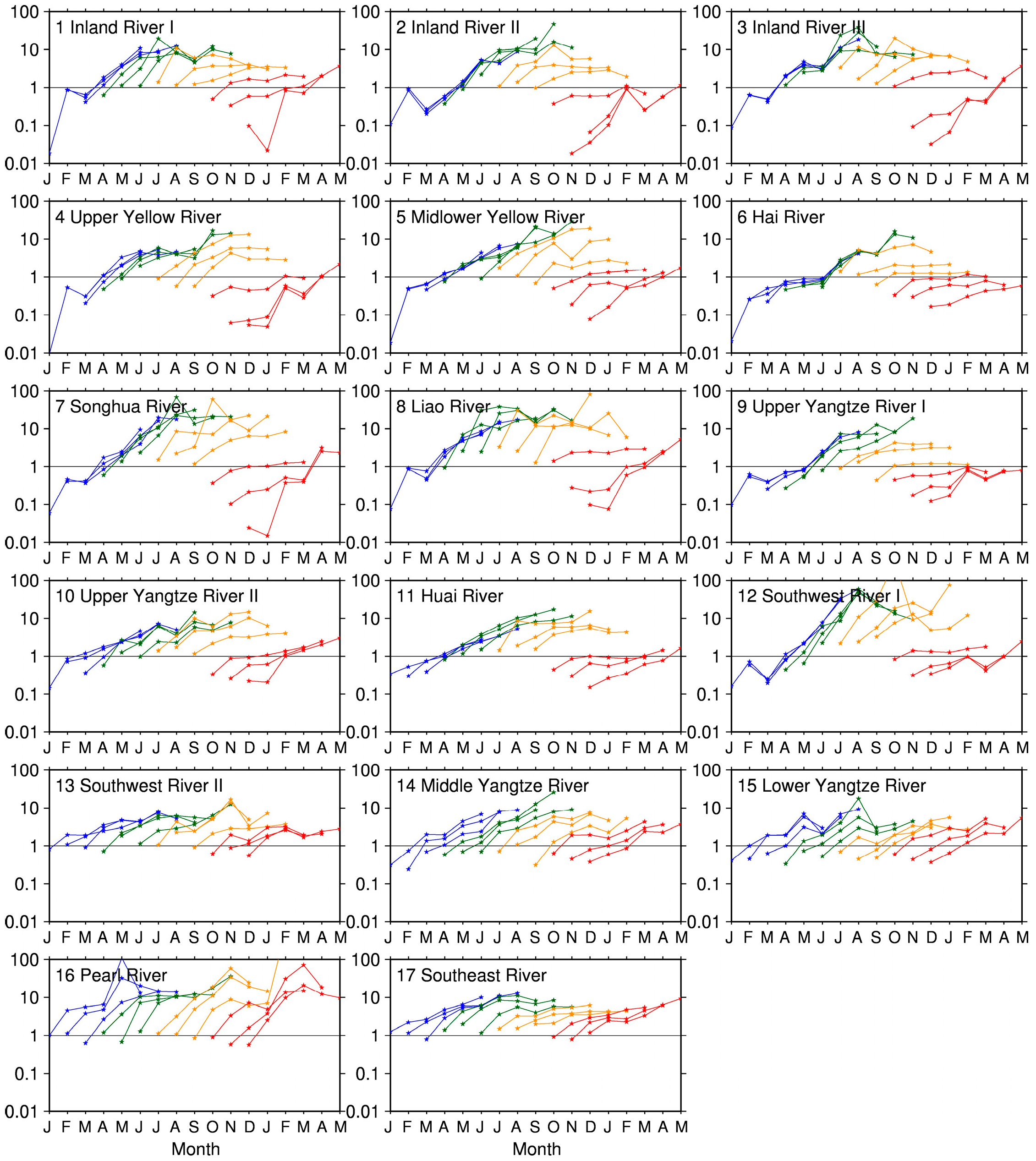
Figure 9 and
Figure 10 show the RPS ratio of six-month CR and SM forecasts, respectively, throughout a year over the 17 hydro-climatic regions. Overall, the spatiotemporal variations of the RPS ratio bear an overall resemblance to those of the RMSE ratio. In terms of CR, the ESP forecasts are more skillful than
revESP forecasts (with RPS ratio < 1) during the dry season (October–April) over the northern 10 regions (regions 1–10), suggesting the leading role of ICs in CR forecasts. Over these regions, the dominance of ICs mostly lies in the first three months, but in some cases (i.e., the forecast initial month from September to November), over three months. Over the other seven humid regions (regions 11–17), the performance of
revESP seems better than ESP (RPS ratio > 1), independent of seasons and lead times, suggesting that skillful forecasts of the future climate can substantially benefit CR forecasts over these regions. When it comes to SM (
Figure 10), almost all the 17 regions have an RPS ratio of less than 1 for the first month, suggesting the effectiveness of ESP in one-month SM forecasts over China. Beyond one month, the difference of ESP and
revESP exhibits obvious spatial heterogeneity. That is, over the northern regions, the ESP still has a significant advantage over
revESP in three-month or even six-month forecasts during the dry season, while the superiority of ESP becomes negligible and inversely the
revESP gains more skills over most southern regions (regions 13–17). Overall, these results are in line with those implied by the deterministic RMSE ratio (see
Figure 5 and
Figure 7), and further confirmed our findings on the relative roles of forecast initialization and forecast forcings.
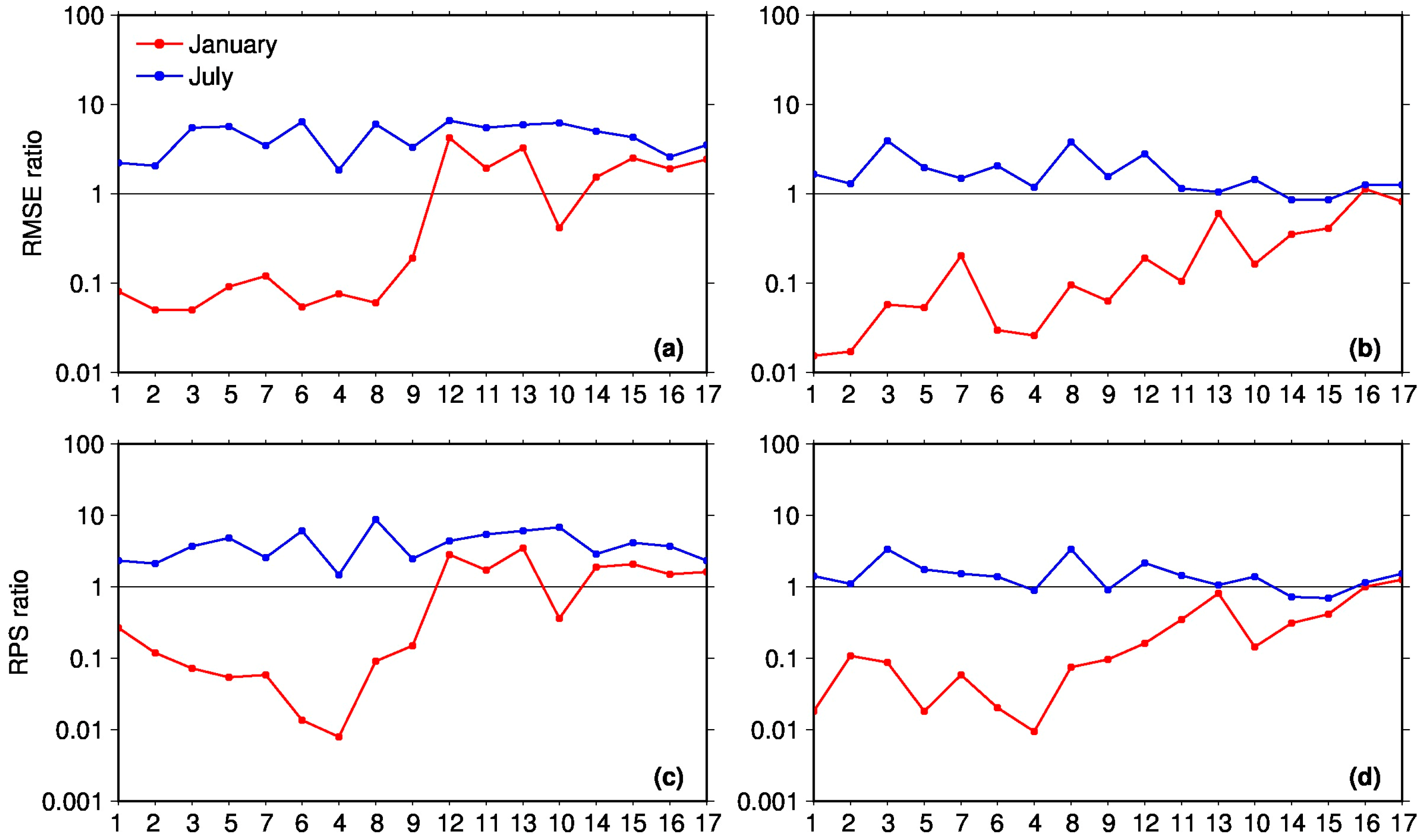
Figure 11 shows the variations of the RMSE ratio and RPS ratio for one-month CR (
Figure 11a,c) and SM (
Figure 11b,d) forecasts with the increases in regional precipitation over 17 hydro-climatic regions (i.e., from dry to wet). That is, the 17 regions and the corresponding metric scores (RMSE ratio and RPS ratio) are sorted in sequence by the increased climatological (1980–2010) mean precipitation (Inland River I < Inland River II < Inland River III < Middle and lower Yellow River < Songhua River < Hai River < Upper Yellow River < Liao River < Upper Yangtze River I < Southwest River I < Huai River < Southwest River II < Upper Yangtze River II < Middle Yangtze River < Lower Yangtze River < Pearl River < Southeast River). Here, the dry January (red line) and wet July (blue line) are chosen as the representative forecast initial months. As regions becoming wet from dry (i.e., with increases in regional precipitation), the corresponding deterministic (RMSE ratio) and probabilistic (RPS ratio) values of January CR forecasts consistently increase from less than 1 to greater than 1. Specifically, the metrics are found below 1 over the first nine relatively dry regions where the regional precipitation is less than 700 mm; whereas, they gradually increase to over 1 with increased regional precipitation. This clearly suggests that ICs have a stronger influence in drier regions, while wetter regions are more prone to CFs’ influence. Consistent with CR forecasts, the skill scores of January SM forecasts, although with values of less than 1, also present an obvious upward trend with increased precipitation. That means that wetter regions tend to have a larger ratio value than drier regions, suggesting that the contribution of ICs in dry regions is usually greater than in wet regions. When it comes to wet season forecasts, the metric scores, either for CR or SM forecasts, is relatively stable with a value greater than or around 1. The negligible sensitivity of skill scores on precipitation variation suggests that the wet season forecasts mostly rely on the CFs for any hydro-climatic regions of China. These analyses provide strong evidence for the statement that colder and drier regions (or seasons) are expected to have a stronger influence of ICs, while wetter and warmer regions (or seasons) are more prone to CFs.
4. Discussion
With the ideal ESP/revESP diagnosis framework, this study identified the key factor that contributes most to CR and SM forecast skill over any specific regions across China and for any particular forecast periods within the year. Generally, it is found that the forecasts (either for CR or for SM) initialized in the dry or wet-to-dry transition period tend to have a strong and long-lead influence of ICs, presumably due to the limited precipitation and reduced activity of soil moisture during the cold season. Additionally, the long memory of antecedent moisture storage is also found in spring months (e.g., April) over the northwestern mountainous region. This may result from the positive contribution of melting snowpack to streamflow. In contrast, the information of CFs seems more critical for the summer hydrological forecasts or across most of southern China. However, it should be noted that in summer months, the antecedent hydrologic conditions still contribute to one-month SM forecasts over the Middle Yangtze River and Lower Yangtze River, which may be attributed to the dry climate regime induced by below-normal rainfalls during this period. These will guide targeted efforts toward improving the seasonal hydrological forecast skill to the greatest extent. For instance, for the regions and time periods with the dominance of ICs, efforts should be devoted to assimilating ground-/satellite remote sensing-based data with model estimates; otherwise improving SM or CR forecast skill has to await further advances in seasonal climate models.
Despite the valuable insights provided in this study, several limitations should be acknowledged when explaining the results. On one hand, the gauge-based VIC off-line simulation is treated as surrogate observations to assess the performance of ESP and
revESP hindcasts, without considering the uncertainty of the model its-self structure. Considerable uncertainties have been demonstrated in model simulations over western China due to the low-density gauging network, and thus the results over these regions should be used with caution. In addition, the ESP/
revESP diagnosis framework only focuses on two end points that reflect zero (i.e., directly taken from observational data) and perfect information (i.e., the ensemble taken from the full climatological period) of CFs and ICs, which prevents a comprehensive understanding of their relative roles at varying levels of uncertainty. What’s more, the initial moisture storage only includes two primary state variables (SM and SWE), without consideration of other water storage components (e.g., surface water, groundwater), which could be important for one-month seasonal streamflow predictions in downstream regions [
19,
24]. This implies that more detailed components of initial storage, rather than the general SM and SWE, should be considered in future assessments.
5. Conclusions
ICs and CFs are the primary two factors governing the performance of seasonal hydrological forecasts. In this study, we investigated their relative roles in CR and SM forecasts under a consistent ESP/revESP diagnosis framework across different hydro-climatic regions of China. Specifically, the six-month ESP and revESP hindcast experiments were conducted with the VIC hydrological model at a 0.25° spatial resolution for each calendar month (January–December) during 1980–2010. In sum, 66,960 months of daily VIC runs over 15,775 grid cells over China for ESP and revESP simulations were presented, respectively. To find out the key influencing factor on seasonal hydrological forecasts, we employed three skill metrics, i.e., the RMSE ratio (RMSEESP/RMSErevESP), κ parameter, and RPS ratio (), to effectively compare the overall performance of ESP and revESP, in terms of the deterministic and probabilistic quality.
The results show that the spatiotemporal variations of the RMSE ratio (deterministic skill score) and RPS ratio (probabilistic skill score) bear an overall resemblance. That is, the knowledge of ICs dominates CR forecast skill in a dry or wet-to-dry transition climate regime that covers the northern and western inland regions during the late fall to early summer. Specifically, the strong influence of ICs can last for one month, three months, and four to six months, respectively, as the forecasts are initialized in spring (March–May), winter (December–February), and late fall (October and November). Here, the large (beyond three months) magnitude of MLT (i.e., the period with RMSE below 1) in winter and late fall months is mostly because the precipitation amount and variability are too low to destroy the prior moisture storage during the dry period. Also, the long-memory of antecedent hydrologic conditions is also found in spring months (March–May), but only over a small portion of snow-dominant regions in Northwest and Northeast China. In contrast, the role of CFs seems more important for a wet climate regime that dominates Southeast China for all seasons or covers North China for summer months (June–September). These findings provide evidence that enhancing the CR forecast skill mostly relies on improving model initialization for those regions and seasons characterized by a dry climate regime, whereas advancing seasonal climate forecasts (e.g., precipitation forecasts) can substantially benefit the CR forecasts in wet regimes.
As for the SM forecasts, the initial hydrologic conditions contribute most to the one-month predictive skill across the whole country for all seasons excluding summer (June–August). Particularly, the strong impact of ICs is expected to extend to three months and in some cases six months for late fall and winter months and over northern China (e.g., Inland River III). Apart from these regions and forecast periods, CFs become the primary source of SM predictability. Furthermore, the contribution of forecast initial conditions to SM prediction tends to cover more extensive regions and last for longer lead times than CR prediction over China, which is mostly attributed to the inherent memory of soil moisture. As the regions become wet from dry (i.e., with increases in regional precipitation), the corresponding metric scores (RMSE ratio and RPS ratio) for January forecasts consistently increase from less than 1 to greater than 1, whereas the ratios of July forecasts seem less sensitive to the variation of precipitation, providing strong evidence for the statement that colder and drier regions (or seasons) tend to exhibit a stronger influence of ICs and wetter and warmer regions (or seasons) are more prone to CFs.
Our work is unique in employing a consistent diagnosis framework to identify the dominant factor that strongly controls the seasonal hydrological forecast skill for any given region, season, and forecast lead across China. The results will contribute to efforts to substantially improve current forecast levels, and thus will largely facilitate the future development of an operational real-time seasonal hydrological prediction system across China.