Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan
Abstract
:1. Introduction
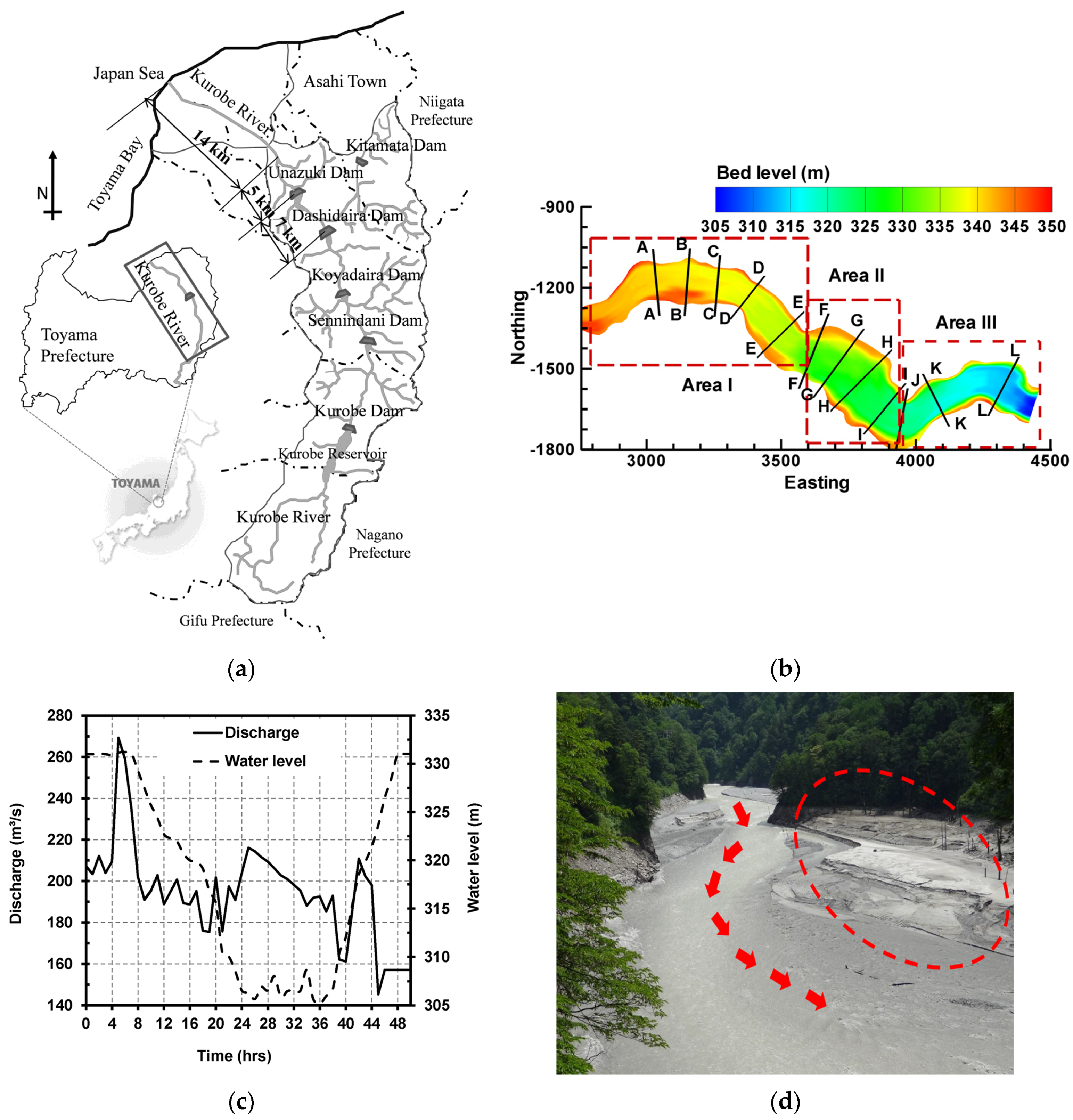
2. Study Case Description
2.1. Site Background
2.2. Field Data Organization
3. Numerical Model
3.1. Flow Field Modeling
3.2. Sediment Transport Modeling
4. Numerical Simulations
4.1. Model Setup and Calibration
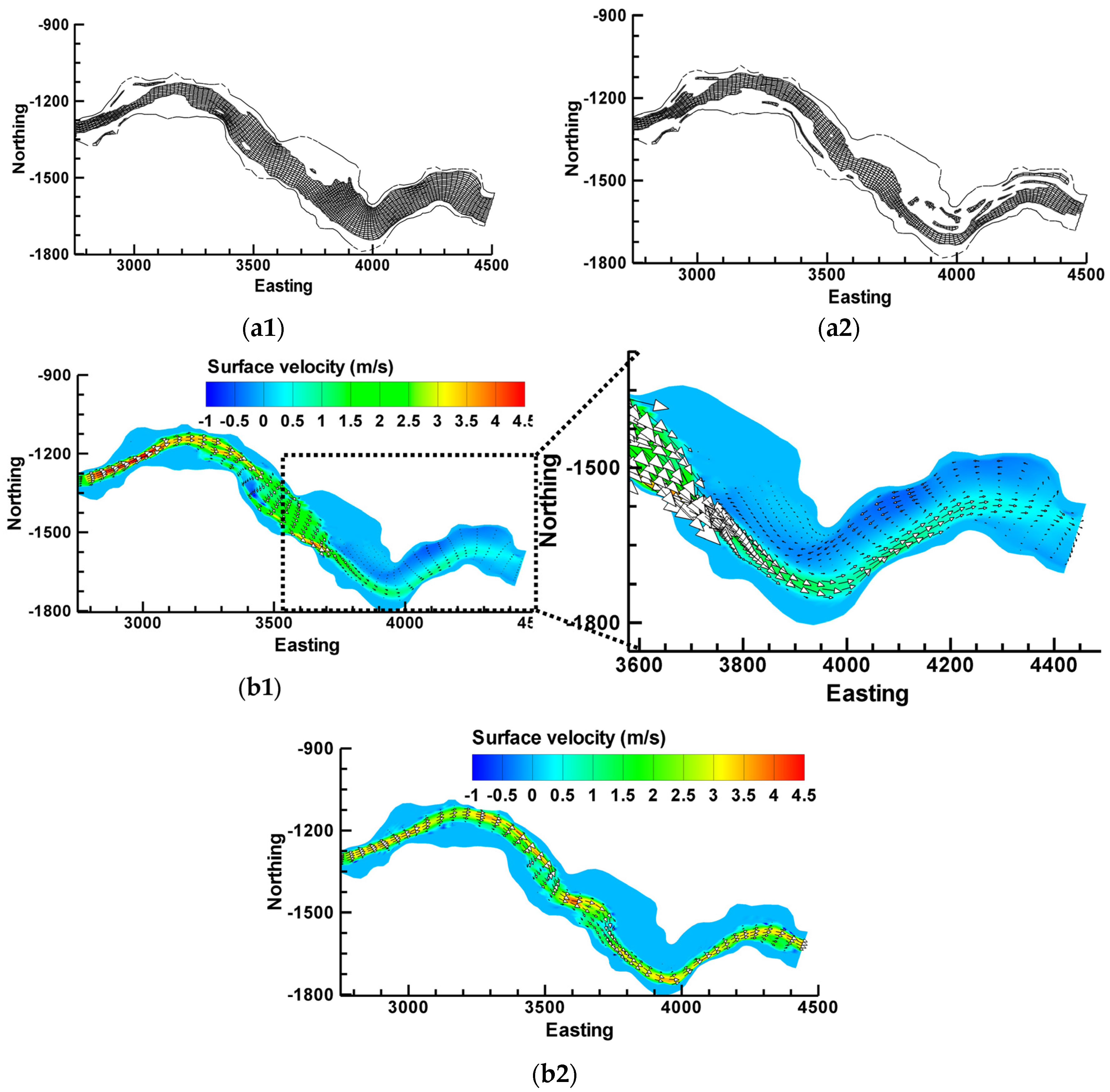
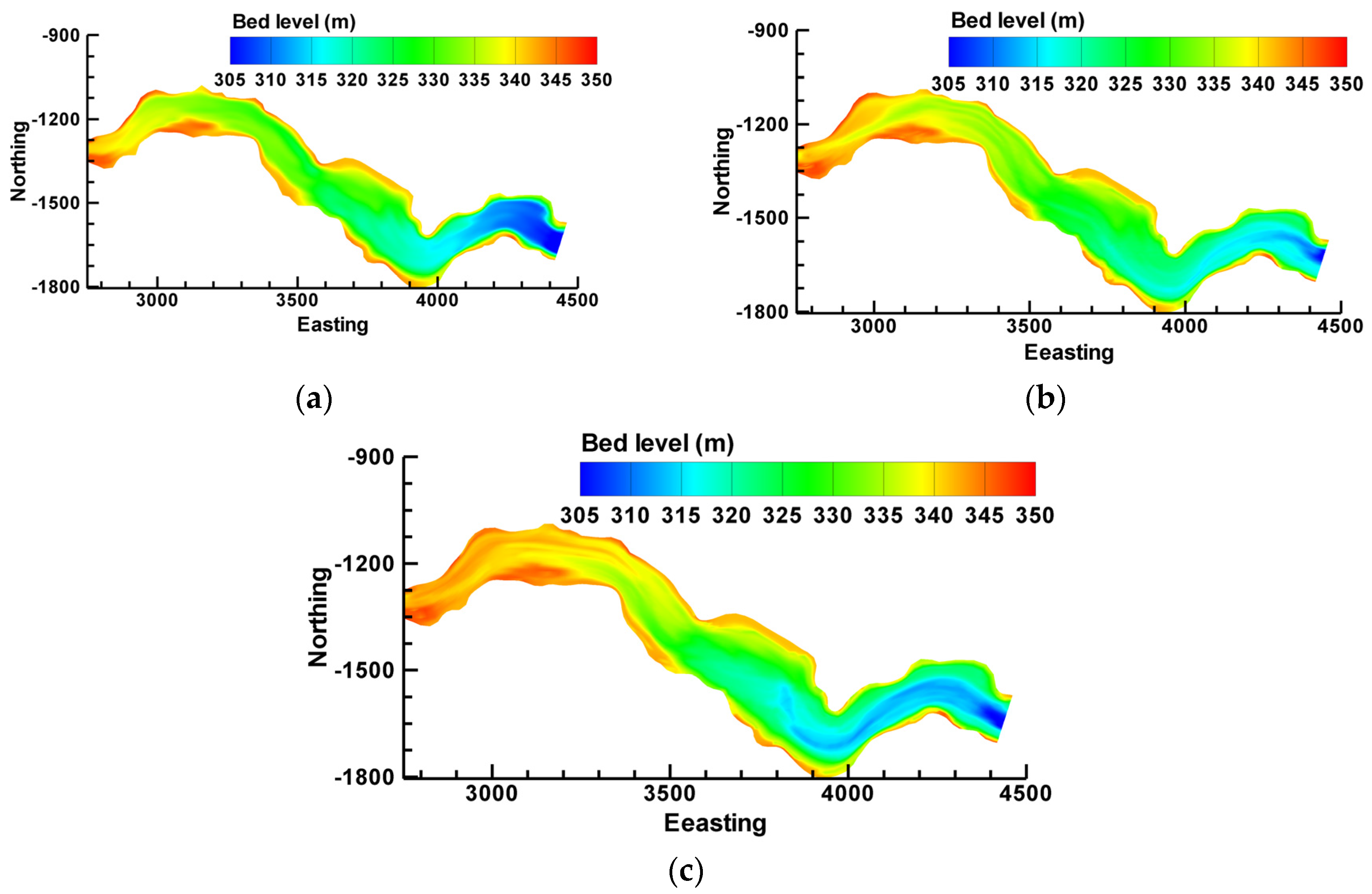
4.2. Evaluation of the Flow Field and Morphological Bed Changes in the Reservoir
5. Discussion
5.1. Hydrodynamic Scenarios and Their Impacts on the Bed Morphology and Flushing Efficiency
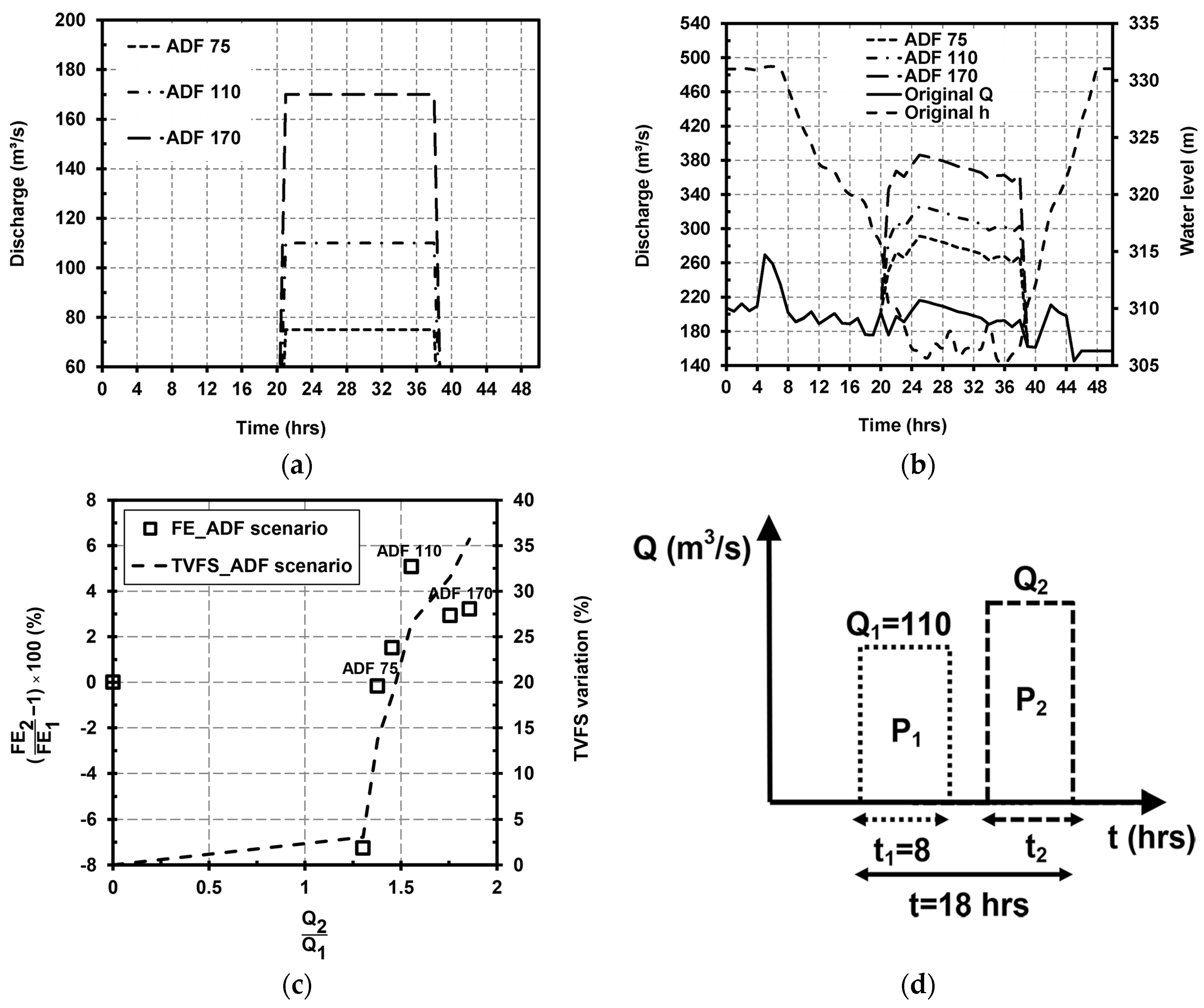
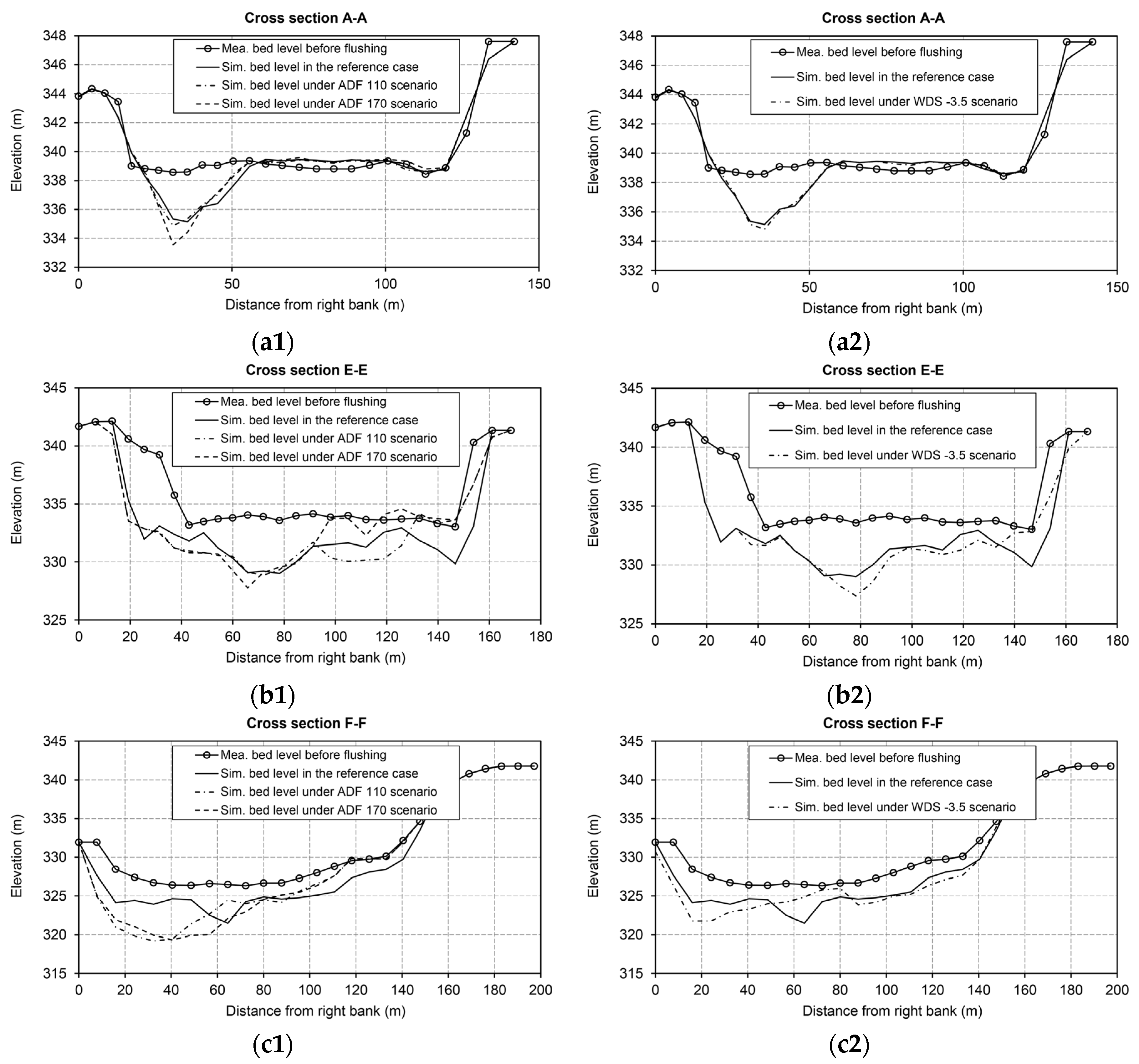
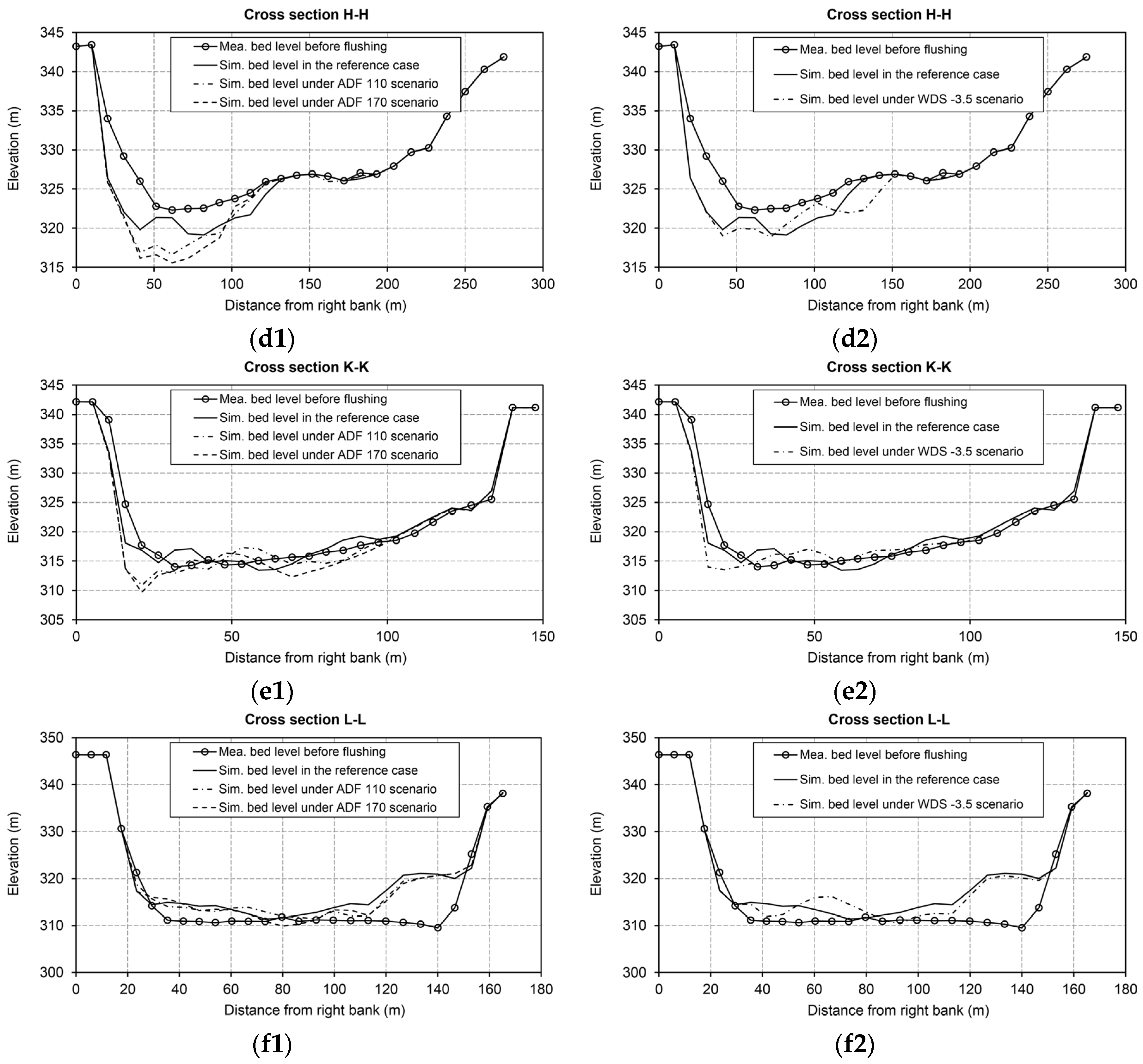
5.1.1. Discharge Scenarios
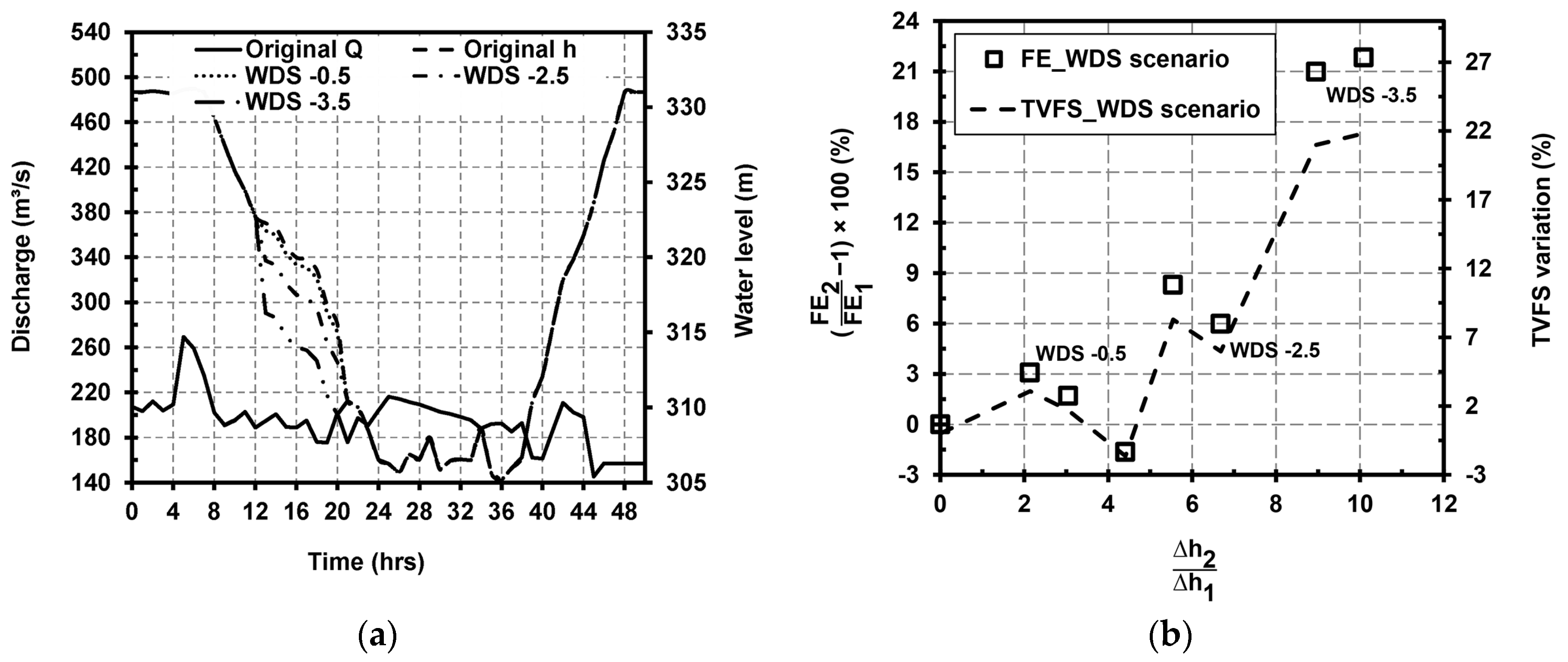
5.1.2. Water Level Scenarios
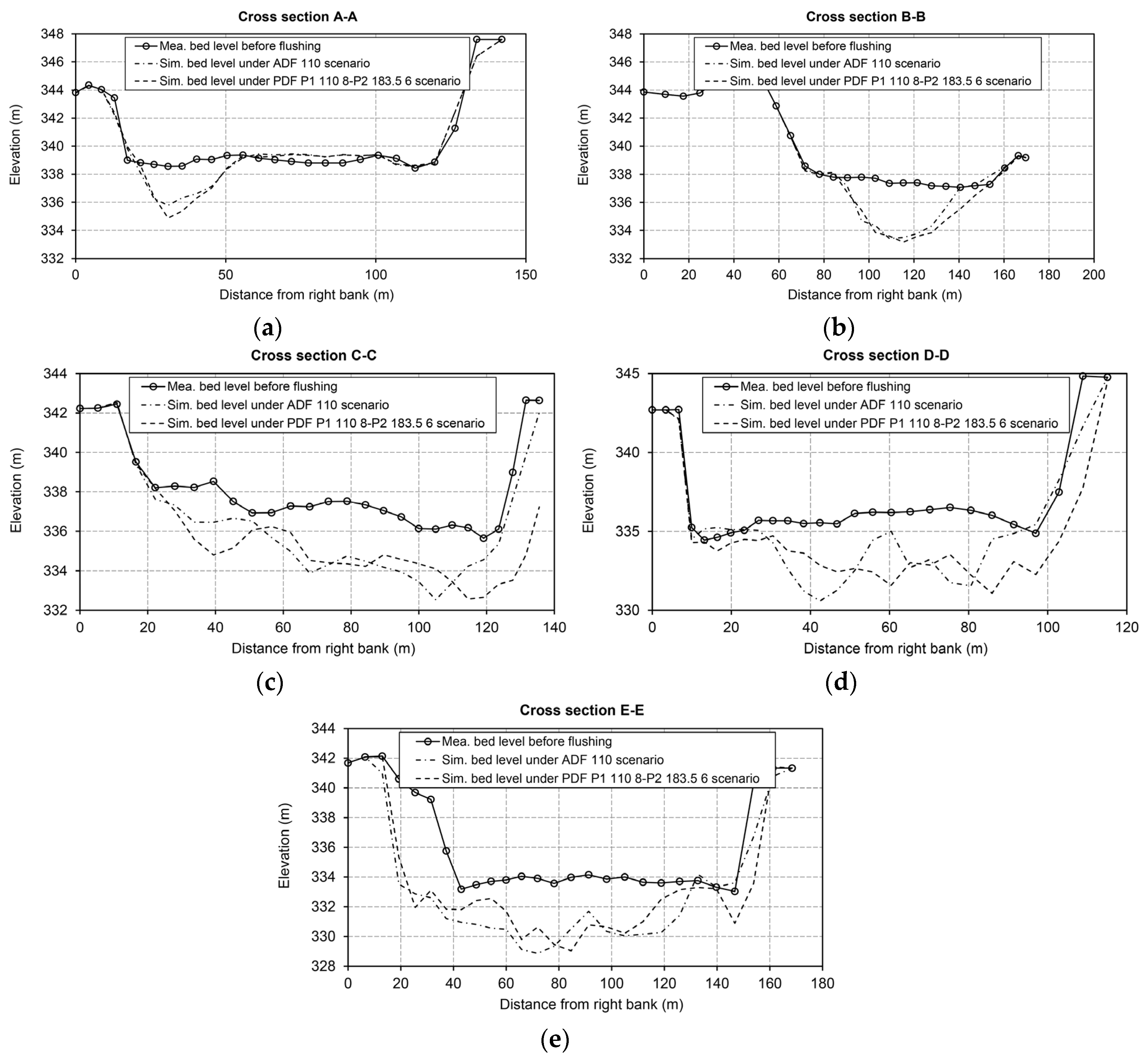
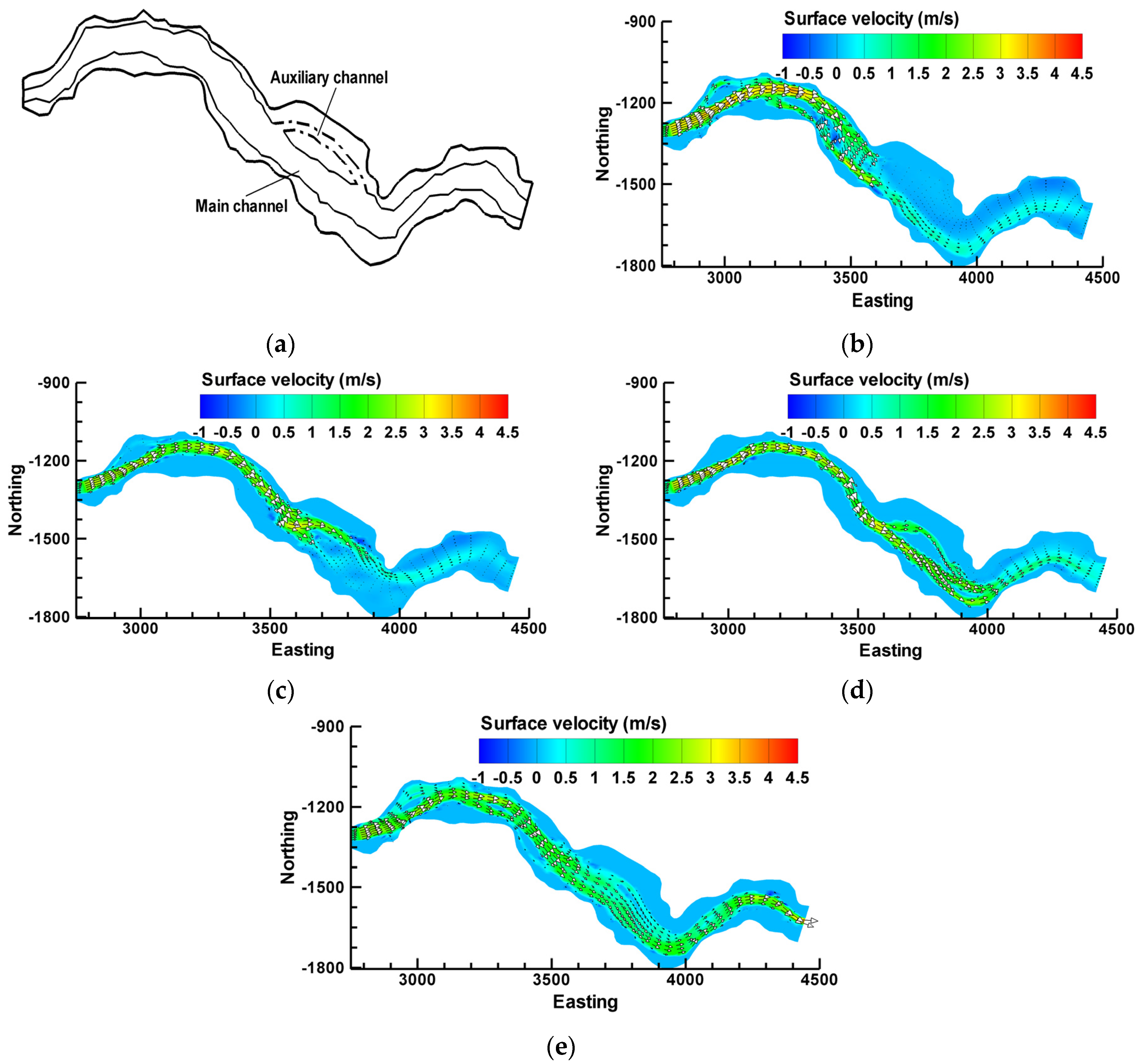
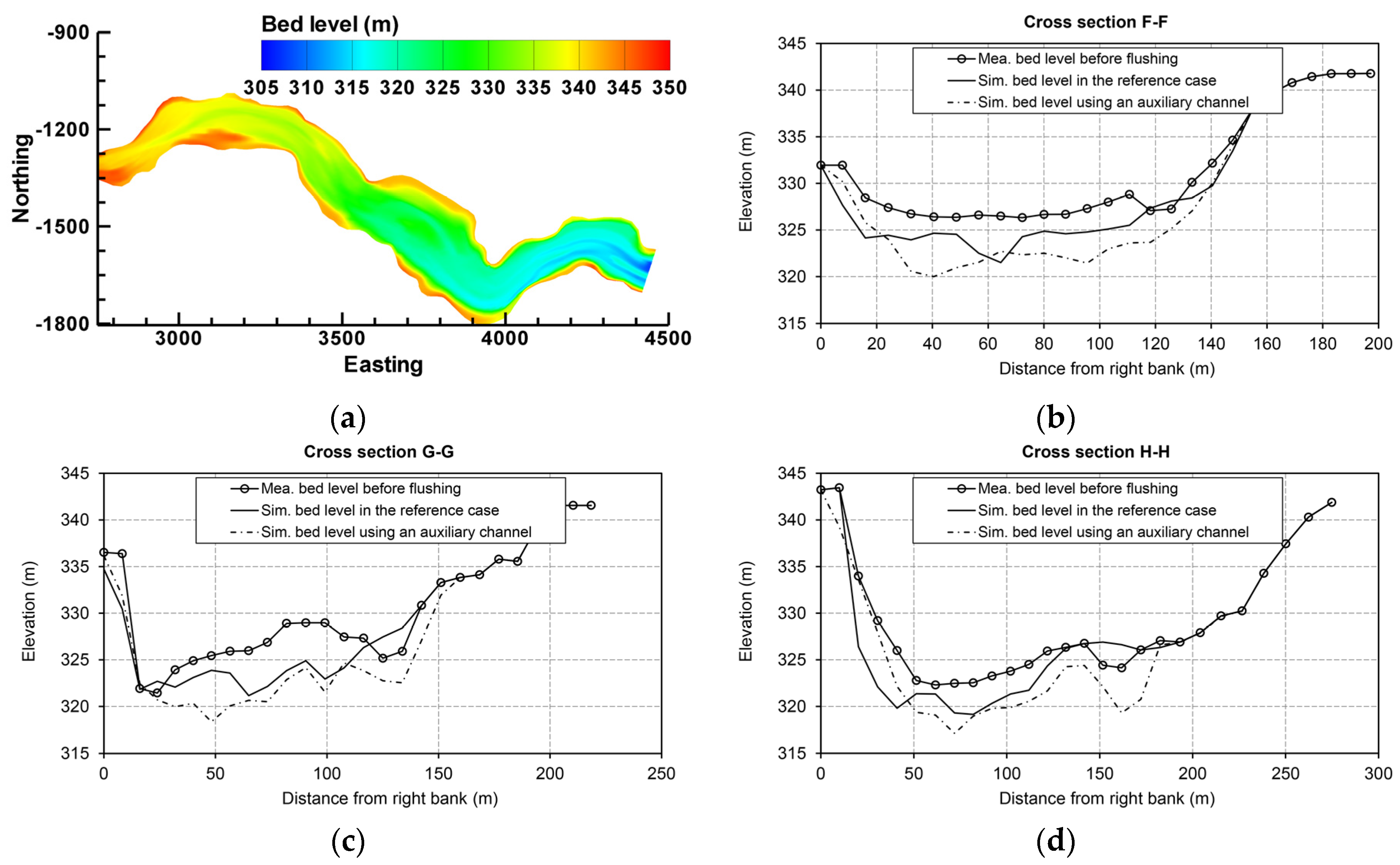
5.2. Auxiliary Channel Scenario
6. Conclusions
- Both the MPM and Van Rijn formulas yielded satisfactory performances in the simulation of bed changes in specific segments of the reservoir during the flushing operation (e.g., MPM formula in the upper half of the reservoir and Van Rijn formula in the vicinity of the Dam). These sediment transport formulas have been developed empirically to calculate the sediment transport for a given set of sediment sizes and hydrodynamic boundary conditions. However, the bed sediment size distribution, bed roughness, and hydrodynamic boundary conditions change dynamically during the free-flow flushing process. Such significant changes cannot be handled by empirical sediment transport formulas due to their inherent limitations. Nevertheless, the MPM bed load sediment transport formula qualitatively and quantitatively performed better than the Van Rijn formula for the entire reservoir. The MPM formula was able to achieve TVFS values that were more than 75% that of the measured TVFS values. Due to the application of the empirical formulas, the alluvial roughness also could not be estimated appropriately, which further magnifies the mentioned inability of the sediment transport formulas to accurately represent the morphological bed changes.
- For the Dashidaira reservoir, introducing an artificial additional discharge during the free-flow stage is practically feasible since this discharge can be supplied from upstream reservoirs. In addition, because this additional discharge is introduced when the flushing gates are fully opened and the water level is low, this discharge can be passed through the bottom outlets if its value is less than the maximum capacity of the outlets. Additional discharge has two major effects: first, it increases the induced bed shear stress and bed erosion and supplies an additional driving force to transport eroded sediments farther downstream in the reservoir and flush them out from the reservoir; second, it causes the water level to increase in the downstream river channel, which can be beneficial from an environmental point of view because it washes away fine materials from the downstream channel terraces (thereby preventing river channel clogging). However, it was found that introducing the extra discharge in the form of two discharge pulses with a larger discharge pulse in the second half of the free-flow stage more efficiently increases the FE ratio and the bed degradation in the upstream areas covered with coarser materials. The numerical outcomes showed that introducing approximately 21% more water from upstream reservoirs (i.e., an approximately 56% increase in the average free-flow discharge) can enhance the FE by approximately 5−13% compared to the reference case (i.e., the 2012 flushing operation), depending on how this additional discharge is delivered.
- The construction of an auxiliary longitudinal flushing channel in the dead zone area of the Dashidaira reservoir causes a portion of the flushing flow to deviate from the main channel into the auxiliary channel and to enter the main channel again via a confluence downstream of the diversion point. The non-diverted flow continues along its original path along the thalweg of the main flushing channel and the diverted flow towards the auxiliary channel scour the deposited sediments from the targeted dead zone in the reservoir. The flushing processes associated with the auxiliary longitudinal channel result in a flushing channel that is overall longer and wider. Hence, the FE is higher by as much as approximately 9% compared to the reference case.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Morris, G.L. Chapter 5: Sediment management and sustainable use of reservoirs. In Modern Water Resources Engineering; Wang, L.K., Yang, C.T., Eds.; Humana Press: Totowa, NJ, USA, 2014; Volume 15, pp. 279–337. [Google Scholar]
- White, R. Evacuation of Sediments from Reservoir; Thomas Telford: London, UK, 2001. [Google Scholar]
- Morris, G.L.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs and Watersheds for Sustainable Use; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Shen, H.W. Flushing sediment through reservoirs. J. Hydraul. Res. 1999, 37, 743–757. [Google Scholar] [CrossRef]
- Sumi, T.; Kantoush, S.A. Integrated management of reservoir sediment routing by flushing, replenishing, and bypassing sediments in Japanese river basins. In Proceedings of the 8th International Symposium on Ecohydraulics, Seoul, Korea, 12–16 September 2010. [Google Scholar]
- Liu, J.; Minami, S.; Otsuki, H.; Liu, B.; Ashida, K. Prediction of concerted sediment flushing. J. Hydraul. Eng. 2004, 130, 1089–1096. [Google Scholar] [CrossRef]
- Kantoush, S.A. Experimental Study on the Influence of the Geometry of Shallow Reservoirs on Flow Patterns and Sedimentation by Suspended Sediments. Ph.D. Thesis, Écolé Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2008. [Google Scholar]
- Sloff, C.J.; Jagers, H.R.A.; Kitamura, Y. Study on the channel development in a wide reservoir. In Proceedings of the 2nd River Flow conference, Napoli, Italy, 23–25 June 2004. [Google Scholar]
- Fukuoka, S.; Sumi, T.; Horiuchi, S. Sediment management on the arase dam removal project. In Proceedings of the 12th International Symposium on River Sedimentation, Kyoto, Japan, 2–5 September 2013. [Google Scholar]
- Asahi, K.; Shimizu, Y.; Nelson, J.; Parker, G. Numerical simulation of river meandering with self-evolving banks. J. Geophysic. Res. 2013, 118, 2208–2229. [Google Scholar] [CrossRef]
- Fukuoka, S.; Uchida, T. Toward integrated multi-scale simulations of flow and sediment transport in rivers. J. Jpn. Soc. Civ. Eng. 2013, 69, II_1–II_10. [Google Scholar] [CrossRef]
- Fang, H.; Rodi, W. Three-dimensional calculation of flow and suspended sediment transport in the neighbourhoods of the dam for the Three Gorges Project (TGP) reservoir in the Yangtze River. J. Hydraul. Res. 2003, 41, 379–394. [Google Scholar] [CrossRef]
- Lu, Y.J.; Wang, Z.Y. 3D numerical simulation for water flows and sediment deposition in dam areas of the Three Gorges project. J. Hydraul. Eng. 2009, 135, 755–769. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of the flushing process of the Kali Gandaki hydropower reservoir. Lakes Reserv. 2012, 17, 25–33. [Google Scholar] [CrossRef]
- Khosronejad, A.; Rennie, C.D.; Salehi Neyshabouri, A.A.; Gholam, I. Three-dimensional numerical modeling of reservoir sediment release. J. Hydraul. Res. 2008, 46, 209–223. [Google Scholar] [CrossRef]
- Harb, G.; Dorfmann, C.; Schneider, J.; Badura, H. Numerical analysis of sediment transport processes during a flushing event of an Alpine reservoir. In Proceedings of the 7th River Flow conference, Lausanne, Switzerland, 3–5 September 2014. [Google Scholar]
- Gallerano, F.; Cannata, G. Compatibility of Reservoir Sediment Flushing and River Protection. J. Hydraul. Eng. 2011, 137, 1111–1125. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of reservoir flushing in a prototype scale. Int. J. River Basin Manag. 2012, 10, 341–349. [Google Scholar] [CrossRef]
- Olsen, N.R.B. A Three Dimensional Numerical Model for Simulation of Sediment Movement in Water Intakes with Multiblock Option; Department of Hydraulic and Environmental Engineering, The Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Haun, S.; Rüther, N. Three-dimensional numerical modelling of flow field in shallow reservoirs. Proc. ICE-Water Manag. 2015, 169, 229–244. [Google Scholar] [CrossRef]
- Dehghani, A.A.; Esmaeili, T.; Chang, W.Y.; Dehghani, N. 3D numerical simulation of local scouring under hydrographs. Proc. ICE-Water Manag. 2013, 166, 120–131. [Google Scholar] [CrossRef]
- Haun, S.; Kjærås, H.; Løvfall, S.; Olsen, N.R.B. Three-dimensional measurements and numerical modelling of suspended sediments in a hydropower reservoir. J. Hydrol. 2013, 479, 180–188. [Google Scholar] [CrossRef]
- Esmaeili, T.; Dehghani, A.A.; Zahiri, A.R.; Suzuki, K. 3D Numerical simulation of scouring around bridge piers (Case Study: Bridge 524 crosses the Tanana River). World Acad. Sci. Eng. Technol. 2009, 58, 1028–1032. [Google Scholar]
- Fischer-Antze, T.; Olsen, N.R.B.; Gutknecht, D. Three-dimensional CFD modeling of morphological bed changes in the Danube River. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Rüther, N.; Olsen, N.R.B. Modelling free-forming meander evolution in a laboratory channel using three-dimensional computational fluid dynamics. Geomorphology 2007, 89, 308–319. [Google Scholar] [CrossRef]
- Ruether, N.; Singh, J.M.; Olsen, N.R.B.; Atkinson, E. 3-D computation of sediment transport at water intakes. Proc. ICE-Water Manag. 2005, 158, 1–7. [Google Scholar] [CrossRef]
- Olsen, N.R.B.; Kjellesvig, H.M. Three-dimensional numerical modelling of bed changes in a sand trap. J. Hydraul. Res. 1999, 37, 189–198. [Google Scholar] [CrossRef]
- Haun, S.; Dorfmann, C.; Harb, G.; Olsen, N.R.B. Numerical modelling of the reservoir flushing of the bodendorf reservoir, Austria. In Proceedings of the 2nd IAHR European Congress, Munich, Germany, 27–29 June 2012. [Google Scholar]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A. Experimental and numerical study of flushing channel formation in shallow reservoirs. J. Jpn. Soc. Civ. Eng. 2014, 70, I_19–I_24. [Google Scholar] [CrossRef]
- Kantoush, S.A.; Sumi, T.; Suzuki, T.; Murasaki, M. Impacts of sediment flushing on channel evolution and morphological processes: Case study of the Kurobe River, Japan. In Proceedings of the 5th River Flow Conference, Braunschweig, Germany, 8–10 June 2010. [Google Scholar]
- Minami, S.; Noguchi, K.; Otsuki, H.; Fukuri, H.; Shimahara, N.; Mizuta, J.; Takeuchi, M. Coordinated sediment flushing and effect verification of fine sediment discharge operation in Kurobe River. In Proceedings of the ICOLD Conference, Kyoto, Japan, 6–8 June 2012. [Google Scholar]
- Sumi, T. Evaluation of efficiency of reservoir sediment flushing in Kurobe River. In Proceedings of the 4th International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: New York, NY, USA, 1980. [Google Scholar]
- Olsen, N.R.B.; Haun, S. Free surface algorithms for 3-D numerical modeling of flushing. In Proceedings of the 5th River Flow Conference, Braunschweig, Germany, 8–10 June 2010. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Van Rijn, L.C. Sediment transport, part III: Bed forms and alluvial roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part II: Suspended load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, IAHR, Stockholm, Sweden, 7–9 June 1948. [Google Scholar]
- Brooks, H. Boundary shear stress in curved trapezoidal channels. J. Hydraul. Div. Am. Soc. Civ. Eng. 1963, 89, 327–333. [Google Scholar]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y.; Haun, S. Numerical study on flushing channel evolution, case study of Dashidaira reservoir, Kurobe river. J. Jpn. Soc. Civ. Eng. 2015, 71, I_115–I_120. [Google Scholar] [CrossRef]
- Kantoush, S.A.; Schleiss, A.J. Channel formation in large shallow reservoirs with different geometries during flushing. J. Environ. Technol. 2009, 30, 855–863. [Google Scholar] [CrossRef] [PubMed]
| Sediment Size (mm) | Cs. A-A (%) | Cs. B-B (%) | Cs. C-C (%) | Cs. D-D (%) | Cs. E-E (%) | Cs. F-F (%) | Cs. G-G (%) | Cs. H-H (%) | Cs. I-I (%) | Cs. J-J (%) | Cs. K-K (%) | Cs. L-L (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 316 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 118.3 | 74 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 40 |
| 37.4 | 6 | 73 | 75 | 70 | 69 | 4 | 1 | 0 | 0 | 0 | 0 | 30 |
| 11.8 | 4 | 7 | 6 | 8 | 13 | 14 | 5 | 0 | 0 | 0 | 0 | 16 |
| 3.7 | 3 | 14 | 11 | 14 | 12 | 25 | 18 | 0 | 0 | 0 | 0 | 3 |
| 1.2 | 5 | 4 | 1 | 3 | 2 | 23 | 21 | 0 | 6 | 13 | 0 | 1 |
| 0.37 | 6 | 2 | 7 | 5 | 4 | 35 | 55 | 100 | 94 | 87 | 100 | 10 |
| Parameter | Active Layer Thickness (m) | Water Content of the Bed Material(%) | Critical Angle of Repose (Degree) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.45 | 0.85 | 50 | 43 | 38 | 33 | 34 | 35 | |
| TVFS (×10−3 m3) | 261.6 | 290.5 | 299.8 | 369.1 | 306.2 | 316.8 | 311.0 | 302.7 | 284.5 |
| MAE (m) | 2.17 | 1.73 | 1.95 | 2.25 | 2.10 | 1.75 | 1.98 | 1.54 | 1.98 |
| Scenario | ADF 75 | ADF 110 | ADF 170 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Area | I | II | III | I | II | III | I | II | III |
| BCI (m) | 0.32 | −0.47 | −0.54 | 0.06 | −0.49 | −0.55 | 0.20 | −0.76 | −0.90 |
| TVFS (×10−3 m3) | 356.0 | 396.1 | 425.0 | ||||||
| Scenario | PDF P1 110 8-P2 137.5 8 | PDF P1 110 8-P2 157 7 | PDF P1 110 8-P2 183.5 6 | ||||||
| Area | I | II | III | I | II | III | I | II | III |
| BCI (m) | −0.01 | −0.09 | −0.21 | 0.02 | −0.04 | −0.20 | −0.09 | 0.01 | 0.04 |
| TVFS (×10−3 m3) | 426.2 | 417.3 | 410.9 | ||||||
| Scenario | WDS −0.5 | WDS −2.5 | WDS −3.5 | ||||||
| Area | I | II | III | I | II | III | I | II | III |
| BCI (m) | 0.03 | −0.14 | 0.02 | 0.10 | −0.13 | −0.23 | −0.08 | −0.33 | −0.22 |
| TVFS (×10−3 m3) | 322.8 | 331.9 | 378.9 | ||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y.; Haun, S.; Rüther, N. Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan. Water 2017, 9, 900. https://doi.org/10.3390/w9110900
Esmaeili T, Sumi T, Kantoush SA, Kubota Y, Haun S, Rüther N. Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan. Water. 2017; 9(11):900. https://doi.org/10.3390/w9110900
Chicago/Turabian StyleEsmaeili, Taymaz, Tetsuya Sumi, Sameh A. Kantoush, Yoji Kubota, Stefan Haun, and Nils Rüther. 2017. "Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan" Water 9, no. 11: 900. https://doi.org/10.3390/w9110900
APA StyleEsmaeili, T., Sumi, T., Kantoush, S. A., Kubota, Y., Haun, S., & Rüther, N. (2017). Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan. Water, 9(11), 900. https://doi.org/10.3390/w9110900








