Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia
Abstract
1. Introduction
2. Materials and Methods
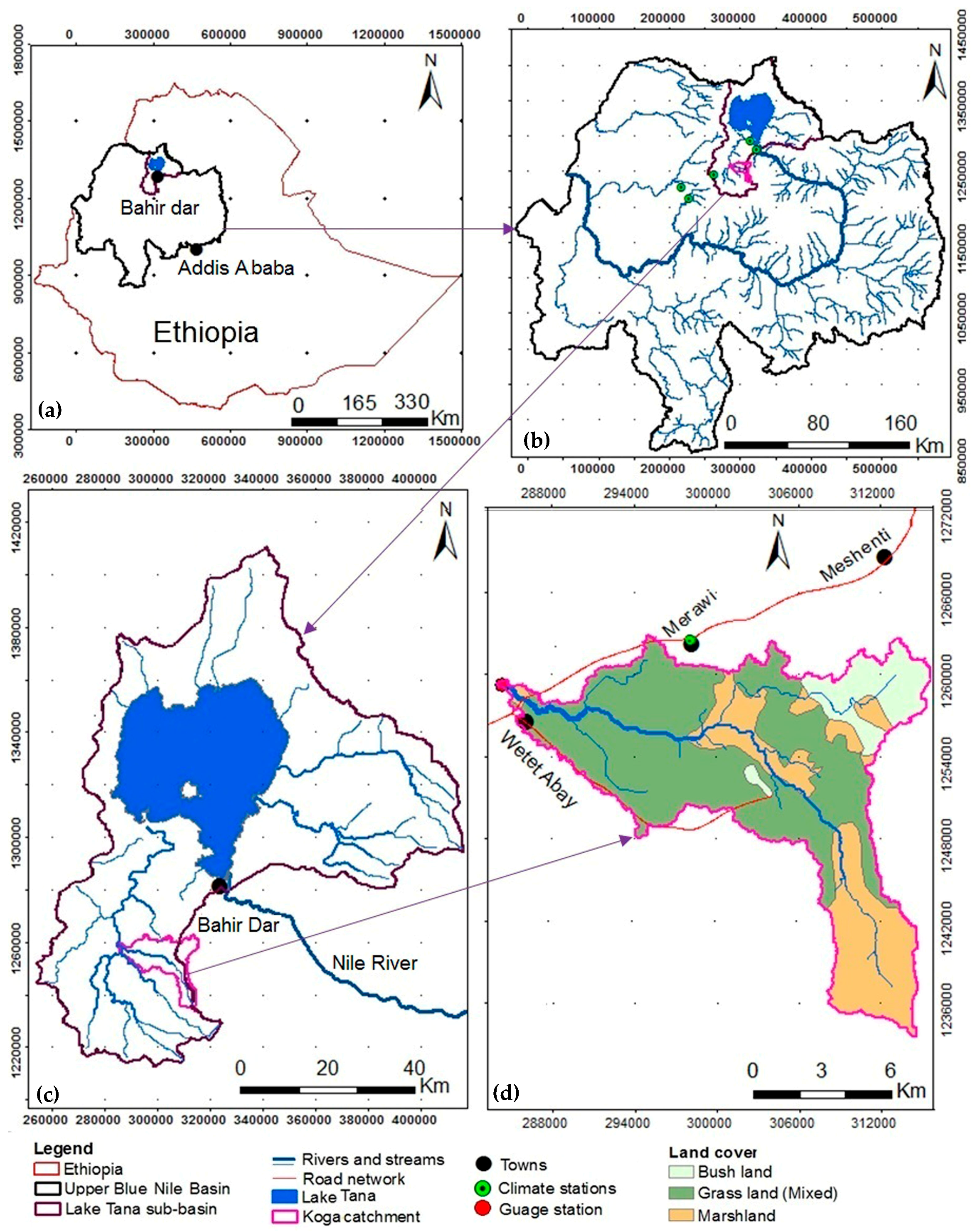
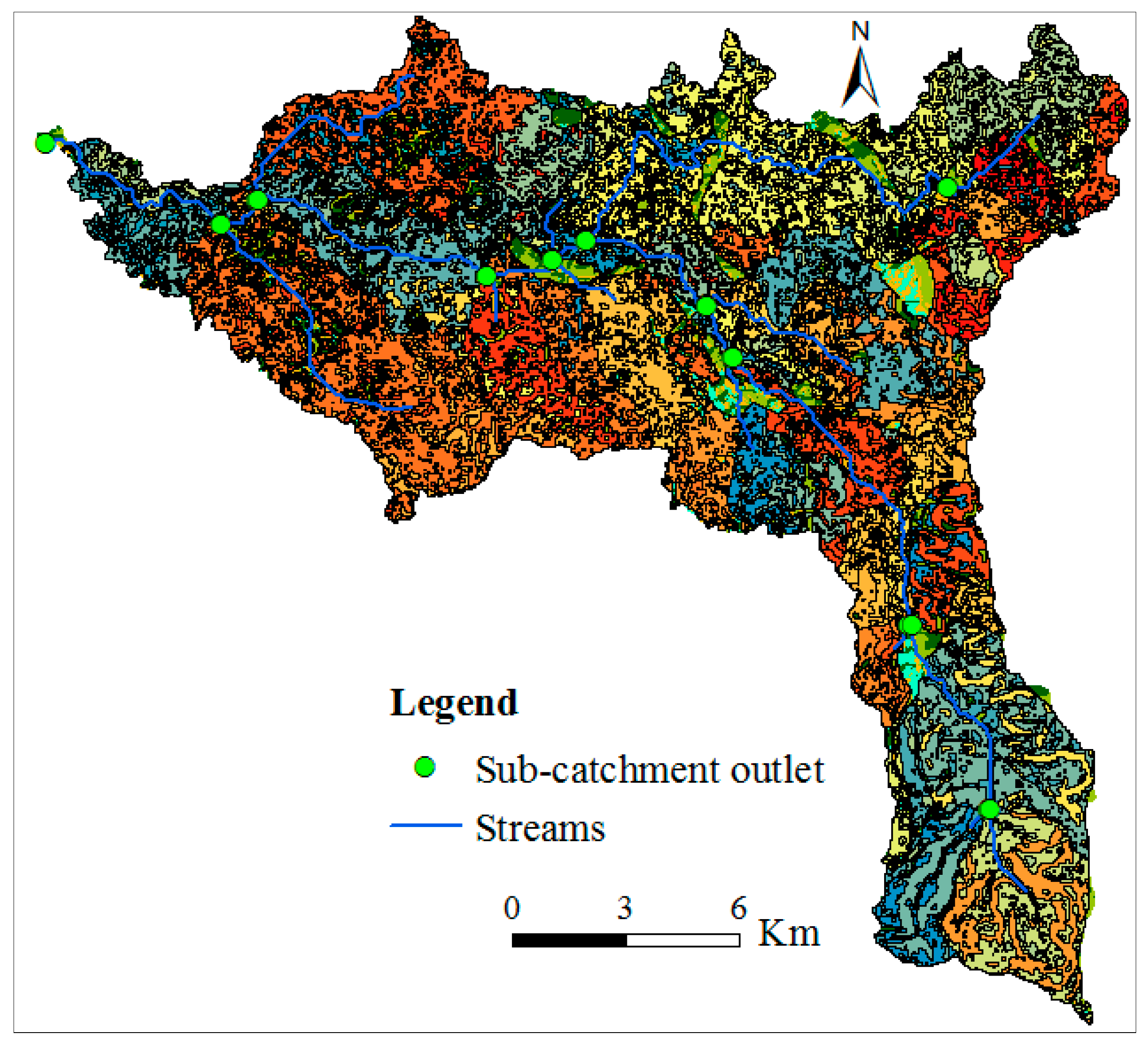
2.1. Study Area
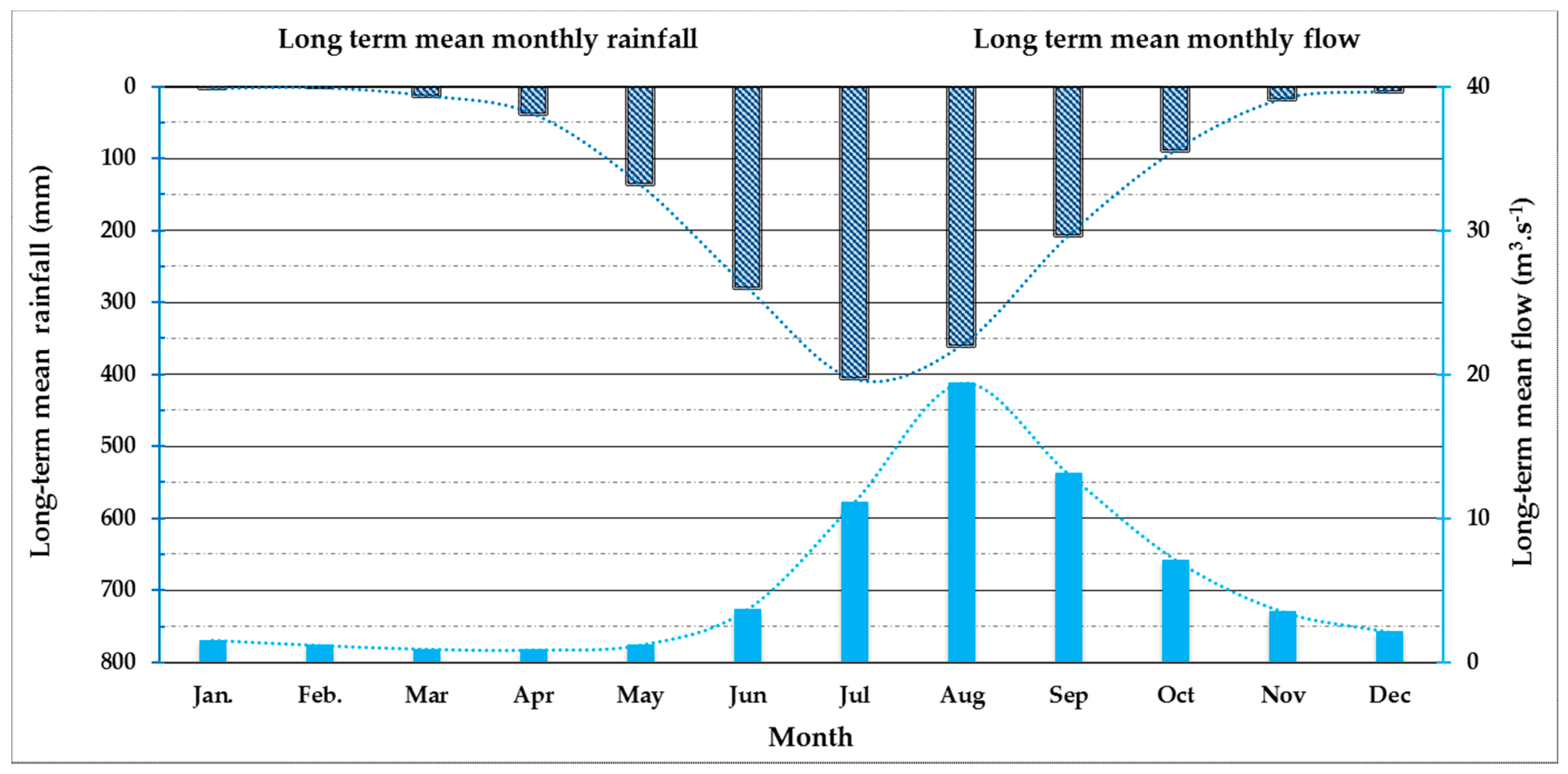
2.2. Input Data
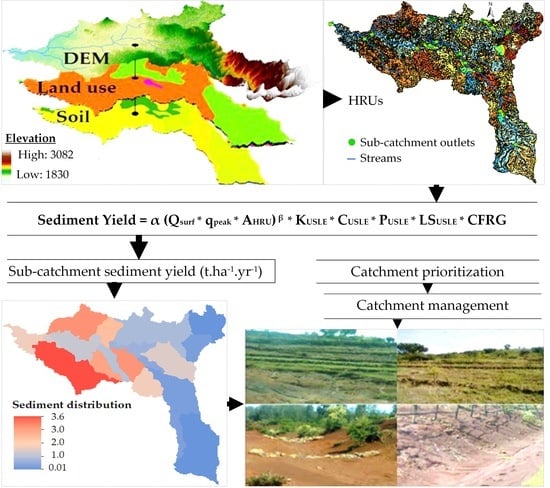
2.3. Model Description
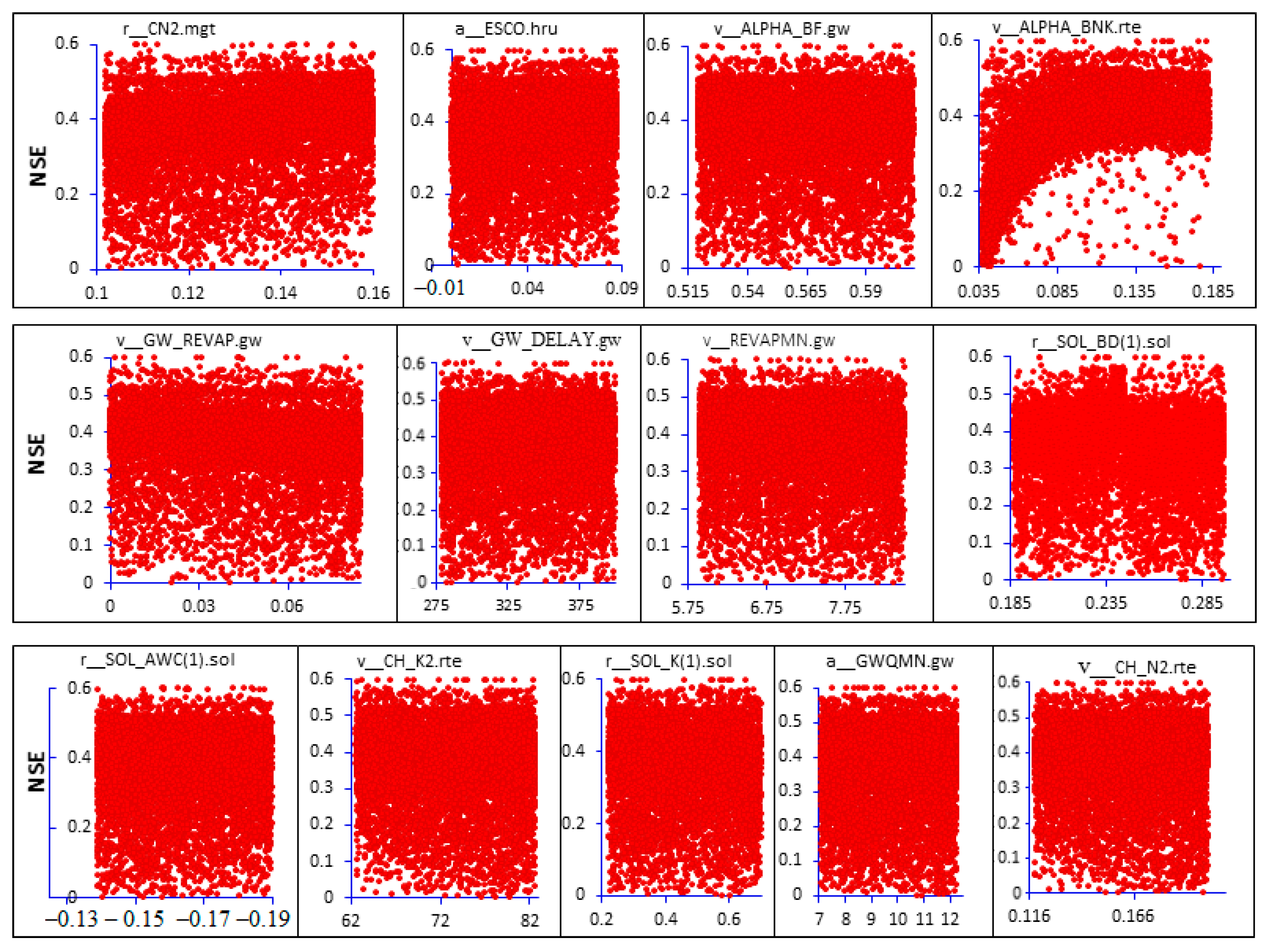
2.3.1. SWAT Model Sensitivity Analysis
2.3.2. Model Prediction Uncertainty
2.3.3. Model Calibration and Validation
2.3.4. Model Performance Evaluation
3. Results and Discussion
3.1. Parameter Sensitivity
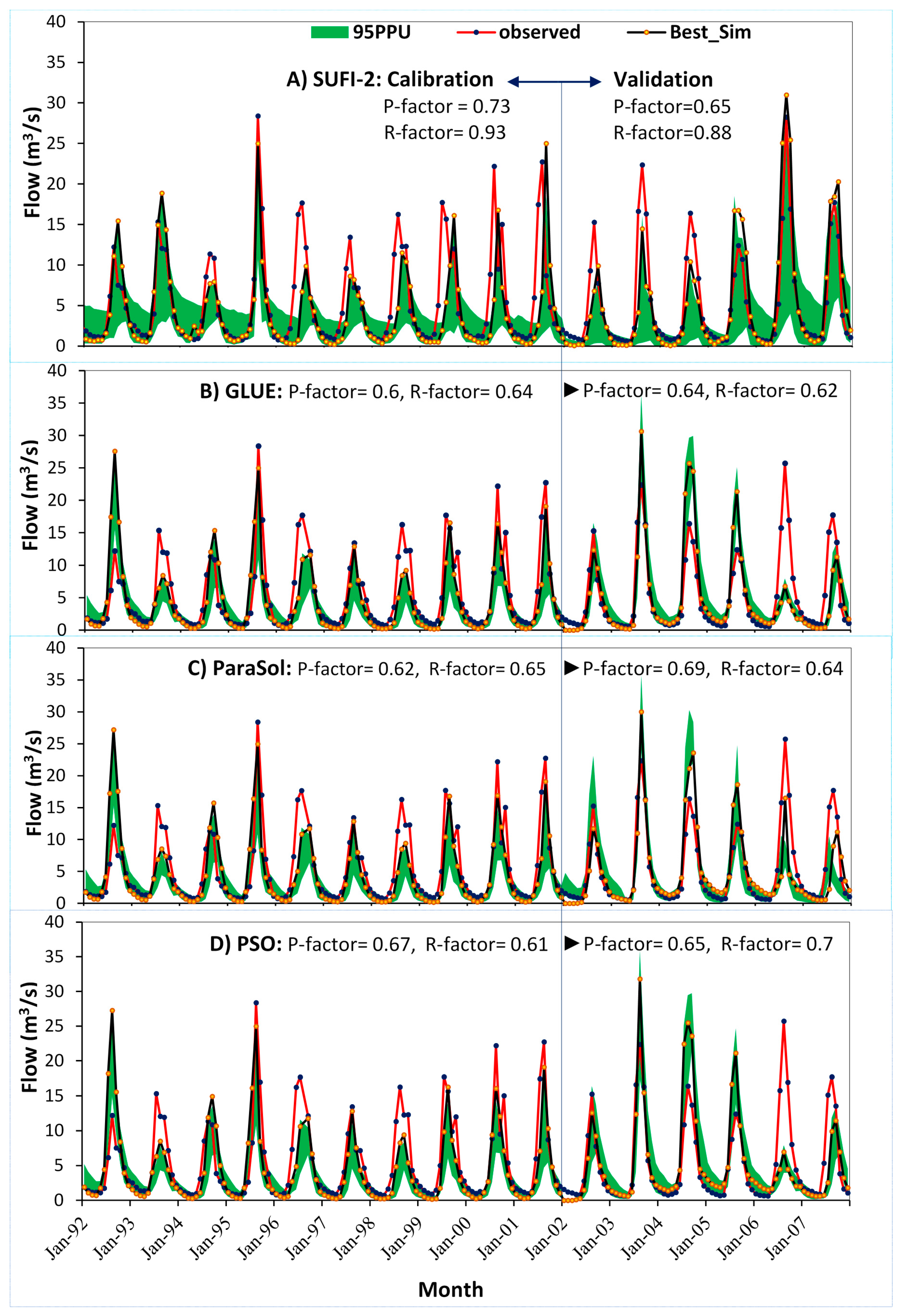
3.2. Flow Calibration and Validation
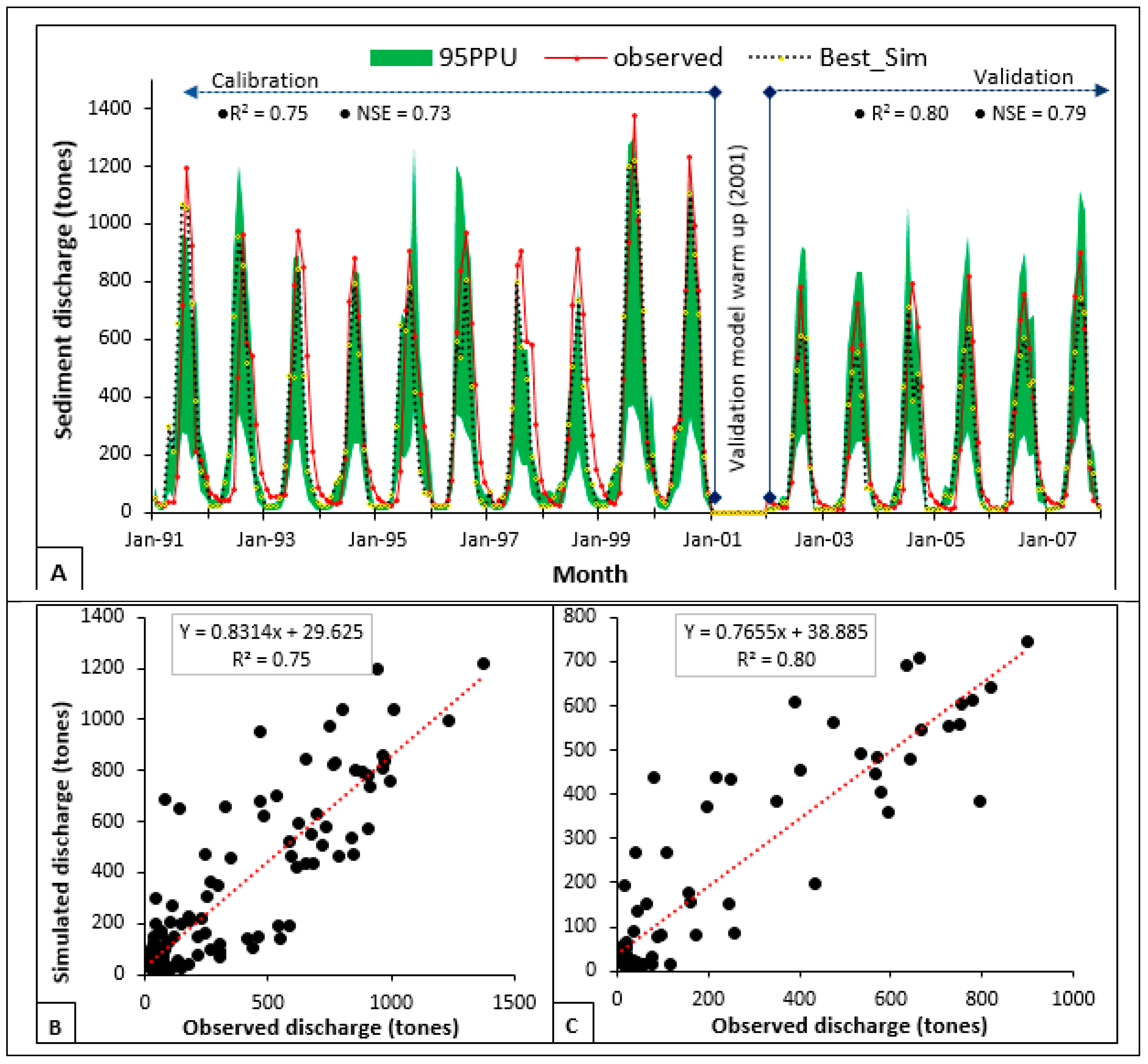
3.3. Sediment Yield Calibration and Validation
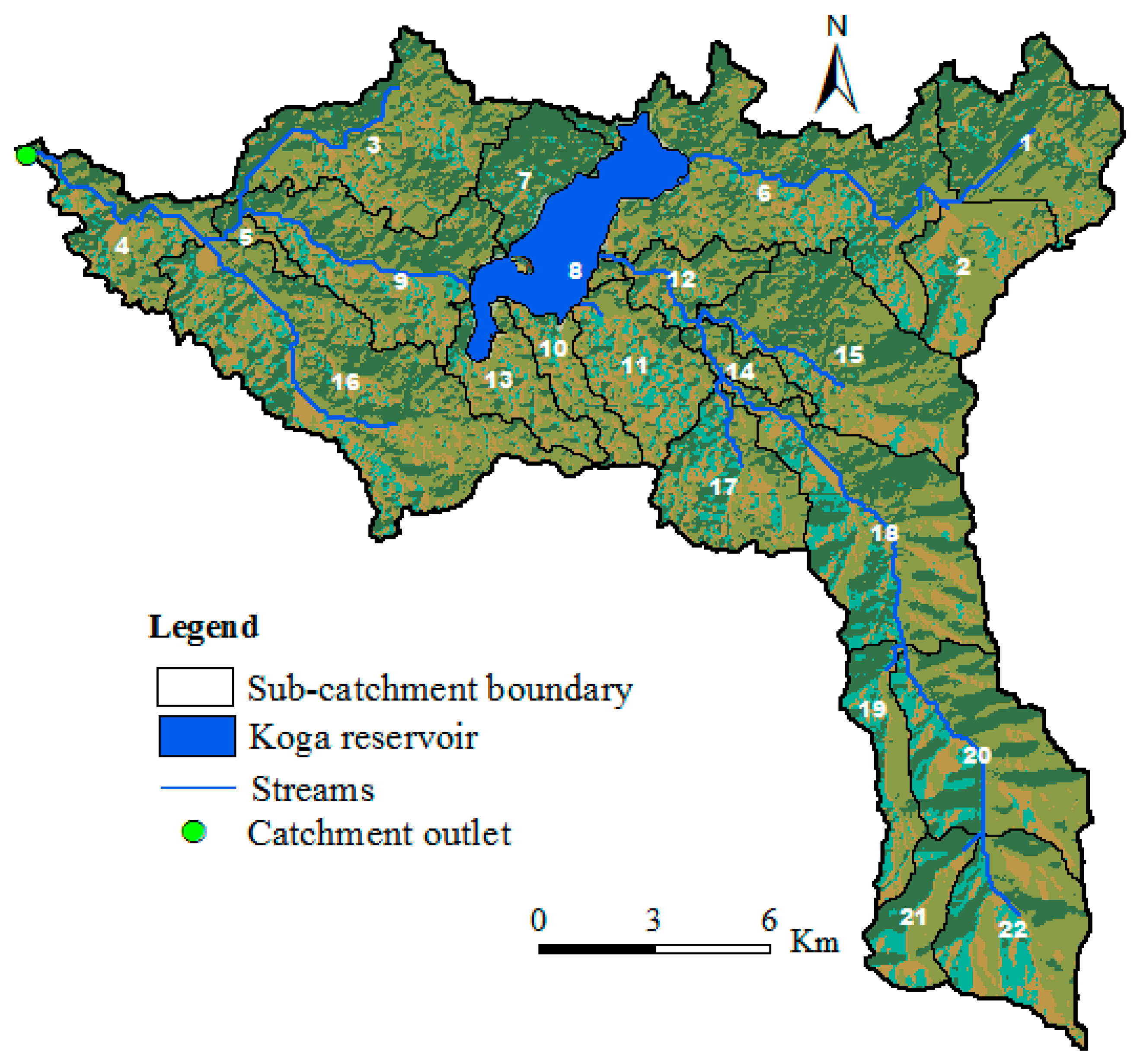
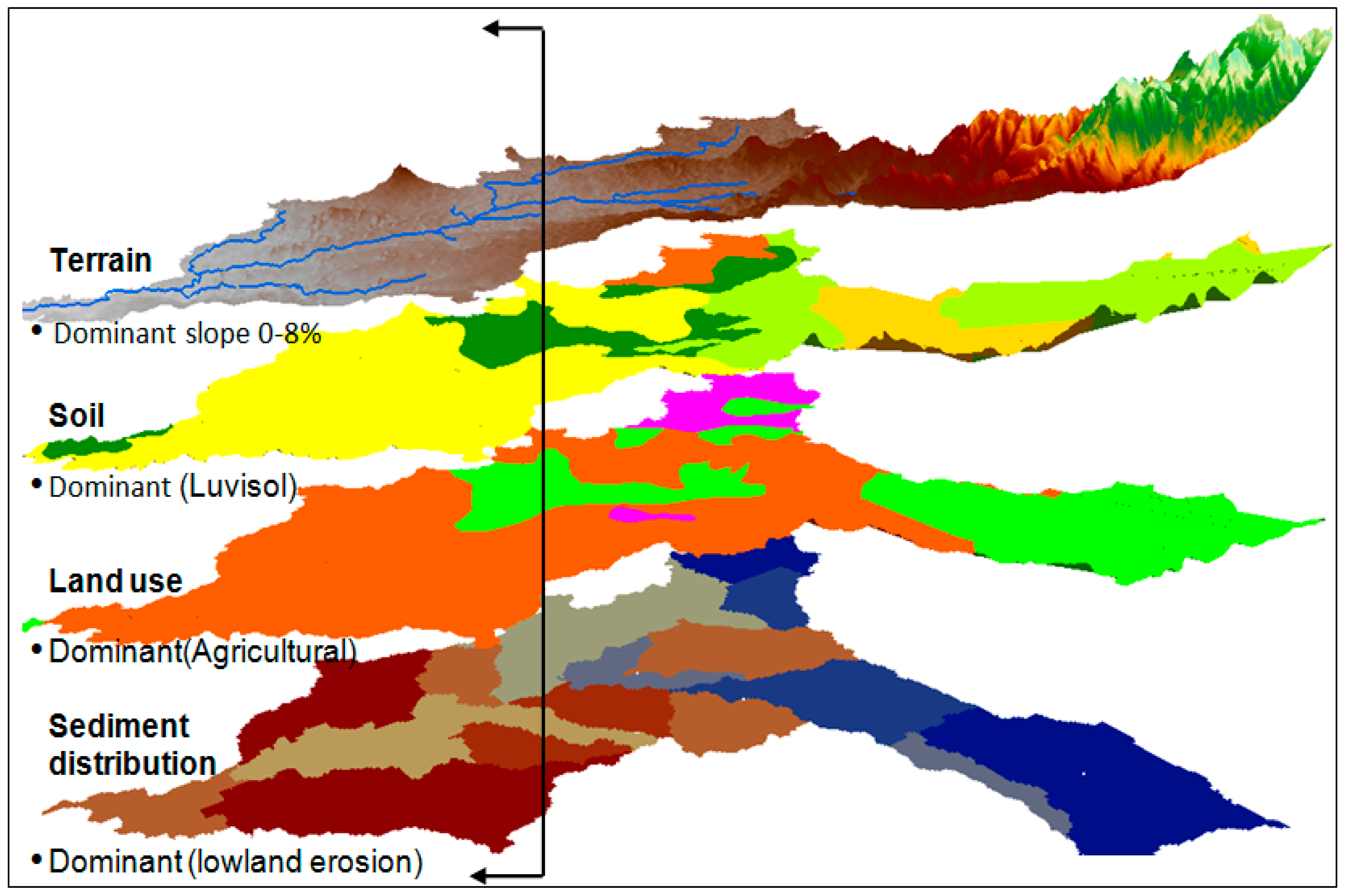
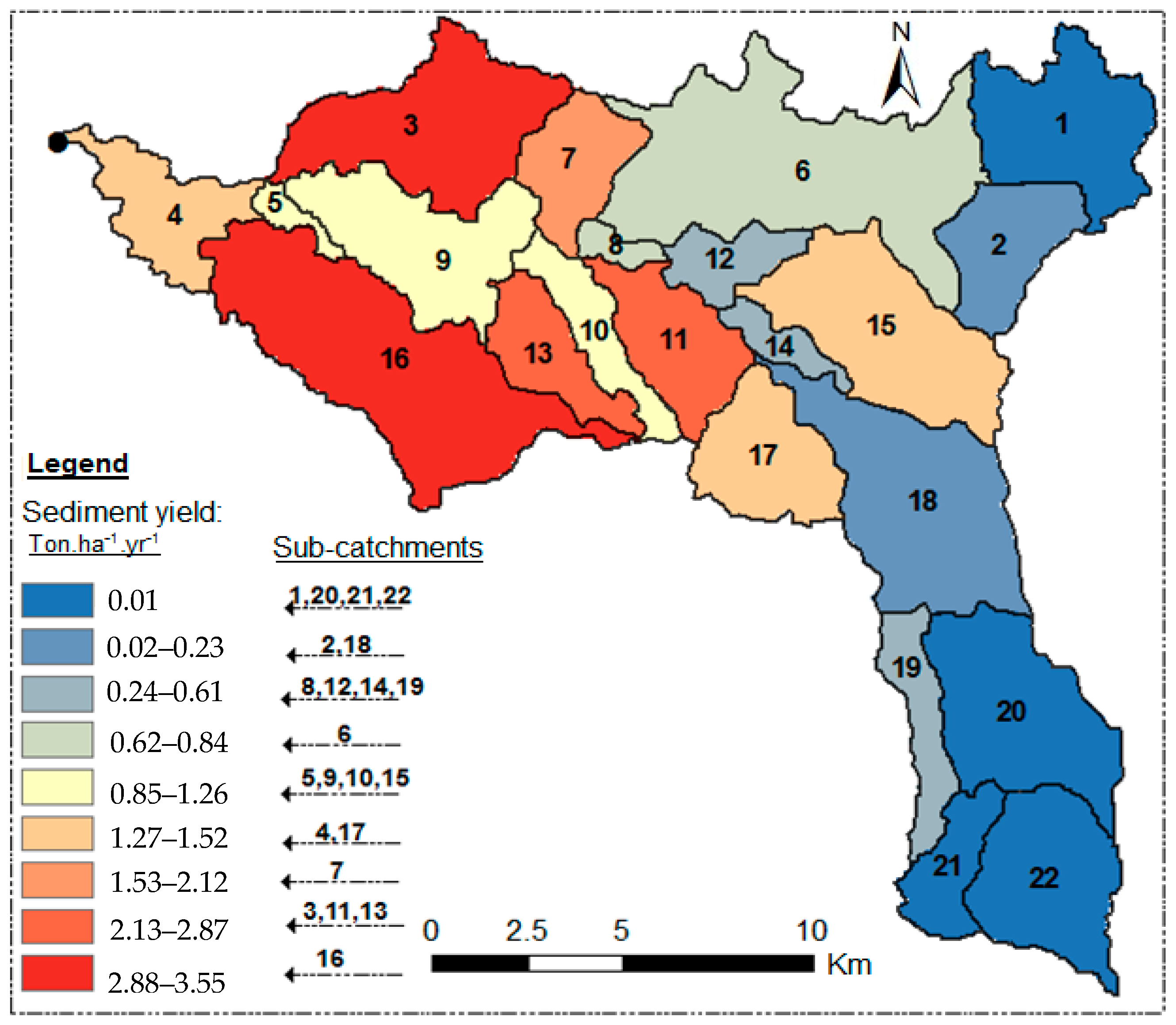
3.4. Spatial Distribution of Sediment Generation and Its Implications
3.4.1. Effect of Distributed Inputs of Soil Type and Land Use on Soil Erosion
3.4.2. Sediment Source Identification
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hurni, H.; Solomon, A.; Amare, B.; Berhanu, D.; Eva, L.; Brigitte, P.; Zeleke, G. Land Degradation and Sustainable Land Management in the Highlands of Ethiopia. In Global Change and Sustainable Development: A Synthesis of Regional Experiences from Research; Hurni, H., Wiesmann, U.M., Eds.; Geographica Bernesia: Bern, Switzerland, 2010; Volume 5, pp. 187–207. [Google Scholar]
- Nyssen, J.; Poesen, J.; Moeyersons, J.; Haile, M.; Deckers, J.; Lang, A. Human impacts on the environment in the Ethiopian and Eritrean Highlands—A states of the art. Earth Sci. 2004, 64, 273–320. [Google Scholar] [CrossRef]
- Reynolds, B. Variability and Change in Koga Reservoir Volume, Blue Nile, Ethiopia. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2013. [Google Scholar]
- Assefa, T.; Manoj, J.; Seifu, A.; Ephrem, Y.; Anwar, A.; Abeyou, W. Identification of Erosion Hotspot Area using GIS and MCE Technique for Koga Watershed in the upper Blue Nile Basin, Ethiopia. Am. J. Environ. Sci. 2015, 4, 245–255. [Google Scholar] [CrossRef]
- Ayele, G.T.; Demessie, S.S.; Mengistu, K.T.; Tilahun, S.A.; Melesse, A.M. Multitemporal land use/land cover change detection for the Batena Watershed, Rift Valley Lakes Basin, Ethiopia. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Melesse, A., Abtew, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 51–72. ISBN 978-3-319-18787-7. [Google Scholar]
- Nyssen, J.; Poesen, J.; Lanckriet, S.; Jacob, M.; Moeyersons, J.; Haile, M.; Deckers, J. Land Degradation in the Ethiopian Highlands. In Landscapes and Landforms of Ethiopia; Paolo, B., Ed.; World Geomorphological Landscapes; Springer: Dodrecht, The Netherlands, 2015; pp. 369–385. [Google Scholar]
- Asres, R.S.; Tilahun, S.A.; Ayele, G.T.; Melesse, A.M. Analyses of land use/land cover change dynamics in the upland watersheds of Upper Blue Nile Basin. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Melesse, A., Abtew, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 73–91. [Google Scholar]
- Guzman, C.; Tilahun, S.; Zegeye, A.; Tammo, S. Suspended sediment concentration-discharge relationships in the sub-humid Ethiopian highlands. Hydrol. Earth Syst. Sci. 2013, 17, 1067–1077. [Google Scholar] [CrossRef]
- Abebayehu, A.; Moges, A. Rill Erosion Assessment in Cultivated Lands and Farmers Perception on Soil Erosion, A Case of Delbo Wogene Micro-Watershed Southern Ethiopia. J. Biol. Agric. Healthc. 2015, 5, 87–115. [Google Scholar]
- Gelagaya, H.S.; Minale, A.S. Soil loss estimation using GIS and Remote sensing techniques: A case of Koga watershed, Northwestern Ethiopia. ISWCR 2016, 4, 126–136. [Google Scholar] [CrossRef]
- Hurni, H. Land degradation, famine and resource scenarios in Ethiopia. In World Soil Erosion and Conservation; David, P., Ed.; Cambridge University Press: Cambridge, UK, 1993; pp. 27–62. [Google Scholar]
- Tadesse, G. Land Degradation: A challenge to Ethiopia. Environ. Manag. 2001, 27, 815–826. [Google Scholar] [CrossRef]
- Nyssen, J.; Poesen, J.; Moeyersons, J.; Haile, M.; Josef, D. Dynamics of soil erosion rates and controlling factors in the Northern Ethiopian Highlands—Towards a sediment budget. Earth Surf. Process. Landf. 2007, 33, 695–711. [Google Scholar] [CrossRef]
- World Bank. The Cost of Land Degradation in Ethiopia: A Review of Past Studies; World Bank: Washington, DC, USA, 2007; pp. 1–21. [Google Scholar]
- Bewket, W.; Teferi, E. Assessment of soil erosion hazard and prioritization for treatment at the watershed level: Case study in the Chemoga watershed, Blue Nile Basin, Ethiopia. Land Degrad. Dev. 2009, 20, 609–622. [Google Scholar] [CrossRef]
- Abraha, A.Z. Assessment of Spatial and Temporal Variability of River Discharge, Sediment Yield and Sediment-Fixed Nutrient Export in Geba River Catchment, Northern Ethiopia; Katholieke Universiteit: Leuven, Belgium, 2009. [Google Scholar]
- Vanmaercke, M.; Zenebe, A.; Poesen, J.; Neyssen, J.; Verstraeten, G.; Deckers, J. Sediment dynamics and the role of flash floods in sediment export from medium-sized catchments: A case study from the semi-arid tropical highlands in northern Ethiopia. J. Soils Sediment. 2010, 10, 611–627. [Google Scholar] [CrossRef]
- Eleni, Y.; Alexander, E.; Günter, B. Temporal variation of suspended sediment transport in the Koga catchment, North Western Ethiopia and environmental implications. Hydrol. Process. 2013, 28, 5972–5984. [Google Scholar]
- Gizachew, A.; Yihenew, G.S. Soil loss estimation for soil conservation planning using geographic information system in Guang watershed, Blue Nile basin. J. Environ. Earth Sci. 2015, 5, 126–134. [Google Scholar]
- Bofu, Y.; David, N. Temporal and spatial variation of sediment yield in the Snowy Mountains region, Australia. In Variability in Stream Erosion and Sediment Transport, Proceedings of the Canberra Symposium, Canberra, Australia, 11–13 May 1994; The Australian Government Publishing Service: Canberra, Australia, 1994. [Google Scholar]
- Marttila, H.; Klöve, B. Dynamics of erosion and suspended sediment transport from drained peatland forestry. J. Hydrol. 2010, 388, 414–425. [Google Scholar] [CrossRef]
- Vincent, B.; Veerle, V.; Atkilt, G.; Jean, P.; Semunesh, G. Human impact on sediment fluxes within the Blue Nile and Atbara River basins. Geomorphology 2012, 181, 231–241. [Google Scholar]
- Awulachew, S.; Ahmed, A.; Haileselassie, Y.A.; Bashar, K.; McCartney, M.; Steenhuis, T. Improved Water and Land Management in the Ethiopian Highlands and Its Impact on Downstream Stake Holders Dependent on the Blue Nile; CPWF Project Report; Consultative Group on International Agricultural Research Challenge Programme on Water and Food: Montpellier, France, 2010. [Google Scholar]
- Klemes, V. Conceptualization and scale in hydrology. J. Hydrol. 1983, 65, 1–23. [Google Scholar] [CrossRef]
- Pandey, A.; Himanshu, S.K.; Mishra, S.; Singh, V.P. Physically based soil erosion and sediment yield models revisited. Catena 2016, 147, 595–620. [Google Scholar] [CrossRef]
- Jeong, J.; Narayanan, K.; Jeff, A.; Glick, R.; Gosselink, L.; Raghavan, S. Development and integration of sub-hourly rainfall–Runoff modeling capability within a watershed model. Water Resour. Manag. 2010, 24, 4505–4527. [Google Scholar] [CrossRef]
- Chanasyk, D.S.; Mapfumo, E.; Willms, W. Quantification and simulation of surface runoff from fescue grassland watersheds. Agric. Water Manag. 2003, 59, 137–153. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the upper Mississippi basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Hunink, J.; Niadas, I.; Antonaropoulos, P.; Droogers, P.; de Vente, J. Targeting of intervention areas to reduce reservoir sedimentation in the Tana catchment (Kenya) using SWAT. Hydrol. Sci. J. 2013, 58, 1–15. [Google Scholar] [CrossRef]
- Arnold, J.G.; Williams, J.R.; Maidment, D.R. Continuous-time water and sediment-routing model for large basins. J. Hydraul. Eng. 1995, 121, 171–183. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.; Williams, J. Large area hydrologic modeling and assessment. Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Arnold, J.; Kiniry, J.; Srinivasan, R.; Williams, J.; Haney, E.; Neitsch, S. Soil and Water Assessment Tool, Input/Output File Documentation; Texas Water Resources Institute: College Station, TX, USA, 2012; pp. 1–650. [Google Scholar]
- Bisantino, T.; Bingner, R.; Chouaib, W.; Gentile, F.; Liuzzi, G. Estimation of runoff, peak discharge and sediment load at the event scale in a medium-size Mediterranean watershed using the ANNAGNPS model. Land Degrad. Dev. 2015, 26, 340–355. [Google Scholar] [CrossRef]
- Taguas, E.V.; Gómez, J.A.; Mateos, P.; Denisi, L. Modelling the rainfall runoff relationships in a large olive orchard catchment in southern Spain. Water Resour. Manag. 2015, 29, 2361–2375. [Google Scholar] [CrossRef]
- MoWR. Spatial and Hydrological Data; Ministry of Water Resources, The Federal Democratic Republic of Ethiopia: Addis Abeba, Ethiopia, 2009.
- Mohamed, Y.A.; van den Hurk, B.J.; Savenije, H.H.; Bastiaanssen, W.G. Hydroclimatology of the Nile: Results from a regional climate model. Hydrol. Earth Syst. Sci. 2005, 9, 263–278. [Google Scholar] [CrossRef]
- Jemberie, M.A.; Awass, A.A.; Melesse, A.M.; Ayele, G.T.; Demissie, S.S. Seasonal rainfall-runoff variability analysis, lake Tana sub-basin, upper Blue Nile basin, Ethiopia. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Melesse, A., Abtew, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 341–363. [Google Scholar]
- NMSA. Metreological Data Agency; The Ethiopian National Metreological Services Agency: Addis Abeba, Ethiopia, 2009. [Google Scholar]
- Arnold, J.G.; Allen, P.M. Estimating hydrologic budgets for three Illinois watersheds. J. Hydrol. 1996, 176, 57–77. [Google Scholar] [CrossRef]
- Gassman, P.; Reyes, M.; Green, C.; Arnold, J. The soil and water assessment tool: Historical development, applications and future directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool (SWAT) User’s Manual; Version 2000; Grassland Soil and Water Research Laboratory: Temple, TX, USA; Texas Water Resources Institute: Collage Station, TX, USA, 2002; pp. 1–506. [Google Scholar]
- Welde, K. Identification and prioritization of sub-watersheds for land and water management in Tekeze dam watershed, Northern Ethiopia. ISWCR 2016, 4, 30–38. [Google Scholar]
- Shawul, A.; Alamirew, T.; Dinka, M. Calibration and validation of SWAT model and estimation of water balance components of Shaya mountainous watershed, Southeastern Ethiopia. Hydrol. Earth Syst. Sci. 2013, 10, 13955–13978. [Google Scholar] [CrossRef]
- Hassen, M.; Assen, M.; Tena, A.; Assefa, M. Modeling of sediment yield in Maybar gauged watershed using SWAT, northeast Ethiopia. Catena 2015, 127, 191–205. [Google Scholar] [CrossRef]
- Dile, Y.; Berndtsson, R.; Setegn, S. Hydrological Response to Climate Change for Gilgel Abay River, in the Lake Tana Basin—Upper Blue Nile Basin of Ethiopia. PLoS ONE 2013, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Seka, A.M.; Awass, A.A.; Melesse, A.M.; Ayele, G.T.; Demissie, S.S. Evaluation of the Effects of Water Harvesting on Downstream Water Availability Using SWAT. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Melesse, A., Abtew, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 763–787. [Google Scholar]
- Moges, M.; Schmitter, P.; Tilahun, S.; Langan, S.; Dagnew, D.; Akale, A.; Steenhuis, T. Suitability of Watershed Models to Predict Distributed Hydrologic Response in the Awramba Watershed in Lake Tana basin. Land Degrad. Dev. 2016, 28, 1386–1397. [Google Scholar] [CrossRef]
- Kaleab, H.; Michael, M.; Manoj, K. Runoff and Sediment Modeling Using SWAT in Gumera Catchment, Ethiopia. OJMH 2013, 3, 196–205. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation; Version 2009; Texas Water Resources Institute: Collage Station, TX, USA, 2011; pp. 1–647. [Google Scholar]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnod, J. Arcswat 2.3 Interface for Swat2005 User’s Guide; Texas Water Resources Institute: Collage Station, TX, USA, 2005. [Google Scholar]
- Williams, J. Sediment-yield prediction with universal equation using runoff energy factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; Agriculture Research Service, US Department of Agriculture: Washington, DC, USA, 1975; pp. 244–252. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion from Cropland East of the Rocky Mountains-Guide for Selection of Practices for Soil and Water Conservation; US Department of Agriculture: Washington, DC, USA, 1965.
- Wlschmeler, W.; Smith, D. Predicting Rainfall-Erosion Losses—A Guide to Conservation Planning; US Department of Agriculture: Washington, DC, USA, 1978; Volume 537, pp. 1–60.
- Chad, F.; Hatim, S.; Jaehak, J. Analysis and simulation of large erosion events at central Texas unit source watersheds. J. Hydrol. 2015, 527, 494–504. [Google Scholar]
- Decoursey, D.G.; Snyder, W.M. Computer-oriented method of optimizing hydrologic model parameters. J. Hydrol. 1969, 9, 34–56. [Google Scholar] [CrossRef]
- Sadeghi, S. Application of MUSLE in prediction of sediment yield in Iranian conditions. In Proceedings of the ISCO 2004—13th International Soil Conservation Organization Conference, Brisbane, Australia, 4–8 July 2004; pp. 1–4. [Google Scholar]
- Cârdei, P. The Dimensional analysis of the USLE—MUSLE Soil Erosion Model. Proc. Rom. Acad. Ser. B 2010, 3, 249–253. [Google Scholar]
- Williams, J.R.; Berndt, H.D. Sediment yield prediction based on watershed hydrology. Trans. ASABE 1977, 20, 1100–1104. [Google Scholar] [CrossRef]
- Banasik, K.; Walling, D.E. Predicting Sedimentgraphs for a Small Agricultural Catchment. Nord. Hydrol. 1996, 27, 275–294. [Google Scholar]
- Madeyski, M.; Banasik, K. Applicability of the modified universal soil loss equation in small Carpathian watersheds. Catena 1989, 14, 75–80. [Google Scholar]
- Savenije, H.G. HESS Opinions “The art of hydrology”. Hydrol. Earth Syst. Sci. 2009, 13, 157–161. [Google Scholar] [CrossRef]
- Sadeghi, S.; Gholami, L.; Darvishan Khaledi, A.; Saeidi, P. A review of the application of the MUSLE model worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef]
- Van Griensven, A. Sensitivity, Auto-Calibration, Uncertainty and Model Evaluation in SWAT2005; UNESCO-IHE: Delft, The Netherlands, 2005. [Google Scholar]
- Saltelli, A.; Torantola, S.; Chan, K. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Saltelli, A. What is sensitivity analysis. In Sensitivity Analysis; Saltelli, A., Chan, K., Scott, E., Eds.; Wiley: New York, NY, USA, 2000; p. 42. ISBN 978-0-471-99892-1. [Google Scholar]
- Muleta, M.; Nicklow, J. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, A.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models e model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T. Methods to quantify and identify the sources of uncertainty for river basin water quality models. Water Sci. Technol. 2006, 53, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, Q.; Guo, B.; Gong, H. The comparative study of multi-site uncertainty evaluation method based on swat model. Hydrol. Process. 2015, 29, 2994–3009. [Google Scholar] [CrossRef]
- Marshall, L.; Nott, D.; Sharma, A. A comparative study of Markov chain Monte Carlo methods for conceptual rainfall-runoff modeling. Water Resour. Res. 2004, 40, 1–11. [Google Scholar] [CrossRef]
- Vrugt, J.; Gupta, H.; Bouten, W.; Sorooshian, S. A shuffled complex evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 1–14. [Google Scholar] [CrossRef]
- Holvoet, K.; Griensven, A.; Seuntjens, P. Sensitivity analysis for hydrology and pesticide supply towards. Phys. Chem. Earth 2003, 30, 518–526. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs; Swiss Federal Institute of Aquatic Science and Technology Eawag: Duebendorf, Switzerland, 2015; pp. 1–100. [Google Scholar]
- Faramarzi, M.; Abbaspour, K.C.; Adamowicz, W.L.; Wei, L.; Fennell, J.; Zehnder, A.J.; Goss, G.G. Uncertainty based assessment of dynamic freshwater scarcity in semi-arid watersheds of Alberta, Canada. J. Hydrol. Reg. Stud. 2017, 9, 48–68. [Google Scholar] [CrossRef]
- Shi, P.; Chen, C.; Srinivasan, R.; Zhang, X.; Cai, T.; Fang, X.; Li, Q. Evaluating the SWAT model for hydrological modeling in Xixian watershed and comparison with the XAJ model. J. Am. Water Resour. Manag. 2011, 25, 2595–2612. [Google Scholar] [CrossRef]
- Koutalakis, P.; Zaimes, G.; Ioannou, K.; Iakovoglou, V. Application of the SWAT model on torrents of the Menoikio, Greece. Fresen. Environ. Bull. 2017, 26, 1210–1215. [Google Scholar]
- Abu El-Nasr, A.; Arnold, J.; Feyen, J.; Berlamont, J. Modeling the hydrology of a catchment using a distributed and a semi distributed model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Beven, K.A. Discussion of distributed hydrological modelling. In Distributed Hydrological Modelling; Abbott, M.R., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 1996; pp. 255–278. [Google Scholar]
- Barrett, E.C. Satellite remote sensing of precipitation: Progress and problems. In Remote Sensing and Hydrology, Wallingford, United Kingdom, 2001; Owe, M., Brubaker, K., Ritchie, J., Rango, A., Eds.; International Association of Hydrological Sciences: Rennes, France, 2001. [Google Scholar]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the SWAT model on a large river basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Shimelis, G.S.; Ragahavan, S.; Assefa, M.M.; Bijan, D. SWAT model application and prediction uncertainty analysis in the Lake Tana basin, Ethiopia. Hydrol. Process. 2009, 24, 357–367. [Google Scholar]
- Iris, K. SWAT for Assessing Negative Impacts of Erosion in Lake Tana Basin; Technical University of Munich: Munich, Germany, 2016. [Google Scholar]
- Clarke, R. A review of some mathematical models used in hydrology, with observations on their calibrations and their use. J. Hydrol. 1973, 19, 1–20. [Google Scholar] [CrossRef]
- Xu, C.-Y. Statistical analysis of parameters and residuals of a conceptual water balance model—Methodology and case study. Water Resour. Manag. 2001, 15, 75–92. [Google Scholar] [CrossRef]
- Guinot, V.; Cappelaere, B.; Delenne, C.; Ruelland, D. Towards improved criteria for hydrological model calibration: Theoretical analysis of distance and weak form-based functions. J. Hydrol. 2011, 401, 1–13. [Google Scholar] [CrossRef]
- Bennett, N.; Croke, B.; Guariso, G.; Guillaume, J.; Hamilton, S.; Jakeman, A.; Andreassian, V. Characterizing performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J. River flow forecasting through conceptual models: Part I. A discussion of principle. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Boskidis, I.; Gikas, G.; Sylaios, G.; Tsihruntzis, V. Hydrologic and Water Quality Modeling of Lower Nestos River Basin. Water Resour. Manag. 2012, 26, 3023–3051. [Google Scholar] [CrossRef]
- Hogue, T.; Sorooshian, S.; Gupta, H.; Holz, A.; Braatz, D. A multistep automatic calibration scheme for river forecasting models. J. Hydrometeorol. 2000, 1, 524–542. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Yang, J.; Abbaspour, K.C.; Reichert, P.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Hurni, H. Soil Conservation Manual for Ethiopia: Field Guide for Conservation Implementation; Ministry of Agriculture: Addis Abeba, Ethiopia, 1985.


| N° | References | Soil Loss in t ha−1 yr−1 | Scale | |
|---|---|---|---|---|
| Spatial | Temporal | |||
| 1 | [11] | 42 | Plot based on cultivated fields | |
| 2 | [12] | 31 | Entire highlands | |
| 3 | [13] | 14.8 | 199 ha agriculture-dominated * | |
| 4 | [14] | 130 | Plot based on cultivated lands | |
| 35 | Entire highlands | |||
| 5 | [15] | 93 | 34,690 ha | |
| 6 | [16] | Tekezie (8,235,000 ha) basin tributaries | ||
| 2.49–3.27 | Genfel (66,000 ha) | seasonal | ||
| 15.62–18.5 | Lower Tankwa (21,300 ha) | seasonal | ||
| 7 | [17] | 4.97–65.43 | 513,300-ha agriculture-dominated catchment in Northern highlands * | |
| 8 | [18] | 25.6 | Small size catchment (9838 ha) | ** |
| 9 | [8] | Small experimental watersheds * | ||
| 5.2 | Andit Tid (477 ha) | seasonal | ||
| 24.7 | Anjeni (113 ha) | seasonal | ||
| 7.4 | Mayba (112 ha) | seasonal | ||
| 10 | [19] | 24.95 | Small size catchment (2500 ha) | |
| Statistical Efficiency Criterion | Model Performance Ratings | |||||
|---|---|---|---|---|---|---|
| Objective Function | Characteristics | Function Category | Reference | Value range | Performance Classification | References |
| R2 | Emphasize on high flows | Weak form-based | [91] | 0.7 < R2 < 1 0.6 < R2 < 0.7 0.5 < R2 < 0.6 R2 < 0.5 | Very good Good Satisfactory Unsatisfactory | [83] |
| ENS | Most common; emphasize on high flows; neglect the low flows | Distance-based | [92,93] | 0.75 < ENS ≤ 1.00 0.65 < ENS ≤ 0.75 0.50 < ENS ≤ 0.65 0.4 < ENS ≤ 0.50 ENS ≤ 0.4 | Very good Good Satisfactory Acceptable Unsatisfactory | [83,94] |
| BIAS | Monotony; cannot be used alone | Weak form-based | [88] | PBIAS < ±10 ±10 ≤ PBIAS < ±15 ±15 ≤ PBIAS < ±25 PBIAS ≥ ±25 | Very good Good Satisfactory Unsatisfactory | [91] |
| RSR | Monotony; cannot be used alone | Distance-based | [95] | 0.00 ≤ RSR ≤ 0.50 0.50 < RSR ≤ 0.60 0.60 < RSR ≤ 0.70 RSR > 0.70 | Very good Good Satisfactory Unsatisfactory | [83] |
| Daily Flow Calibration | |||||||||
| Parameter Name | Range | SUFI-2 | GLUE | ParaSol | PSO | ||||
| Rank | OM * | Rank | OM * | Rank | OM * | Rank | OM * | ||
| V__ALPHA_BNK.rte | 0–1 | 1 | 0.11 | 1 | 0.13 | 1 | 0.07 | 1 | 0.12 |
| R__CN2.mgt | ±0.2 | 2 | 0.13 | 3 | 0.12 | 2 | 0.12 | 2 | 0.14 |
| A__ESCO.hru | 0.01–1 | 3 | 0.04 | 4 | 0.01 | 7 | 0.03 | 8 | 0.13 |
| R__SOL_K(..).sol | −0.8–0.8 | 4 | 0.49 | 9 | 0.67 | 12 | 0.27 | 9 | 0.19 |
| V__CH_K2.rte | 5–130 | 5 | 72.68 | 5 | 84.38 | 3 | 76.42 | 3 | 84.10 |
| R__SOL_BD(..).sol | −0.5–0.6 | 6 | 0.24 | 6 | 0.23 | 5 | 0.25 | 12 | 0.24 |
| V__ALPHA_BF.gw | 0–1 | 7 | 0.56 | 8 | 0.61 | 11 | 0.55 | 13 | 0.57 |
| R__SOL_AWC(..).sol | −0.2–0.4 | 8 | −0.17 | 10 | −0.14 | 8 | −0.15 | 11 | −0.16 |
| A__GWQMN.gw | 0–5000 | 9 | 9.69 | 12 | 8.24 | 10 | 9.00 | 10 | 8.14 |
| V__GW_DELAY.gw | 30–450 | 10 | 351.27 | 13 | 269.37 | 9 | 307.70 | 5 | 223.89 |
| V__GW_REVAP.gw | 0–0.2 | 11 | 0.04 | 2 | 0.05 | 4 | 0.04 | 7 | 0.05 |
| V__REVAPMN.gw | 0–500 | 12 | 7.20 | 11 | 5.39 | 13 | 7.23 | 6 | 5.17 |
| V__CH_N2.rte | 0–0.3 | 13 | 0.16 | 7 | 0.17 | 6 | 0.20 | 4 | 0.19 |
| Monthly Flow Calibration | |||||||||
| Parameter Name | Range | SUFI-2 | GLUE | ParaSol | PSO | ||||
| Rank | OM * | Rank | OM * | Rank | OM * | Rank | OM * | ||
| V__ALPHA_BNK.rte | 0–1 | 1 | 0.17 | 1 | 0.12 | 2 | 0.12 | 1 | 0.11 |
| R__CN2.mgt | ±0.2 | 2 | 0.11 | 2 | 0.16 | 1 | 0.16 | 2 | 0.16 |
| A__ESCO.hru | 0.01–1 | 5 | −0.05 | 3 | 0.05 | 4 | 0.07 | 4 | 0.09 |
| R__SOL_K(..).sol | −0.8–0.8 | 3 | 0.16 | 4 | 0.57 | 13 | 0.69 | 11 | 0.39 |
| V__CH_K2.rte | 5–130 | 4 | 71.65 | 5 | 76.45 | 5 | 80.55 | 5 | 75.54 |
| R__SOL_BD(..).sol | −0.5–0.6 | 12 | 0.33 | 6 | 0.24 | 9 | 0.24 | 7 | 0.24 |
| V__ALPHA_BF.gw | 0–1 | 8 | 0.54 | 7 | 0.53 | 10 | 0.58 | 10 | 0.56 |
| R__SOL_AWC(..).sol | −0.2–0.4 | 6 | −0.13 | 8 | −0.16 | 11 | −0.17 | 8 | −0.17 |
| A__GWQMN.gw | 0–5000 | 13 | 17.62 | 9 | 9.72 | 12 | 9.47 | 12 | 7.22 |
| V__GW_DELAY.gw | 30–450 | 9 | 267.66 | 10 | 375.54 | 7 | 379.18 | 13 | 284.70 |
| V__GW_REVAP.gw | 0.02–0.2 | 7 | 0.16 | 11 | 0.03 | 3 | 0.00 | 3 | 0.02 |
| V__REVAPMN.gw | 0–500 | 11 | 3.98 | 12 | 6.03 | 6 | 6.27 | 9 | 6.44 |
| V__CH_N2.rte | 0–0.3 | 10 | 0.19 | 13 | 0.19 | 8 | 0.20 | 6 | 0.16 |
| SWAT-CUP Calibration | ||||||||
| Variables | SUFI-2 | GLUE | ParaSol | PSO | ||||
| Daily | Monthly | Daily | Monthly | Daily | Monthly | Daily | Monthly | |
| P-factor | 0.8 | 0.73 | 0.53 | 0.6 | 0.76 | 0.62 | 0.55 | 0.67 |
| R-factor | 0.81 | 0.93 | 0.5 | 0.64 | 0.6 | 0.65 | 0.47 | 0.61 |
| R2 | 0.37 | 0.65 | 0.38 | 0.63 | 0.47 | 0.64 | 0.37 | 0.63 |
| NSE | 0.33 | 0.58 | 0.32 | 0.57 | 0.31 | 0.58 | 0.32 | 0.59 |
| bR2 | 0.17 | 0.39 | 0.16 | 0.41 | 0.16 | 0.42 | 0.16 | 0.4 |
| PBIAS | 21.7 | 24.5 | 24.2 | 17.56 | 25.8 | 18.6 | 23.1 | 18.1 |
| KGE | 0.46 | 0.6 | 0.43 | 0.72 | 0.4 | 0.7 | 0.53 | 0.66 |
| RSR | 0.79 | 0.65 | 0.78 | 0.65 | 0.83 | 0.68 | 0.79 | 0.66 |
| SWAT-CUP Validation | ||||||||
| Variables | SUFI-2 | GLUE | ParaSol | PSO | ||||
| Daily | Monthly | Daily | Monthly | Daily | Monthly | Daily | Monthly | |
| P-factor | 0.72 | 0.65 | 0.46 | 0.64 | 0.5 | 0.69 | 0.53 | 0.65 |
| R-factor | 1.09 | 0.88 | 0.56 | 0.62 | 0.39 | 0.64 | 0.54 | 0.7 |
| R2 | 0.43 | 0.67 | 0.31 | 0.58 | 0.4 | 0.62 | 0.3 | 0.58 |
| NSE | 0.36 | 0.58 | 0.21 | 0.54 | 0.35 | 0.59 | 0.22 | 0.55 |
| bR2 | 0.25 | 0.47 | 0.15 | 0.43 | 0.12 | 0.4 | 0.13 | 0.43 |
| PBIAS | 23 | 8.8 | 6.94 | 2.70 | 21.5 | 4.32 | 17.3 | 1.5 |
| KGE | 0.62 | 0.66 | 0.53 | 0.78 | 0.51 | 0.72 | 0.5 | 0.72 |
| RSR | 0.77 | 0.64 | 0.86 | 0.74 | 0.8 | 0.76 | 0.86 | 0.73 |
| Parameter | Range | Rank | t-Stat | p-Value | Fitted Value |
|---|---|---|---|---|---|
| v__USLE_P.mgt | 0–1 | 1 | −111.8 | 0 | 0.07 |
| r__CH_COV.rte | −0.001−1 | 2 | 0.85 | 0.40 | 0.17 |
| v__SPEXP.bsn | 1–2 | 3 | 0.79 | 0.43 | 1.82 |
| v__SPCON.bsn | 0.0001−0.01 | 4 | 0.28 | 0.78 | 0.0015 |
| r__CH_EROD.rte | 0–1 | 5 | −0.16 | 0.87 | 0.26 |
| Component | P-Factor | R-Factor | R2 | NSE | bR2 | PBIAS | KGE | RSR |
|---|---|---|---|---|---|---|---|---|
| Calibration | 0.64 | 0.75 | 0.75 | 0.73 | 0.61 | 7.8 | 0.83 | 0.52 |
| Validation | 0.67 | 0.84 | 0.80 | 0.79 | 0.62 | 6.4 | 0.81 | 0.45 |
 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayele, G.T.; Teshale, E.Z.; Yu, B.; Rutherfurd, I.D.; Jeong, J. Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia. Water 2017, 9, 782. https://doi.org/10.3390/w9100782
Ayele GT, Teshale EZ, Yu B, Rutherfurd ID, Jeong J. Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia. Water. 2017; 9(10):782. https://doi.org/10.3390/w9100782
Chicago/Turabian StyleAyele, Gebiaw T., Engidasew Z. Teshale, Bofu Yu, Ian D. Rutherfurd, and Jaehak Jeong. 2017. "Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia" Water 9, no. 10: 782. https://doi.org/10.3390/w9100782
APA StyleAyele, G. T., Teshale, E. Z., Yu, B., Rutherfurd, I. D., & Jeong, J. (2017). Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia. Water, 9(10), 782. https://doi.org/10.3390/w9100782