Generalized Storage–Yield–Reliability Relationships for Analysing Shopping Centre Rainwater Harvesting Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection and Acquisition of Data
2.2. Simulation Analysis
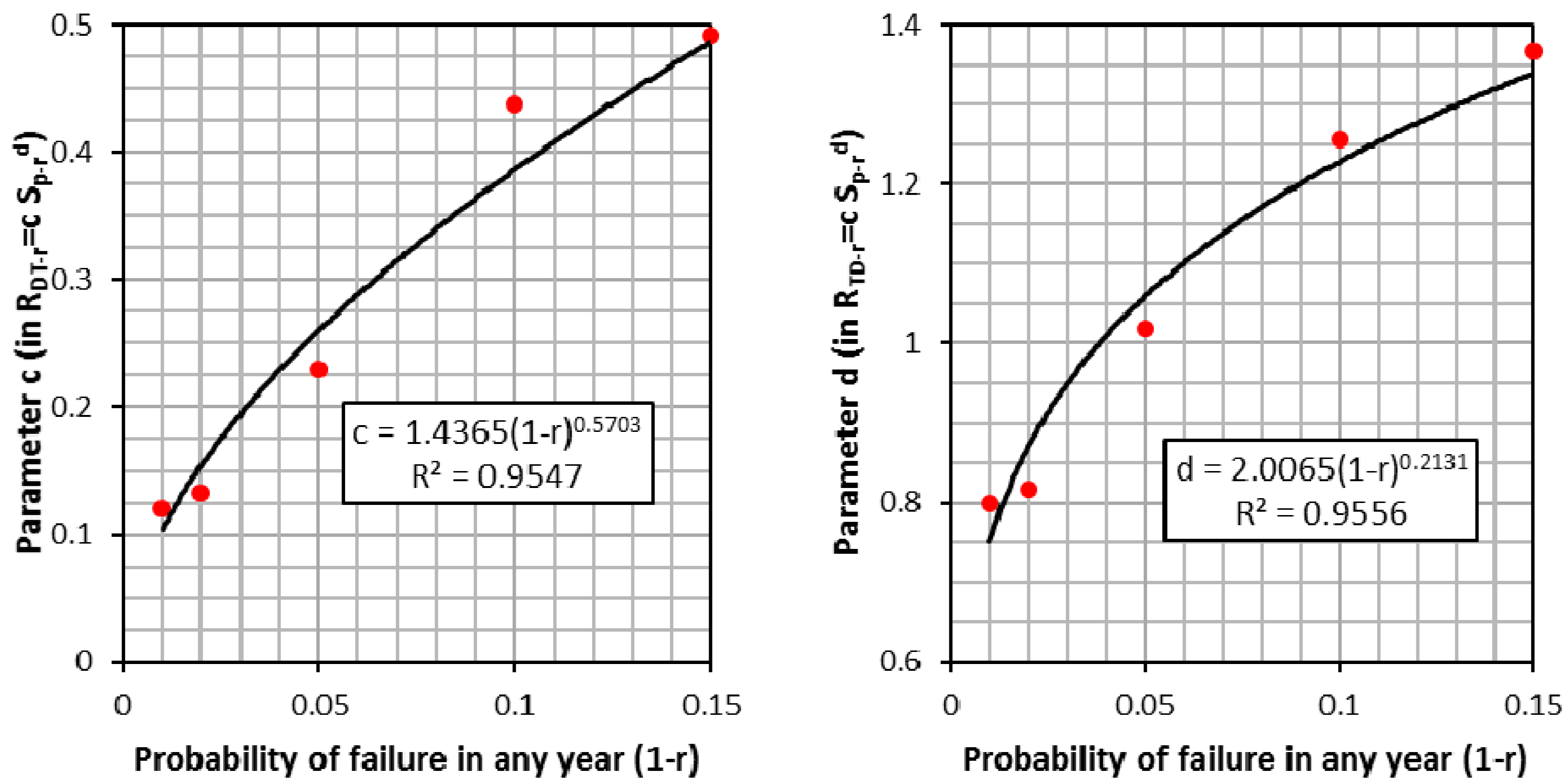
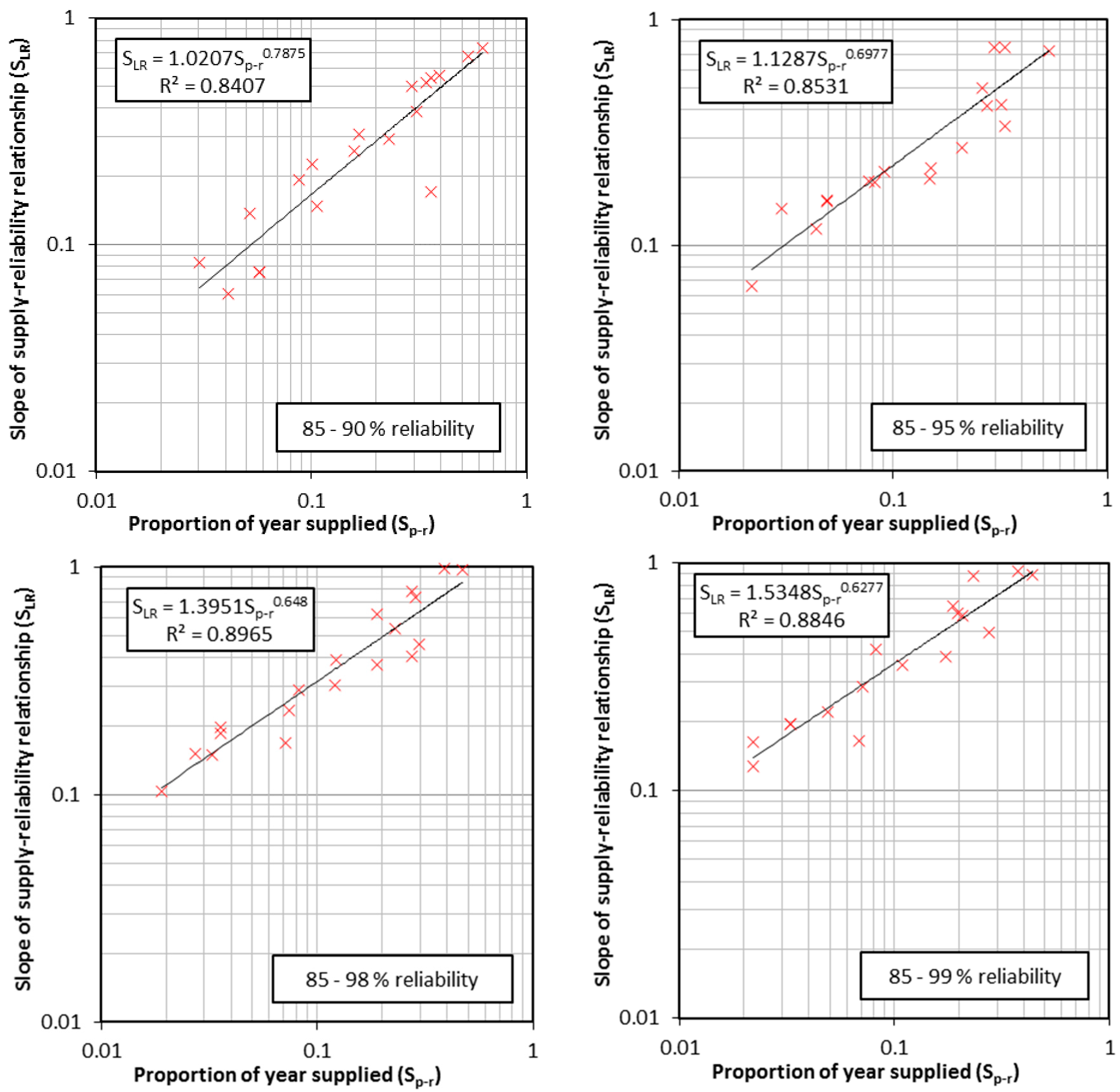
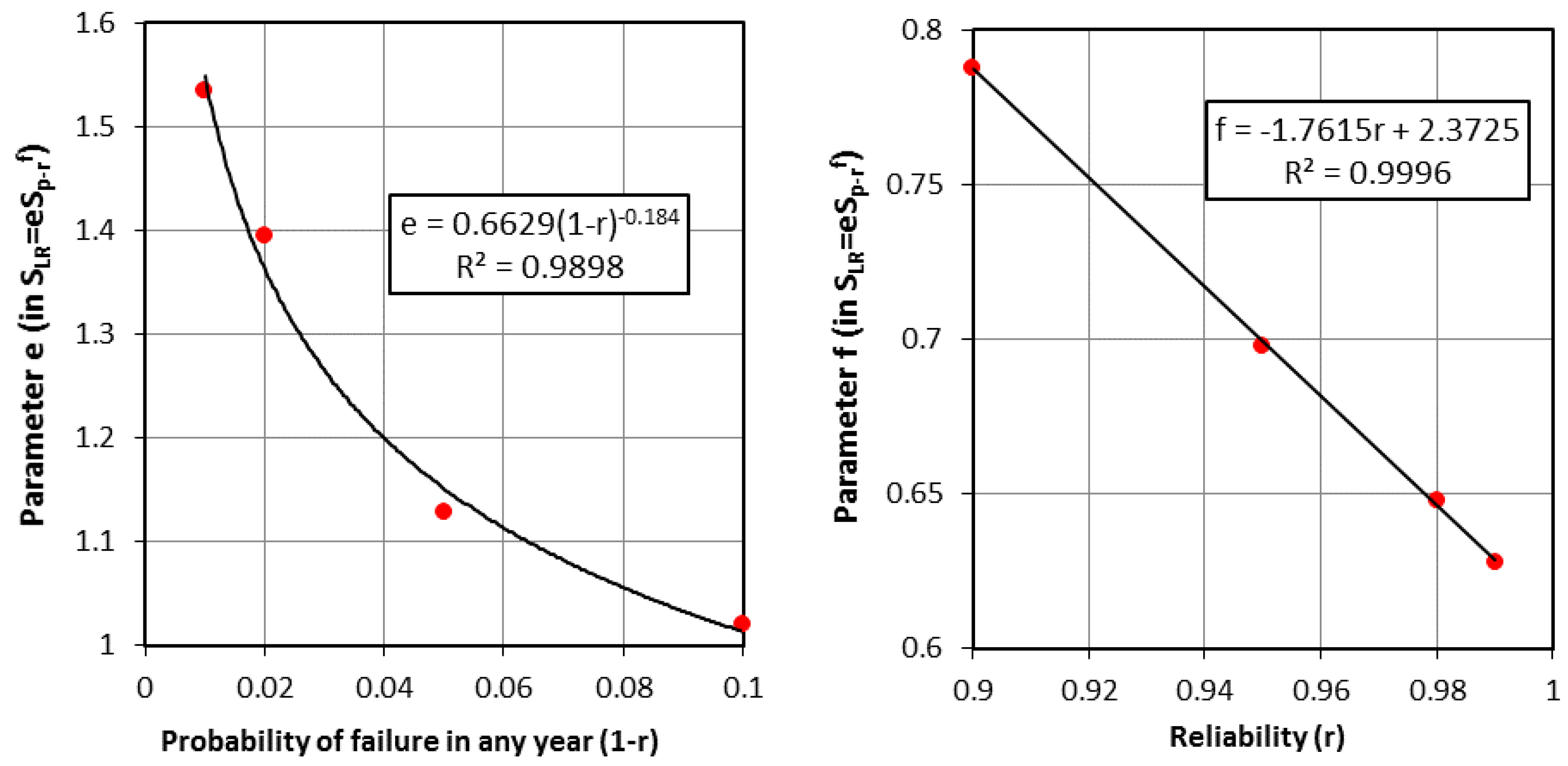
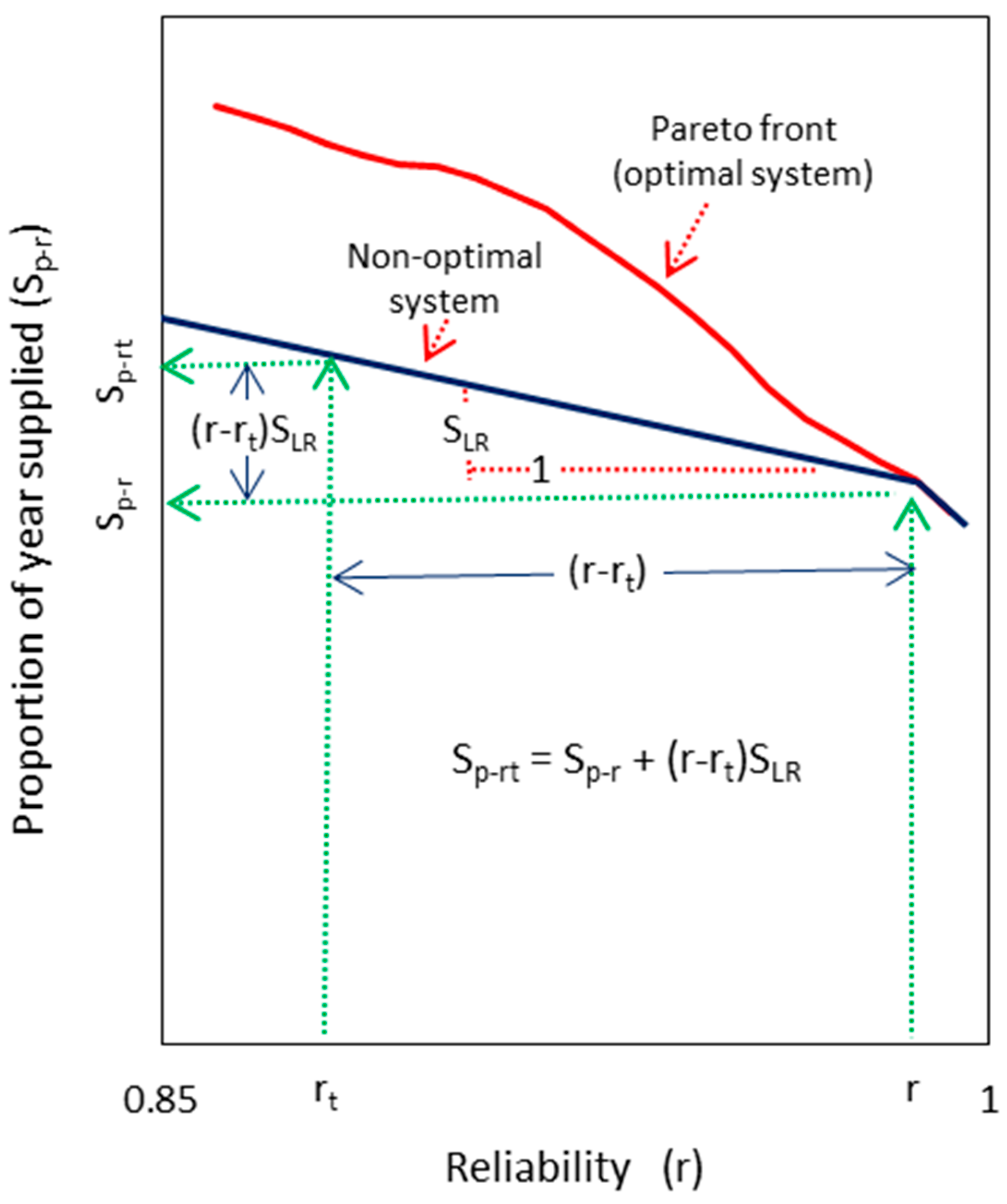
2.3. Formulating Generalized Storage–Yield–Reliability Relationships
3. Results
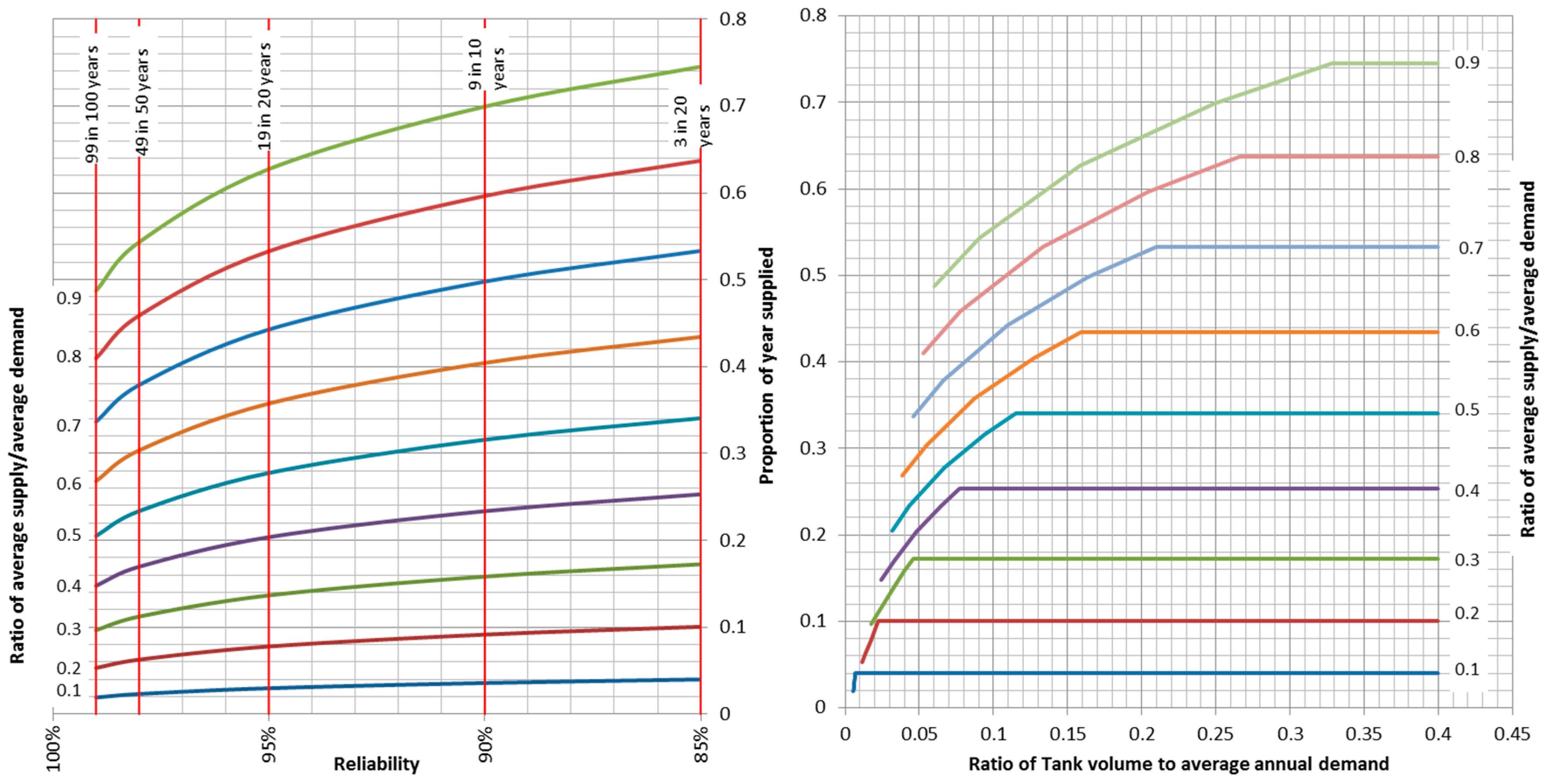
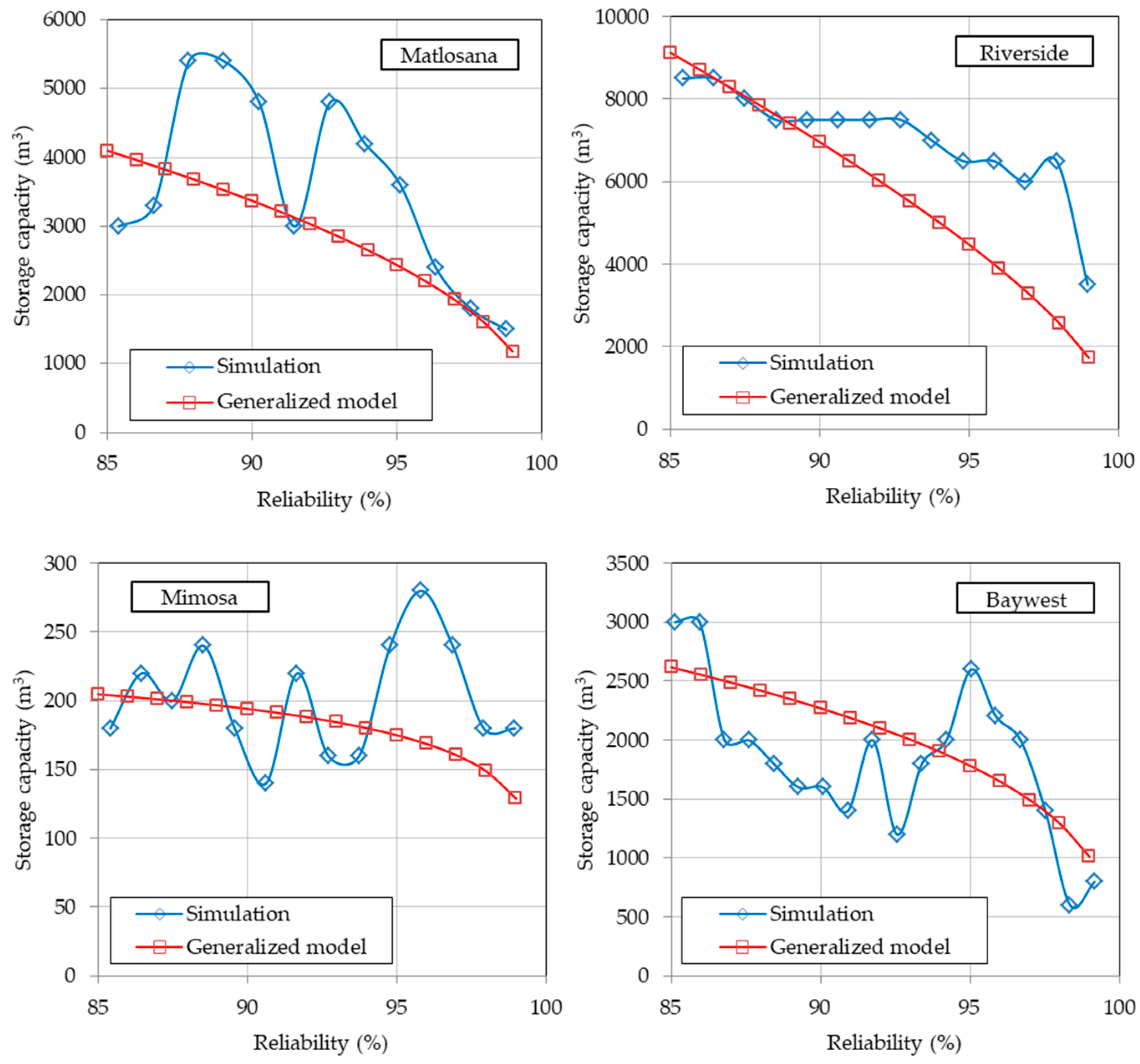
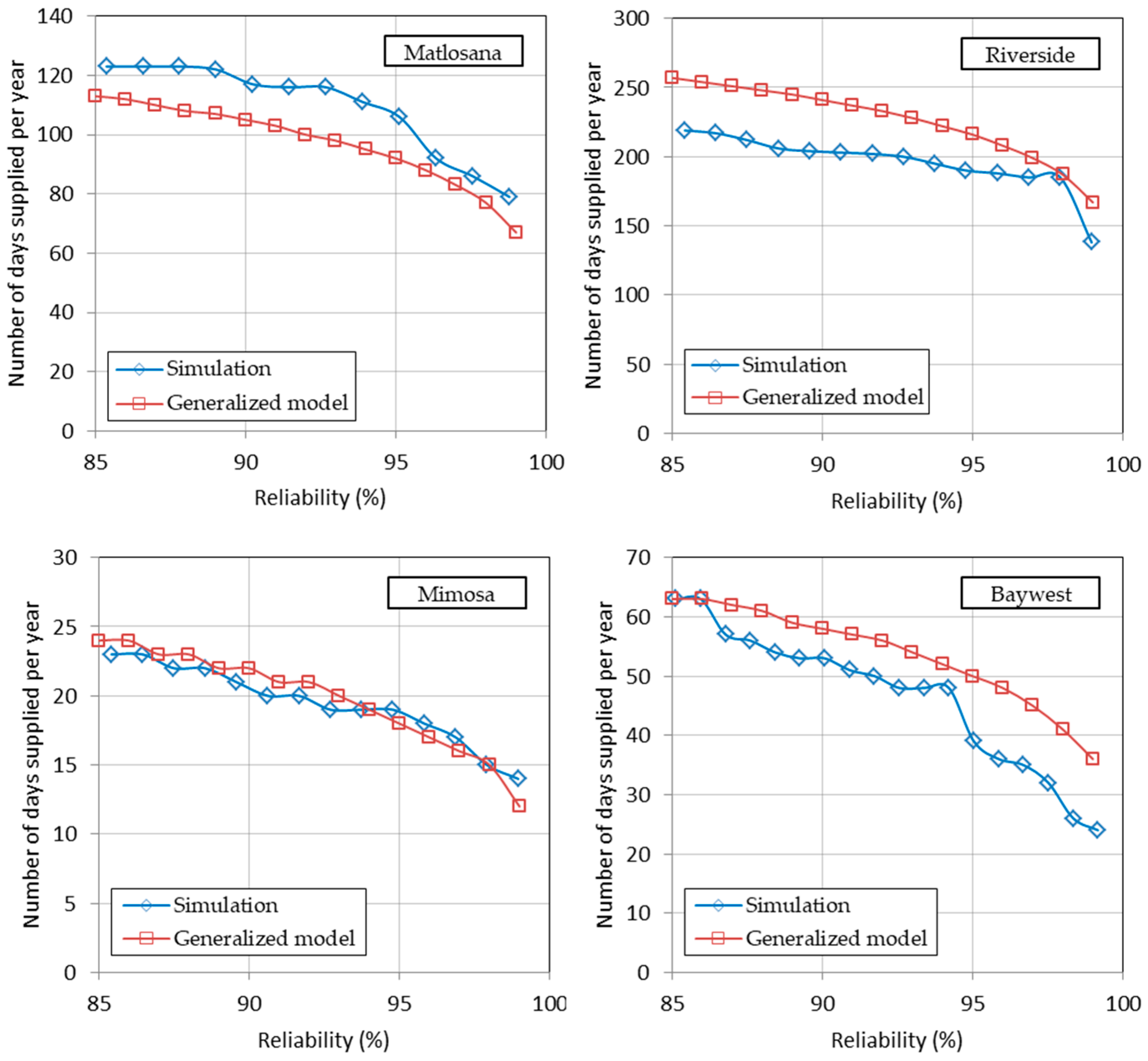
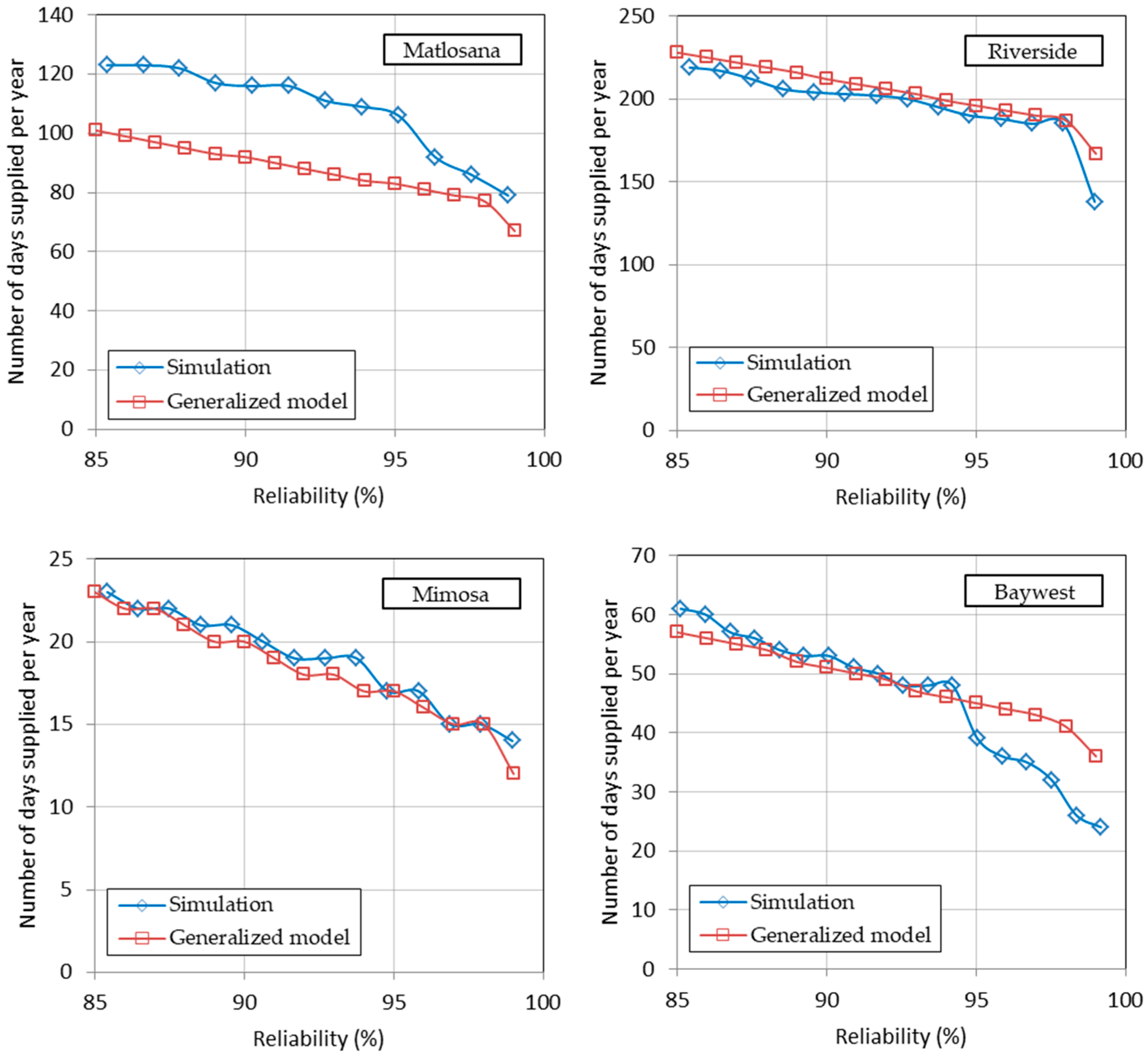
3.1. Simulation Analysis
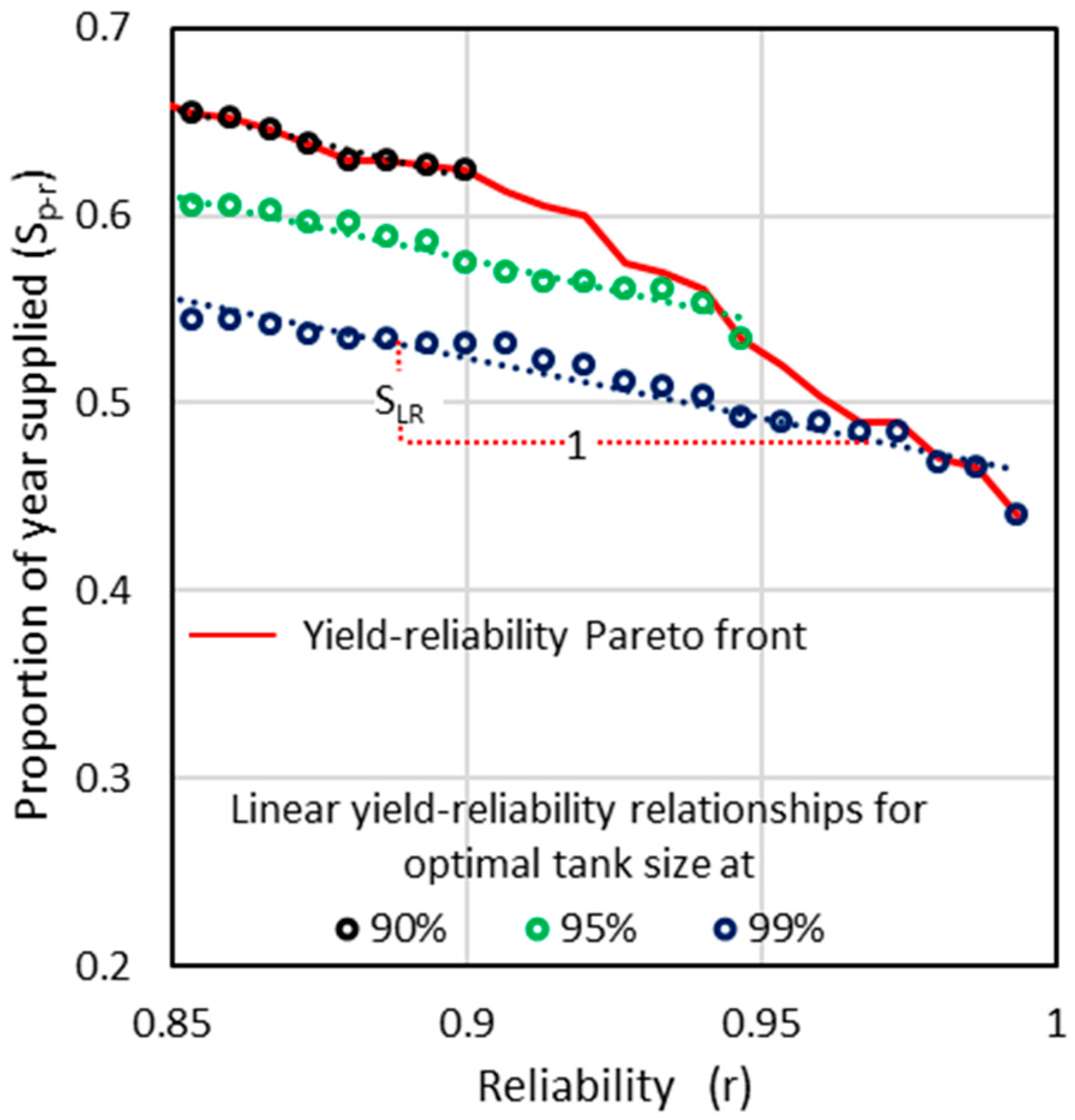
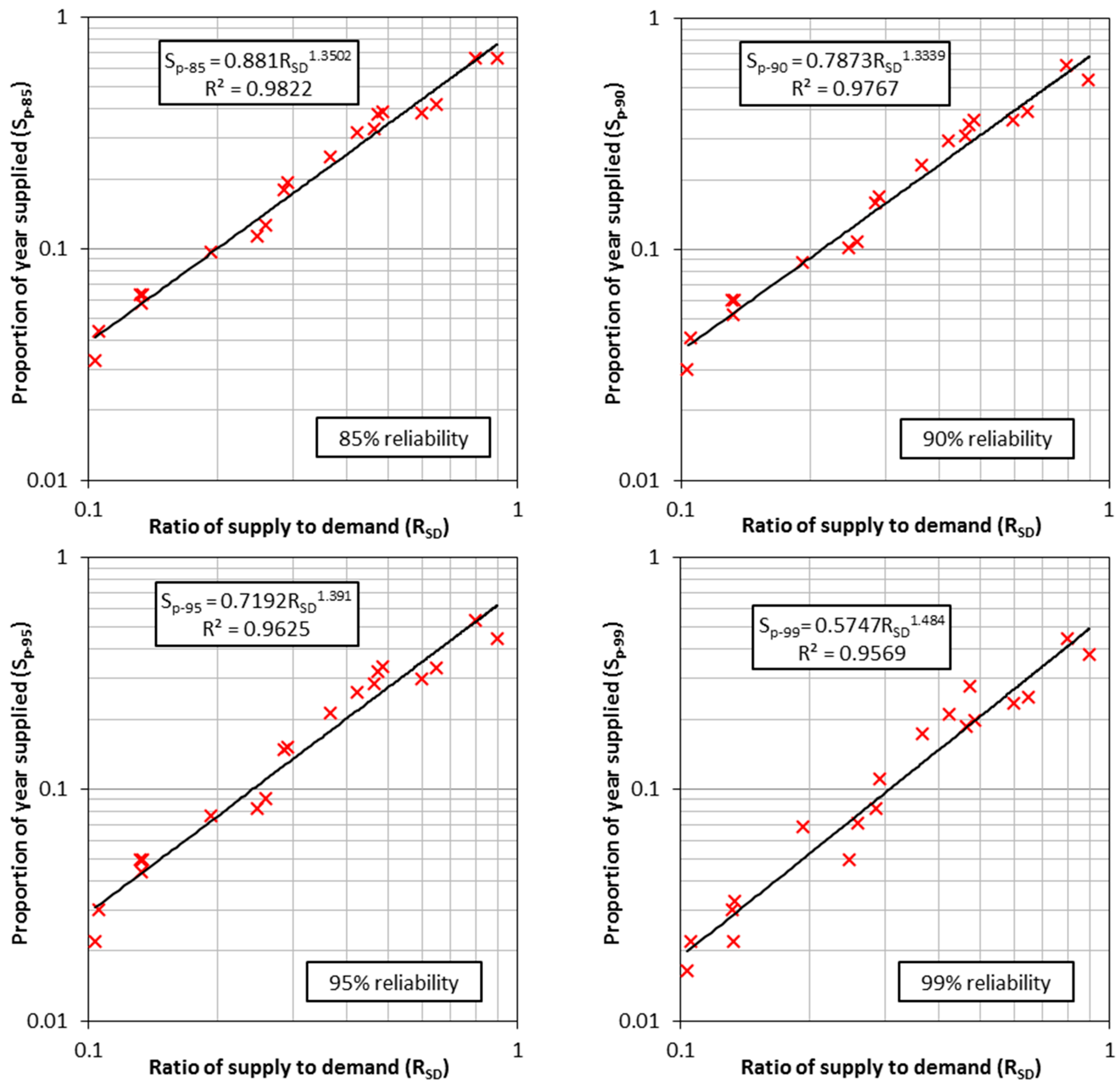
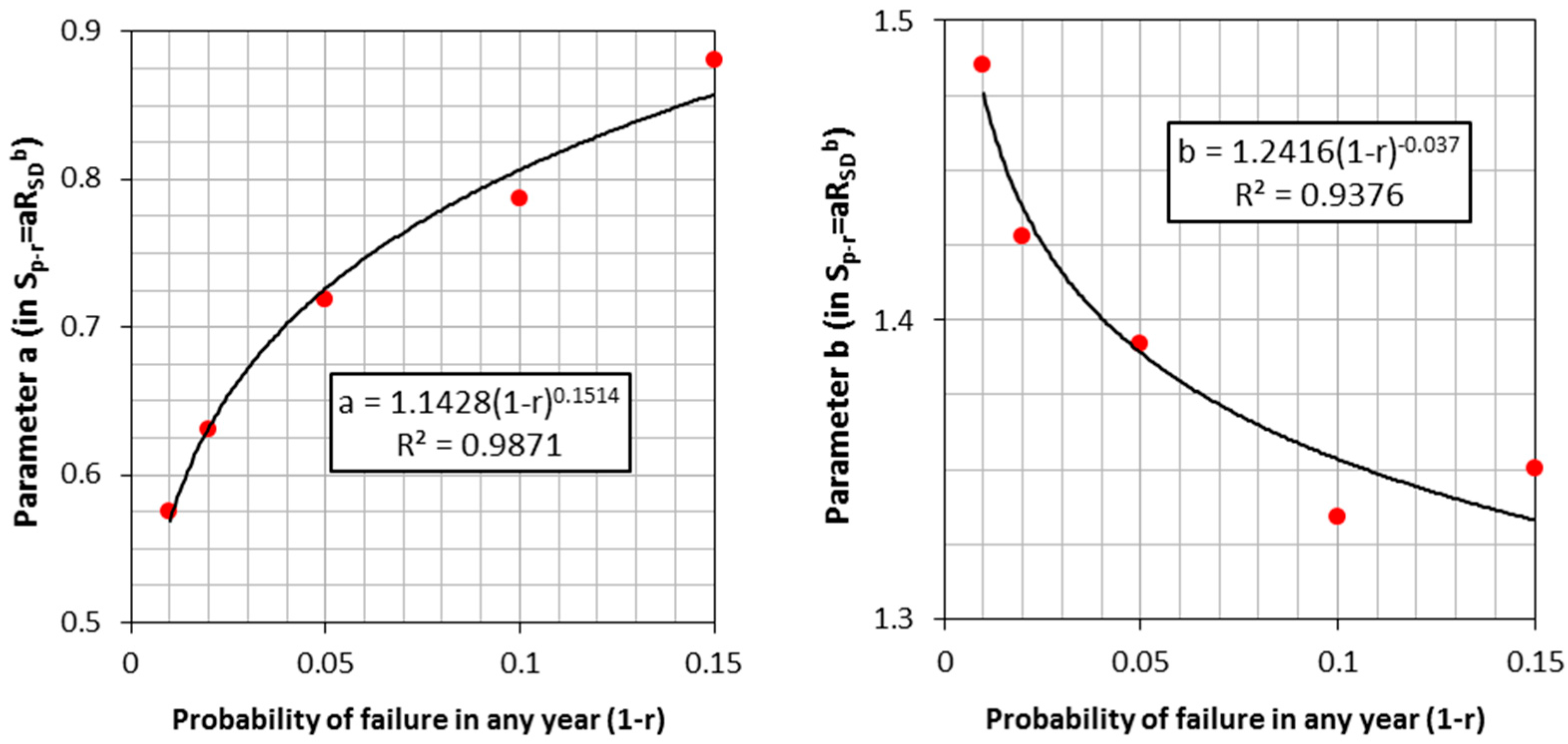
3.2. Generalized Storage–Yield–Reliability Relationships
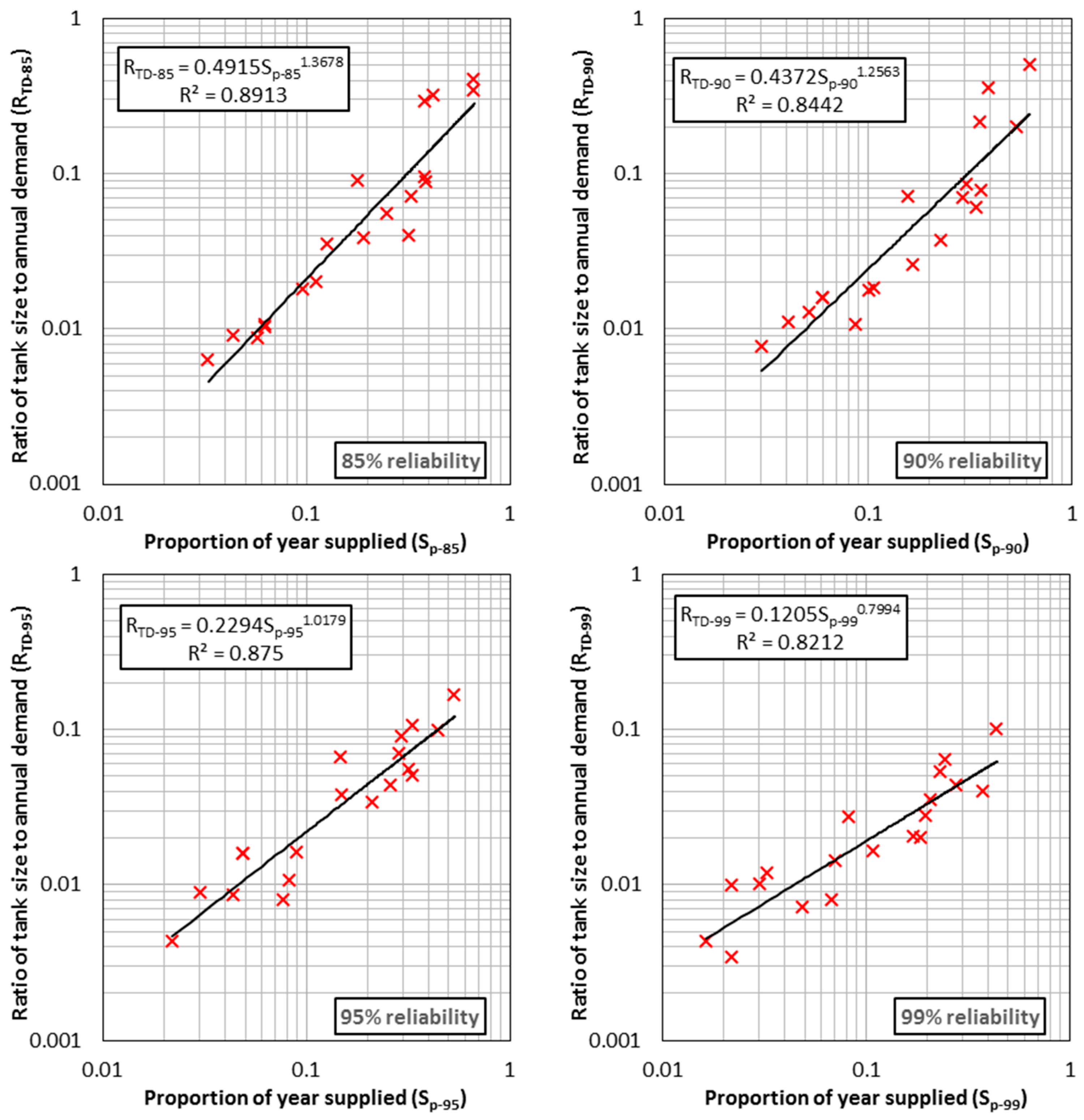
3.3. Verification of Generalized Model
4. Case Study: RWH System for Maponya Mall
5. Discussion and Conclusions
Author Contributions
Conflicts of Interest
References
- United Nations Educational, Scientific and Cultural Organization (UNESCO). The United Nations World Water Development Report 3: Water in a Changing World; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2009. [Google Scholar]
- United Nations Educational, Scientific and Cultural Organization (UNESCO). World Water Development Report Volume 4: Managing Water under Uncertainty and RISK; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2012; Volume 1. [Google Scholar]
- Department of Water Affairs. National Water Resource Strategy: South Africa; Department of Water Affairs: Pretoria, South Africa, 2013; 201p.
- O’Brien, O. Domestic Water Demand for Consumers with Rainwater Harvesting Systems. Master’s Thesis, Department of Civil Engineering, Division of Water and Environmental Engineering, Stellenbosch University, Stellenbosch, South Africa, 2014. [Google Scholar]
- Tito, M.P. Modelling and Sustainable Management of Rainwater Harvesting in Urban Systems. Ph.D. Thesis, Universitat Autònoma de Barcelona (UAB), Barcelona, Spain, 2012. [Google Scholar]
- Rahman, A.; Keane, J.; Imteaz, M.A. Rainwater harvesting in Greater Sydney: Water savings, reliability and economic benefits. Resour. Conserv. Recycl. 2012, 61, 16–21. [Google Scholar] [CrossRef]
- Ghisi, E.; Schondermark, P.N. Investment Feasibility Analysis of Rainwater Use in Residences. Water Resour. Manag. 2013, 27, 2555–2576. [Google Scholar] [CrossRef]
- Farreny, R.; Gabarrell, X.; Rieradevall, J. Cost-efficiency of rainwater harvesting strategies in dense Mediterranean neighbourhoods. Resour. Conserv. Recycl. 2011, 55, 686–694. [Google Scholar] [CrossRef]
- Campisano, A.; Butler, D.; Ward, S.; Burns, M.J.; Friedler, E.; DeBusk, K.; Fisher-Jeffes, L.N.; Ghisi, E.; Rahman, A.; Furumai, H.; et al. Urban rainwater harvesting systems: Research, implementation and future perspectives. Water Res. 2017, 115, 195–209. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.S. Cost Recovery in Urban Water Services: Select Experiences in Indian Cities; Water and Sanitation Program, World Bank: Washington, DC, USA, March 2011. [Google Scholar]
- Farolfi, S.; Gallego-Ayala, J. Domestic water access and pricing in urban areas of Mozambique: Between equity and cost recovery for the provision of a vital resource. Int. J. Water Resour. Dev. 2014, 30, 728–744. [Google Scholar] [CrossRef]
- Sample, D.J.; Liu, J. Optimizing rainwater harvesting systems for the dual purposes of water supply and runoff capture. J. Clean. Prod. 2014, 75, 174–194. [Google Scholar] [CrossRef]
- Chiu, Y.R.; Tsai, Y.L.; Chiang, Y.C. Designing rainwater harvesting systems cost-effectively in a urban water-energy saving scheme by using a GIS-simulation based design system. Water 2015, 7, 6285–6300. [Google Scholar] [CrossRef]
- Dobrowksy, P.H.; Mannel, D.; De Kwaadsteniet, M.; Prozesky, H.; Khan, W.; Cloete, T.E. Quality assessment and primary uses of harvested rainwater in Kleinmond, South Africa. Water SA 2014, 40, 401–406. [Google Scholar] [CrossRef]
- Abbott, S.E.; Douwes, J.; Caughley, B.P. A survey of the microbiological quality of roof-collected rainwater of private dwellings in New Zealand. N. Z. J. Environ. Health 2006, 29, 6–16. [Google Scholar]
- Evans, C.A.; Coombes, P.J.; Dunstan, R.H. Wind, rain and bacteria: The effect of weather on the microbial composition of roof-harvested rainwater. Water Res. 2006, 40, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.; McBroom, M.W.; Scott Beasley, R. Roofing as a source of nonpoint water pollution. J. Environ. Manag. 2004, 73, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Evison, L.; Sunna, N. Microbial regrowth in household water storage tanks. J. Am. Water Work Assoc. 2001, 93, 85–94. [Google Scholar]
- Van der Sterren, M.; Rahman, A.; Dennis, G.R. Quality and Quantity Monitoring of Five Rainwater Tanks in Western Sydney, Australia. J. Environ. Eng. 2013, 139, 332–340. [Google Scholar] [CrossRef]
- Sazakli, E.; Alexopoulos, A.; Leotsinidis, M. Rainwater harvesting, quality assessment and utilization in Kefalonia Island, Greece. Water Res. 2007, 41, 2039–2047. [Google Scholar] [CrossRef] [PubMed]
- Mwenge Kahinda, J.; Taigbenu, A.E. Rainwater harvesting in South Africa: Challenges and opportunities. Phys. Chem. Earth 2011, 36, 968–976. [Google Scholar] [CrossRef]
- Ndiritu, J.G.; McCarthy, S.; Tshirangwana, N. Probabilistic assessment of the rainwater harvesting potential of schools in South Africa. Proc. Int. Assoc. Hydrol. Sci. 2014, 364, 435–440. [Google Scholar] [CrossRef]
- Prinsloo, D.A. Classification and Hierarchy of Retail Facilities in South Africa; Urban Studies: Johannesburg, South Africa, 2010; 76p. [Google Scholar]
- Green Building Council of South Africa. Green Star South Africa: Office V1.1 Technical Manual; Green Building Council of South Africa: Cape Town, South Africa, 2014. [Google Scholar]
- Fonseca, C.R.; Hidalgo, V.; Díaz-Delgado, C.; Vilchis-Francés, A.Y.; Gallego, I. Design of optimal tank size for rainwater harvesting systems through use of a web application and geo-referenced rainfall patterns. J. Clean. Prod. 2017, 145, 323–335. [Google Scholar] [CrossRef]
- Hanson, L.S.; Vogel, R.M. Generalized storage-reliability-yield relationships for rainwater harvesting systems. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Optimal sizing of storage tanks for domestic rainwater harvesting in Sicily. Resour. Conserv. Recycl. 2012, 63, 9–16. [Google Scholar] [CrossRef]
- Liaw, C.H.; Chiang, Y.C. Dimensionless analysis for designing domestic rainwater harvesting systems at the regional level in Northern Taiwan. Water 2014, 6, 3913–3933. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Ahsan, A.; Shanableh, A. Reliability analysis of rainwater tanks using daily water balance model: Variations within a large city. Resour. Conserv. Recycl. 2013, 77, 37–43. [Google Scholar] [CrossRef]
- Liaw, C.; Tsai, Y. Optimum Storage Volume of Rooftop Rain Water Harvesting Systems for Domestic Use. J. Am. Water Resour. Assoc. 2004, 901–912. [Google Scholar] [CrossRef]
- Notaro, V.; Liuzzo, L.; Freni, G. Reliability Analysis of Rainwater Harvesting Systems in Southern Italy. Procedia Eng. 2016, 162, 373–380. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Adeboye, O.B.; Rayburg, S.; Shanableh, A. Rainwater harvesting potential for southwest Nigeria using daily water balance model. Resour. Conserv. Recycl. 2012, 62, 51–55. [Google Scholar] [CrossRef]
- Prinsloo, D.A. Benchmarking the South African Shopping Centre Industry International and Local Trends; South African Council of Shopping Centres, Shopping Centre Directory: Gauteng, South Africa, 2013. [Google Scholar]
- Lynch, S. The Development of a Raster Database of Annual, Monthly and Daily Rainfall for Southern Africa; WRC Report No. 1156/0/1; Water Research Commission: Pretoria, Southern Africa, 2003. [Google Scholar]
- Council for Science and Industiral Research. Guidelines for Human Settlement Plannning and Design; Council for Science and Industiral Research: New Delhi, Delhi, 2005; Volume 2. [Google Scholar]
- Saunders, A. Shopping Centre Water Efficiency Report; HFM Asset Management: Perth, Australia, 2012. [Google Scholar]
- Santos, C.; Taveira-Pinto, F. Analysis of different criteria to size rainwater storage tanks using detailed methods. Resour. Conserv. Recycl. 2013, 71, 1–6. [Google Scholar] [CrossRef]
- Ndiritu, J.; Odiyo, J.O.; Makungo, R.; Ntuli, C.; Mwaka, B. Yield-reliability analysis for rural domestic water supply from combined rainwater harvesting and run-of-river abstraction. Hydrol. Sci. J. 2011, 56, 238–248. [Google Scholar] [CrossRef]
- Ward, S.; Memon, F.A.; Butler, D. Rainwater harvesting: Model-based design evaluation. Water Sci. Technol. 2010, 61, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Su, M.D.; Lin, C.H.; Chang, L.F.; Kang, J.L.; Lin, M.C. A probabilistic approach to rainwater harvesting systems design and evaluation. Resour. Conserv. Recycl. 2009, 53, 393–399. [Google Scholar] [CrossRef]
- Yaziz, M.I.; Gunting, H.; Sapari, N.; Ghazali, A.W. Variations in rainwater quality from roof catchments. Water Res. 1989, 23, 761–765. [Google Scholar] [CrossRef]
- Silva Vieira, A.; Weeber, M.; Ghisi, E. Self-cleaning filtration: A novel concept for rainwater harvesting systems. Resour. Conserv. Recycl. 2013, 78, 67–73. [Google Scholar] [CrossRef]
- Fewkes, A. Modelling the performance of rainwater collection systems: Towards a generalised approach. Urban Water. 2000, 1, 323–333. [Google Scholar] [CrossRef]
- Berwanger, H.; Ghisi, E. Investment feasibility analysis of rainwater harvesting in the city of Itapiranga, Brazil. Int. J. Sustain. Hum. Dev. 2014, 2, 104–114. [Google Scholar]
- Melville-Shreeve, P.; Ward, S.; Butler, D. Rainwater harvesting typologies for UK houses: A multi criteria analysis of system configurations. Water 2016, 8. [Google Scholar] [CrossRef]
- Mashau, F. Rainwater Harvesting for Multiple Uses in Siloam Village of Limpopo Province, South Africa; Unpublished Honours Research Dissertation; University of Venda: Thohoyandou, South Africa, 2006. [Google Scholar]
- Ghisi, E.; Tavares, D.D.F.; Rocha, V.L. Rainwater harvesting in petrol stations in Brasília: Potential for potable water savings and investment feasibility analysis. Resour. Conserv. Recycl. 2009, 54, 79–85. [Google Scholar] [CrossRef]
- Basson, M.S.; Allen, R.B.; Pegram, G.G.S.; Van Rooyen, J. Probabilistic Management of Water Resource and Hydropower Systems; Water Resources Publications: Littleton, CO, USA, 1994. [Google Scholar]
- Basson, M.S.; van Rooyen, J.A. Practical Application of Probabilistic Approaches to the Management of Water Resource Systems. J. Hydrol. 2001, 241, 53–61. [Google Scholar] [CrossRef]
- Ndiritu, J.; Odiyo, J.; Makungo, R.; Mwaka, B.; Mthethwa, N.; Ntuli, C.; Andanje, A. Development of probabilistic operating rules for Hluhluwe Dam, South Africa. Phys. Chem. Earth 2017, 100, 343–352. [Google Scholar] [CrossRef]
- Weibull, W. A statistical theory of strength of materials. Ing. Vetensk. Akad. Handl. 1939, 151, 1–45. [Google Scholar]
- Cunnane, C. Unbiased plotting positions—A review. J. Hydrol. 1978, 37, 205–222. [Google Scholar] [CrossRef]
- Makkonen, L. Plotting positions in extreme value analysis. J. Appl. Meteorol. Climatol. 2006, 45, 334–340. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Shanableh, A.; Rahman, A.; Ahsan, A. Optimisation of rainwater tank design from large roofs: A case study in Melbourne, Australia. Resour. Conserv. Recycl. 2011, 55, 1022–1029. [Google Scholar] [CrossRef]
- City of Johannesburg. Climate Change Adaptation Plan; City of Johannesburg: Johannesburg, South Africa, 2009. [Google Scholar]

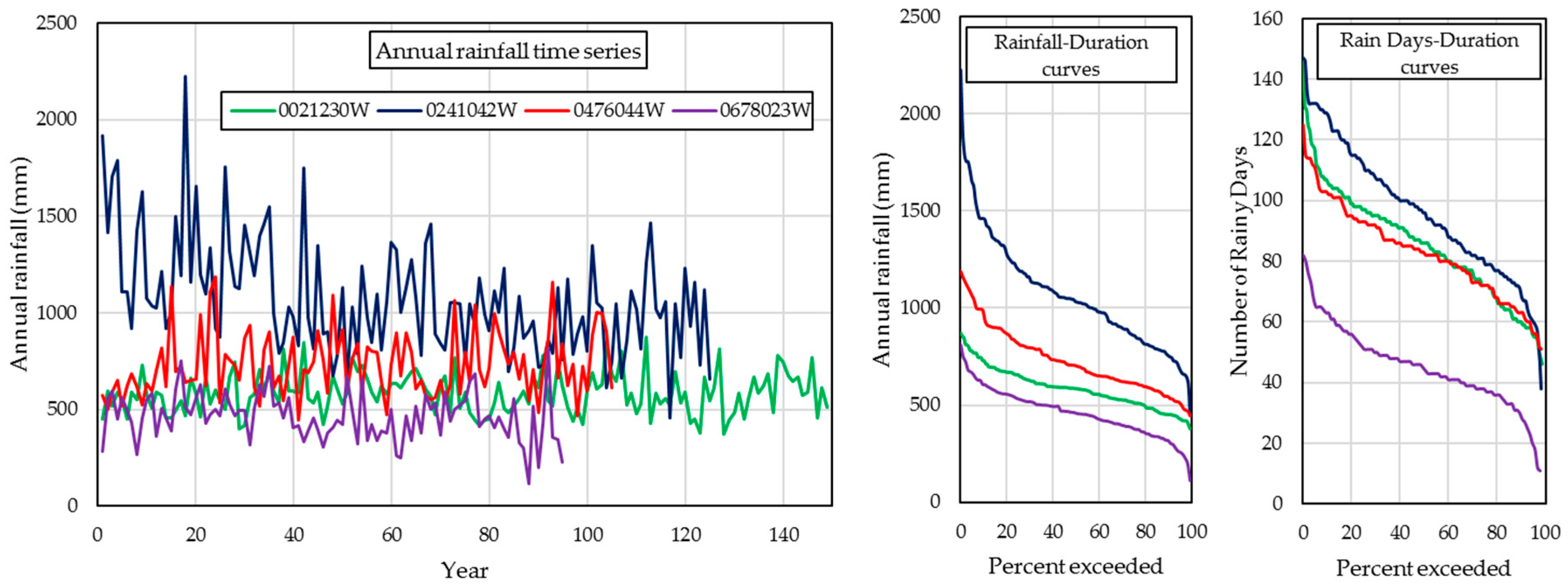
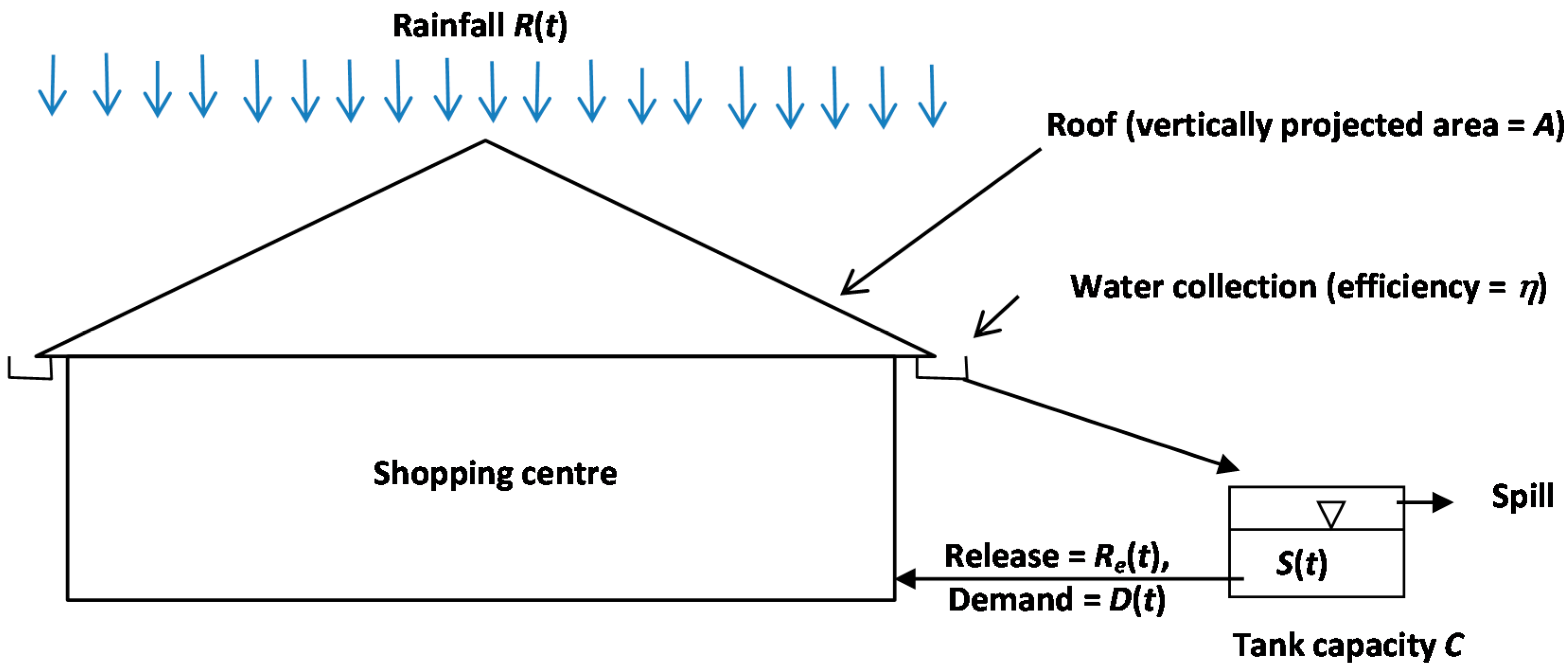
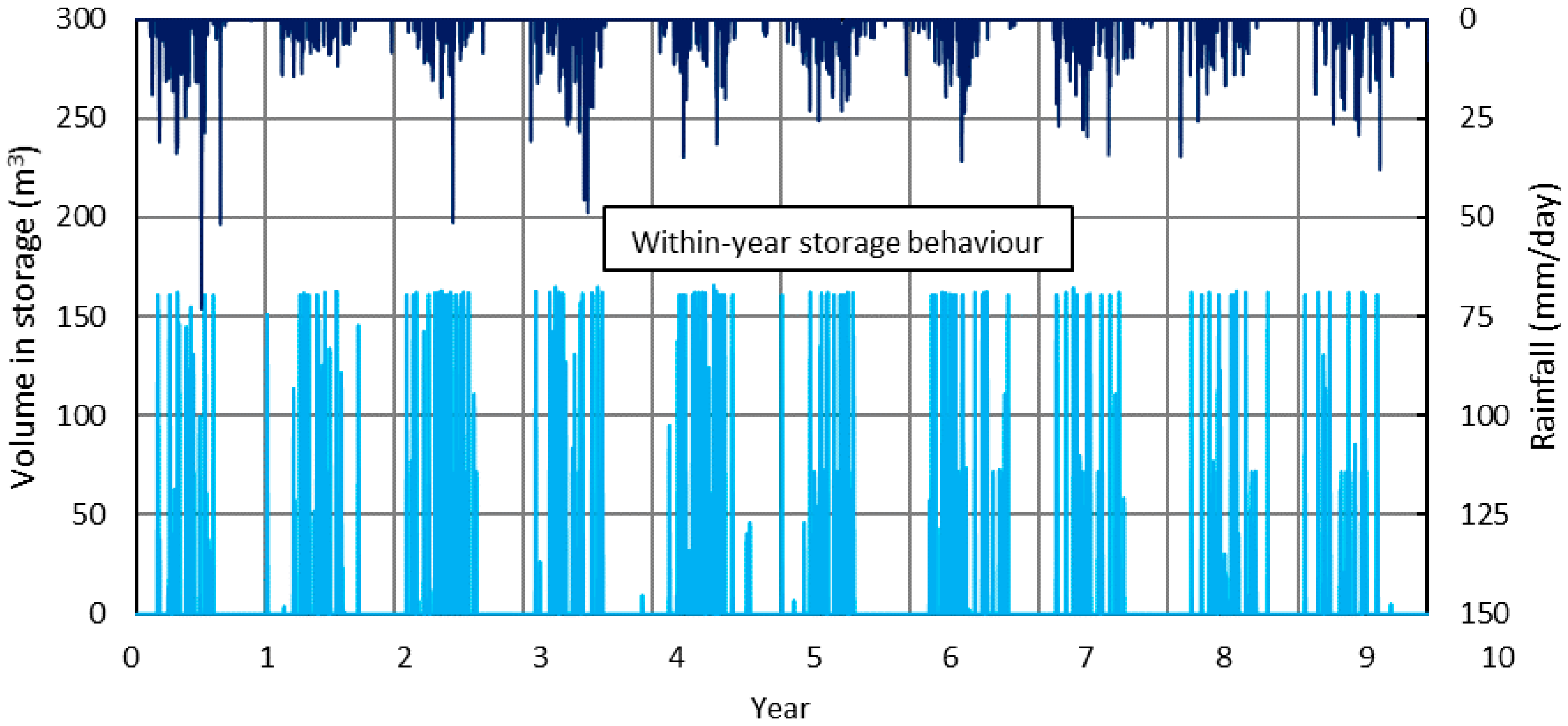
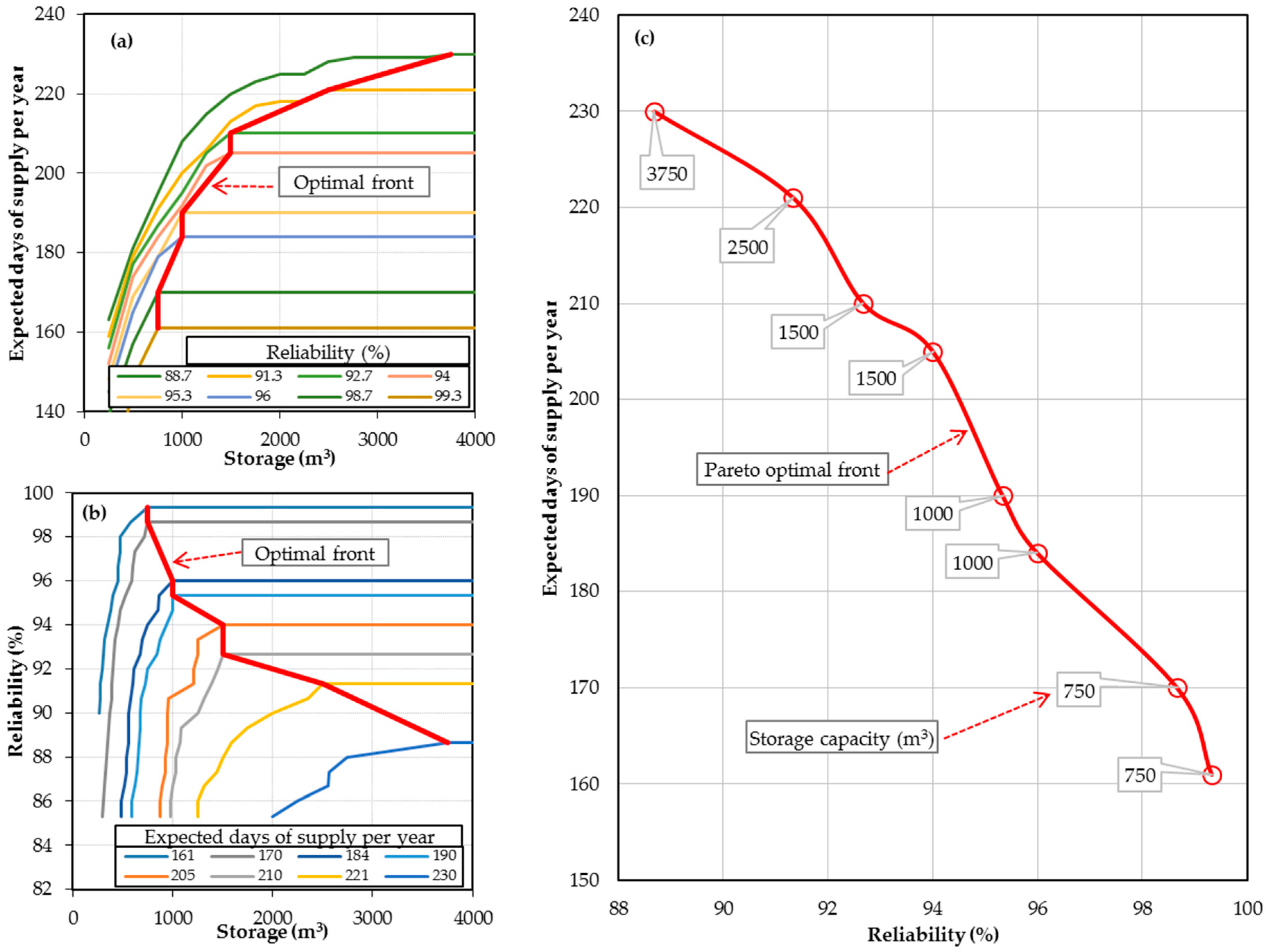
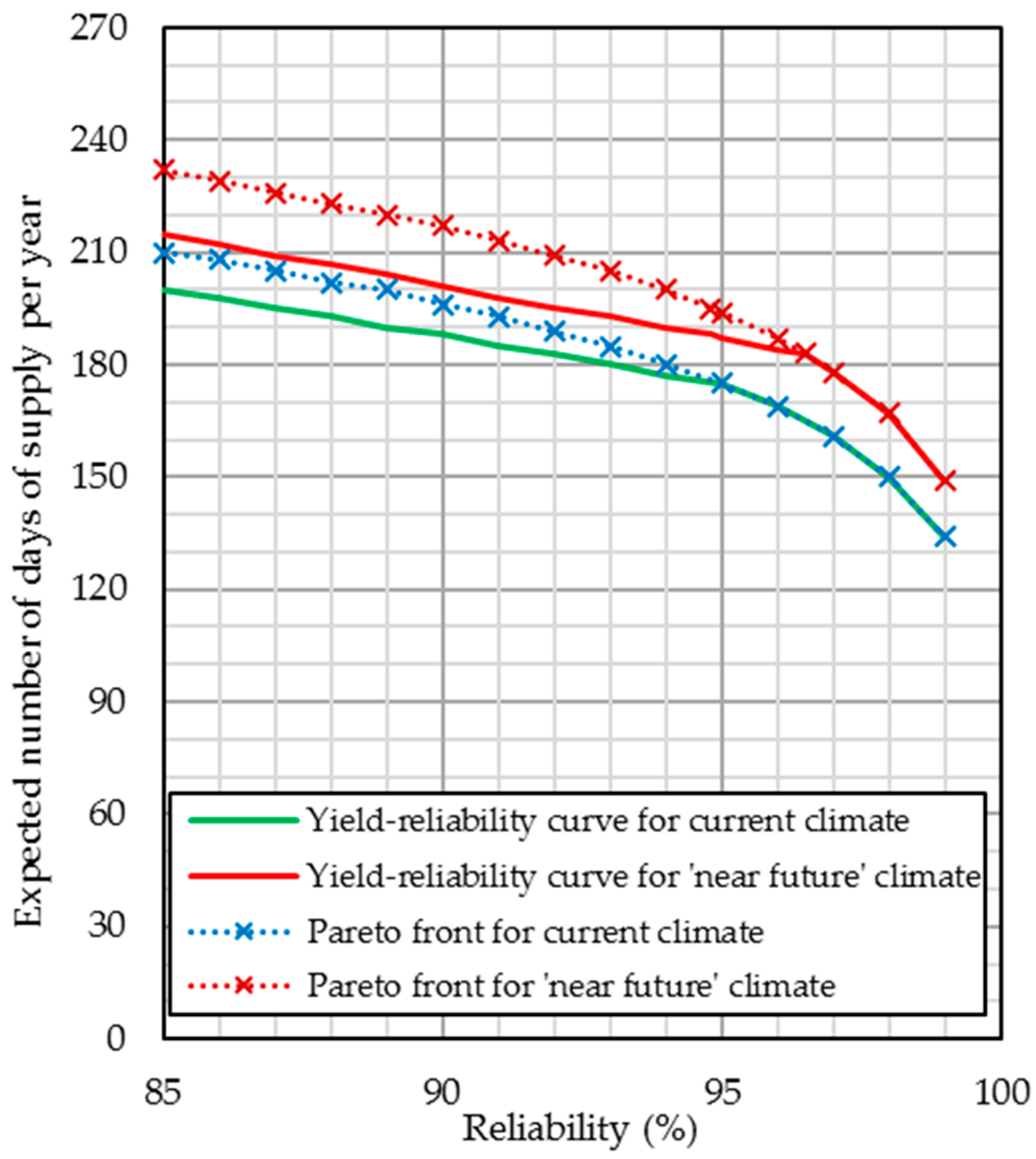
| Region | Mall | Retail Area (m2) | Roof Area (m2) | Rainfall Station No. | Distance from Mall (km) |
|---|---|---|---|---|---|
| Gauteng | Sandton City | 128,000 | 83,472 | 0476093 W | 6.67 |
| South Gate Mall | 89,700 | 45,349 | 0476044 W | 6.24 | |
| Norwood Mall | 32,344 | 32,194 | 0476129 W | 0.43 | |
| Braamfontein Centre | 21,309 | 3416 | 0475881 W | 0.97 | |
| Grayston Centre | 5000 | 4198 | 0476093 W | 5.68 | |
| Cape Town | Canal Walk | 141,000 | 26,082 | 0020896 W | 4.38 |
| Tygervally Centre | 90,000 | 55,403 | 0021230 W | 4.74 | |
| Willow Bridge | 40,051 | 23,390 | 0021230 W | 3.95 | |
| Howard Centre | 15,000 | 14,052 | 0021055 w | 2.88 | |
| Capricon Square | 5889 | 6374 | 0020839 W | 13.11 | |
| Limpopo | Mall of the North | 75,000 | 35,199 | 0678023 W | 1.26 |
| Savanah Mall | 37,000 | 17,880 | 0677834 W | 2.15 | |
| Limpopo Mall | 27,766 | 7446 | 0677834 W | 1.81 | |
| Cycad Shopping Centre | 12,000 | 5267 | 0677834 W | 0.94 | |
| Kwa Zulu Natal | Gateway Mall | 180,000 | 123,498/73,313 * | 0241103 W | 0.97 |
| Liberty Midlands Mall | 75,000 | 74,702/55,241 * | 0239605 P | 3.21 | |
| Musgrave Centre | 39,886 | 20,058 | 0240738 W | 8.36 | |
| Phoenix Plaza | 24,162 | 29,307/18,070 * | 0241042 W | 2.72 | |
| Granada Square | 5818 | 2097 | 0241103 W | 2.15 | |
| NW | Matlosana | 65,000 | 50,100/40,000 ! | 0436495 W | 8.03 |
| FS | Mimosa | 25,000 | 5297 | 0261368 W | 2.30 |
| MP | Riverside | 49,529 | 45,000 | 0556088 W | 9.02 |
| EC | Baywest | 90,000 | 45,351 | 0035209 W | 14.85 |
| Rainfall Station No. | MAP (mm/Year) | Length of Data (Years) | Percentage of Observed of Data | Percentage of In-Filled Data | Percentage of Missing Data |
|---|---|---|---|---|---|
| 0476093 W | 552 | 107 | 55.2 | 40.9 | 3.9 |
| 0476044 W | 727 | 107 | 75.7 | 20.4 | 3.9 |
| 0476129 W | 752 | 107 | 73.7 | 22.4 | 3.9 |
| 0475881 W | 788 | 107 | 84.4 | 11.7 | 3.9 |
| 0020896 W | 563 | 149 | 44.3 | 54.7 | 1.0 |
| 0021230 W | 586 | 150 | 47.8 | 52.1 | 0.1 |
| 0021055 W | 483 | 149 | 60.6 | 38.4 | 1.0 |
| 0020839 W | 1183 | 149 | 44.4 | 54.6 | 1.0 |
| 0678023 W | 464 | 96 | 83.1 | 16.9 | 0.0 |
| 0677834 W | 485 | 96 | 92.9 | 7.1 | 0.0 |
| 0241103 W | 1144 | 125 | 59.6 | 37.5 | 2.9 |
| 0239605 P | 925 | 107 | 67.9 | 31.2 | 0.9 |
| 0240738 W | 876 | 127 | 45.7 | 52.4 | 1.9 |
| 0241042 W | 1072 | 125 | 49.1 | 48.0 | 2.9 |
| 0436495 W | 588 | 82 | 97.9 | 2.1 | 0.0 |
| 0556088 W | 718 | 98 | 69.4 | 30.6 | 0.0 |
| 0261368 W | 550 | 97 | 91.9 | 8.1 | 0.0 |
| 0035209 W | 590 | 124 | 54.0 | 45.8 | 0.2 |
| Shopping Centre | Reliability (%) | 85 | 90 | 95 | 98 | 99 |
|---|---|---|---|---|---|---|
| South Gate | Yield * | 142 | 132 | 122 | 101 | 72 |
| Storage ** | 4750 | 4250 | 2750 | 1500 | 1500 | |
| Braamfontein | Yield | 12 | 11 | 8 | 7 | 6 |
| Storage | 130 | 160 | 90 | 130 | 90 | |
| Grayston | Yield | 70 | 61 | 55 | 45 | 40 |
| Storage | 240 | 165 | 240 | 150 | 105 | |
| Norwood | Yield | 116 | 107 | 95 | 84 | 76 |
| Storage | 1800 | 3200 | 2000 | 1600 | 1600 | |
| Sandton | Yield | 120 | 112 | 104 | 69 | 68 |
| Storage | 6800 | 6800 | 5600 | 2000 | 1600 | |
| Capricon | Yield | 242 | 228 | 195 | 172 | 161 |
| Storage | 3000 | 3750 | 1250 | 1000 | 750 | |
| Howard | Yield | 91 | 84 | 77 | 69 | 63 |
| Storage | 800 | 550 | 500 | 350 | 300 | |
| Willow Bridge | Yield | 35 | 32 | 28 | 26 | 25 |
| Storage | 1000 | 600 | 450 | 450 | 450 | |
| Tyger Valley | Yield | 139 | 125 | 117 | 108 | 101 |
| Storage | 5100 | 3300 | 3000 | 2400 | 2400 | |
| Canal Walk | Yield | 21 | 19 | 16 | 12 | 8 |
| Storage | 750 | 1125 | 750 | 450 | 300 | |
| Mall of North | Yield | 65 | 58 | 54 | 44 | 30 |
| Storage | 4000 | 3250 | 3000 | 2000 | 1250 | |
| Savanah | Yield | 23 | 22 | 18 | 13 | 11 |
| Storage | 525 | 825 | 825 | 525 | 525 | |
| Limpopo | Yield | 16 | 15 | 11 | 10 | 8 |
| Storage | 240 | 300 | 240 | 390 | 270 | |
| Cycad | Yield | 23 | 22 | 18 | 13 | 12 |
| Storage | 160 | 240 | 240 | 160 | 180 | |
| Gateway-Reduced area | Yield | 140 | 131 | 108 | 101 | 85 |
| Storage | 32,000 | 24,000 | 10,000 | 8000 | 6000 | |
| Liberty-reduced area | Yield | 243 | 196 | 162 | 142 | 138 |
| Storage | 15,300 | 9000 | 4500 | 2700 | 1800 | |
| Musgrave | Yield | 41 | 37 | 30 | 27 | 18 |
| Storage | 1100 | 1000 | 600 | 600 | 400 | |
| Phoenix-reduced area | Yield | 153 | 143 | 121 | 104 | 90 |
| Storage | 7500 | 8500 | 2500 | 1500 | 1500 | |
| Granada | Yield | 46 | 39 | 33 | 27 | 26 |
| Storage | 255 | 135 | 120 | 90 | 105 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndiritu, J.; Moodley, Y.; Guliwe, M. Generalized Storage–Yield–Reliability Relationships for Analysing Shopping Centre Rainwater Harvesting Systems. Water 2017, 9, 771. https://doi.org/10.3390/w9100771
Ndiritu J, Moodley Y, Guliwe M. Generalized Storage–Yield–Reliability Relationships for Analysing Shopping Centre Rainwater Harvesting Systems. Water. 2017; 9(10):771. https://doi.org/10.3390/w9100771
Chicago/Turabian StyleNdiritu, John, Yashiren Moodley, and Mondli Guliwe. 2017. "Generalized Storage–Yield–Reliability Relationships for Analysing Shopping Centre Rainwater Harvesting Systems" Water 9, no. 10: 771. https://doi.org/10.3390/w9100771
APA StyleNdiritu, J., Moodley, Y., & Guliwe, M. (2017). Generalized Storage–Yield–Reliability Relationships for Analysing Shopping Centre Rainwater Harvesting Systems. Water, 9(10), 771. https://doi.org/10.3390/w9100771





