An Integrated Modelling System to Predict Hydrological Processes under Climate and Land-Use/Cover Change Scenarios
Abstract
1. Introduction
2. Case Study and Method
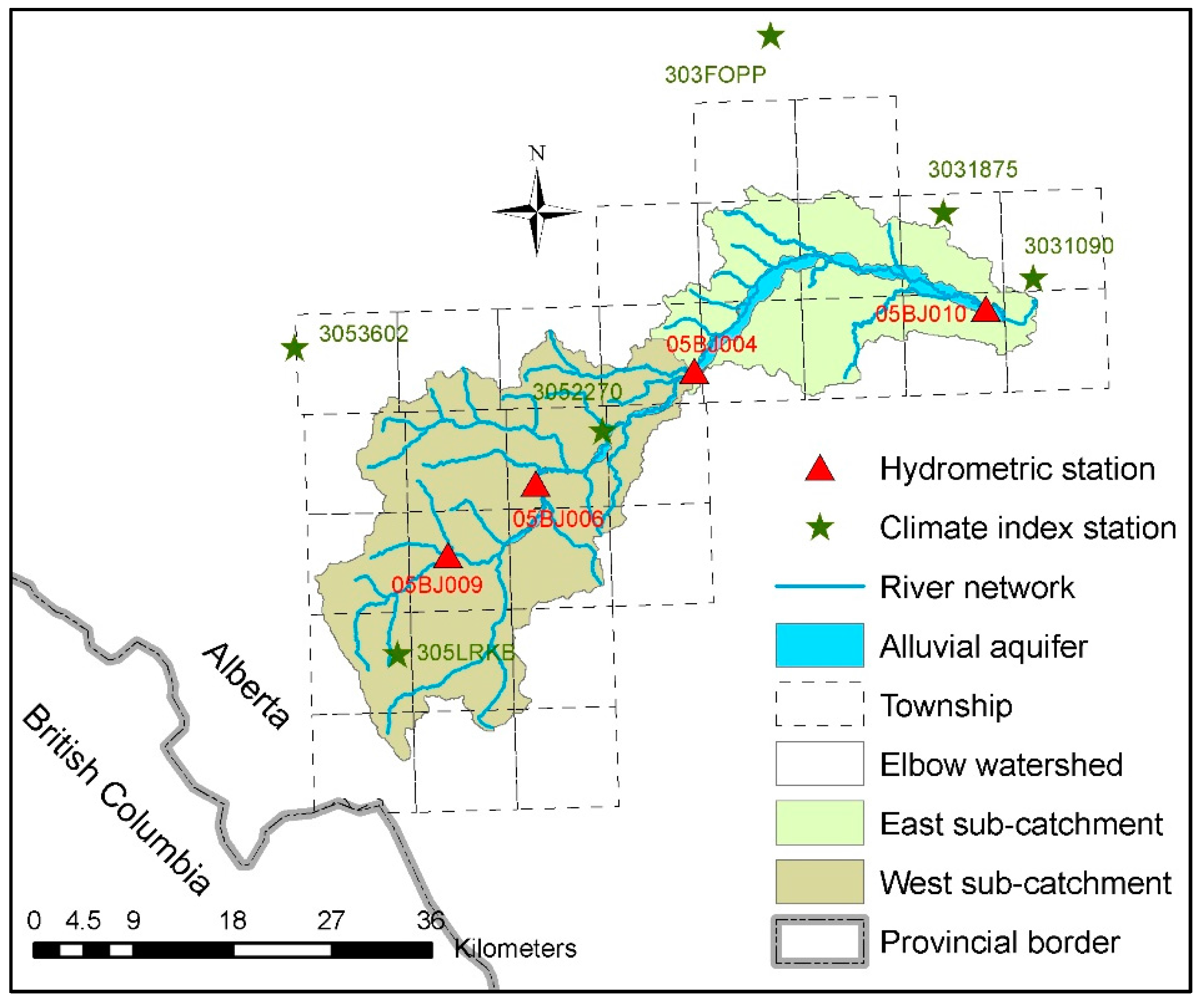
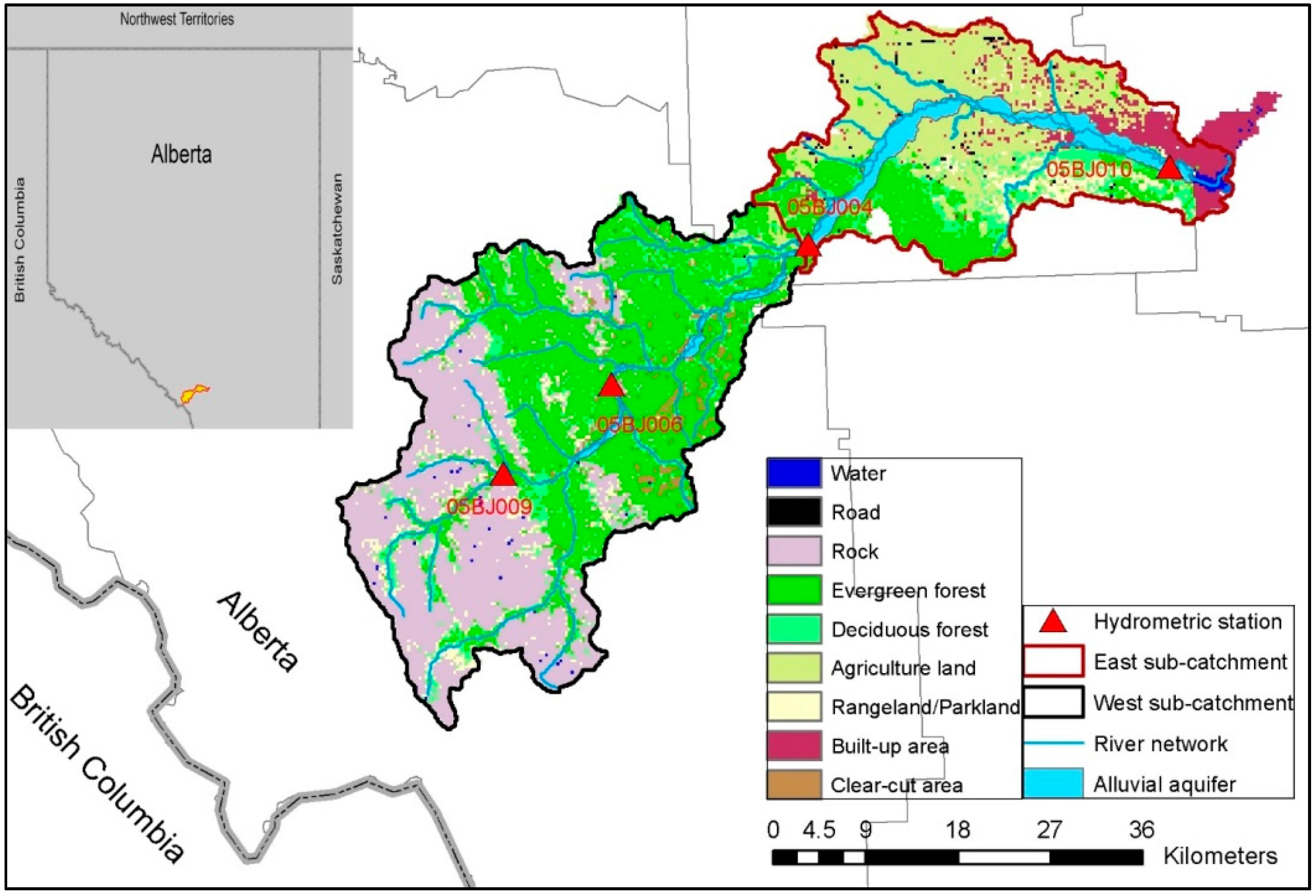
2.1. The Elbow River Watershed
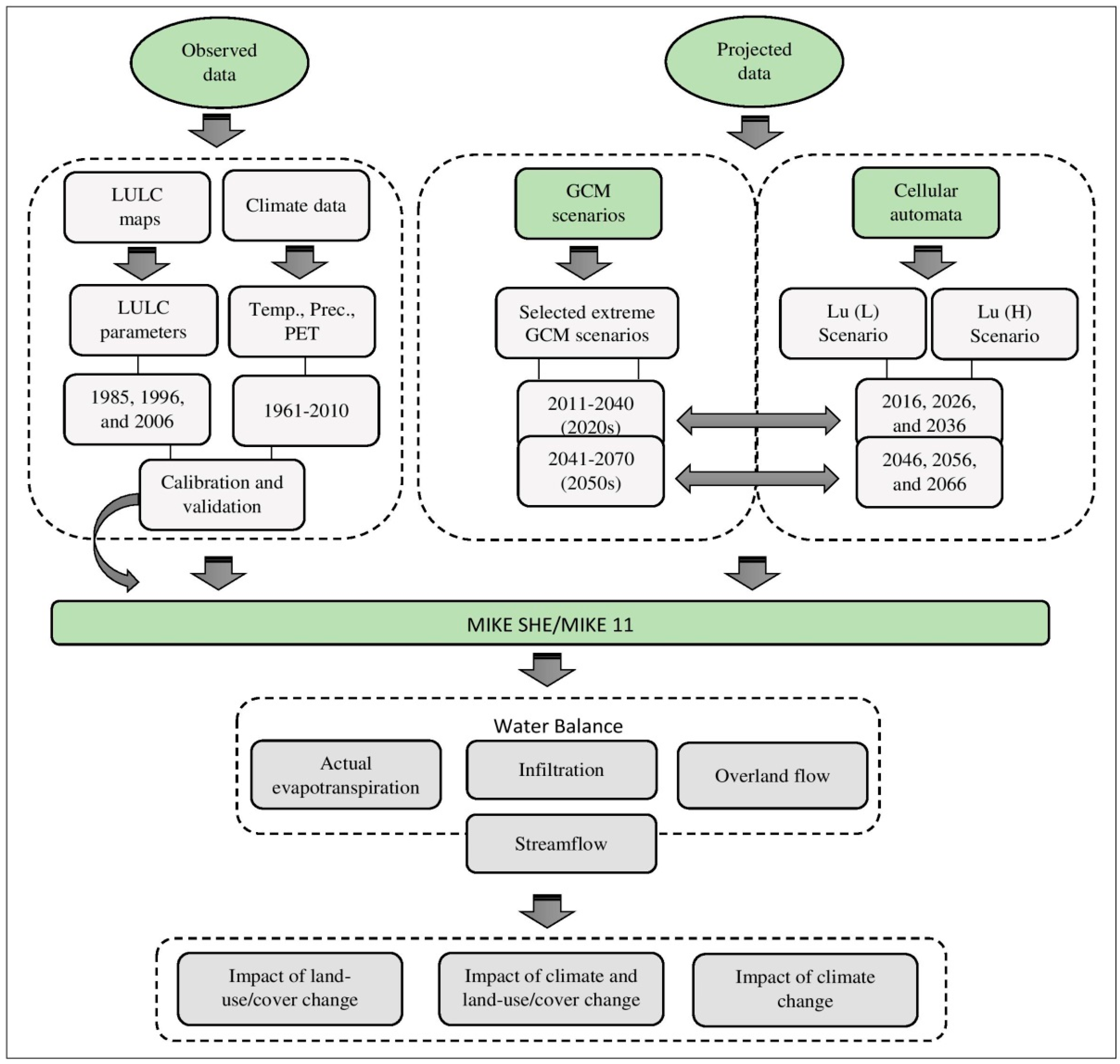
2.2. Methodological Framework
2.2.1. Observed Climate and LULC Data
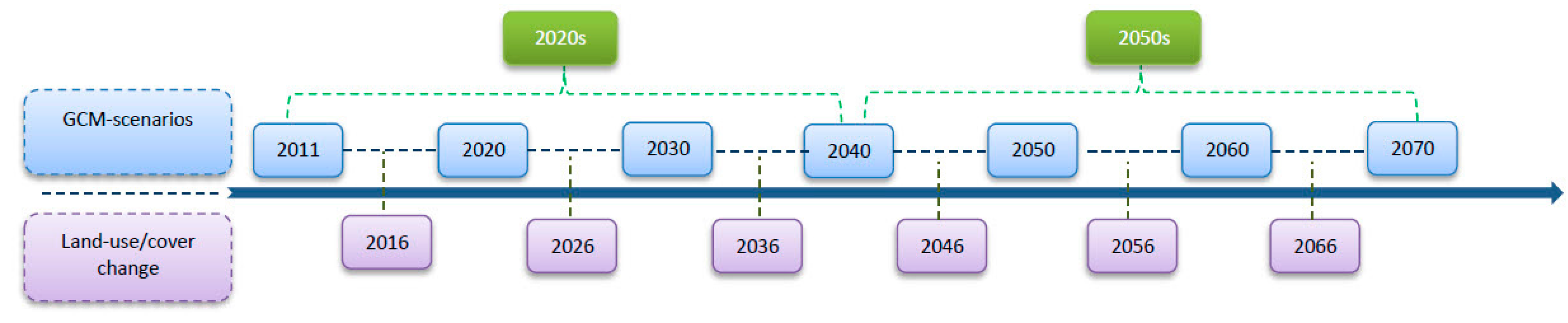
2.2.2. GCMs-Scenarios
2.2.3. LULC Change Modeling and Scenarios
2.2.4. Hydrological Modeling
2.2.5. Simulated Scenarios
- (1)
- Impact of LULC change on hydrological processes:
- (a)
- LU-H scenario: This scenario assumes constant baseline climate (1961–1990) while LULC changes for the 2020s and 2050s under the Lu-(PH) scenario.
- (b)
- LU-L scenario: This scenario assumes constant baseline climate (1961–1990) while LULC changes for the 2020s and 2050s under the Lu-(PL) scenario.
- (2)
- Impact of climate change on hydrological process:
- (a)
- A1B scenario: This scenario considers the A1B climate scenario while LULC is constant.
- (b)
- B2 scenario: This scenario considers the B2 climate scenario while LULC is constant.
- (3)
- Impact of climate and LULC change on hydrological processes:
- (a)
- LU(H)-A1B scenario: This scenario considers the A1B climate scenario with the LU-PH scenario.
- (b)
- LU(L)-A1B scenario: This scenario considers the A1B climate scenario with the LU-PL scenario.
- (c)
- LU(H)-B2 scenario: This scenario considers the B2 climate scenario with the LU-PH scenario.
- (d)
- LU(L)-B2 scenario: This scenario considers the B2 climate scenario with the LU-PL scenario.
3. Results and Discussion
3.1. Annual and Seasonal Changes in Climate Scenarios
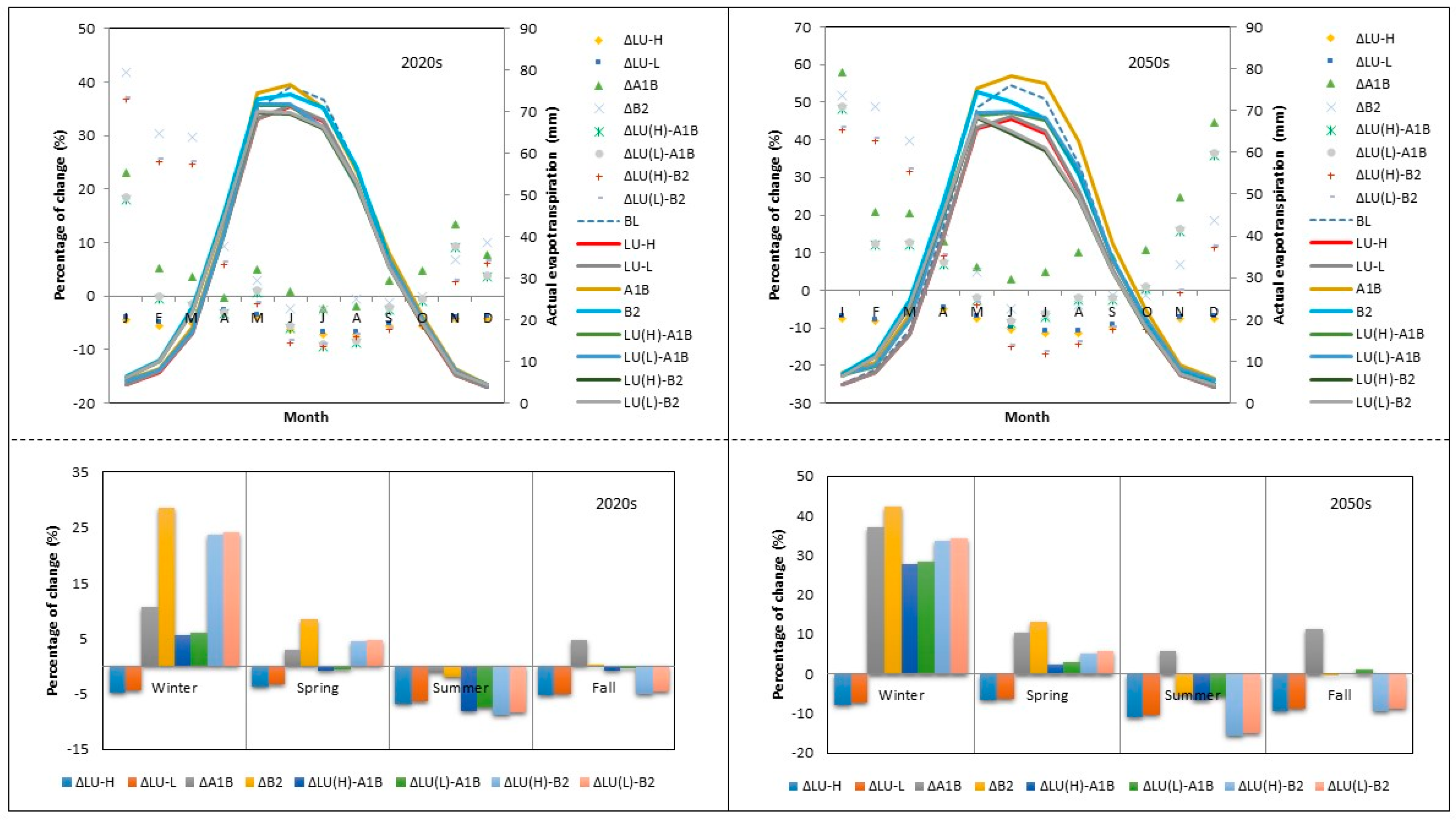
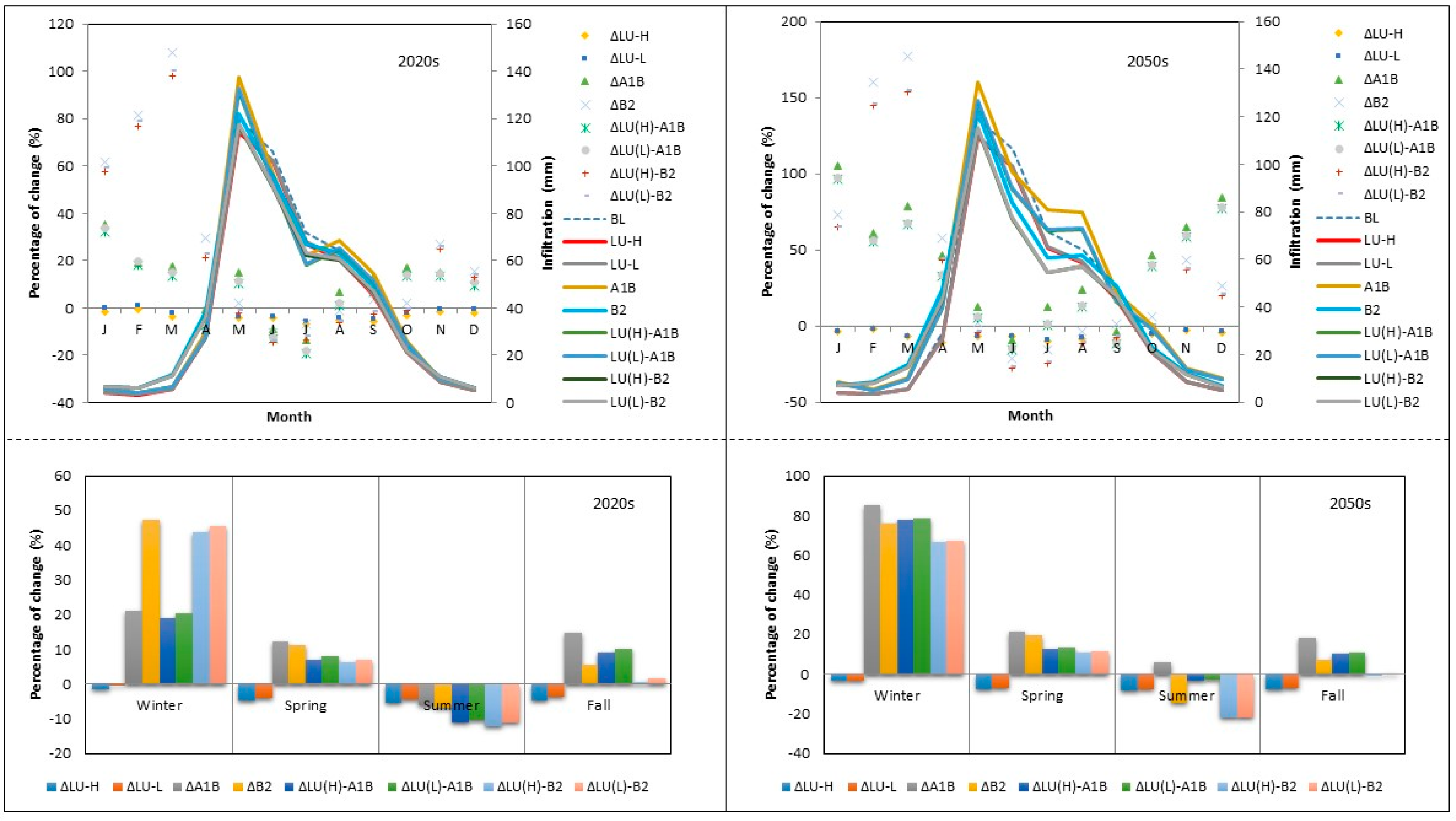
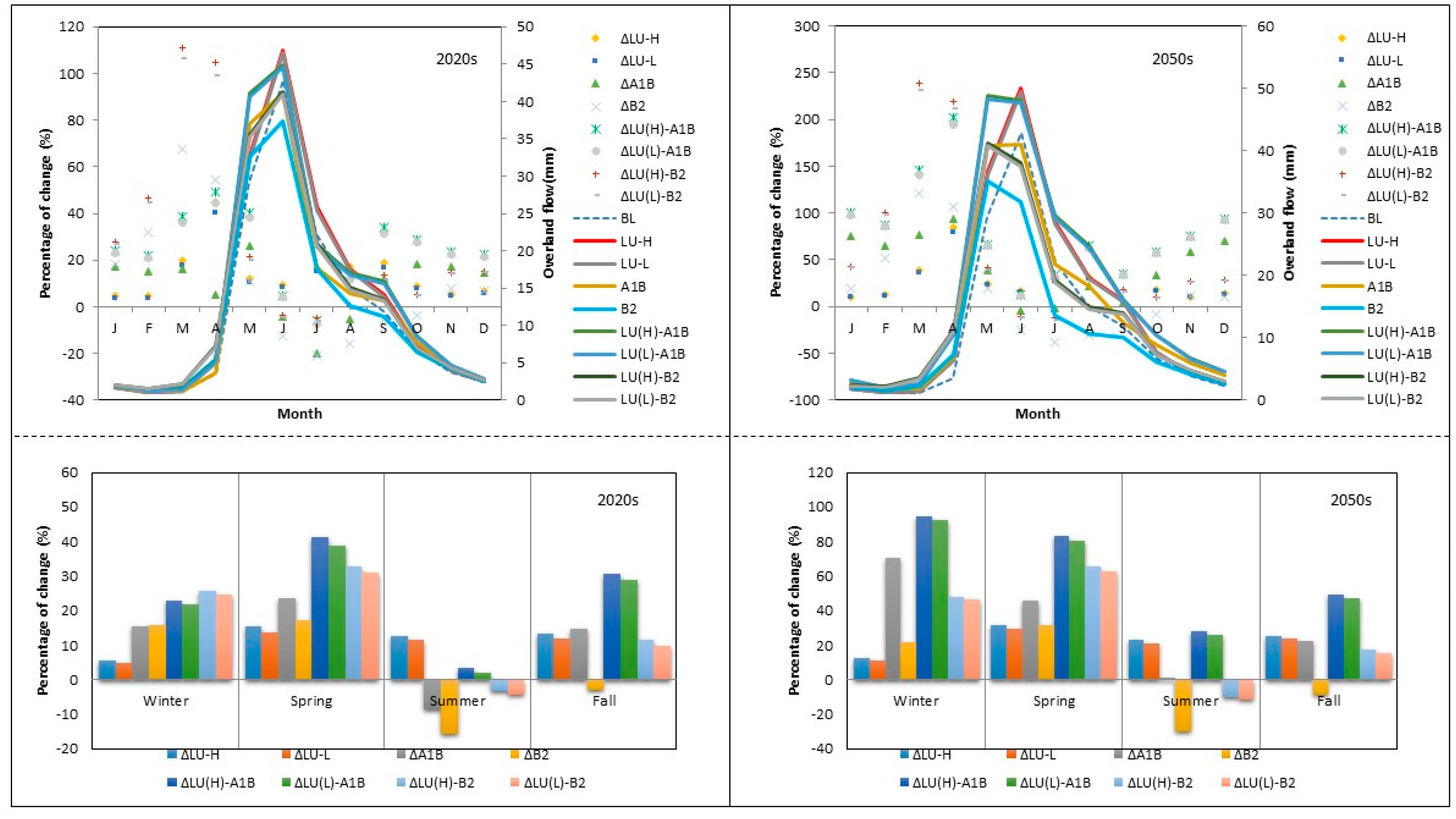
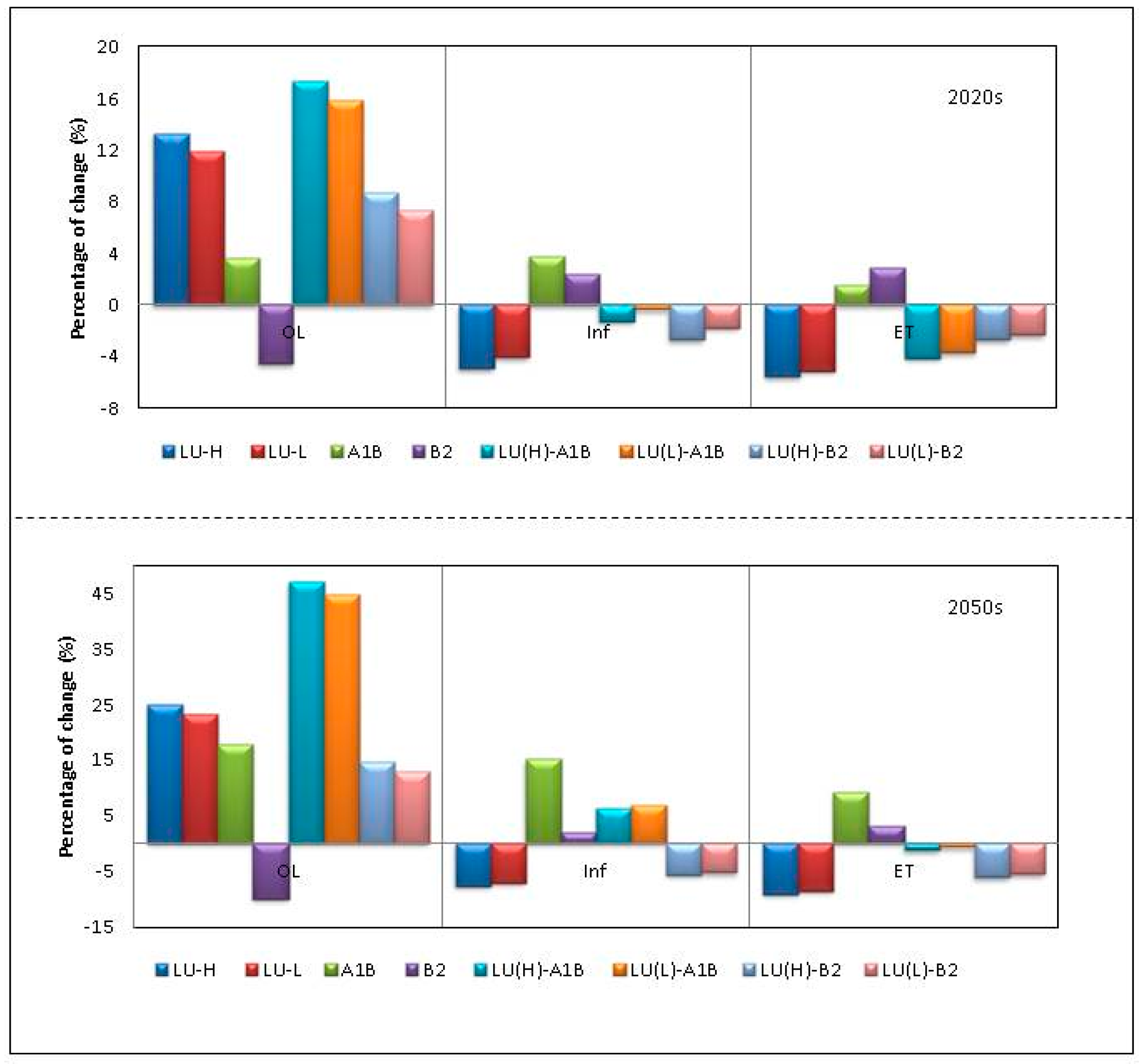
3.2. Impact of LULC and Climate Change on Water Balance
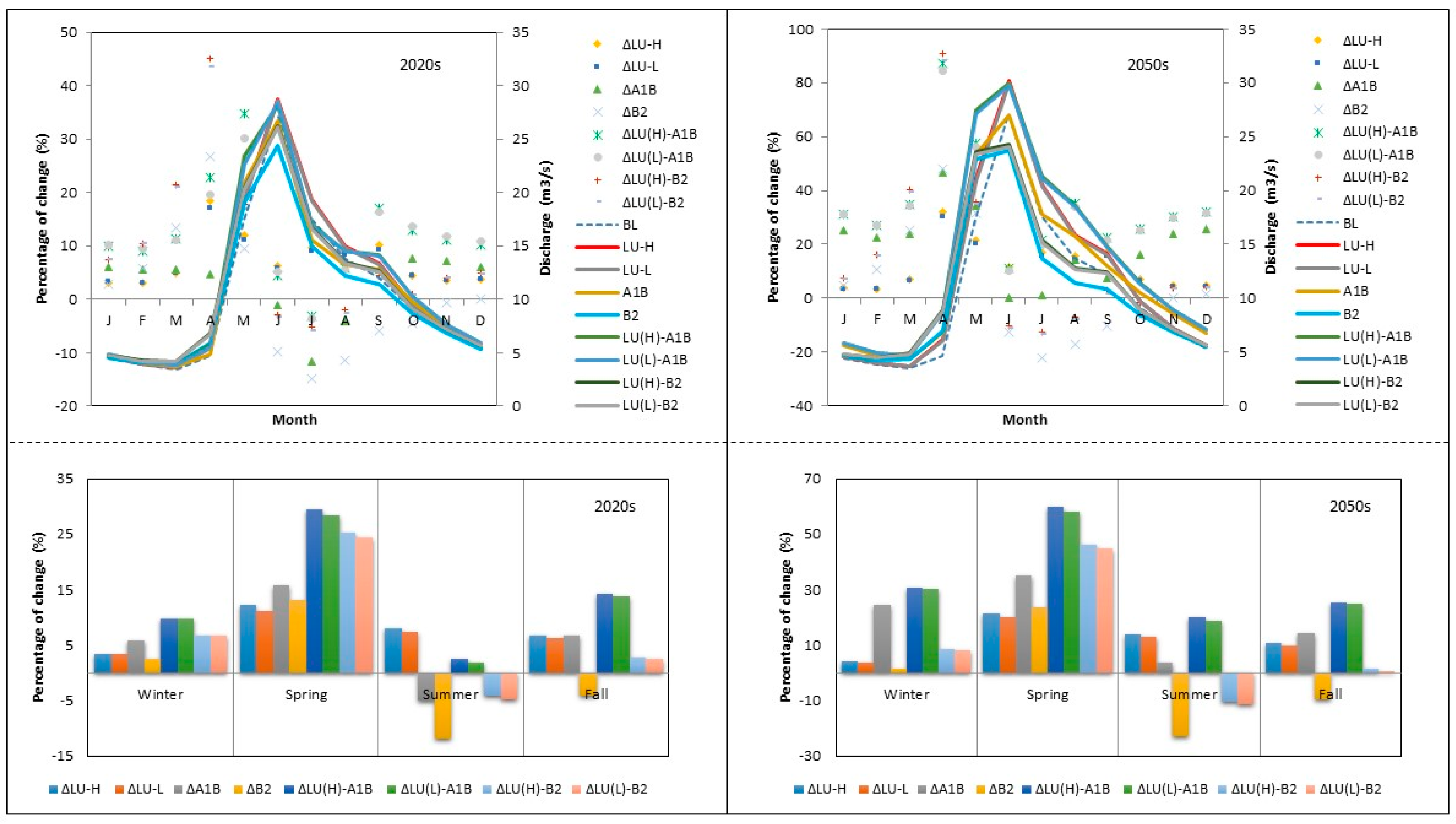
3.2.1. Average Seasonal Changes in Water Balance
Actual Evapotranspiration
Infiltration
Overland Flow
3.2.2. Average Annual Changes in Water Balance
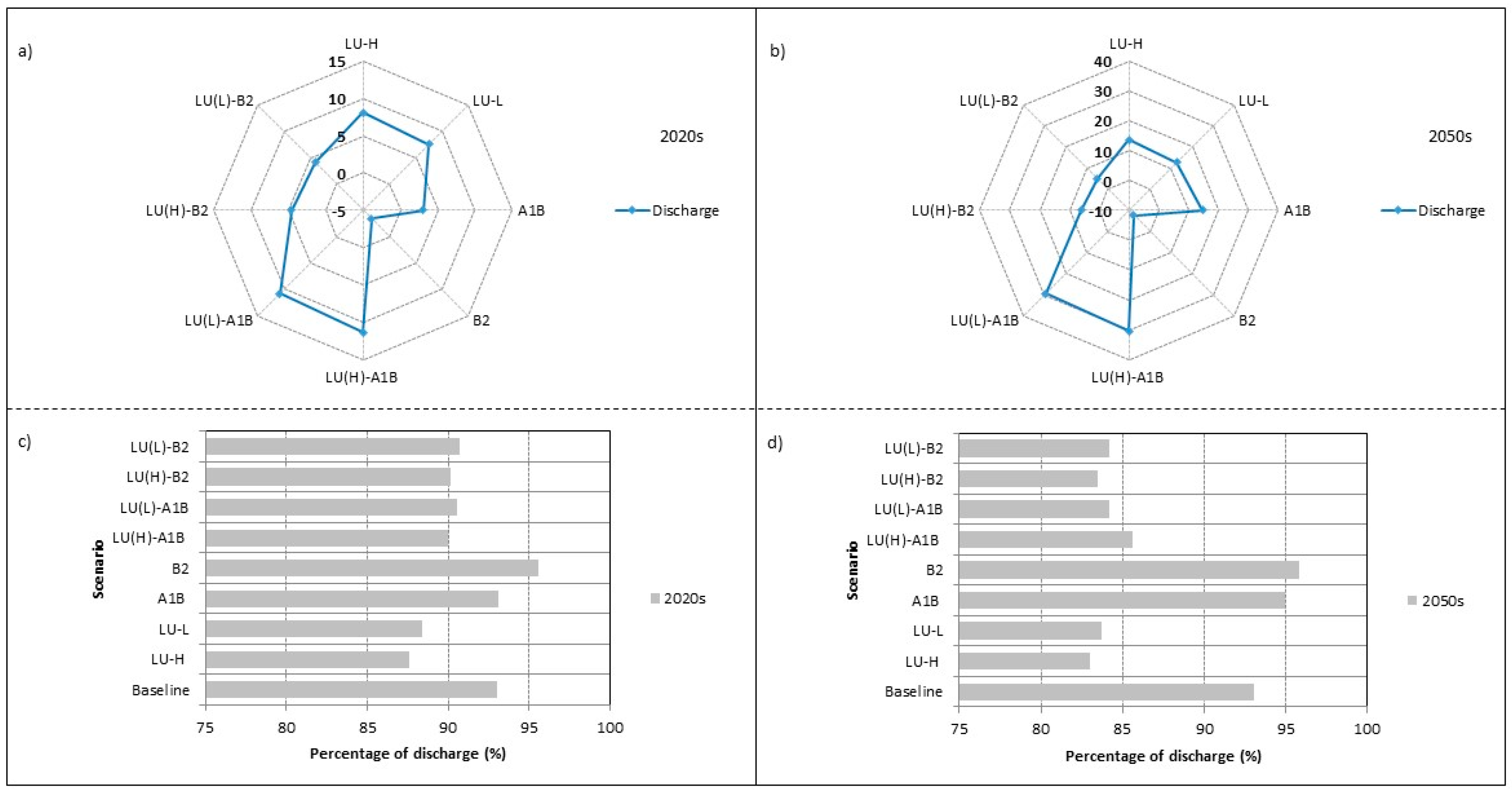
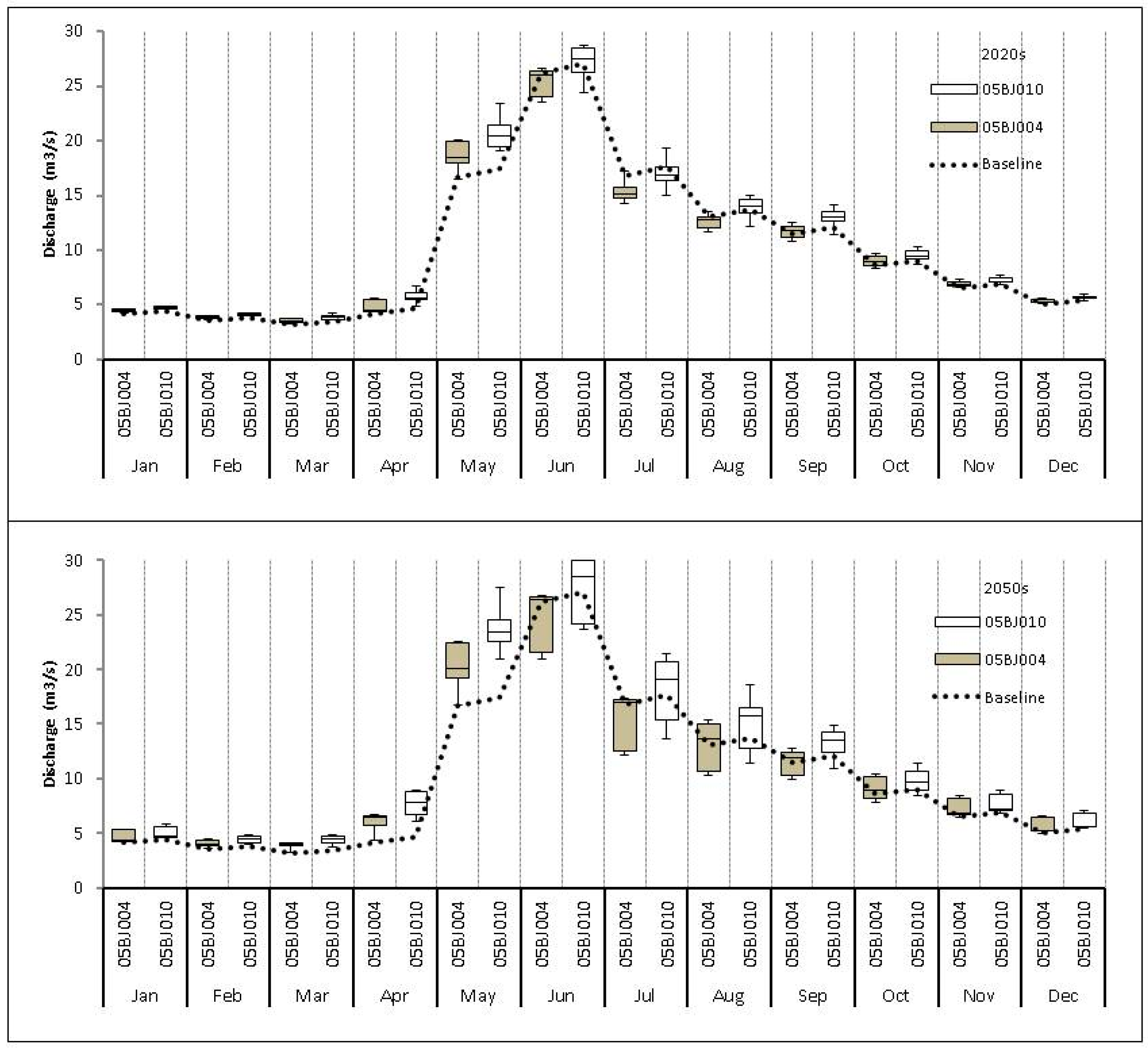
3.2.3. Streamflow
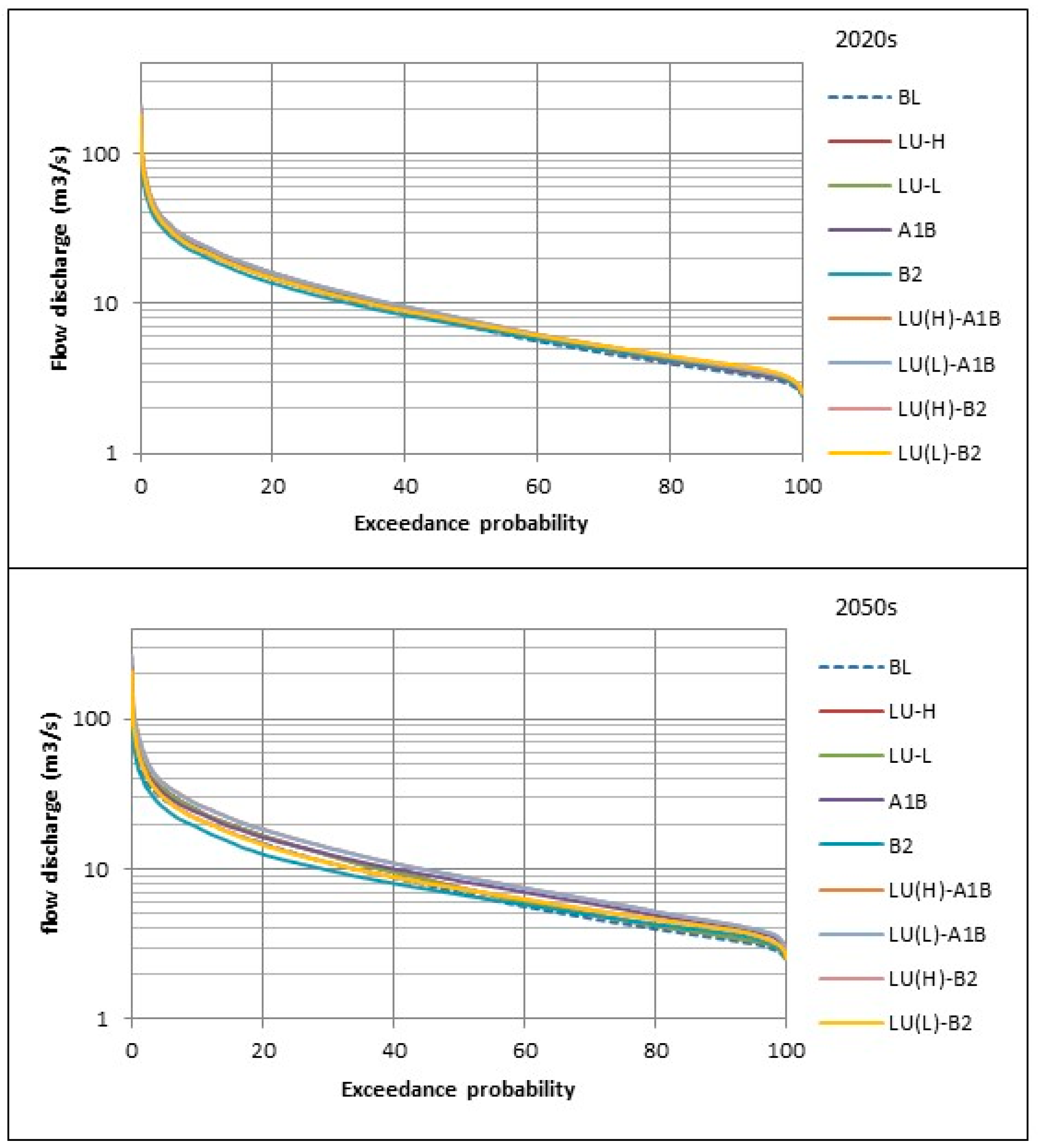
Flow Duration Curve
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
| Climate Station (ID) | Elevation |
|---|---|
| 3031090 | 1067 |
| 3031875 | 1235 |
| 303FOPP | 1303 |
| 3052270 | 1400 |
| 3053602 | 1463 |
| 305LRKB | 2120 |
References
- Legesse, D.; Vallet-Coulomb, C.; Gasse, F. Hydrological response of a catchment to climate and land use changes in Tropical Africa: Case study South Central Ethiopia. J. Hydrol. 2003, 275, 67–85. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Gathenya, M.; Mwangi, H.; Coe, R.; Sang, J. Climate-and land use-induced risks to watershed services in the Nyando River Basin, Kenya. Exp. Agric. 2011, 47, 339–356. [Google Scholar] [CrossRef]
- Weatherhead, E.K.; Howden, N.J.K. The relationship between land use and surface water resources in the UK. Land Use Policy 2009, 26, S243–S250. [Google Scholar] [CrossRef]
- Dias, L.C.P.; Macedo, M.N.; Costa, M.H.; Coe, M.T.; Neill, C. Effects of land cover change on evapotranspiration and streamflow of small catchments in the Upper Xingu River Basin, Central Brazil. J. Hydrol. Reg. Stud. 2015, 4, 108–122. [Google Scholar] [CrossRef]
- Hundecha, Y.; Bárdossy, A. Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model. J. Hydrol. 2004, 292, 281–295. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Mata, L.J.; Arnell, N.W.; Döll, P.; Jimenez, B.; Miller, K.; Oki, T.; Şen, Z.; Shiklomanov, I. The implications of projected climate change for freshwater resources and their management. Hydrol. Sci. J. 2008, 53, 3–10. [Google Scholar] [CrossRef]
- Farjad, B.; Gupta, A.; Marceau, D.J. Hydrological regime responses to climate change for the 2020s and 2050s periods in the Elbow River watershed in southern Alberta, Canada. In Environmental Management of River Basin Ecosystems; Springer: Cham, Switzerland, 2015; pp. 65–89. [Google Scholar]
- Farjad, B.; Gupta, A.; Marceau, D.J. Annual and Seasonal Variations of Hydrological Processes under Climate Change Scenarios in Two Sub-Catchments of a Complex Watershed. Water Resour. Manag. 2016, 30, 2851–2865. [Google Scholar] [CrossRef]
- Bell, R.; Hodges, K.; Vidale, P.L.; Strachan, J.; Roberts, M. Simulation of the global ENSO–tropical cyclone teleconnection by a high-resolution coupled general circulation model. J. Clim. 2014, 27, 6404–6422. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T.; Kaspar, F. Estimating the impact of global change on flood and drought risks in Europe: A continental, integrated analysis. Clim. Chang. 2006, 75, 273–299. [Google Scholar] [CrossRef]
- Hosseinizadeh, A.; SeyedKaboli, H.; Zareie, H.; Ali, M.A.; Farjad, B. Impact of climate change on the severity, duration and frequency of drought in a semi-arid agricultural basin. Geoenviron. Disasters 2015, 2, 1–9. [Google Scholar] [CrossRef]
- Loukas, A.; Quick, M.C. The Effect of Climate Change on Hydrologic Regime of Two Climatically Different Watersheds. ASCE J. Hydrol. Eng. 1996, 1, 77–87. [Google Scholar] [CrossRef]
- Boyer, C.; Chaumont, D.; Chartier, I.; Roy, A.G. Impact of climate change on the hydrology of St. Lawrence tributaries. J. Hydrol. 2010, 384, 65–83. [Google Scholar] [CrossRef]
- Barron, O.; Silberstein, R.; Ali, R.; Donohue, R.; McFarlane, D.J.; Davies, P.; Donn, M. Climate change effects on water-dependent ecosystems in south-western Australia. J. Hydrol. 2012, 434, 95–109. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Coulibaly, P. Hydrologic impact of climate change in the Saguenay watershed: Comparison of downscaling methods and hydrologic models. J. Hydrol. 2005, 307, 145–163. [Google Scholar] [CrossRef]
- Forbes, K.A.; Kienzle, S.W.; Coburn, C.A.; Byrne, J.M.; Rasmussen, J. Simulating the hydrological response to predicted climate change on a watershed in southern Alberta, Canada. Clim. Chang. 2011, 105, 555–576. [Google Scholar] [CrossRef]
- He, J.; Valeo, C.; Chu, A.; Neumann, N.F. Stormwater quantity and quality response to climate change using artificial neural networks. Hydrol. Process 2011, 25, 1298–1312. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Kienzle, S.W.; Nemeth, M.W.; Byrne, J.M.; MacDonald, R.J. Simulating the hydrological impacts of climate change in the upper North Saskatchewan River basin, Alberta, Canada. J. Hydrol. 2012, 412, 76–89. [Google Scholar] [CrossRef]
- Gädeke, A.; Hölzel, H.; Koch, H.; Pohle, I.; Grünewald, U. Analysis of uncertainties in the hydrological response of a model-based climate change impact assessment in a subcatchment of the Spree River, Germany. Hydrol. Process. 2014, 28, 3978–3998. [Google Scholar] [CrossRef]
- Velázquez, J.A.; Schmid, J.; Ricard, S.; Muerth, M.J.; St-Denis, B.G.; Minville, M.; Turcotte, R. An ensemble approach to assess hydrological models’ contribution to uncertainties in the analysis of climate change impact on water resources. Hydrol. Earth Syst. Sci. 2013, 17, 565. [Google Scholar] [CrossRef]
- Poulin, A.; Brissette, F.; Leconte, R.; Arsenault, R.; Malo, J.S. Uncertainty of hydrological modelling in climate change impact studies in a Canadian, snow-dominated river basin. J. Hydrol. 2011, 409, 626–636. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Jung, I.W. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrol. Process. 2011, 25, 2814–2826. [Google Scholar] [CrossRef]
- Nolan, P.; O’Sullivan, J.; McGrath, R. Impacts of climate change on mid-twenty-first-century rainfall in Ireland: A high-resolution regional climate model ensemble approach. Int. J. Climatol. 2017. [Google Scholar] [CrossRef]
- Chaudhuri, C.; Srivastava, R. A novel approach for statistical downscaling of future precipitation over the Indo-Gangetic Basin. J. Hydrol. 2017, 547, 21–38. [Google Scholar] [CrossRef]
- Bronstert, A. Rainfall-runoff modelling for assessing impacts of climate and land-use change. Hydrol. Process. 2004, 18, 567–570. [Google Scholar] [CrossRef]
- Thanapakpawin, P.; Richey, J.; Thomas, D.; Rodda, S.; Campbell, B.; Logsdon, M. Effects of landuse change on the hydrologic regime of the Mae Chaem river basin, NW Thailand. J. Hydrol. 2007, 334, 215–230. [Google Scholar] [CrossRef]
- Wijesekara, G.N.; Farjad, B.; Gupta, A.; Qiao, Y.; Delaney, P.; Marceau, D.J. A Comprehensive Land-Use/Hydrological Modeling System for Scenario Simulations in the Elbow River Watershed, Alberta, Canada. Environ. Manag. 2014, 53, 357–381. [Google Scholar] [CrossRef] [PubMed]
- Jakeman, A.J.; Littlewood, I.G.; Whitehead, P.G. An assessment of the dynamic response characteristics of streamflow in the Balquhidder catchments. J. Hydrol. 1993, 145, 337–355. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Système Hydrologique Européen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Dunn, S.M.; Mackay, R. Spatial variation in evapotranspiration and the influence of land use on catchment hydrology. J. Hydrol. 1995, 171, 49–73. [Google Scholar] [CrossRef]
- Hendriks, M. Introduction to Physical Hydrology; Oxford University Press: Oxford, UK, 2010; p. 331. [Google Scholar]
- Notebaert, B.; Verstraeten, G.; Ward, P.; Renssen, H.; Van Rompaey, A. Modeling the sensitivity of sediment and water runoff dynamics to Holocene climate and land use changes at the catchment scale. Geomorphology 2011, 126, 18–31. [Google Scholar] [CrossRef]
- Tu, J. Combined impact of climate and land use changes on streamflow and water quality in eastern Massachusetts, USA. J. Hydrol. 2009, 379, 268–283. [Google Scholar] [CrossRef]
- Antonellini, M.; Dentinho, T.; Khattabi, A.; Masson, E.; Mollema, P.N.; Silva, V.; Silveira, P. An integrated methodology to assess future water resources under land use and climate change: An application to the Tahadart drainage basin (Morocco). Environ. Earth Sci. 2014, 71, 1839–1853. [Google Scholar] [CrossRef]
- Gan, T.Y.; Burges, S.J. An assessment of a conceptual rainfall-runoff model’s ability to represent the dynamics of small hypothetical catchments: 2. Hydrologic responses for normal and extreme rainfall. Water Resour. Res. 1990, 26, 1605–1619. [Google Scholar]
- Khoi, D.N.; Suetsugi, T. The responses of hydrological processes and sediment yield to land-use and climate change in the Be River Catchment, Vietnam. Hydrol. Process. 2014, 28, 640–652. [Google Scholar] [CrossRef]
- Montenegro, S.; Ragab, R. Impact of possible climate and land use changes in the semi arid regions: A case study from North Eastern Brazil. J. Hydrol. 2012, 434, 55–68. [Google Scholar] [CrossRef]
- Wilbanks, T.J.; Kates, R.W. Global change in local places: How scale matters. Clim. Chang. 1999, 43, 601–628. [Google Scholar] [CrossRef]
- Strengers, B.; Leemans, R.; Eickhout, B.; de Vries, B.; Bouwman, L. The land-use projections and resulting emissions in the IPCC SRES scenarios as simulated by the IMAGE 2.2 model. GeoJournal 2004, 61, 381–393. [Google Scholar] [CrossRef]
- Sleeter, B.M.; Sohl, T.L.; Bouchard, M.A.; Reker, R.R.; Soulard, C.E.; Acevedo, W.; Zhu, Z. Scenarios of land use and land cover change in the conterminous United States: Utilizing the special report on emission scenarios at ecoregional scales. Glob. Environ. Chang. 2012, 22, 896–914. [Google Scholar] [CrossRef]
- Kankaanpää, S.; Carter, T.R. Construction of European Forest Land Use Scenarios for the 21st Century; Finnish Environment Institute: Helsinki, Finland, 2004; p. 57. [Google Scholar]
- Verburg, P.H.; Schulp, C.J.E.; Witte, N.; Veldkamp, A. Downscaling of land use change scenarios to assess the dynamics of European landscapes. Agric. Ecosyst. Environ. 2006, 114, 39–56. [Google Scholar] [CrossRef]
- Abildtrup, J.; Audsley, E.; Fekete-Farkas, M.; Giupponi, C.; Gylling, M.; Rosato, P.; Rounsevell, M. Socio-economic scenario development for the assessment of climate change impacts on agricultural land use: A pairwise comparison approach. Environ. Sci. Policy 2006, 9, 101–115. [Google Scholar] [CrossRef]
- Rounsevell, M.D.A.; Reginster, I.; Araújo, M.B.; Carter, T.R.; Dendoncker, N.; Ewert, F.; Tuck, G. A coherent set of future land use change scenarios for Europe. Agric. Ecosyst. Environ. 2006, 114, 57–68. [Google Scholar] [CrossRef]
- Solecki, W.D.; Oliveri, C. Downscaling climate change scenarios in an urban land use change model. J. Environ. Manag. 2004, 72, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Tong, S.T.; Sun, Y.; Ranatunga, T.; He, J.; Yang, Y.J. Predicting plausible impacts of sets of climate and land use change scenarios on water resources. Appl. Geogr. 2012, 32, 477–489. [Google Scholar] [CrossRef]
- Wang, R.; Kalin, L.; Kuang, W.; Tian, H. Individual and combined effects of land use/cover and climate change on Wolf Bay watershed streamflow in southern Alabama. Hydrol. Process. 2014, 28, 5530–5546. [Google Scholar] [CrossRef]
- Alberta Treasury Board and Finance, Alberta Population Projections, by Census Division. 2014. Available online: http://finance.alberta.ca/aboutalberta/population-projections/index.html (accessed on 31 July 2015).
- Gan, T.Y. Hydroclimatic trends and possible climatic warming in the Canadian Prairies. Water Resour. Res. 1998, 34, 3009–3015. [Google Scholar] [CrossRef]
- He, M.; Hogue, T.S. Integrating hydrologic modeling and land use projections for evaluation of hydrologic response and regional water supply impacts in semi-arid environments. Environ. Earth Sci. 2012, 65, 1671–1685. [Google Scholar] [CrossRef]
- GeoBase. 2008. Available online: www.Geobase.ca (accessed on 9 October 2017).
- Di Baldassarre, G.; Montanari, A. Uncertainty in river discharge observations: A quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, X.; Zhang, X.; Hagemann, S. Projection of glacier runoff in Yarkant River basin and Beida River basin, Western China. Hydrol. Process 2012, 26, 2773–2781. [Google Scholar] [CrossRef]
- Zhang, X.C.; Liu, W.Z.; Li, Z.; Chen, J. Trend and uncertainty analysis of simulated climate change impacts with multiple GCMs and emission scenarios. Agric. For. Meteorol. 2011, 151, 1297–1304. [Google Scholar] [CrossRef]
- Snover, A.K.; Hamlet, A.F.; Lettenmaier, D.P. Climate-change scenarios for water planning studies: Pilot applications in the Pacific Northwest. Bull. Am. Meteorol. Soc. 2003, 84, 1513–1518. [Google Scholar] [CrossRef]
- Hay, L.E.; McCabe, G.J. Hydrologic effects of climate change in the Yukon River Basin. Clim. Chang. 2010, 100, 509–523. [Google Scholar] [CrossRef]
- Arnell, N.W.; Reynard, N.S. The effects of climate change due to global warming on river flows in Great Britain. J. Hydrol. 1996, 183, 397–424. [Google Scholar] [CrossRef]
- Köplin, N.; Schädler, B.; Viviroli, D.; Weingartner, R. The importance of glacier and forest change in hydrological climate-impact studies. Hydrol. Earth Syst. Sci. 2013, 17, 619–635. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Ambient Air Temperature; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1985; p. 85. [Google Scholar]
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Espadafor, M.; Lorite, I.J.; Gavilán, P.; Berengena, J. An analysis of the tendency of reference evapotranspiration estimates and other climate variables during the last 45 years in Southern Spain. Agric. Water Manag. 2011, 98, 1045–1061. [Google Scholar] [CrossRef]
- Kristensen, K.J.; Jensen, S.E. A model for estimating actual evapotranspiration from potential evapotranspiration. Nordic Hydrol. 1975, 6, 170–188. [Google Scholar]
- Yan, J.; Smith, K.R. Simulation of integrated surface water and ground water system-model formulation. J. Am. Water Resour. Assoc. 1994, 30, 879–890. [Google Scholar] [CrossRef]
- Huntington, T.G.; Sheffield, J.; Hayhoe, K. Impacts of climate change on wintertime precipitation, snowmelt regime, surface runoff, and infiltration in the northeastern USA during the 21st century. In Proceedings of the 64th Eastern Snow Conference, St. Johns, NL, Canada, 29 May–1 June 2007; Volume 29, pp. 181–189. [Google Scholar]
- Troendle, C.A.; Olsen, W.K. Potential effects of timber harvest and water management on streamflow dynamics and sediment transport. In Sustainable Ecological Systems: Implementing an Ecological Approach to Land Management. USDA Forest Service General Technical Report RM-247; U.S. Department of Agriculture: Fort Collins, CO, USA, 1994; pp. 34–41. [Google Scholar]
- Costa, M.H.; Botta, A.; Cardille, J.A. Effects of large-scale changes in land cover on the discharge of the Tocantins River, Southeastern Amazonia. J. Hydrol. 2003, 283, 206–217. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Schilling, K.E. Increasing streamflow and baseflow in Mississippi River since the 1940s: Effect of land use change. J. Hydrol. 2006, 324, 412–422. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; van Dijk, A.I.; Guerschman, J.P.; Mulligan, M.; Bruijnzeel, L.A.; McVicar, T.R. Detecting changes in streamflow after partial woodland clearing in two large catchments in the seasonal tropics. J. Hydrol. 2012, 416, 60–71. [Google Scholar] [CrossRef]

| Procedure | Calibration/Validation Period | NSE (Daily) | NSE (Monthly) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 05B-J009 | 05B-J006 | 05B-J004 | 05B-J010 | 05B-J009 | 05B-J006 | 05B-J004 | 05B-J010 | ||
| Calibration | 1981–1991 | 0.53 | 0.63 | 0.72 | 0.63 | 0.63 | 0.75 | 0.83 | 0.75 |
| Validation | 1991–2000 | N/A | N/A | 0.73 | 0.71 | N/A | N/A | 0.87 | 0.86 |
| 2001–2010 | N/A | N/A | 0.61 | 0.63 | N/A | N/A | 0.70 | 0.71 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farjad, B.; Gupta, A.; Razavi, S.; Faramarzi, M.; Marceau, D.J. An Integrated Modelling System to Predict Hydrological Processes under Climate and Land-Use/Cover Change Scenarios. Water 2017, 9, 767. https://doi.org/10.3390/w9100767
Farjad B, Gupta A, Razavi S, Faramarzi M, Marceau DJ. An Integrated Modelling System to Predict Hydrological Processes under Climate and Land-Use/Cover Change Scenarios. Water. 2017; 9(10):767. https://doi.org/10.3390/w9100767
Chicago/Turabian StyleFarjad, Babak, Anil Gupta, Saman Razavi, Monireh Faramarzi, and Danielle J. Marceau. 2017. "An Integrated Modelling System to Predict Hydrological Processes under Climate and Land-Use/Cover Change Scenarios" Water 9, no. 10: 767. https://doi.org/10.3390/w9100767
APA StyleFarjad, B., Gupta, A., Razavi, S., Faramarzi, M., & Marceau, D. J. (2017). An Integrated Modelling System to Predict Hydrological Processes under Climate and Land-Use/Cover Change Scenarios. Water, 9(10), 767. https://doi.org/10.3390/w9100767






