An Economic Assessment of the Global Potential for Seawater Desalination to 2050
Abstract
1. Introduction
2. Materials and Methods
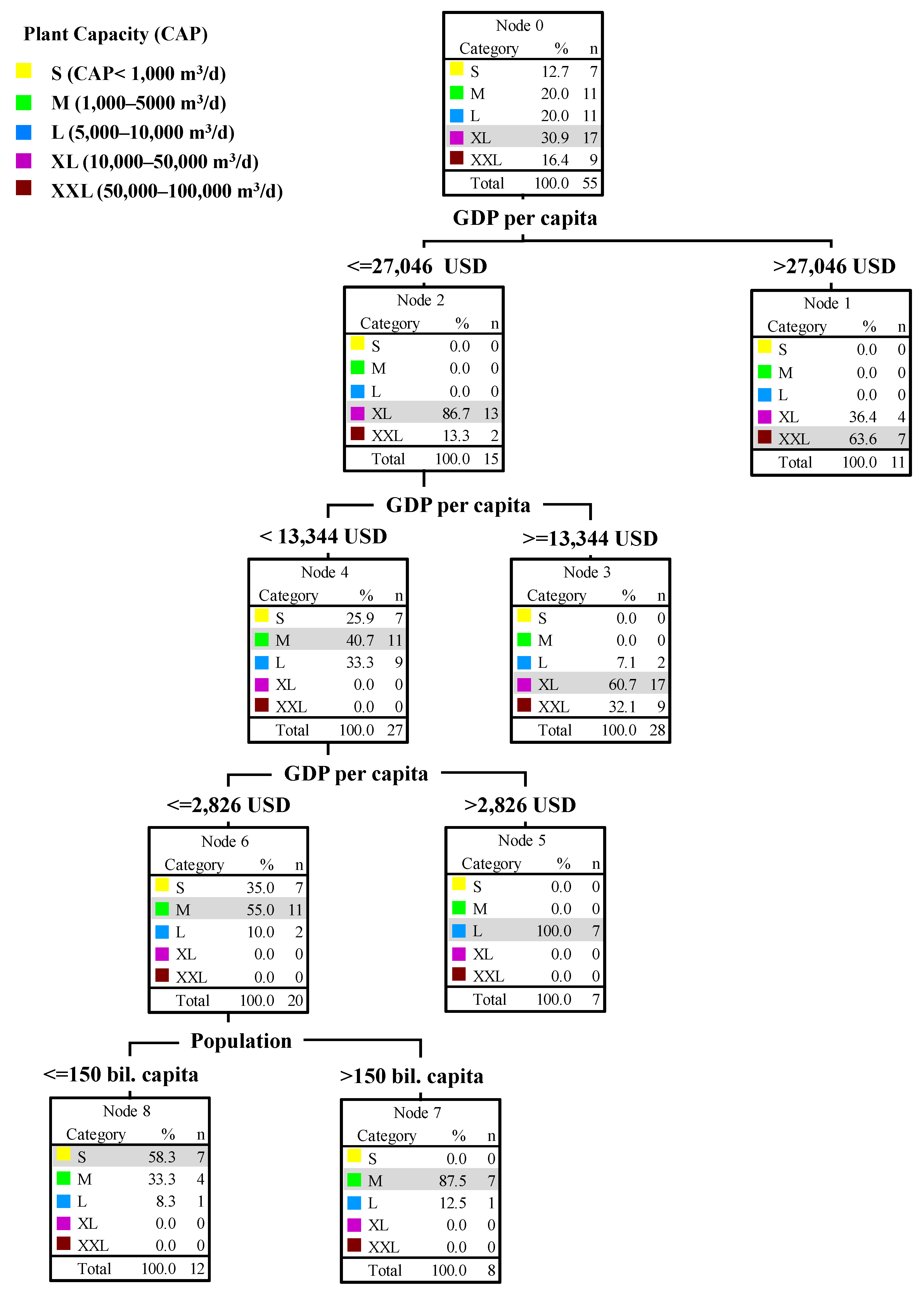
2.1. Data Collection
2.2. Methodology for Assessment of Economic Feasibility of SWRO
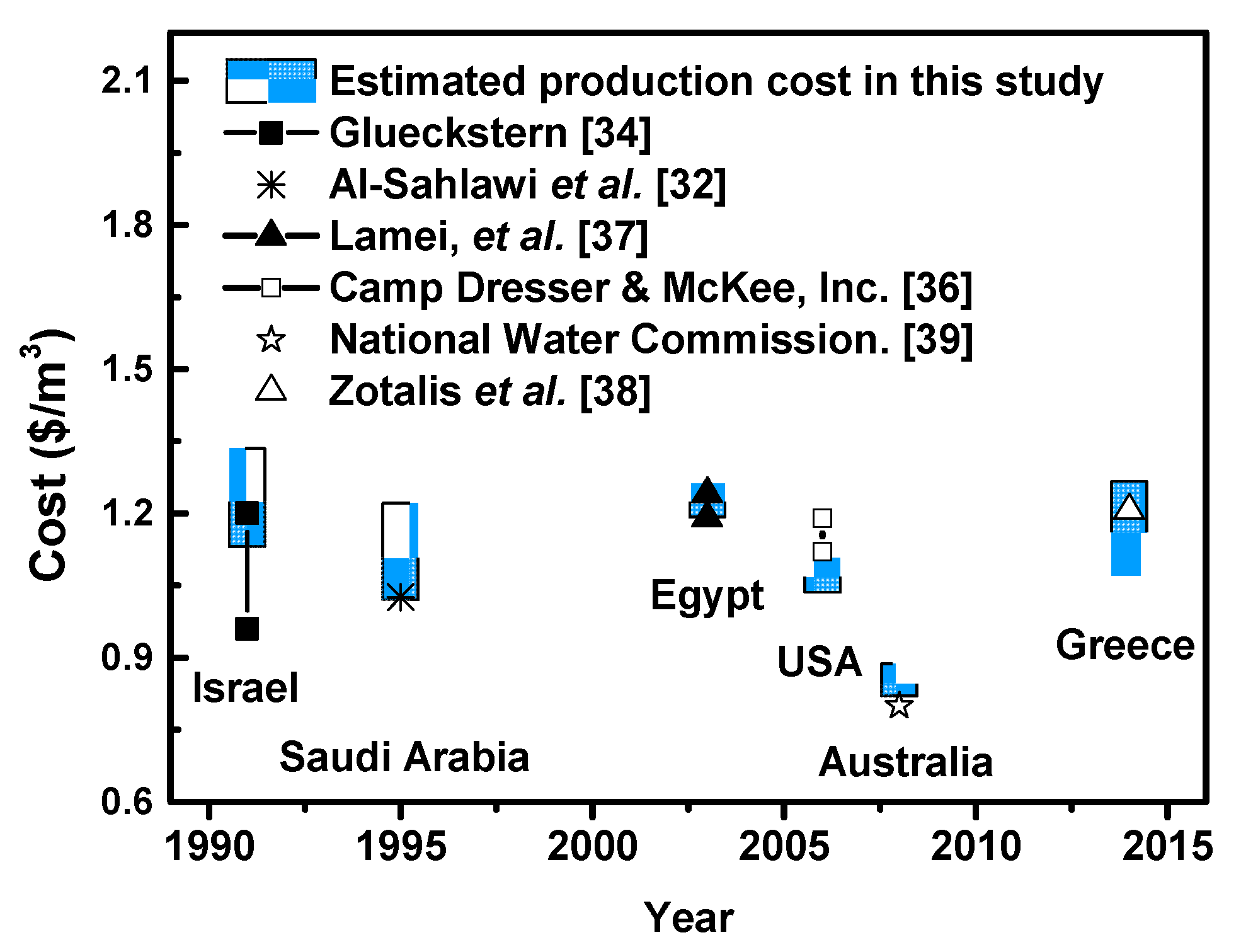
2.3. Statistical Production Cost (PC) Model
2.3.1. Capital Cost Option
t-statistic: (18.9) (156.3) (−18.9) (2.5)
t-statistic: (6.5) (29.3) (−6.5)
t-statistic: (4.8) (9.6) (−4.6)
t-statistic: (4.7) (11.9) (−4.4)
2.3.2. Capacity Option
2.3.3. O&M Cost Option
2.4. Statistical Water Price (WP) Model
t-statistic: (−1.7) (9.8) (3.7)
t-statistic: (−0.4) (2.7) (1.7)
2.5. Future Simulations with Developed PC and WP Models
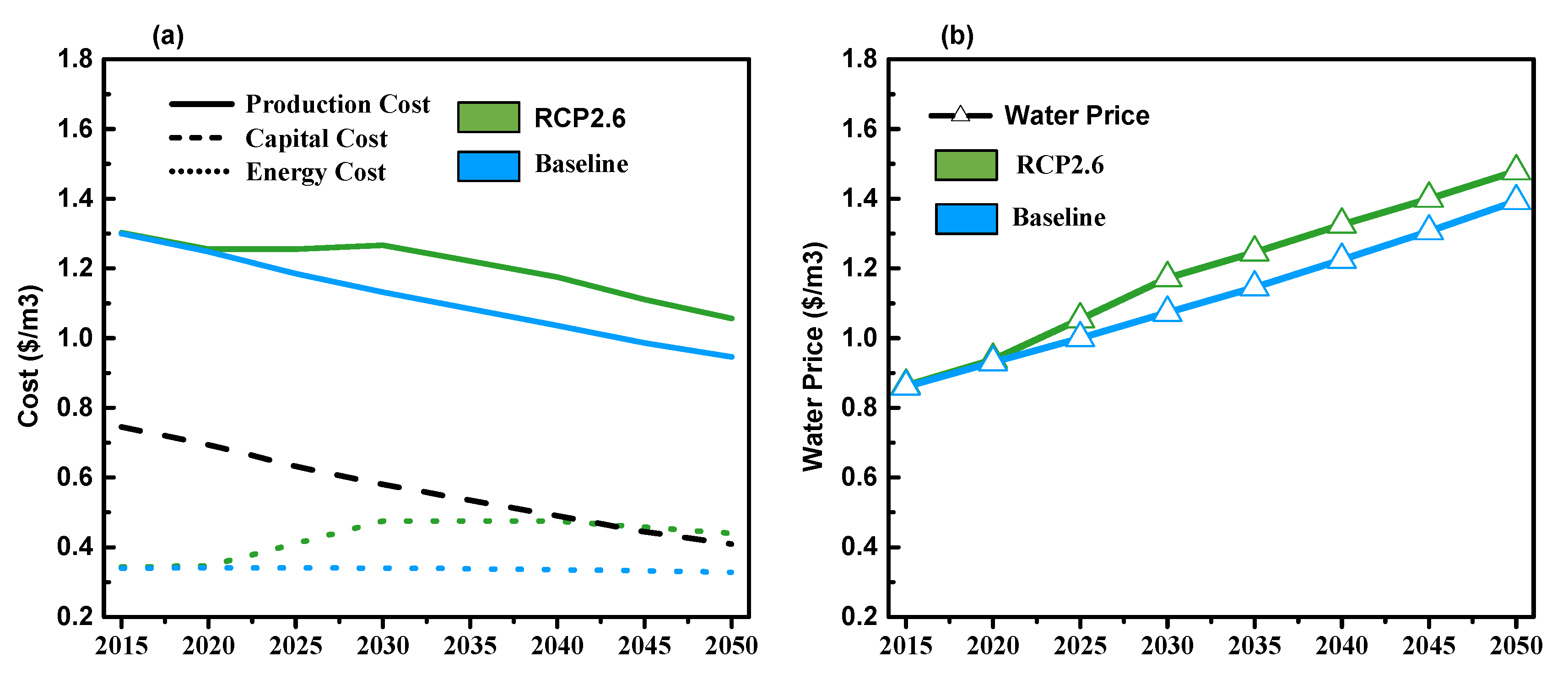
- Capital cost: Capital cost is estimated using Equations (5)–(8). In these equations, plant capacity selection for each country is based on the results of the decision trees. We assume that each country tends to build the SWRO plant with the largest capacity that is also affordable. For the total installed capacity, Ghaffour, et al. [3] estimate that the current growth rate would be ~55%; here, that same past growth rate is used for the future simulations. Additionally, as in the past simulation, a discount rate of 8% and a 20-year plant life are also used for future periods [30].
- O&M cost: In both the past and the future periods, labor, membrane exchange, and chemical costs are assumed to be constant, as summarized in Table 1. Equation (10) is used to calculate the energy cost.
- Water price: The water price is estimated using Equations (12) and (13) for the two scenarios. First, these functions are used to simulate the change in the water price in each country during different years. In our long-term future simulation, the future projected water price is assumed to change uniformly every year. Second, the function, developed based on data from 56 countries, is applied to compute the deficient water price in the other 84 countries that were not included in the observed dataset. For domestic water withdrawal per capita, Hanasaki, et al. [43] estimate that the growth rate would be ~7.3 × 10−4 m3 person−1 year−1; here, that same past growth rate is used for the future simulations.
- Socioeconomic condition: Shared Socioeconomic Pathways (SSPs) are newly developed socioeconomic scenarios for use in global climate policy studies. They depict five possible future global situations (SSP1–5). In this study, we perform the future simulations primarily under the SSP2, which involves a middle-of-the road scenario with an intermediate GDP per capita and intermediate population growth. This scenario was selected because it is consistent with the development patterns that have been observed over the past century [48].
- Climate policy: As mentioned above, energy cost is an integral part of the unit production cost. This may be greatly affected by future climate policies, as different policies lead to different energy prices [27]. In the present study, to clarify the effect of climate policy on future SWRO diffusion, future simulations of PC and WP models are carried out under the following two climate policy scenarios [49]:
- No climate policy scenario (Baseline): this assumes changes in the socioeconomic conditions in different countries under SSP2 and does not account for the effect of a climate policy (i.e., it assumes there are no constraints on greenhouse gas emissions). Under such a scenario, the energy sources are dependent on traditional fossil fuels.
- Stringent climate policy scenario (RCP2.6): this assumes changes in the socioeconomic conditions in different countries under SSP2 and accounts for the effect of the stringent climate policy of RCP2.6 (i.e., it assumes a stringent constraint on greenhouse gas emissions aimed at keeping the global mean temperature increase below 2 °C by the year 2100). The RCP2.6 scenarios generally involve more renewable energy resources and a higher carbon tax than does the baseline scenario.
3. Results and Discussion
3.1. Production Cost Prediction by Future Simulation of the PC Model
3.2. Water Price Prediction According to Future Simulations of the WC Model
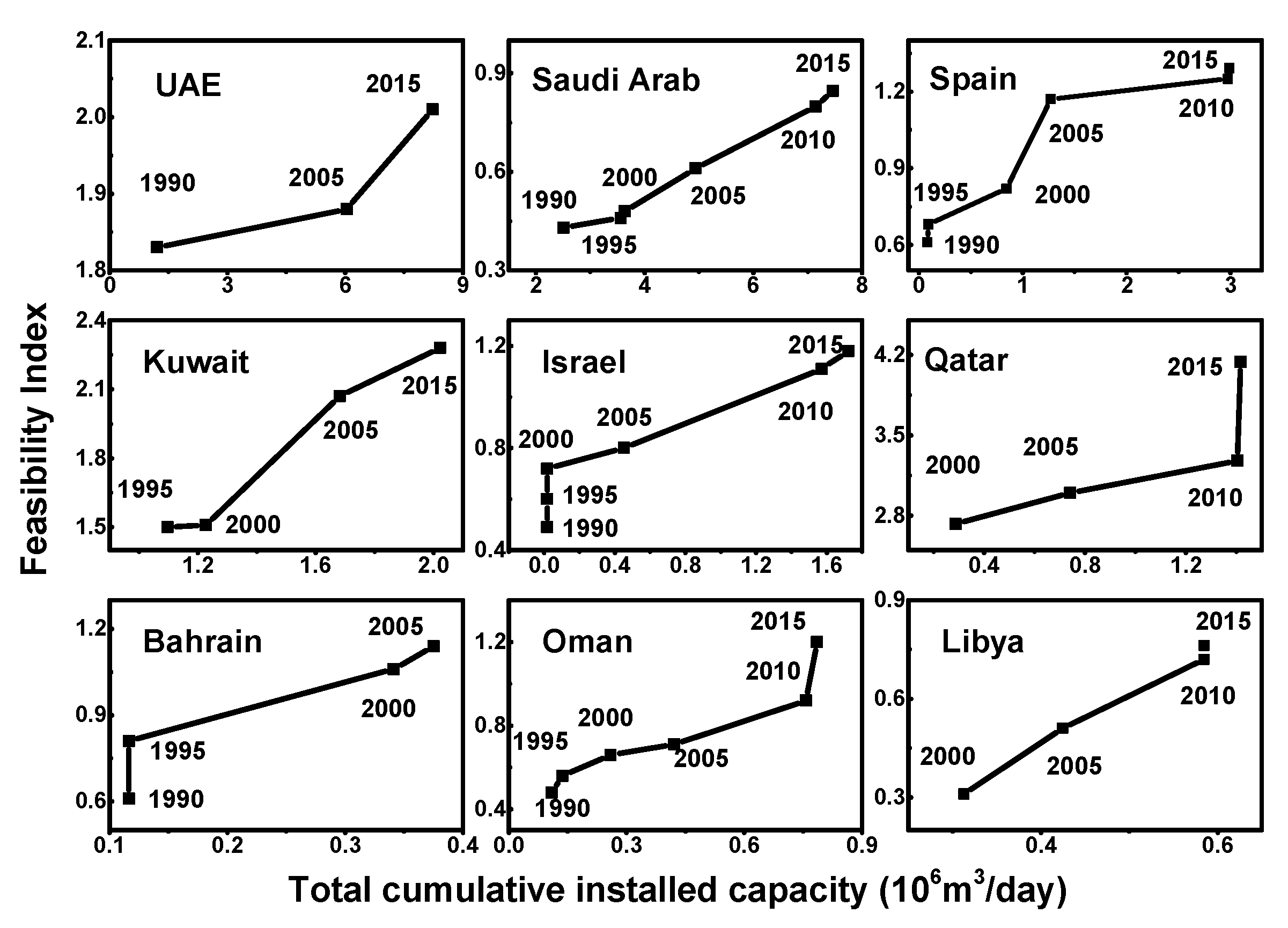
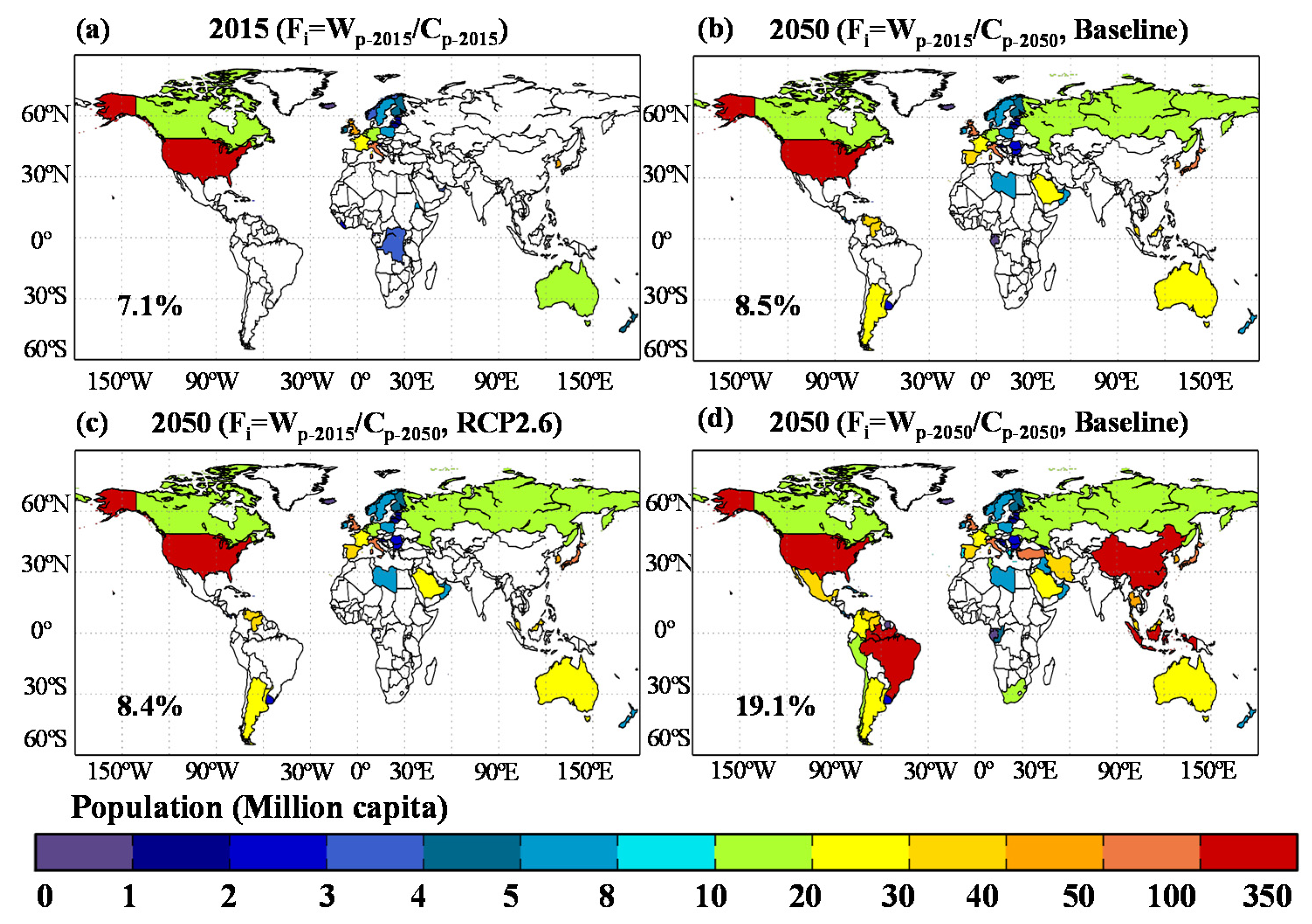
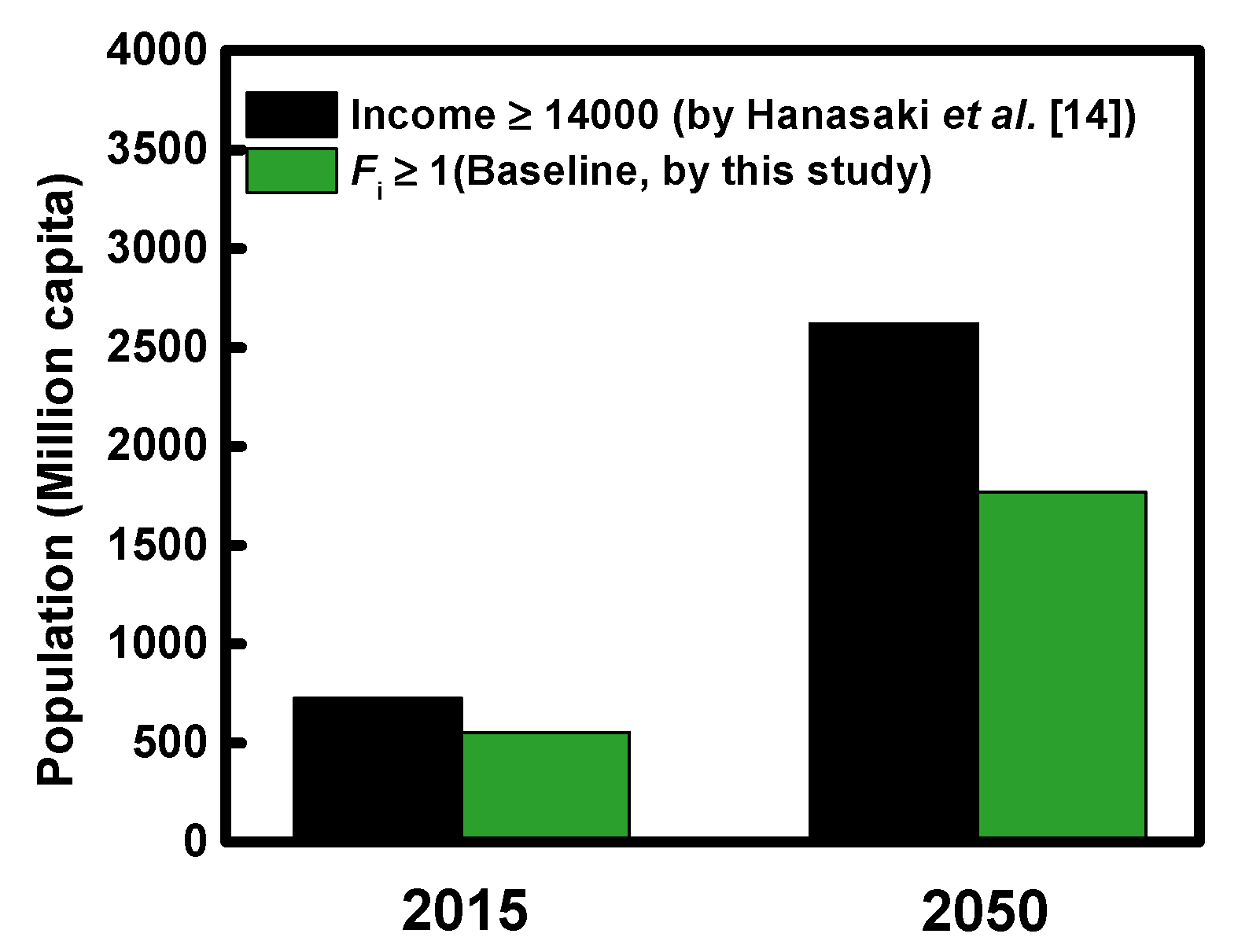
3.3. Economic Feasibility Assessment of SWRO on a Global Scale
3.3.1. Assessment Using the Constant Water Price in 2015
3.3.2. Assessment Incorporating Changes in Water Prices
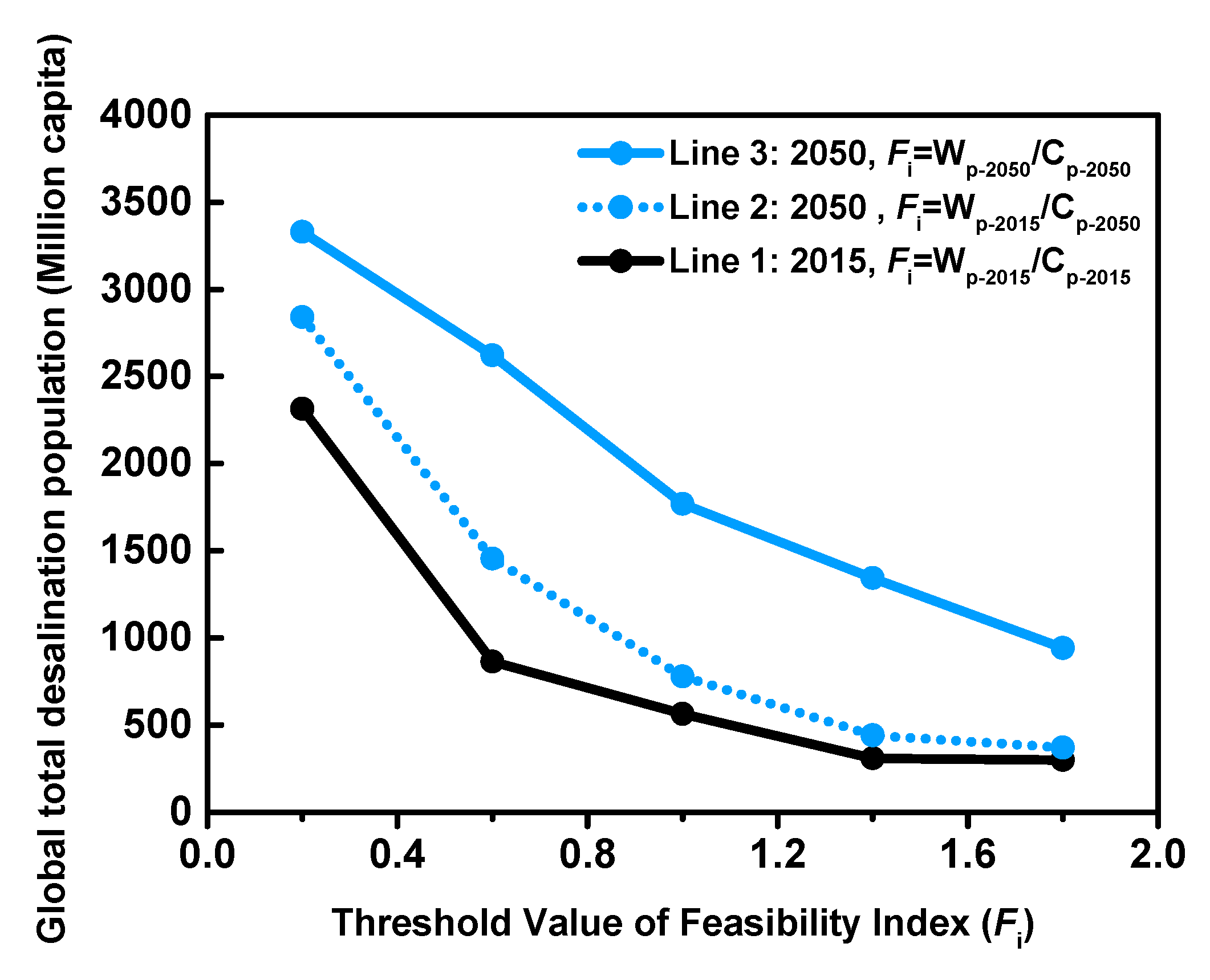
3.3.3. Sensitivity Analysis of the Feasibility Index
3.4. Data Limitations and Uncertainties
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Kundzewicz, Z.W.; Dieter, G. Grand Challenges Related to the Assessment of Climate Change Impacts on Freshwater Resources. J. Hydrol. Eng. 2015, 20, 1943–5584. [Google Scholar] [CrossRef]
- Ghaffour, N.; Missimer, T.M.; Amy, G.L. Technical review and evaluation of the economics of water desalination: Current and future challenges for better water supply sustainability. Desalination 2013, 309, 197–207. [Google Scholar] [CrossRef]
- Mays, L.W. Groundwater Resources Sustainability: Past, Present, and Future. Water Resour. Manag. 2013, 27, 4409–4424. [Google Scholar] [CrossRef]
- Miller, S.; Shemer, H.; Semiat, R. Energy and environmental issues in desalination. Desalination 2015, 366, 2–8. [Google Scholar] [CrossRef]
- Schallenberg-Rodríguez, J.; Veza, J.M.; Blanco-Marigorta, A. Energy efficiency and desalination in the Canary Islands. Renew. Sustain. Energy Rev. 2014, 40, 741–748. [Google Scholar] [CrossRef]
- Peñate, B.; García-Rodríguez, L. Current trends and future prospects in the design of seawater reverse osmosis desalination technology. Desalination 2012, 284, 1–8. [Google Scholar] [CrossRef]
- Al-Sahali, M.; Ettouney, H. Developments in thermal desalination processes: Design, energy, and costing aspects. Desalination 2007, 214, 227–240. [Google Scholar] [CrossRef]
- DesalData. Availabe online: http://www.desaldata.com/ (accessed on 5 October 2015).
- Bremere, I.; Kennedy, M.; Stikker, A.; Schippers, J. How water scarcity will effect the growth in the desalination market in the coming 25 years. Desalination 2001, 138, 7–15. [Google Scholar] [CrossRef]
- Kirshen, P. Adaptation Options and Cost in Water Supply; Tufts University: Medford, MA, USA, 2007. [Google Scholar]
- Kim, S.H.; Hejazi, M.; Liu, L.; Calvin, K.; Clarke, L.; Edmonds, J.; Kyle, P.; Patel, P.; Wise, M.; Davies, E. Balancing global water availability and use at basin scale in an integrated assessment model. Clim. Chang. 2016, 136, 217–231. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; Bierkens, M.F.P. Modelling global water stress of the recent past: On the relative importance of trends in water demand and climate variability. Hydrol. Earth Syst. Sci. 2011, 15, 3785–3808. [Google Scholar] [CrossRef]
- Hanasaki, N.; Yoshikawa, S.; Kakinuma, K.; Kanae, S. A seawater desalination scheme for global hydrological models. Hydrol. Earth Syst. Sci. 2016, 20, 4143–4157. [Google Scholar] [CrossRef]
- Ziolkowska, J.R. Is Desalination Affordable?—Regional Cost and Price Analysis. Water Resour. Manag. 2015, 29, 1385–1397. [Google Scholar] [CrossRef]
- Zhou, Y.; Tol, R.S.J. Evaluating the costs of desalination and water transport. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Ali, E.S.; Alsaman, A.S.; Harby, K.; Askalany, A.A.; Diab, M.R.; Ebrahim Yakoot, S.M. Recycling brine water of reverse osmosis desalination employing adsorption desalination: A theoretical simulation. Desalination 2017, 408, 13–24. [Google Scholar] [CrossRef]
- Caldera, U.; Bogdanov, D.; Breyer, C. Local cost of seawater RO desalination based on solar PV and wind energy: A global estimate. Desalination 2016, 385, 207–216. [Google Scholar] [CrossRef]
- Choi, Y.; Cho, H.; Shin, Y.; Jang, Y.; Lee, S. Economic Evaluation of a Hybrid Desalination System Combining Forward and Reverse Osmosis. Membranes 2016, 6, 3. [Google Scholar] [CrossRef] [PubMed]
- World Bank. Availabe online: http://databank.worldbank.org/data/home.aspx (accessed on 29 June 2016).
- IEA Database. Availabe online: http://www.iea.org/statistics/ (accessed on 9 May 2017).
- Gleick, P.H.; Michael, J.C. The world’s Water 2008–2009; Island Press: Washington, DC, USA, 2009. [Google Scholar]
- IBNET Tariff Database. Availabe online: https://tariffs.ib-net.org/ (accessed on 27 May 2017).
- Yoshikawa, S.; Cho, J.; Yamada, H.G.; Hanasaki, N.; Kanae, S. An assessment of global net irrigation water requirements from various water supply sources to sustain irrigation: Rivers and reservoirs (1960–2050). Hydrol. Earth Syst. Sci. 2014, 18, 4289–4310. [Google Scholar] [CrossRef]
- Shared Socioeconomic Pathway (SSP) Database. Availabe online: https://tntcat.iiasa.ac.at/SspDb/dsd?Action=htmlpage&page=about (accessed on 18 October 2016).
- Murakami, D.; Yamagata, Y. Estimation of gridded population and GDP scenarios with spatially explicit statistical downscaling. arXiv 2016, arXiv:1610.09041. [Google Scholar]
- Fujimori, S.; Hasegawa, T.; Masui, T.; Takahashi, K.; Herran, D.S.; Dai, H.; Hijioka, Y.; Kainuma, M. SSP3: AIM implementation of Shared Socioeconomic Pathways. Global. Environ. Chang. 2017, 42, 268–283. [Google Scholar] [CrossRef]
- Kesieme, U.K.; Milne, N.; Aral, H.; Cheng, C.Y.; Duke, M. Economic analysis of desalination technologies in the context of carbon pricing, and opportunities for membrane distillation. Desalination 2013, 323, 66–74. [Google Scholar] [CrossRef]
- Ziolkowska, J.R. Desalination leaders in the global market—Current trends and future perspectives. Water Sci. Technol. Water Supply 2016. [Google Scholar] [CrossRef]
- Papapetrou, M.; Cipollina, A.; La Commare, U.; Micale, G.; Zaragoza, G.; Kosmadakis, G. Assessment of methodologies and data used to calculate desalination costs. Desalination 2017, 419, 8–19. [Google Scholar] [CrossRef]
- Loutatidou, S.; Chalermthai, B.; Marpu, P.R.; Arafat, H.A. Capital cost estimation of RO plants: GCC countries versus southern Europe. Desalination 2014, 347, 103–111. [Google Scholar] [CrossRef]
- Al-Karaghouli, A.; Kazmerski, L.L. Energy consumption and water production cost of conventional and renewable-energy-powered desalination processes. Renew. Sustain. Energy Rev. 2013, 24, 343–356. [Google Scholar] [CrossRef]
- Semiat, R. Energy Issues in Desalination Processes. Environ. Sci. Technol. 2008, 42, 8193–8201. [Google Scholar] [CrossRef] [PubMed]
- Glueckstern, P. Cost estimates of large RO systems. Desalination 1991, 81, 49–56. [Google Scholar] [CrossRef]
- Al-Sahlawi, M.A. Seawater desalination in Saudi Arabia: Economic review and demand projections. Desalination 1999, 123, 143–147. [Google Scholar] [CrossRef]
- CDM. Water Supply Cost Estimation Study; South Florida Water Management District: West Palm Beach, FL, USA, 2007.
- Lamei, A.; Van der Zaag, P.; Von Münch, E. Basic cost equations to estimate unit production costs for RO desalination and long-distance piping to supply water to tourism-dominated arid coastal regions of Egypt. Desalination 2008, 225, 1–12. [Google Scholar] [CrossRef]
- Zotalis, K.; Dialynas, E.; Mamassis, N.; Angelakis, A. Desalination Technologies: Hellenic Experience. Water 2014, 6, 1134–1150. [Google Scholar] [CrossRef]
- Commission, N.W. Emerging Trends in Desalination: A Review; National Water Commission: Canberra, Australia, 2008. [Google Scholar]
- Wilderer, P. Treatise on Water Science; Elsevier Science: Amsterdam, The Netherlands, 2011. [Google Scholar]
- McKenzie, D.; Ray, I. Urban water supply in India: Status, reform options and possible lessons. Water Policy 2009, 11, 442–460. [Google Scholar] [CrossRef]
- Li, L.; Wu, X.; Tang, Y. Adoption of increasing block tariffs (IBTs) among urban water utilities in major cities in China. Urban. Water J. 2017, 14, 661–668. [Google Scholar] [CrossRef]
- Hanasaki, N.; Fujimori, S.; Yamamoto, T.; Yoshikawa, S.; Masaki, Y.; Hijioka, Y.; Kainuma, M.; Kanamori, Y.; Masui, T.; Takahashi, K.; et al. A global water scarcity assessment under Shared Socio-economic Pathways—Part 2: Water availability and scarcity. Hydrol. Earth Syst. Sci. 2013, 17, 2393–2413. [Google Scholar] [CrossRef]
- Alexander, Q.; Christine, S.; Kevin, F.; Vanessa, L. National Economic & Labor Impacts of the Water Utility Sector: Technical Report; Water Reserch Foundation: San Francisco, CA, USA, 2014. [Google Scholar]
- Linda, J.R. Electricity Use and Management in the Municipal Water Supply and Wastewater Industries; Water Reserch Foundation: San Francisco, CA, USA, 2013. [Google Scholar]
- Piper, S. Impact of water quality on municipal water price and residential water demand and implications for water supply benefits. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Zachariadis, T. Residential Water Scarcity in Cyprus: Impact of Climate Change and Policy Options. Water 2010, 2, 788–814. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Riahi, K.; Ebi, K.L.; Hallegatte, S.; Carter, T.R.; Mathur, R.; van Vuuren, D.P. A new scenario framework for climate change research: The concept of shared socioeconomic pathways. Clim. Chang. 2014, 122, 387–400. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Stehfest, E.; den Elzen, M.G.J.; Kram, T.; van Vliet, J.; Deetman, S.; Isaac, M.; Klein Goldewijk, K.; Hof, A.; Mendoza Beltran, A.; et al. RCP2.6: Exploring the possibility to keep global mean temperature increase below 2 °C. Clim. Chang. 2011, 109, 95. [Google Scholar] [CrossRef]
- Ruester, S.; Zschille, M. The impact of governance structure on firm performance: An application to the German water distribution sector. Util. Policy 2010, 18, 154–162. [Google Scholar] [CrossRef]
- March, H.; Saurí, D.; Rico-Amorós, A.M. The end of scarcity? Water desalination as the new cornucopia for Mediterranean Spain. J. Hydrol. Part C 2014, 519, 2642–2651. [Google Scholar] [CrossRef]
| Parameter | Data | Year | Ref. |
|---|---|---|---|
| Capital cost | 56 countries (764 plants) | 1990–2014 | [9] |
| GDP | 56 countries | 1990–2014 | [20] |
| Population | 56 countries | 1990–2014 | [20] |
| Electricity | 56 countries | 1990–2014 | [21] |
| Water price | 56 countries | 1990–2014 | [22,23] |
| Water withdrawal | 56 countries | 1990–2000 | [24] |
| Water demand | 56 countries | 1990–2001 | [24] |
| For future period | |||
| GDP | 140 countries | 2015–2050 | [25] |
| Population | 140 countries | 2015–2050 | [26] |
| Electricity | 17 Regions | 2015–2050 | [27] |
| Economic Parameters | |||
| Labor cost | 0.1 US $/m3 | [15] | |
| Chemical cost | 0.07 US $/m3 | [15] | |
| Membrane exchange cost | 0.03 US $/m3 | [15] | |
| Energy consumption | 4 kWh/m3 | [6] | |
| Maintenance cost | 2% of capital cost | [28] | |
| Baseline | RCP2.6 | Baseline | ||||||
|---|---|---|---|---|---|---|---|---|
| (Fi = Wp-2015/Cp-2015) | (Fi = Wp-2015/Cp-2050) | (Fi = Wp-2015/Cp-2050) | (Fi = Wp-2050/Cp-2050) | |||||
| 2015 | 2050 | 2050 | 2050 | |||||
| Class | Population | Percent | Population | Percent | Population | Percent | Population | Percent |
| (Million) | (Million) | (Million) | (Million) | |||||
| 1 (Fi < 0.5) | 1086.8 | 14% | 1622.2 | 18% | 1695.4 | 19% | 610.4 | 7% |
| 2 (0.5 < Fi < 1) | 382.9 | 5% | 995.7 | 11% | 929.1 | 10% | 1018.1 | 11% |
| 3 (1 < Fi < 2) | 358.4 | 5% | 411.1 | 4% | 410.1 | 4% | 1238.8 | 14% |
| 4 (2 < Fi < 4) | 193.2 | 2% | 364.5 | 4% | 361.9 | 4% | 514.9 | 6% |
| 5 (4 < Fi < 7) | 0.0 | 0.0% | 3.1 | 0.0% | 0.0 | 0.0% | 14.3 | 0.2% |
| Global population | 7811.3 | 9149.4 | 9149.4 | 9149.4 | ||||
| Class > 2 | 551.6 | 7.1% | 778.6 | 8.5% | 771.9 | 8.4% | 1768.0 | 19.3% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Yoshikawa, S.; Iseri, Y.; Fujimori, S.; Kanae, S. An Economic Assessment of the Global Potential for Seawater Desalination to 2050. Water 2017, 9, 763. https://doi.org/10.3390/w9100763
Gao L, Yoshikawa S, Iseri Y, Fujimori S, Kanae S. An Economic Assessment of the Global Potential for Seawater Desalination to 2050. Water. 2017; 9(10):763. https://doi.org/10.3390/w9100763
Chicago/Turabian StyleGao, Lu, Sayaka Yoshikawa, Yoshihiko Iseri, Shinichiro Fujimori, and Shinjiro Kanae. 2017. "An Economic Assessment of the Global Potential for Seawater Desalination to 2050" Water 9, no. 10: 763. https://doi.org/10.3390/w9100763
APA StyleGao, L., Yoshikawa, S., Iseri, Y., Fujimori, S., & Kanae, S. (2017). An Economic Assessment of the Global Potential for Seawater Desalination to 2050. Water, 9(10), 763. https://doi.org/10.3390/w9100763





