Abstract
This study integrates and develops methods, namely low impact development (LID) selection method and an LID spatial planning model, to enable decision-making to minimize pluvial flooding for a community. The objective is to minimize the flood risk under the worst case of the design storm within the budget constraints. Design storms in current and future climate scenarios are analyzed as input to the Storm Water Management Model (SWMM). Then, LID practices are selected based on the proposed procedure and a spatial planning model is built to identify the optimal LID layouts using the simulated annealing (SA) algorithm. The lower and upper bounds of the generated rainfall intensities of a five-year 1-h duration design storms for the Hadley Centre Global Environment Model version 2 for the atmosphere and oceans (HadGEM2-AO), the Norwegian Earth System Model (NorESM1-ME), and the CSIRO-Mk3.6.0 Atmosphere-Ocean GCM (CSIRO-Mk3.6.0) during 2021–2040 are derived. The LID selection helps efficiently identify appropriate LID. Results show that nearly no flood occurs under the optimal LID layouts found by the LID spatial planning model. Moreover, it is more optimal to invest in LID in the lower sub-catchments in LID planning when the budget is limited. These methods are generally applicable for a community using LIDs as adaptation measures against pluvial flooding.
1. Introduction
Many densely populated cities are flood-prone, and existing infrastructure may not be resilient enough facing the increased peak flows that may occur with climate change [1]. As such, many approaches to adaptation against floods have been proposed [2,3]. To achieve more sustainable land use practices against floods, small-scale source-control structures have received more attention in recent years over traditional engineered defenses [4,5,6,7]. These source-control structures disperse the perviousness in the developed area and retain storm water at its source, resulting in decreased surface runoff, lower peak flow rates, and eventual reduction of the flood [8]. Among the terms used to describe the practices, low impact development (LID) practices are used in this study as adaptation measures. The purpose of LID is to reduce the negative effects of urbanization on local hydrology [9]. These practices are already applied to reduce urban flooding, for example the rain garden of the new Hyderabad airport, the High Point Community Revitalization plan [10], and the flood plain in Benthemplein [11]. Appropriate design of LIDs prevents pluvial floods and provides more livable space.
Some studies have explored and quantified the effects of LID on storm water quantity and quality for specific rainfall characteristics. Qin et al. (2013) [12] simulated the performance of LIDs in Shenzhen, southeast China. Swales, permeable pavements, and green roofs perform best in total flood volume reduction during storm events with an early, middle, and late peak, respectively. It can be attributed to the setting of the storage height of each LID. Moreover, the result shows that swales, permeable pavements, and green roofs reduce floods more effectively during heavier and shorter events and that the performance depends on the location of peak rainfall intensity. However, other studies have shown that LID performs better for small storms [13,14]. Hood et al. [13] conducted a study in Southeastern Connecticut and found that the amount, duration, and antecedent moisture condition of the storms influence the performance of LIDs. The reductions of the runoff depth and peak discharge are mainly due to the infiltration in permeable pavement, bioretention, and grassed swales. Based on the previous studies, it is certain that LID designs and rainfall characteristics, such as the location of peak rainfall intensity, need to be considered.
Site constraints are important factors in in screen out suitable LIDs because they may limit the use of some LIDs, unless the LIDs are with specific design to adapt to the constraints. This study proposed a LID selection method based on the site constraints, providing users with a way to isolate the most suitable LID options when needed. Common site restrictions include land use type, local pollution loading, soil type and depth, groundwater table depth, topography, available space, drainage area, and impervious area. Pollution load control may be the main objective of LID implementation, rather than flood control. In that case, the pollution load of the site is not only treated as a constraint; instead, the effects of LIDs on the reduction of pollution loads are considered in the objective of adaptation. In Southern California, even the landslide risk is taken into account [15]. Other considerations include the required setback from buildings/building foundations, roads, water bodies, and other infrastructure [16,17,18]. Some studies also consider system reliability and robustness as selection criteria, but it is difficult to verify the methods used to score these factors for each LID practice [19,20].
Considerations involving subjective judgment, such as local experience or resident preference, can also be applied in LID selection [21]. Not all of the aforementioned factors are exclusively independent; moreover, overlap of these considerations may reduce the efficiency of selecting LID. For example, the impervious area is related to the land use type to some extent, and the buffer distances to buildings, roads, etc. are associated with the available space. Research that assigns quantitative benchmarks for the implementation of various LID practices under certain site conditions is rare. Moreover, studies exploring quantitative benchmarks seldom elaborate on the application of those benchmarks and usually do not establish an LID selection procedure. Among the very few that do describe selection procedures, Jia et al. (2013) [17] proposed an approach for selecting LID practices based on site constraints, cost, and effectiveness by creating a score table. However, the self-defined weights used in the scoring method affect the results of the LID selection and therefore cannot guarantee the reliability. In this case, evaluating the cost and efficacy using hydrological or planning models is another alternative.
Widely applied models created to support LID planning and decision-making usually combine the Storm Water Management Model (SWMM) and optimization methods to help identify the optimal types, configurations, and locations of LID practices [22,23]. System for Urban Stormwater Treatment and Analysis Integration (SUSTAIN; Lai et al., 2007 [22]) is one example, developed to assist the decision-making of the planning of the flow and pollution control measures. The optimization algorithm of SUSTAIN are scatter search and non-dominated sorting genetic algorithm-II (NSGA-II). Other optimization methods have also been applied in LID planning, including downhill simplex method combined with genetic algorithm [24], linear programming [25], and grey stochastic programming [26]. These are potential decision support tools for LID planning. However, decision support for future climate scenario analysis and LID selection to screen suitable LIDs is not included in SUSTAIN, although site condition information can be imported using geographic information systems. Moreover, the application of SUSTAIN relies heavily on the knowledge of the tool of geographic information systems in addition to the optimization methods. Therefore, the major contribution of this study is to propose LID selection method and a spatial planning model to assist LID planning under climate change.
Considering the site constraints and the cost-effectiveness of the LID measures under both current and future climate conditions, implementation of these LID measures in a target area is a complex task. Observed precipitation is required to derive the design storms for current conditions. Future daily rainfall estimates are often produced by stochastic weather generators [27,28] based on climate scenarios derived from the projections of general circulation models (GCMs). To obtain direct flood-related rainfall characteristics, design storms needs to be derived [29]. To conclude, integrated and systematic methodologies are necessary to assist community-scale implementation of LID practices. The goal of this study is to develop procedures to support adaptation decision-making for implementing LID of a community against pluvial flooding when experiencing climate change. The procedures of LID selection method and an LID spatial planning model intended to be transferrable to any region are highlighted in this study. Decision-making is applied to a design case, which demonstrates the steps necessary in LID planning for a community.
2. Materials and Methods
This study focuses on community-scale risk analysis of pluvial flooding and spatial planning of LID as adaptation measures by integrating existing methods and developing methodologies for each step of the systematic framework of adaptation decision-making (Figure 1). Adaptation to future climate scenarios is the process of adjustment to expected climate and its effects [30]. The framework is based on the European Union (EU) Adaptation Supporting Tool and the United Kingdom Climate Impacts Program adaptation wizard [31]. This study used a regional five-year design storm in flood analysis and proposed methods of LID selection and LID spatial planning to support the adaptation framework, which advances the current state-of-the-art approach [32,33,34,35].
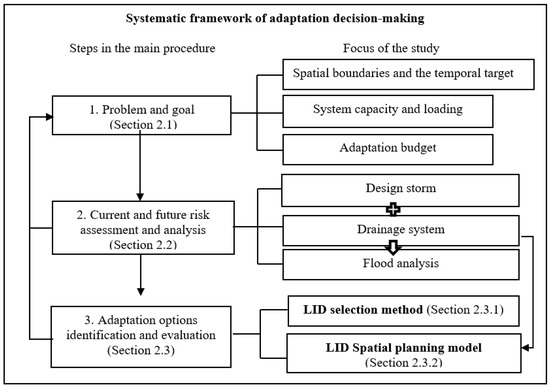
Figure 1.
Systematic framework of adaptation decision-making.
Because floods may occur under the extreme rainfall in future climate scenarios, it is crucial to strengthen the carrying capacity to help a community adapt to potential pluvial flooding. The carrying capacity of the drainage system is the ability to drain the stormwater of the design storm event that is mandated by local law without causing inundation, a five-year design storm for the study case. The drainage system is the current storm drains plus the LID components as adaptation measures in the future climate scenarios. For risk assessment, this study conducted flood analysis using the rainfall intensity of the future worst scenario derived from the projections of selected GCMs. The method of LID selection is developed as an option for users to isolate the most suitable LID options, and an LID spatial planning model is proposed to evaluate the efficacy. The two procedures embedded in the framework are marked in Figure 1. The corresponding sections describing the procedures are shown in parentheses.
2.1. Problem and Goal
In the first step, the problem and the goal should be clarified before identifying climate adaptation measures. The problem of concern is pluvial flooding in a community under climate change conditions; therefore, external water from outside the community is not considered. The spatial boundaries and concerned future period are clarified in the problem setup, as are the capacity and loading of the drainage system. In this study, the concerned future period is 2021–2040 and the spatial boundaries are the sub-catchments of the study case. The site description is included in the section of design case because the methods are intended to be transferrable to any region. The loading means the flow caused by the stormwater and depends on the storm events the system faces. The value of the peak flow quantifying the flood risk is derived from the engineering designs and rainfall records of the concerned region, in this study the design case of the reference community. Then, the budget of the local authorities or stakeholders for implementing LID is considered. The goal is to effectively reduce flooding using the drainage system combining the storm drains and LID measures, under the estimated maximum rainfall intensity of the five-year design storms in the future climate scenarios derived from the GCM projections, e.g., the worst design storm. Here, a design storm with five-year return period (denoted as a five-year storm) is selected to meet the legal requirement for the study case. Specifically, the maximal depth and the maximal duration of inundation among all manholes are identified, respectively. Then, the objective function is to minimize the linear combination of the maximal depth, the maximal duration, and the number of inundated points spatially within the budget constraints, which is three million New Taiwan Dollars (NTD) for the study case.
2.2. Risk Assessment and Analysis
The second and the third steps are to assess current and future risks. When storm water reaches the surface and the drainage system fails to transport the water efficiently, inundation occurs. Therefore, this section elaborates on the details of design storms and flood analysis. Design storm is a storm event of specific duration and return period used to calculate the runoff volume and peak discharge, for designing hydrology-related measures in engineering. Observed hourly precipitation is used to derive the design storm by frequency analysis [36] and hyetograph analysis [37]. The design storm is the input of flood analysis in assessing current flood risk. Future daily rainfall is generated using a Richardson-type weather generator [27], based on future climate scenarios derived from GCM projections. To evaluate the design storm in the future climate scenario, the increase of the rainfall intensity is assumed the same as the increase of daily precipitation in the future climate scenarios. The hyetograph suitable for the target area, in this study the Hsinchu County for the study case, can be analyzed using the Simple Scaling Gauss–Markov method [37]. This method can also be applied to other areas if the normality and the correlation coefficients of the rainfall-event records fulfill the assumptions of the Gauss–Markov model. Then, the identified worst design storm is used in the flood simulation for future risk assessment.
In this study, flooding caused by storm water is simulated using SWMM (version 5.1.010), a physically based deterministic model developed by the Environmental Protection Agency of the United States. SWMM is used to assess the effects of development or adaptation measures on the runoff quantity and quality through the rainfall-runoff, urban drainage, and routing processes [38,39,40]. SWMM is selected because it has the embedded LID simulation modules that can be used to assess the effects of LIDs on runoff quantity. The Horton equation has been used for simulating infiltration and the routing method is the dynamic wave method. To depict the interaction between the pipe flow of the sewer system and the street flow on the surface, a dual system is developed. The dual system assumes that street gutters and sewer pipes are parallel and connected vertically by manholes. Therefore, the water spills onto the streets and causes flooding in the SWMM simulation when the flow is above the pipe crown. The gutter design of the dual system is flexible in this method; users are able to adjust the inlet/outlet offset, cross-section, and street slope according to local records. Simulation of LID is also included in SWMM to analyze subsequent effects on flood reduction. Given proper parameters, the design of LID practices can be simulated by SWMM LID modules. The LIDs are stratified into the surface, soil, storage, and drainage layers, with corresponding parameters such as the thickness, the porosity, and the conductivity of the soil layer. The users are encouraged to collect the parameters from the manufacturers before applying the proposed framework. Notice that the different objectives of installing LID also influence the selection of the parameters. More detailed descriptions of LID modeling can be found in the SWMM user’s manual [38].
2.3. Efficacy Evaluation of Adaptation Measures
In the fourth step, adaptation measures are selected to increase the capacity of the targeted community to reduce flood risk under climate change conditions. Two parts are included in this section: LID selection method and the LID spatial planning model.
2.3.1. LID Selection Method
This study developed a procedure for LID selection to isolate the most suitable LID options. Some LID options may need additional design considerations to be implemented under certain local site constraints. The proposed LID selection provide decision-makers an approach to efficiently limit the potential LIDs to those appropriate to the site, by calculating the score of the commonly-seen site-constraint factors (Table 1). Here is an example showing how the score of the pollution loading constraint is calculated from one of the collected studies providing the benchmarks. Twelve LIDs including infiltration trench, infiltration basin, dry detention pond, wet detention pond, vegetated filter strip, grassed swale, constructed wetlands, sand filter, green roof, rain barrel, porous pavement, and bioretention are considered in the reference [17]. All LIDs are applicable in low-pollution loading sites, while some are not as useful in medium-pollution loading sites, namely green roof, rain barrel, porous pavement, and bioretention. Moreover, only vegetated filter strip is applicable in high-pollution loading site. To summarize, there are 1, 8, and 12 out of 12 LID measures on the selection list applicable for the category of high-, medium-, and low-pollution loading sites, respectively, with regard to the pollution loading constraint [17]. Each site constraint factor is viewed as the selection criteria of suitable LIDs. The score of selection criteria is developed to determine key criteria and rank the selection criteria, which are further used to screen suitable LIDs.

Table 1.
Frequency and score for site constraints in low impact development (LID) selection.
Some LID measures are applicable for more than one category. No LID measures are limited by the pollution-loading factor if the real world situation lies in the low-pollution loading category, which is viewed as inefficient to isolate the most suitable LID options. The score is calculated by averaging the absolute difference between the ratio (ri) of applicable LIDs without additional design considerations (NLID in category i) and the average ratio (ravg) of LID for all categories (Nall LID options/C) (Equation (1)). The score of the pollution-loading factor in the aforementioned example can be calculated by Equation (2). Here, C = 3 refers to the high-, medium- and low- pollution loading categories. The lowest score (0) occurs if each category contains the same amounts of LIDs (four LIDs). It is because then only four LIDs without additional design considerations remain applicable for a real-world condition lying in one of the three categories. Therefore, the lower the score of the factor is, the faster the factor can screen out LIDs without additional design considerations. The numbers of the categories are different for each study and each constraint within the studies, which can be found in the reference studies [15,16,17,18]. For instance, according to the reference studies [41,42] which are reviewed by the study mentioning the pollution loading constraint [17], LIDs ability to address low, medium, and high pollution loading means the removal efficiencies of pollutants such as total suspended solids and total phosphorus lie in 0–30%, 31–65%, and > 65%, respectively. Moreover, the small, medium, and large area required for BMP are defined as land <10 acres, 10–40 acres, and >40 acres [42].
where ri is the ratio of applicable LIDs to the number of all LIDs; NLID in category i is the number of applicable LIDs in the category i among the C categories of the site constraint factor; Nall LID options is number of all LIDs; ravg is the ratio of average LIDs in each category (Nall LID options/C) to the number of all LIDs (Nall LID options); and Score(pollu) is the score of the pollution-loading factor.
The score of the selection criteria of LIDs based on specified benchmarks exhaustively collected in previous studies is shown in Table 1 [16,17,18,40]. The site-constraint factors that limit the implementation of LIDs are reviewed based on the national or local guidance of several countries. The countries include North and South America, Europe, Africa, Asia, and Australia together with Oceania [16,18,19,20,43,44,45,46,47]. The frequency that each site-constraint is mentioned in the literatures is also shown in Table 1. Seven of the 11 most frequently mentioned factors are defined as primary site constraints because some factors overlap. For example, land use type, drainage area, and impervious area are usually correlated, and buffer or setback is related to the available area for LID. Moreover, some factors such as landslide risk are not a universal concern. Therefore, clarifying the primary factors helps identify the most-often considered crucial aspects.
Because the consideration of the buffer or setback in each region varies greatly, the score of that is neglected in this study and should be considered together with the available area. The priority of considering the site constraint factors is derived based on the average values of the score in Table 1, in the order of available area, ground water table depth, pollution loading, depth to impermeable bedrock, slope, land use type, and soil type. The benchmarks include LID options from available LID experiments or implementations in the United States, Canada, and Europe. Although the benchmarks may not be as useful in the places with very different site characteristics such as the soils in tropical regions, the proposed LID selection procedure is generally applicable in regions adopting similar type of LID measures. After identifying the LID options, the design of the LID needs to be addressed. The study optimizes the LID layouts with given LID parameters. However, further studies are recommended to optimize both LID layouts and parameters to fit particular objectives or site conditions.
2.3.2. LID Spatial Planning Model
Owing to budget constraints, decision makers must allocate LID practices in the most effective manner for alleviating floods. Therefore, a spatial planning model with the ability to minimize flood from a five-year storm in the worst future climate scenario is proposed to determine the optimal layouts of LID. In the spatial planning model, the objective is to minimize the maximal depth, the maximal duration, and the number of inundated points in the watershed within the budget constraints under the worst design storm. The decision variables include the type and amount of LID in each sub-catchment, which constitute a LID layout and form a solution. The combined use of LID practices can be considered in the spatial optimization model, either by dividing the sub-catchments into more sub-catchments or by redesigning decision variables for sub-catchments. To demonstrate the effects of the type and location of LIDs, only one of the LID measures is applied for each sub-catchment in this study.
To assimilate the planning process to the behavior of decision-making, the weighting method [48] is used. The setting of the weights helps to identify optimal solutions among all Pareto solutions in a multi-objective problem. The objective function of the spatial planning model is to minimize the highest depth (Di) and duration (Ti) of inundation among all sub-catchments as well as the number of inundated points (H) in the watershed after implementing LID, as shown in Equation (3), and the constraints are expressed in Equations (4)–(8). ωD, ωT, and ωH are weights. Notice that both the objective function and weights should be determined collaboratively with stakeholders from practical perspective. The maximal depth (m3), the maximal duration (hour), and the number of inundated points (-) of the floods in the objective function are normalized to ensure the rationality of adding up the terms with different units. This is accomplished by dividing Di, Ti, and H by the possible maximal values (Dmax_noLID, Tmax_noLID, and HnoLID) obtained before implementing LID under the worst case of the future climate scenarios. Di, Ti, and H are non-linear functions because the dynamic wave method accounts for pressure changes, such as backwater effects. Moreover, the simulated annealing (SA) algorithm is used because it is usually applied to problems related to allocation, such as the traveling salesman decision problem, and assures effective and efficient optimization [49].
where M is the set of sub-catchments with m elements; N is the set of LID measures with n elements; pi is a random number ensuring only one of the LID measures is selected for each sub-catchment; ε is a random number representing the number of the selected LID units, generated from a uniform distribution between 0 and the allowed maximum amounts; xij is the number of the jth LID in the ith sub-catchment; Sij is the limit of the amount of the jth LID in the ith sub-catchment according to the site constraint factors; Cj is the cost of the jth LID; B is the total budget; and ZD, ZT , and ZH are the maximal depth, the maximal duration, and the inundated points of the flood, respectively.
The SA algorithm combined with SWMM is used to conduct the procedure for planning. The procedure includes changing the LID layout, simulating flood risk, and evaluating the objective function to guide the exploration of the solution space. The neighboring solution is generated by changing the types and amounts of LID practices in a randomly selected sub-catchment. To ensure the applicability of the spatial planning model, several executions of SA with different random initial states are required to check the characteristics of the optimal solutions. The spatial planning procedure is mainly programmed using the R statistical package, whereas the integration of SWMM and SA are programmed using C++. Based on the results of the optimization, the effects of the LID layouts on flood reduction are examined. By changing the setting of the storm drains and the design of LIDs, the LID spatial planning model is transferable to any other region.
3. Design Case
To test the validity of the proposed procedures, the framework of adaptation decision-making is applied to the artificial rural community. The reference village of the design case is the Xingshi Village, located in Hukou Township, Hsinchu County in northern Taiwan (Figure 2). The area marked by a square is where the drainage system located. Xingshi Village is a rural community involved in the community empowerment plan, mainly composed by residential area and the surrounded paddy fields. It belongs to subtropical climate zone, with annual average temperature of 22 °C and annual precipitation of 1550 mm. The precipitation is unevenly distributed, mostly comes from the thunderstorms in the wet seasons (May to October in Taiwan). The storm drains in Xingshi Village are designed to convey the peak flow from a five-year storm. The LIDs are relatively new in the history of the village, and only the junior high school has applied the rainwater harvesting and permeable pavements at the parking lots. According to the characteristics of the reference village, the types and the ratios of land uses, the ground water depth, and soil characteristics (Table 2) are designed. The designed community is divided into 61 blocks. Each sub-catchment consists of a certain number of blocks based on the surface slope, concentration time, and distribution of the roads. Each sub-catchment has a given land use and drainage area, and the rainwater is drained to the northeast direction (Figure 3). In this study, the stormwater overflow from the paddy fields is assumed drained from the farmland drainage and will not enter the sub-catchments.
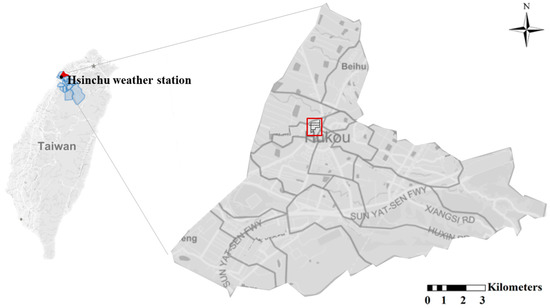
Figure 2.
Location of the weather station and the study case of Xingshi Village, Hukou Township, Hsinchu County, northern Taiwan.

Table 2.
Characteristics for the design case.
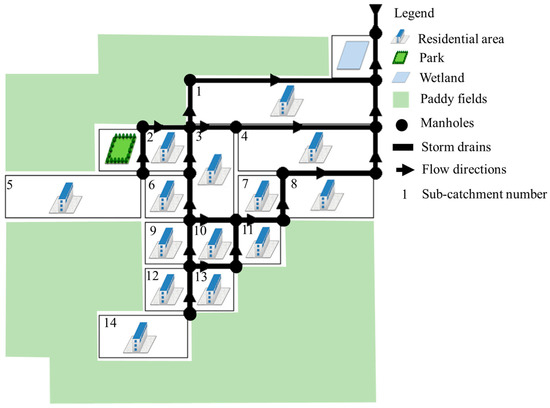
Figure 3.
Design case in Storm Water Management Model (SWMM).
The weather data used for the designed community are obtained from the station closest to the reference community (Hsinchu station). The GCMs are selected based on the criteria of the trend similarity (R2) and differences (root mean square error; RMSE) of the baseline mean monthly precipitation (1986–2005) between the data produced by different GCMs at the nearest data point and the observed data of Hsinchu station [50]. Three GCMs are selected taking into consideration the required computation efforts. In this study, the Hadley Centre Global Environment Model version 2 for the atmosphere and oceans (HadGEM2-AO) [51], the Norwegian Earth System Model (NorESM1-ME) [52], and the CSIRO-Mk3.6.0 Atmosphere-Ocean GCM (CSIRO-Mk3.6.0) [53] are selected to project the future climate. Scenarios representing future greenhouse gases concentration follow the Representative Concentration Pathway (RCP) proposed by IPCC [30]. The high-end scenario RCP 8.5 is used and GCM climate projections are downscaled using bias-correction and spatial disaggregation by the National Science and Technology Center for Disaster Reduction (NCDR) [54]. The increment of daily precipitation in future climate scenarios comparing to the precipitation in baseline scenarios for the selected GCMs are used to estimate the rainfall intensity of the five-year storm in future climate scenarios. After determining the distribution ratio of hourly rainfall based on the historical data and obtaining the Intensity-Duration-Frequency (IDF) curves, the worst design storm is then determined by choosing a suitable hyetograph for the design case. The hyetograph is location-dependent and need to be derived from historical observed weather data. In this study the designed hyetograph analyzed from a previous study for Taiwan is used [35]. The duration of the storm is 1 h, as determined by the simulated time for the runoff to flow from the most remote point in the community to the outlet. The 1-h (denoted as 1-h) events are distributed into 12 equal periods for the convenience of generating the hyetograph.
The storm drains in the study case are able to convey the runoff from the design storm in the current scenario, as mentioned in the Disaster Prevention and Protection Act of Taiwan currently applied to the storm drains of the reference community. The average flow velocity for the sewers remains between 0.8 m/s and 3 m/s, and the safety factor of 0.85 is used. The storm drains of the design case in SWMM are setup to imitate the reference community, using the methods proposed by Gironás et al. (2009) [55]. The manhole discharges of SWMM have been validated under a similar case in Taiwan [56]. In the simulation setup, each sub-catchment is assigned one of four land use types, including residential area, green area, paddy field, and wetland. The wetland located in the upper-right corner of Figure 1 is used for natural water treatment. The site characteristics affecting the selection of LID are also noted in Table 2. Other characteristics that may limit the application of LID, such as the vegetation, eco-region, sensitivity, and restricted areas, are already included in the variables of available space. The results of applying the adaptation framework to the case study are presented in Section 4, within which the subsections correspond to those in Section 2.
4. Results and Discussions
4.1. Problem and Goal
This study focuses on pluvial flooding, particularly under climate change conditions under the high-end scenario RCP 8.5 in the near-term future during 2021–2040. Considering the acceptable level of risk, the design objective for the future climate scenario is set to convey the runoff from a five-year storm without surface flooding, based on the Disaster Prevention and Protection Act of Taiwan. For adaptation using LID, the capital and maintenance cost limit is assumed three million NTD, which is roughly equivalent to the current policies promoting the implementation of LID in a community. The goal of the adaptation is to minimize the most severe flood depth, the most severe flood duration, and the number of inundated points under future climate scenarios.
4.2. Risk Assessment and Analysis
The design storms in the current and future climate scenarios are derived as the input of SWMM in flood-risk assessment. The rainfall intensity of a five-year storm with 1-h duration is 63.2 mm/h, based on the observed precipitation of Hsinchu weather station. Moreover, the increase of the daily precipitation of the three GCMs derived from the climate projections are analyzed. Because this study focuses on extreme storm events, the average of three maximum increased percentages of the monthly precipitation from HadGEM2-AO, NorESM1-ME, and CSIRO-Mk 3.6.0 in wet seasons (May to October) is evaluated to estimate the worst future climate scenario. The average of the maximum increased percentages of the monthly precipitation of the GCMs is 39% during 2021–2040 in RCP 8.5. To evaluate the effects of adaptation using LID measures in the worst climate scenario, the rainfall intensity of the design storm in the worst case is set 50% more than that of the current rainfall intensity, which is 94.8 mm/h calculated by multiplying 63.2 mm/h by 1.5. It is also found that the LID layouts optimal in the worst case help the drainage system to convey stormwater until 2061–2080, based on the increased percentages of the monthly precipitation. The worst design storm would overwhelm the existing storm drains that meets the current standard and lead to flooding. According to the legal requirement, the storm drains are designed for a five-year storm. The storm drains of the reference community are able to convey the runoff from a five-year storm and experience no flood in the current condition. However, flood risk exists in the near-term future (Table 3). To achieve the goal of minimizing flooding under the worst design storm in the future climate scenarios, LID practices are applied to the design case. The selection of suitable LID measures and the corresponding parameters are described in Section 4.3.1.

Table 3.
Increase of flood risk for future climate scenarios.
4.3. Adaptation Options Identification and Evaluation
4.3.1. LID Selection Method
Technically, the LID measures mentioned in the source references of Table 1 are options for the design case. Based on the priority of site characteristics identified in Section 2.3.1, the LID selection criteria are applied to the community beginning with the available area. First, the references defining the area required for different LID are examined, and the applicable LID appearing in more than one reference is checked [16,17,18,40]. Four LID measures fitting the small available area of the design case are deemed applicable: media filter [16,17,18], green roof [16,17], rain barrel [16,17,18], and permeable pavements [16,17]. Because the depth to the water table of the design case is deep, it does not limit the use of any aforementioned LID practice. The remaining factors do not exclude any of the LID practices. However, the media filter is not considered in the design case because it is mainly used to remove pollutants and additional assumptions are required for simulation as it is not included in SWMM LID modules [57]. Users can decide whether to keep the media filters as options in their own cases and in this study only green roofs (G), permeable pavements (P), and rain barrels (R) are selected as adaptation measures for the design case. The parameter setup of each layer of the LID influences flood inundation in the design community. The storage capacity of the rain barrel is designed assuming the average (85%) of the usually analyzed range of water supply reliability (70–100%) in Taiwan for each building with an effective roof area of 100 m2, according to the results of Hsinchu County in previous research [58]. The parameters of the other LID practices in SWMM are also assumed based on previous research [12,59]. The facility costs of the green roofs, permeable pavements, and rain barrels are 3370 NTD/100 m2, 3400 NTD/100 m2, and 1097 NTD/barrel, while the maintenance cost for the first two LIDs are 2400 NTD/100 m2 and 1761 NTD/100 m2 assuming 20 years of the lifespan and planning horizon, respectively [60]. Notice that the maintenance costs of rain barrels with capacities around 200 liters are covered by households themselves. The facility cost of a rain barrel is calculated by multiplying the capacity of each unit (0.3656 m3) by the cost per unit (3000 NTD/m3) [17].
4.3.2. LID Spatial Planning Model
The proposed spatial planning model using the SA algorithm aims to optimize the layout of the LID practices. As an example, the weights are set as 0.33 for each of the four terms in the objective function. Because the building coverage ratio is 60% of the residential area, the allowed maximum coverage ratios are designed as half of the roof area and the pavement area, which equates to 30% and 20% of the residential area for green roofs and permeable pavements, respectively. The maximum coverage ratio of the above ground rain barrels is 20% of the available space in the residential area [60]. The unit surface areas of the above LID practices are 2916, 2916, and 0.4 m2. The parameters of the SA algorithm are shown in Table 4, which are selected in accordance with the recommended settings reviewed in Chen et al. (2015) [49].

Table 4.
Design parameters in the cooling schedule of simulated annealing (SA) algorithm.
The spatial planning model is used to find the optimal LID layouts with the input of the worst design storm (94.8 mm/h). In this study, three executions of SA with different random initial states are conducted to examine the operability of the model, namely initial solution 1, 2, and 3 (LID1, LID2, and LID3). The initial solutions of the executions of SA are composed by randomly assigned LID type and amount in each sub-catchment. The value of the objective function of LID1, LID2, and LID3 and the corresponding optimal solution found by SA are listed in Table 5. The results show that there is nearly no flood (e.g., inundated depths are less than 0.01 m) when applying the optimal LID layouts in the design case. Moreover, the effectiveness of the spatial planning model are ensured because the maximum inundated depth, the maximum inundated duration, and the number of inundated points under the optimal layouts of the initial solution 1, 2 and 3 are similar.

Table 5.
Increase of flood risk for future climate scenarios.
The relationship between the costs of the LID layouts and the objective function for optimization of LID1 is shown in Figure 4. The vertical axis is multiply by minus 1 so that higher values indicate better performance of the LID. The solutions are dispersed, with some reaching high efficacy of flood mitigation with relatively low LID cost. Therefore, the layouts represented by these solutions show the possibility of flood reduction under limited budgets. The minimal costs for reaching different levels of flood reduction are shown by the straight line in Figure 3. That is, the location and type of LIDs may be more important than the amount of them when the number of LIDs is up to a certain extent, and additional LID is not always necessary to reduce flooding.
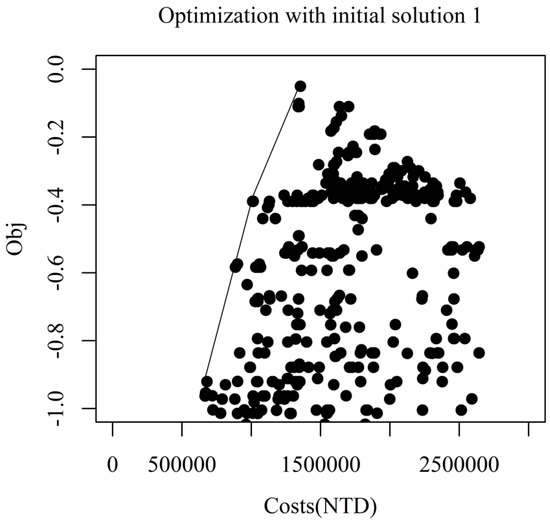
Figure 4.
Relation between low impact development (LID) cost and objective function
The objective function of LID1 converges from 1.3 to 0 through 826 iterations of the SA algorithm, which represents the reduction of the flood. The optimal layouts can be viewed as the best performance of the implemented LID within the budget constraint under the worst future climate scenarios, which assured nearly no flood in the community. Otherwise, raising the budget may be necessary to reduce floods. If the goal is to achieve the most cost-effective flood mitigation, further research on marginal effect is necessary to assess the trade-off between allocated budget and reduction in objective values. Because several LID layouts performed equally effectively, their patterns are analyzed. Here only the optimal layouts are examined. Because the optimization algorithm tends to find better solutions; therefore, the worst solutions found in the optimization process are not as bad as other possible solutions that are not even searched for in the solution space.
The optimal LID layouts of the three executions of SA are shown in Figure 4. Notice that brown, white, and green represent green roofs, permeable pavements, and rain barrels, respectively. The percentage (%) of the LIDs is derived from dividing the amounts of LID by the allowed maximum amounts. The percentages shown in parenthesis in Figure 5 are high in general, which indicates the flood-reduction effects of the LIDs. The reason that the optimal layouts differ is that the SA algorithm goes through the solutions space randomly and records different near optimal solutions. However, useful information for decision-making in LID planning is derived.
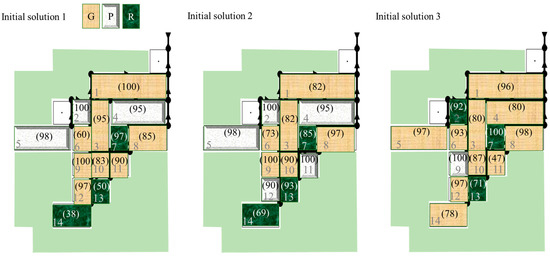
Figure 5.
Types and percentages of the optimal layouts for different initial solutions.
The green roofs appeared most often in the best solutions. It may be because the delay of runoff for green roofs is significantly longer than that of permeable pavements. Moreover, although the rain barrels can effectively store stormwater, the cost of rain barrels is significantly greater than green roofs and permeable pavements for the same effect on reducing flood. Because the green roofs and the permeable pavements demonstrated in this study do not have storage layer, the flood-reduction effect of the optimal LID layouts is mainly attributed to the staggered timing of the peak flow in each sub-catchment, rather than to the magnitude of the captured or collected stormwater. Large amounts of green roofs in sub-catchment 1 are crucial in reducing flood. It prevents flooding in the upstream manholes, and therefore large amounts of green roofs in sub-catchment 2 and 4 may not be necessary. Large amounts of green roofs in sub-catchment 10 are found for the three optimal layouts, which may be because the corresponding manhole connects water from two pipes with relatively small diameters. Moreover, because the sub-catchments 9 and 10 preferably include more LIDs, the amount of LIDs in sub-catchments 13 and 14 can be substantially reduced. To conclude, the LIDs at downstream sub-catchments are important in reducing flood for the adjacent upstream sub-catchments and also the whole community, and therefore should be first considered in LID planning when the budget is limited.
5. Discussion
In this study, the rainfall intensity of the worst design storm in future climate scenarios is assumed 1.5 times the intensity of the current design storm for the design case, derived from the daily-precipitation projections of the selected GCMs. The assumption is that the increased percentages of rainfall intensities of design storms are the same as the increased percentages of the daily precipitation. The changes of rainfall intensities of design storms are less discussed; however, methods of downscaling daily precipitation into hourly rainfall have been proposed, such as K Nearest Neighbor method [29]. With the projected hourly rainfall series, design storms can be estimated using frequency analysis [34] combined with a hyetograph suitable for the target area. Generating hourly precipitation in future climate scenarios provides the range of the uncertainty of estimating the change of the rainfall intensity of design storms due to climate change. Therefore, the method is worth discussing and is recommended for future studies applying adaptation framework against flooding.
The LID selection method is developed trying to help screen out suitable LIDs efficiently based on the site characteristics, which also enhances the application of the benchmarks of the selection criteria (e.g., the site constraint factors) proposed by previous studies. The conditions particularly marked in the reference of the benchmarks, such as the terms “if” and “with”, are treated as LIDs with additional requirement. However, the additional requirements defined in the studies may be embedded in some of the LID practices and are not necessary exclude the use of the LIDs. Although the reference studies are review, more studies list the specified benchmarks are required to provide the information of detailed selection criteria for LIDs. The proposed LID planning model identifies the optimal LID layouts for the study case and found that it is more optimal to invest in LIDs in the lower sub-catchments than the upper sub-catchments. The result complies with a previous study comparing the performance of evenly distributed LIDs and optimal LID layouts on peak flow reduction in a different design case [61]. The study concludes that the performance of installing 20% of the area with LID at downstream is the same as installing 40–50% of the area with evenly distributed LID for a five-year storm in Hsinchu. It indicates that the spatial planning model provides useful information. However, it is possible for the estimated flood risk to change in the future after implementation of LID owing to better climate projections. In such cases, an adaptation revision mechanism and principles would be necessary for adjusting the adaptation plan to meet the goal under different scenarios.
Although this study demonstrated the application of the framework as practically as possible, further studies are still necessary to optimize both LID layouts and parameters to fit particular objectives or site conditions. For example, the rainfall patterns and reused water demands are influential factors in the water supply performance of a rain barrel; therefore, these factors need to be considered when designing the storage capacity of rain barrels. Furthermore, the marginal value assessment of flood mitigation is recommended. Aspects such as water supply, human thermal comfort, and biodiversity may be influenced by the implementation of the LID. Proper indicators can be selected and included in the objective function to find the most favored LID layouts. In addition, stakeholder opinions should be included in the entire decision process, from clarifying the problem and setting up the goal of adaptation to identifying adaptation options from the local environment and experience and setting special requirements as criteria for LID selection. All of these issues require further study.
6. Conclusions
This study developed procedures for supporting a systematic framework of climate adaptation decision-making to clarify the problem and goal, evaluate current and future climate risk, and assess the adaptation options. LID practices are used as adaptation measures to strengthen the carrying capacity of the drainage system for a five-year return period storm, helping to offset the increased flows associated with climate change. The goal of adaptation is to minimize the maximal depth, the maximal duration, and the number of the inundated points in a community under limited budget conditions, when facing the worst design storm, a design storm with five-year return period (a five-year storm) with 1-h duration, under the high-end scenario RCP 8.5 during 2021–2040. To assist the evaluation of climate risk and implementation of LID practices, procedures of LID selection method and an LID spatial planning model are proposed. The increase of the rainfall intensity of the design storm in the future climate scenarios is assumed the same as that of the daily precipitation. The worst design storm is estimated as 1.5 times of the current rainfall intensity, which is 94.8 mm/hr. For the steps of identifying and evaluating the adaptation options, LID options are reduced based on site constraints, and an LID spatial planning model is then constructed to consider the cost and effectiveness. The decision variables are the type and amount of LID practices for each sub-catchment. The SA algorithm is used in the LID spatial planning model as a searching algorithm and is combined with SWMM. The adaptation decision-making framework is applied to a design case to demonstrate the steps required to assess the flood risk and to adapt to flood for a community.
The results showed that the systematic framework of climate adaptation decision-making helps the planning of LID under the uncertainty of climate change. The proposed procedure of LID selection provides users with a way to isolate the most suitable LID options when needed. The results of the LID spatial planning model show that nearly no flood occurs when applying the optimal LID layouts in the design case under the worst design storm. From the relationship between the cost of the LID and its flood-reduction effect, some LID layouts are found having a considerable effect on flood reduction with relatively lower costs than other layouts. Moreover, the patterns of the optimal LID layouts from different execution of SA are analyzed. The results show that LIDs at downstream sub-catchments have a considerable effect on the adjacent upstream sub-catchments and also the whole community and should be first considered in LID planning when the budget is limited. In conclusion, the adaptation framework is generally helpful in LID planning for a community to adapt to pluvial flooding.
Acknowledgments
This study is funded by the National Science Council (NSC) of Taiwan under Contract No. MOST 102-2628-B-002-020-MY3.
Author Contributions
Pei-Yuan Chen conducted the analysis and wrote the paper. Ching-Pin Tung supervised this study and also edited the manuscript. Moreover, Yuan-Hua Li contributed by developing the study case and the simulation using SWMM.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ward, P.J.; Pauw, W.; Van Buuren, M.; Marfai, M.A. Governance of flood risk management in a time of climate change: The cases of Jakarta and Rotterdam. Environ. Politics 2013, 22, 518–536. [Google Scholar] [CrossRef]
- Digman, C. Retrofitting to Manage Surface Water; CIRIA: London, UK, 2012. [Google Scholar]
- Karavokiros, G.; Lykou, A.; Koutiva, I.; Batica, J.; Kostaridis, A.; Alves, A.; Makropoulos, C. Providing evidence-based, intelligent support for flood resilient planning and policy: The pearl knowledge base. Water 2016, 8, 392. [Google Scholar] [CrossRef]
- Perez-Pedini, C.; Limbrunner, J.F.; Vogel, R.M. Optimal location of infiltration-based best management practices for storm water management. J. Water Resour. Plan. Manag. 2005, 131, 441–448. [Google Scholar] [CrossRef]
- Dietz, M.E.; Clausen, J.C. Stormwater runoff and export changes with development in a traditional and low impact subdivision. J. Environ. Manag. 2008, 87, 560–566. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2014, 12, 1–18. [Google Scholar] [CrossRef]
- Avila, H.; Avila, L.; Sisa, A. Dispersed storage as stormwater runoff control in consolidated urban watersheds with flash flood risk. J. Water Resour. Plan. Manag. 2016, 142, 04016056. [Google Scholar] [CrossRef]
- Coombes, P.J.; Kuczera, G.; Kalma, J.D.; Argue, J.R. An evaluation of the benefits of source control measures at the regional scale. Urban Water 2002, 4, 307–320. [Google Scholar] [CrossRef]
- Lee, J.G.; Heaney, J.P. Estimation of urban imperviousness and its impacts on storm water systems. J. Water Resour. Plan. Manag. 2003, 129, 419–426. [Google Scholar] [CrossRef]
- Johnson, R.L.; Staeheli, P. City of seattle—Stormwater low impact development practices. In Proceedings of the World Environmental and Water Resource Congress: Examining the Confluence of Environmental and Water Concerns, Omaha, NE, USA, 21–25 May 2006; pp. 1–10. [Google Scholar]
- Urbanisten, D. Water square Benthemplein in Rotterdam, the Netherlands. Landsc. Archit. Front. 2013, 1, 136–143. [Google Scholar]
- Qin, H.-P.; Li, Z.-X.; Fu, G. The effects of low impact development on urban flooding under different rainfall characteristics. J. Environ. Manag. 2013, 129, 577–585. [Google Scholar] [CrossRef] [PubMed]
- Hood, M.J.; Clausen, J.C.; Warner, G.S. Comparison of stormwater lag times for low impact and traditional residential development. J. Am. Water Resour. Assoc. 2007, 43, 1036–1046. [Google Scholar] [CrossRef]
- Damodaram, C.; Giacomoni, M.H.; Prakash Khedun, C.; Holmes, H.; Ryan, A.; Saour, W.; Zechman, E.M. Simulation of combined best management practices and low impact development for sustainable stormwater management. J. Am. Water Resour. Assoc. 2010, 46, 907–918. [Google Scholar] [CrossRef]
- Low Impact Development Center, Inc. Low Impact Development Manual for Southern California: Technical Guidance and Site Planning Strategies. California State Water Resources Control Board and Low Impact Development Center, Inc., 2010. Available online: https://www.casqa.org/sites/default/files/downloads/socallid-manual-final-040910.pdf (accessed on 29 September 2017).
- City of Edmonton. Low Impact Development Best Management Practices Design Guide Edition 1.0. City of Edmonton, 2011. Available online: http://rcflood.org/downloads/NPDES/Documents/LIDManual/LID_BMP_Design_Handbook.pdf (accessed on 30 September 2017).
- Jia, H.; Yao, H.; Tang, Y.; Shaw, L.Y.; Zhen, J.X.; Lu, Y. Development of a multi-criteria index ranking system for urban runoff best management practices (BMPs) selection. Environ. Monit. Assess. 2013, 185, 7915–7933. [Google Scholar] [CrossRef] [PubMed]
- United States Department of Defense. United Facilities Criteria, Low impact Development Manual: UFC 3-210-10; United States Department of Defense: Washington, DC, USA, 2015.
- Pittner, C.; Allerton, G. Suds for Roads; WSP Development and Transport: Edinburgh, Scotland, 2009. [Google Scholar]
- Consultancy, D.D. Greater Dublin Strategic Drainage Study (GDSDS). New Development Policy–Technical Guidance Document 2005. pp. 1–5. Available online: https://www.dublincity.ie/sites/default/files/content/WaterWasteEnvironment/WasteWater/Drainage/GreaterDublinStrategicDrainageStudy/Documents/Vol%203%20-%20Chapter%206%20-%20Sustainable%20Drainage%20Systems.pdf (accessed on 29 September 2017).
- Kulbicki, L. Does Welsh national Planning Policy Effectively Address Low Impact Development in the Open Countryside? The Lammas Community. 2011. Available online: http://lammas.org.uk/wp-content/uploads/2013/03/Does_Welsh_National_Planning_Policy_effectively_address_Low_Impact_Development_in_the_open_countryside_Louise_Kulbicki_2011.pdf (accessed on 27 September 2017).
- Lai, F.-H.; Dai, T.; Zhen, J.; Riverson, J.; Alvi, K.; Shoemaker, L. SUSTAIN-AN EPA BMP process and placement tool for urban watersheds. In Proceedings of the Water Environment Federation, Bellevue, WA, USA, 24–27 June 2007. [Google Scholar]
- Heaney, J.P.; Lee, J.G. Methods for Optimizing Urban Wet-Weather Control System; U.S. Environmental Protection Agency: Washington, DC, USA, 2006.
- Reichold, L.; Zechman, E.M.; Brill, E.D.; Holmes, H. Simulation-optimization framework to support sustainable watershed development by mimicking the predevelopment flow regime. J. Water Resour. Plan. Manag. 2009, 136, 366–375. [Google Scholar] [CrossRef]
- Zoltay, V.I.; Vogel, R.M.; Kirshen, P.H.; Westphal, K.S. Integrated watershed management modeling: Generic optimization model applied to the Ipswich River Basin. J. Water Resour. Plan. Manag. 2010, 136, 566–575. [Google Scholar] [CrossRef]
- Chang, N.-B.; Rivera, B.J.; Wanielista, M.P. Optimal design for water conservation and energy savings using green roofs in a green building under mixed uncertainties. J. Clean. Prod. 2011, 19, 1180–1188. [Google Scholar] [CrossRef]
- Richardson, C.W.; Wright, D.A. WGEN: A Model for Generating Daily Weather Variables; US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1984.
- Semenov, M.A.; Barrow, E.M.; Lars-Wg, A. A Stochastic Weather Generator for Use in Climate Impact Studies; Rothamsted Research: Hertfordshire, UK, 2002. [Google Scholar]
- Solaiman, T.A.; Simonovic, S.P. Development of Probability Based Intensity-Duration-Frequency Curves under Climate Change; Department of Civil and Environmental Engineering, The University of Western Ontario: London, ON, Canada, 2011. [Google Scholar]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- UKCIP Tools: Adaptation Wizard. Available online: www.ukcip.org.uk/resources/tools/adapt.asp (accessed on 23 January 2016).
- Liu, Y.; Cibin, R.; Bralts, V.F.; Chaubey, I.; Bowling, L.C.; Engel, B.A. Optimal selection and placement of BMPs and LID practices with a rainfall-runoff model. Environ. Model. Softw. 2016, 80, 281–296. [Google Scholar] [CrossRef]
- Kirshen, P.; Caputo, L.; Vogel, R.M.; Mathisen, P.; Rosner, A.; Renaud, T. Adapting urban infrastructure to climate change: A drainage case study. J. Water Resour. Plan. Manag. 2014, 141, 04014064. [Google Scholar] [CrossRef]
- Lee, J.G.; Heaney, J.P.; Lai, F.-H. Optimization of integrated urban wet-weather control strategies. J. Water Resour. Plan. Manag. 2005, 131, 307–315. [Google Scholar] [CrossRef]
- Åstebøl, S.O.; Hvitved-Jacobsen, T.; Simonsen, Ø. Sustainable stormwater management at Fornebu—From an airport to an industrial and residential area of the city of Oslo, Norway. Sci. Total Environ. 2004, 334, 239–249. [Google Scholar] [CrossRef] [PubMed]
- Chow, V.T. A general formula for hydrologic frequency analysis. Eos Trans. Am. Geophys. Union 1951, 32, 231–237. [Google Scholar] [CrossRef]
- Cheng, K.S.; Hueter, I.; Hsu, E.C.; Yeh, H.C. A scale-invariant gauss-markov model for design storm hyetographs. J. Am. Water Resour. Assoc. 2001, 37, 723–735. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; US Environmental Protection Agency: Cincinnati, OH, USA, 2010.
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.1; US Environmental Protection Agency: Washington, DC, USA, 2015.
- Rossman, L.; Huber, W. Storm Water Management Model Reference Manual Volume I—Hydrology (Revised); US Environmental Protection Agency: Cincinnati, OH, USA, 2016.
- Abbasi, S.A.; Koskelo, A. Pollutant Load Reductions for Total Maximum Daily Loads for Highways; Transportation Research Board: Washington, DC, USA, 2013; Volume 444. [Google Scholar]
- United States Environmental Protection Agency (EPA). Handbook: Urban Runoff Pollution Prevention and Control Planning; Diane Pub Co.: Cincinnati, OH, USA, 1993. [Google Scholar]
- Armitage, N.; Vice, M.; Fisher-Jeffes, L.; Winter, K.; Spiegel, A.; Dunstan, J. The South African Guidelines for Sustainable Drainage Systems; Water Research Commission: Pretoria, South Africa, 2012. [Google Scholar]
- Blacktown City Council. Developer Handbook for Water Sensitive Urban Design; Blacktown City Council: Blacktown City, Australia, 2013. Available online: https://www.blacktown.nsw.gov.au/Plan-build/Stage-2-plans-and-guidelines/Engineering-Design-Guide-library/Water-Sensitive-Urban-Design (accessed on 29 September 2017).
- Practicum, S.P.; Barboza, N.; Bedard, M.; Jensen, R. The Study of Impervious versus Pervious Surfaces, and Low Impact Development (LID) Designs Within the City of Trinidad; Humboldt State University: Arcata, CA, USA, 2006. [Google Scholar]
- Woods-Ballard, B.; Kellagher, R.; Martin, P.; Jefferies, C.; Bray, R.; Shaffer, P. The SUDS Manual; Ciria: London, UK, 2007; Volume 697. [Google Scholar]
- United Nations Economic and Social Commission for Asia and the Pacific (ESCAP). Low Carbon Green Growth Roadmap for Asia and the Pacific; ESCAP: Bangkok, Thailand, 2012. [Google Scholar]
- Zadeh, L. Optimality and non-scalar-valued performance criteria. IEEE Trans. Autom. Control 1963, 8, 59–60. [Google Scholar] [CrossRef]
- Chen, P.Y.; Tung, C.P.; Lin, W.C.; Li, Y.H. Spatial optimization procedure for land-use arrangement in a community based on a human comfort perspective. Paddy Water Environ. 2016, 14, 71–83. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Tung, C.-P. Procedure for selecting GCM datasets for climate risk assessment. Terr. Atmos. Ocean. Sci. 2017, 28, 43–55. [Google Scholar] [CrossRef]
- Collins, W.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Hinton, T.; Jones, C.; Liddicoat, S.; Martin, G.; O’Connor, F.; Rae, J. Evaluation of the HadGEM2 model. Hadley Cent. Tech. Note 74. 2008. Available online: http://www.inscc.utah.edu/~reichler/publications/papers/Collins_08_MetOffice_74.pdf (accessed on 27 September 2017).
- Tjiputra, J.; Roelandt, C.; Bentsen, M.; Lawrence, D.; Lorentzen, T.; Schwinger, J.; Seland, Ø.; Heinze, C. Evaluation of the carbon cycle components in the norwegian earth system model (NorESM). Geosci. Model Dev. 2013, 6, 301–325. [Google Scholar] [CrossRef]
- Rotstayn, L.; Jeffrey, S.; Collier, M.; Dravitzki, S.; Hirst, A.; Syktus, J.; Wong, K. Aerosol-and greenhouse gas-induced changes in summer rainfall and circulation in the Australasian region: A study using single-forcing climate simulations. Atmos. Chem. Phys. 2012, 12, 6377–6404. [Google Scholar] [CrossRef]
- Hong, N.-M.; Lee, T.-Y.; Chen, Y.-J. Daily weather generator with drought properties by copulas and standardized precipitation indices. Environ. Monit. Assess. 2016, 188, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Gironás, J.; Roesner, L.A.; Davis, J.; Rossman, L.; Supply, W. Storm Water Management Model Applications Manual; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Washington, DC, USA, 2009.
- Lin, S.-S.; Chang, H.-K.; Hsieh, S.-H.; Kuo, J.-T.; Lai, J.-S. An Integrated Approach for Inundation Simulation in an Urban Area; IAHS PUBLICATION: Wallingford, UK, 2004; pp. 151–156. [Google Scholar]
- Consultants, G. Guidelines for Evaluating and Selecting Modifications to Existing Roadway Drainage Infrastructure to Improve Water Quality in Ultra-Urban Areas; Transportation Research Board: Washington, DC, USA, 2012; Volume 728. [Google Scholar]
- Liaw, C.-H.; Chiang, Y.-C. Dimensionless analysis for designing domestic rainwater harvesting systems at the regional level in northern Taiwan. Water 2014, 6, 3913–3933. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y. SWMM simulation of the storm water volume control performance of permeable pavement systems. J. Hydrol. Eng. 2014, 20, 06014010. [Google Scholar] [CrossRef]
- Construction and Planning Agency of Ministry of Interior (CPAMI). Operating Manual of Low Impact Development Implementation for Water Environment; CPAMI: Taipei, Taiwan, 2015. (In Chinese)
- Huang, Y.; Tung, C. Development of sustainable stormwater management using simulation-optimization approach under climate change. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 12–17 April 2015; Volume 17. EGU2015-4986-1. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).