Estimating River Depth from SWOT-Type Observables Obtained by Satellite Altimetry and Imagery
Abstract
1. Introduction
2. Case Study
- The Po River with its narrow width (150–650 m) highlights the limitations of both altimetry and imagery.
- We have access to a variety of in situ data for the validation purposes.
3. Data
3.1. In Situ Data
3.2. Water Level from Satellite Altimetry
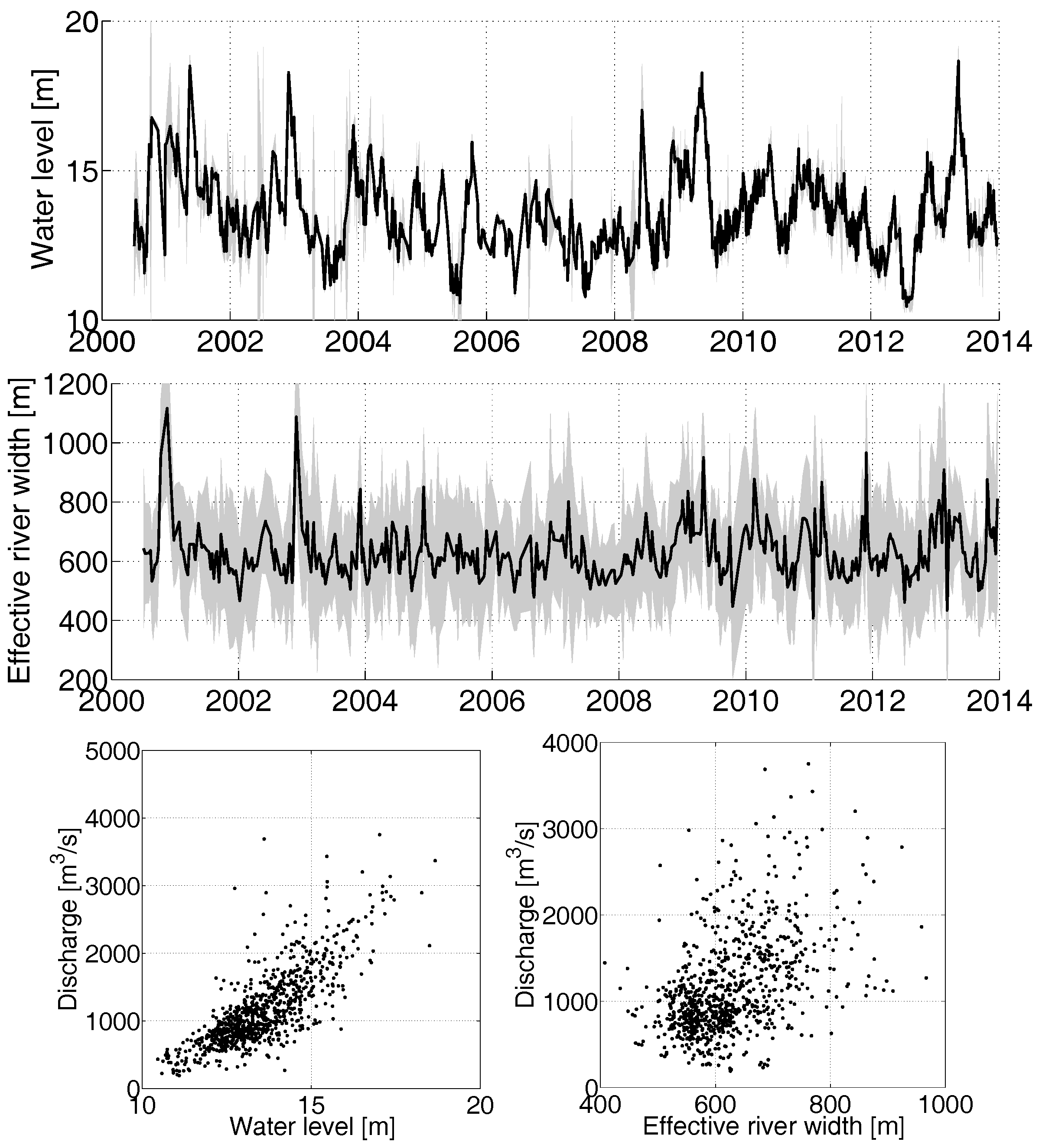
- Normalization of the data between zero and one: The measurements are merged by normalizing the time series according to their statistical characteristics. This step helps to make the range for the distribution of water level variations at different virtual stations consistent. For the merging process, the data of each virtual station is normalized by assigning the third percentile to zero and the 85th percentile to one.
- Confidence limit definition of 99% of a Student’s t-test for a sliding time window: The length of the time window can be experimented with to achieve the best performance. Here, a time window of one month (15 days before and 15 days after the selected measurement) is chosen as it leads to optimal results in terms of time series behavior and the number of identified outliers.
- Outlier identification and rejection: The identification and the rejection of the outliers is carried out by an iterative data snooping method and by iteratively updating the confidence limits. The data snooping method searches for the observation (always one observation) with the largest gross error [42].
- Rescaling of normalized values to their corresponding river water level heights: After removing the outliers, the combined normalized altimetric values are ready to be rescaled back to their true water level values.
- Constructing the time series: After rescaling, we now have a cloud of measurements with their corresponding uncertainty for the selected location along the river, which is free from outliers. The dense time series of water level can then be obtained by connecting the measurements using a three-point distance weighted moving averaging.
3.3. River Width from Satellite Imagery
4. Methodology to Estimate River Depth
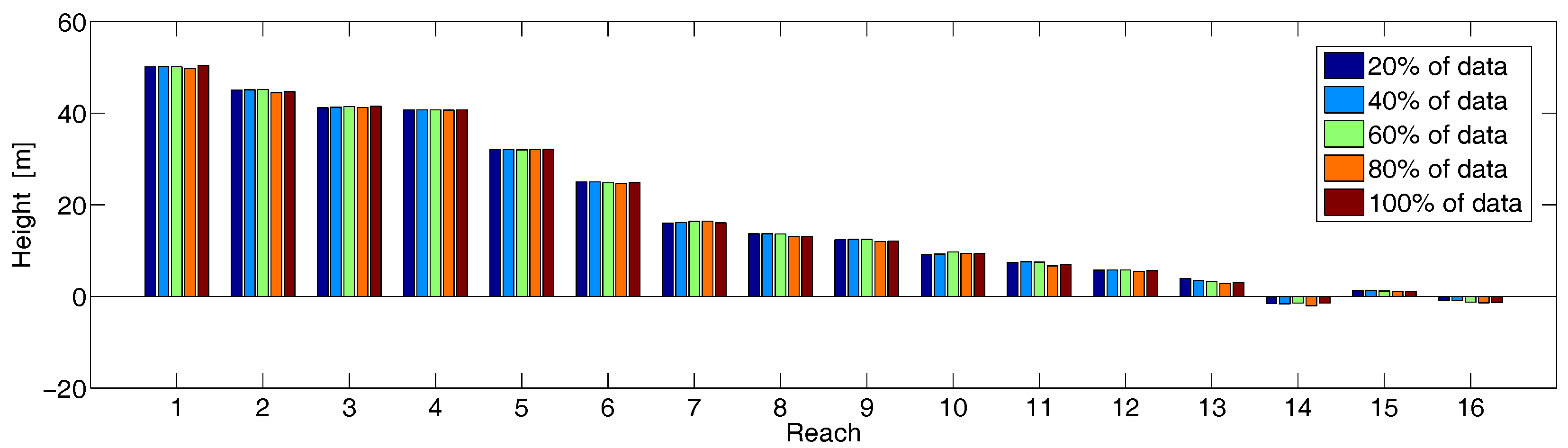
5. Results, Validation and Discussion
6. Perspective for the SWOT Mission
- Satellite altimetry is put on an operational footing through the Sentinel 3 series of the European Copernicus program. At the same time, research satellites such as CryoSat-2, SARAL/AltiKa or Jason-3 remain in orbit and provide complementary space-time sampling. This constellation addresses many current limitations and opens a significant area of investigation into the operational use of altimetry missions for hydrological purposes. Developing methods to generate dense time series of water level using altimetry data, demonstrated in this study, raise the hope of using operational altimetry together with SWOT data in the future for a better monitoring of temporal dynamics in many rivers around the world.
- Remote sensing techniques have been introduced as viable choices to monitor surface water variations [5]. Optical and SAR satellite imagery missions provide the opportunity to monitor surface water extent repeatedly at appropriate time intervals. Recent missions provide images with better spatial and temporal resolution. Different Landsat missions have been gathering images in various multispectral bands from the Earth since 1980. Recently, Landsat 8 with 30 m spatial resolution has provided monthly images of the Earth’s surface. Applications that demand a high temporal resolution preferably make use of the daily snapshots of MODIS imagery with 250-m resolution. Since 2015, Sentinel-2 has provided images with better resolution (10 m, 20 m, 60 m) and also a high revisit time (five days). On the other hand, SAR missions with images from ERS-1, ERS-2 and ENVISAT in C-band are the main sources for spatial water area monitoring in the tropical area, which is cloudy and rainy most of the year [12]. TerraSAR-X in X-band provides high resolution images with 1-, 2- and-3 meter pixel size every two days. From 2014 onwards, Sentinel-1A has provided continuous imagery (day, night and all weather) in C-band, expanding our understanding of surface water. Therefore, developing reliable algorithms to obtain reliable dynamic river masks, as developed by [38] and implemented in this study, gives the perspective of the SWOT mission that the results from different imagery sensors could be combined with the results from SWOT for a better monitoring of river masks in the future.
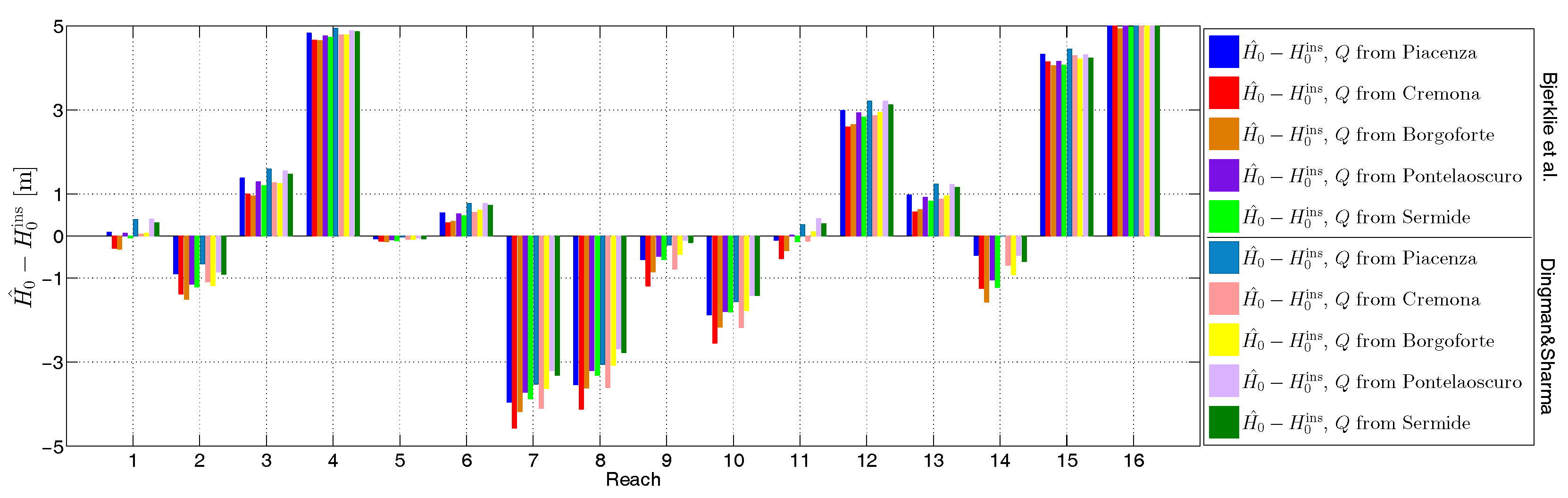
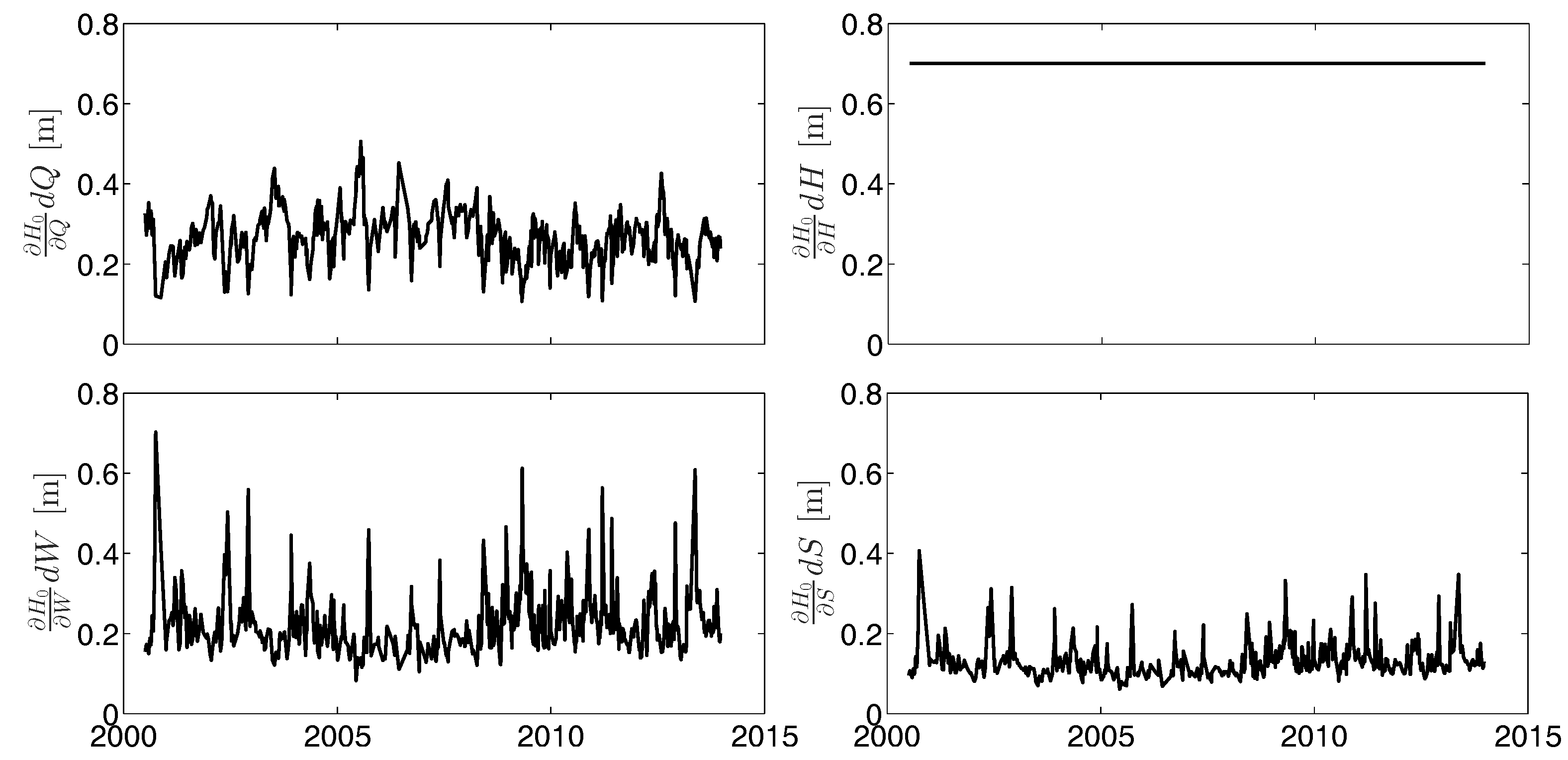
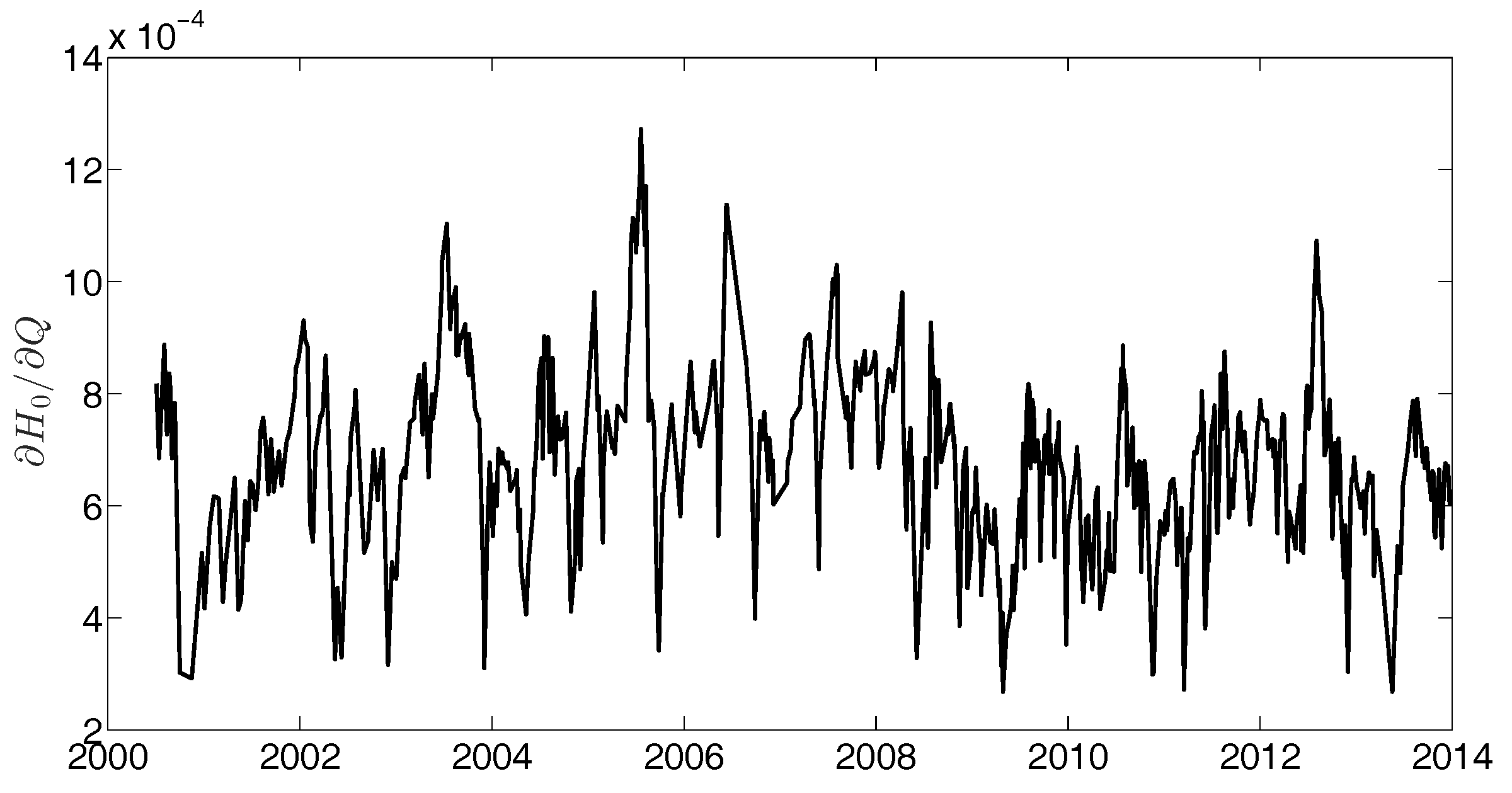
- In terms of river depth estimation, our results in Figure 11, Figure 12 and Figure 13 highlight the weaker dependency of error in river depth estimation to the error of river width and river discharge. This means that a preliminary result of river width and a coarse river discharge would be enough to estimate river depth. This is especially important for discharge algorithms, which work based on Manning’s flow resistance equation, and the initial values of variables play an important role in the fast and precise estimation of discharge. Moreover, this result would mean that one could use a rough estimation of river discharge instead of in situ data and still receive acceptable results for river depth.
7. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Comparison of Water Level and Effective River Width with Discharge
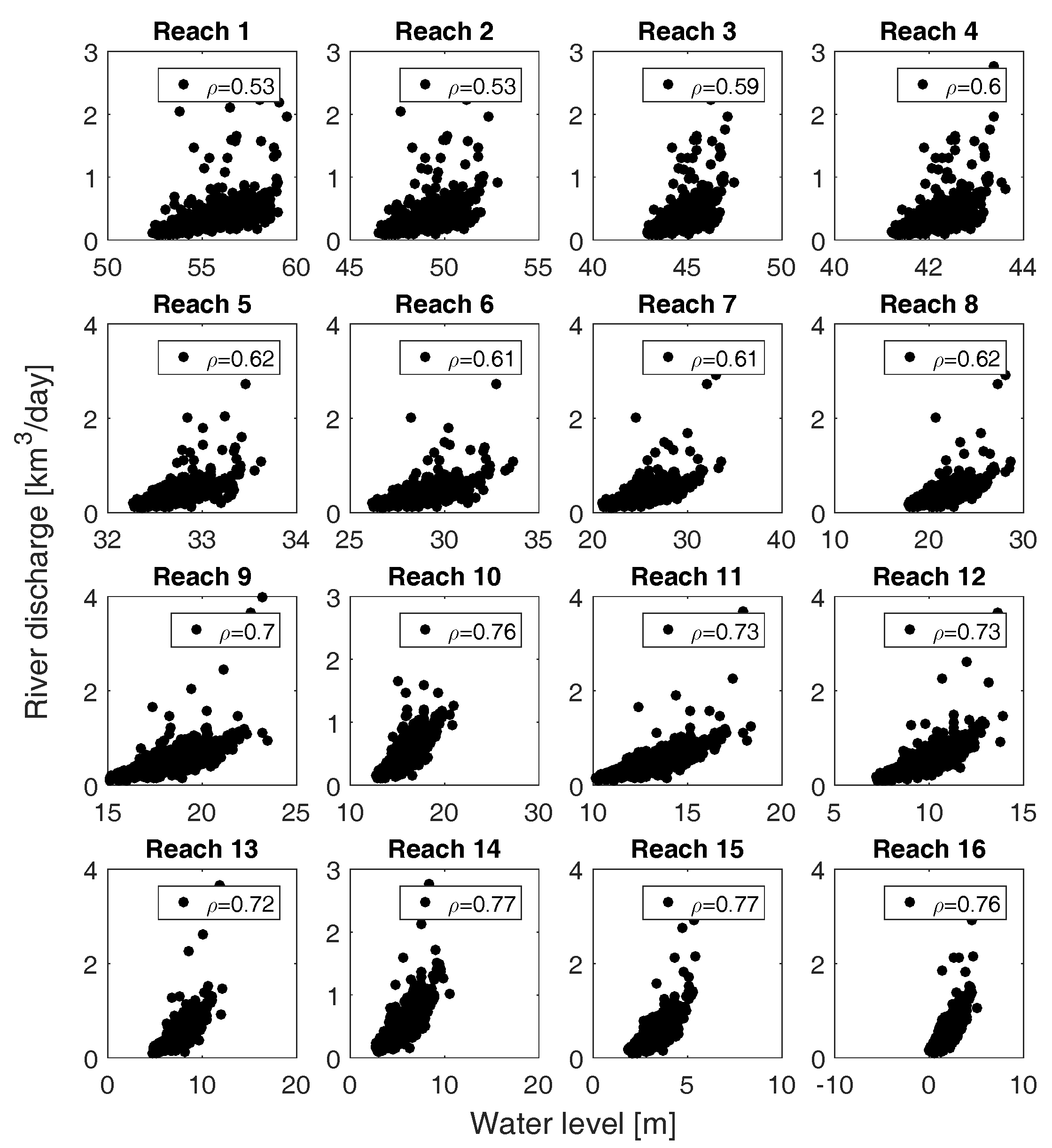
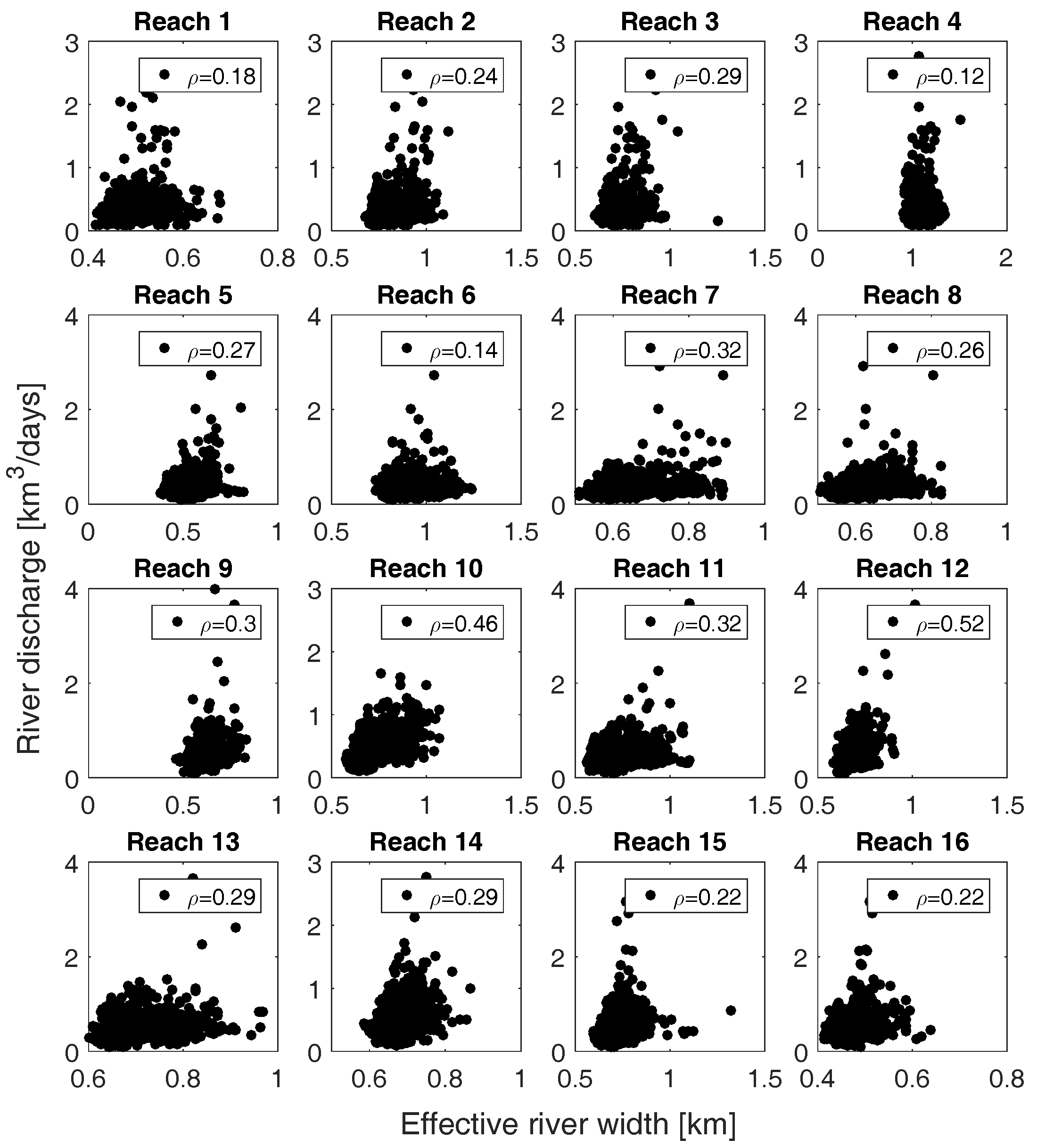
References
- Dingman, S.L.; Bjerklie, D.M. Estimation of River Discharge. In Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lorenz, C.; Devaraju, B.; Tourian, M.J.; Riegger, J.; Kunstmann, H.; Sneeuw, N. Large-scale runoff from landmasses: A global assessment of the closure of the hydrological and atmospheric water balances. J. Hydrometeorol. 2014, 15, 2111–2139. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J. The current status of global river discharge monitoring and potential new technologies complementing traditional discharge measurements. In Predictions in Ungauged Basins: PUB Kick-Off, Proceedings of the PUB Kick-Off Meeting, Brasilia, Brazil, 20–22 November 2002; IAHS Publication: Wallingford, UK, 2007; Volume 309. [Google Scholar]
- Tourian, M.J.; Sneeuw, N.; Bárdossy, A. A quantile function approach to discharge estimation from satellite altimetry (ENVISAT). Water Resour. Res. 2013, 49, 1–13. [Google Scholar] [CrossRef]
- Alsdorf, D.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River Discharge Estimation by Using Altimetry Data and Simplified Flood Routing Modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Lett. 2008, 35, L20401. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Smith, L.C. RivWidth: A software tool for the calculation of river widths from remotely sensed imagery. Geosci. Remote Sens. Lett. IEEE 2008, 5, 70–73. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Dingman, S.L.; Vörösmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Elmi, O.; Tourian, M.J.; Sneeuw, N. River discharge estimation using channel width from satellite imagery. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 727–730. [Google Scholar]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Smith, L.C.; Isacks, B.L.; Bloom, A.L.; Murray, A.B. Estimation of discharge from three braided rivers using synthetic aperture radar satellite imagery: Potential application to ungaged basins. Water Resour. Res. 1996, 32, 2021–2034. [Google Scholar] [CrossRef]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Lettenmaier, D.P.; Alsdorf, D.E. Prospects for river discharge and depth estimation through assimilation of swath-altimetry into a raster-based hydrodynamics model. Geophys. Res. Lett. 2007, 34, 481–496. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Natl. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef] [PubMed]
- Durand, M.; Neal, J.; Rodriguez, E.; Andreadis, K.M.; Smith, L.C.; Yoon, Y. Estimating reach-averaged discharge for the River Severn from measurements of river water surface elevation and slope. J. Hydrol. 2014, 511, 92–104. [Google Scholar] [CrossRef]
- Garambois, P.A.; Monnier, J. Inference of effective river properties from remotely sensed observations of water surface. Adv. Water Resour. 2015, 79, 103–120. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Durand, M.T.; Hossain, F. Spatiotemporal interpolation of discharge across a river network by using synthetic SWOT satellite data. Water Resour. Res. 2015, 51, 430–449. [Google Scholar] [CrossRef]
- Lorenz, C.; Tourian, M.J.; Devaraju, B.; Sneeuw, N.; Kunstmann, H. Basin-scale runoff prediction: An Ensemble Kalman Filter framework based on global hydrometeorological data sets. Water Resour. Res. 2015, 51, 8450–8475. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F. Inverse streamflow routing. Hydrol. Earth Syst. Sci. 2013, 17, 4577–4588. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River discharge estimation at daily resolution from satellite altimetry over an entire river basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Bates, P.; Buytaert, W.; Matgen, P.; Pappenberger, F. A data assimilation approach to discharge estimation from space. Hydrol. Process. 2009, 23, 3641–3649. [Google Scholar] [CrossRef]
- Yoon, Y.; Durand, M.; Merry, C.J.; Clark, E.A.; Andreadis, K.M.; Alsdorf, D.E. Estimating river bathymetry from data assimilation of synthetic {SWOT} measurements. J. Hydrol. 2012, 464–465, 363–375. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Collischonn, W.; Bonnet, M.P.; de Gonçalves, L.G.G.; Calmant, S.; Getirana, A.; Santos da Silva, J. Assimilating in situ and radar altimetry data into a large-scale hydrologic-hydrodynamic model for streamflow forecast in the Amazon. Hydrol. Earth Syst. Sci. 2013, 17, 2929–2946. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Durand, M.T.; Andreadis, K.M.; Beighley, R.E.; Paiva, R.C.; Allen, G.H.; Miller, Z.F. Assessing the potential global extent of SWOT river discharge observations. J. Hydrol. 2014, 519 Pt B, 1516–1525. [Google Scholar] [CrossRef]
- Mersel, M.K.; Smith, L.C.; Andreadis, K.M.; Durand, M.T. Estimation of river depth from remotely sensed hydraulic relationships. Water Resour. Res. 2013, 49, 3165–3179. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A.; Marcus, W.A.; Fonstad, M.A. Passive optical remote sensing of river channel morphology and in-stream habitat: Physical basis and feasibility. Remote Sens. Environ. 2004, 93, 493–510. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A.; Lawrence, R.L. Spectrally based remote sensing of river bathymetry. Earth Surf. Proc. Landf. 2009, 34, 1039–1059. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A. A forward image model for passive optical remote sensing of river bathymetry. Remote Sens. Environ. 2009, 113, 1025–1045. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Marcus, W.A. Remote sensing of stream depths with hydraulically assisted bathymetry (HAB) models. Geomorphology 2005, 72, 320–339. [Google Scholar] [CrossRef]
- Leon, J.; Calmant, S.; Seyler, F.; Bonnet, M.P.; Cauhop, M.; Frappart, F.; Filizola, N.; Fraizy, P. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. J. Hydrol. 2006, 328, 481–496. [Google Scholar] [CrossRef]
- Bjerklie, D.M. Estimating the bankfull velocity and discharge for rivers using remotely-sensed river morphology information. J. Hydrol. 2007, 341, 144–155. [Google Scholar] [CrossRef]
- Biancamaria, S.; Durand, M.; Andreadis, K.; Bates, P.; Boone, A.; Mognard, N.; Rodríguez, E.; Alsdorf, D.; Lettenmaier, D.; Clark, E. Assimilation of virtual wide swath altimetry to improve Arctic river modeling. Remote Sens. Environ. 2011, 115, 373–381. [Google Scholar] [CrossRef]
- Durand, M.; Rodriguez, E.; Alsdorf, D.E.; Trigg, M. Estimating river depth from remote sensing swath interferometry measurements of river height, slope, and width. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 20–31. [Google Scholar] [CrossRef]
- Gejadze, I.; Malaterre, P.O. Discharge estimation under uncertainty using variational methods with application to the full Saint-Venant hydraulic network model. Int. J. Numer. Methods Fluids 2017, 83, 405–430. [Google Scholar] [CrossRef]
- Dingman, S.L.; Sharma, K.P. Statistical development and validation of discharge equations for natural channels. J. Hydrol. 1997, 199, 13–35. [Google Scholar] [CrossRef]
- Raggi, M.; Ronchi, D.; Sardonini, L. Po Basin Case Study Status Report; Deliverable D32; University of Bologna: Bologna, Italy, 2007. [Google Scholar]
- Elmi, O.; Tourian, M.J.; Sneeuw, N. Dynamic River Masks from Multi-Temporal Satellite Imagery: An Automatic Algorithm Using Graph Cuts Optimization. Remote Sens. 2016, 8, 1005. [Google Scholar] [CrossRef]
- Tourian, M.J.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series by multimission satellite altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef]
- Moramarco, T.; Singh, V.P. Simple Method for Relating Local Stage and Remote Discharge. J. Hydrol. Eng. 2001, 6, 78–81. [Google Scholar] [CrossRef]
- Ponce, V.M. Engineering Hydrology: Principles and Practices; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks; Netherlands Geodetic Commission: Delft, The Netherlands, 1968; Volume 2. [Google Scholar]
- Kohli, P.; Torr, P. Measuring Uncertainty in Graph Cut Solutions efficiently Computing Min-marginal Energies Using Dynamic Graph Cuts. Comput. Vis. ECCV 2006, 1, 30–43. [Google Scholar]
- Te Chow, V. Open Channel Hydraulics; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1959. [Google Scholar]
- Helmert, F.R. Die Ausgleichungsrechnung nach der Methode der Kleinsten Quadrate: Mit Anwendungen auf die Geodäsie und die Theorie der Messinstrumente; BG Teubner: Leipzig, Germany, 1872; Volume 1. [Google Scholar]
- Roese-Koerner, L.R. Convex Optimization for Inequality Constrained Adjustment Problems. Ph.D. Thesis, Universitäts-und Landesbibliothek Bonn, Bonn, Germany, 2015. [Google Scholar]
- Biancamaria, S.; Lettenmaier, D.; Pavelsky, T. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Pavelsky, T. Recent Progress in Development of SWOT river Discharge Algorithms. In Proceedings of the 2012 SWOT Discharge Algorithms Workshop, Chapel Hill, NC, USA, 18–20 June 2012; pp. 18–20. [Google Scholar]

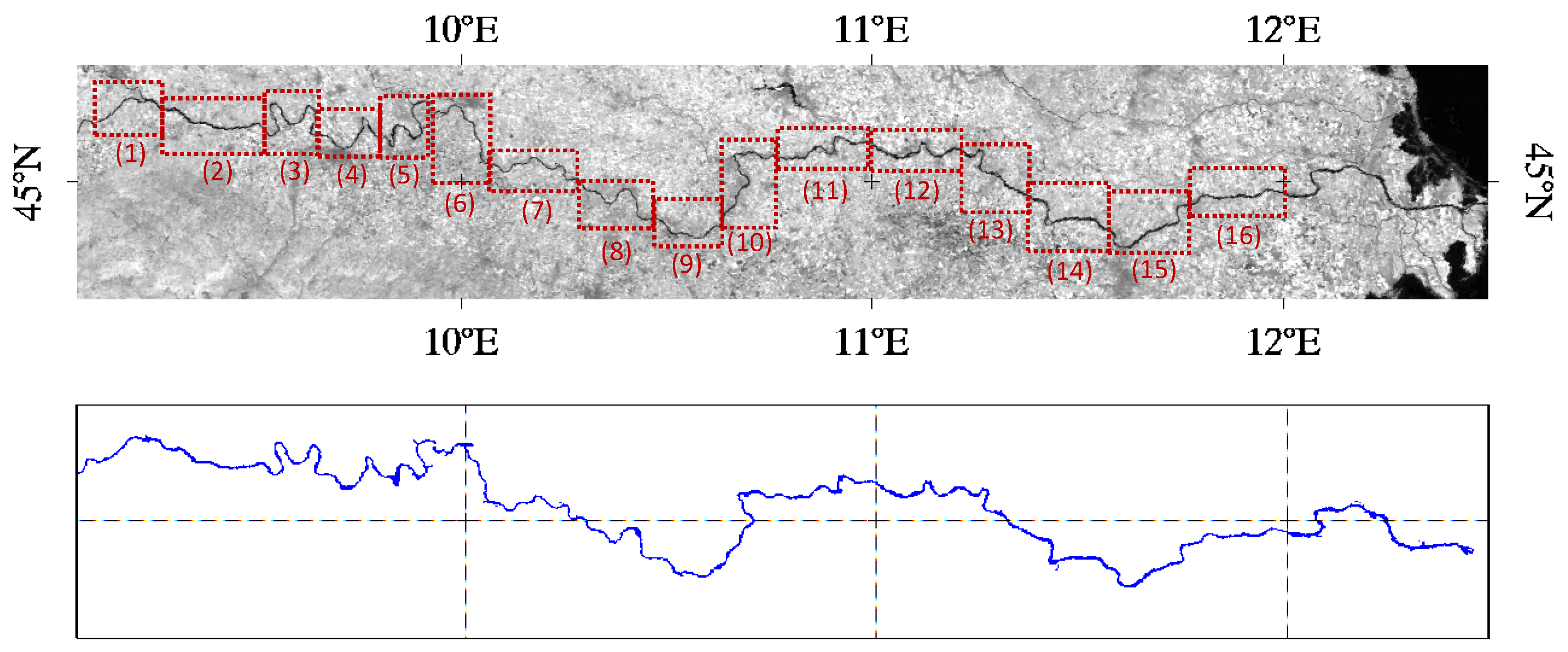




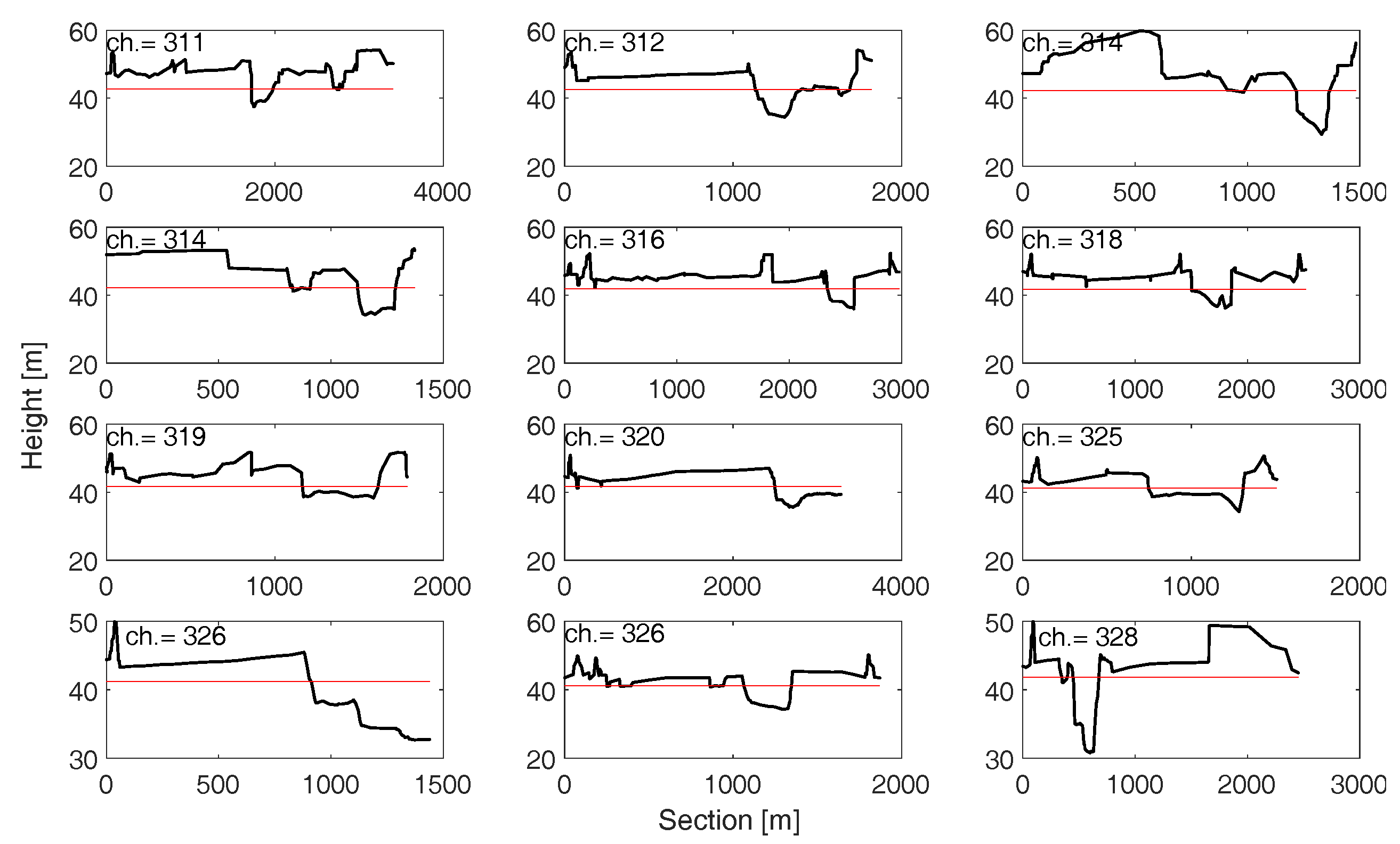
| Reach Number | Starting Point | Ending Point | Reach Length | ||||
|---|---|---|---|---|---|---|---|
| Lat. | Lon. | Chainage | Lat. | Lon. | Chainage | ||
| () | () | (km) | () | () | (km) | (km) | |
| 1 | 45.11 | 9.12 | 250.00 | 45.10 | 9.34 | 270.00 | 20.00 |
| 2 | 45.10 | 9.34 | 270.00 | 45.11 | 9.55 | 290.00 | 20.00 |
| 3 | 45.11 | 9.55 | 290.00 | 45.08 | 9.66 | 310.00 | 20.00 |
| 4 | 45.08 | 9.66 | 310.00 | 45.07 | 9.82 | 329.36 | 19.35 |
| 5 | 45.07 | 9.82 | 329.36 | 45.09 | 9.90 | 341.16 | 11.80 |
| 6 | 45.09 | 9.90 | 341.16 | 45.03 | 10.07 | 369.36 | 28.20 |
| 7 | 45.03 | 10.07 | 369.36 | 45.00 | 10.28 | 389.34 | 19.98 |
| 8 | 45.00 | 10.28 | 389.34 | 44.94 | 10.46 | 409.37 | 20.02 |
| 9 | 44.94 | 10.46 | 409.37 | 44.96 | 10.66 | 429.37 | 20.00 |
| 10 | 44.96 | 10.66 | 429.37 | 45.04 | 10.79 | 449.36 | 20.00 |
| 11 | 45.04 | 10.79 | 449.36 | 45.07 | 11.00 | 469.33 | 19.97 |
| 12 | 45.07 | 11.00 | 469.33 | 45.06 | 11.21 | 489.36 | 20.03 |
| 13 | 45.06 | 11.21 | 489.36 | 44.97 | 11.39 | 509.36 | 20.00 |
| 14 | 44.97 | 11.39 | 509.36 | 44.92 | 11.57 | 529.34 | 19.98 |
| 15 | 44.92 | 11.57 | 529.34 | 44.96 | 11.75 | 549.36 | 20.02 |
| 16 | 44.96 | 11.75 | 549.36 | 44.98 | 11.98 | 569.35 | 19.99 |
| Variable | Dataset | Resolution | Time Period | Source | |
|---|---|---|---|---|---|
| Spatial | Temporal | ||||
| Effective river width W | MODIS | 250 m | 8 d | 2000–2014 | [38] |
| Variable Surface water level H and slope S | – | 3 d | 2000–2014 | [39] | |
| TOPEX/Poseidon | – | 10 d | 1992–2002 | ||
| ENVISAT | – | 35 d | 2002–2010 | ||
| TOPEX/Poseidon XT | – | 10 d | 2002–2005 | ||
| ENVISAT XT | – | 30 d | 2010–2012 | ||
| CryoSat-2 | – | 369 d | 2012–2014 | ||
| Jason-2 | – | 10 d | 2008–2016 | ||
| River discharge Q | in situ | – | 1 d | 1995–2013 | AIPO |
| Channel sections | surveyed | every 250 m | – | – | AIPO |
| Name | Lat. | Lon. | Elevation | Average Width | Average Flow Velocity | Average Discharge |
|---|---|---|---|---|---|---|
| () | () | (m) | (km) | (m/s) | (m/s) | |
| Piacenza | 45.06 | 9.70 | 42.37 | 106 | 0.61 | 933 |
| Cremona | 45.13 | 9.99 | 29.03 | 157 | 0.82 | 1075 |
| Borgoforte | 45.05 | 10.75 | 14.05 | 164 | 0.84 | 1313 |
| Sermide | 45.02 | 11.29 | 9.50 | 329 | 0.44 | 1378 |
| Pontelagoscuro | 44.89 | 11.61 | 3.48 | 175 | 3.01 | 1477 |
| Reach | (m) | Model by Bjerklie et al. [9] | Model by Dingman and Sharma [36] | ||||
|---|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | ||||
| 1 | 50.27 | 0.69 | 50.37 ± 0.15 | 0.10 | 0.39 | 50.66 ± 0.14 | 0.39 |
| 2 | 45.62 | 0.60 | 44.72 ± 0.15 | 0.89 | 0.30 | 44.96 ± 0.14 | 0.66 |
| 3 | 40.09 | 1.36 | 41.47 ± 0.10 | 1.38 | 0.67 | 41.69 ± 0.09 | 1.59 |
| 4 | 35.91 | 2.06 | 40.73 ± 0.03 | 4.83 | 0.88 | 40.85 ± 0.03 | 4.94 |
| 5 | 32.20 | 29.20 | 32.07 ± 0.01 | 0.12 | 11.95 | 32.13 ± 0.01 | 0.07 |
| 6 | 24.60 | 0.80 | 24.91 ± 0.09 | 0.31 | 0.40 | 25.16 ± 0.08 | 0.57 |
| 7 | 20.63 | 0.22 | 16.06 ± 0.31 | 4.56 | 0.13 | 16.53 ± 0.31 | 4.10 |
| 8 | 17.18 | 0.27 | 13.06 ± 0.26 | 4.12 | 0.16 | 13.58 ± 0.26 | 3.60 |
| 9 | 12.92 | 0.74 | 12.07 ± 0.14 | 0.85 | 0.42 | 12.48 ± 0.13 | 0.44 |
| 10 | 11.54 | 0.50 | 9.37 ± 0.16 | 2.17 | 0.27 | 9.77 ± 0.16 | 1.77 |
| 11 | 7.38 | 0.53 | 7.04 ± 0.16 | 0.34 | 0.29 | 7.48 ± 0.16 | 0.10 |
| 12 | 2.70 | 1.40 | 5.64 ± 0.07 | 2.94 | 0.73 | 5.91 ± 0.07 | 3.21 |
| 13 | 2.08 | 1.25 | 3.00 ± 0.10 | 0.92 | 0.66 | 3.31 ± 0.09 | 1.23 |
| 14 | −0.26 | 0.58 | −1.49 ± 0.20 | 1.23 | 0.34 | −0.87 ± 0.19 | 0.61 |
| 15 | −3.00 | 4.83 | 1.07 ± 0.04 | 4.07 | 2.28 | 1.23 ± 0.04 | 4.24 |
| 16 | −6.29 | 4.97 | −1.32 ± 0.08 | 4.97 | 2.64 | −1.07 ± 0.07 | 5.22 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tourian, M.J.; Elmi, O.; Mohammadnejad, A.; Sneeuw, N. Estimating River Depth from SWOT-Type Observables Obtained by Satellite Altimetry and Imagery. Water 2017, 9, 753. https://doi.org/10.3390/w9100753
Tourian MJ, Elmi O, Mohammadnejad A, Sneeuw N. Estimating River Depth from SWOT-Type Observables Obtained by Satellite Altimetry and Imagery. Water. 2017; 9(10):753. https://doi.org/10.3390/w9100753
Chicago/Turabian StyleTourian, Mohammad J., Omid Elmi, Abolfazl Mohammadnejad, and Nico Sneeuw. 2017. "Estimating River Depth from SWOT-Type Observables Obtained by Satellite Altimetry and Imagery" Water 9, no. 10: 753. https://doi.org/10.3390/w9100753
APA StyleTourian, M. J., Elmi, O., Mohammadnejad, A., & Sneeuw, N. (2017). Estimating River Depth from SWOT-Type Observables Obtained by Satellite Altimetry and Imagery. Water, 9(10), 753. https://doi.org/10.3390/w9100753





