Assessing Agricultural Drought in the Anthropocene: A Modified Palmer Drought Severity Index
Abstract
:1. Introduction
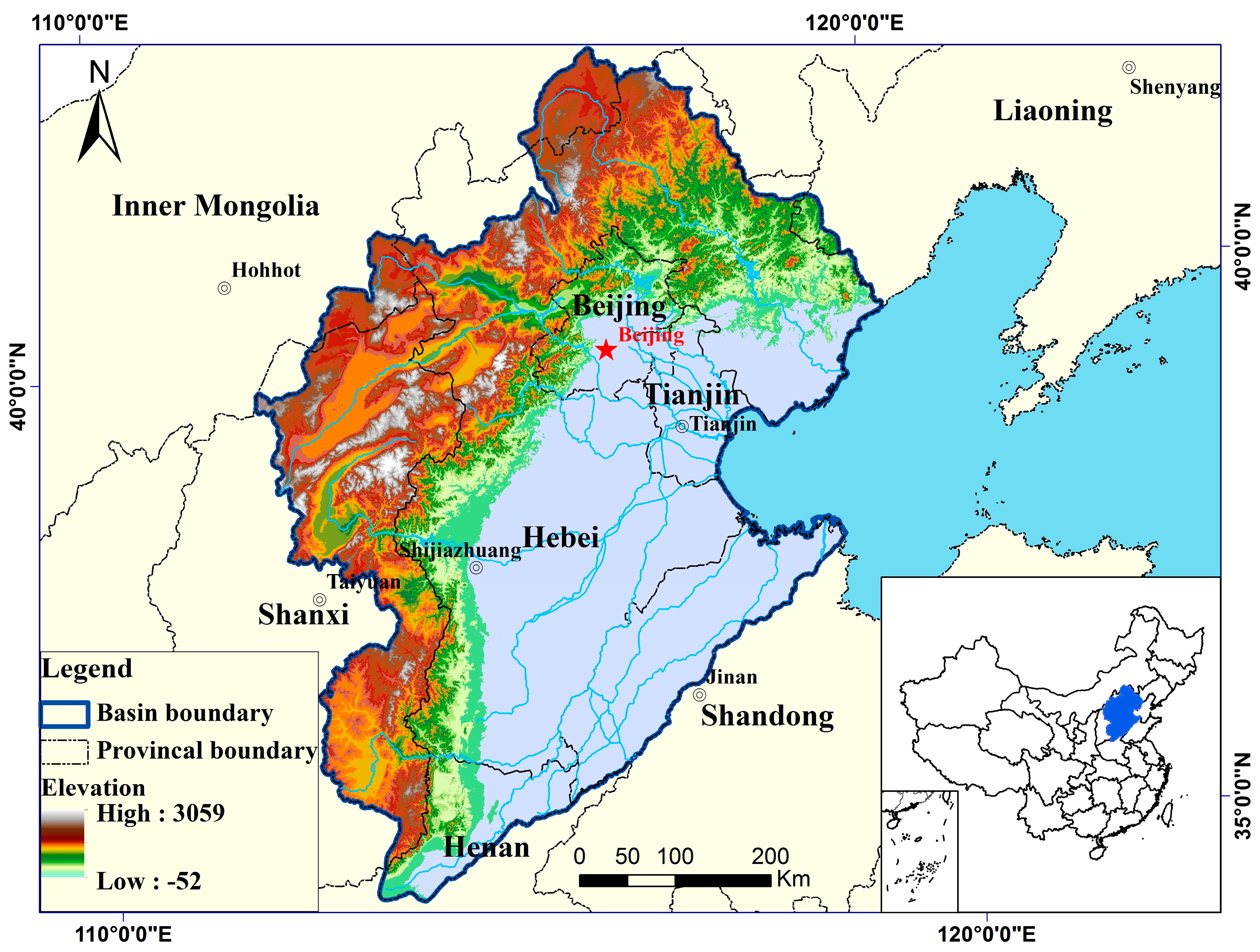
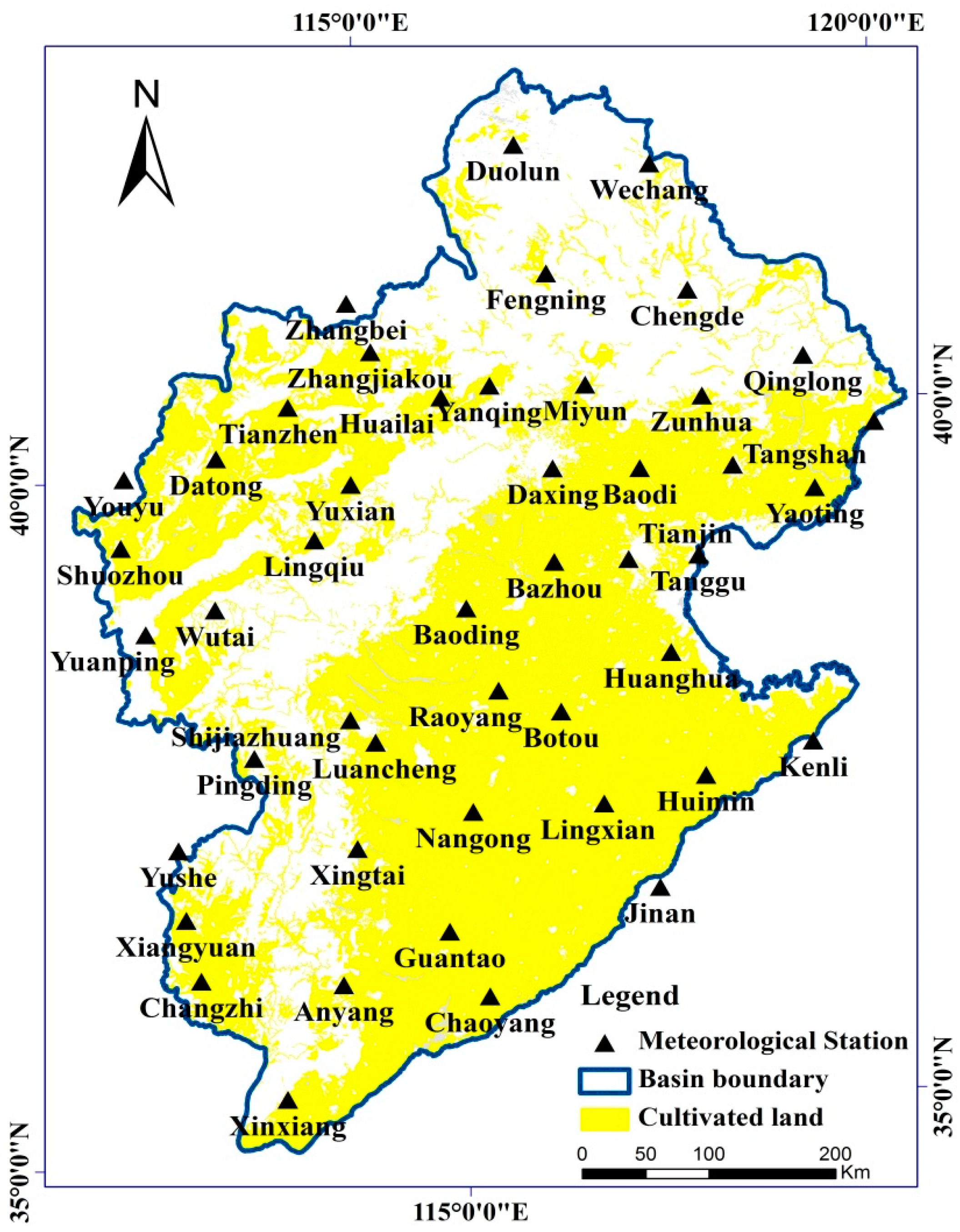
2. Description of the Study Area
3. Data and Methodology
3.1. Data Sources
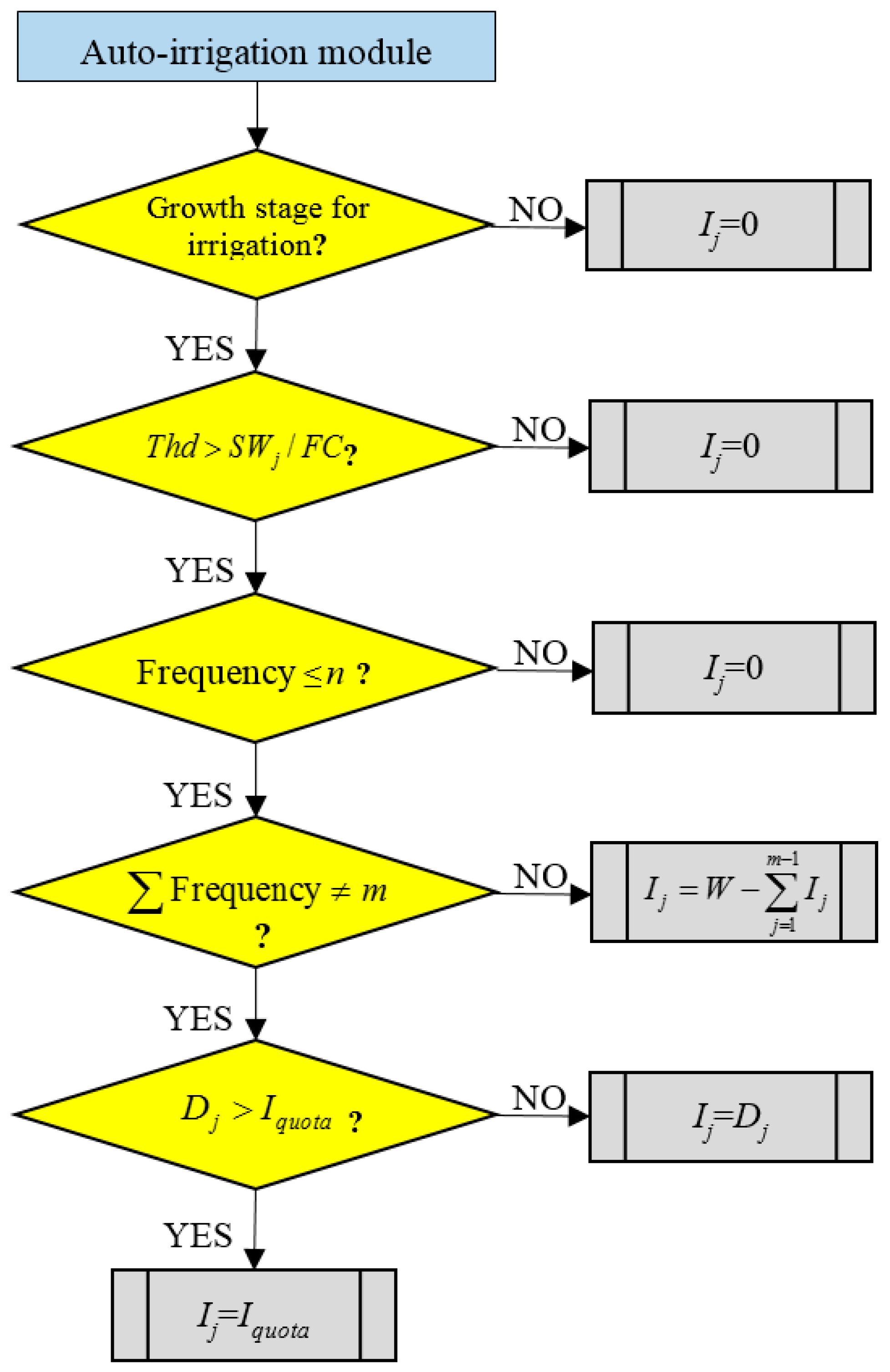
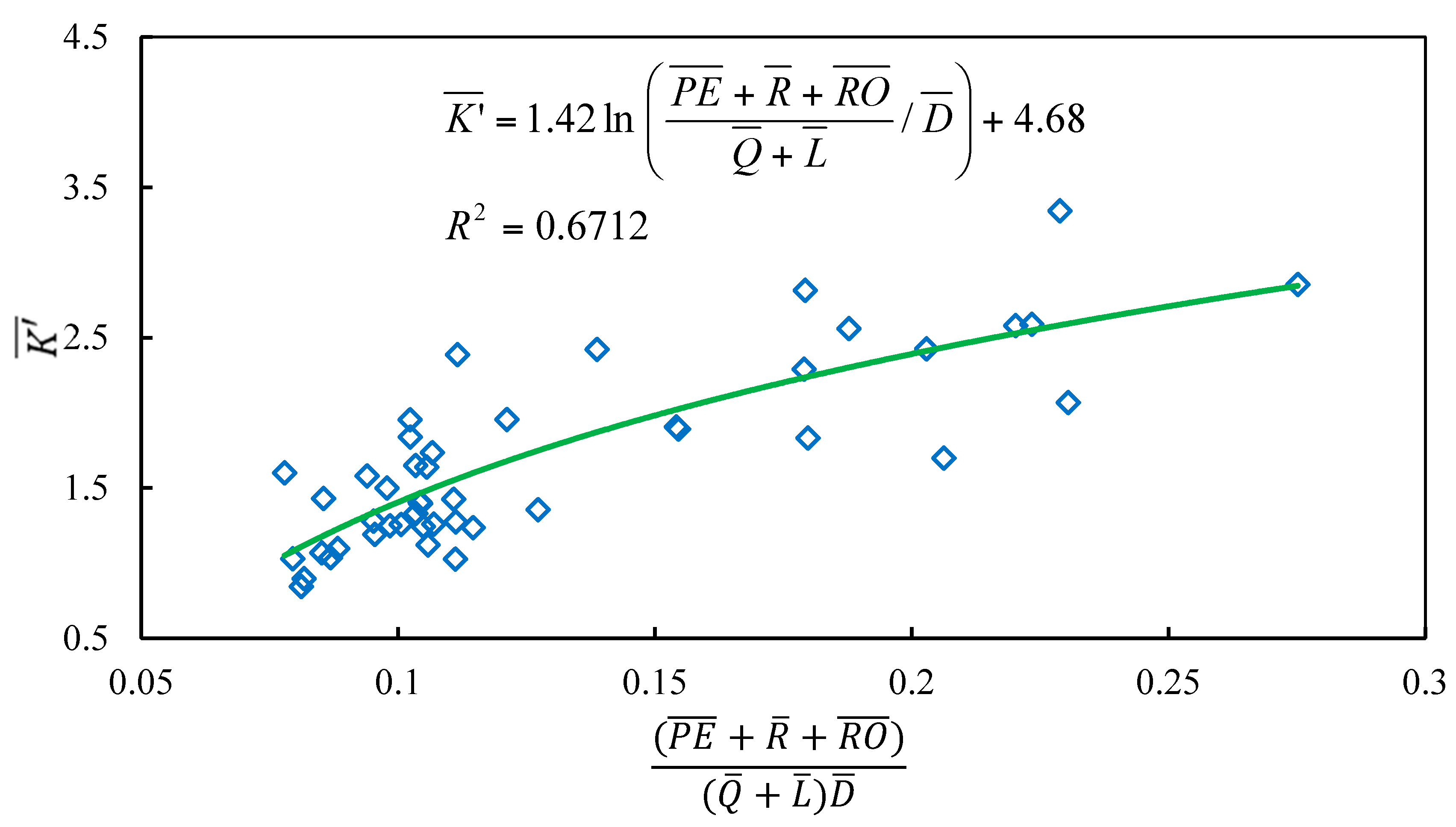
3.2. Methodology
4. Results and Discussion
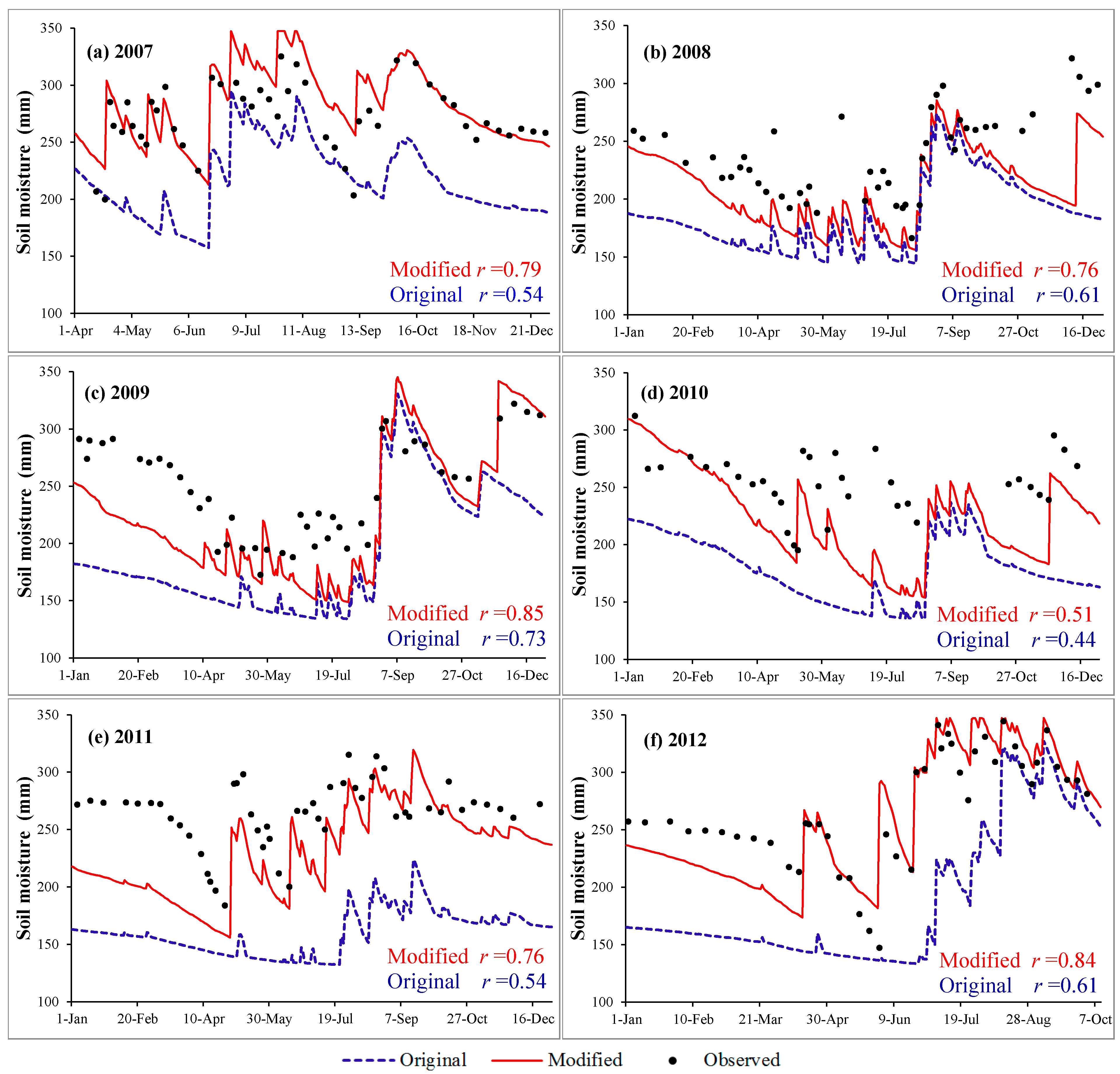
4.1. Soil Moisture Analyses
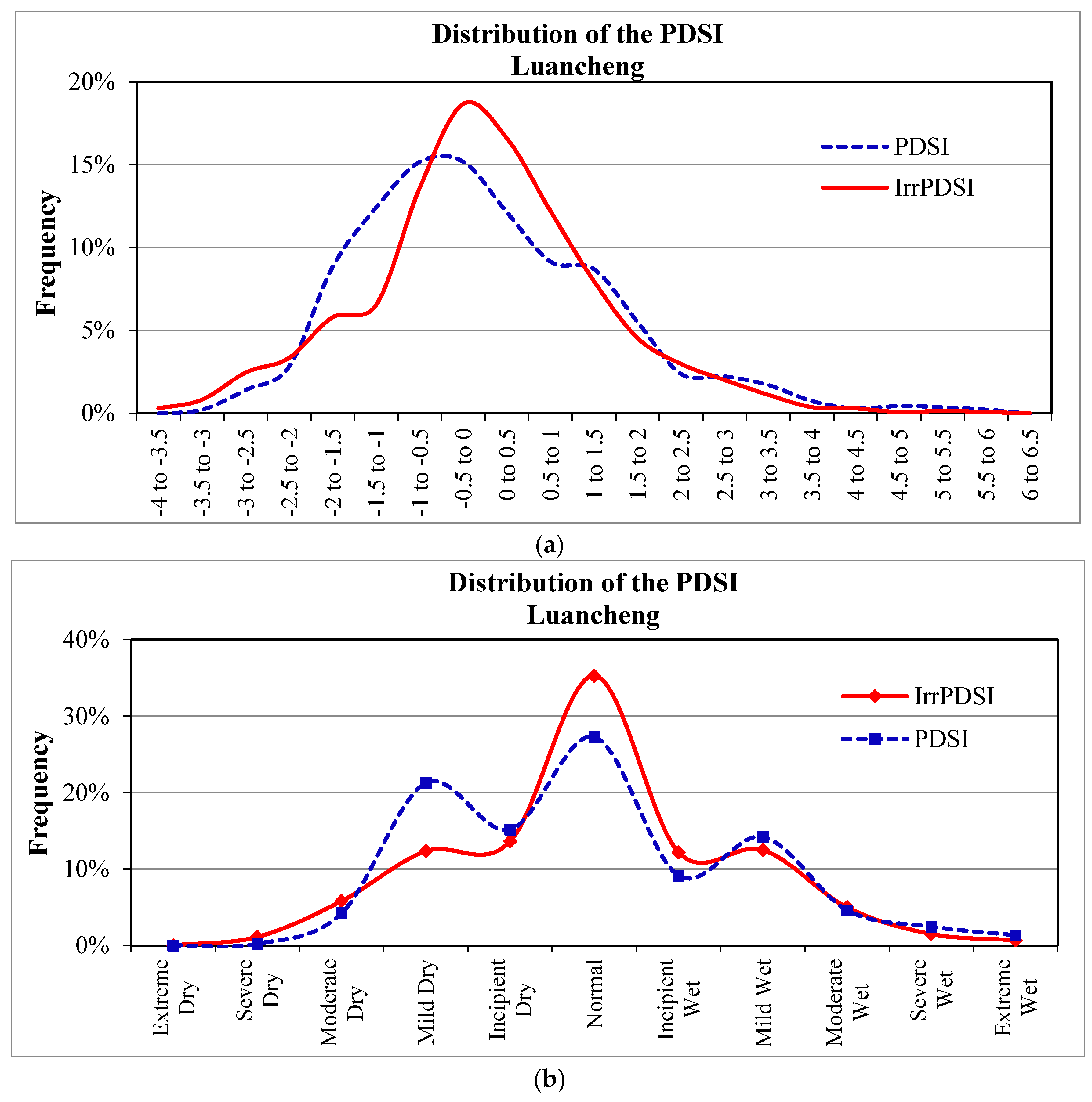
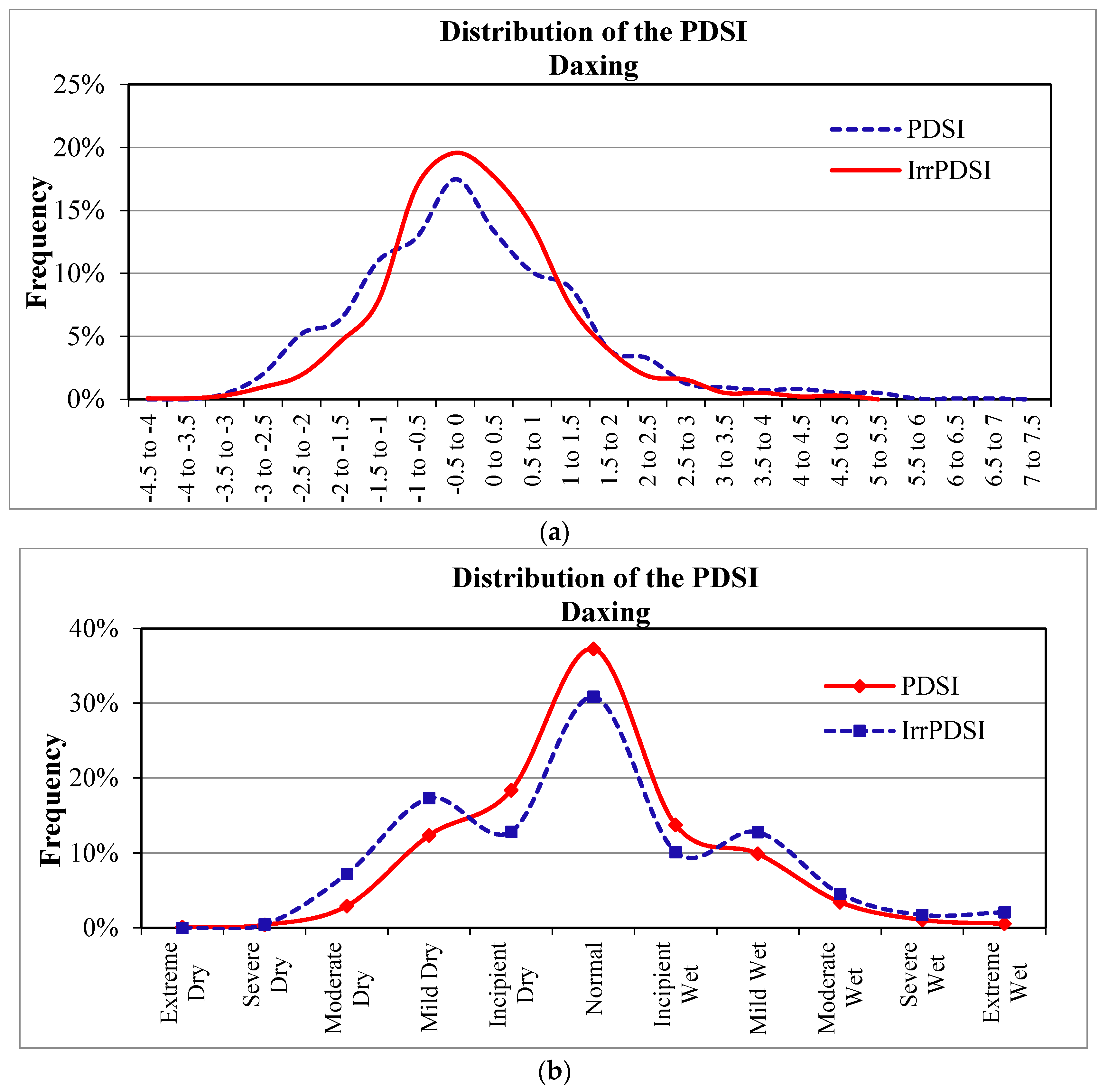
4.2. Frequency Analyses
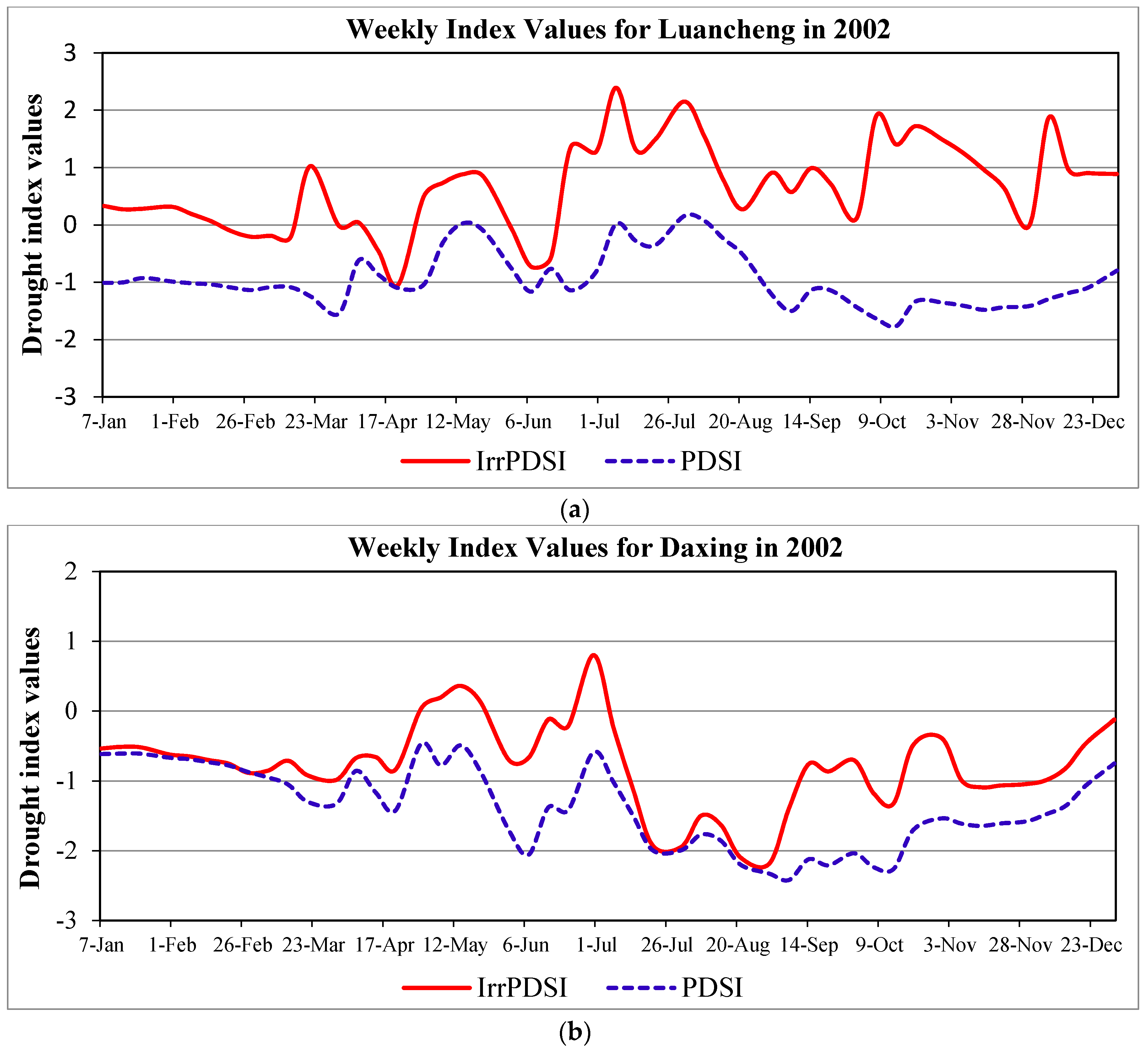
4.3. Time Series Analyses
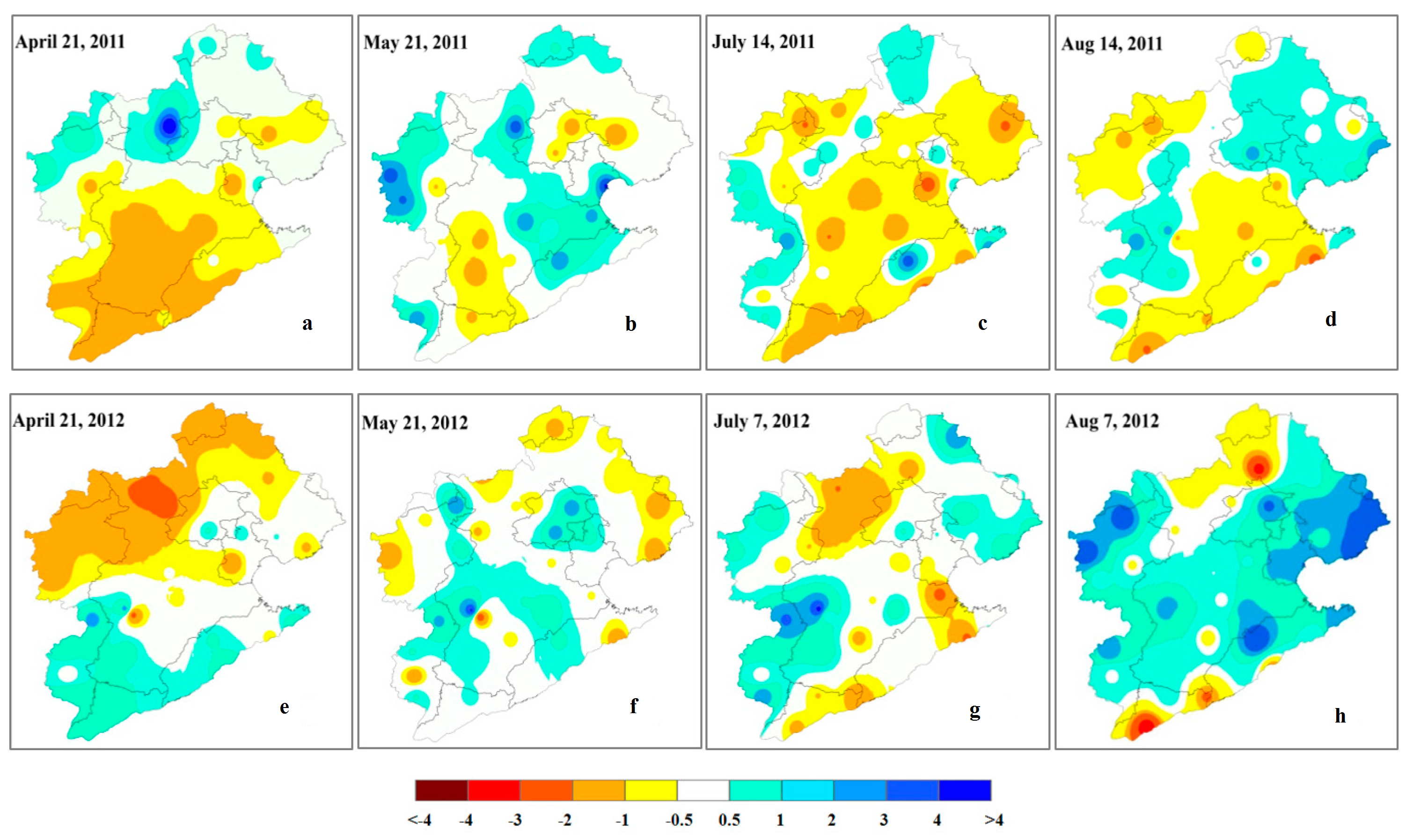
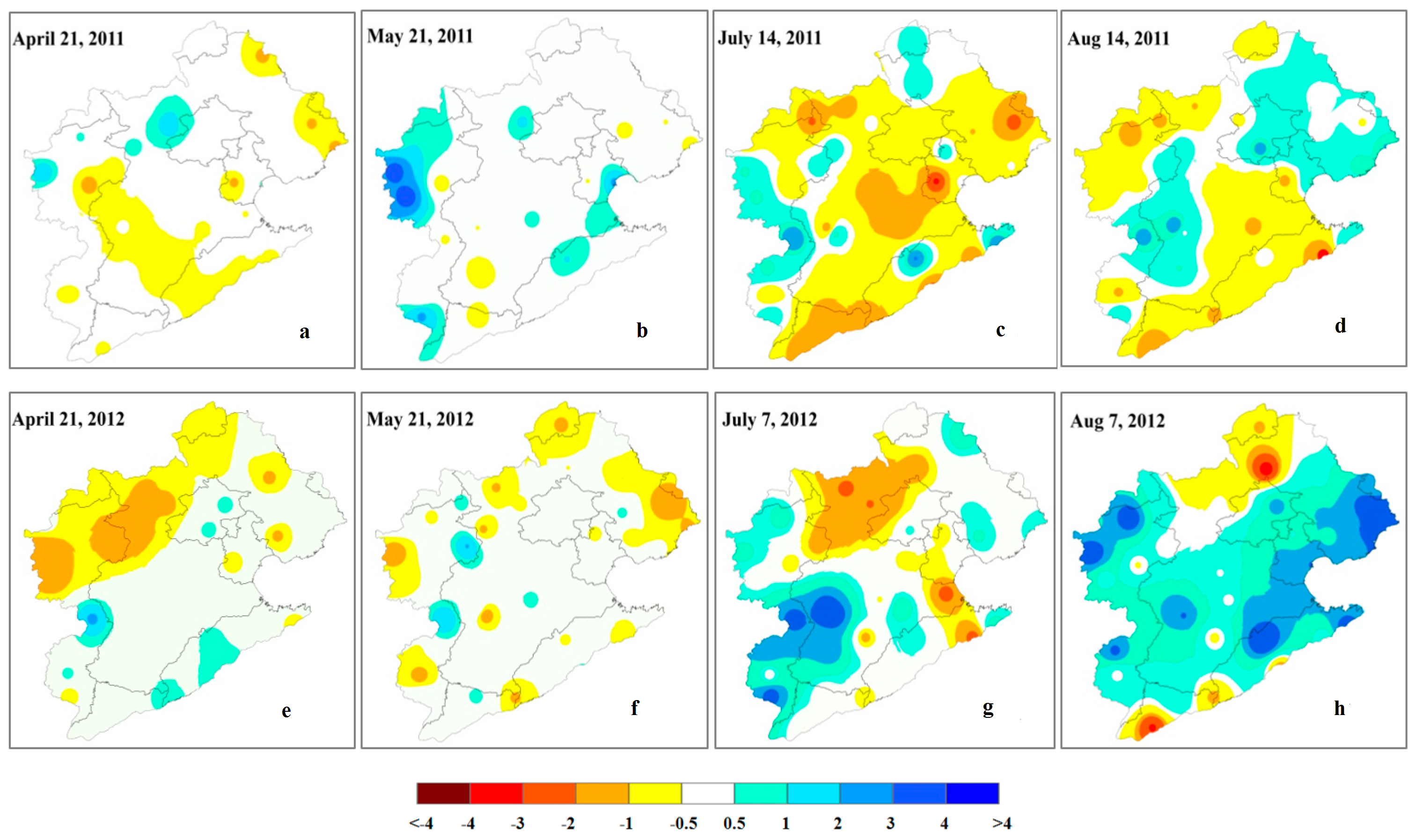
4.4. Spatial Analyses
5. Conclusions
- (1)
- Comparing the farmland soil moisture in Luancheng station, the correlation coefficients between the results simulated by the modified model and the observed values from 2007 to 2012 were 0.73, 0.76, 0.85, 0.51, 0.76 and 0.84, respectively; which had increased by 32.7%, 24.6%, 16.4%, 15.9%, 40.7% and 37.7%, respectively, compared with the performance of the original method. It turned out that the simulation results were ideal and provided a more objective response to the farmland moisture-changing process.
- (2)
- The statistical analyses indicated that the frequencies of mild dry and wet reported by the PDSI were 21% and 14% for Luancheng, and 17% and 13% for Daxing, respectively, which did not fit with the belief that the frequency of mild dry should be approximately equal to mild wet. Contrarily, the IrrPDSI reported a nearly normal distribution, and mild dry and wet occurred with a close frequency (12% for Luancheng and 10% for Daxing, respectively). Moreover, the results showed that 39 of the 47 stations in the study area based on IrrPDSI had nearly normal distributed values, whereas only half of the stations examined based on the PDSI did.
- (3)
- The time series plot of the two PDSIs showed that the IrrPDSI reported a normal or mild wet category in Luancheng station and incipient or mild dry in Daxing station during July and December 2002, respectively; whereas the PDSI reported more negative results than the IrrPDSI. The report of agricultural disasters confirmed that the results reported by the IrrPDSI were more consistent with the real conditions.
- (4)
- The spatial analyses showed that the results reported by IrrPDSI matched historical records better than the PDSI during the irrigated season, which showed that irrigation can usually effectively relieve drought conditions. There were insignificant differences between the distributions of dry–wet based on the two indices during the non-irrigated season as a result of infrequent irrigation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Masud, M.B.; Khaliq, M.N.; Wheater, H.S. Future changes to drought characteristics over the Canadian Prairie Provinces based on NARCCAP multi-RCM ensemble. Clim. Dyn. 2016, 48, 1–21. [Google Scholar] [CrossRef]
- Masud, M.B.; Khaliq, M.N.; Wheater, H.S. Analysis of meteorological droughts for the Saskatchewan River Basin using univariate and bivariate approaches. J. Hydrol. 2015, 522, 452–466. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Research Paper No. 45; U.S. Department of Commerce Weather Bureau: Washington, DC, USA, 1965.
- Palmer, W.C. Keeping track of crop moisture conditions, nationwide: The new Crop Moisture Index. Weather Wise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Shafer, B.A.; Dezman, L.E. Development of a Surface Water Supply Index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. In Proceedings of the 50th Annual Western Snow Conference, Reno, NV, USA, 19 April 1982; Colorado State University: Fort Collins, CO, USA, 1982; pp. 164–175. [Google Scholar]
- Meyer, S.J.; Hubbard, K.G.; Wilhite, D.A. A crop-specific drought index for corn: I. Model development and validation. Agron. J. 1993, 85, 388–395. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar-orbiting satellite data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Patel, N.R.; Chopra, P.; Dadhwal, V.K. Analyzing spatial patterns of meteorological drought using standardized precipitation index. Meteorol. Appl. 2007, 14, 329–336. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. A nonparametric multivariate multi-index drought monitoring framework. J. Hydrometeorol. 2014, 15, 89–101. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Gleeson, T.; Clark, J.; Van Dijk, A.I.; Stahl, K.; Hannaford, J.; Di Baldassarre, G.; Teuling, A.J.; Tallaksen, L.M.; Uijlenhoet, R.; et al. Drought in the Anthropocene. Nat. Geosci. 2016, 9, 89–91. [Google Scholar] [CrossRef]
- Sadri, S.; Kam, J.; Sheffield, J. Nonstationarity of low flows and their timing in the eastern United States. Hydrol. Earth Syst. Sci. 2016, 20, 633–649. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Buchanan-Smith, M. Drought and Water Crises: Science, Technology, and Management Issues; CRC Press: Boca Raton, FL, USA, 2005; pp. 4–29. [Google Scholar]
- Hosseini, S.M.; Sharifzadeh, A.; Akbari, M. Causes, effects and management mechanisms of drought crisis in rural and nomadic communities in southeastern Iran as perceived by agricultural/rural managers and specialist. J. Hum. Ecol. 2009, 27, 189–200. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. Comment on “Characteristics and trends in various forms of the Palmer Drought Severity Index (PDSI) during 1900–2008” by Aiguo Dai. J. Geophys. Res. 2011, 116, D19112. [Google Scholar] [CrossRef]
- O’Farrell, P.J.; Anderson, P.M.L.; Milton, S.J.; Dean, W.R.J. Human response and adaptation to drought in the arid zone: Lessons from southern Africa. S. Afr. J. Sci. 2009, 105, 34–39. [Google Scholar]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Droughts: A Global Assesment; Routledge: London, UK, 2000; Volume 1, pp. 3–18. [Google Scholar]
- Li, Z.; Hao, Z.; Shi, X.; Déry, S.J.; Li, J.; Chen, S.; Li, Y. An agricultural drought index to incorporate the irrigation process and reservoir operations: A case study in the Tarim River Basin. Glob. Planet. Chang. 2016, 143, 10–20. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ines, A.V.; Das, N.N.; Khedun, C.P.; Singh, V.P.; Sivakumar, B.; Hansen, J.W. Anatomy of a local-scale drought: Application of assimilated remote sensing products, crop model, and statistical methods to an agricultural drought study. J. Hydrol. 2015, 526, 15–29. [Google Scholar] [CrossRef]
- Sauer, T.; Havlík, P.; Schneider, U.A.; Schmid, E.; Kindermann, G.; Obersteiner, M. Agriculture and resource availability in a changing world: The role of irrigation. Water Resour. Res. 2010, 46, 666–669. [Google Scholar] [CrossRef]
- Portmann, F.T.; Siebert, S.; Döll, P. MIRCA2000—Global monthly irrigated and rainfed crop areas around the year 2000: A new high-resolution data set for agricultural and hydrological modeling. Glob. Biogeochem. Cycles 2010, 24, 2013–2024. [Google Scholar] [CrossRef]
- Narayanamoorthy, A. Development and composition of irrigation in India: Temporal trends and regional patterns. Irrig. Drain. 2011, 60, 431–445. [Google Scholar] [CrossRef]
- State Statistical Bureau. Statistical Yearbook; Statistical Press of China: Beijing, China, 2014. (In Chinese)
- Cao, X.; Wang, Y.; Wu, P.; Zhao, X.; Wang, J. An evaluation of the water utilization and grain production of irrigated and rain-fed croplands in China. Sci. Total Environ. 2015, 529, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Van Loon, A.F.; Stahl, K.; Di Baldassarre, G.; Clark, J.; Rangecroft, S.; Wanders, N.; Gleeson, T.; Van Dijk, A.I.; Tallaksen, L.M.; Hannaford, J.; et al. Drought in a human-modified world: Reframing drought definitions, understanding, and analysis approaches. Hydrol. Earth Syst. Sci. 2016, 20, 3631–3650. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A. Hydrological response to meteorological drought using the Palmer drought indices in Thessaly, Greece. Desalination 2009, 237, 3–21. [Google Scholar] [CrossRef]
- Sun, L.; Mitchell, S.W.; Davidson, A. Multiple drought indices for agricultural drought risk assessment on the Canadian prairies. Int. J. Climatol. 2012, 32, 1628–1639. [Google Scholar] [CrossRef]
- Gobena, A.K.; Gan, T.Y. Assessment of trends and possible climate change impacts on summer moisture availability in western Canada based on Metrics of the Palmer Drought Severity Index. J. Clim. 2013, 26, 4583–4595. [Google Scholar] [CrossRef]
- Yuan, S.; Quiring, S.M. Drought in the U.S. Great Plains (1980–2012): A sensitivity study using different methods for estimating potential evapotranspiration in the Palmer Drought Severity Index. J. Geophys. Res. 2014, 119, 10996–11010. [Google Scholar] [CrossRef]
- Tei, S.; Yonenobu, H.; Sugimoto, A.; Ohta, T.; Maximov, T.C. Reconstructed summer Palmer Drought Severity Index since 1850 AD based on δ 13 C of larch tree rings in eastern Siberia. J. Hydrol. 2015, 529, 442–448. [Google Scholar] [CrossRef]
- Zou, L.; Xia, J.; She, D. Drought characteristic analysis based on an improved PDSI in the Wei River Basin of China. Water 2017, 9, 178. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer Drought Severity Index: Limitations and assumptions. J. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Sepulcrecanto, G.; Horion, S.; Singleton, A. Development of a combined drought indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef]
- Quiring, S.M.; Papakryiakou, T.N. An evaluation of agricultural drought indices for the Canadian prairies. Agric. For. Meteorol. 2003, 118, 49–62. [Google Scholar] [CrossRef]
- Ye, J.; Shen, S.; Lu, H. Application of modified palmer drought severity index in agricultural drought monitoring. Chin. J. Agro-Meteorol. 2009, 30, 257–261. (In Chinese) [Google Scholar]
- Cai, Y.; Wang, M.; Zhou, Z.; Chen, D.; Zhang, Y. Palmer drought severity model and its application in Mianyang. Plateau Mt. Meteorol. Res. 2010, 30, 55–59. (In Chinese) [Google Scholar]
- Mika, J.; Horváth, S.; Makra, L.; Dunkel, Z. The palmer drought severity index (PDSI) as an indicator of soil moisture. Phys. Chem. Earth Parts A/B/C 2005, 30, 223–230. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. WIREs Clim. Chang. 2011, 3, 45–65. [Google Scholar] [CrossRef]
- Ren, X.S.; Hu, Z.L.; Cao, Y.B.; He, S. Water Resources Assessment in the Haihe River Basin; Water Resources and Electricity Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Fang, Q.X.; Ma, L.; Green, T.R.; Yu, Q.; Wang, T.D.; Ahuja, L.R. Water resources and water use efficiency in the North China plain: Current status and agronomic management options. Agric. Water Manag. 2010, 97, 1102–1116. [Google Scholar] [CrossRef]
- Chen, S.; Li, R. Assessment of surface water resources and evapotranspiration in the Haihe River Basin of China using SWAT model. Hydrol. Process. 2013, 27, 1200–1222. [Google Scholar]
- Gao, G.; Xu, C.Y.; Chen, D.; Singh, V.P. Spatial and temporal characteristics of actual evapotranspiration over Haihe River Basin in China. Stoch. Environ. Res. Risk Assess. 2012, 26, 1–15. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S. A self-calibrating palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, A.L.; Qiao, C.L. Research on application of palmer drought model in Jinghuiqu irrigation area. Agric. Res. Arid Areas 2010, 28, 259–264. (In Chinese) [Google Scholar]
- Xiao, J.F.; Liu, Z.D.; Liu, X.F.; Liu, Z.G.; Chen, Y.M. Analysis and study on irrigation problem of main spring maize area of China. Water Sav. Irrig. 2010, 4, 1–3. (In Chinese) [Google Scholar]
- Water Industry Standard of the People’s Republic of China (SL568-2012): Soil Moisture Evaluation; Ministry of Water Resources of PRC: Beijing, China, 2012. (In Chinese)
- Gu, R.; Tang, Z. Analysis of the cause of drought in Shandong in the summer 2002. Meteorol. Mon. 2004, 30, 22–26. (In Chinese) [Google Scholar]
- Zou, X.; Zhai, P.; Zhang, Q. Variations in droughts over China: 1951–2003. Geophys. Res. Lett. 2005, 32, 353–368. [Google Scholar] [CrossRef]
- Xue, D.; Wang, J.; Wang, X. Characteristic analysis of change into drought in Shandong Province. J. Nat. Disasters 2007, 16, 60–65. (In Chinese) [Google Scholar]
| Region | Crop Type | Growth Stage for Irrigation | Irrigation | Auto-Irrigation Threshold d | |
|---|---|---|---|---|---|
| Frequency | Amount (mm) | ||||
| Western Hebei, Beijing, Tianjing and south Shanxi a | Winter wheat | Sowing (1–10 Octobor) | 1 | 58 | 0.6 |
| Tillering (20 November–10 December) | 1 | 80 | 0.5 | ||
| Jointing (10 March–14 April) | 1 | 65 | 0.55 | ||
| Heading (10–30 April) | 1 | 68 | 0.55 | ||
| Filling (1–30 May) | 2 | 75 | 0.55 | ||
| 67 | 0.55 | ||||
| Summer maize | Jointing (1–30 July) | 1 | 64 | 0.55 | |
| Filling (20 August–20 September) | 1 | 64 | 0.6 | ||
| Northern Shandong, northern Henan and eastern Hebei b | Winter wheat | Sowing (15–30 Octobor) | 1 | 63 | 0.6 |
| Tillering (20 November–10 December) | 1 | 70 | 0.5 | ||
| Jointing (10 March–14 April) | 1 | 65 | 0.55 | ||
| Heading (10–30 April) | 1 | 70 | 0.55 | ||
| Filling (1–30 May) | 2 | 67 | 0.55 | ||
| 65 | 0.55 | ||||
| Summer maize | Jointing (1–20 July) | 1 | 61 | 0.55 | |
| Filling (1–30 August) | 1 | 71 | 0.6 | ||
| Northern Shanxi and northern Hebei c | Spring maize | Jointing (10 June–10 July) | 1 | 75 | 0.55 |
| Tasseling (20–30 July) | 1 | 75 | 0.6 | ||
| Filling (1–30 August) | 1 | 75 | 0.6 | ||
| PDSI Value | Class |
|---|---|
| ≥4.00 | Extreme wet |
| 3.00 to 3.99 | Severe wet |
| 2.00 to 2.99 | Moderate wet |
| 1.00 to 1.99 | Mild wet |
| 0.50 to 0.99 | Incipient wet |
| 0.49 to −0.49 | Normal |
| −0.50 to −0.99 | Incipient drought |
| −1.00 to −1.99 | Mild drought |
| −2.00 to −2.99 | Moderate drought |
| −3.00 to −3.99 | Severe drought |
| ≤−4.00 | Extreme drought |
| PDSI | IrrPDSI |
|---|---|
| - | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Xiao, W.; Zhao, Y.; Li, X.; Lu, F.; Lu, C.; Chen, Y. Assessing Agricultural Drought in the Anthropocene: A Modified Palmer Drought Severity Index. Water 2017, 9, 725. https://doi.org/10.3390/w9100725
Yang M, Xiao W, Zhao Y, Li X, Lu F, Lu C, Chen Y. Assessing Agricultural Drought in the Anthropocene: A Modified Palmer Drought Severity Index. Water. 2017; 9(10):725. https://doi.org/10.3390/w9100725
Chicago/Turabian StyleYang, Mingzhi, Weihua Xiao, Yong Zhao, Xudong Li, Fan Lu, Chuiyu Lu, and Yan Chen. 2017. "Assessing Agricultural Drought in the Anthropocene: A Modified Palmer Drought Severity Index" Water 9, no. 10: 725. https://doi.org/10.3390/w9100725
APA StyleYang, M., Xiao, W., Zhao, Y., Li, X., Lu, F., Lu, C., & Chen, Y. (2017). Assessing Agricultural Drought in the Anthropocene: A Modified Palmer Drought Severity Index. Water, 9(10), 725. https://doi.org/10.3390/w9100725






