Influence of Rack Slope and Approaching Conditions in Bottom Intake Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Laboratory Flume
2.2. Instruments
2.3. Numerical Simulations
2.4. Experimental and Numerical Campaign
3. Results and Discussion
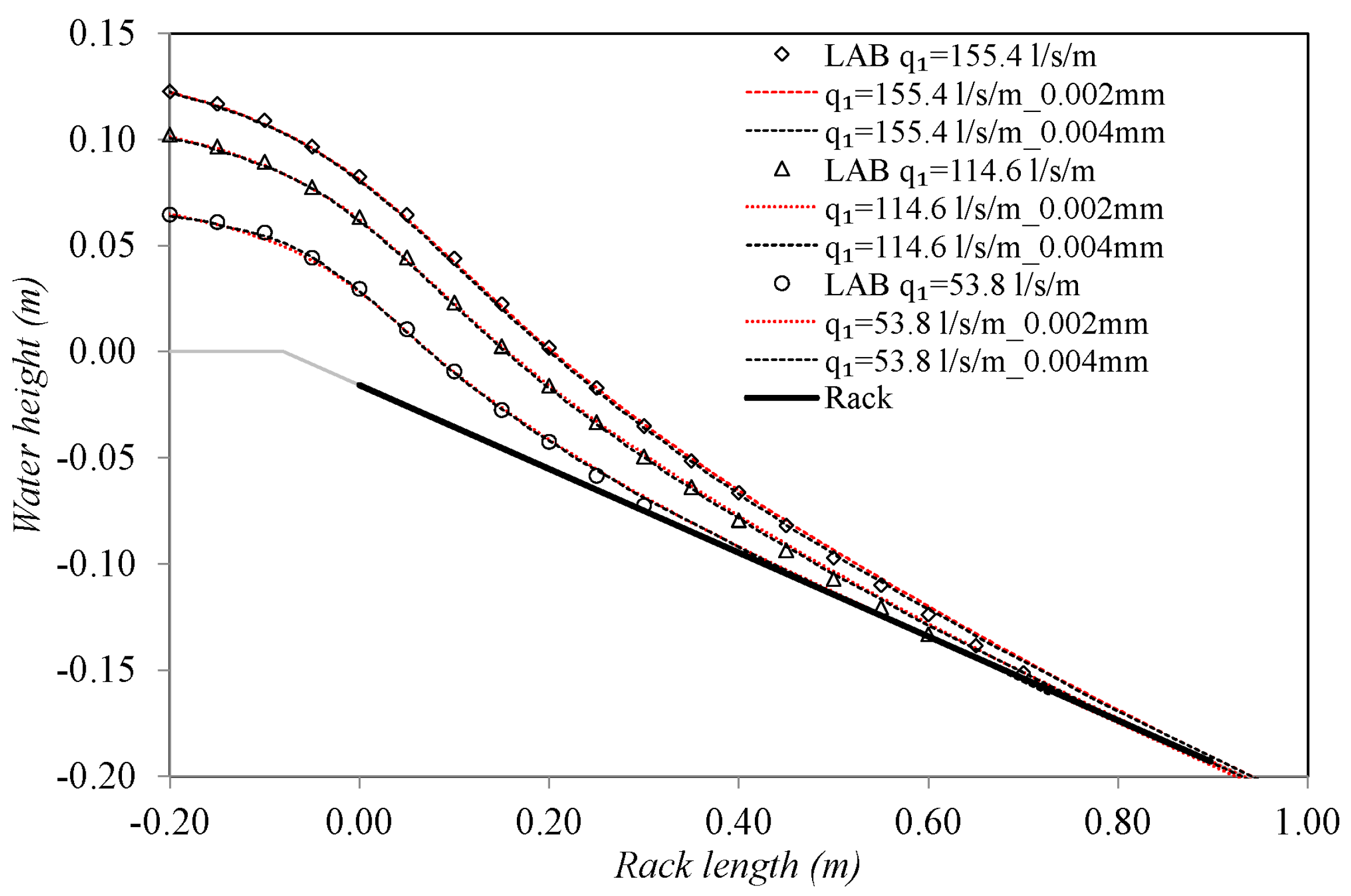
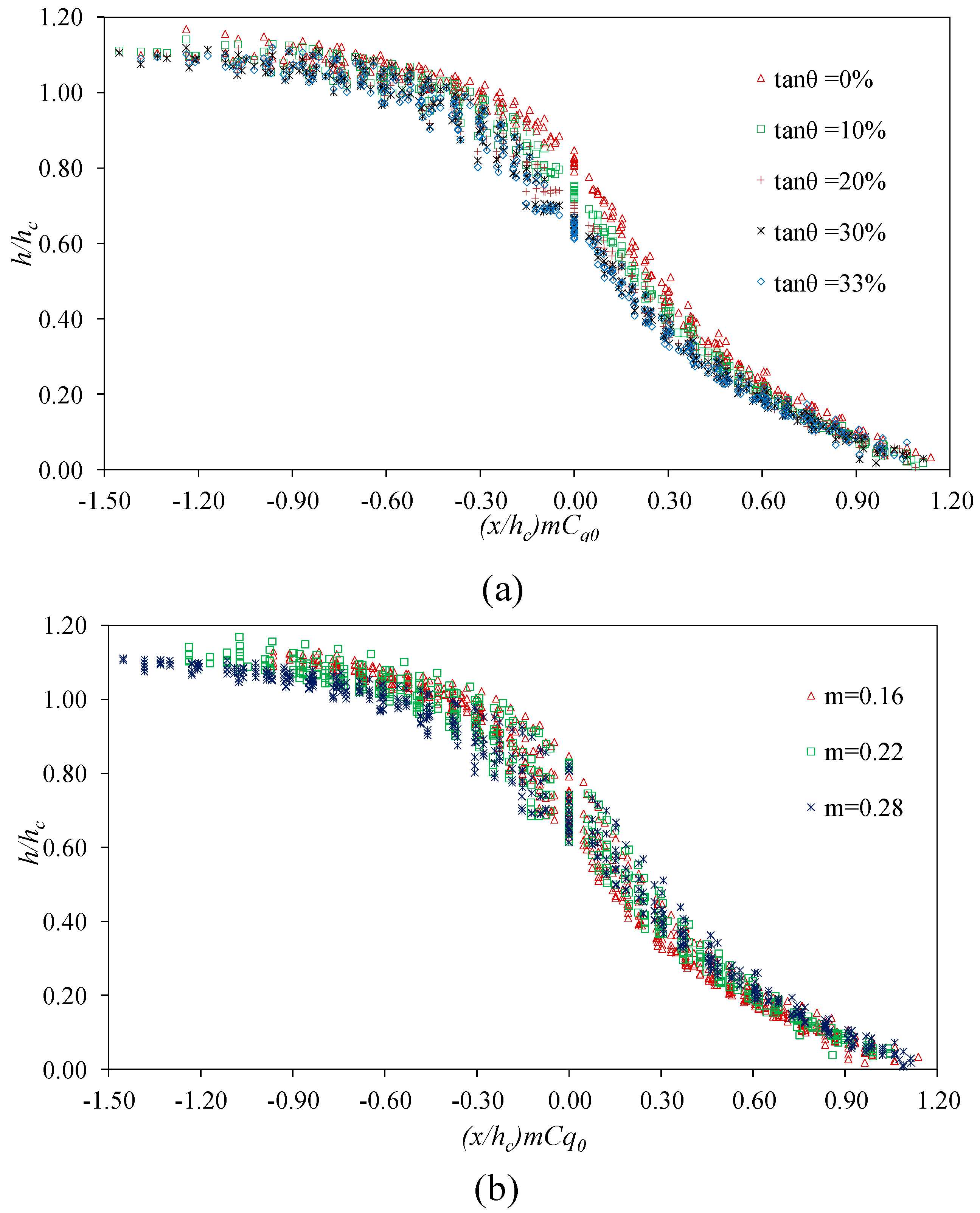
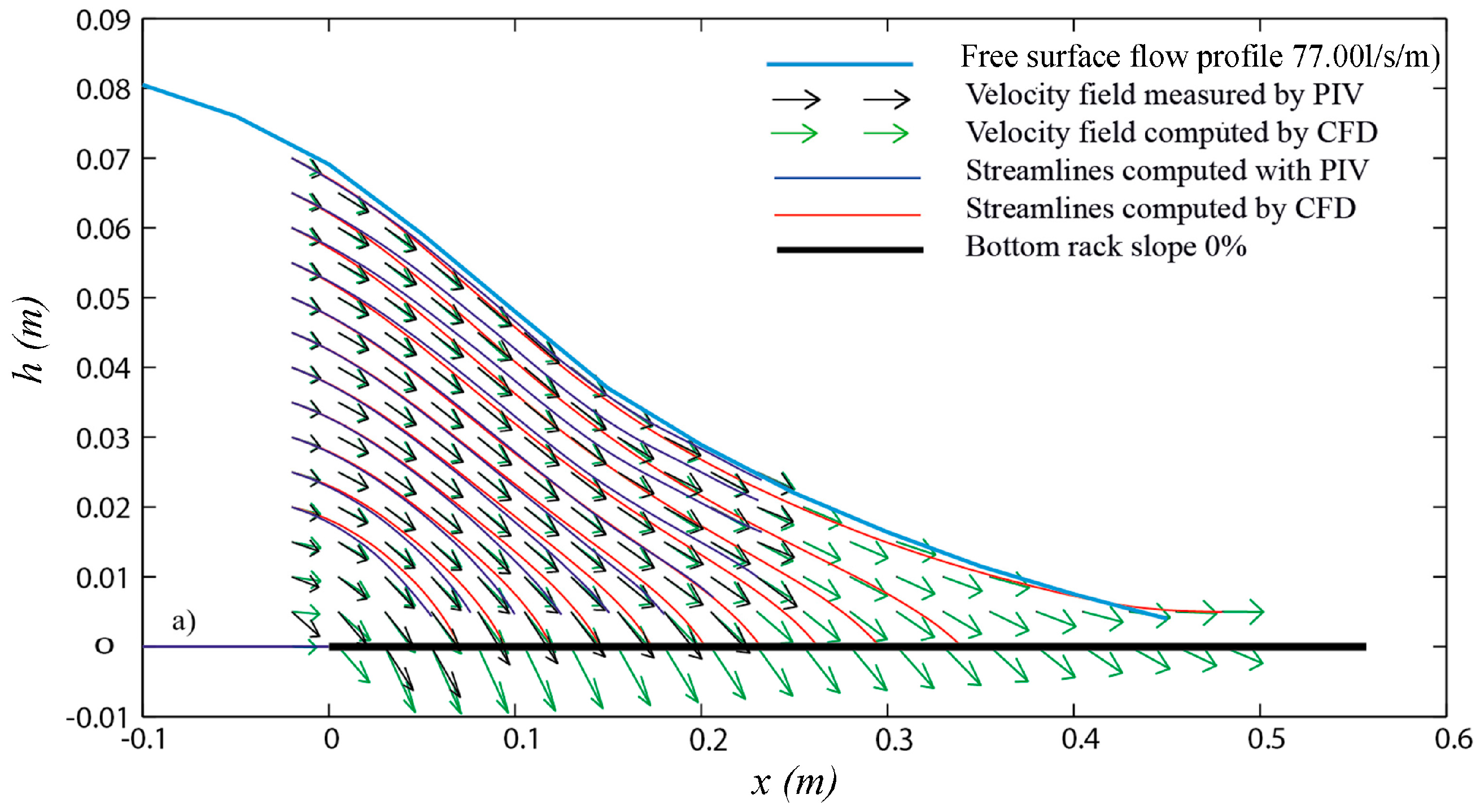
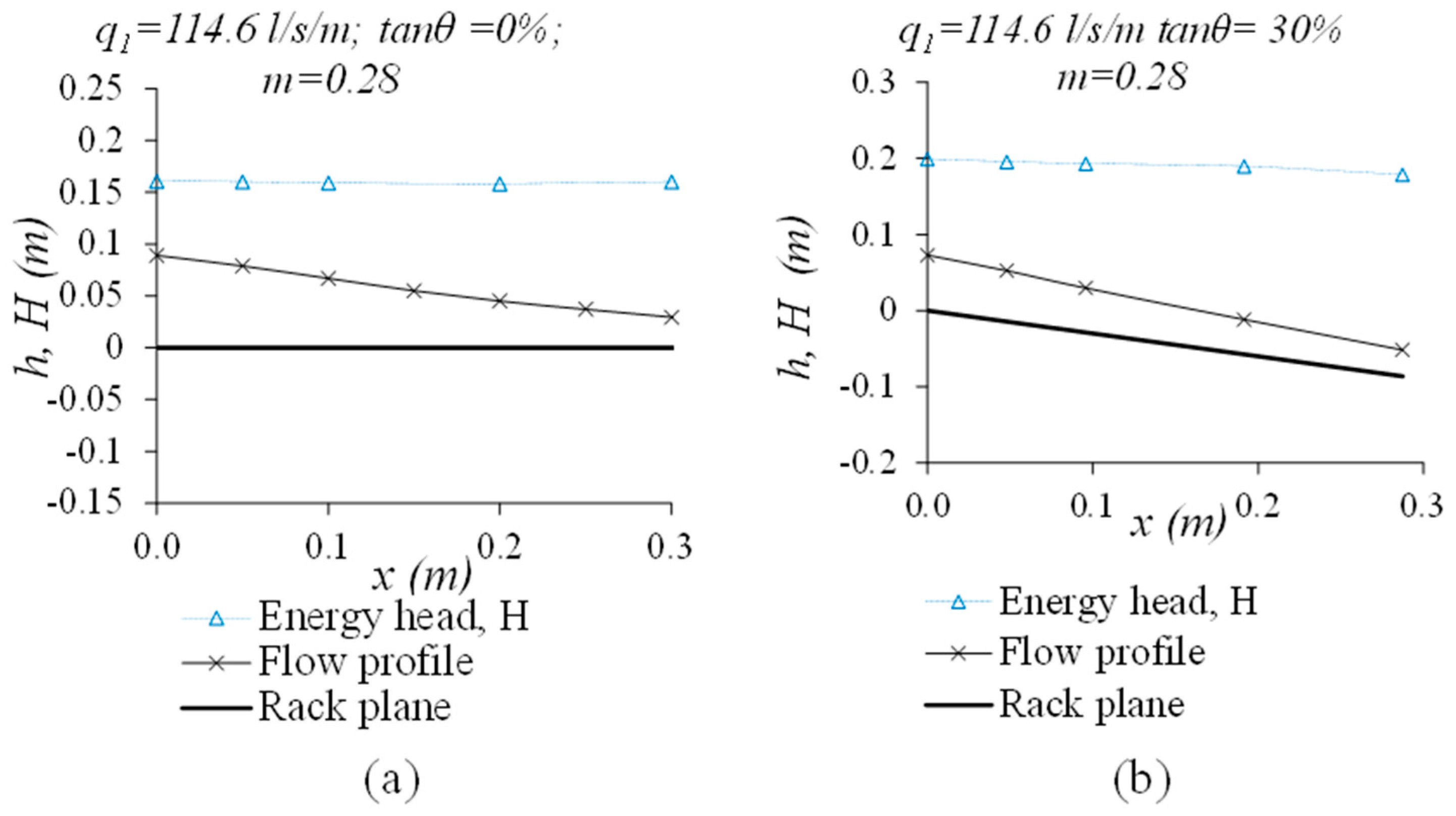
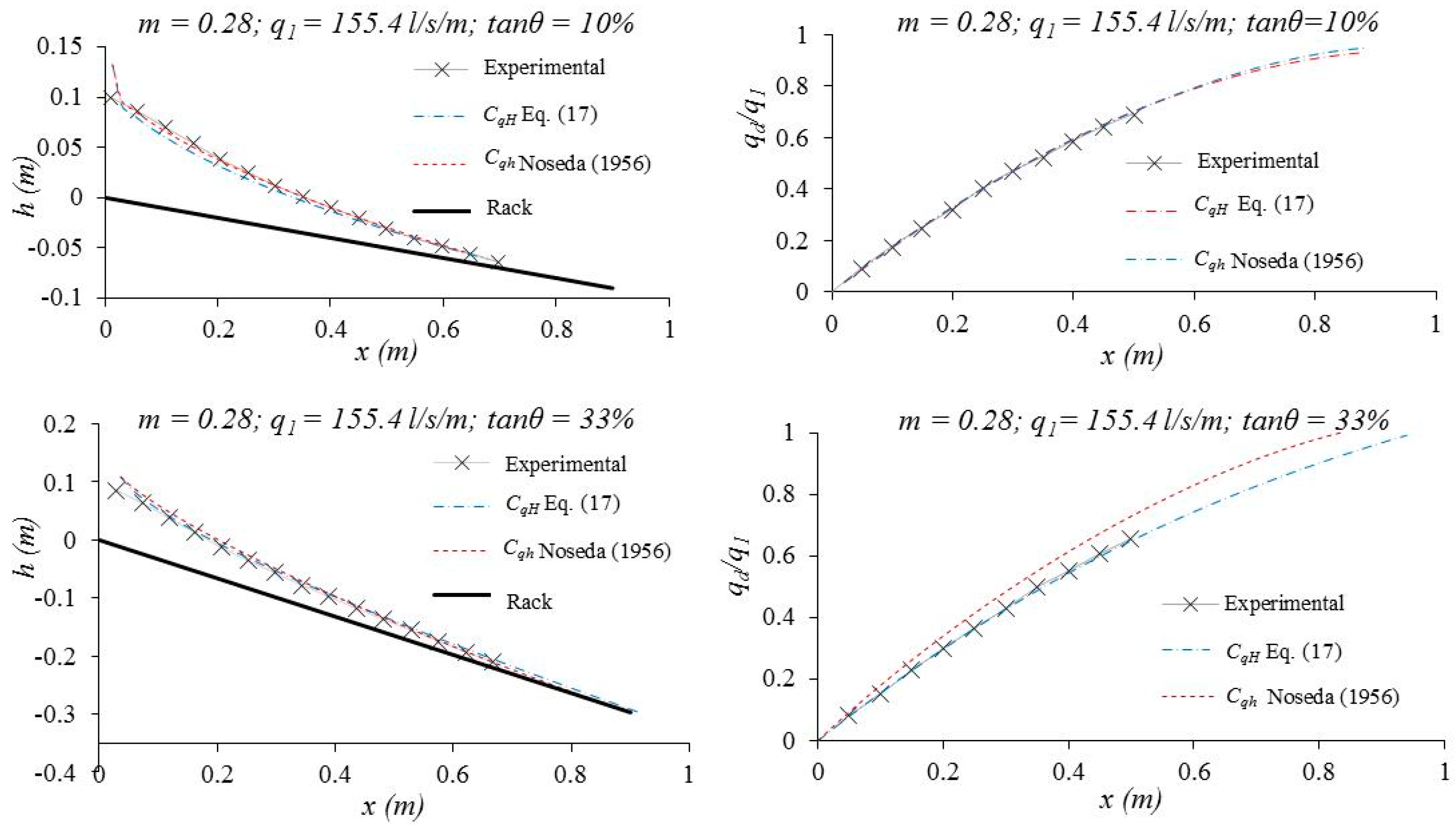
3.1. Free Surface Flow Profile
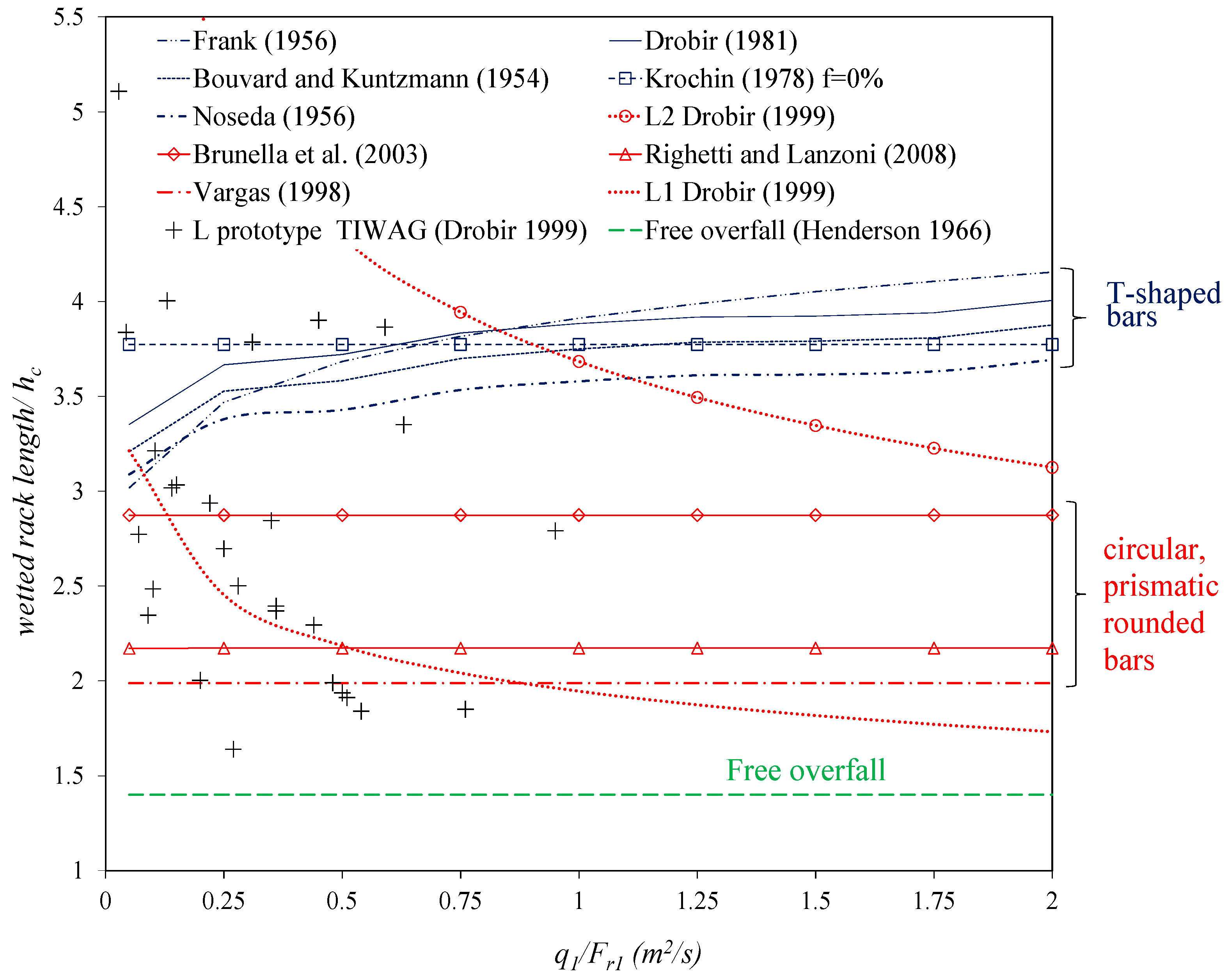
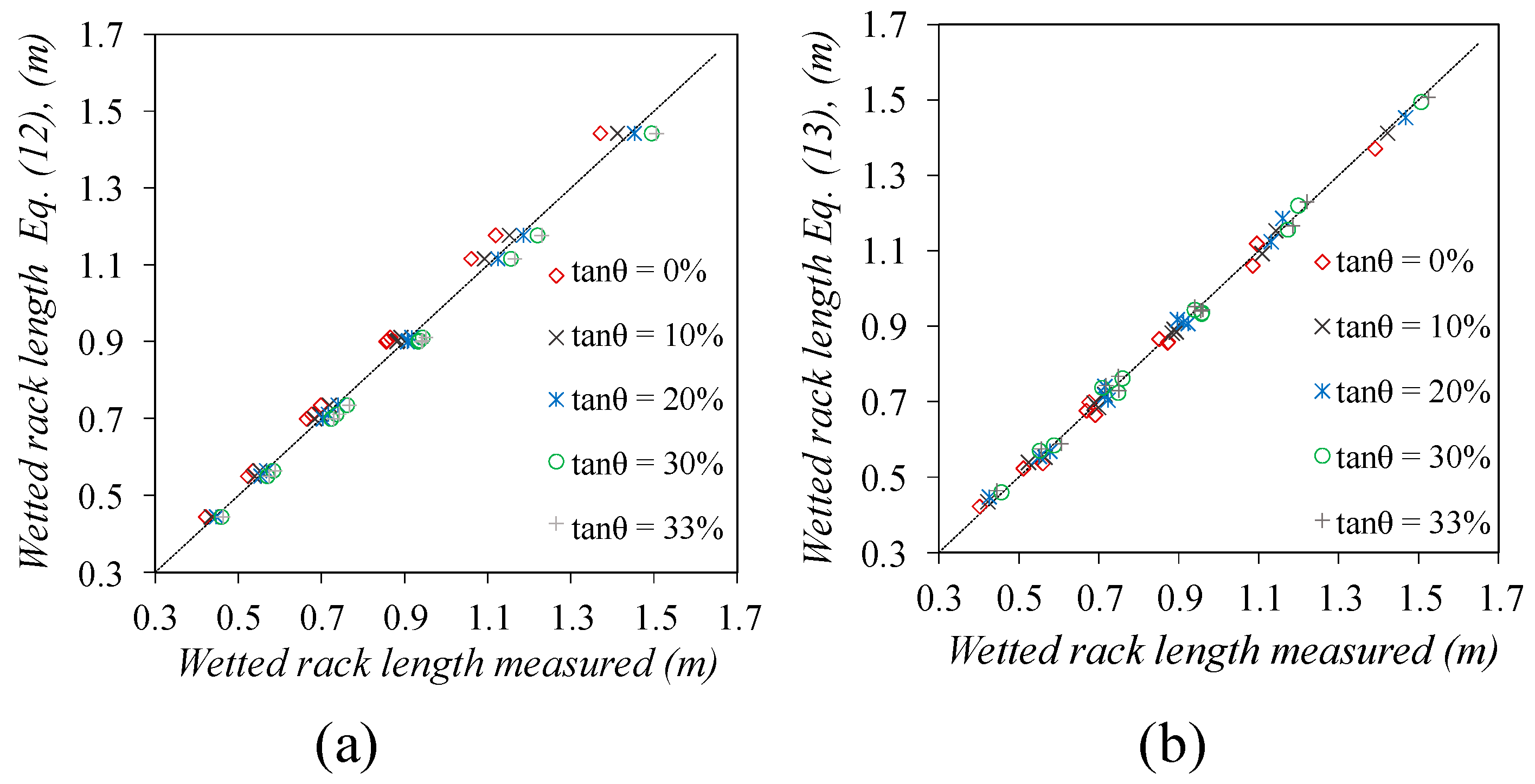
3.2. Wetted Rack Length
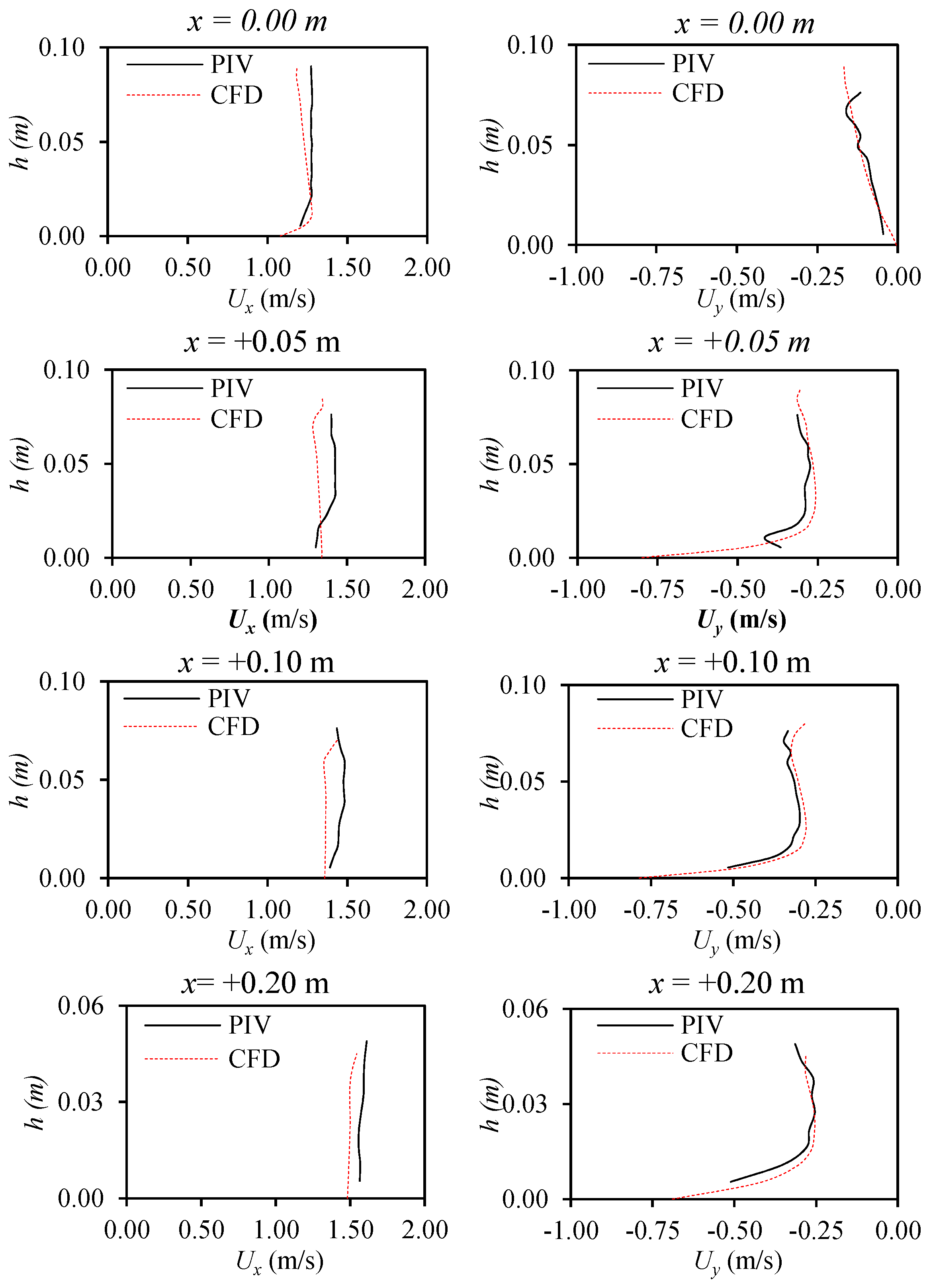
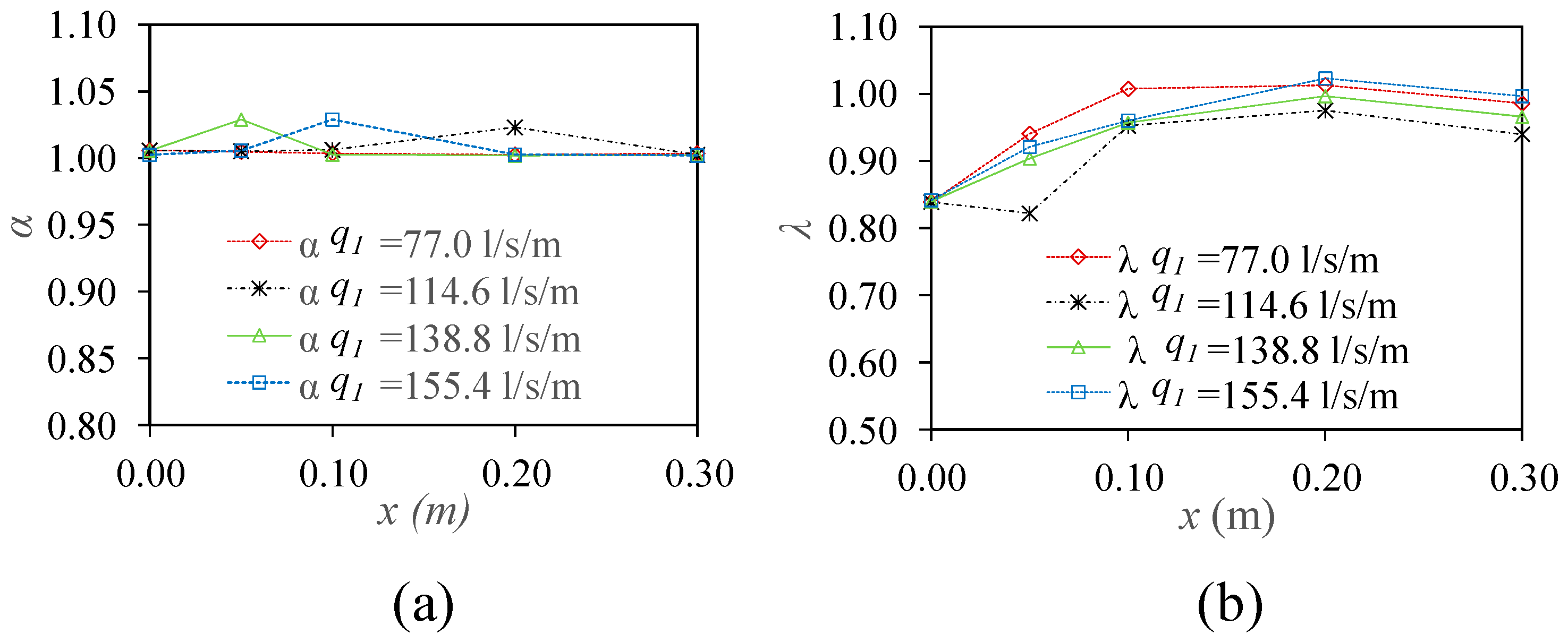
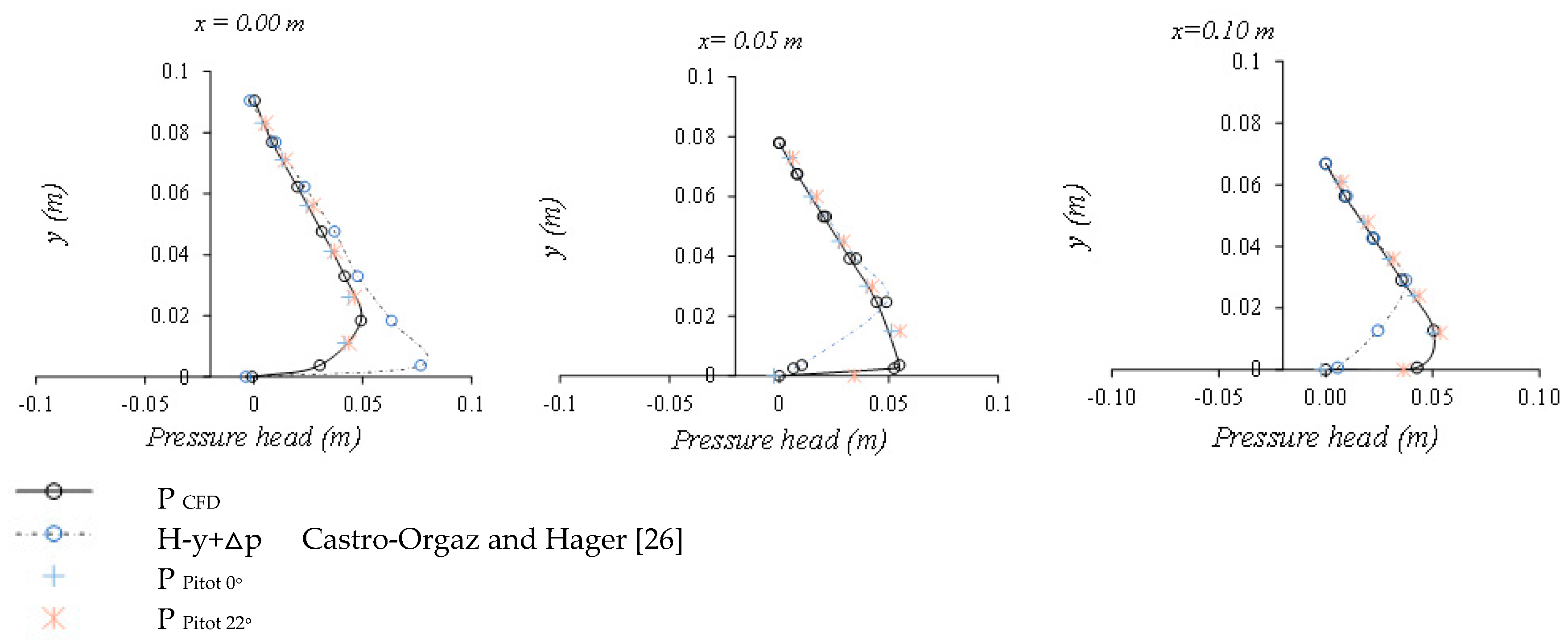
3.3. Velocity and Pressure Fields over the Rack
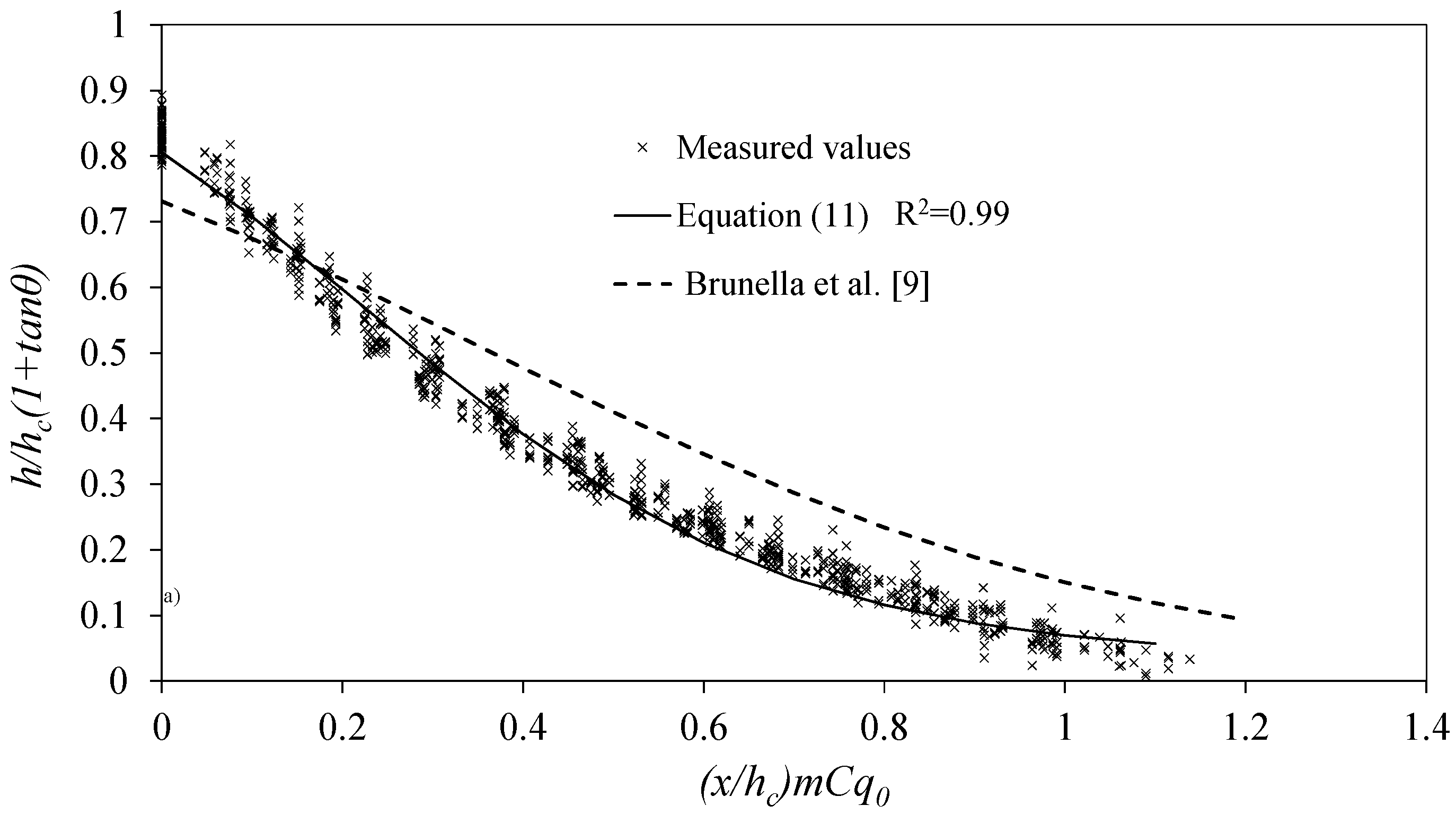
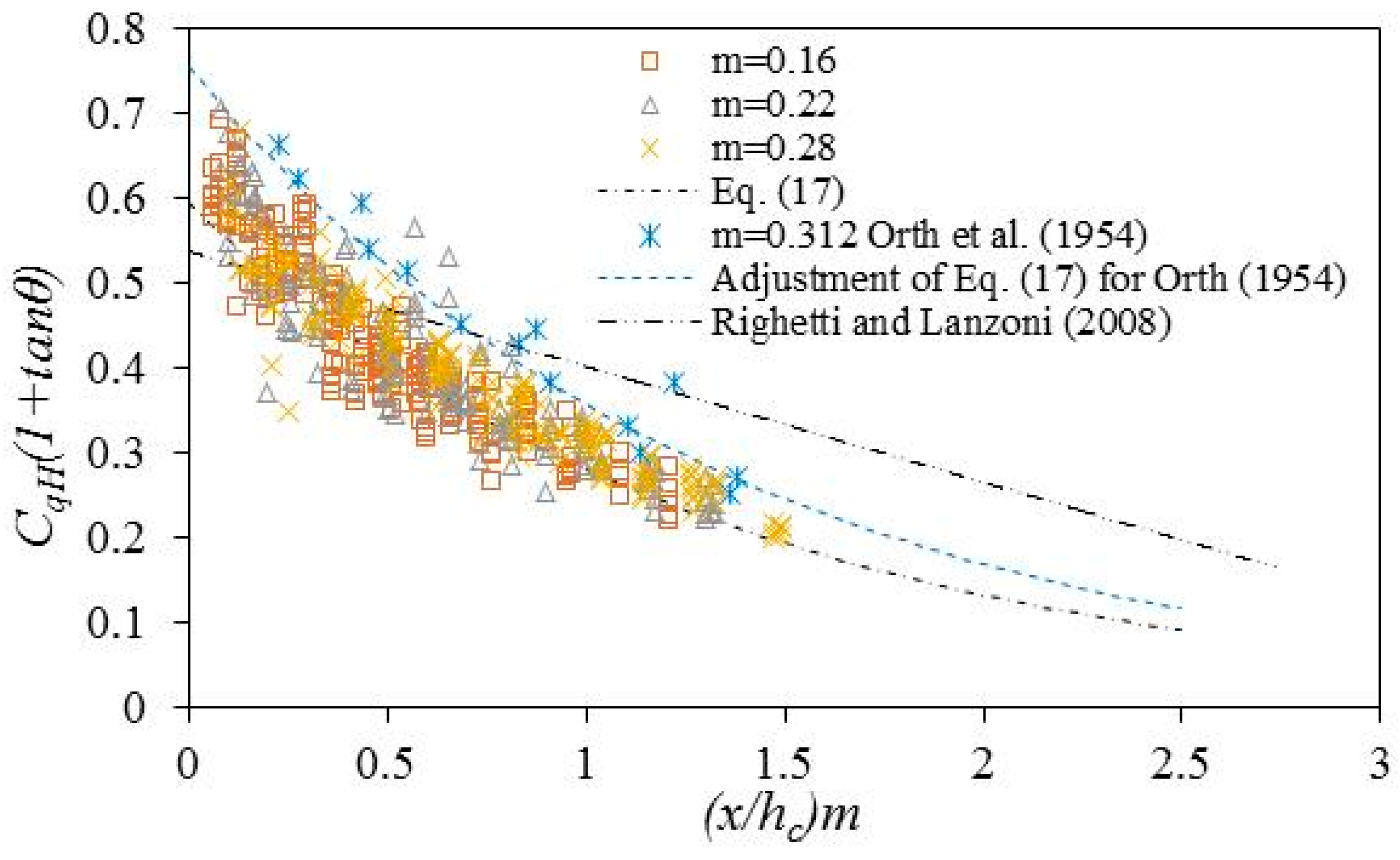
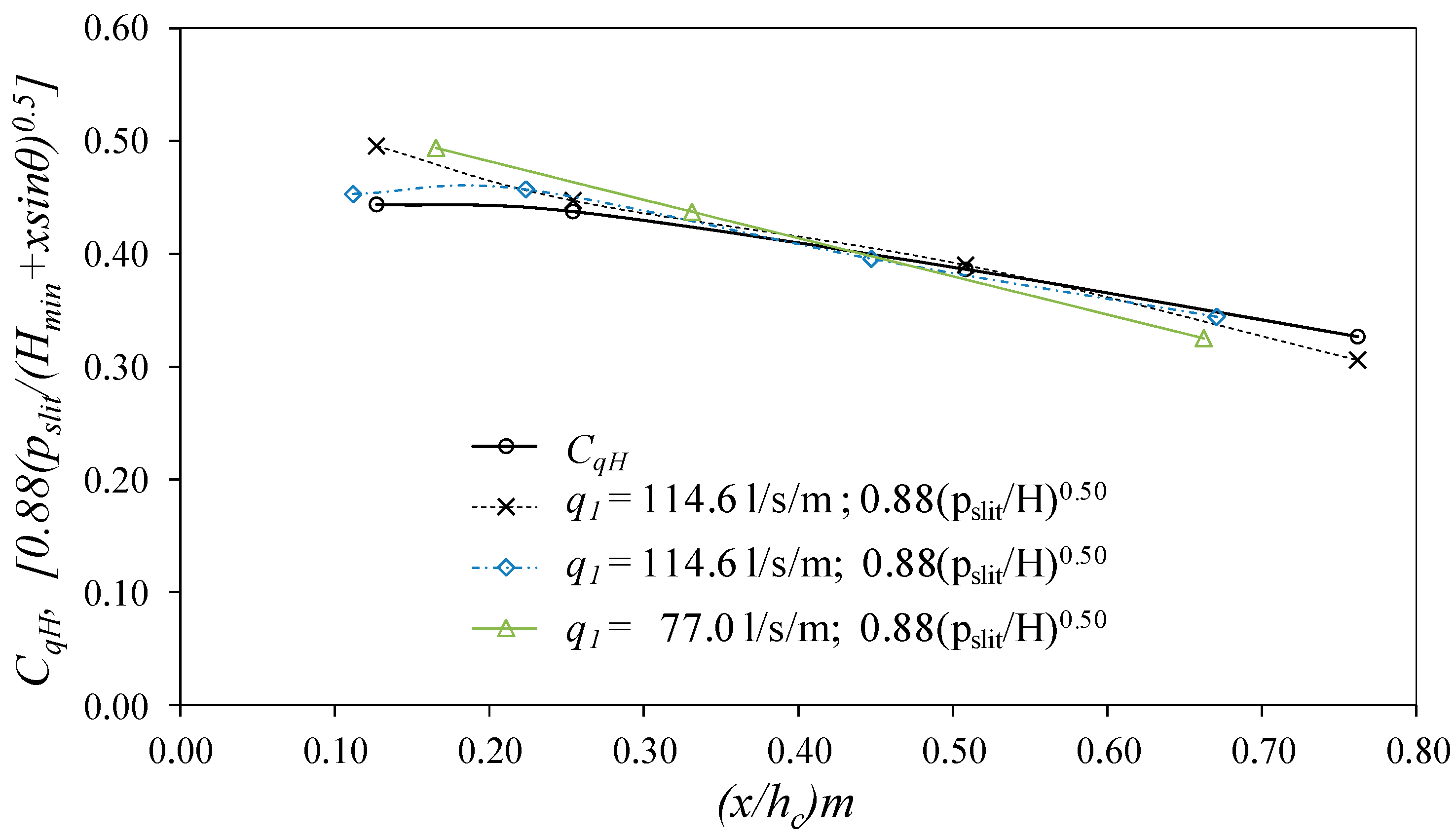
3.4. Discharge Coefficient
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| a | constant depending on the shape of bars in Equation (10); |
| b1 | space between bars; |
| bw | bar width; |
| Cc | contraction coefficient for effective flow area; |
| CqH | discharge coefficient for energy head; |
| Cqh | discharge coefficient for flow depth; |
| Cq0 | static discharge coefficient; |
| f | percentage of occluded rack in Equation of Krochin [3] included in Appendix A; |
| g | gravitational acceleration; |
| H | energy head along the rack referred to the rack plane; |
| H0 | energy head at the beginning of the rack referred to the rack plane; |
| hc | critical depth; |
| h1, h2 | flow depth at the beginning and end of the rack, respectively; |
| i | longitudinal slope, tanθ; |
| k1, k2 | constants of wetted rack length formulations of Krochin [3] and Vargas [15] respectively included in Appendix A; |
| L | wetted rack length; |
| L1, L2 | maximum wetted length over the bar and in the slit, respectively; |
| m | void ratio; |
| P | static pressure; |
| pt, β | total pressure measured in Pitot tube tip in the direction of the axis with inclination β with the horizontal; |
| pslit | static pressure in the slit between two bars; |
| q1 | specific approaching flow; |
| q2 | specific flow at the end of the rack; |
| U | mean velocity vector; |
| Ui | module of the velocity vector located in the position i; |
| Ux, Uy | component of the velocity vector in the longitudinal and perpendicular coordinate, respectively; |
| Uβ | component of velocity vector in the direction of the axe of inclination β; |
| x | longitudinal coordinate; |
| y | perpendicular coordinate; |
| α | velocity coefficient of the energy equation; |
| β | angle of inclination of the Pitot tube; |
| ρ | density; |
| θ | angle of the rack plane with the horizontal; and |
| λ | pressure coefficient of the energy equation |
Appendix A
| References | Experimental Setup | Wetted Rack Length, L (m) |
|---|---|---|
| Noseda [8] | q1max = 100 L/s; B = 0.50 m; 0.16 < m < 0.28; 0.57 < b1 < 1.17 cm; T-shaped bars; slopes: 0%–20% | ; ; |
| Bouvard and Kuntzmann [14] | Information from Noseda [8] | |
| Frank [13] | Information from Noseda [8] | ; ; |
| Krochin [3] | Information from Melik-Nubarov [24]; prismatic and flat bars. | ; ; ; |
| Drobir [4] | Information from Frank [13] and Bouvard and Kuntzmann [14] | ; ; |
| Drobir et al. [16] | q1max = 20 L/s; B = 0.50 m; m = 0.6; b1 = 1.50 cm; bw = 1 cm; Circular bars; Slope: 0%–20% | L TIWAG |
| Brunella et al. [9] | q1max = 100 L/s; B = 50 cm; circular bars Two setups: (a) b1 = 1.20 cm; bw = 0.6 cm; m = 0.352 (b) b1 = 0.6 cm; bw = 0.3 cm; m = 0.664; Slope: 0°–51° | ; |
| Righetti and Lanzoni [10,39] | q1max = 37.5 L/s; B = 25 cm; prismatic with rounded edge; m = 0.20; b1 = 0.50 cm; bw = 2.00 cm | ; ; ; |
| Vargas [15] | q1max = 40 L/s; B = 55.20 cm; circular bars slope: 0°–20°; Two setups: (a) m = 0.33; b1 = 0.50 cm; bw = 1 cm; (b) m = 0.5; b1 = 1 cm; bw = 1 cm | ; |
| Henderson [17] | - | Free overfall; |
References
- Orth, J.; Chardonnet, E.; Meynardi, G. Étude de grilles pour prises d’eau du type en dessous. Houille Blanche 1954, 9, 343–351. (In French) [Google Scholar] [CrossRef]
- Ract-Madoux, M.; Bouvard, M.; Molbert, J.; Zumstein, J. Quelques réalisations récentes de prises en-dessous à haute altitude en Savoie. Houille Blanche 1955, 10, 852–878. (In French) [Google Scholar] [CrossRef]
- Krochin, S. Diseño Hidráulico, 2nd ed.; Escuela Politécnica Nacional (EPN): Quito, Ecuador, 1978; pp. 97–106. (In Spanish) [Google Scholar]
- Drobir, H. Entwurf von Wasserfassungen im Hochgebirge. Österreichische Wasserwirtsch 1981, 11, 243–253. (In German) [Google Scholar]
- Bouvard, M. Mobile Barrages and Intakes on Sediment Transporting Rivers; A.A. Balkema: Rotterdam, The Netherlands, 1992. [Google Scholar]
- Raudkivi, A.J. Hydraulic Structures Design Manual; IAHR Monograph: Rotterdam, The Netherlands, 1993; pp. 92–105. [Google Scholar]
- Castillo, L.G.; García, J.T.; Carrillo, J.M. Experimental and Numerical Study of Bottom Rack Occlusion by Flow with Gravel-Sized Sediment. Application to Ephemeral Streams in Semi-Arid Regions. Water 2016, 8, 166. [Google Scholar] [CrossRef]
- Noseda, G. Correnti permanenti con portata progressivamente decrescente, defluenti su griglie di fondo. L’Energia Elettrica 1956, 33, 565–588. (In Italian) [Google Scholar]
- Brunella, S.; Hager, W.; Minor, H. Hydraulics of Bottom Rack Intake. J. Hydraul. Eng. 2003, 129, 2–10. [Google Scholar] [CrossRef]
- Righetti, M.; Lanzoni, S. Experimental Study of the Flow Field over Bottom Intake Racks. J. Hydraul. Eng. 2008, 134, 15–22. [Google Scholar] [CrossRef]
- Garot, F. De Watervang met liggend rooster. Ing. Ned. Indie 1939, 6, 115–132. (In German) [Google Scholar]
- White, J.K.; Charlton, J.A.; Ramsay, C.A.W. On the Design of Bottom Intakes for Diverting Stream Flows. In Proceedings of the Institution of Civil Engineers, London, UK, 18–21 April 1972; Volume 51, pp. 337–345.
- Frank, J. Fortschritte in der hydraulic des Sohlenrechens. Bauingenieur 1959, 34, 12–18. [Google Scholar]
- Bouvard, M.; Kuntzmann, J. Étude théorique des grilles de prises d’eau du type En dessous. Houille Blanche 1956, 5, 569–574. (In French) [Google Scholar]
- Vargas, V. Tomas de Fondo. In Proceedings of the XVIII Congreso Latinoamericano de Hidráulica, Oaxaca, Mexico, 13–16 October 1998. (In Spanish)
- Drobir, H.; Kienberger, V.; Krouzecky, N. The Wetted Rack Length of the Tyrolean Weir. In Proceedings of the IAHR-28th Congress, Graz, Austria, 22–27 August 1999.
- Henderson, F.M.N. Open Channel Flow; MacMillan: New York, NY, USA, 1966. [Google Scholar]
- Motskow, M. Sur le calcul des grilles de prise d’eau. Houille Blanche 1957, 4, 570–580. [Google Scholar]
- Venkataraman, P. Discharge Characteristics of an Idealised Bottom Intake. J. Inst. Civ. Eng. (India) 1977, 58, 99–104. [Google Scholar]
- Nasser, M.S.; Venkataraman, P.; Ramamurthy, A.S. Flow in a channel with a slot in the bed. J. Hydraul. Res. 1980, 18, 359–367. [Google Scholar] [CrossRef]
- Nasser, M.S.; Venkataraman, P.; Ramamurthy, A.S. Curvature corrections in open channel flow. Can. J. Civ. Eng. 1980, 7, 421–431. [Google Scholar] [CrossRef]
- Ramamurthy, A.; Satish, M. Discharge Characteristics of Flow Past a Floor Slot. J. Irrig. Drain. 1986, 112, 20–27. [Google Scholar] [CrossRef]
- Righetti, M.; Rigon, R.; Lanzoni, S. Indagine Sperimentale del Deflusso Attraverso una Griglia di Fondo a Barre Longitudinali. In Proceedings of the XXVII Convegno di Idraulica e Costruzioni Idrauliche, Genova, Italy, 12–15 September 2000; Volume 3, pp. 457–464. (In Italian)
- Melik-Nubarow, S.G. Type perfectionnè de prise d’eau à grille horizontale. Revue 1939, N10–N11. (In French). Available online: https://es.scribd.com/doc/283882848/Diseno-Hidraulico-KROCHIN-pdf (accessed on 20 January 2017). [Google Scholar]
- Nakagawa, H. On Hydraulic performance of bottom diversion Works. Bull. Disaster Prev. Res. Inst. 1969, 18, 29–48. [Google Scholar]
- Castro-Orgaz, O.; Hager, W.H. Spatially-varied open channel flow equations with vertical inertia. J. Hydraul. Res. 2011, 49, 667–675. [Google Scholar] [CrossRef]
- García, J.T. Estudio Experimental y Numérico de los Sistemas de Captación de Fondo. Ph.D. Thesis, Universidad Politécnica de Cartagena, Murcia, Spain, 2016. [Google Scholar]
- Adrian, R.J.; Westerweel, J. Particle Image Velocimetry; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Time-Resolved Digital Particle Image Velocimetry Tool for MATLAB (version: 1.4). J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS CFX. Solver Theory Guide. Release 16.2; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. ASME J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B. Sensitivity of turbulent Schmidt number and turbulence model to simulations of jets in crossflow. Environ. Model. Softw. 2016, 82, 218–228. [Google Scholar] [CrossRef]
- Castillo, L.; Carrillo, J.M. Numerical simulation and validation of intake systems with CFD methodology. In Proceedings of the 2nd IAHR European Congress, Munich, Germany, 27–29 June 2012.
- Castillo, L.G.; Carrillo, J.M.; Sordo-Ward, A. Simulation of overflow nappe impingement jets. J. Hydroinf. 2014, 16, 922–940. [Google Scholar] [CrossRef]
- Castillo, L.G.; García, J.T.; Carrillo, J.M. Experimental Measurements of Flow and Sediment Transport through Bottom Racks-Influence of Gravels Sizes on the Rack. In Proceedings of the River Flow, Lausanne, Switzerland, 3–5 September 2014; pp. 2165–2172.
- Castillo, L.G.; Carrillo, J.M.; Bombardelli, F.A. Distribution of mean flow and turbulence statistics in plunge pools. J. Hydroinf. 2016. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Khatchatrian, R. Analyse de Prise d’eau de Montagne à Grille du Type en Dessous. Thèse, Erévan, 1955. (In French)Available online: http://www.shf-lhb.org/articles/lhb/pdf/1957/06/lhb1957048.pdf (accessed on 20 January 2017).
- Righetti, M.; Lanzoni, S. Closure to “Experimental Study of the Flow Field over Bottom Intake Racks” by Maurizio Righetti and Stefano Lanzoni. J. Hydraul. Eng. 2009, 135, 865–868. [Google Scholar] [CrossRef]




| Author | Flow | Flume Width | Shape | Setting | Slope |
|---|---|---|---|---|---|
| Noseda [8] | q1max = 100 L/s | B = 0.50 m | T-shaped | 0.16 < m < 0.28 0.57 < b1 < 1.17 cm | 0%–20% |
| Brunella et al. [9] | q1max = 100 L/s | B = 0.50 m | Circular | Two setups: (a) b1 = 0.60 or 0.30 cm; bw = 1.20 or 0.60 cm; m = 0.352 (b) b1 = 1.80 or 0.90 cm; bw = 1.20 or 0.60 cm; m = 0.664 | 0%–123% |
| Righetti and Lanzoni [10] | q1max = 37.5 L/s | B = 0.25 m | Prismatic with rounded edge | m = 0.20; b1 = 0.50 cm; bw = 2.00 cm | <3.5% |
| tanθ (-) | q1 (L/s/m) | Rack A (m = 0.16) (b1 = 0.0057 m; bw = 0.03 m) | Rack B (m = 0.22) (b1 = 0.0085 m; bw = 0.03 m) | Rack C (m = 0.28) (b1 = 0.0117 m; bw = 0.03 m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h1 (m) | H0 (m) | Fr1 (-) | q2/q1 (%) | h1 (m) | H0 (m) | Fr1 (-) | q2/q1 (%) | h1 (m) | H0 (m) | Fr1 (-) | q2/q1 (%) | ||
| 0 | 53.8 | 0.053 | 0.106 | 1.42 | 1.9 | 0.055 | 0.104 | 1.32 | 1.9 | 0.055 | 0.104 | 1.34 | 1.9 |
| 77.0 | 0.069 | 0.132 | 1.36 | 2.6 | 0.070 | 0.132 | 1.33 | 1.3 | 0.069 | 0.132 | 1.35 | 1.3 | |
| 114.6 | 0.090 | 0.163 | 1.36 | 4.4 | 0.091 | 0.162 | 1.33 | 1.7 | 0.089 | 0.164 | 1.38 | 0.9 | |
| 155.4 | 0.114 | 0.208 | 1.28 | 20.6 | 0.110 | 0.212 | 1.36 | 3.2 | 0.109 | 0.212 | 1.37 | 2.6 | |
| 0.10 | 53.8 | 0.049 | 0.111 | 1.59 | 1.9 | 0.048 | 0.112 | 1.64 | 1.9 | 0.048 | 0.112 | 1.63 | 1.9 |
| 77.0 | 0.062 | 0.141 | 1.61 | 3.9 | 0.063 | 0.140 | 1.57 | 1.3 | 0.061 | 0.142 | 1.62 | 1.3 | |
| 114.6 | 0.083 | 0.181 | 1.54 | 5.2 | 0.082 | 0.182 | 1.57 | 1.7 | 0.080 | 0.185 | 1.63 | 1.7 | |
| 155.4 | 0.102 | 0.221 | 1.53 | 21.2 | 0.100 | 0.224 | 1.58 | 3.9 | 0.100 | 0.223 | 1.56 | 3.2 | |
| 0.20 | 53.8 | 0.044 | 0.121 | 1.89 | 3.7 | 0.044 | 0.120 | 1.85 | 1.9 | 0.044 | 0.120 | 1.85 | 1.9 |
| 77.0 | 0.057 | 0.150 | 1.80 | 3.9 | 0.058 | 0.148 | 1.77 | 1.3 | 0.057 | 0.149 | 1.79 | 2.6 | |
| 114.6 | 0.076 | 0.191 | 1.73 | 6.1 | 0.077 | 0.191 | 1.73 | 2.6 | 0.076 | 0.191 | 1.73 | 2.6 | |
| 155.4 | 0.096 | 0.230 | 1.68 | 21.9 | 0.096 | 0.230 | 1.68 | 4.5 | 0.095 | 0.232 | 1.70 | 4.5 | |
| 0.30 | 53.8 | 0.042 | 0.126 | 2.00 | 3.7 | 0.041 | 0.127 | 2.04 | 1.9 | 0.042 | 0.126 | 2.00 | 3.7 |
| 77.0 | 0.054 | 0.157 | 1.94 | 5.2 | 0.054 | 0.157 | 1.95 | 2.6 | 0.054 | 0.157 | 1.95 | 3.9 | |
| 114.6 | 0.073 | 0.197 | 1.86 | 7.0 | 0.072 | 0.198 | 1.91 | 3.5 | 0.072 | 0.199 | 1.90 | 2.6 | |
| 155.4 | 0.090 | 0.242 | 1.84 | 23.2 | 0.090 | 0.242 | 1.84 | 4.5 | 0.090 | 0.241 | 1.83 | 4.5 | |
| 0.33 | 53.8 | 0.042 | 0.127 | 2.02 | 3.7 | 0.041 | 0.129 | 2.07 | 3.7 | 0.041 | 0.129 | 2.08 | 3.7 |
| 77.0 | 0.054 | 0.159 | 1.99 | 6.5 | 0.054 | 0.158 | 1.97 | 2.6 | 0.053 | 0.160 | 2.00 | 3.9 | |
| 114.6 | 0.073 | 0.199 | 1.87 | 7.0 | 0.072 | 0.201 | 1.90 | 4.4 | 0.071 | 0.203 | 1.92 | 2.6 | |
| 155.4 | 0.088 | 0.248 | 1.91 | 25.1 | 0.089 | 0.244 | 1.86 | 5.1 | 0.091 | 0.241 | 1.82 | 5.1 | |
| tanθ (-) | q1 (L/s/m) | Rack A (m = 0.16) | Rack B (m = 0.22) | Rack C (m = 0.28) |
|---|---|---|---|---|
| h/hc (x = −0.50 m) | ||||
| 0 | 53.8 | 1.091 | 1.169 | 1.121 |
| 77.0 | 1.095 | 1.134 | 1.093 | |
| 114.6 | 1.072 | 1.106 | 1.087 | |
| 155.4 | 1.065 | 1.065 | 1.062 | |
| 0.10 | 53.8 | 1.130 | 1.142 | 1.122 |
| 77.0 | 1.099 | 1.105 | 1.098 | |
| 114.6 | 1.076 | 1.089 | 1.080 | |
| 155.4 | 1.041 | 1.041 | 1.044 | |
| 0.20 | 53.8 | 1.100 | 1.119 | 1.082 |
| 77.0 | 1.087 | 1.081 | 1.088 | |
| 114.6 | 1.072 | 1.048 | 1.059 | |
| 155.4 | 1.024 | 1.015 | 1.031 | |
| 0.30 | 53.8 | 1.100 | 1.119 | 1.082 |
| 77.0 | 1.087 | 1.081 | 1.088 | |
| 114.6 | 1.072 | 1.048 | 1.059 | |
| 155.4 | 1.024 | 1.015 | 1.031 | |
| 0.33 | 53.8 | 1.119 | 1.103 | 1.112 |
| 77.0 | 1.087 | 1.076 | 1.081 | |
| 114.6 | 1.062 | 1.056 | 1.049 | |
| 155.4 | 1.015 | 1.002 | 1.035 | |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo, L.G.; García, J.T.; Carrillo, J.M. Influence of Rack Slope and Approaching Conditions in Bottom Intake Systems. Water 2017, 9, 65. https://doi.org/10.3390/w9010065
Castillo LG, García JT, Carrillo JM. Influence of Rack Slope and Approaching Conditions in Bottom Intake Systems. Water. 2017; 9(1):65. https://doi.org/10.3390/w9010065
Chicago/Turabian StyleCastillo, Luis G., Juan T. García, and José M. Carrillo. 2017. "Influence of Rack Slope and Approaching Conditions in Bottom Intake Systems" Water 9, no. 1: 65. https://doi.org/10.3390/w9010065
APA StyleCastillo, L. G., García, J. T., & Carrillo, J. M. (2017). Influence of Rack Slope and Approaching Conditions in Bottom Intake Systems. Water, 9(1), 65. https://doi.org/10.3390/w9010065








