Measuring Spatiotemporal Features of Land Subsidence, Groundwater Drawdown, and Compressible Layer Thickness in Beijing Plain, China
Abstract
:1. Introduction
2. Materials and Methods
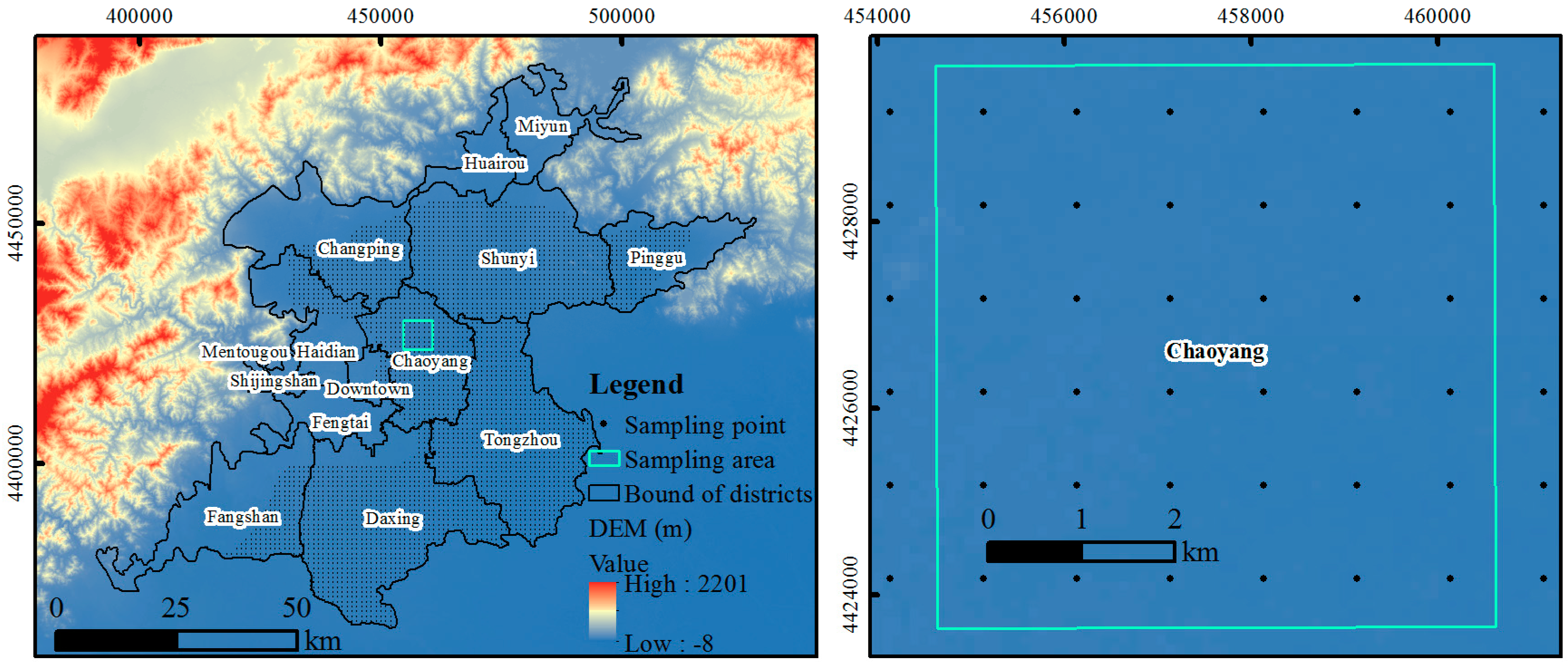
2.1. Study Area
2.2. Available Datasets
2.3. Gravity Center Analysis
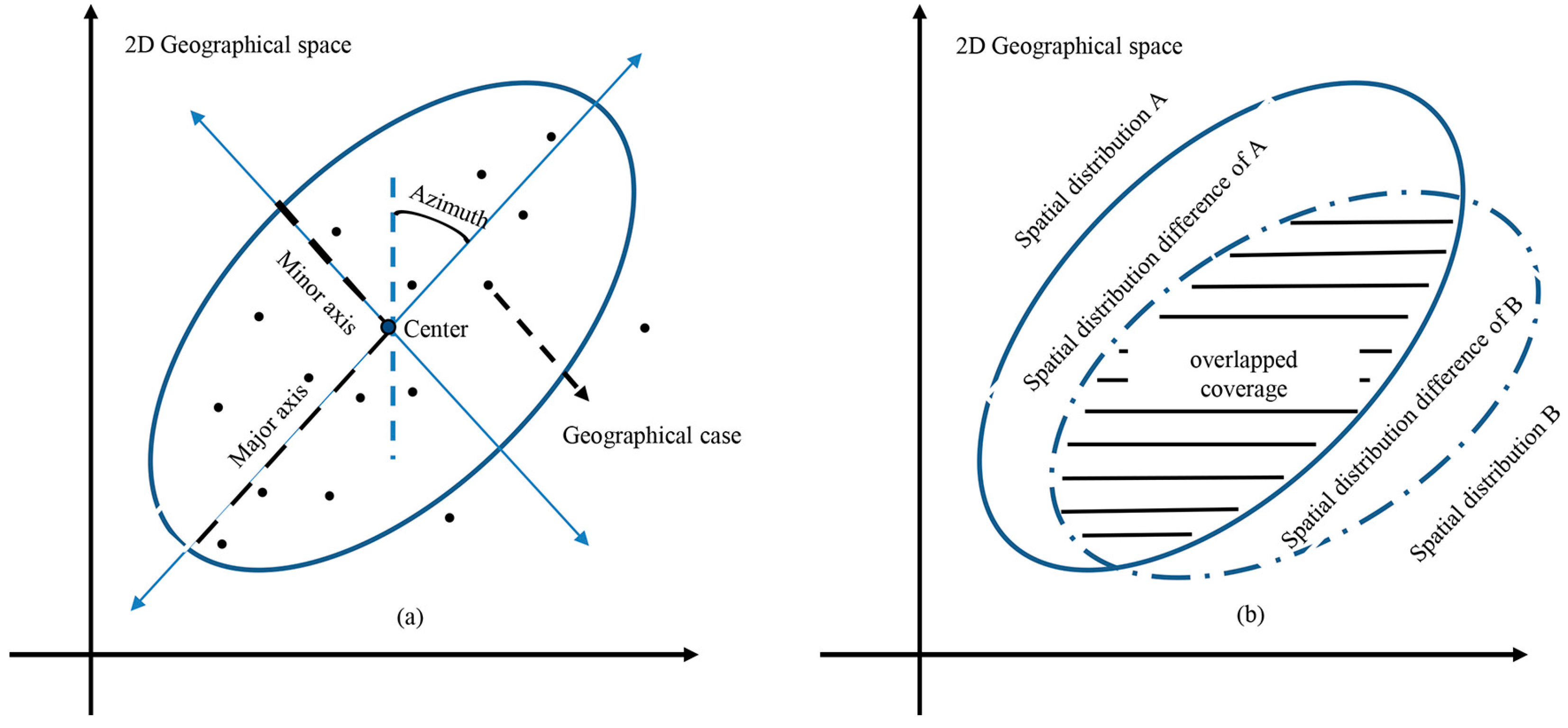
2.4. Standard Deviational Ellipse Analysis
3. Results
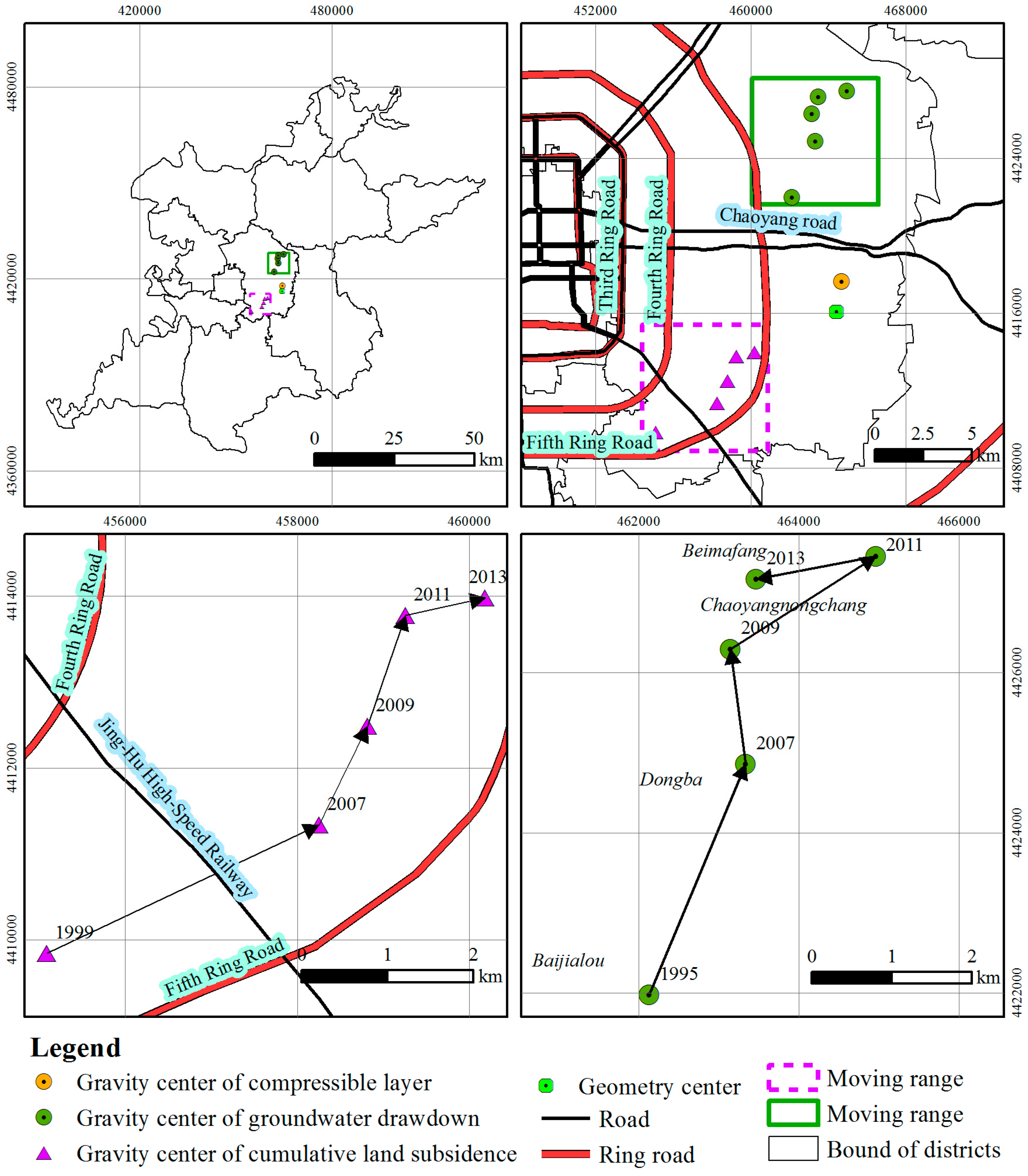
3.1. Gravity Center Evolution Analysis
3.1.1. Gravity Center of Land Subsidence
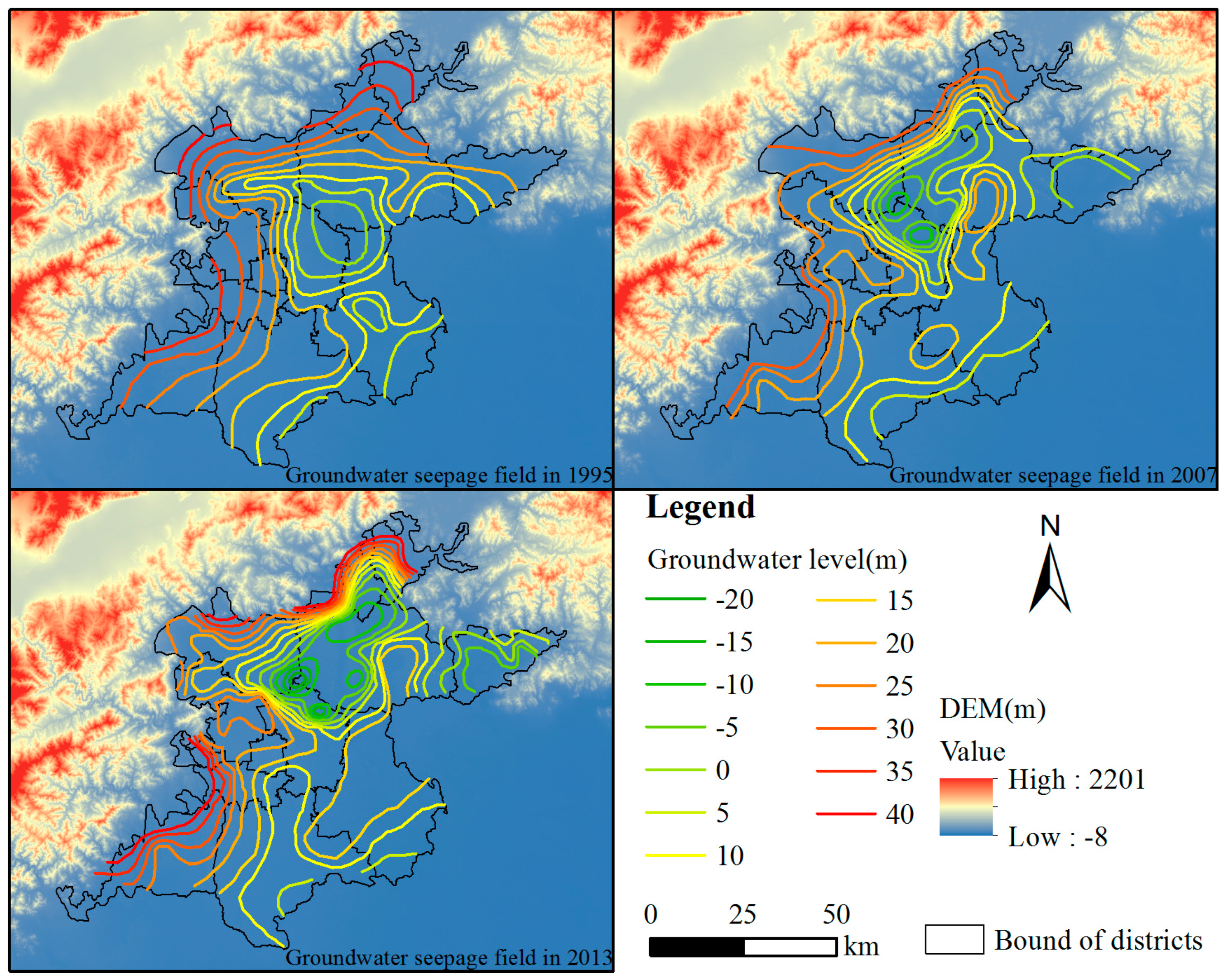
3.1.2. Gravity Center of Groundwater Drawdown and Compressible Layer Thickness
3.1.3. Coupling Analysis of the Gravity Center
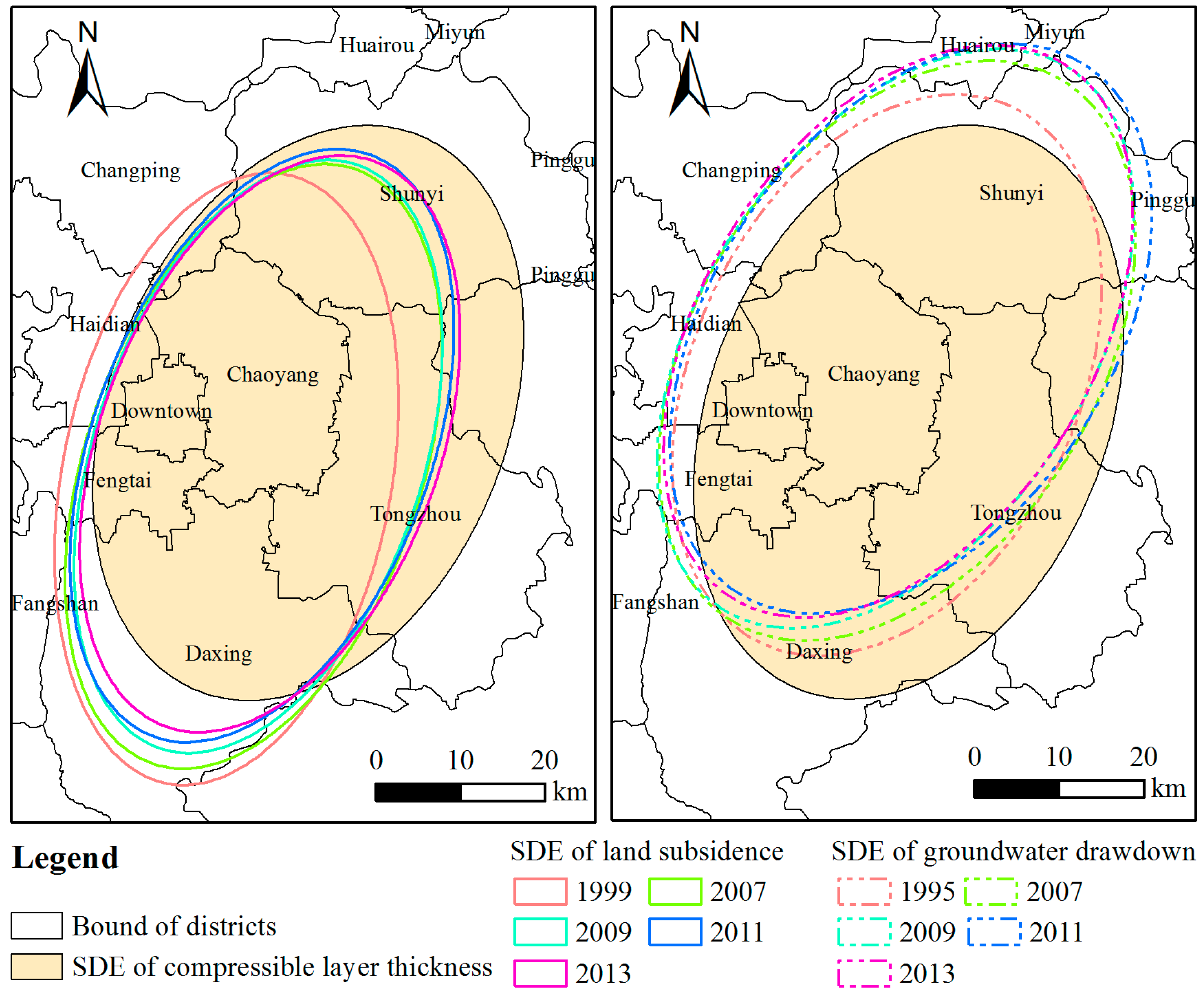
3.2. Development Orientation Comparison Analysis
3.3. Dispersion Tendency Comparison Analysis
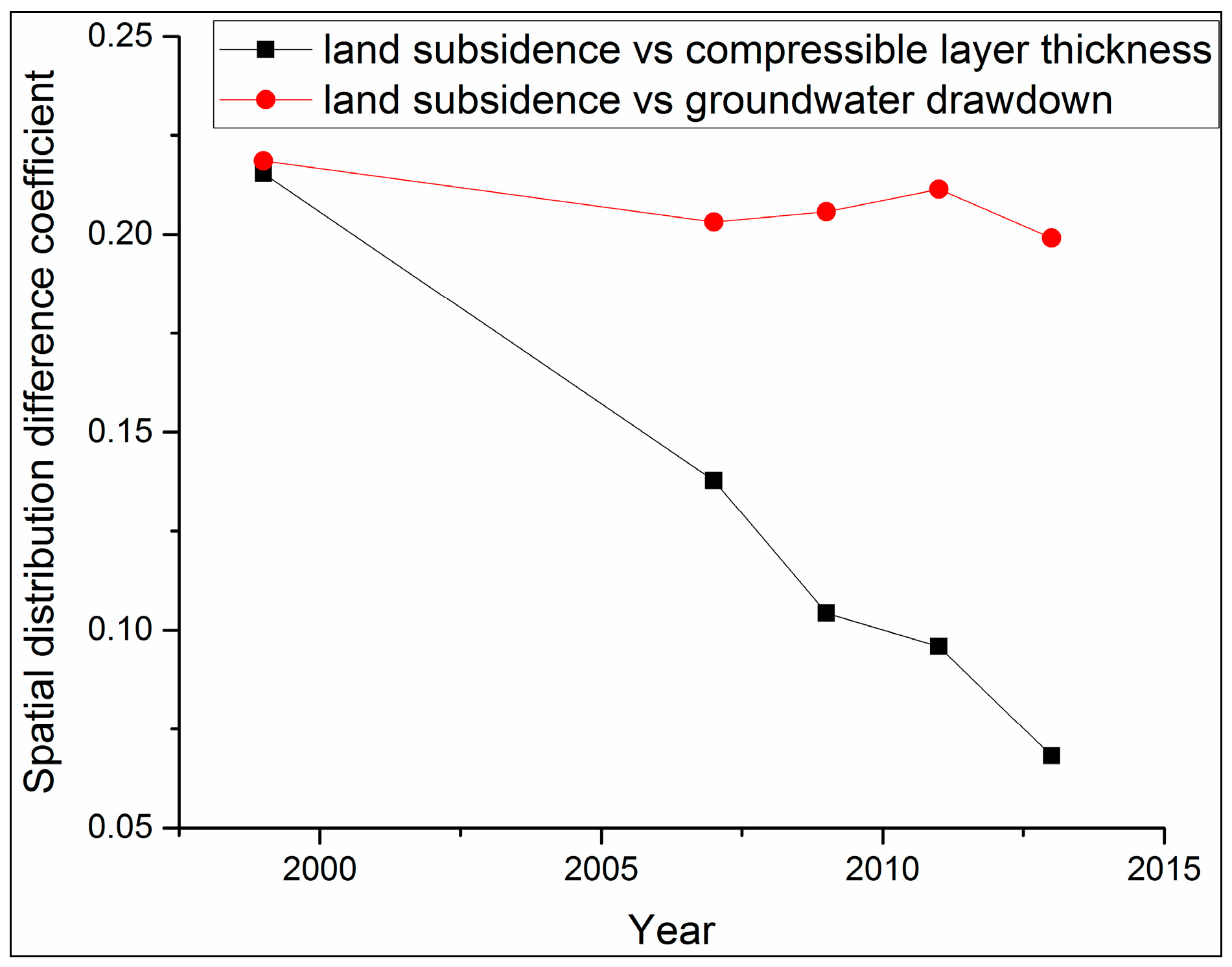
3.4. Spatial Differentiation Coefficient Comparison Analysis
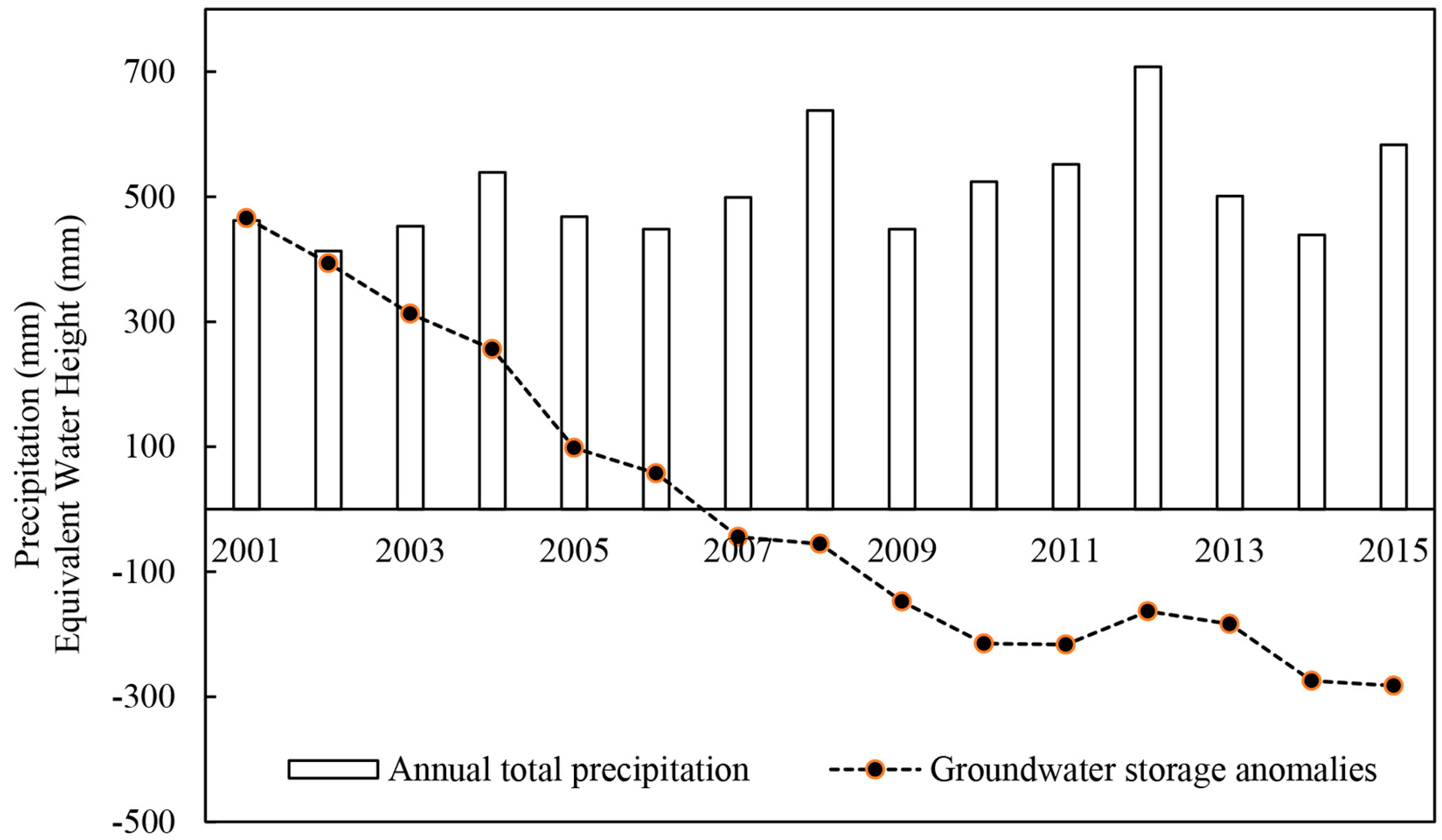
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Galloway, D.L.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Gambolati, G.; Teatini, P. Geomechanics of subsurface water withdrawal and injection. Water Resour. Res. 2015, 51, 3922–3955. [Google Scholar] [CrossRef]
- Calderhead, A.I.; Therrien, R.; Rivera, A.; Martel, R.; Garfias, J. Simulating pumping-induced regional land subsidence with the use of InSAR and field data in the Toluca valley, Mexico. Adv. Water Resour. 2011, 34, 83–97. [Google Scholar] [CrossRef]
- Shi, X.Q.; Fang, R.; Wu, J.C.; Xu, H.X.; Sun, Y.Y.; Yu, J. Sustainable development and utilization of groundwater resources considering land subsidence in Suzhou, China. Eng. Geol. 2012, 124, 77–89. [Google Scholar] [CrossRef]
- Modoni, G.; Darini, G.; Spacagna, R.L.; Saroli, M.; Russo, G.; Croce, P. Spatial analysis of land subsidence induced by groundwater withdrawal. Eng. Geol. 2013, 167, 59–71. [Google Scholar] [CrossRef]
- Raspini, F.; Loupasakis, C.; Rozos, D.; Adam, N.; Moretti, S. Ground subsidence phenomena in the delta municipality region (northern Greece): Geotechnical modeling and validation with persistent scatterer interferometry. Int. J. Appl. Earth Obs. 2014, 28, 78–89. [Google Scholar] [CrossRef]
- Brown, S.; Nicholls, R.J. Subsidence and human influences in mega deltas: The case of the Ganges-Grahmaputra-Meghna. Sci. Total Environ. 2015, 527–528, 362–374. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudpour, M.; Khamhechiyan, M.; Nikudel, M.R.; Ghassemi, M.R. Numerical simulation and prediction of regional land subsidence caused by groundwater exploitation in the southwest plain of Tehran, Iran. Eng. Geol. 2015, 201, 6–28. [Google Scholar] [CrossRef]
- Castellazzi, P.; Arroyo-Domínguez, N.; Martel, R.; Calderhead, A.I.; Normand, J.C.L.; Gárfias, J. Land subsidence in major cities of central Mexico: Interpreting InSAR-derived land subsidence mapping with hydrogeological data. Int. J. Appl. Earth Obs. 2016, 47, 102–111. [Google Scholar] [CrossRef]
- Chen, M.; Tomás, R.; Li, Z.H.; Motagh, M.; Li, T.; Hu, L.Y.; Gong, H.L.; Li, X.J.; Yu, J.; Gong, X.L. Imaging land subsidence induced by groundwater extraction in Beijing (China) using satellite radar interferometry. Remote Sens.-Basel 2016, 8, 468. [Google Scholar] [CrossRef]
- Zou, L.; Kent, J.; Lam, N.; Cai, H.; Qiang, Y.; Li, K.N. Evaluating Land Subsidence Rates and Their Implications for Land Loss in the Lower Mississippi River Basin. Water 2016, 8, 10. [Google Scholar] [CrossRef]
- Syvitski, J.; Kettner, A.; Overeem, I.; Hutton, E.; Hannon, M.; Brakenridge, G.; Day, J.; Vörösmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A. Groundwater extraction, land subsidence, and sea-level rise in the Mekong delta, Vietnam. Environ. Res. Lett. 2014, 9, 1–6. [Google Scholar] [CrossRef]
- Sušnik, J.; Vamvakeridou-Lyroudia, L.S.; Baumert, N.; Kloos, J.; Renaud, F.G.; La Jeunesse, I. Interdisciplinary assessment of sea-level rise and climate change impacts on the lower Nile delta, Egypt. Sci. Total Environ. 2015, 503–504, 279–288. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Yu, D.P.; Wilby, R. Modelling the impact of land subsidence on urban pluvial flooding: A case study of downtown Shanghai, China. Sci. Total Environ. 2016, 544, 744–753. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, J.; Zebker, H.A.; Galloway, D.L.; Amelung, F. Seasonal subsidence and rebound in Las Vegas valley, Nevada, observed by synthetic aperture radar interferometry. Water Resour. Res. 2001, 37, 1551–1566. [Google Scholar] [CrossRef]
- Bell, J.W.; Amelung, F.; Ramelli, A.R.; Blewitt, G. Land subsidence in Las Vegas, Nevada, 1935–2000: New geodetic data show evolution, revised spatial patterns, and reduced rates. Environ. Eng. Geosci. 2002, 8, 155–174. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Wegmüller, U.; Rizzetto, F. Mapping regional land displacements in the Venice coastland by an integrated monitoring system. Remote Sens. Environ. 2005, 98, 403–413. [Google Scholar] [CrossRef]
- Teatini, P.; Ferronato, M.; Gambolati, G.; Gonella, G. Groundwater pumping and land subsidence in the Emilia-Romagna coastland, Italy: Modeling the past occurrence and the future trend. Water Resour. Res. 2006, 42, W01406. [Google Scholar] [CrossRef]
- Anderssohn, J.; Wetzel, H.U.; Walter, T.R.; Motagh, M.; Djamour, Y.; Kaufmann, H. Land subsidence pattern controlled by old alpine basement faults in the Kashmar valley, northeast Iran: Results from InSAR and levelling. Geophys. J. Int. 2008, 174, 287–294. [Google Scholar] [CrossRef]
- Jia, S.M.; Wang, H.G.; Zhao, S.S.; Luo, Y. A tentative study of the mechanism of land subsidence in Beijing. City Geol. 2007, 2, 20–26. (In Chinese) [Google Scholar]
- Zhang, Y.Q.; Gong, H.L.; Gu, Z.Q.; Wang, R.; Li, X.J.; Zhao, W.J. Characterization of land subsidence induced by groundwater withdrawals in the plain of Beijing city, China. Hydrogeol. J. 2014, 22, 397–409. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.L.; Li, X.J.; Wang, R.; Chen, B.B.; Dai, Z.X.; Teatini, P. Land subsidence due to groundwater withdrawal in the northern Beijing plain, China. Eng. Geol. 2015, 193, 243–255. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hudnut, K.W.; Ingebritsen, S.E.; Phillips, S.P.; Peltzer, G.; Rogez, F.; Rosen, P.A. Detection of aquifer system compaction and land subsidence using interferometric synthetic aperture radar, Antelope Valley, Mojave Desert, California Water. Resour. Res. 1998, 34, 2573–2585. [Google Scholar] [CrossRef]
- Mitchell, A. The ESRI Guide to GIS Analysis Volume 2: Spatial Measurements & Statistics; ESRI Press: Redlands, CA, USA, 2005; pp. 21–61. [Google Scholar]
- Li, X.B. Visulizing spatial equality of development. Sci. Geogr. Sin. 1999, 19, 254–257. (In Chinese) [Google Scholar]
- Xu, J.H.; Yue, W.Z. Evolvement and comparative analysis of the population center gravity and the economy gravity center in recent twenty years in china. Sci. Geogr. Sin. 2001, 21, 385–389. (In Chinese) [Google Scholar]
- Lefever, D.W. Measuring geographic concentration by means of the standard deviational ellipse. Am. J. Soc. 1926, 32, 88–94. [Google Scholar] [CrossRef]
- Furfey, P.H. A note on Lefever’s “standard deviational ellipse”. Am. J. Soc. 1927, 33, 94–98. [Google Scholar] [CrossRef]
- Warntz, W.; Neft, D. Contributions to a statistical methodology for areal distributions. Reg. Sci. 2006, 2, 47–66. [Google Scholar] [CrossRef]
- Robert, S. The standard deviational ellipse; an updated tool for spatial description. Geogr. Ann. 1971, 53, 28–39. [Google Scholar]
- Wang, B.; Shi, W.Z.; Miao, Z.L. Confidence analysis of standard deviational ellipse and its extension into higher dimensional Euclidean space. PLoS ONE 2015, 10, e0118537. [Google Scholar] [CrossRef] [PubMed]
- Bashshur, R.L.; Metzner, C.A. The application of three-dimensional analogue models to the distribution of medical care facilities. Med. Care 1970, 8, 395–407. [Google Scholar] [CrossRef] [PubMed]
- Vanhulsel, M.; Beckx, C.; Janssens, D.; Vanhoof, K.; Wets, G. Measuring dissimilarity of geographically dispersed space-time paths. Transportation 2011, 38, 65–79. [Google Scholar] [CrossRef]
- Yue, T.X.; Fan, Z.M.; Liu, J.Y. Changes of major terrestrial ecosystems in China since 1960. Glob. Planet. Chang. 2005, 48, 287–302. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.P.; Liu, Q.F.; Yu, Y. Dynamic change of wetland landscape patterns in Songnen plain. Wetl. Sci. 2008, 6, 167–172. (In Chinese) [Google Scholar]
- Wang, B.J.; Shi, B.; Inyang, H.I. GIS-based quantitative analysis of orientation anisotropy of contaminant barrier particles using standard deviational ellipse. Soil Sediment Contam. 2008, 17, 437–447. [Google Scholar]
- Mamuse, A.; Porwal, A.; Kreuzer, O.; Beresford, S. A new method for spatial centrographic analysis of mineral deposit clusters. Ore Geo. Rev. 2009, 36, 293–305. [Google Scholar] [CrossRef]
- Eryando, T.; Susanna, D.; Pratiwi, D.; Nugraha, F. Standard Deviational Ellipse (SDE) models for malaria surveillance, case study: Sukabumi district-Indonesia, in 2012. Malar. J. 2012, 11. [Google Scholar] [CrossRef]
- O’Loughlin, J.; Witmer, F.D.W. The localized geographies of violence in the north Caucasus of Russia, 1999–2007. Ann. Assoc. Am. Geogr. 2011, 101, 178–201. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, Z.Q. Projecting the spatial variation of economic based on the specific ellipses in China. Sci. Geogr. Sin. 2014, 34, 979–986. (In Chinese) [Google Scholar]
- Peng, J.; Chen, S.; Lü, H.L.; Liu, Y.X.; Wu, J.S. Spatiotemporal patterns of remotely sensed PM 2.5, concentration in China from 1999 to 2011. Remote Sens. Environ. 2016, 174, 109–121. [Google Scholar] [CrossRef]
- Jia, S.M.; Ye, C.; Liu, J.R.; Zhao, S.S.; Wang, R.; Yang, Y.; Wang, H.G.; Dong, D.W. Investigation of Land Subsidence in Beijing; Beijing Institute of Hydrogeology and Engineering Geology: Beijing, China, 2006; p. 5. (In Chinese) [Google Scholar]
- Liu, Y.; Ye, C.; Jia, S.M. Division of water-bearing zones and compressible layers in Beijing’s land subsidence areas. City Geol. 2007, 2, 10–15. (In Chinese) [Google Scholar] [CrossRef]
- Beijing Water Authority, Government Affairs, Statistical Information. Available online: http://www.bjwater.gov.cn/pub/bjwater/zfgk/tjxx/ (accessed on 5 May 2016).
- Griffith, D. Theory of Spatial Statistics. In Spatial Statistics and Models; Gaile, G.L., Willmott, C.J., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984; pp. 3–15. [Google Scholar]
- Krugman, P. First nature, second nature, and metropolitan location. Reg. Sci. 1993, 33, 129–144. [Google Scholar] [CrossRef]
- Chen, F.; Lin, H.; Yeung, K.; Cheng, S.L. Detection of Slope Instability in Hong Kong Based on Multi-baseline Differential SAR Interferometry Using ALOS PALSAR Data. GISci. Remote Sens. 2010, 47, 208–220. [Google Scholar] [CrossRef]
- Ng, H.M.; Ge, L.L.; Li, X.J.; Abidin, H.Z.; Andreas, H.; Zhang, K. Mapping land subsidence in Jakarta, Indonesia using persistent scatterer interferometry (PSI) technique with Alos Palsar. Int. J. Appl. Earth Obs. 2012, 18, 232–242. [Google Scholar] [CrossRef]
- Strozzi, T.; Teatini, P.; Tosi, L.; Wegmüller, U.; Werner, C. Land subsidence of natural transitional environments by satellite radar interferometry on artificial reflectors. Geophys. Res. Earth Surf. 2013, 118, 1177–1191. [Google Scholar] [CrossRef]
- Samsonov, S.V.; D’Oreye, N.; González, P.J.; Tiampo, K.F.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the greater Vancouver region from two decades of ERS-ENVISAT-RADARSAT-2 DInSAR measurements. Remote Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef]
- Dehghan-Soraki, Y.; Sharifikia, M.; Sahebi, M.R. A comprehensive interferometric process for monitoring land deformation using ASAR and PALSAR satellite interferometric data. GISci. Remote Sens. 2015, 52, 58–77. [Google Scholar] [CrossRef]
- Yeh, P.J.-F.; Swenson, S.C.; Famiglietti, J.S.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42, W12203. [Google Scholar] [CrossRef]
- Wang, X.W.; de Linage, C.; Famiglietti, J.; Zender, C.S. Gravity Recovery and Climate Experiment (GRACE) detection of water storage changes in the Three Gorges Reservoir of China and comparison with in situ measurements. Water Resour. Res. 2011, 47, W12502. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Pan, Y.; Gong, H.L.; Yeh, P.J.-F.; Li, X.J.; Zhou, D.M.; Zhao, W.J. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, C.; Gong, H.L.; Yeh, P.J.-F.; Shen, Y.J.; Guo, Y.; Huang, Z.Y.; Li, X.J. Detection of human-induced evapotranspiration using GRACE satellite observations in the Haihe River basin of China. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef]


| Subsidence Funnel Zone | 1999 | 2005 | 2007 | 2009 | 2011 | 2013 | |
|---|---|---|---|---|---|---|---|
| A | Balizhuang-Dajiaoting in Chaoyang | 700 | 750 | 750 | 800 | 1050 | 1300 |
| B | Laiguangying in Chaoyang | 500 | 650 | 800 | 950 | 1000 | 1400 |
| C | Shahe-Baxianzhaung in Changpiing | 650 | 1050 | 1100 | 1150 | 1200 | 1400 |
| D | Lixian-Yufa in Daxing | 650 | 800 | 850 | 950 | 1050 | 1200 |
| E | Pinggezhuang in Shunyi | 250 | 400 | ||||
| F | Yang town in Shunyi | 150 | 200 | 250 | 300 | 400 |
| Parameter | Equation | |
|---|---|---|
| Azimuth angle | ||
| Standard deviation | ||
| Year | x | y | Distance (m) | Direction | Rate (m/Year) | Relative Distance (m) | Relative Direction | |
|---|---|---|---|---|---|---|---|---|
| Cumulative land subsidence | 1999 | 455,082.73 | 4,409,843.56 | 11,221.13 | South by West 33.70° | |||
| 2007 | 458,249.82 | 4,411,339.05 | 3502.42 | North by East 64.72° | 437.80 | 7773.48 | South by West 37.49° | |
| 2009 | 458,814.36 | 4,412,488.92 | 1280.98 | North by East 26.15° | 640.49 | 6650.08 | South by West 32.58° | |
| 2011 | 459,259.27 | 4,413,771.85 | 1357.88 | North by East 19.13° | 678.94 | 5647.37 | South by West 24.01° | |
| 2013 | 460,186.49 | 4,413,978.36 | 949.93 | North by East 77.44° | 474.97 | 4720.14 | South by West 26.30° | |
| Groundwater drawdown | 1995 | 462,135.93 | 4,421,975.89 | 6331.38 | North by West 21.13° | |||
| 2007 | 463,338.85 | 4,424,859.60 | 3124.55 | North by East 22.64° | 260.38 | 8855.55 | North by West 7° | |
| 2009 | 463,147.88 | 4,426,294.86 | 1447.90 | North by West 7.58° | 723.95 | 10,303.39 | North by West 7.08° | |
| 2011 | 464,963.60 | 4,427,455.10 | 2154.77 | North by East 57.42° | 1077.38 | 11,398.14 | North by East 2.74° | |
| 2013 | 463,472.92 | 4,427,165.65 | 1518.53 | South by West 10.99° | 759.27 | 11,135.78 | North by West 4.87° | |
| Compressible layer thickness | 464,698.89 | 4,417,620.02 | 1575.25 | North by East 10.28° | ||||
| Geometry center | 464,417.87 | 4,416,070.03 | ||||||
| Year | 1995 (1999) | 2007 | 2009 | 2011 | 2013 |
|---|---|---|---|---|---|
| Land subsidence vs. groundwater drawdown (m) | 14,033.57 | 14,446.58 | 14,470.08 | 14,824.67 | 13,590.63 |
| Land subsidence vs. compressible layer thickness (m) | 12,367.04 | 9002.28 | 7807.42 | 6663.16 | 5798.57 |
| SDE Parameters | Year | Short Axis (m) | Long Axis (m) | Rotation Angle (°) | Long Axis/Short Axis | Area (km2) |
|---|---|---|---|---|---|---|
| Cumulative land subsidence | 1999 | 19,346.19 | 36,550.69 | 11.19 | 1.89 | 2221.28 |
| 2007 | 19,789.50 | 36,998.78 | 18.72 | 1.87 | 2300.04 | |
| 2009 | 19,348.78 | 36,293.81 | 18.67 | 1.88 | 2205.97 | |
| 2011 | 19,875.39 | 36,567.86 | 20.58 | 1.84 | 2283.12 | |
| 2013 | 19,904.22 | 35,492.24 | 20.51 | 1.78 | 2219.19 | |
| Groundwater drawdown | 1995 | 22,751.85 | 34,974.82 | 24.96 | 1.54 | 2499.73 |
| 2007 | 23,714.93 | 37,426.64 | 31.52 | 1.58 | 2788.20 | |
| 2009 | 22,851.41 | 37,940.96 | 32.96 | 1.66 | 2723.58 | |
| 2011 | 23,416.54 | 37,325.74 | 33.87 | 1.59 | 2745.69 | |
| 2013 | 23,009.21 | 37,143.34 | 31.94 | 1.61 | 2684.74 | |
| Compressible layer thickness | 23,473.52 | 35,233.51 | 21.62 | 1.50 | 2598.10 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Gong, H.; Zhu, L.; Li, X. Measuring Spatiotemporal Features of Land Subsidence, Groundwater Drawdown, and Compressible Layer Thickness in Beijing Plain, China. Water 2017, 9, 64. https://doi.org/10.3390/w9010064
Li Y, Gong H, Zhu L, Li X. Measuring Spatiotemporal Features of Land Subsidence, Groundwater Drawdown, and Compressible Layer Thickness in Beijing Plain, China. Water. 2017; 9(1):64. https://doi.org/10.3390/w9010064
Chicago/Turabian StyleLi, Yongyong, Huili Gong, Lin Zhu, and Xiaojuan Li. 2017. "Measuring Spatiotemporal Features of Land Subsidence, Groundwater Drawdown, and Compressible Layer Thickness in Beijing Plain, China" Water 9, no. 1: 64. https://doi.org/10.3390/w9010064
APA StyleLi, Y., Gong, H., Zhu, L., & Li, X. (2017). Measuring Spatiotemporal Features of Land Subsidence, Groundwater Drawdown, and Compressible Layer Thickness in Beijing Plain, China. Water, 9(1), 64. https://doi.org/10.3390/w9010064






