Identifying the Correlation between Water Quality Data and LOADEST Model Behavior in Annual Sediment Load Estimations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Water Quality Data Statistics for Annual Sediment Load Estimates
2.2. Water Quality Data Selection for LOADEST Runs
3. Results and Discussion
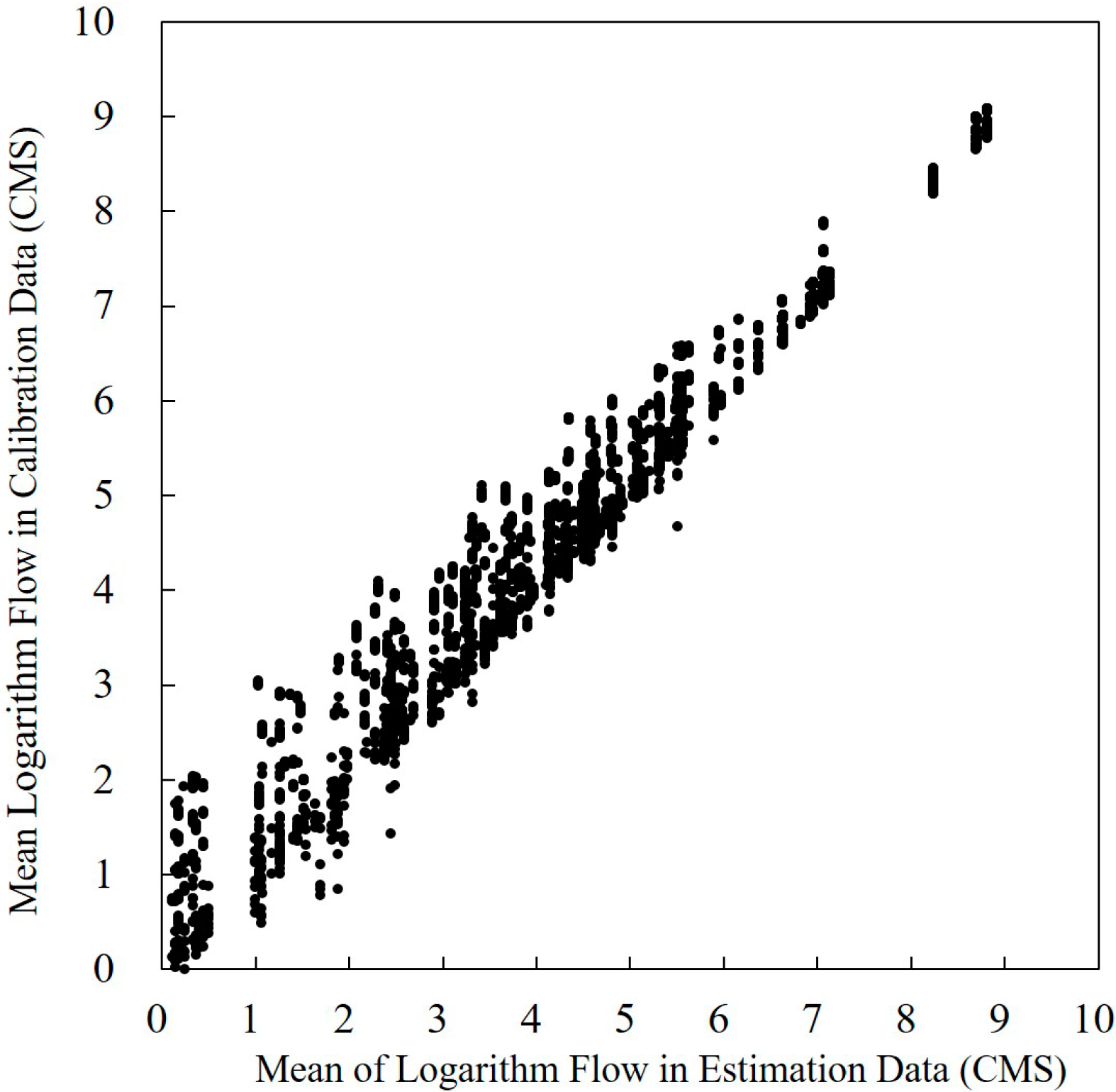
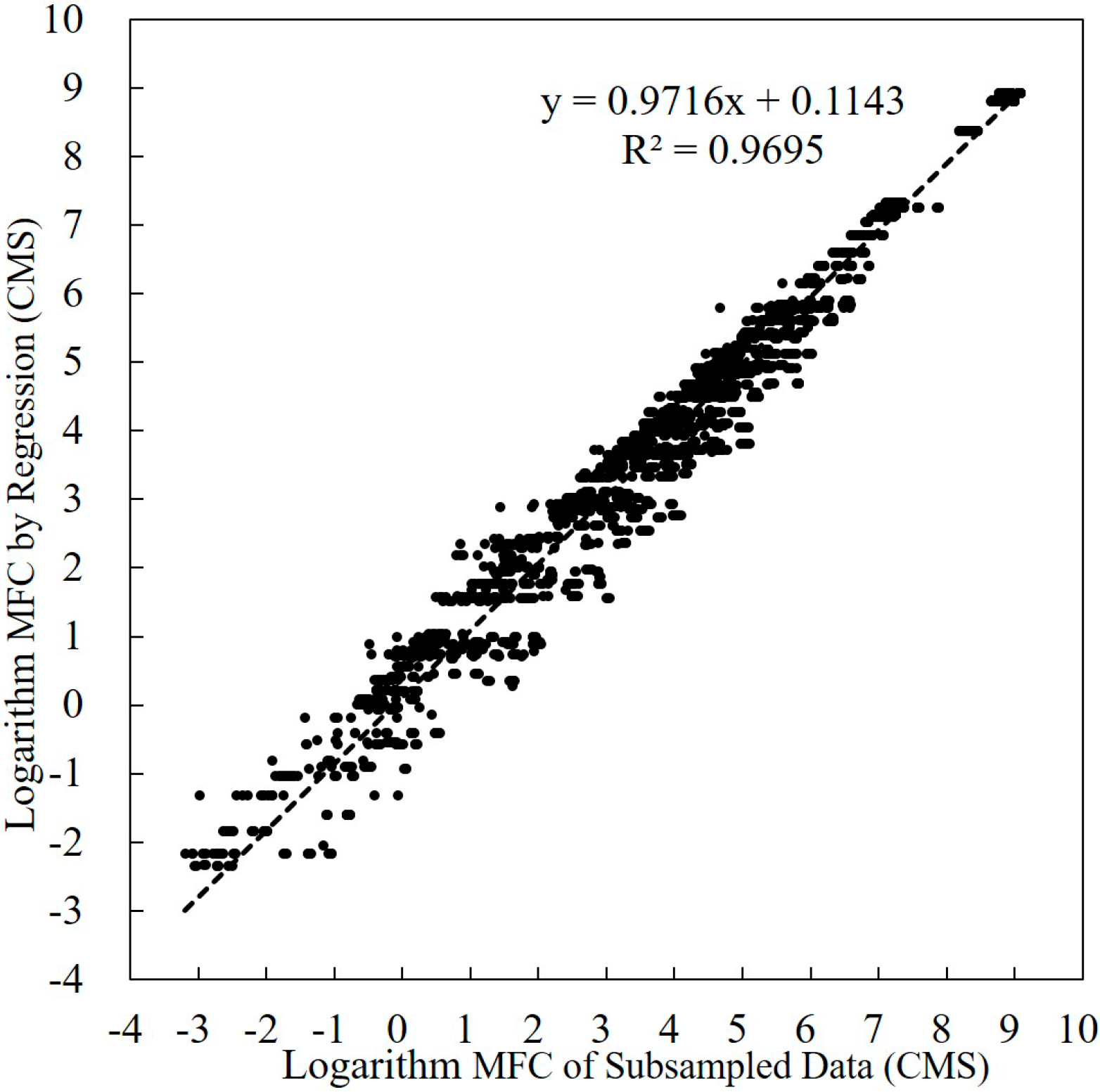
3.1. Required Statistics for Annual Sediment Load Estimates
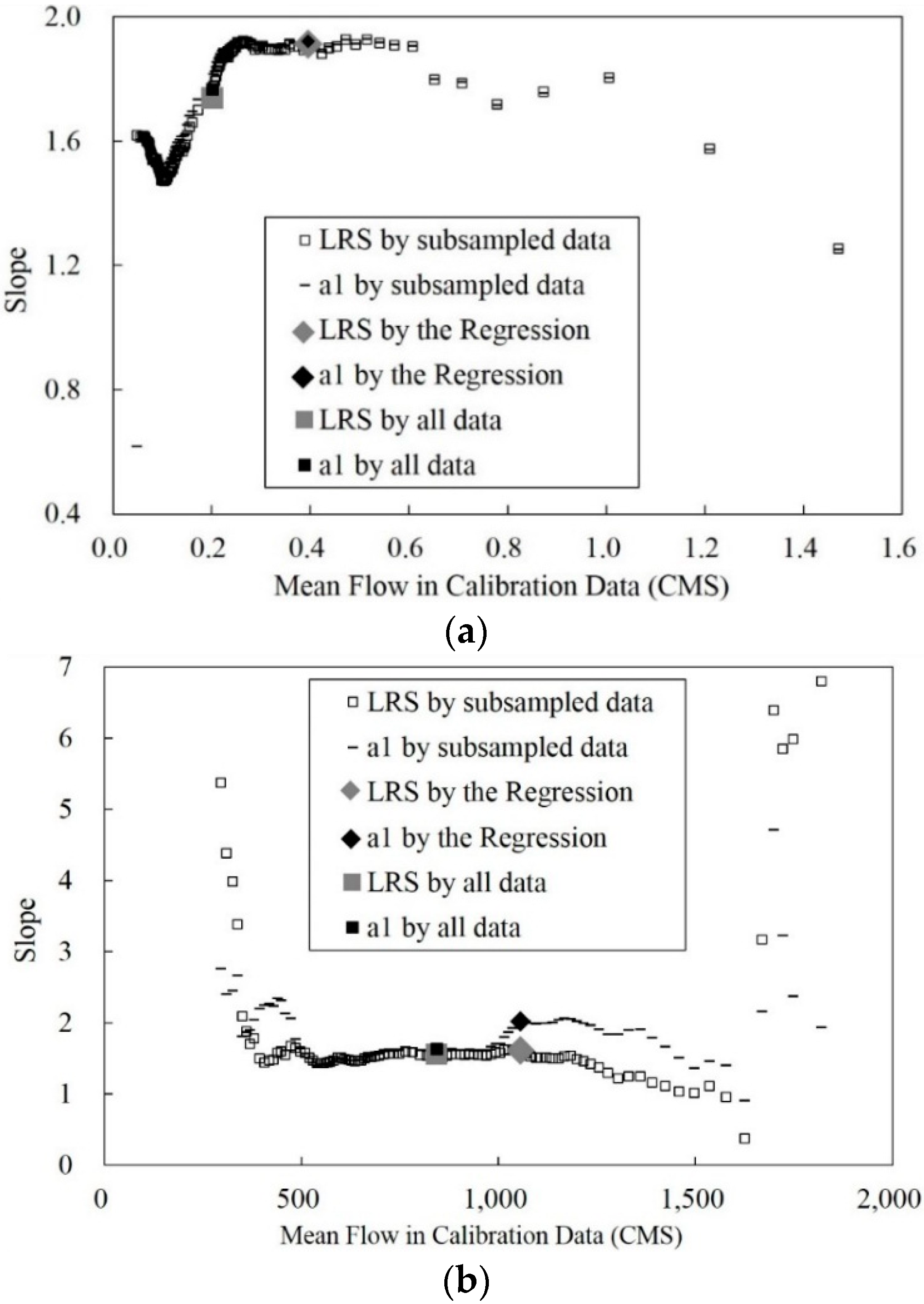
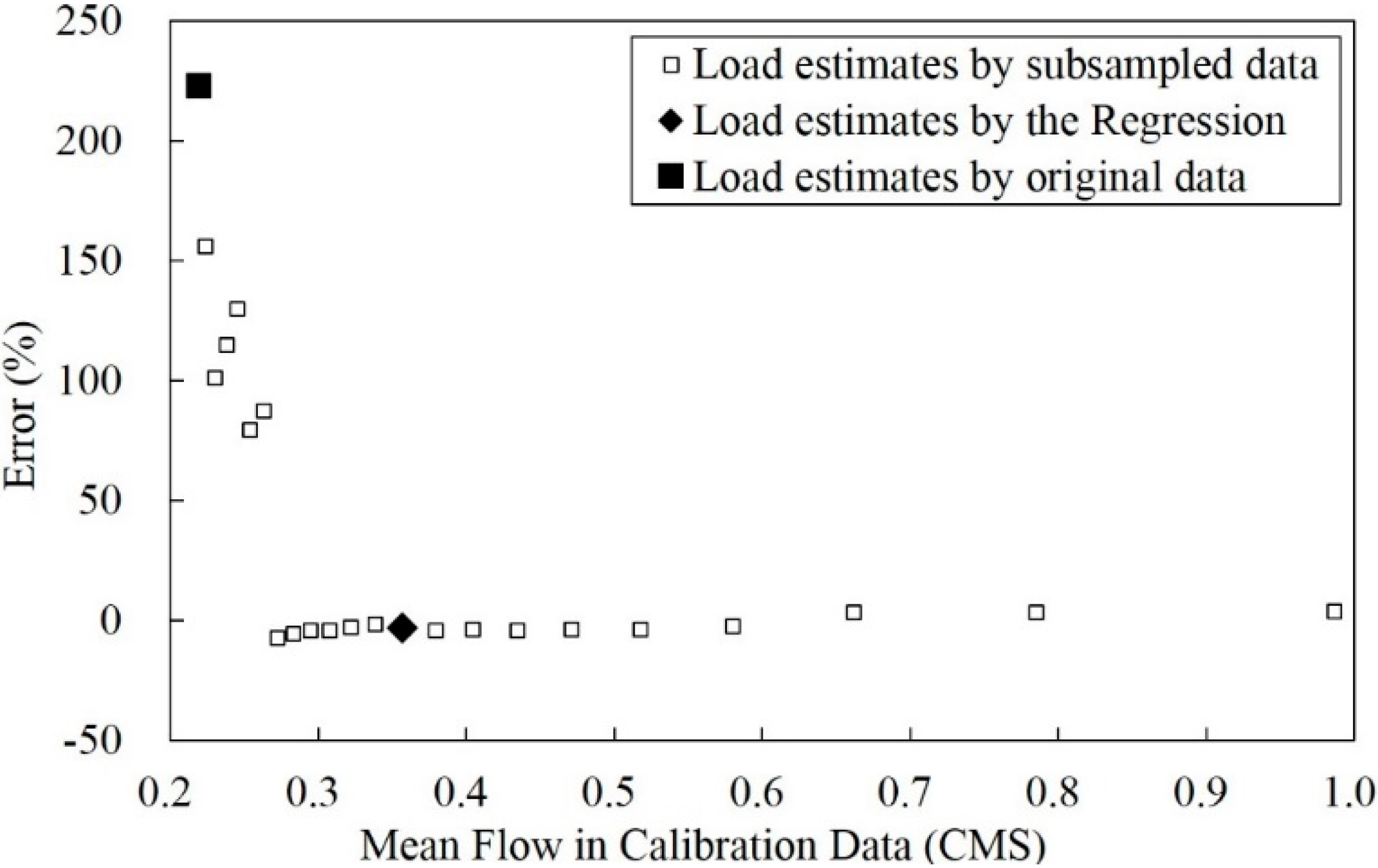
3.2. Mean Flow in Calibration Data and Annual Sediment Load Estimates
- (1)
- Compute MFCo using the regression equation with a mean flow of historical data prior to initiating a water quality monitoring program;
- (2)
- Collect a few water quality samples based on MFCo;
- (3)
- Compute MFCi using the regression equation with the mean flow from the beginning of water quality monitoring program;
- (4)
- Collect water quality samples from low flow if MFCi is greater than the required MFC by regression equation, collect water quality samples from high flow (storm events) if MFCi is smaller than the required MFC by regression equation;
- (5)
- Repeat processes 3 and 4 by the end of water quality monitoring program.
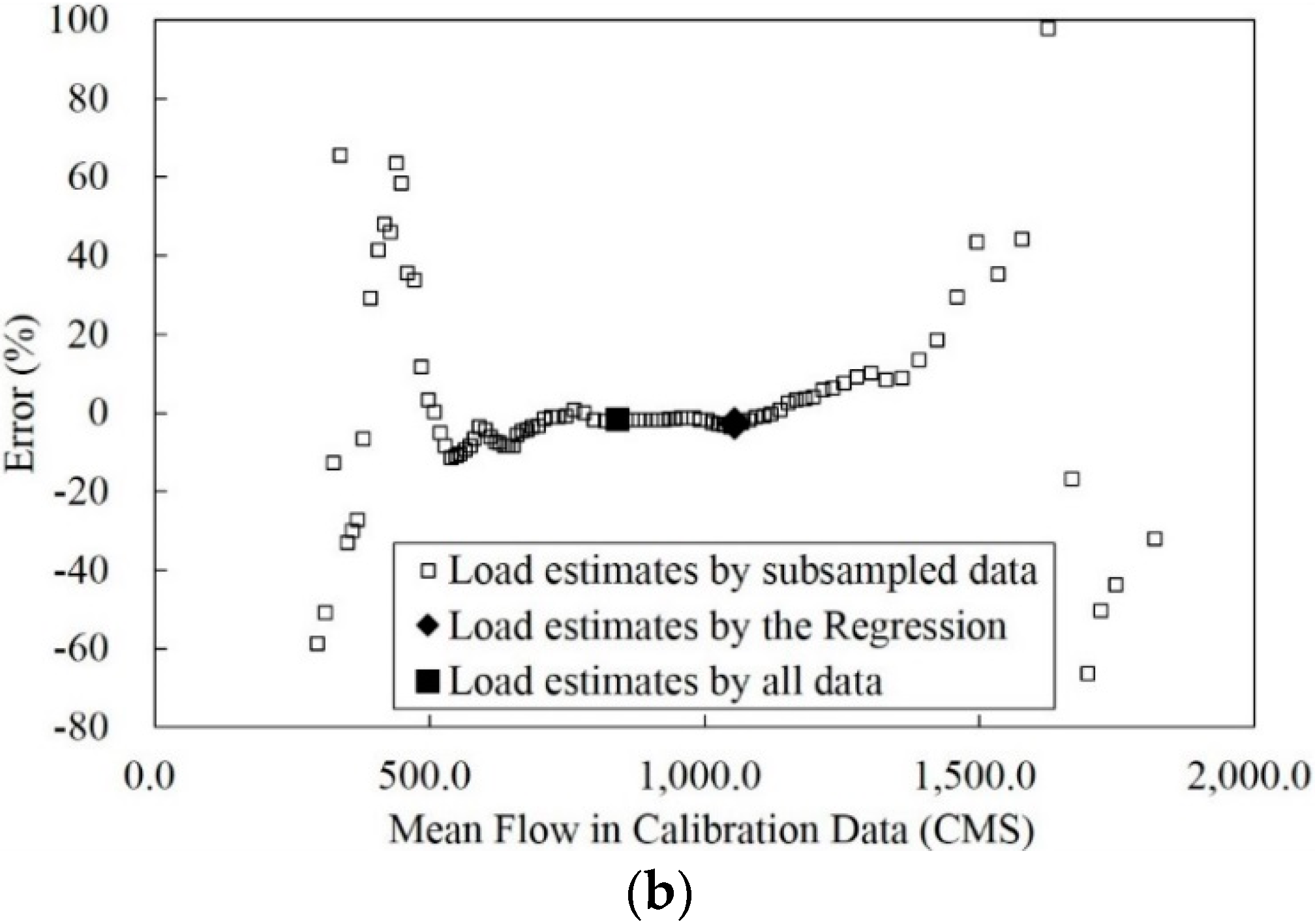
3.3. Improvement of the Poorest Annual Sediment Load Estimates
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brigham, M.E.; Wentz, D.A.; Aiken, G.R.; Krabbenhoft, D.P. Mercury cycling in stream ecosystems. 1. Water column chemistry and transport. Environ. Sci. Technol. 2009, 43, 2720–2725. [Google Scholar] [CrossRef] [PubMed]
- King, K.W.; Harmel, R.D. Considerations in selecting a water quality sampling strategy. Trans. ASAE 2003, 46, 63–73. [Google Scholar]
- Halliday, S.J.; Skeffington, R.A.; Bowes, M.J.; Gozzard, E.; Newman, J.R.; Lowewnthal, M.; Palmer-Felgate, E.J.; Jarvie, H.P.; Wade, A.J. The water quality of the River Enborne, UK: Observations from high-frequency monitoring in a rural, lowland river system. Water 2014, 6, 150–180. [Google Scholar] [CrossRef]
- Sanders, E.C.; Yuan, Y.; Pitchford, A. Fecal coliform and E. coli concentrations in effluent-dominated streams of the Upper Santa Cruz watershed. Water 2013, 5, 243–261. [Google Scholar] [CrossRef]
- Valero, E. Characterization of the water quality status on a stretch of River Lerez around a small hydroeletric power station. Water 2012, 4, 815–834. [Google Scholar] [CrossRef]
- Robertson, D.M.; Roerish, E.D. Influence of various water quality sampling strategies on load estimates for small streams. Water Resour. Res. 1999, 35, 3747–3759. [Google Scholar] [CrossRef]
- Gilroy, E.J.; Hirsch, R.M.; Cohn, T.A. Mean square error of regression-based constituent transport estimates. Water Resour. Res. 1990, 26, 2069–2077. [Google Scholar] [CrossRef]
- Johnson, A.H. Estimating solute transport in streams from grab samples. Water Resour. Res. 1979, 15, 1224–1228. [Google Scholar] [CrossRef]
- Coynel, A.; Schafer, J.; Hurtrez, J.; Dumas, J.; Etcheber, H.; Blanc, G. Sampling frequency and accuracy of SPM flux estimates in two contrasted drainage basins. Sci. Total Environ. 2004, 330, 233–247. [Google Scholar] [CrossRef] [PubMed]
- Henjum, M.B.; Hozalski, R.M.; Wennen, C.R.; Novak, P.J.; Arnold, W.A. A comparison of total maximum daily load (TMDL) calculations in urban streams using near real-time and periodic sampling data. J. Environ. Monit. 2010, 12, 234–241. [Google Scholar] [CrossRef]
- Horowitz, A.J. An evaluation of sediment rating curves for estimating suspended sediment concentrations for subsequent flux calculations. Hydrol. Process. 2003, 17, 3387–3409. [Google Scholar] [CrossRef]
- Johnes, P.J. Uncertainties in annual riverine phosphorus load estimation: Impact of load estimation methodology, sampling frequency, baseflow index and catchment population density. J. Hydrol. 2007, 332, 241–258. [Google Scholar] [CrossRef]
- Kronvang, B.; Bruhnm, A.J. Choice of sampling strategy and estimation method for calculating nitrogen and phosphorus transport in small lowland streams. Hydrol. Process. 1996, 10, 1483–1501. [Google Scholar] [CrossRef]
- Robertson, D.M. Influence of different temporal sampling strategies on estimating total phosphorus and suspended sediment concentration and transport in small streams. J. Am. Water Resour. Assoc. 2003, 39, 1281–1308. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1963. [Google Scholar]
- U.S. Environmental Protection Agency. Monitoring Guidance for Determining the Effectiveness of Nonpoint Source Controls; USEPA Office of Water Nonpoint Source Control Branch: Washington, DC, USA, 1997.
- Zar, J.H. Biostatistical Analysis, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Haggard, B.E.; Soerens, T.S.; Green, W.R.; Richards, R.P. Using regression methods to estimate stream phosphorus loads at the Illinois River, Arkansas. Appl. Eng. Agric. 2003, 19, 187–194. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Effect of Storm-Sampling Frequency on Estimation of Water-Quality Loads and Trends in two Tributaries to Chesapeake Bay in Virginia; Water-Resources Investigations Report 01-4136; U.S. Geological Survey: Richmond, VA, USA, 2001.
- U.S. Geological Survey. Computer Programs for Describing the Recession of Ground-Water Discharge and for Estimating Mean Ground-Water Recharge and Discharge from Streamflow Records-Update; Water-Resources Investigation Report 98-4148; U.S. Geological Survey: Reston, VA, USA, 1998.
- Park, Y.S.; Engel, B.A. Use of pollutant load regression models with various sampling frequencies for annual load estimation. Water 2014, 6, 1658–1697. [Google Scholar] [CrossRef]
- Park, Y.S.; Engel, B.A. Analysis for regression model behavior by sampling strategy for annual pollutant load estimation. J. Environ. Qual. 2015, 44, 1843–1851. [Google Scholar] [CrossRef] [PubMed]
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST): A Fortran Program for Estimating Constituent Loads in Streams and Rivers; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2004.
- Powell, J.L. Least absolute deviations estimation for the censored regression model. J. Econom. 1984, 25, 303–325. [Google Scholar] [CrossRef]
- Jones, C.S.; Schilling, K.E. Carbon export from the Raccoon River, Iowa: Patterns, processes, and opportunities. J. Environ. Qual. 2013, 42, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Sprague, L.A.; Gronberg, J.A. Relating management practices and nutrient export in agricultural watersheds of the United States. J. Environ. Qual. 2012, 41, 1939–1950. [Google Scholar] [CrossRef] [PubMed]
- Dornblaser, M.M.; Striegl, R.G. Suspended sediment and carbonate transport in the Yukon river basin, Alska: Flouxes and potential future responses to climate change. Water Resour. Res. 2009, 45, W06411. [Google Scholar] [CrossRef]
- Spencer, R.G.M.; Aiken, G.R.; Bulter, K.D.; Dornblaser, M.M.; Striegl, R.G.; Hernes, P.J. Utilizing chromophoric dissolves organic matter measurements to derive export and reactivity of dissolved organic carbon exported to the Arctic Ocean: A case study of the Yukon river, Alaska. Geophy. Res. Lett. 2009, 36, L06401. [Google Scholar] [CrossRef]
- Carey, R.O.; Migliaccio, K.W.; Brown, M.T. Nutrient discharges to Biscayne Bay, Florida: Trends, loads, and a pollutant index. Sci. Total Environ. 2011, 409, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Das, S.K.; Ng, A.W.M.; Perera, B.J.C. Assessment of nutrient and sediment loads in the Yarra river catchment. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; pp. 3490–3496.
- Oh, J.; Sankarasubramanian, A. Interannual hydroclimatic variability and its influence on winter nutrients variability over the southeast United States. Hydrol. Earth Syst. Sci. Discuss. 2011, 8, 10935–10971. [Google Scholar] [CrossRef]
- Duan, S.; Kaushal, S.S.; Groffman, P.M.; Band, L.E.; Belt, K.T. Phosphorus export across an urban to rural gradient in the Chesapeake Bay watershed. J. Geophy. Res. 2012, 117. [Google Scholar] [CrossRef]
- USGS Water Quality Data for the Nation Homepage. Available online: http://waterdata.usgs.gov/nwis/qw (accessed on 23 March 2013).
- National Center for Water Quality Research of Heidelberg University Homepage. Available online: http://www.heidelberg.edu/academiclife/distinctive/ncwqr (accessed on 23 March 2013).
- U.S. Environmental Protection Agency. An Approach for Using Load Duration Curves in the Development of TMDLs; US EPA Office of Wetlands, Ocean and Watersheds: Washington, DC, USA, 2007.
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; The R Foundation: Vienna, Austria, 2012. [Google Scholar]


| Water Quality Parameter | Sample Size | Period | Number of Sites | Reference |
|---|---|---|---|---|
| Mercury | 30–47 samples (monthly sampling) | 2002–2006 | 8 | [1] |
| Suspended sediment | ±30 samples (6–8 per year) | 2001–2005 | 5 | [27] |
| Chromophoric dissolved organic matter | 39 samples | 2004–2005 | 1 | [28] |
| NOx-N, NH3-N, Total phosphorus | 88–155 samples (Monthly sampling) | 1992–2006 | 18 | [29] |
| Total nitrogen, Total phosphorus, Total suspended solids | Monthly sampling | 1970–2009 | 12 | [30] |
| Total nitrogen | 54–152 samples | 12–22 years | 18 | [31] |
| Soluble reactive phosphorus, Total phosphorus | Weekly sampling | 1998–2007 | 8 | [32] |
| Parameter | From Calibration Data | From Estimation Data |
|---|---|---|
| Q (1) | Minimum, Maximum, Mean, Standard deviation | Minimum, Maximum, Mean, Standard deviation |
| C (2) | Minimum, Maximum, Mean, Standard deviation | Minimum, Maximum, Mean, Standard deviation |
| Q, C, and L (3) | Correlation Coefficient of: Q and C, log(Q) and C, (log(Q))2 and C, Q and L, log(Q) and L, (log(Q))2 and L | |
| Coefficient of determination of: Q and C, log(Q) and C, (log(Q))2 and C, Q and L, log(Q) and L, (log(Q))2 and L | ||
| Percentage of Q with C data in high, moist, mid-range, dry, and low flow regimes (4) | ||
| Minimum Q in calibration data/Minimum flow in estimation data | ||
| Maximum Q in calibration data/Maximum flow in estimation data | ||
| Mean Q in calibration data/Mean flow in estimation data | ||
| Standard deviation Q in calibration data/Standard deviation Q in estimation data | ||
| Station Number | Station Name | Data Period | Drainage Area (km2) |
|---|---|---|---|
| 02119400 | Third Creek near Stony Point, NC, USA | 1959–1968 | 12.5 |
| 07287150 | Abiaca Creek near Seven Pines, MS, USA | 1993–2002 | 246.6 |
| 03265000 | Stillwater River at Pleasant Hill, OH, USA | 1967–1973 | 1302.8 |
| 12334550 | Clark Fork at Turah Bridge nr Bonner, MT, USA | 1993–2002 | 9430.1 |
| 06486000 | Missouri River at Sioux City, IA, USA | 1992–1999 | 814,810.3 |
| USGS Station Number (Data Period) | Error in Annual Sediment Load Estimates (%) (Percentage of Calibration Data from High Flow, %) | |
|---|---|---|
| Regression | All Data | |
| 02119400 (1959–1963) | 6.4 | −13.0 |
| (36.8) | (11.1) | |
| 02119400 (1964–1968) | 2.5 | −8.7 |
| (36.2) | (10.3) | |
| 07287150 (1993–1997) | 13.0 | 22.4 |
| (16.8) | (10.1) | |
| 07287150 (1998–2002) | 8.1 | −5.1 |
| (17.4) | (10.1) | |
| 03265000 (1967–1969) | 14.8 | −29.5 |
| (20.3) | (10.1) | |
| 03265000 (1970–1973) | −10.8 | −39.7 |
| (18.8) | (10.2) | |
| 12334550 (1993–1997) | 7.5 | −16.6 |
| (17.1) | (10.1) | |
| 12334550 (1998–2002) | 0.7 | −12.7 |
| (16.7) | (10.3) | |
| 06486000 (1992–1995) | −2.9 | −1.7 |
| (18.4) | (10.1) | |
| 06486000 (1995–1999) | −5.8 | −2.8 |
| (21.7) | (10.1) | |
| USGS Station Number (Sampling Strategy) | MFE (1) | R. MFC (2) | MFC (3) (Error, %) | Num. Data (6) (PCH (7), %) | ||
|---|---|---|---|---|---|---|
| Original (4) | Regression (5) | Original (4) | Regression (5) | |||
| 02119400 | 0.18 | 0.36 | 0.19 | 0.35 | 120 | 45 |
| (monthly on 18th) | (195.5) | (1.7) | (10.0) | (26.7) | ||
| 02119400 | 0.18 | 0.36 | 0.22 | 0.36 | 120 | 57 |
| (monthly on 19th) | (223.0) | (−3.0) | (12.5) | (26.3) | ||
| 02119400 | 0.18 | 0.36 | 0.21 | 0.36 | 120 | 52 |
| (monthly on 20th) | (132.8) | (−13.0) | (12.5) | (28.8) | ||
| 02119400 | 0.18 | 0.36 | 0.17 | 0.36 | 261 | 65 |
| (fortnightly on 12th) | (144.7) | (1.4) | (7.7) | (30.8) | ||
| 05291000 | 1.43 | 2.50 | 1.78 | 2.51 | 84 | 59 |
| (monthly on 25th) | (204.0) | (−27.0) | (9.5) | (13.6) | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.S.; Engel, B.A. Identifying the Correlation between Water Quality Data and LOADEST Model Behavior in Annual Sediment Load Estimations. Water 2016, 8, 368. https://doi.org/10.3390/w8090368
Park YS, Engel BA. Identifying the Correlation between Water Quality Data and LOADEST Model Behavior in Annual Sediment Load Estimations. Water. 2016; 8(9):368. https://doi.org/10.3390/w8090368
Chicago/Turabian StylePark, Youn Shik, and Bernie A. Engel. 2016. "Identifying the Correlation between Water Quality Data and LOADEST Model Behavior in Annual Sediment Load Estimations" Water 8, no. 9: 368. https://doi.org/10.3390/w8090368
APA StylePark, Y. S., & Engel, B. A. (2016). Identifying the Correlation between Water Quality Data and LOADEST Model Behavior in Annual Sediment Load Estimations. Water, 8(9), 368. https://doi.org/10.3390/w8090368





