Developing a Conjunctive Use Optimization Model for Allocating Surface and Subsurface Water in an Off-Stream Artificial Lake System
Abstract
:1. Introduction
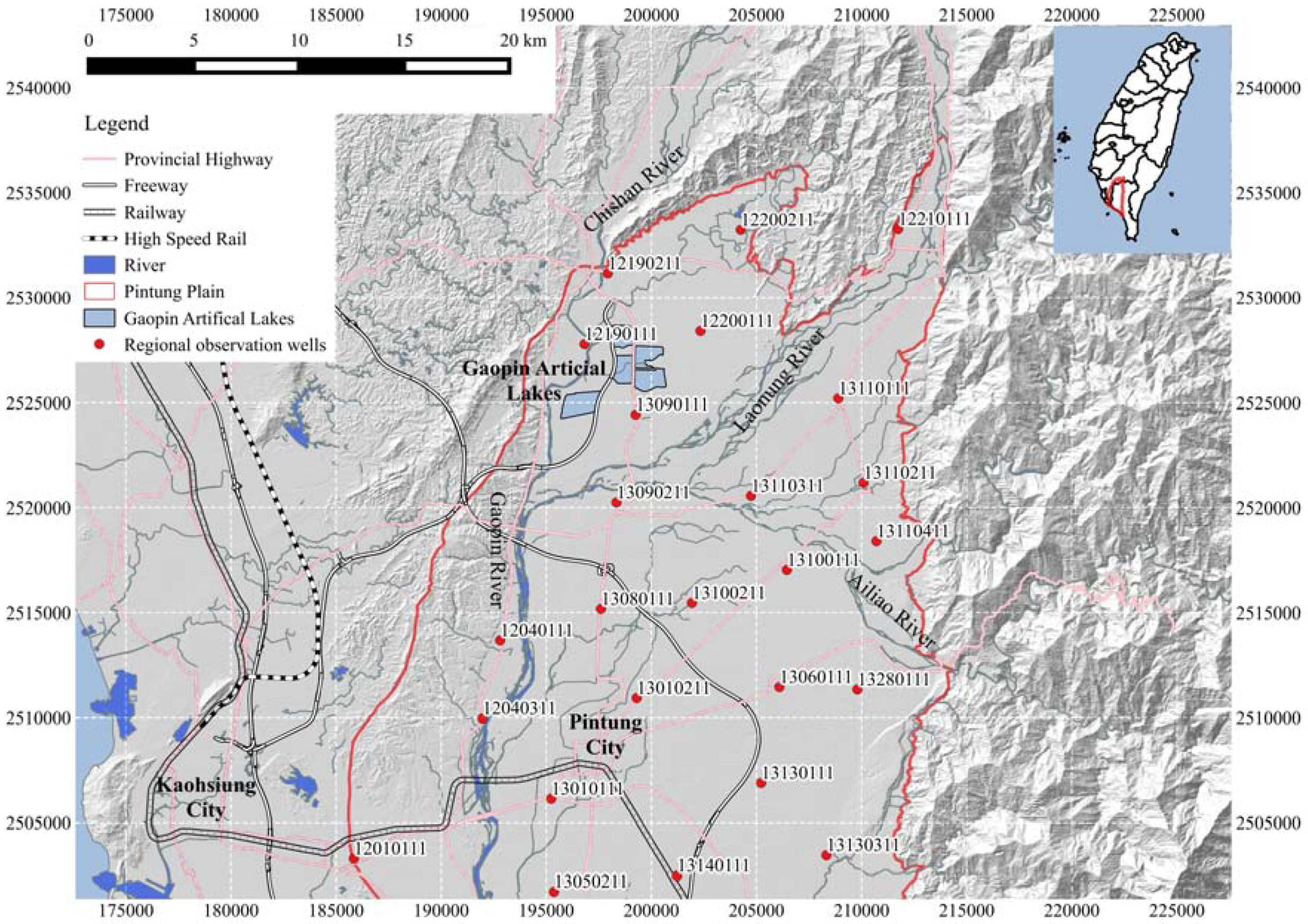
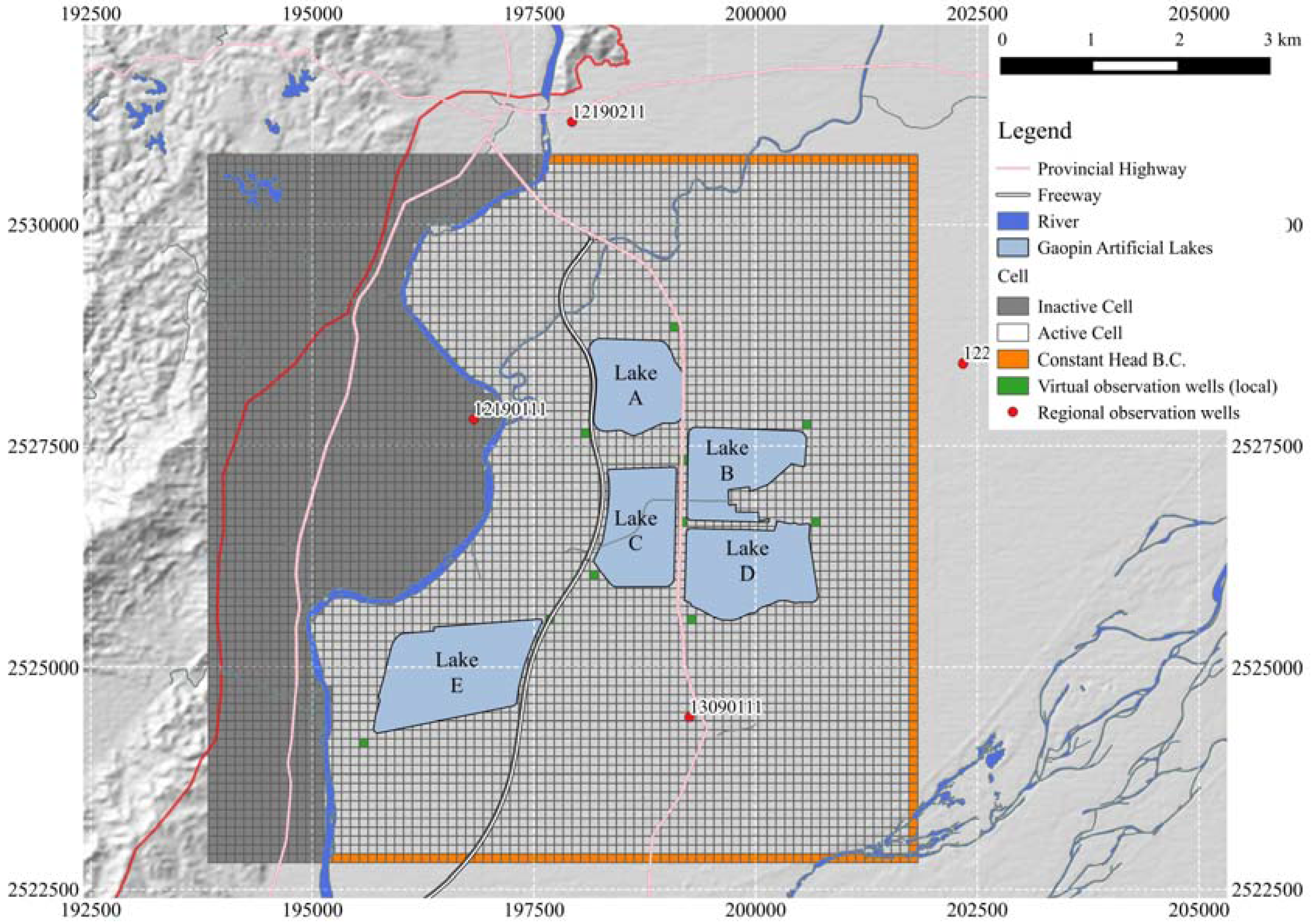
2. Study Area
3. Lake–Groundwater CUMM Model Formulation
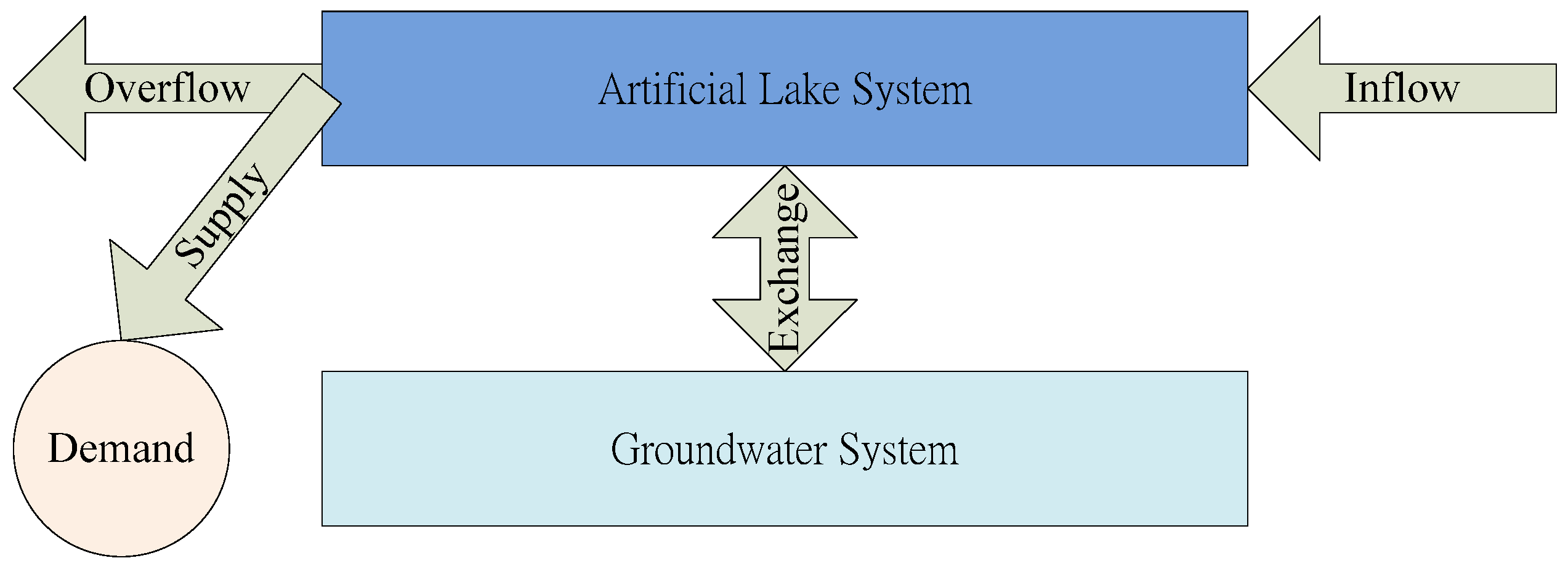
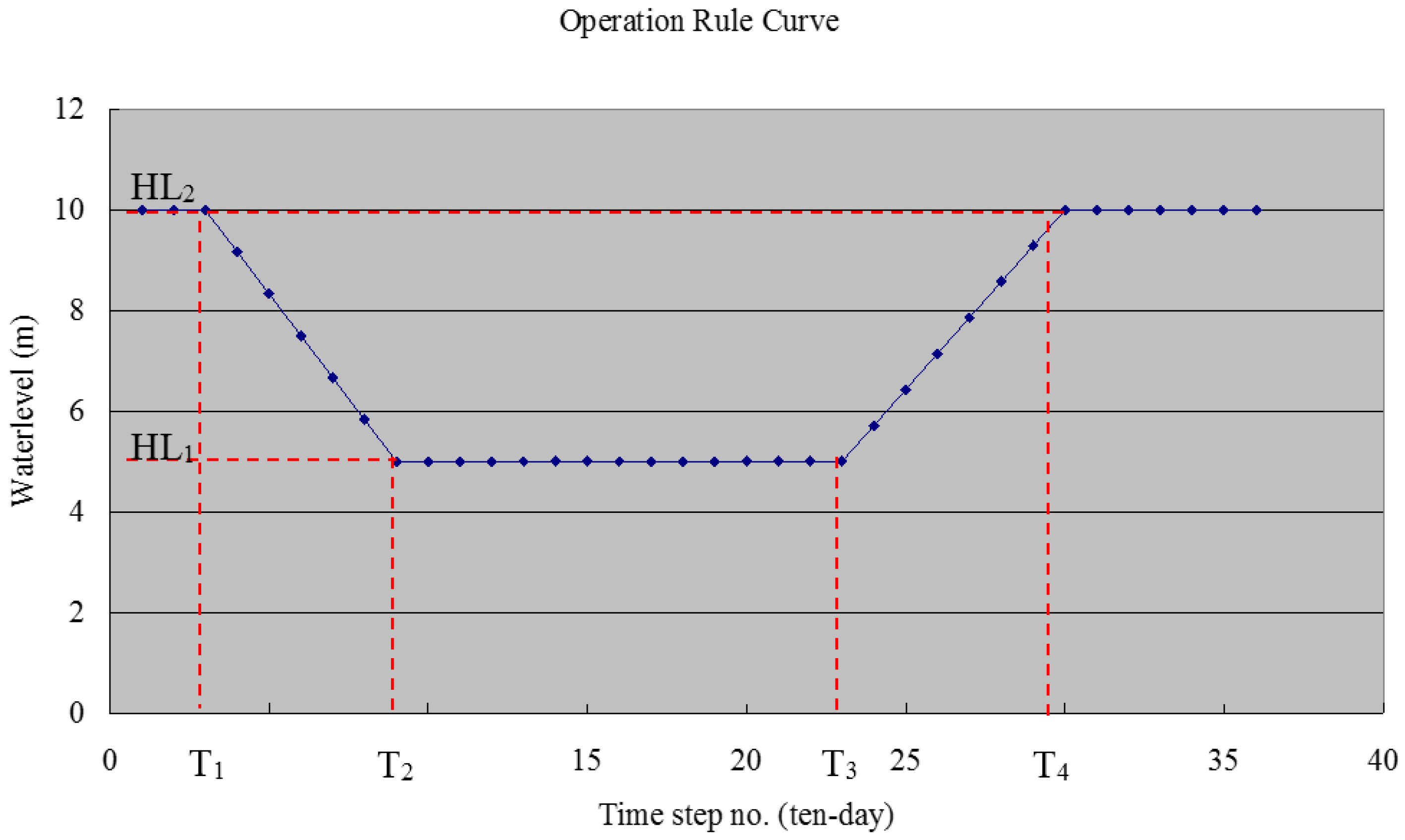
3.1. Model Formulation
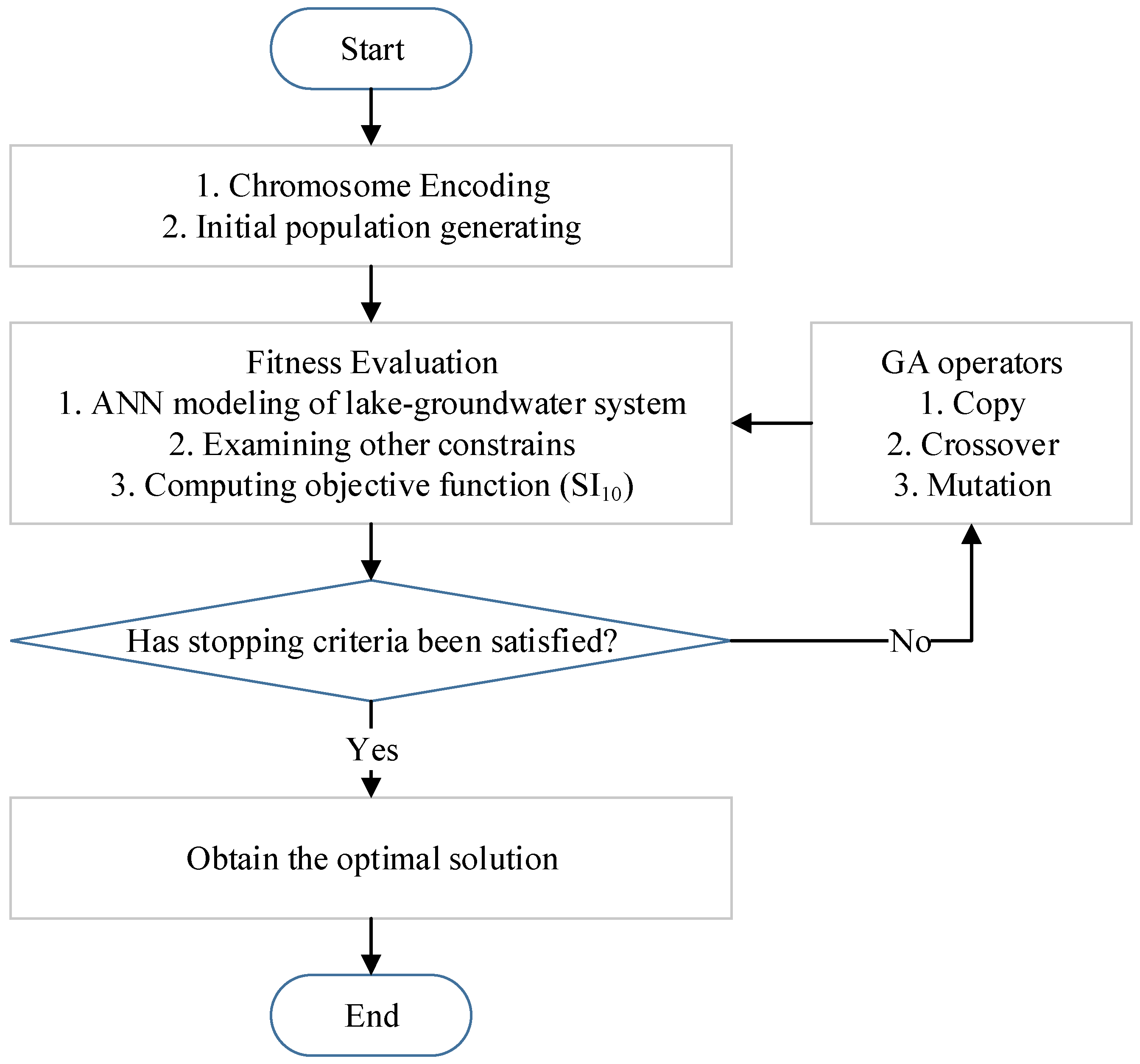
3.2. Optimal Solution
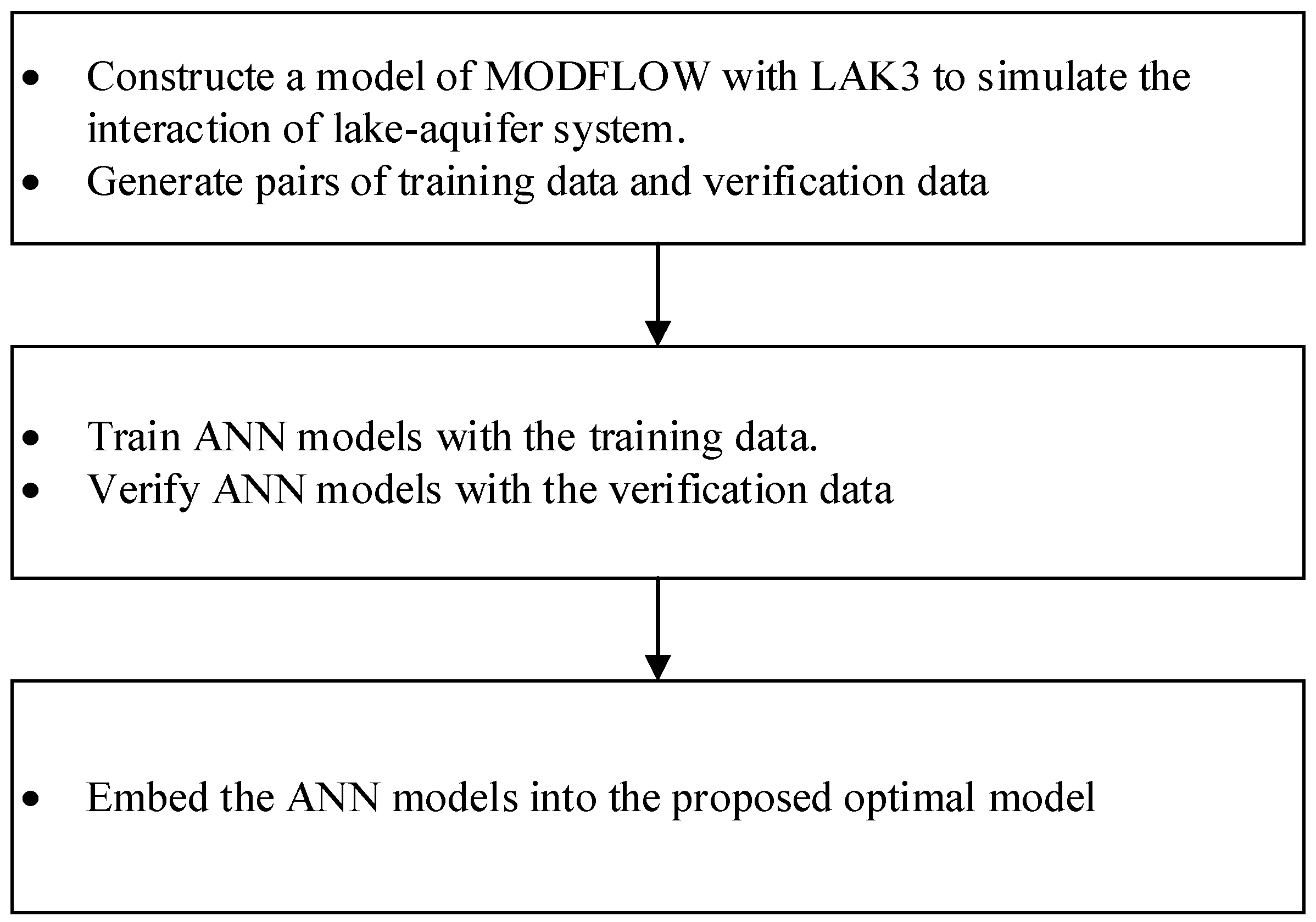
4. Development of Lake–Groundwater ANN Model
4.1. Simulation of Lake–Groundwater System Using LAK3 Package
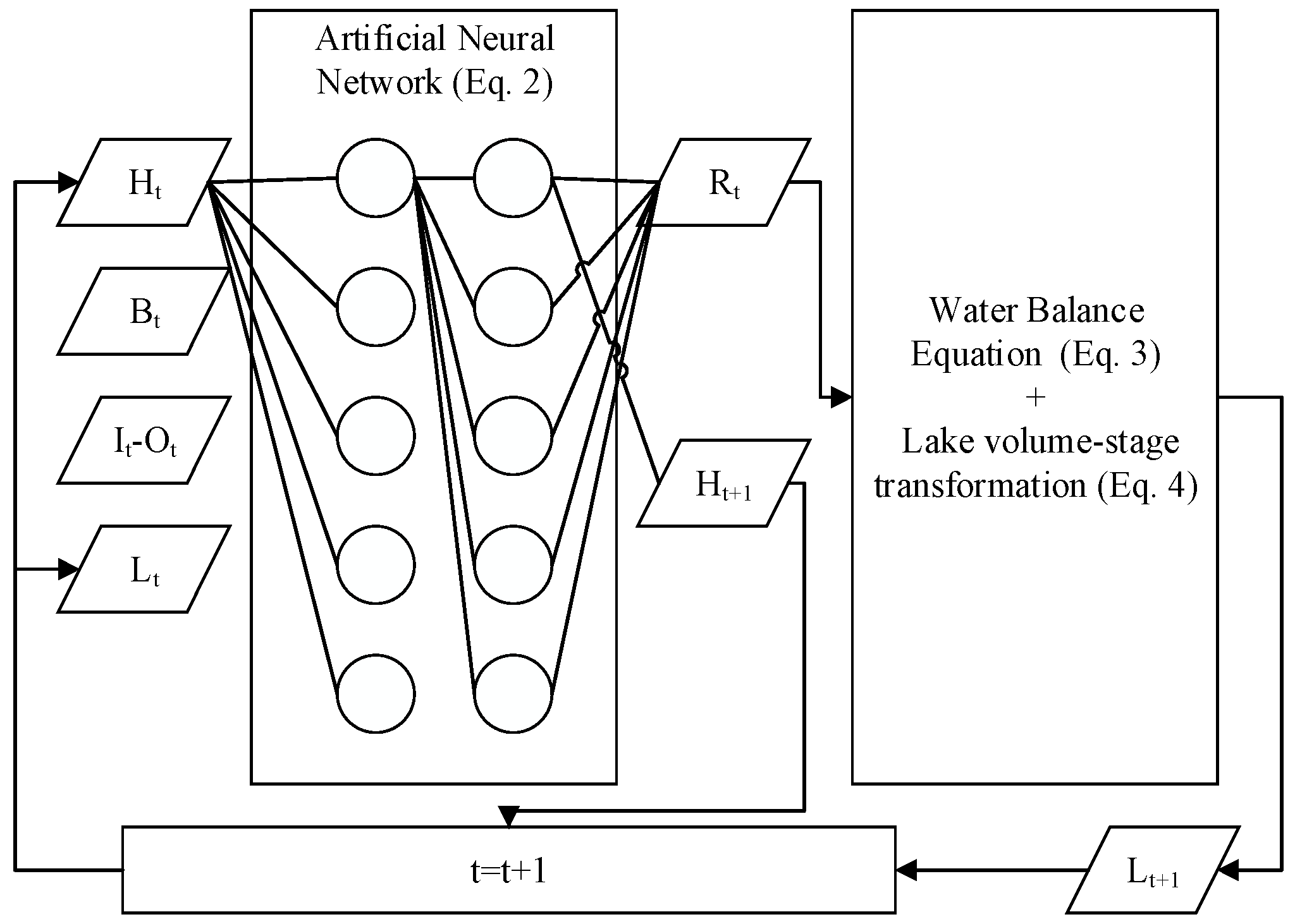
4.2. Lake–Groundwater ANN Model
5. Results and Discussion
5.1. Effectiveness of Lake–Groundwater CUMM
5.2. Model Calibration and Validation of Lake–Groundwater ANN Model
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, Y.W.; Chang, L.C.; Huang, C.W.; Chu, H.J. Applying genetic algorithm and neural network to the conjunctive use of surface and subsurface water. Water Resour. Manag. 2013, 27, 4731–4757. [Google Scholar] [CrossRef]
- Singh, A. Conjunctive use of water resources for sustainable irrigated agriculture. J. Hydrol. 2014, 519, 1688–1697. [Google Scholar] [CrossRef]
- Sandoval-Solis, S.; McKinney, D.; Loucks, D. Sustainability index for water resources planning and management. J. Water Resour. Plan. Manag. 2010, 137, 381–390. [Google Scholar] [CrossRef]
- Khare, D.; Jat, M. Assessment of counjunctive use planning options: A case study of Sapon irrigation command area of Indonesia. J. Hydrol. 2006, 328, 764–777. [Google Scholar] [CrossRef]
- Gemma, M.; Tsur, Y. The stabilization value of groundwater and conjunctive water management under uncertainty. Appl. Econ. Perspect. Policy 2007, 29, 540–548. [Google Scholar] [CrossRef]
- Yeh, Y.-L.; Chen, T.-C. Application of grey correlation analysis for evaluating the artificial lake site in Pingtung Plain, Taiwan. Can. J. Civ. Eng. 2004, 31, 56–64. [Google Scholar] [CrossRef]
- March, J.G.; Benstead, J.P.; Pringle, C.M.; Scatena, F.N. Damming tropical island streams: Problems, solutions, and alternatives. BioScience 2003, 53, 1069–1078. [Google Scholar] [CrossRef]
- Dougherty, M.; Bayne, D.; Curtis, L.; Reutebuch, E.; Seesock, W. Water quality in a non-traditional off-stream polyethylene-lined reservoir. J. Environ. Manag. 2007, 85, 1015–1023. [Google Scholar] [CrossRef] [PubMed]
- Singh, A. An overview of the optimization modelling applications. J. Hydrol. 2012, 466, 167–182. [Google Scholar] [CrossRef]
- An-Vo, D.-A.; Mushtaq, S.; Reardon-Smith, K. Estimating the value of conjunctive water use at a system-level using nonlinear programing model. J. Econ. Soc. Policy 2015, 17, 163–182. [Google Scholar]
- Joodavi, A.; Zare, M.; Mahootchi, M. Development and application of a stochastic optimization model for groundwater management: Crop pattern and conjunctive use consideration. Stoch. Environ. Res. Risk Assess. 2015, 29, 1637–1648. [Google Scholar] [CrossRef]
- Schmid, W.; Hanson, R.; Leake, S.; Hughes, J.D.; Niswonger, R.G. Feedback of land subsidence on the movement and conjunctive use of water resources. Environ. Model. Softw. 2014, 62, 253–270. [Google Scholar] [CrossRef]
- Rao, S.V.N.; Bhallamudi, S.M.; Thandaveswara, B.S.; Mishra, G.C. Conjunctive use of surface and groundwater for coastal and deltaic systems. J. Water Resour. Plan. Manag. ASCE 2004, 130, 255–267. [Google Scholar] [CrossRef]
- Peralta, R.C.; Forghani, A.; Fayad, H. Multiobjective genetic algorithm conjunctive use optimization for production, cost, and energy with dynamic return flow. J. Hydrol. 2014, 511, 776–785. [Google Scholar] [CrossRef]
- Stets, E.G.; Winter, T.C.; Rosenberry, D.O.; Striegl, R.G. Quantification of surface water and groundwater flows to open- and closed-basin lakes in a headwaters watershed using a descriptive oxygen stable isotope model. Water Resour. Res. 2010, 46, W03515. [Google Scholar] [CrossRef]
- Bocanegra, E.; Londono, O.Q.; Martínez, D.; Romanelli, A. Quantification of the water balance and hydrogeological processes of groundwater-lake interactions in the Pampa Plain, Argentina. Environ. Earth Sci. 2013, 68, 2347–2357. [Google Scholar] [CrossRef]
- Yihdego, Y.; Becht, R. Simulation of lake–aquifer interaction at Lake Naivasha, Kenya using a three-dimensional flow model with the high conductivity technique and a DEM with bathymetry. J. Hydrol. 2013, 503, 111–122. [Google Scholar] [CrossRef]
- Karan, S.; Kidmose, J.; Engesgaard, P.; Nilsson, B.; Frandsen, M.; Ommen, D.; Flindt, M.; Andersen, F.Ø.; Pedersen, O. Role of a groundwater–lake interface in controlling seepage of water and nitrate. J. Hydrol. 2014, 517, 791–802. [Google Scholar] [CrossRef]
- Matott, L.S.; Tolson, B.A.; Asadzadeh, M. A benchmarking framework for simulation-based optimization of environmental models. Environ. Model. Softw. 2012, 35, 19–30. [Google Scholar] [CrossRef]
- Chu, H.J.; Chang, L.C. Optimal control algorithm and neural network for dynamic groundwater management. Hydrol. Process. 2009, 23, 2765–2773. [Google Scholar] [CrossRef]
- Grundmann, J.; Schütze, N.; Schmitz, G.H.; Al-Shaqsi, S. Towards an integrated arid zone water management using simulation-based optimisation. Environ. Earth Sci. 2012, 65, 1381–1394. [Google Scholar] [CrossRef]
- Merritt, M.L.; Konikow, L.F. Documentation of a Computer Program to Simulate Lake-Aquifer Interaction Using the MODFLOW Ground-Water Flow Model and the MOC3D Solute-Transport Model; U.S. Geological Survey: Tallahassee, FL, USA, 2000.
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operating rule curves by genetic algorithms. Hydrol. Process. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Chang, L.-C.; Ho, C.-C.; Chen, Y.-W. Applying multiobjective genetic algorithm to analyze the conflict among different water use sectors during drought period. J. Water Resour. Plan. Manag. 2009, 136, 539–546. [Google Scholar] [CrossRef]
| Case | Conjunctive Use or Not | Operating Rule Curve | Lakebed Condition |
|---|---|---|---|
| Case 1 | Use surface water only | - | Impermeable |
| Case 2 | Conjunctive use of surface and ground water | - | Permeable |
| Case 3 | Conjunctive use of surface and ground water | One single optimized operating curve and discount ratio for all sub-lakes delivered by the proposed CUMM. | Permeable |
| Case 4 | Conjunctive use of surface and ground water | Optimized operating curves and discount ratios for each sub-lake delivered by the proposed CUMM. | Permeable |
| Name of Variables | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| 21.10 | 5.44 | 4.26 | 2.37 | |
| Total shortage time (days) | 2080 | 930 | 1780 | 1810 |
| Total shortage volume (thousand cubic meters) | 630,287 | 274,635 | 325,499 | 247,404 |
| Average shortage volume (thousand cubic meters per day) | 303 | 295 | 183 | 181 |
| Total supply volume (thousand cubic meters) | 732,546 | 1,088,198 | 1,037,333 | 1,115,429 |
| Recharge volume from lakes to aquifer (thousand cubic meters) | - | 168,671 | 189,077 | −31,739 |
| The Parameters of Operating Rule Curve | Case 2 | Case 3 | Case 4 | ||||
|---|---|---|---|---|---|---|---|
| Sub-Lake A | Sub-Lake B | Sub-Lake C | Sub-Lake D | Sub-Lake E | |||
| - | 3 | 4 | 4 | 4 | 4 | 4 | |
| - | 10 | 11 | 11 | 11 | 11 | 11 | |
| - | 21 | 20 | 20 | 20 | 20 | 20 | |
| - | 23 | 29 | 29 | 29 | 29 | 29 | |
| - | 2.32 | 2.96 | 6.19 | 2.32 | 5.87 | 2.32 | |
| - | 11.48 | 11.40 | 11.80 | 6.07 | 6.46 | 5.756 | |
| - | 0.82 | 0.52 | 0.84 | 0.90 | 0.98 | 0.98 | |
| Sub-Lake | Number of Perceptrons | Output Variables | RMSE (m) | ||
|---|---|---|---|---|---|
| First Hidden Layer | Second Hidden Layer | Output Layer | |||
| Sub-lake A | 3 | - | 4 | Lake level | 0.24 |
| Upstream groundwater level | 0.26 | ||||
| Downstream groundwater level | 0.29 | ||||
| Sub-lake B | 5 | 5 | 4 | Lake level | 0.21 |
| Upstream groundwater level | 0.25 | ||||
| Downstream groundwater level | 0.23 | ||||
| Sub-lake C | 15 | - | 4 | Lake level | 0.29 |
| Upstream groundwater level | 0.23 | ||||
| Downstream groundwater level | 0.40 | ||||
| Sub-lake D | 7 | - | 4 | Lake level | 0.26 |
| Upstream groundwater level | 0.23 | ||||
| Downstream groundwater level | 0.51 | ||||
| Sub-lake E | 5 | - | 4 | Lake level | 0.41 |
| Upstream groundwater level | 0.43 | ||||
| Downstream groundwater level | 0.55 | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.-C.; Chen, Y.-W.; Chang, L.-C.; Huang, C.-W. Developing a Conjunctive Use Optimization Model for Allocating Surface and Subsurface Water in an Off-Stream Artificial Lake System. Water 2016, 8, 315. https://doi.org/10.3390/w8080315
Pan C-C, Chen Y-W, Chang L-C, Huang C-W. Developing a Conjunctive Use Optimization Model for Allocating Surface and Subsurface Water in an Off-Stream Artificial Lake System. Water. 2016; 8(8):315. https://doi.org/10.3390/w8080315
Chicago/Turabian StylePan, Chen-Che, Yu-Wen Chen, Liang-Cheng Chang, and Chun-Wei Huang. 2016. "Developing a Conjunctive Use Optimization Model for Allocating Surface and Subsurface Water in an Off-Stream Artificial Lake System" Water 8, no. 8: 315. https://doi.org/10.3390/w8080315





