Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study
Abstract
:1. Introduction
- 1)
- Proposing a new methodology for determining the flows throughout the year in an irrigation network demand, considering the need of the crop, the historic consumption and the irrigation farmers’ habits
- 2)
- Estimating the flow rate and pressures with the time
- 3)
- Quantifying the energy balance in pressurized irrigation distribution systems to determine the energy footprint of water in the distribution system, and the estimated recoverable energy
- 4)
- Applying these procedures to a real case study
2. Methods and Materials
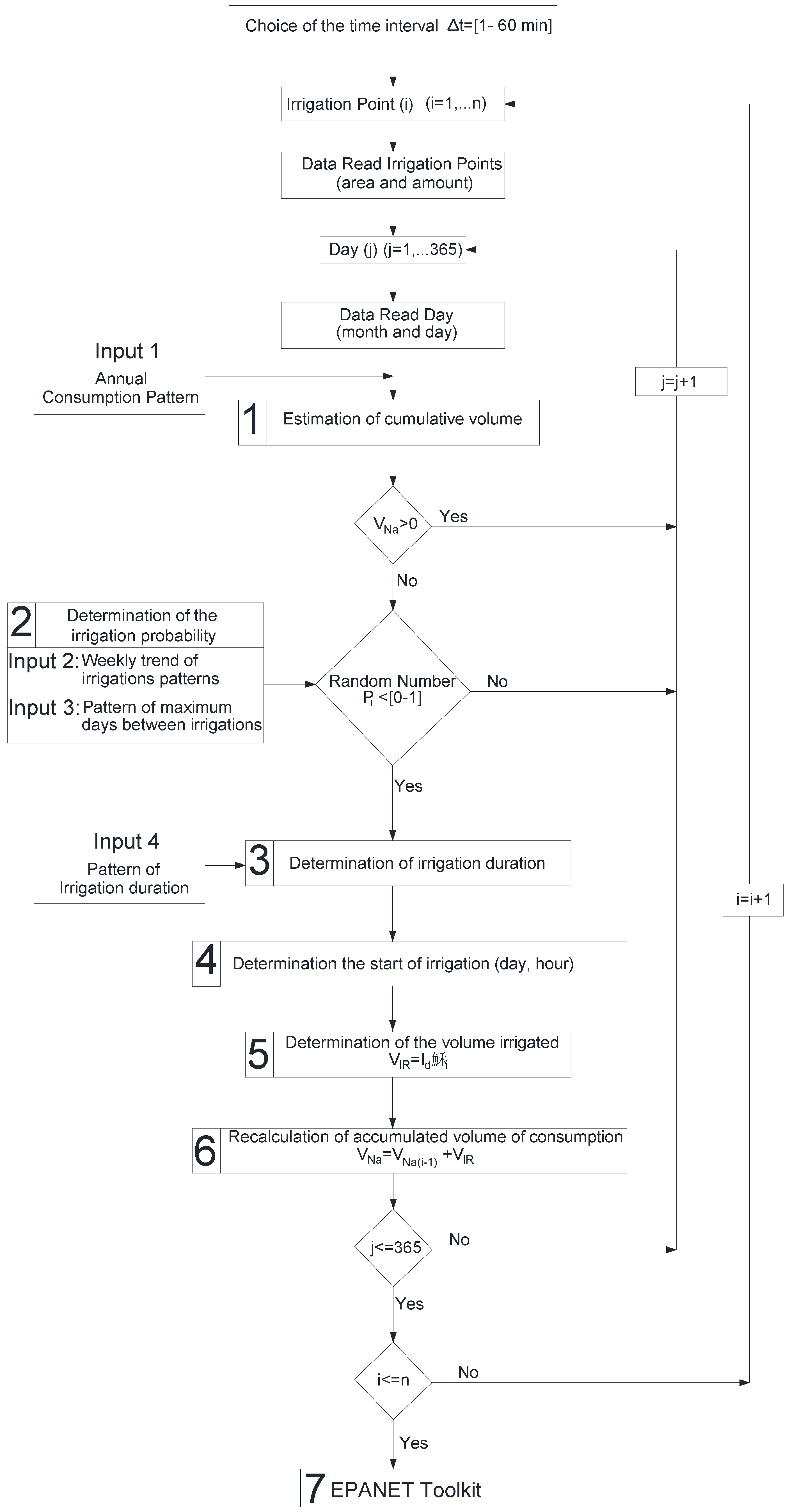
2.1. Methodology for Determining the Flow
- Estimation of cumulative volume consumed by the irrigation point
- 2.
- The determination of the irrigation probability (PI)
- i = numbers of days inside of interval;
- j = day of decision making;
- wdj = pattern to irrigate one particular day inside the interval;
- = total addition of patterns.
- 3.
- The determination of the irrigation duration
- 4.
- The start of irrigation
- 5.
- Determination of irrigation volume
- 6.
- Calculation of cumulative consumption
- 7.
- The pressure and flow modeled for each node in the network
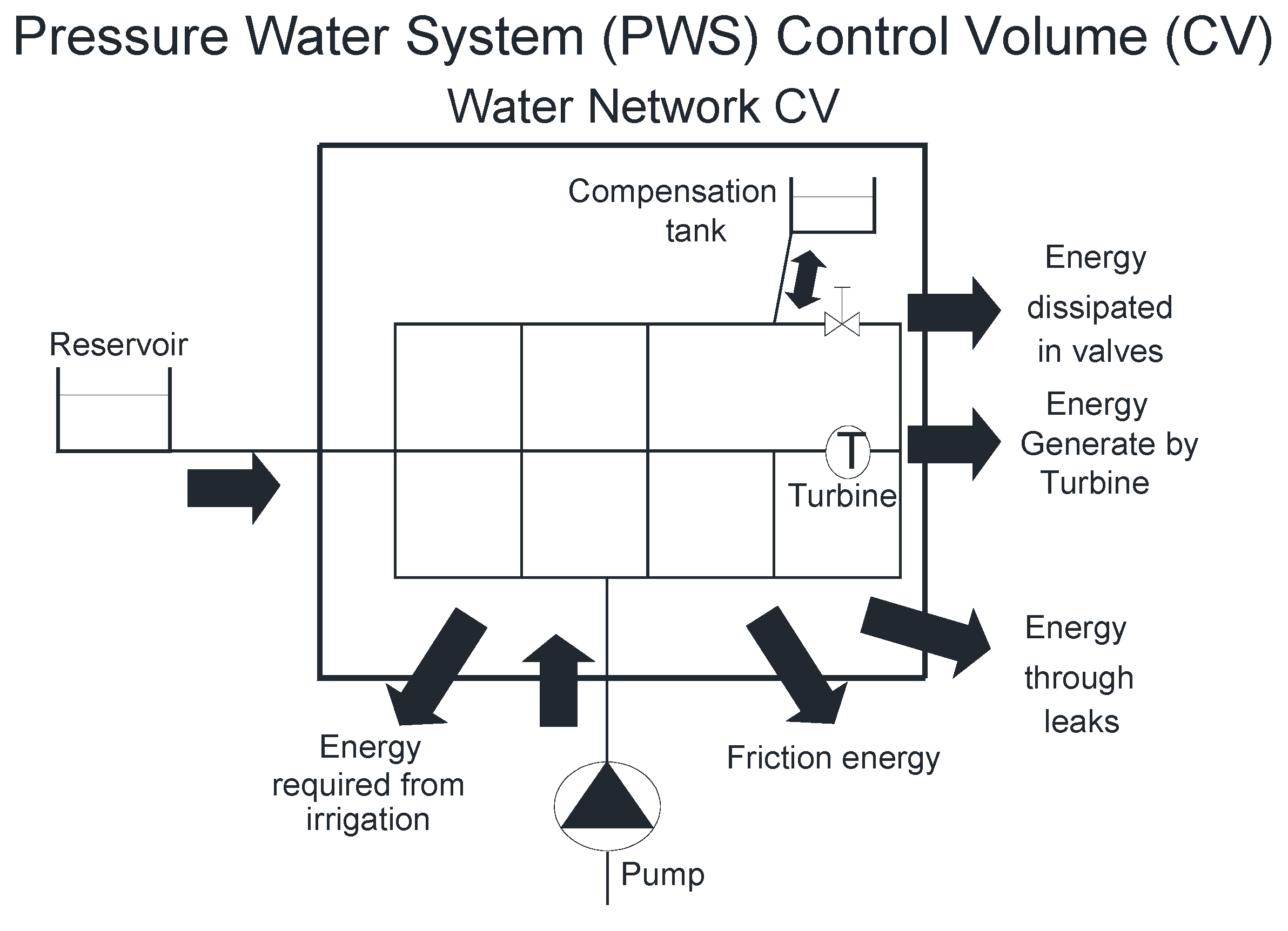
2.2. Balance of Energy
- = exchange of energy per unit time in the control system;
- = exchange of heat per unit of time (heat power);
- = power transmitted directly to or from the fluid (e.g., pump);
- = differential volume of control volume for integration;
- = velocity vector of fluid;
- = differential area of control surface for integration;
- = fluid density;
- = potential energy per unit mass;
- = internal energy per unit mass;
- = kinetic energy per unit mass;
- = height of pressure per unit mass;
- = time interval (s);
- n = total number of irrigation points;
- i = individual irrigation points;
- = specific weight of the fluid (N/m3);
- = total flow demanded by the network (m3/s);
- = piezometric head of the reservoir. For a pumped system, the value is the manometric height;
- = flow demanded by each irrigation point (m3/s);
- = piezometric head of the consumption node (m);
- = total energy (kW) supplied to the system. This term is equal to ET, which is later defined;
- = energy consumed by all irrigation points (kW). This term will be defined as ERI plus ETRI;
- = Exchange of internal energy. In an adiabatic system, it is equal to friction losses. This term will be defined as EFR.
- -
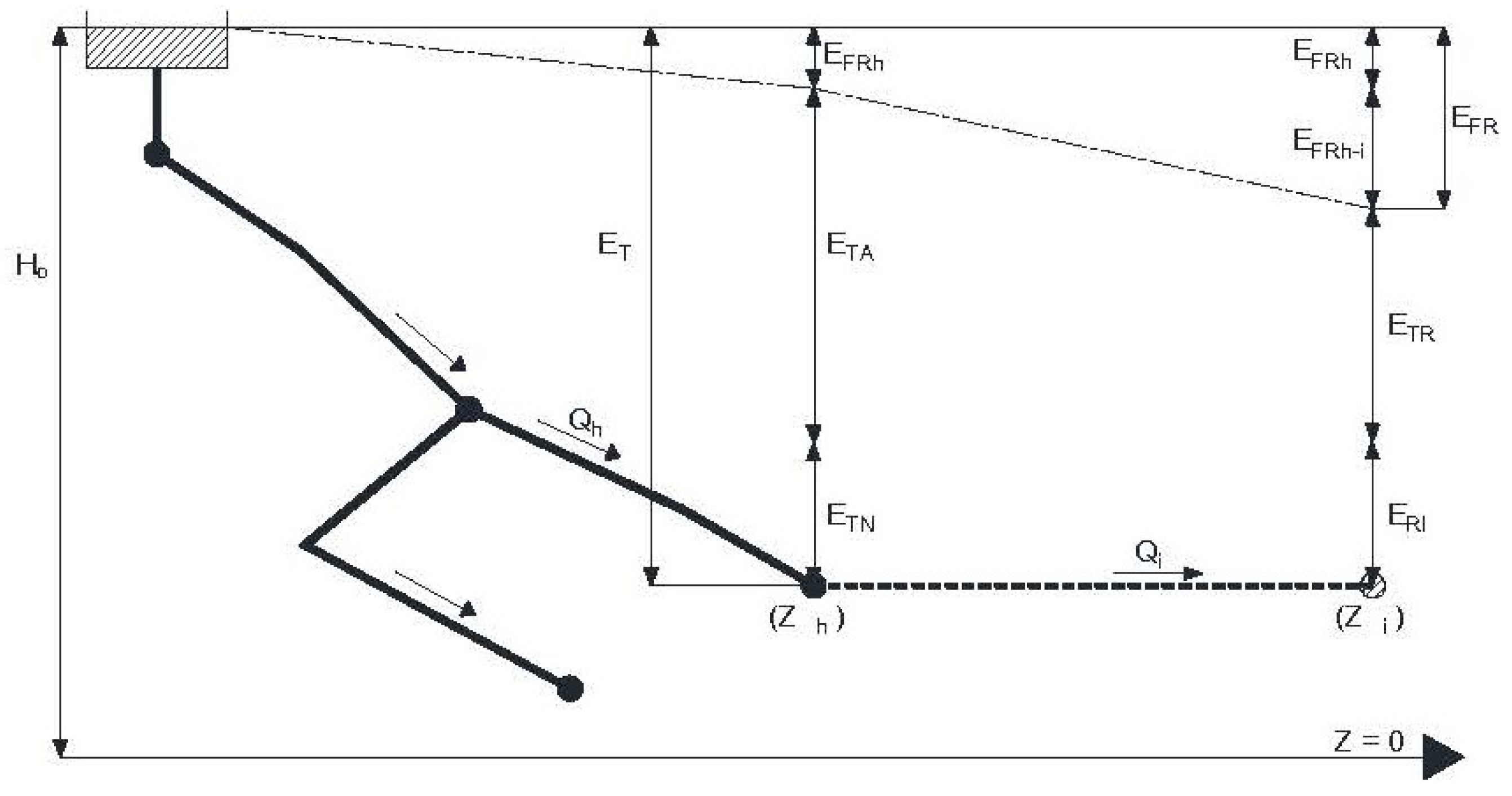
- Total Energy (ETi): potential total energy in an irrigation point when the consumption is null in the entire network. It corresponds to the static energy (i.e., potential) of the node. For an irrigation point along a time interval, the value is:
- -
- Friction Energy (EFRi): for a time interval, it is the energy dissipated in the network by the water coming from head until the irrigation point.
- -
- Theoretical Energy Necessary (ETNi): it is the minimum energy required in a hydrant or line to ensure the minimum pressure of irrigation in the more unfavorable point. The value is:
- -
- Energy Required for Irrigation (ERIi): during an interval of time, it is the minimum energy required at an irrigation point to ensure the irrigation water evenly. The value is:
- -
- Theoretical Available Energy (ETAi): it is the available energy for recovery in a hydrant or line. The recovery coefficient in a hydrant or line (CRT) depends on losses existent between the hydrant (or pipeline) and the most disadvantageous consumption node. It is equal to the sum of the theoretical energy recoverable plus the theoretical energy unrecoverable (ENRT). The value of this energy for a particular time duration, is defined as:
- -
- Theoretical Recoverable Energy (ETRi): it is the maximum theoretical recoverable energy in an irrigation point, hydrant or line of the network, ensuring at downstream the minimum pressure of irrigation.
- -
- Theoretical unrecoverable Energy (ENTRi): it is the energy in a hydrant or line on the network that cannot be recovered. This energy is necessary to assume the losses from the line or hydrant to the more unfavorable irrigation point.
- -
- Recovery coefficient in hydrant or line (CRTi): it is the quotient between ETRi and ETAi in an irrigation point, hydrant or line of the network. It represents the proportion of recovery energy over available energy.
- i)
- In plot of cultivation—in this case, the private user needs to reduce pressure down to 30 m w.c. to carry out drip irrigation. Generally, the user installs a pressure reducer to dissipate the excess energy. This element can be replaced by a pico-turbine to generate energy for self-consumption. This energy can be used in remote-control system, cleaning of filters, lighting and others similar consumptions.
- ii)
- In the hydrant pipe—when the hydrant supplies to flat topography, reduction of pressure can be done. In an operating network, this reduction is carried out with a pressure reducing valve. This recovery could potentially be done if a suitable turbine could be installed.
- iii)
- In pipe branch—in networks with large extension and irregular orography, some parts of the network can achieve higher pressure than necessary, forcing pressure to be reduced on a pipe branch. Currently, this reduction is possible by using a reducing valve installed on this branch. These valves can be replaced by turbines or pumps as turbines (PAT) [14] depending on the system characteristics to increase the energy efficiency of the network.
3. Case Study
3.1. Description
- a)
- To make use of records of the water metered in the irrigation points. There are records since 2003 (year that network began to operate). In each plot, registers were taken quarterly corresponding to the months of March, June, September and December.
- b)
- To calculate the flow design (water requirements) for each of the considered plot, according to the crop and characteristics of the irrigation installation (distance between drippers and type). The number of sectors is established depending on the area of plots. This has allowed an allocation of irrigation according to the existing installation (Figure 1).
- c)
- To perform interviews of users and operating staff for estimating farmer habits. The type of irrigation management at the annual, monthly, weekly and daily levels has been analyzed in this questionnaire. Based on these interviews, different consumption patterns have been established. These patterns take in to account the irrigation habits of farmers: weekly trend, maximum days between irrigations and irrigation duration (Inputs 2, 3 and 4 in Figure 1).
3.2. Methodology
3.2.1. Historical Consumption Data and Probability Function
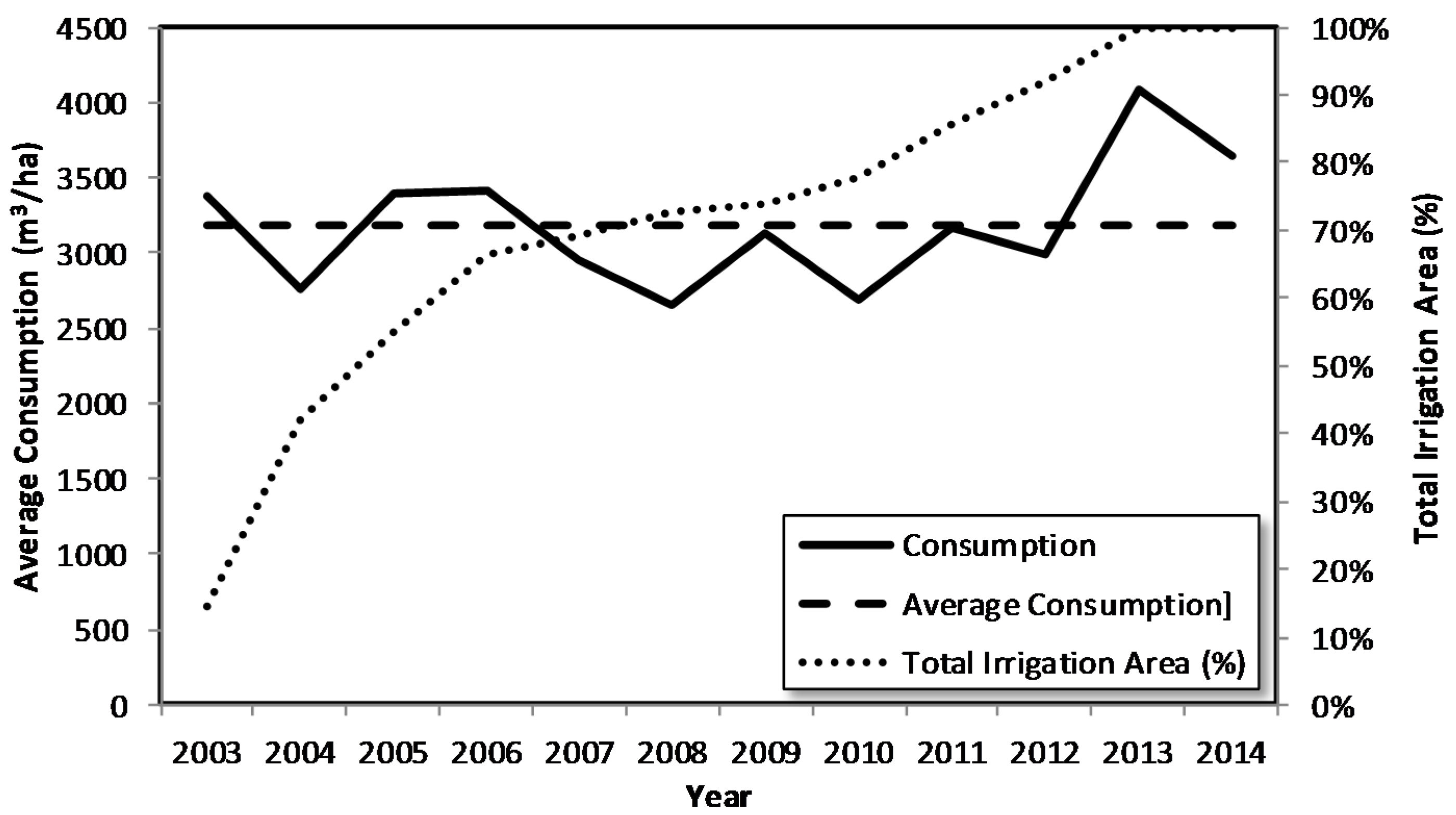
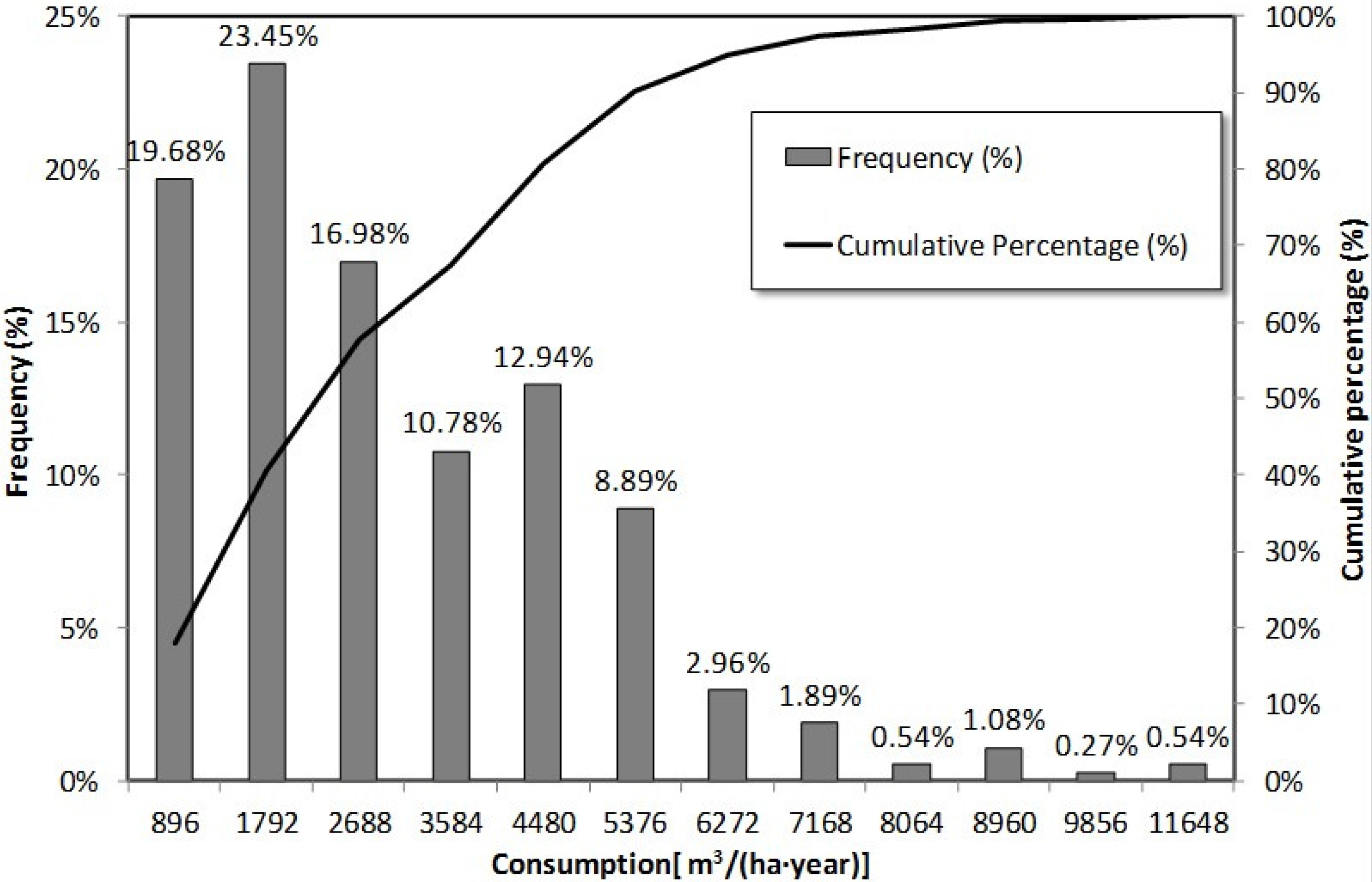
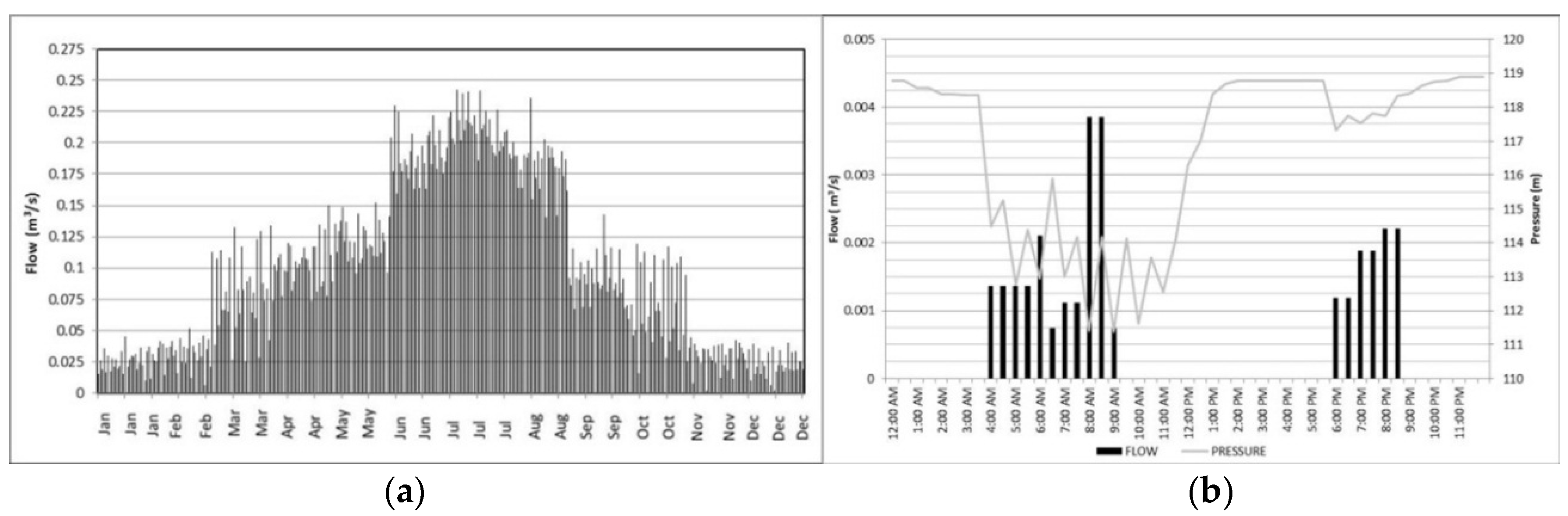
- The annual consumption is estimated for each irrigation point, grouping them in terms of similar consumptions. This classification has provided the distribution presented in Figure 7.
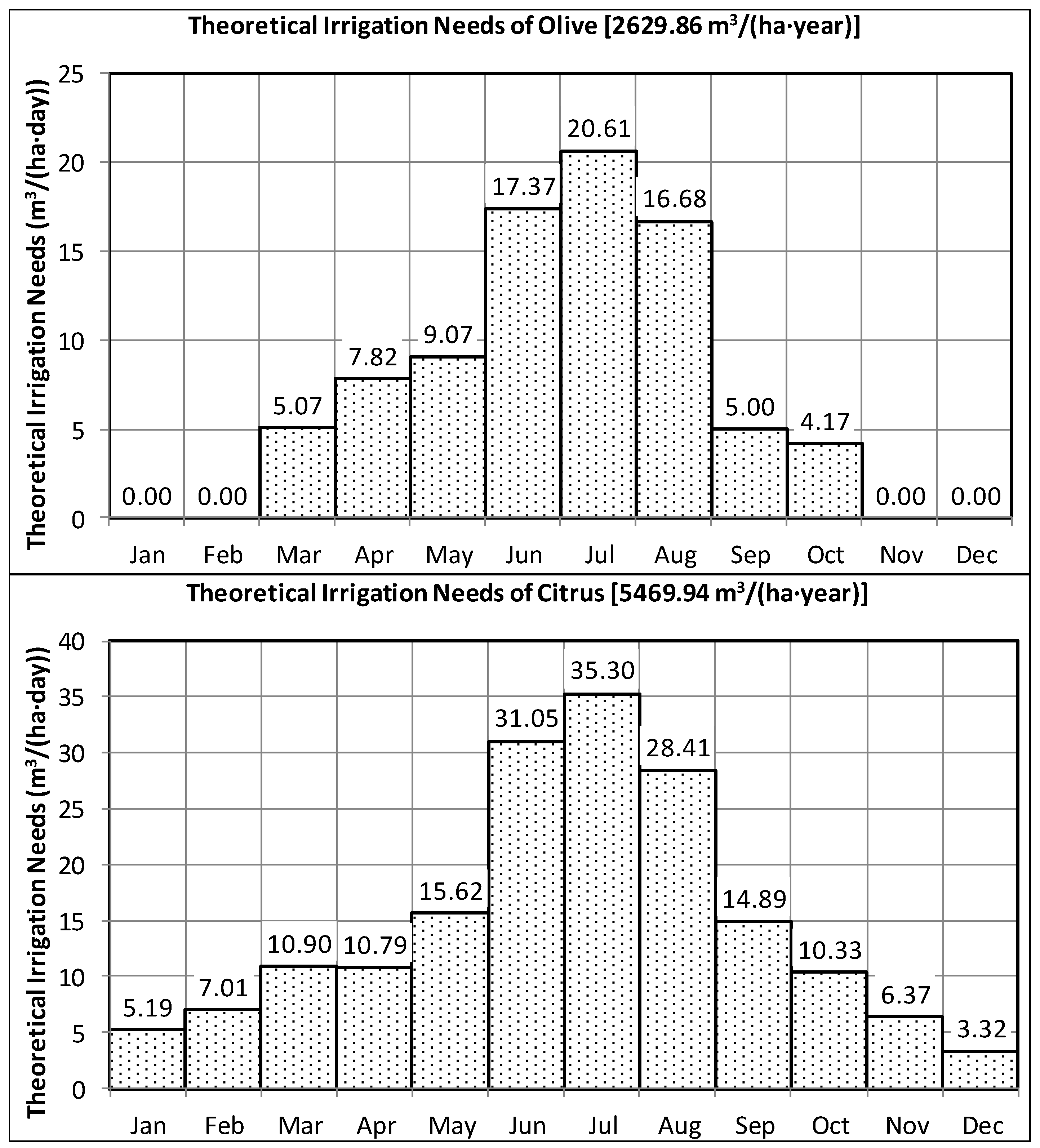
- In order to determine the distribution of daily consumption, specific weights for crops of citrus and olive needs to be considered, according to the registered consumptions. The monthly pattern of irrigation needs has been set taking into account consumer groups (Figure 7). On the one hand, the irrigation points with consumptions lower than 3584 m3/ha have been assigned the patterns of consumption under the name “Crop of Olive” (Figure 8). On the other hand, the irrigation points with consumptions higher than 4480 m3/ha have been assigned the patterns of consumption under the name “Crop of Citrus” (Figure 8).
3.2.2. Pattern of Irrigation Habits
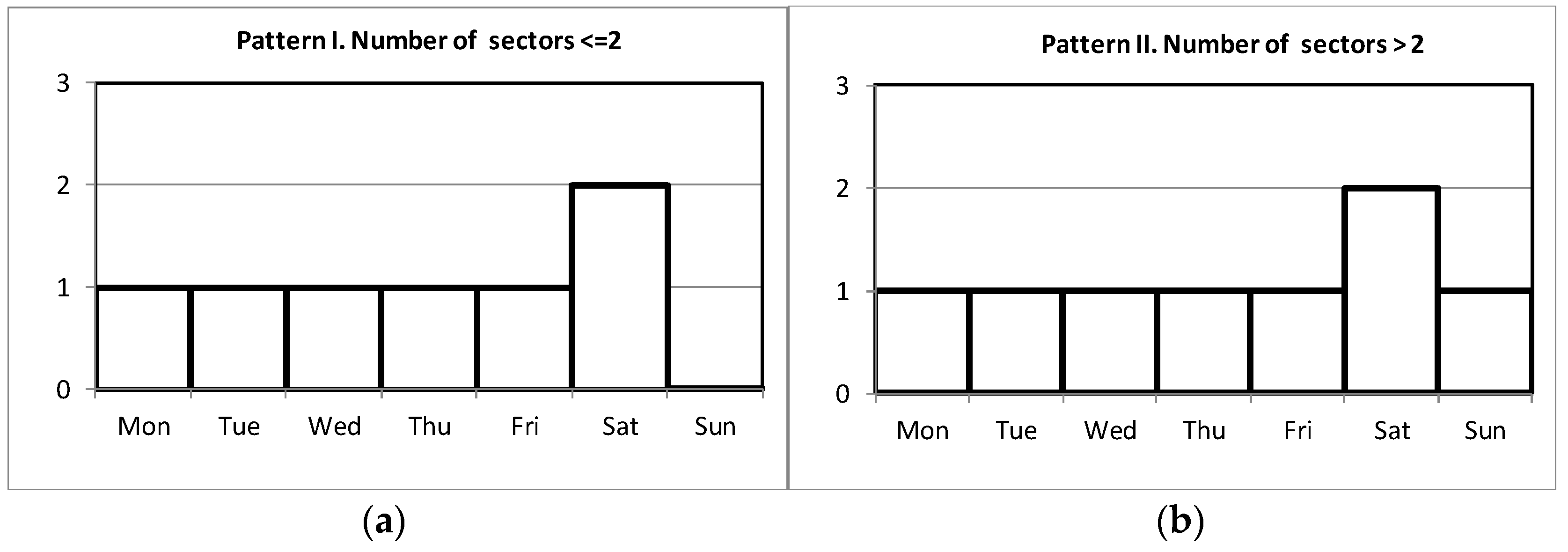
- Analyzing the information obtained from interviews, two trends of irrigations have been depicted. Small farmers avoid Sunday as irrigation day and Saturday appears with double preference than the rest of the days (Figure 9a). Big farmers also have double preference for Saturday, but do not avoid irrigation on Sunday (Figure 9b).
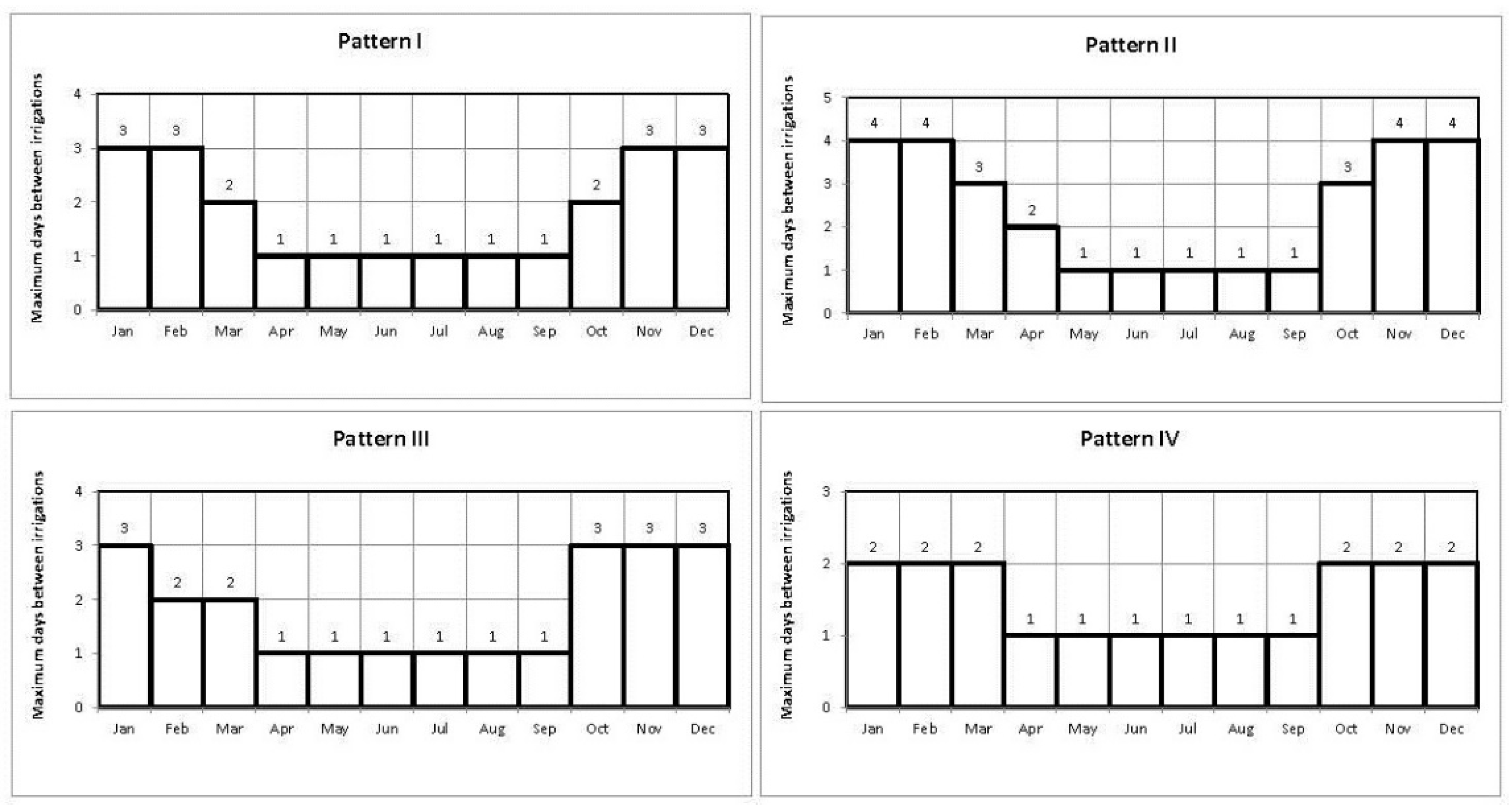
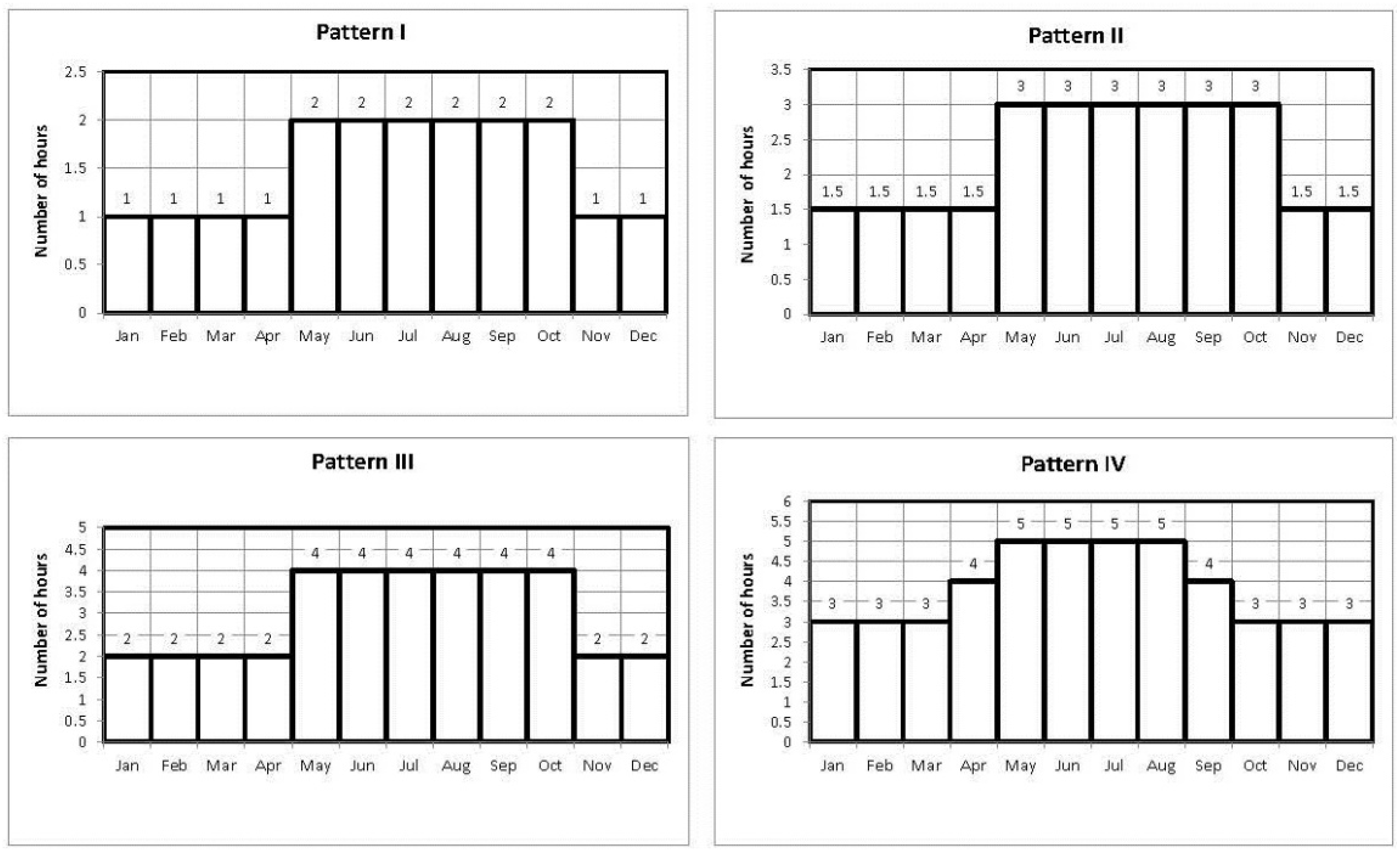
- Distribution of maximum days between irrigations: these patterns refer to the maximum interval between watering. Irrigation occurs every day during the months of higher consumption (May, June, July, August and September). In remaining months, the intervals of irrigation increase, being not a clear and well-defined pattern for all farmers. Each farmer chooses the interval according to different factors (e.g., rain, availability and soil properties). Based on the results of the interviews, four distributions have been defined. According to the results of the requested data for farmer habits across surveys, patterns have been assigned. Pattern I has been assigned approximately to 40% of the irrigation points, pattern II to 20%, pattern III to 20% and pattern IV to the other 20%. This assignment has been carried out randomly (Figure 10).
- Patterns of irrigation duration: based on the requested information four distributions have been proposed. Again, pattern I has been assigned approximately to 40% of the irrigation points, pattern II to 20%, pattern III to 20% and pattern IV to other 20%. This assignment has been carried out randomly (Figure 11).
- Distribution of irrigation start probability: farmers tend to irrigate in certain particular hours of the day. This aspect is considered in this methodology by using the patterns for the probability of starting irrigation in the different schedules. The watering schedule between 10 A.M. and 4 P.M. is chosen in the months of January, February, March, April, October, November and December. However, farmers irrigate in different light hours in summer months to avoid warmer hours and night. Therefore, three patterns have been developed to define the probability (see Figure 1, step 4).
4. Results
4.1. Basic Characteristics
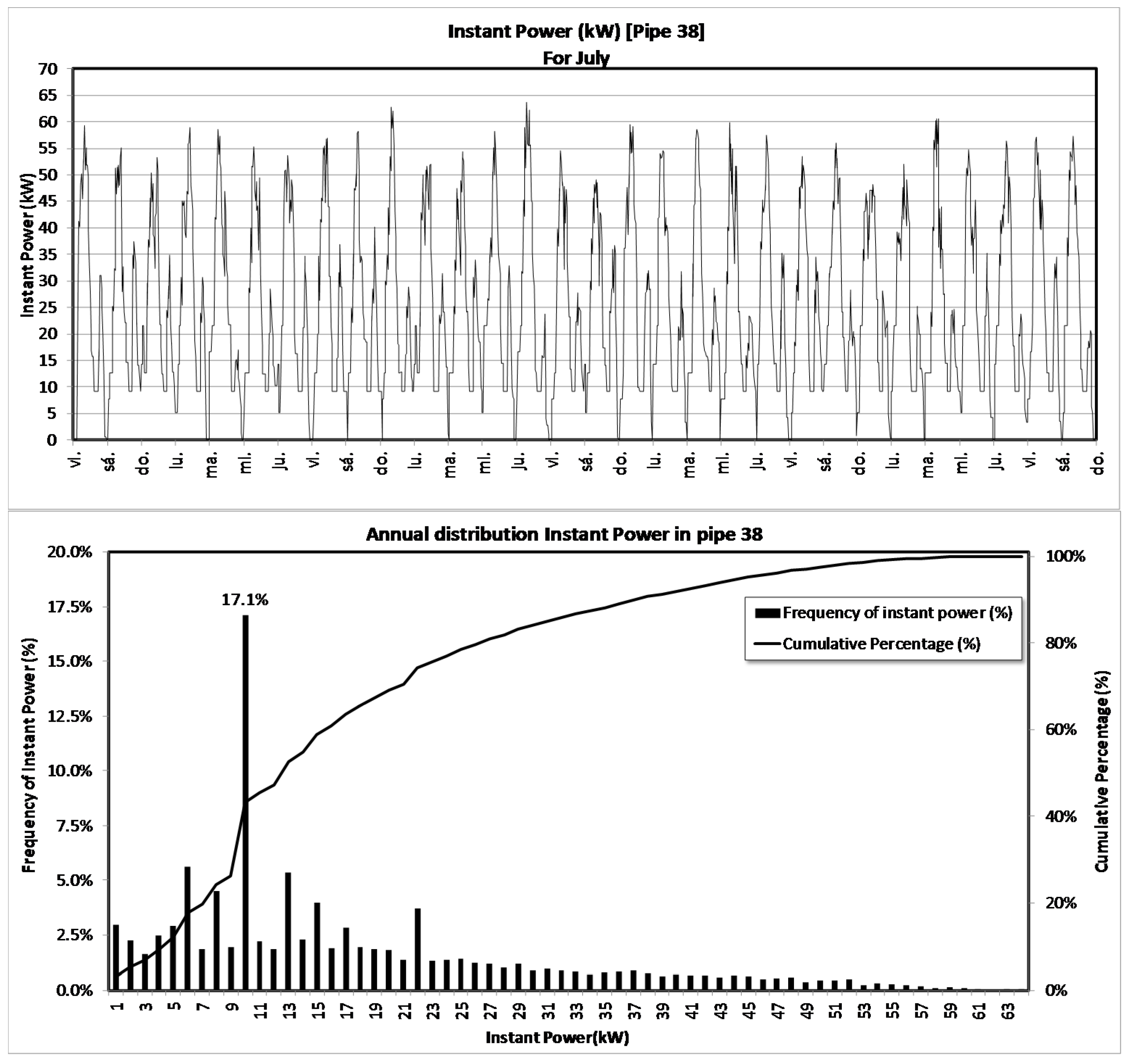
4.2. Flows in the Network
4.3. Water-Energy Nexus Estimation
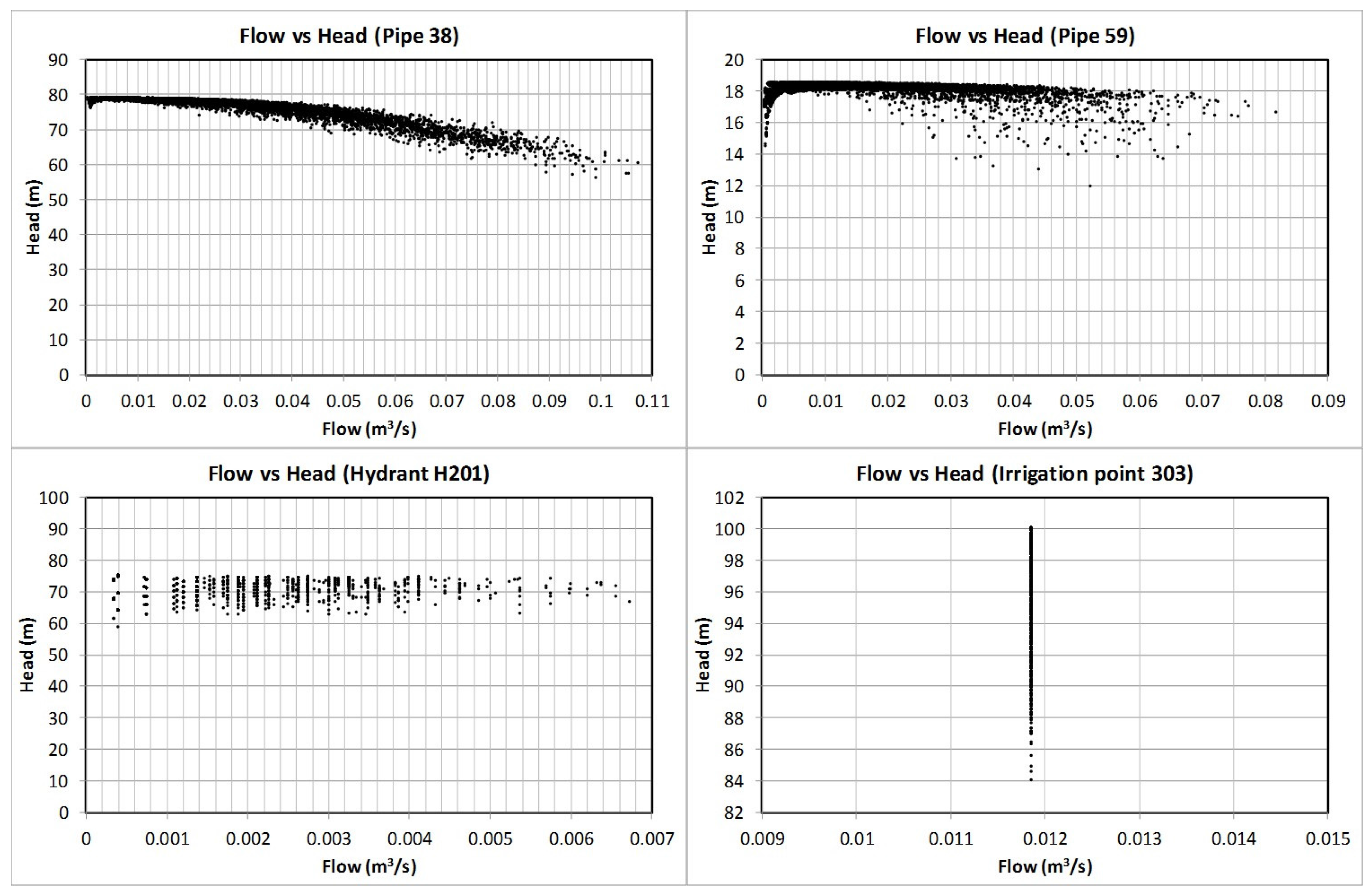
4.4. Theoretical Recoverable Energy
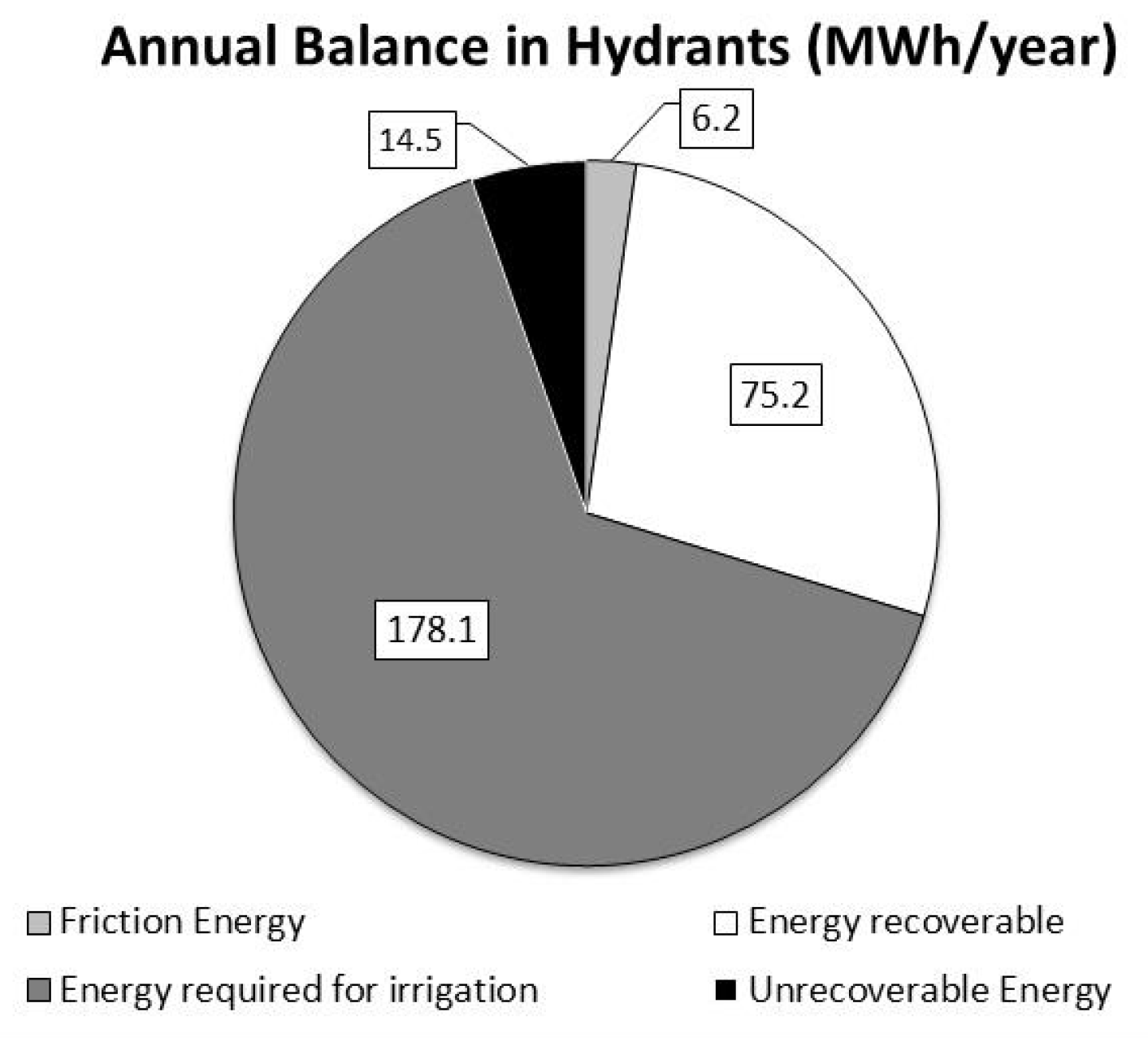
4.5. Global Energy Balance
4.6. Economic Feasibility
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kahil, M.; Albiac, J.; Dinar, A. Improving the performance of water policies: Evidence from drought in Spain. Water 2016, 8, 34. [Google Scholar] [CrossRef]
- Llop, M.; Ponce-Alfonso, X. Water and agriculture in a Mediterranean region: The search for a sustainable water policy strategy. Water 2016, 8, 66. [Google Scholar] [CrossRef]
- Corominas, J. Agua y Energía en el riego en la época de la sostenibilidad. Ing. Agua 2010, 17, 219–233. [Google Scholar] [CrossRef]
- Seoane, P.; Allué, R.; Postigo, M.J.; Cordón, M.A. Boletín Mensual de Estadística; Ministerio de Agricultura, Alimentación y Medio Ambiente: Madrid, Spain, 2013. [Google Scholar]
- FAO. Agua Y Cultivos; FAO: Rome, Italy, 2002; Availiable online: http://www.fao.org/docrep/005/y3918s/y3918s10.htm (accessed on 30 April 2016).
- MAGRAMA. El riego Localizado Alcanza el 48.23% de la Superficie Regada en España. Minist Agric Aliment y Medio Ambient. Available online: http://www.magrama.gob.es/gl/prensa/noticias/el-riego-localizado-alcanza-el-4823--de-la-superficie-regada-en-espa%C3%B1a-/tcm7-312671-16 (accessed on 15 April 2016).
- FAO. Superficie Equipada para el Riego. Available online: http://www.fao.org/nr/water/aquastat/infographics/Irrigation_esp.pdf (accessed on 15 April 2016).
- Pardo, M.A.; Manzano, J.; Cabrera, E.; García-Serra, J. Energy audit of irrigation networks. Biosyst. Eng. 2013, 115, 89–101. [Google Scholar] [CrossRef]
- Coelho, B.; Andrade-Campos, A. Efficiency achievement in water supply systems—A review. Renew Sustain. Energy. Rev. 2014, 30, 59–84. [Google Scholar] [CrossRef]
- Baki, S.; Makropoulos, C. Tools for energy footprint assessment in urban water systems. Procedia Eng. 2014, 89, 548–556. [Google Scholar] [CrossRef]
- Okadera, T.; Chontanawat, J.; Gheewala, S.H. Water footprint for energy production and supply in Thailand. Energy 2014, 77, 49–56. [Google Scholar] [CrossRef]
- Herath, I.; Deurer, M.; Horne, D.; Singh, R.; Clothier, B. The water footprint of hydroelectricity: A methodological comparison from a case study in New Zealand. J. Clean. Prod. 2011, 19, 1582–1589. [Google Scholar] [CrossRef]
- Endo, A.; Burnett, K.; Orencio, P. Methods of the water-energy-food nexus. Water 2015, 7, 5806–5830. [Google Scholar] [CrossRef]
- Mendoza-Grimón, V.; Hernández-Moreno, J.; Palacios-Díaz, M. Improving water use in fodder production. Water 2015, 7, 2612–2621. [Google Scholar] [CrossRef]
- Ramos, H.M.; Vieira, F.; Covas, D.I.C. Energy efficiency in a water supply system: Energy consumption and CO2 emission. Water Sci. Eng. 2010, 3, 331–340. [Google Scholar]
- Choulot, A. Energy Recovery in Existing Infrastructures with Small Hydropower Plants; FP6 Project Shapes (Work Package 5—WP5); European Directorate for Transport and Energy: Brussels, Belgium, 2010. [Google Scholar]
- Carravetta, A.; Fecarotta, O.; Del Giudice, G.; Ramos, H. Energy recovery in water systems by PATs: A comparisons among the different installation schemes. Procedia Eng. 2014, 70, 275–284. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Pump as turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Energy production in water distribution networks: A PAT design strategy. Water Resour. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Oreste, F.; Ramos, H. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Ramos, H.; Borga, A.; Simão, M. New design solutions for low-power energy production in water pipe systems. Water Sci. Eng. 2009, 2, 69–84. [Google Scholar]
- Adhau, S.P.; Moharil, R.M.; Adhau, P.G. Mini-hydro power generation on existing irrigation projects: Case study of Indian sites. Renew. Sustain. Energy Rev. 2012, 16, 4785–4795. [Google Scholar] [CrossRef]
- Butera, I.; Balestra, R. Estimation of the hydropower potential of irrigation networks. Renew. Sustain. Energy. Rev. 2015, 48, 140–151. [Google Scholar] [CrossRef]
- Tilmant, A.; Goor, Q.; Pinte, D. Agricultural-to-hydropower water transfers: Sharing water and benefits in hydropower-irrigation systems. Hydrol. Earth Syst. Sci. 2009, 13, 1091–1101. [Google Scholar] [CrossRef]
- Tarragó, E.F.; Ramos, H. Micro-Hydro Solutions in Alqueva Multipurpose Project (AMP) towards Water-Energy-Environmental Efficiency Improvements. Bachelor’s Thesis, Universidade de Lisboa, Lisboa, Portugal, 2015. [Google Scholar]
- Clément, R. Calcul des débits dans le réseaux d’irrigation fonctionnant á la demande. La Houille Blanche 1966, 5, 553–575. [Google Scholar] [CrossRef]
- Mavropoulos, T.I. Sviluppo di una nuova formula per il calcolo delle portate di punta nelle reti irrigue con esercizio alla domanda. Riv. Irrig. Dren. 1997, 44, 27–35. [Google Scholar]
- Maidment, D.R.; Hutchinson, P.D. Modeling water demands of irrigation projects. J. Irrig. Drain. Eng. 1983, 109, 405–418. [Google Scholar] [CrossRef]
- Alandi, P.P.; Pérez, P.C.; Álvarez, J.F.O.; Hidalgo, M.; Martín-Benito, J.M.T. Pumping selection and regulation for water-distribution networks. J. Irrig. Drain. Eng. 1997, 131, 273–281. [Google Scholar] [CrossRef]
- Aliod, R.; Eizaguerri, A.; Estrada, C. Dimensionado y análisis hidráulico de redes de distribución a presión en riego a la demanda: Aplicación del programa GESTAR. Riegos Dren. XXI 1997, 92, 22–38. [Google Scholar]
- Pereira, L.S.; Teixeira, J.L. Modelling for Irrigation Delivery Scheduling: Simulation of Demand at Sector Level with Models ISAREG and IRRICEP; FAO: Rome, Italy, 1994. [Google Scholar]
- Lamaddalena, N.; Sagardoy, J.A. Performance Analysis of On-Demand Pressurized Irrigation Systems; FAO: Roma, Italy, 2007. [Google Scholar]
- Rossman, L.A. EPANET 2 User’s Manual; U.S. Environmental Protection Agency (EPA): Cincinnati, OH, USA, 2000.
- White, F.M. Fluid Mechanics, 6th ed.; McGrau-Hill: Madrid, Spain, 2008. [Google Scholar]
- Cabrera, E.; Cobacho, R.; Soriano, J. Towards an energy labelling of pressurized water networks. Procedia Eng. 2014, 70, 209–217. [Google Scholar] [CrossRef]
- Klein, G.; Krebs, M.; Hall, V.; O’Brien, T.; Blevins, B.B. California’s Water–Energy Relationship; California Energy Commission: Sacramento, CA, USA, 2005.
- Shrestha, S.; Dhakal, S.; Shrestha, A.; Kaneko, S.; Kansal, A. Water-Energy-Carbon Nexus in Cities: Cases from Bangkok, New Delhi, Tokyo. In Water Energy Food Nexus: International Cooperation and Technology Transfer; Asian Institute of Technology: Paris, France, 2015. [Google Scholar]
- Spadaro, J.V.; Langlois, L.; Hamilton, B. Greenhouse Gas Emissions of Electricity Generation Chains: Assessing the Difference. IAEA Bull. 2000, 42, 19–28. [Google Scholar]
- Weisser, D. A guide to life-cycle greenhouse gas (GHG) emissions from electric supply technologies. Energy 2007, 32, 1543–1559. [Google Scholar] [CrossRef]
- Arora, M.; Aye, L.; Malano, H.; Ngo, T. Water-energy-GHG emissions accounting for urban water supply: A case study on an urban redevelopment in Melbourne. Water Util. J. 2013, 6, 9–18. [Google Scholar]
- Nair, S.; George, B.; Malano, H.M.; Arora, M.; Nawarathna, B. Water–energy–greenhouse gas nexus of urban water systems: Review of concepts, state-of-art and methods. Resour. Conserv. Recycl. 2014, 89, 1–10. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Tamburino, V.; Zimbone, S.M. A simple method to evaluate the technical and economic feasibility of micro hydro power plants in existing irrigation systems. Renew. Energy 2016, 85, 498–506. [Google Scholar] [CrossRef]
- Castro, A. Minicentrales Hidroeléctricas; Instituto para la Diversificación y Ahorro de la Energía: Madrid, Spain, 2006. [Google Scholar]
- Elbatran, A.H.; Yaakob, O.B.; Ahmed, Y.M.; Shabara, H.M. Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. Renew. Sustain. Energy Rev. 2015, 43, 40–50. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]


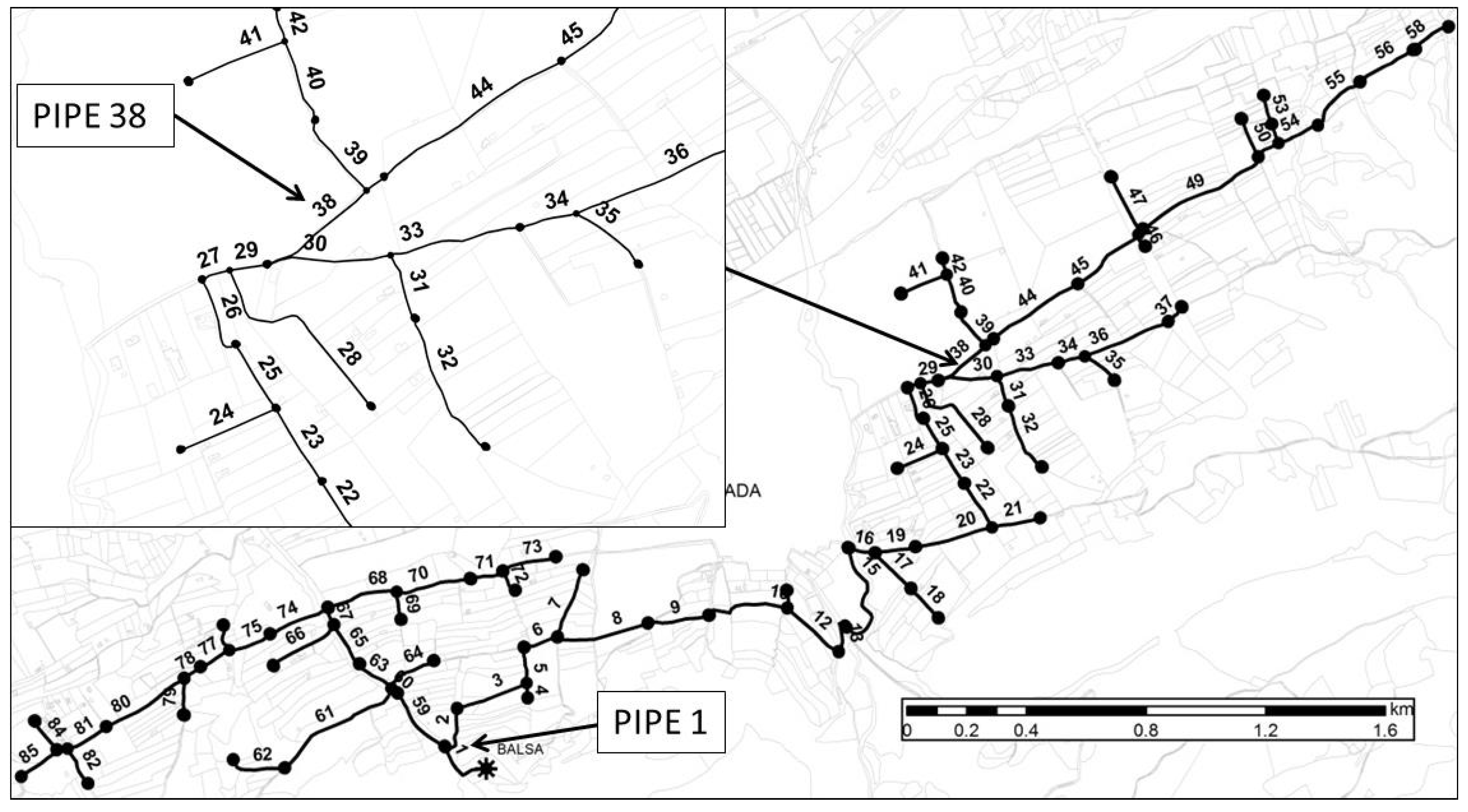
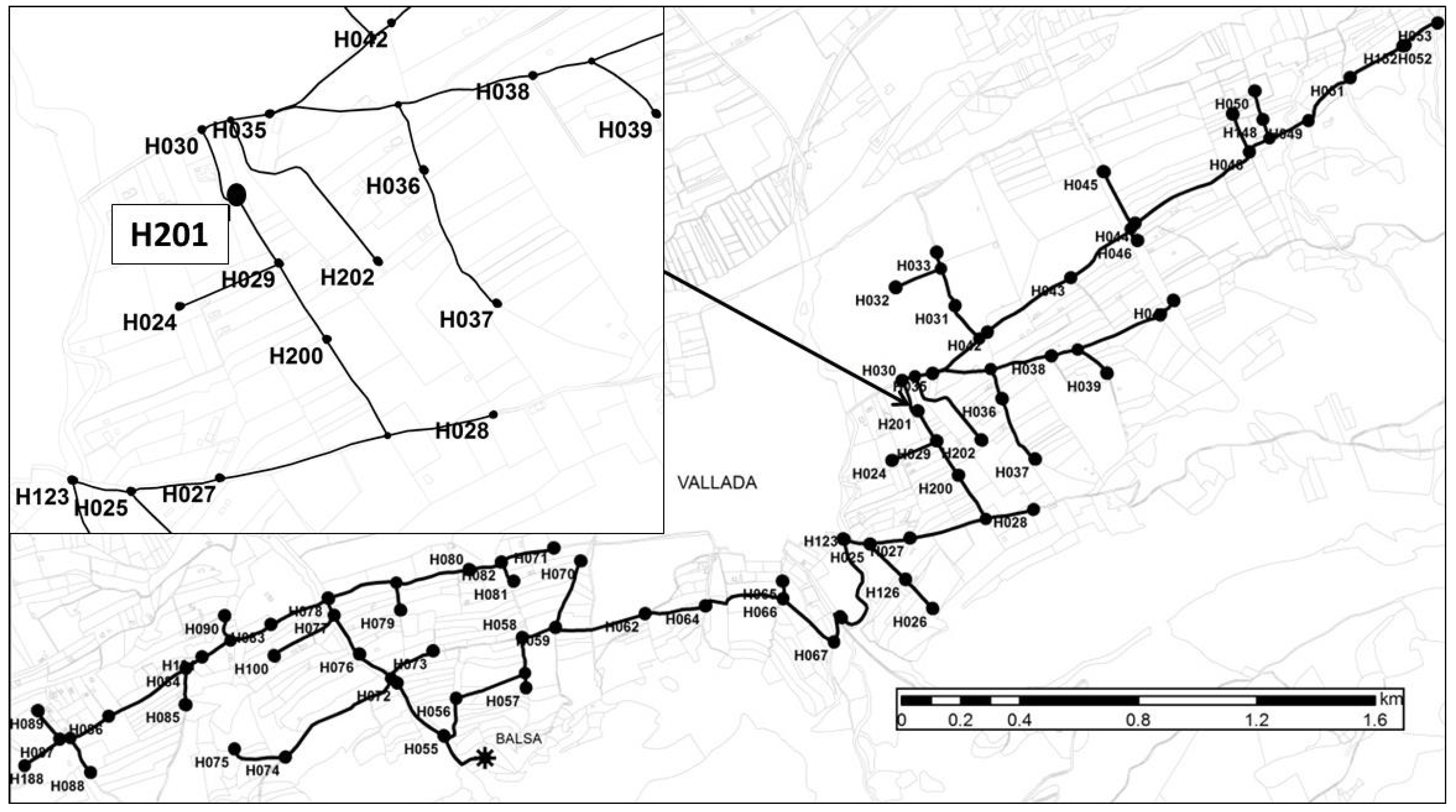
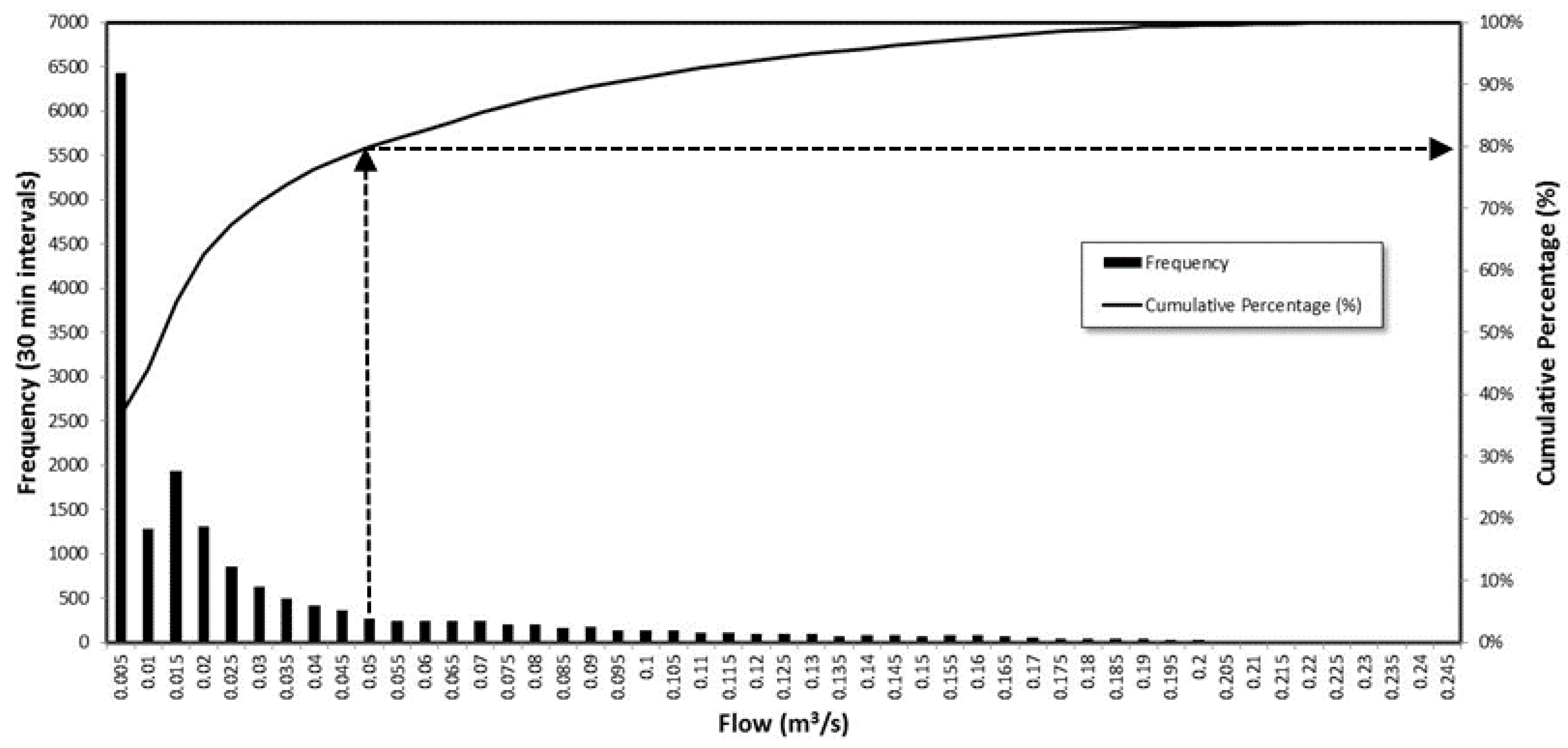
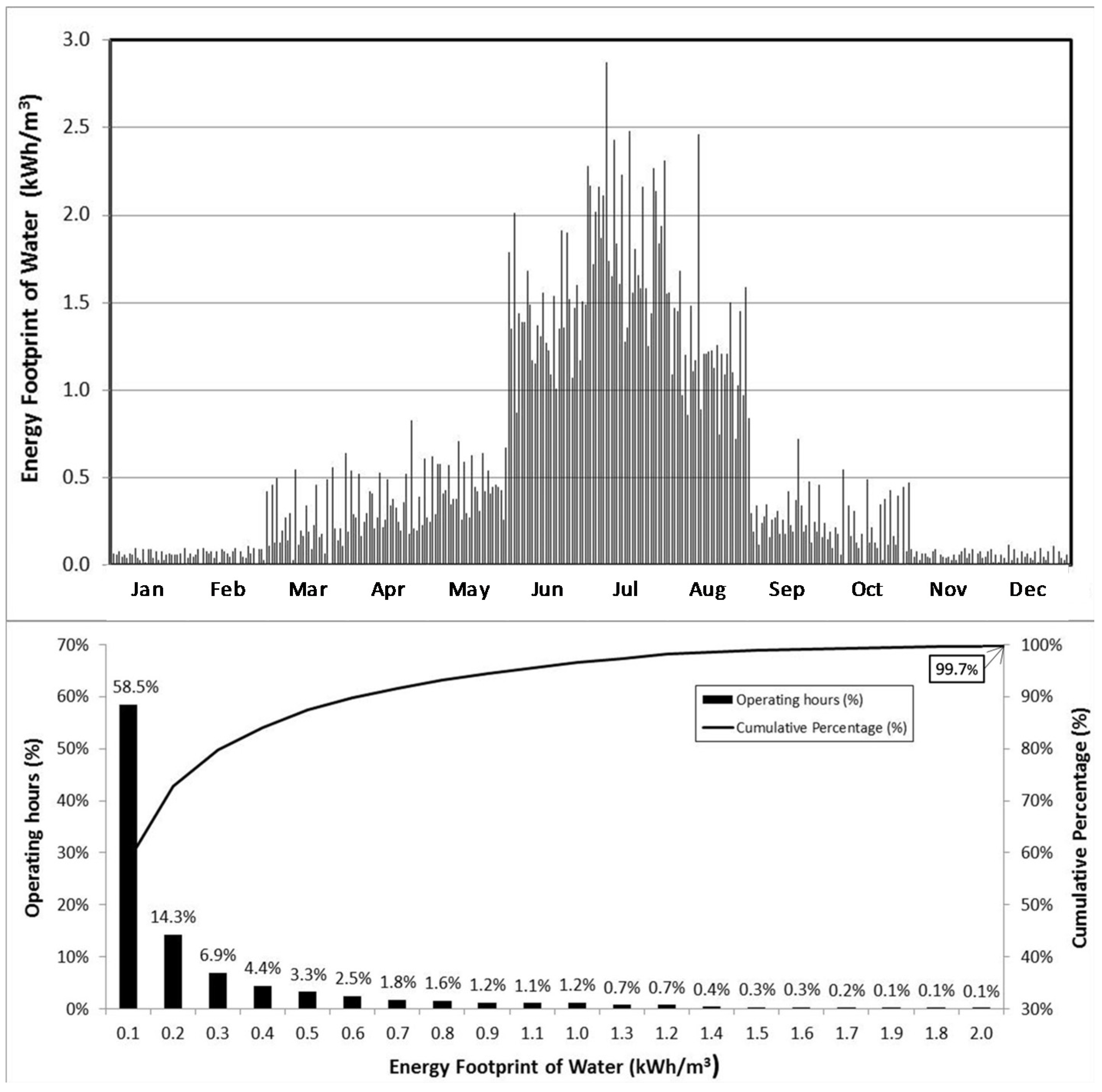
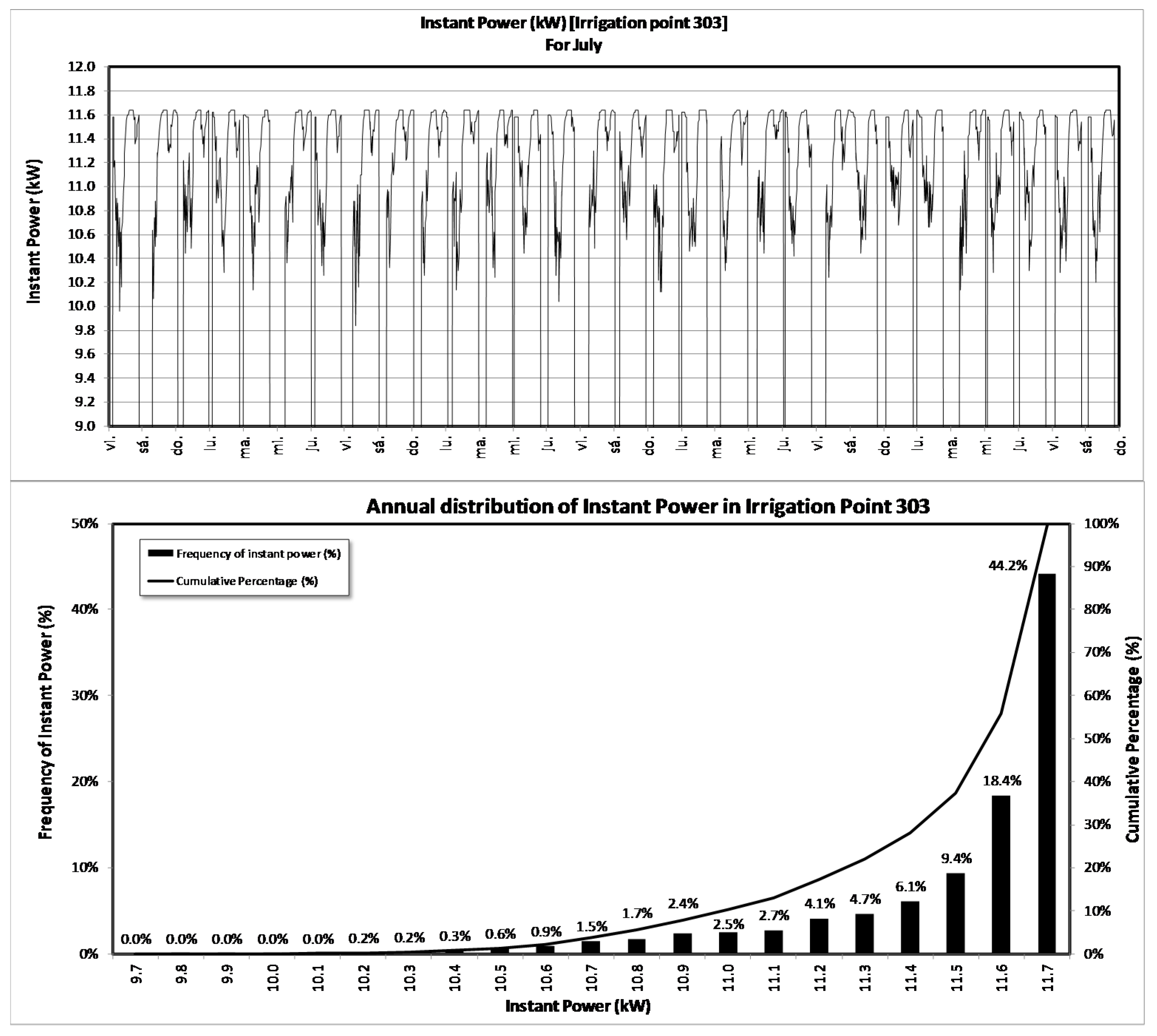
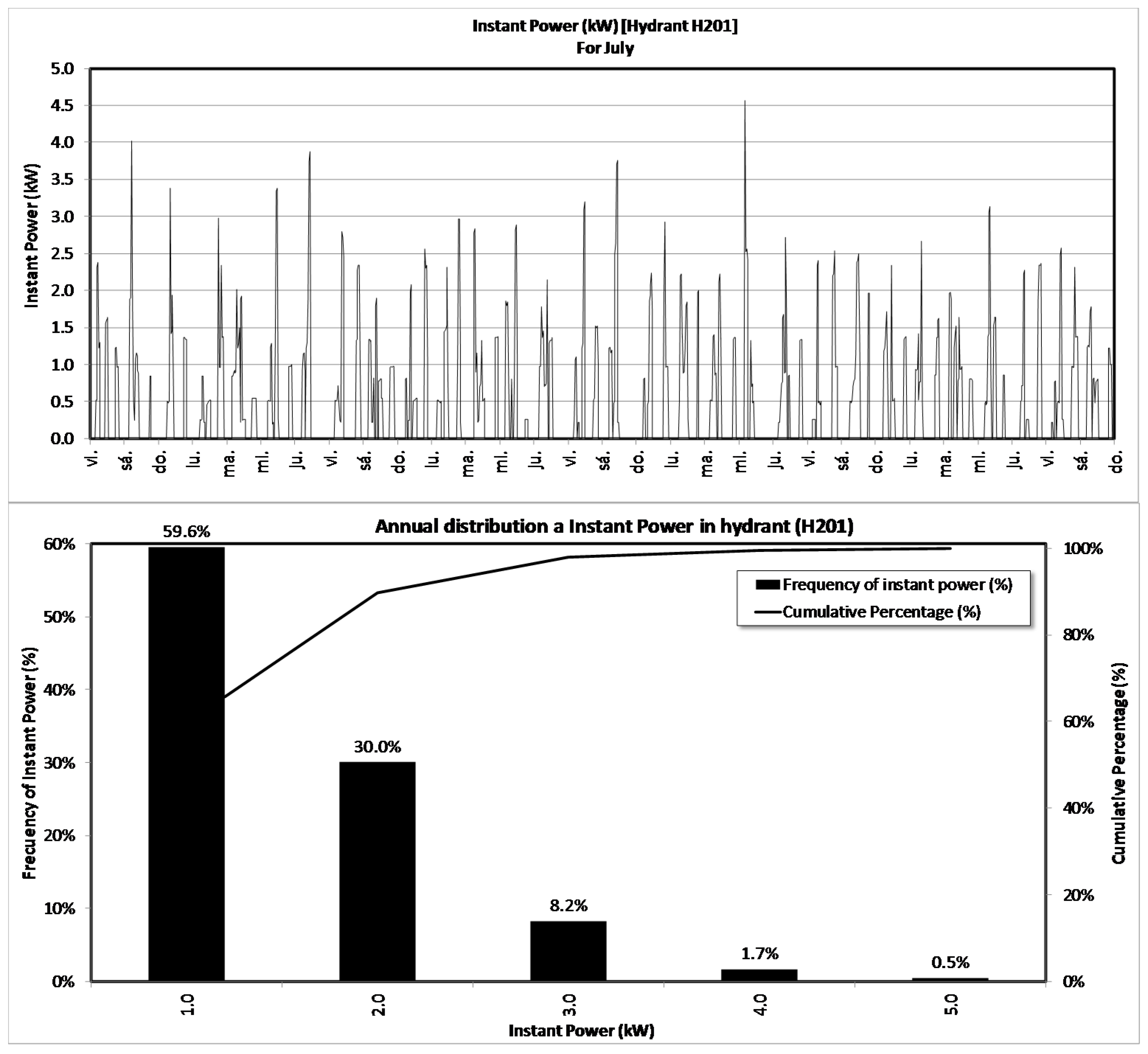
| HYDRANT | ERT | CRT | HYDRANT | ERT | CRT |
|---|---|---|---|---|---|
| MWh/Year | MWh/Year | ||||
| H024 | 1.99 | 0.66 | H065 | 0.80 | 0.63 |
| H025 | 1.56 | 0.76 | H066 | 0.13 | 0.57 |
| H026 | 0.48 | 0.59 | H067 | 0.22 | 0.53 |
| H027 | 1.92 | 0.67 | H070 | 1.40 | 0.69 |
| H028 | 0.12 | 0.46 | H071 | 0.40 | 0.72 |
| H029 | 2.27 | 0.72 | H072 | 0.28 | 0.35 |
| H030 | 0.77 | 0.80 | H073 | 0.22 | 0.45 |
| H031 | 1.36 | 0.81 | H074 | 0.64 | 0.40 |
| H032 | 3.94 | 0.73 | H075 | 0.31 | 0.54 |
| H033 | 4.19 | 0.81 | H076 | 1.34 | 0.55 |
| H035 | 3.57 | 0.79 | H077 | 0.52 | 0.64 |
| H036 | 2.50 | 0.76 | H078 | 3.68 | 0.69 |
| H037 | 1.12 | 0.69 | H079 | 0.76 | 0.53 |
| H038 | 3.54 | 0.71 | H080 | 1.41 | 0.66 |
| H039 | 0.64 | 0.69 | H081 | 0.40 | 0.72 |
| H040 | 3.57 | 0.65 | H082 | 1.28 | 0.71 |
| H042 | 33.73 | 0.80 | H083 | 0.87 | 0.72 |
| H043 | 9.13 | 0.81 | H084 | 0.80 | 0.67 |
| H044 | 5.60 | 0.78 | H085 | 1.50 | 0.58 |
| H045 | 16.12 | 0.83 | H086 | 0.48 | 0.52 |
| H046 | 5.14 | 0.72 | H087 | 0.27 | 0.58 |
| H047 | 5.03 | 0.80 | H088 | 0.51 | 0.26 |
| H048 | 13.37 | 0.80 | H089 | 0.73 | 0.59 |
| H049 | 0.26 | 0.82 | H090 | 0.59 | 0.69 |
| H050 | 1.93 | 0.77 | H100 | 0.89 | 0.65 |
| H051 | 2.67 | 0.59 | H101 | 1.05 | 0.63 |
| H052 | 0.86 | 0.77 | H123 | 1.78 | 0.79 |
| H053 | 11.05 | 0.84 | H126 | 0.47 | 0.68 |
| H055 | 0.04 | 0.14 | H140 | 0.73 | 0.74 |
| H056 | 0.01 | 0.28 | H148 | 0.32 | 0.82 |
| H057 | 0.55 | 0.26 | H152 | 2.47 | 0.72 |
| H058 | 0.99 | 0.60 | H188 | 2.81 | 0.68 |
| H059 | 0.46 | 0.61 | H200 | 1.35 | 0.77 |
| H062 | 2.32 | 0.57 | H201 | 1.58 | 0.68 |
| H064 | 0.22 | 0.28 | H202 | 2.08 | 0.76 |
| PIPE | ERT | CRT | PIPE | ERT | CRT |
|---|---|---|---|---|---|
| MWh/year | MWh/year | ||||
| 1 | 4.29 | 0.16 | 44 | 55.58 | 0.64 |
| 2 | 17.56 | 0.29 | 45 | 48.35 | 0.63 |
| 3 | 18.64 | 0.23 | 46 | 5.14 | 0.72 |
| 4 | 0.55 | 0.26 | 47 | 16.12 | 0.83 |
| 5 | 26.83 | 0.26 | 48 | 32.61 | 0.62 |
| 6 | 26.41 | 0.25 | 49 | 28.13 | 0.60 |
| 7 | 1.40 | 0.69 | 50 | 5.03 | 0.80 |
| 8 | 25.85 | 0.25 | 51 | 14.49 | 0.60 |
| 9 | 24.84 | 0.29 | 52 | 2.24 | 0.81 |
| 10 | 41.64 | 0.40 | 53 | 1.93 | 0.77 |
| 11 | 0.80 | 0.63 | 54 | 12.88 | 0.58 |
| 12 | 41.10 | 0.33 | 55 | 12.70 | 0.59 |
| 13 | 40.96 | 0.28 | 56 | 12.62 | 0.72 |
| 14 | 40.96 | 0.28 | 57 | 0.86 | 0.77 |
| 15 | 40.96 | 0.25 | 58 | 11.05 | 0.84 |
| 16 | 40.42 | 0.24 | 59 | 10.56 | 0.46 |
| 17 | 0.77 | 0.42 | 60 | 10.18 | 0.43 |
| 18 | 0.48 | 0.59 | 61 | 0.85 | 0.39 |
| 19 | 39.40 | 0.27 | 62 | 0.31 | 0.54 |
| 20 | 38.64 | 0.35 | 63 | 5.79 | 0.21 |
| 21 | 0.12 | 0.46 | 64 | 0.22 | 0.45 |
| 22 | 83.51 | 0.57 | 65 | 5.27 | 0.17 |
| 23 | 82.51 | 0.52 | 66 | 0.89 | 0.65 |
| 24 | 1.99 | 0.66 | 67 | 4.90 | 0.16 |
| 25 | 79.32 | 0.50 | 68 | 3.01 | 0.47 |
| 26 | 78.15 | 0.50 | 69 | 0.76 | 0.53 |
| 27 | 77.67 | 0.49 | 70 | 3.29 | 0.66 |
| 28 | 2.08 | 0.76 | 71 | 1.96 | 0.66 |
| 29 | 76.15 | 0.48 | 72 | 0.40 | 0.72 |
| 30 | 9.88 | 0.48 | 73 | 0.40 | 0.72 |
| 31 | 2.84 | 0.52 | 74 | 3.08 | 0.15 |
| 32 | 1.12 | 0.69 | 75 | 2.90 | 0.16 |
| 33 | 7.68 | 0.57 | 76 | 0.59 | 0.69 |
| 34 | 4.83 | 0.59 | 77 | 2.78 | 0.16 |
| 35 | 0.64 | 0.69 | 78 | 2.51 | 0.17 |
| 36 | 4.20 | 0.64 | 79 | 1.50 | 0.58 |
| 37 | 3.57 | 0.65 | 80 | 1.78 | 0.19 |
| 38 | 89.99 | 0.64 | 81 | 1.60 | 0.21 |
| 39 | 8.86 | 0.75 | 82 | 0.51 | 0.26 |
| 40 | 7.59 | 0.72 | 83 | 2.98 | 0.59 |
| 41 | 3.94 | 0.73 | 84 | 0.73 | 0.59 |
| 42 | 4.19 | 0.81 | 85 | 2.81 | 0.68 |
| 43 | 82.74 | 0.64 | -- | -- | -- |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study. Water 2016, 8, 234. https://doi.org/10.3390/w8060234
Pérez-Sánchez M, Sánchez-Romero FJ, Ramos HM, López-Jiménez PA. Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study. Water. 2016; 8(6):234. https://doi.org/10.3390/w8060234
Chicago/Turabian StylePérez-Sánchez, Modesto, Francisco Javier Sánchez-Romero, Helena M. Ramos, and P. Amparo López-Jiménez. 2016. "Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study" Water 8, no. 6: 234. https://doi.org/10.3390/w8060234
APA StylePérez-Sánchez, M., Sánchez-Romero, F. J., Ramos, H. M., & López-Jiménez, P. A. (2016). Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study. Water, 8(6), 234. https://doi.org/10.3390/w8060234









