Frequency Analysis of High Flow Extremes in the Yingluoxia Watershed in Northwest China
Abstract
:1. Introduction
2. Study Area and Data Description
3. Methodology Description
3.1. Probability Modeling
3.2. Stationarity and Independence Tests
3.3. Return Level Estimations
4. Results and Discussion
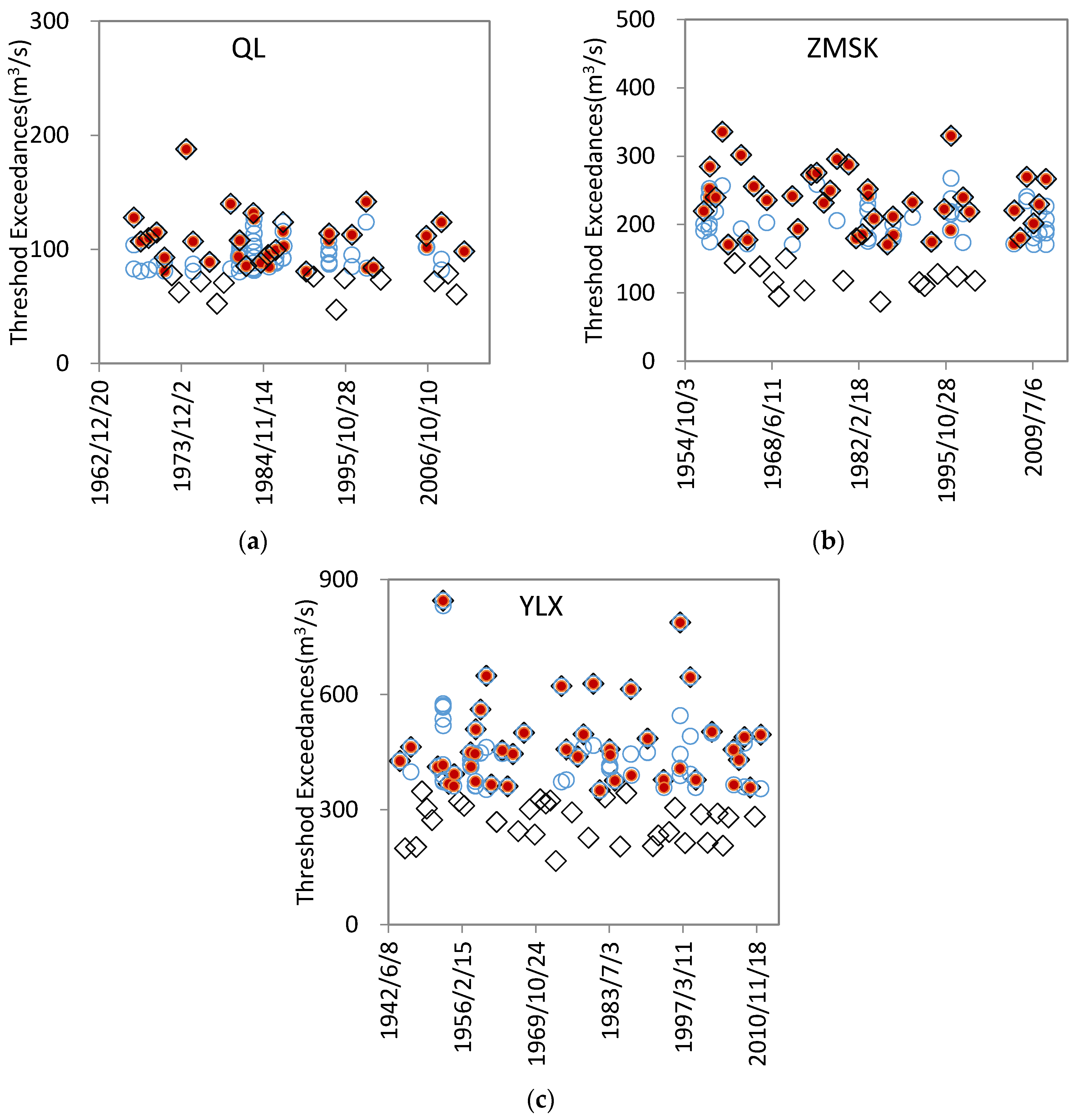
4.1. Threshold Selection and POT Series
4.2. AM Series and Stationarity and Independence Tests
4.3. Frequency Analysis for High Flow Extremes
4.3.1. Probability Modeling
4.3.2. Return Level Estimation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dahlke, H.E.; Lyon, S.W.; Stedinger, J.R.; Jansson, P. Contrasting trends in floods for two sub-arctic catchments in northern Sweden—Does glacier presence matter? Hydrol. Earth Syst. Sci. 2012, 16, 2123–2141. [Google Scholar] [CrossRef]
- Kay, A.L.; Jones, D.A. Transient changes in flood frequency and timing in Britain under potential projections of climate change. Int. J. Climatol. 2012, 32, 489–502. [Google Scholar] [CrossRef]
- Jha, M.K.; Singh, A.K. Trend analysis of extreme runoff events in major river basins of Peninsular Malaysia. Int. J. Water 2013, 7, 142–158. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Baeck, M.L.; Vitolo, R.; Stephenson, D.B.; Krajewski, W.F. On the frequency of heavy rainfall for the Midwest of the United States. J. Hydrol. 2011, 400, 103–120. [Google Scholar] [CrossRef]
- Du, H.; Xia, J.; Zeng, S.D.; She, D.X.; Zhang, Y.Y.; Yan, Z.Q. Temporal and spatial variations and statistical models of extreme runoff in Huaihe River Basin. Acta Geogr. Sin. 2012, 67, 398–409. (In Chinese) [Google Scholar]
- Xia, J.; Du, H.; Zeng, S.; She, D.; Zhang, Y.; Yan, Z.; Ye, Y. Temporal and spatial variations and statistical models of extreme runoff in Huaihe River basin during 1956–2010. J. Geogr. Sci. 2012, 22, 1045–1060. [Google Scholar] [CrossRef]
- Asl, S.J.; Khorshiddoust, A.M.; Dinpashoh, Y.; Sarafrouzeh, F. Frequency analysis of climate extreme events in Zanjan, Iran. Stoch. Environ. Res. Risk Assess. 2013, 27, 1637–1650. [Google Scholar]
- Rao, A.R.; Hamed, K.H. Flood frequency Analysis; CRC Press LLC: New York, NY, USA, 1999. [Google Scholar]
- Madsen, H.; Rasmussen, P.F.; Rosbjerg, D. Comparison of annual maximum series and partial duration series methods for modeling extreme hydrologic events. Water Resour. Res. 1997, 33, 747–757. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Comparison between the peaks-over-threshold method and the annual maximum method for flood frequency analysis. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Benyahya, L.; Gachon, P.; St-Hilaire, A.; Laprise, R. Frequency analysis of seasonal extreme precipitation in sounthern Quebec (Canada): An evaluation of regional climate model simulation with respect to two gridded datasets. Hydrol. Res. 2014, 45, 115–133. [Google Scholar] [CrossRef]
- Li, Z.; Brissette, F.; Chen, J. Assessing the applicability of six precipitation probability distribution models on the Loess Plateau of China. Int. J. Climatol. 2014, 34, 462–471. [Google Scholar] [CrossRef]
- Rahmani, V.; Hutchinson, S.L.; Hutchinson, J.M.S.; Anandhi, A. Extreme daily rainfall event distribution patterns in Kansas. J. Hydrol. Eng. 2014, 19, 707–716. [Google Scholar] [CrossRef]
- Du, H.; Xia, J.; Zeng, S.; She, D.; Liu, J. Variations and statistical probability characteristic analysis of extreme precipitation events under climate change in Haihe River Basin, China. Hydrol. Process. 2014, 28, 913–925. [Google Scholar] [CrossRef]
- Shamir, E.; Georgakakos, K.P.; Murphy, M.J. Frequency analysis of the 7–8 December 2010 extreme precipitation in the Panama Canal watershed. J. Hydrol. 2013, 480, 136–148. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D.; Makropoulos, C. How extreme is extreme? An assessment of daily rainfall distribution tails. Hydrol. Earth Syst. Sci. 2013, 17, 851–862. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Ling, H.B.; Xu, H.L.; Fu, J.Y. High- and low-flow variations in annual runoff and their response to climate change in the headstreams of the Tarim River, Xinjiang, China. Hydrol. Process. 2013, 27, 975–988. [Google Scholar] [CrossRef]
- Chen, X.H.; Zhang, L.J.; Xu, C.Y.; Zhang, J.M.; Ye, C.Q. Hydrological design of nonstationary flood extremes and durations in Wujiang river, South China: changing properties, causes and impacts. Math. Probl. Eng. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Fawcett, L.; Walshaw, D. Improved estimation for temporally clustered extremes. Environmetrics 2007, 18, 173–188. [Google Scholar] [CrossRef]
- Fawcett, L.; Walshaw, D. Estimating return levels from serially dependent extremes. Environmetrics 2012, 23, 272–283. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.X.; Hao, Z.C.; Chen, X.; Zhang, Z.; Xu, C.Y.; Sun, L. Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin, China. J. Hydrol. 2010, 380, 386–405. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Xiao, M.; Xu, C.Y. Flood frequency under the influence of trends in the Pearl River basin, China: Changing patterns, causes and implications. Hydrol. Process. 2015, 29, 1406–1417. [Google Scholar] [CrossRef]
- Yin, Z.L.; Xiao, H.L.; Zou, S.B.; Zhu, R.; Lu, Z.X.; Lan, Y.C.; Shen, Y.P. Simulation of hydrological processes of mountainous watersheds in inland river basins: taking the Heihe Mainstream River as an example. J. Arid Land 2014, 6, 16–26. [Google Scholar] [CrossRef]
- Guhathakurta, P.; Sreejith, O.P.; Menon, P.A. Impact of climate change on extreme rainfall events and flood risk in India. J. Earth Syst. Sci. 2011, 120, 359–373. [Google Scholar] [CrossRef]
- Qin, J.; Ding, Y.J.; Wu, J.K.; Gao, M.J.; Yi, S.H.; Zhao, C.C.; Ye, B.S.; Li, M.; Wang, S.X. Understanding the impact of mountain landscapes on water balance in the upper Heihe River watershed in northwestern China. J. Arid Land 2013, 5, 366–383. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Nagi, S.A.; Khalaf, S.S. Maximum likelihood estimation from record-breaking data for the generalized Pareto distribution. Metron 2004, 3, 377–389. [Google Scholar]
- Deidda, R.; Puliga, M. Performances of some parameter estimators of the Generalized Pareto Distribution over rounded-off samples. Phys. Chem. Earth. 2009, 34, 626–634. [Google Scholar] [CrossRef]
- Zaman, M.A.; Rahman, A.; Haddad, K. Regional flood frequency analysis in arid regions: A case study for Australia. J. Hydrol. 2012, 475, 74–83. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 23, 126–135. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Robson, A.J. Change detection in hydrological records—A review of the methodology. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Page, K.J.; McElroy, L. Comparison of annual and partial duration series floods on the Murrumbidgee river. Water Resour. Bull. 1981, 17, 286–289. [Google Scholar] [CrossRef]
- Scarrott, C.; Macdonald, A. A review of extreme value threshold estimation and uncertainty quantification. Revstat Stat. J. 2012, 10, 33–60. [Google Scholar]
- Jiang, Z.H.; Ding, Y.G.; Zhu, L.F.; Zhang, J.L.; Zhu, L.H. Extreme precipitation experimentation over Eastern China based on Generalized Pareto Distribution. Plateau Meteorol. 2009, 28, 573–580. (In Chinese) [Google Scholar]
- Si, B.; Yu, J.H.; Ding, Y.G. Research on extreme value distribution of short-duration heavy precipitation in the Sichuan Basin. Sci. Meteorol. Sin. 2012, 32, 403–410. (In Chinese) [Google Scholar]
- Northrop, P.J.; Coleman, C.L. Improved threshold diagnostic plots for extreme value analyses. Extremes 2014, 17, 289–303. [Google Scholar] [CrossRef]
- Wadsworth, J.L. Exploiting Structure of Maximum Likelihood Estimators for Extreme Value Threshold Selection. Technometrics 2016, 58, 116–126. [Google Scholar] [CrossRef]
- Lang, M.; Ouardab, T.B.M.J.; Bobee, B. Towards operational guidelines for over-threshold modeling. J. Hydrol. 1999, 255, 103–117. [Google Scholar] [CrossRef]
- Shao, Q.X.; Wong, H.; Xia, J.; Ip, W.C. Models for extremes using the extended three-parameter Burr XII system with application to flood frequency analysis. Hydrol. Sci. J. 2004, 49, 685–702. [Google Scholar] [CrossRef]
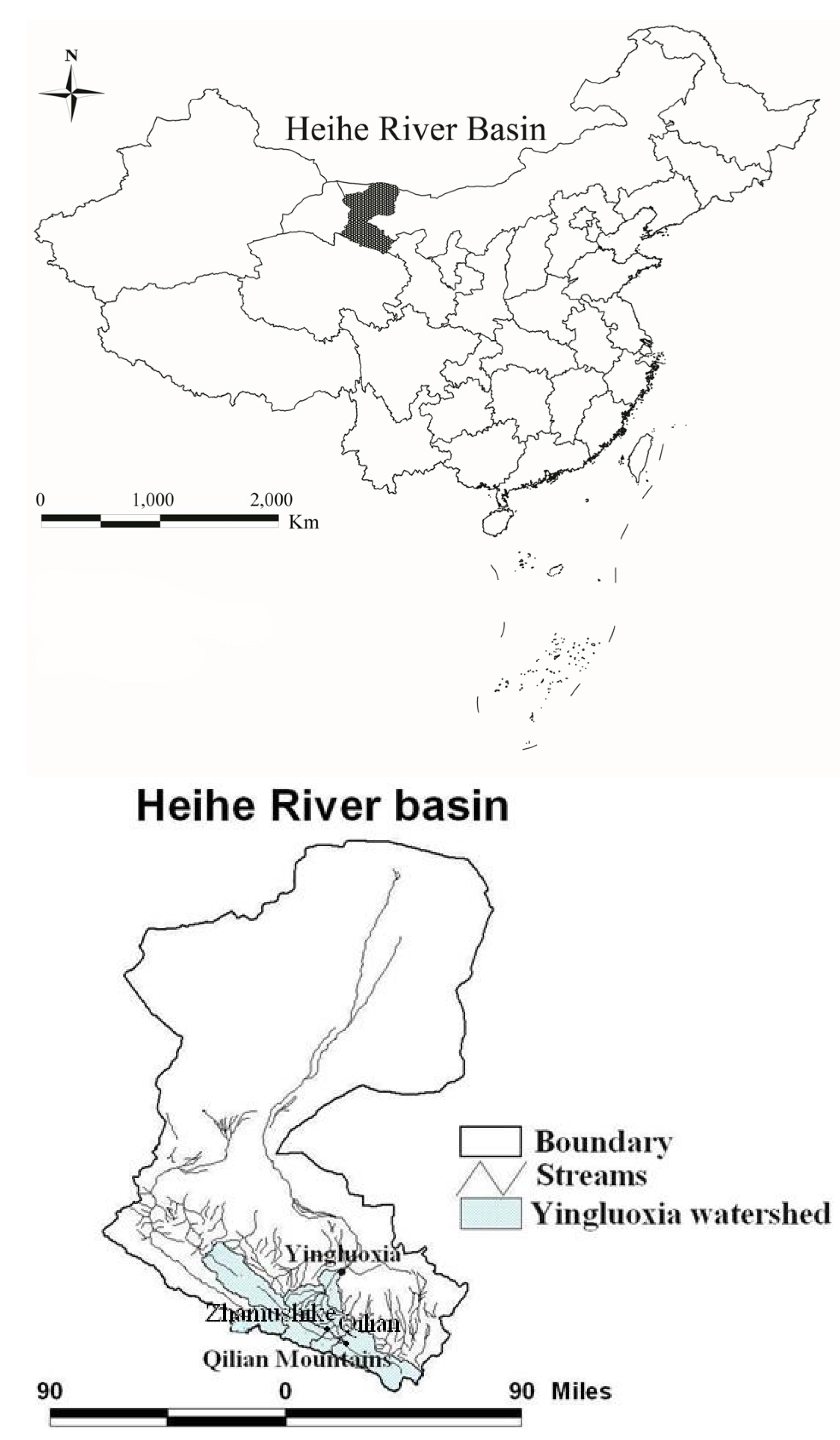
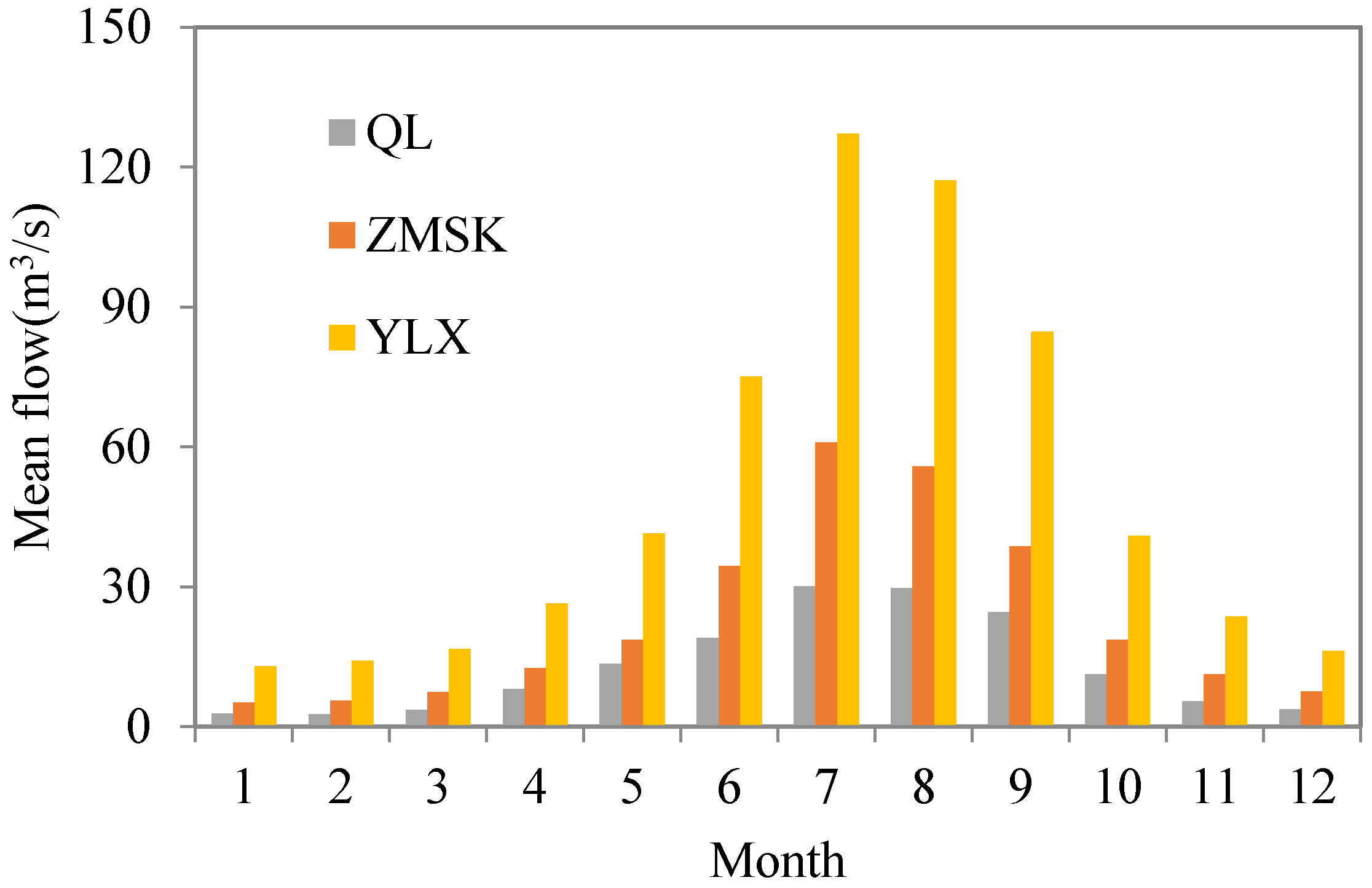
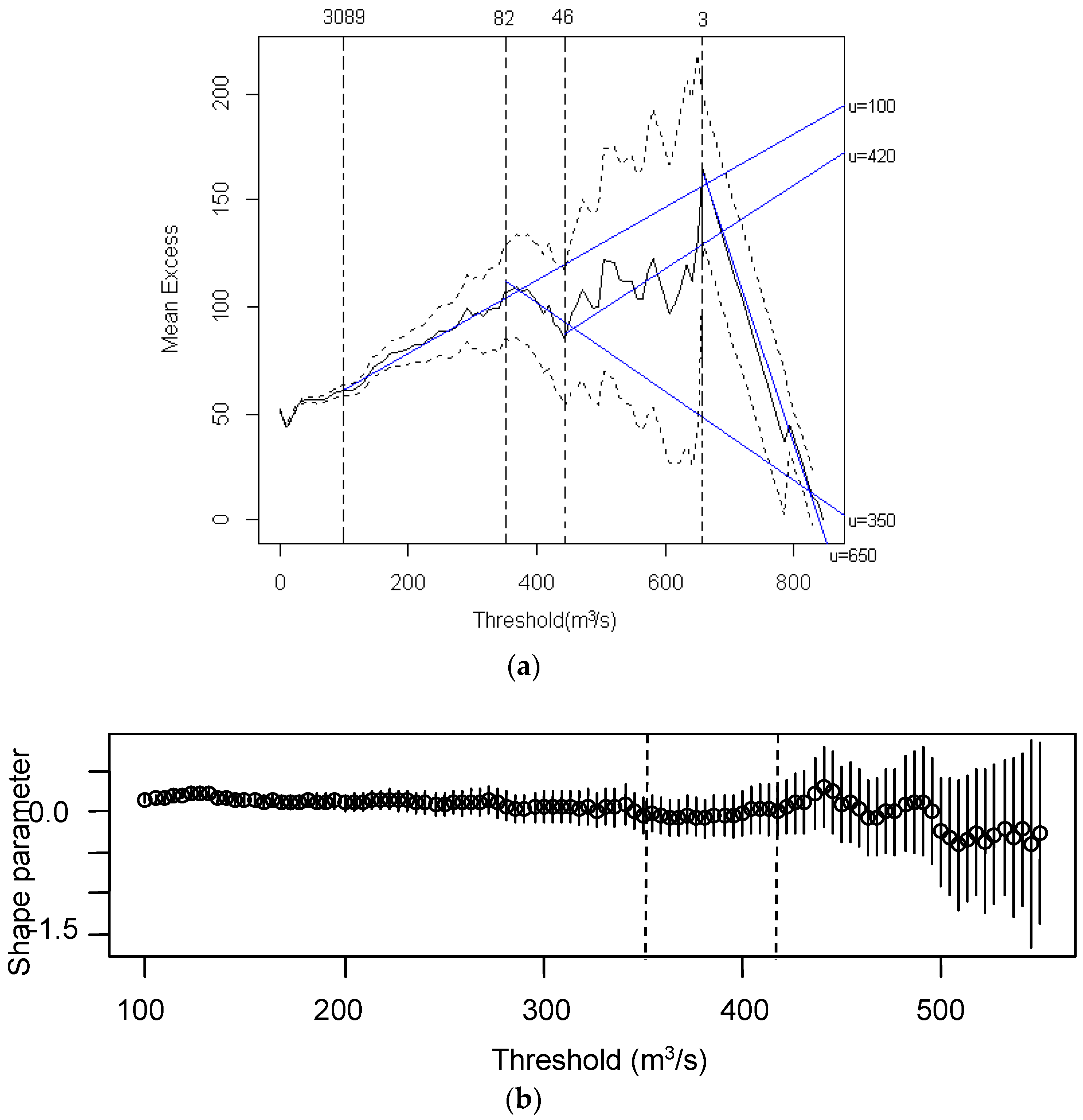
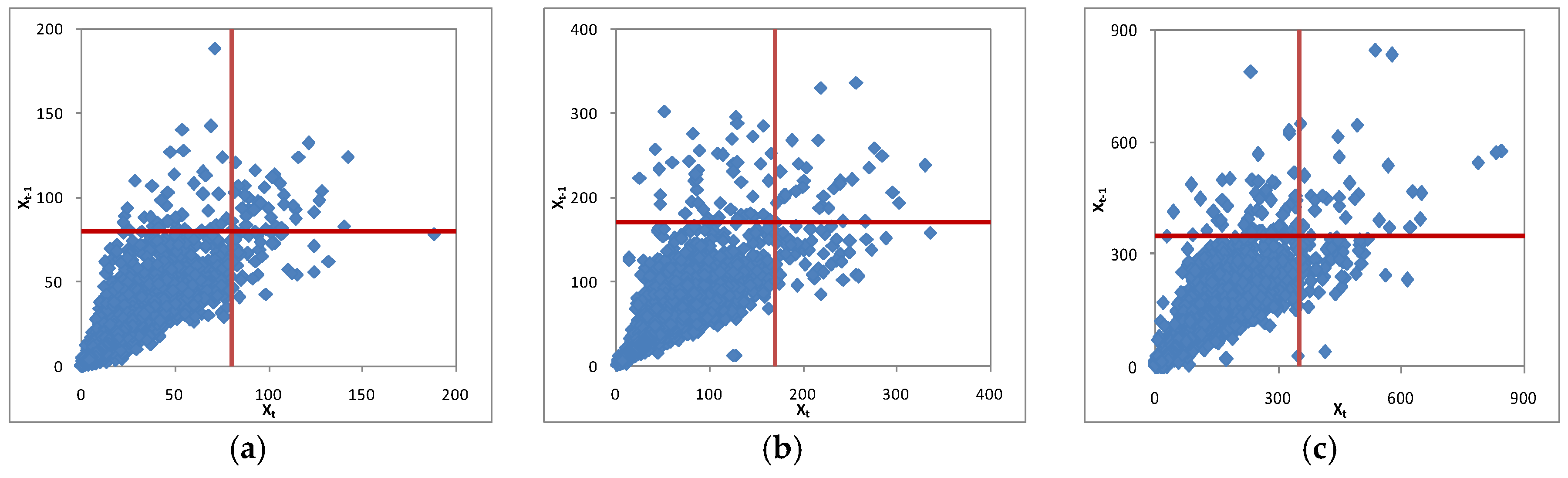


| Station Name (Abbreviation) | Longitude | Latitude | Elevation (m asl) | Data Period | Data Length | Annual Mean (m3/s) | Cv | Skewness |
|---|---|---|---|---|---|---|---|---|
| Qilian (QL) | 100°15′ E | 38°11′ N | 2787 | 1967–2011 | 36 | 13.00 | 1.11 | 2.67 |
| Zhamushike (ZMSK) | 99°59′ E | 38°14′ N | 2810 | 1957–2011 | 48 | 23.16 | 1.16 | 3.52 |
| Yingluoxia (YLX) | 100°11′ E | 38°49′ N | 1700 | 1944–2011 | 66 | 51.64 | 1.07 | 3.21 |
| Station | AM | POT | ||||||
|---|---|---|---|---|---|---|---|---|
| Sample Size | Maximum (m3/s) | Minimum (m3/s) | Mean (m3/s) | Threshold (m3/s) | Sample Size | Minimum (m3/s) | Mean (m3/s) | |
| QL | 36 | 188 (1974) | 47 (1994) | 97 | 80 | 32 | 81 (1990) | 109 |
| ZMSK | 48 | 336 (1960) | 87 (1985) | 205 | 170 | 45 | 171 (1961, 1986, 2009) | 228 |
| YLX | 66 | 845 (1952) | 166 (1973) | 384 | 350 | 45 | 351 (1981) | 467 |
| Station | Change Point | Trend | Independence Test | |||
|---|---|---|---|---|---|---|
| Critical Value (P = 0.05) | Q | Lag 1 | Critical Value(α = 0.05) | |||
| QL | 69 | 171.7 | −1.10 | −0.05 | −0.08 | 0.33 |
| ZMSK | 119 | 263.5 | −0.45 | −0.39 | −0.05 | 0.28 |
| YLX | 139 | 423.6 | −0.23 | −0.25 | −0.11 | 0.24 |
| Station | K-S | A-D | Parameter Estimation | ||||
|---|---|---|---|---|---|---|---|
| AM-GEV | |||||||
| QL | 0.09 | 0.22 | 0.19 | 2.50 | 84.76 (4.4943) | 24.1494 (3.1982) | −0.0694 (0.1126) |
| ZMSK | 0.08 | 0.20 | 0.33 | 2.50 | 183.48 (10.6038) | 65.6735 (7.8552) | −0.3364 (0.1094) |
| YLX | 0.06 | 0.16 | 0.26 | 2.50 | 316.48 (15.4693) | 108.1400 (11.6639) | 0.0436 (0.1116) |
| POT-GPD | |||||||
| QL | 0.10 | 0.24 | 0.34 | 2.50 | – | 33.9589 (7.3896) | −0.2107 (0.1322) |
| ZMSK | 0.08 | 0.20 | 0.42 | 2.50 | – | 86.9987 (16.6579) | −0.4716 (0.1392) |
| YLX | 0.08 | 0.20 | 0.33 | 2.50 | – | 125.4130 (26.9464) | −0.0702 (0.1551) |
| Station | T = 10 | T = 50 | T = 100 | T = 200 |
|---|---|---|---|---|
| AM_GEV (m3/s) | ||||
| QL | 135 (118,152) | 167 (135,200) | 180 (137,222) | 192 (138,245) |
| ZMSK | 287 (266,308) | 326 (296,356) | 337 (300,374) | 346 (303,389) |
| YLX | 572 (498,646) | 776 (589,964) | 867 (604,1131) | 956 (604,1308) |
| POT_GPD (m3/s) | ||||
| QL | 143 (125,162) | 169 (144,194) | 179 (148,209) | 187 (150,224) |
| ZMSK | 295 (274,316) | 325 (303,346) | 333 (308,357) | 339 (311,367) |
| YLX | 591 (519,664) | 743 (609,877) | 807 (625,989) | 869 (626,1112) |
| Difference (%) | ||||
| QL | 5.59 | 1.18 | −0.56 | −2.67 |
| ZMSK | 2.71 | −0.31 | −1.20 | −2.06 |
| YLX | 3.21 | −4.44 | −7.43 | −10.00 |
| Station | T = 10 | T = 50 | T = 100 | T = 200 |
|---|---|---|---|---|
| QL | 126 (111,141) | 151 (126,175) | 162 (133,192) | 173 (137,209) |
| ZMSK | 279 (262,297) | 314 (294,333) | 325 (302,347) | 334 (306,361) |
| YLX | 581 (515,647) | 725 (598, 851) | 787 (619, 954) | 847 (631,1063) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, Y.; Zhao, W.; Xu, Z.; Li, Z. Frequency Analysis of High Flow Extremes in the Yingluoxia Watershed in Northwest China. Water 2016, 8, 215. https://doi.org/10.3390/w8050215
Li Z, Wang Y, Zhao W, Xu Z, Li Z. Frequency Analysis of High Flow Extremes in the Yingluoxia Watershed in Northwest China. Water. 2016; 8(5):215. https://doi.org/10.3390/w8050215
Chicago/Turabian StyleLi, Zhanling, Yuehua Wang, Wei Zhao, Zongxue Xu, and Zhanjie Li. 2016. "Frequency Analysis of High Flow Extremes in the Yingluoxia Watershed in Northwest China" Water 8, no. 5: 215. https://doi.org/10.3390/w8050215
APA StyleLi, Z., Wang, Y., Zhao, W., Xu, Z., & Li, Z. (2016). Frequency Analysis of High Flow Extremes in the Yingluoxia Watershed in Northwest China. Water, 8(5), 215. https://doi.org/10.3390/w8050215





