Using High-Resolution Data to Test Parameter Sensitivity of the Distributed Hydrological Model HydroGeoSphere
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Model Description
2.3. Conceptual Model
2.4. Data Base
2.5. Parameterization and Calibration
2.6. Modeling Procedure
2.7. Measures of Model Performance
3. Results
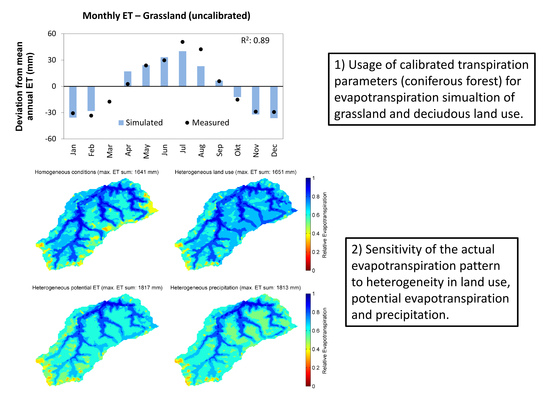
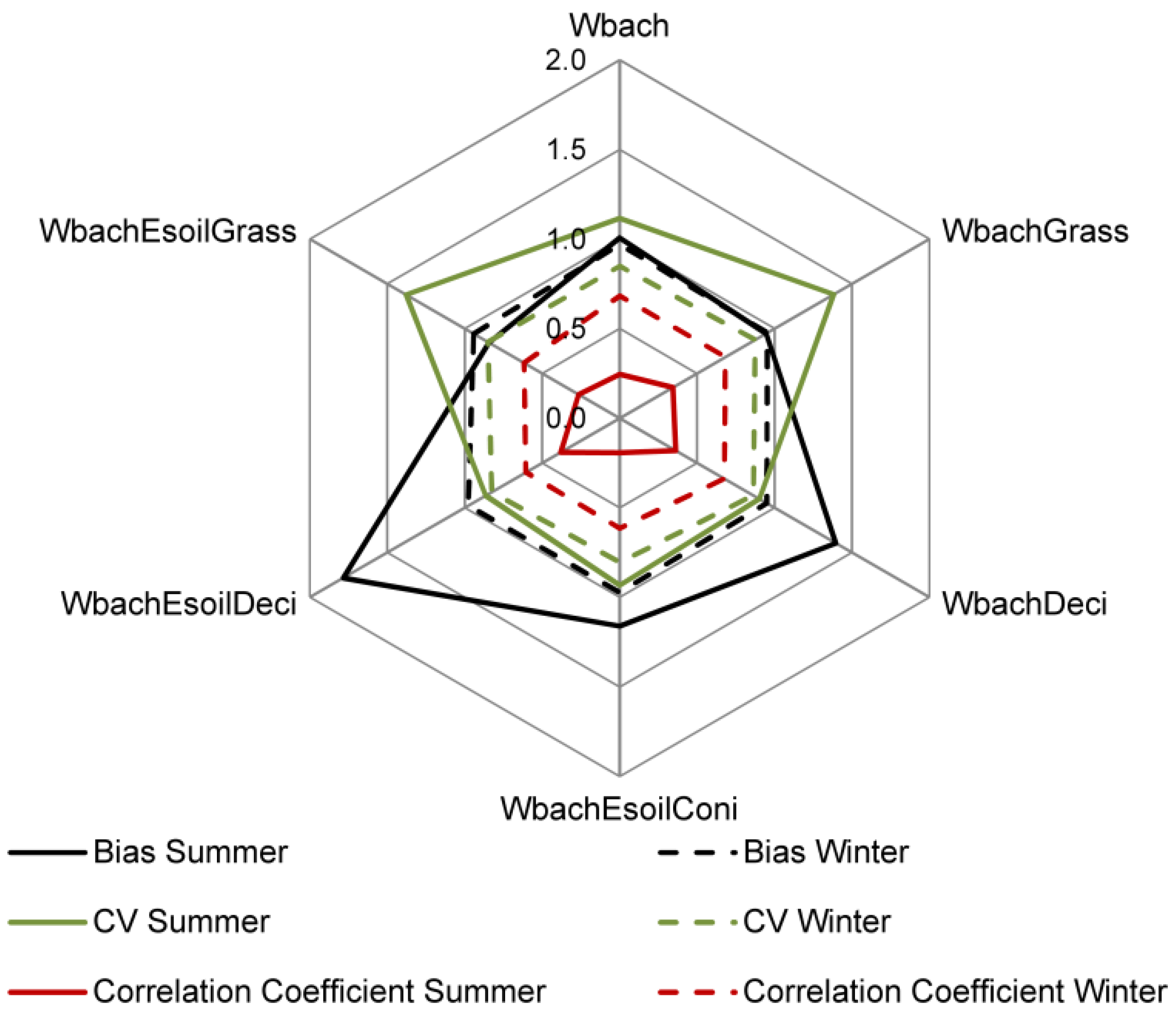
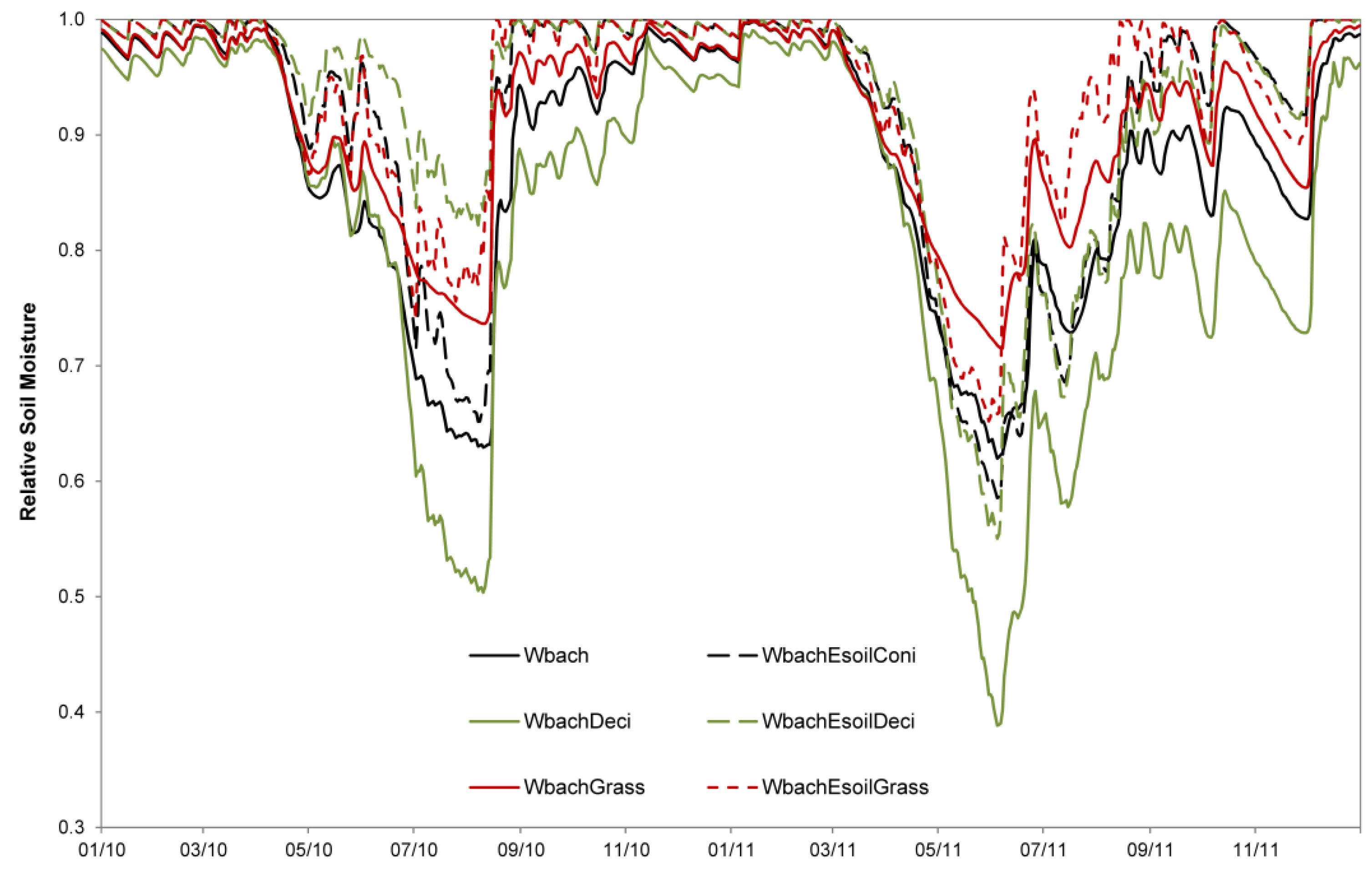
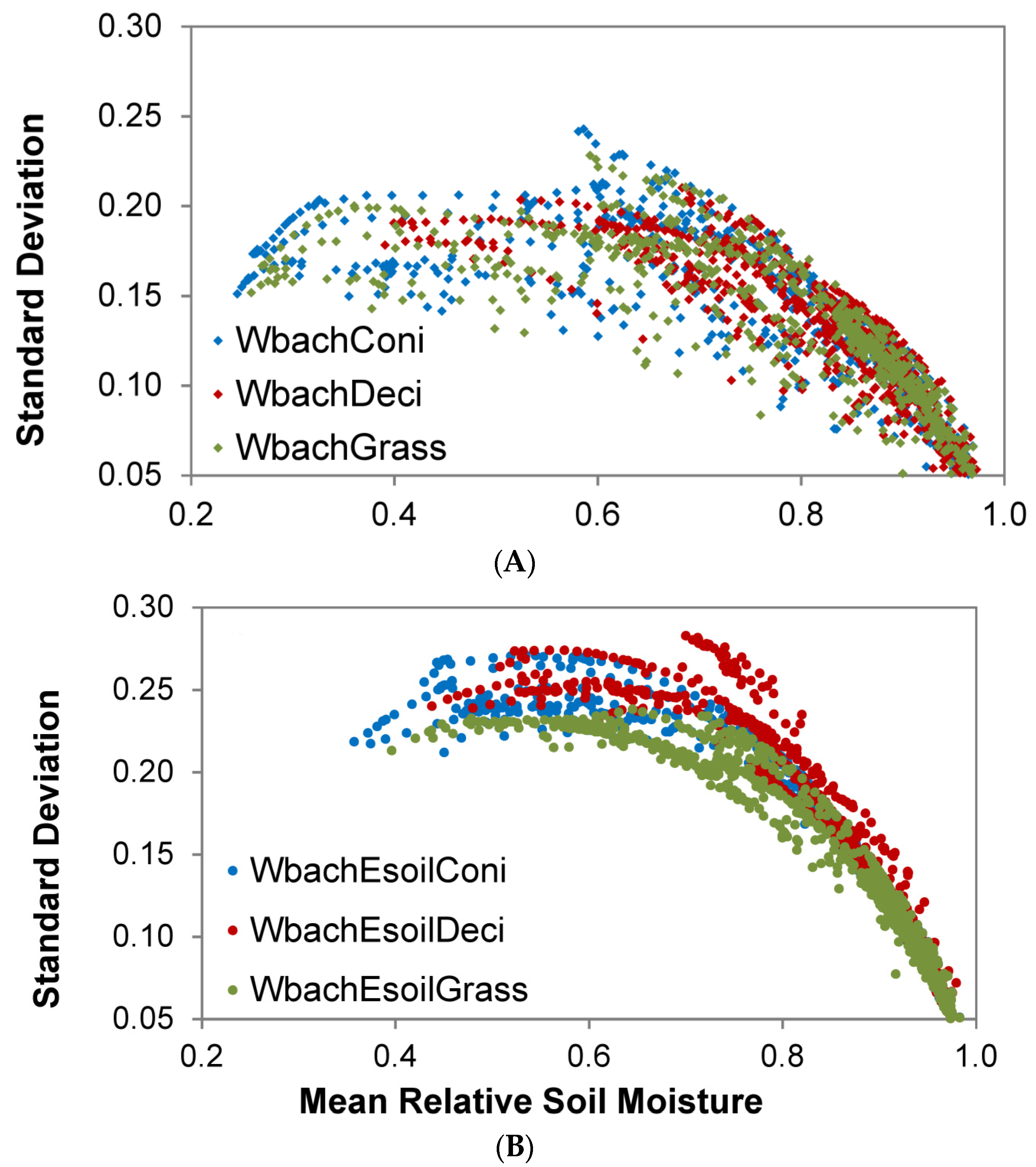
3.1. Influence of Mesoscale Soil and Land Use Parameterization on the Simulation of the Headwater Catchment
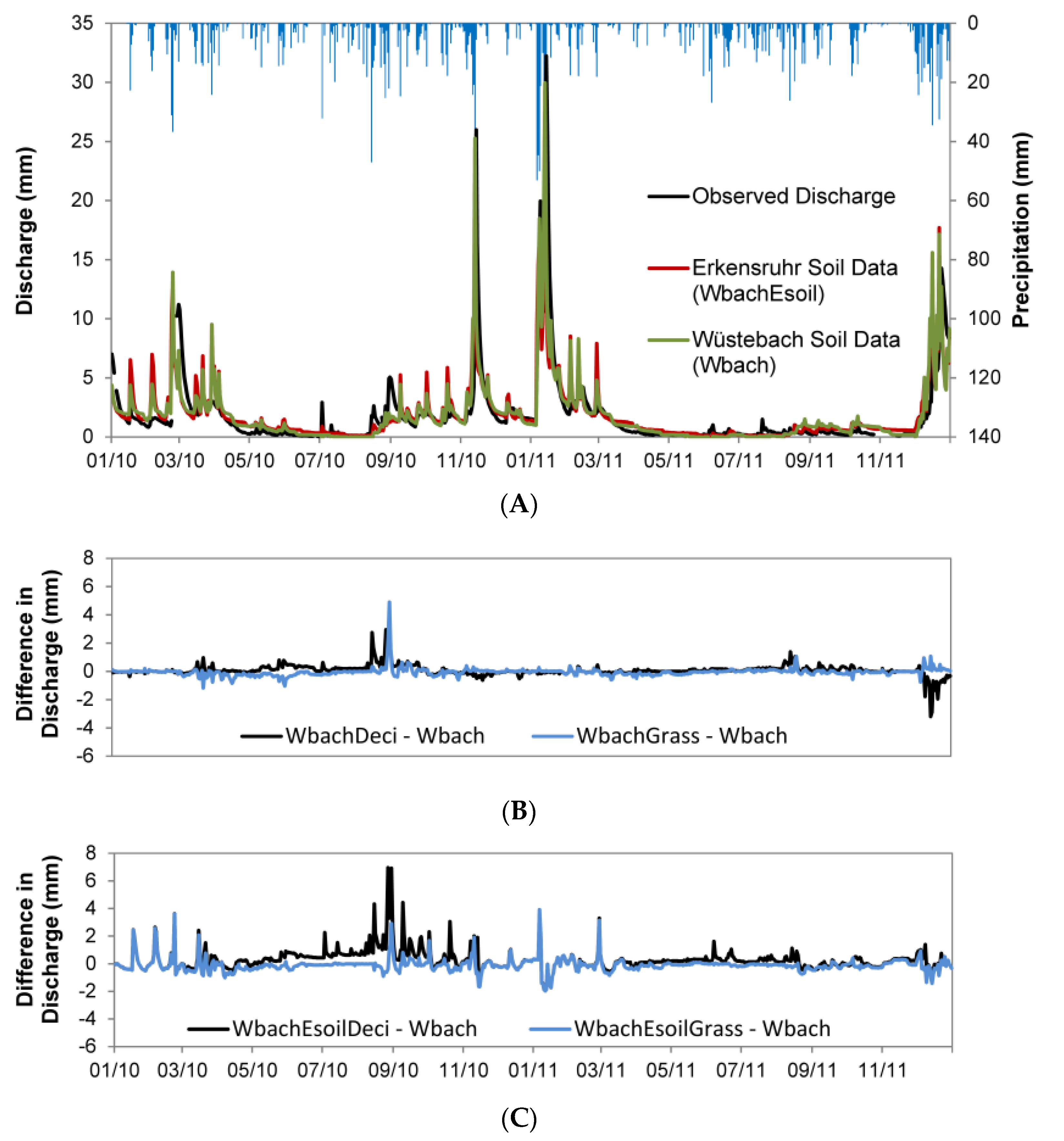
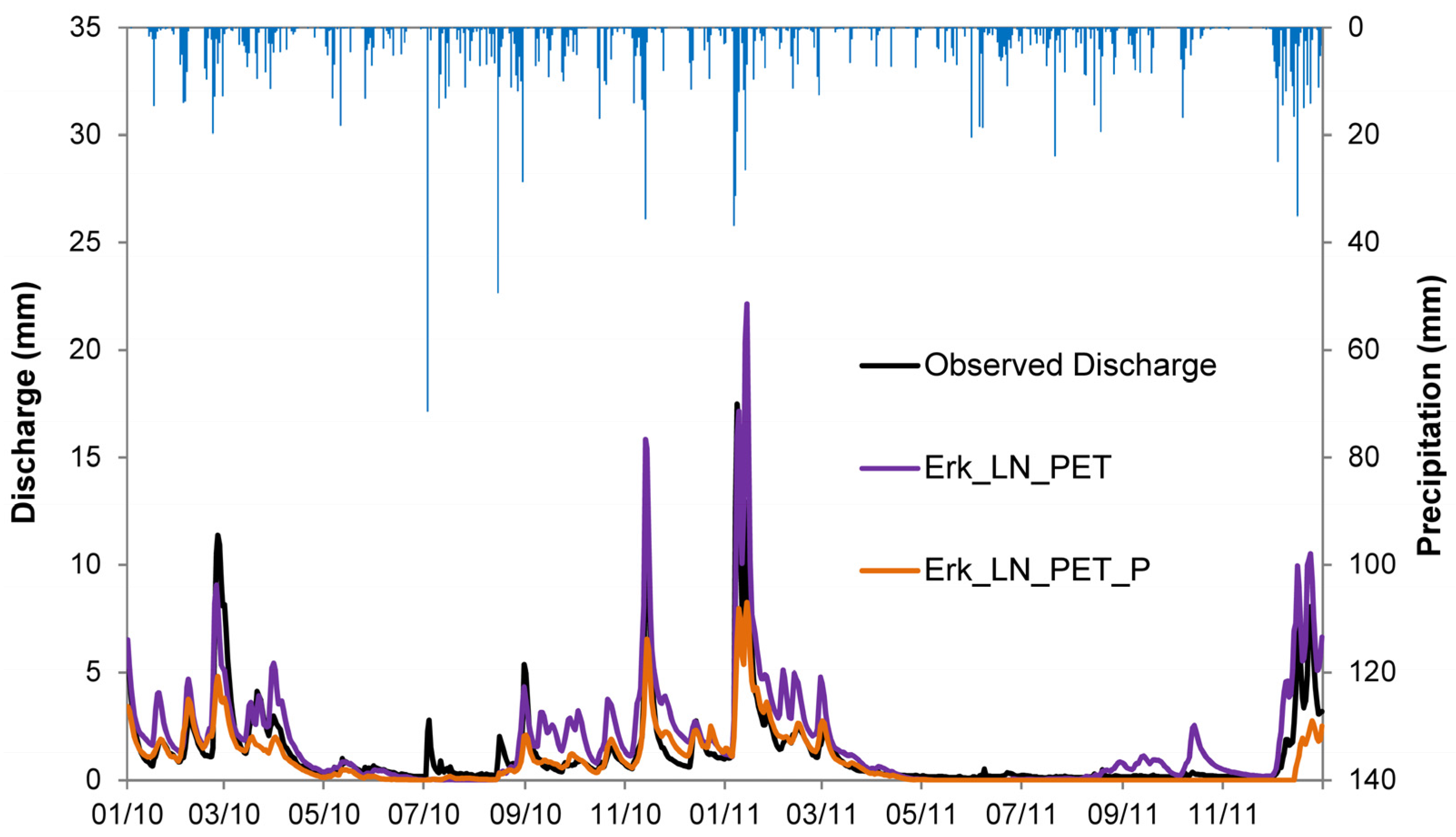
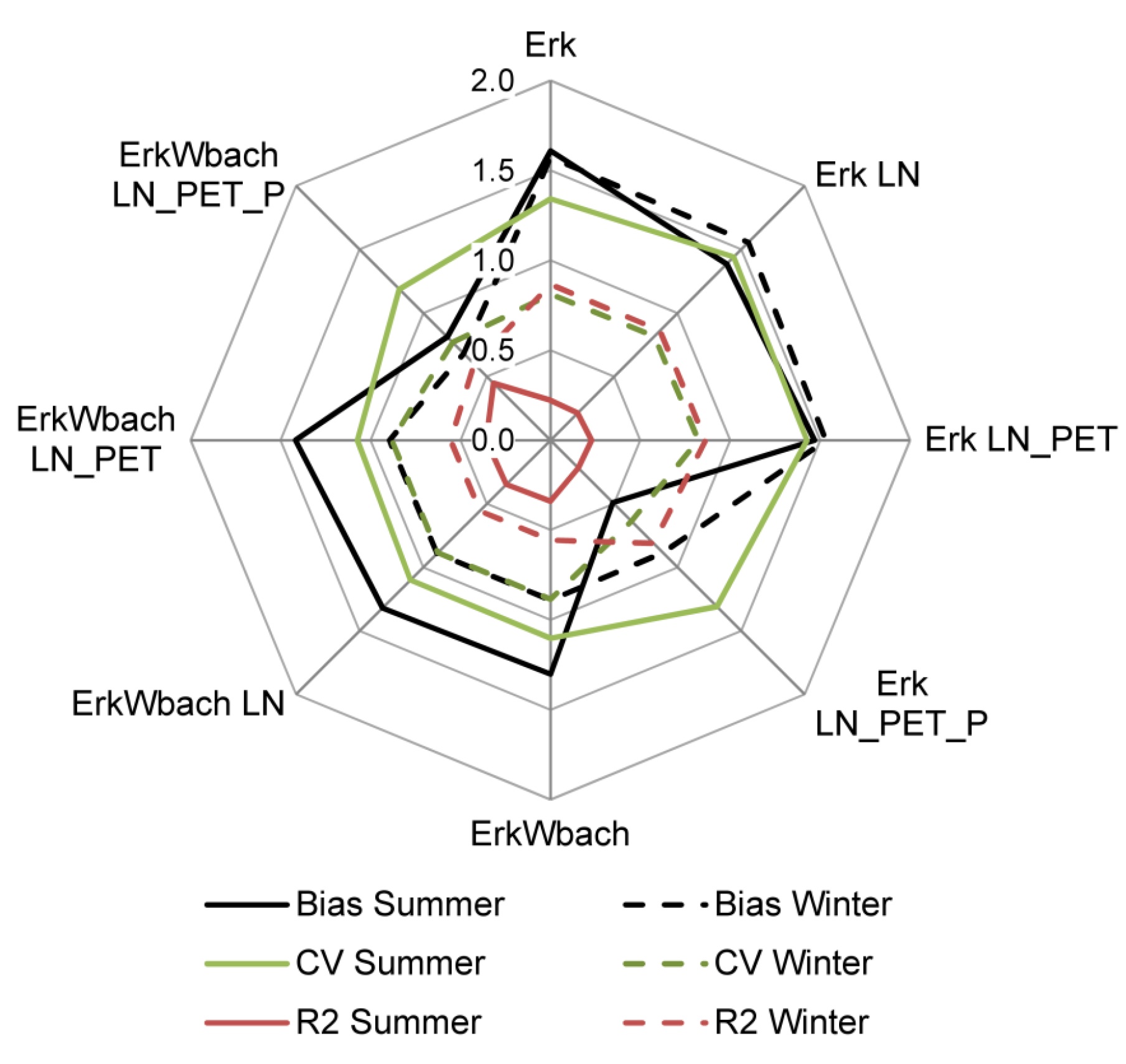
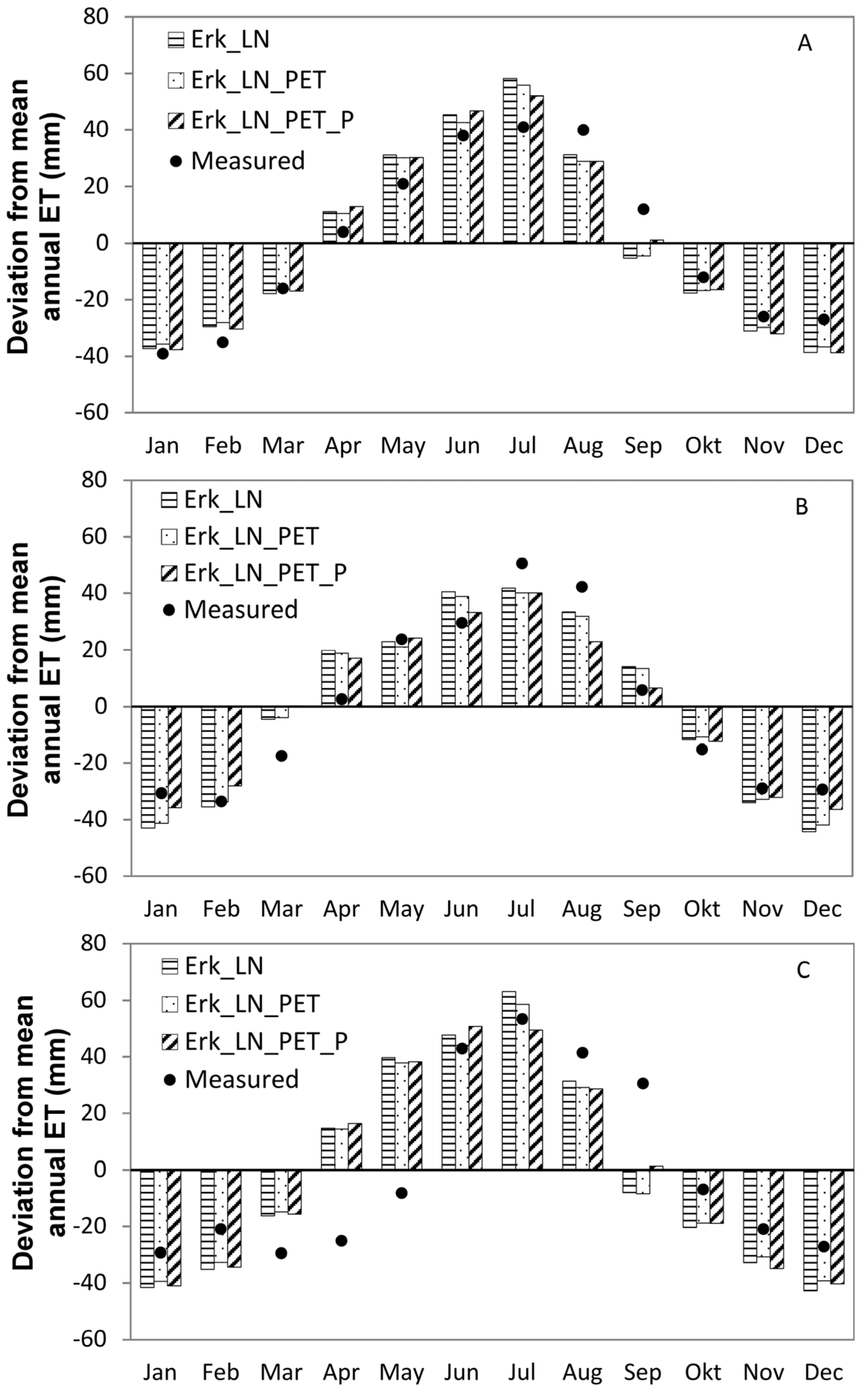
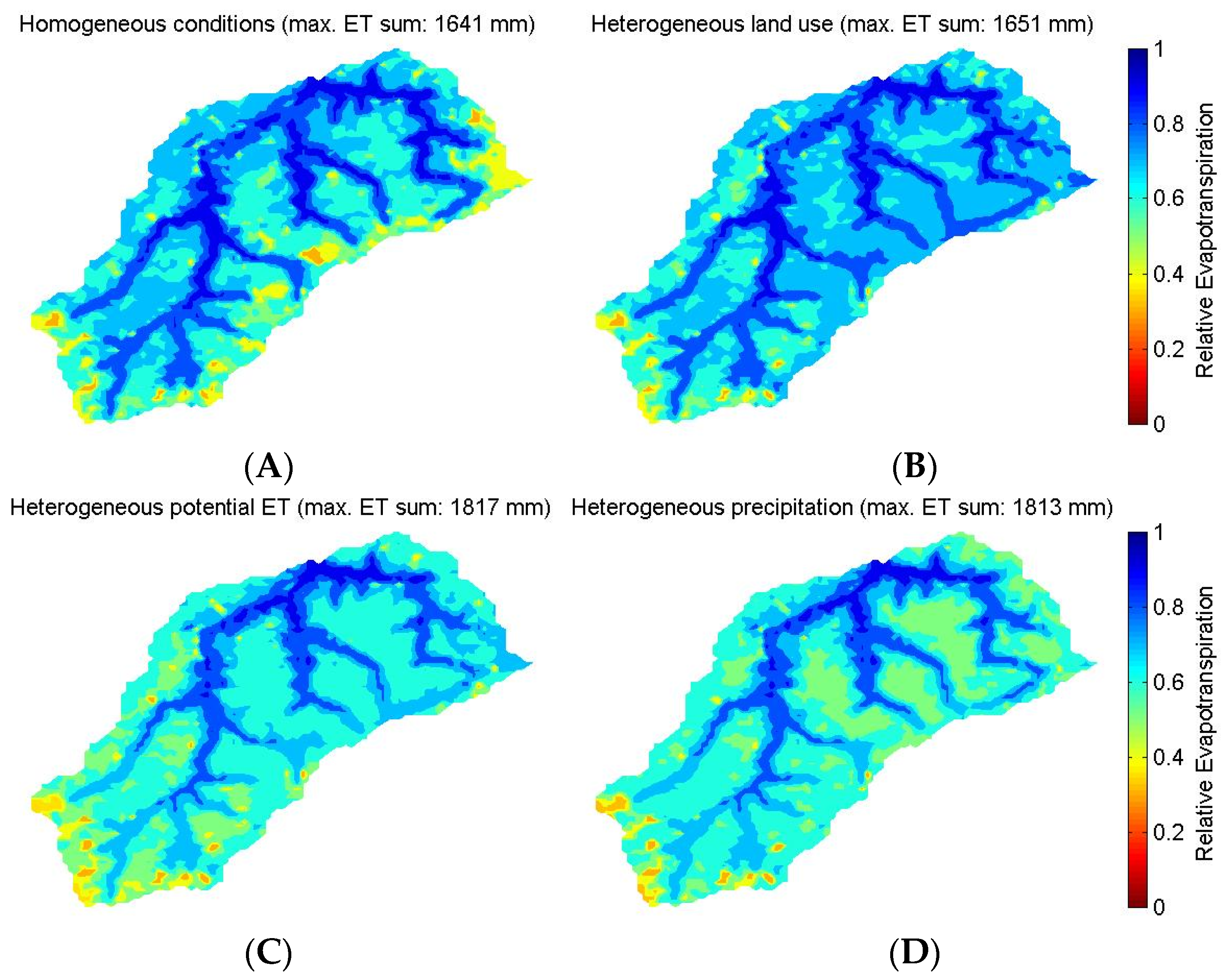
3.2. Influence of Parameter Regionalization and Spatially Distributed Input Data on the Simulation of the Mesoscale Catchment
4. Discussion
4.1. Influence of Mesoscale Soil and Land Use Parameterization on the Simulation of the Headwater Catchment
4.2. Influence of Parameter Regionalization and Spatially Distributed Input Data on the Simulation of the Mesoscale Catchment
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FAO | Food and Agriculture Organization of the United Nations |
| HGS | HydroGeoSphere |
| LAI | Leaf Area Index |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| PET | Potential Evapotranspiration |
| TERENO | Terrestrial Environmental Observatories |
| VGM | Van-Genuchten-Mualem |
References
- Panday, S.; Huyakorn, P.S. A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed watershed model. Water Resour. Res. 2008, 44, W02402. [Google Scholar] [CrossRef]
- Graham, D.N.; Butts, M.B. Flexible, integrated watershed modelling with MIKE SHE. In Watershed Models; Singh, V.P., Frevert, D.K., Eds.; CRC Press: Boca Raton, FL, USA, 2005; pp. 245–271. [Google Scholar]
- Camporese, M.; Paniconi, C.; Putti, M.; Orlandini, S. Surface-subsurface flow modeling with path-based runoff routing, boundary condition-based coupling, and assimilation of multisource observation data. Water Resour. Res. 2010, 46, W02512. [Google Scholar] [CrossRef]
- Ala-aho, P.; Rossi, P.M.; Isokangas, E.; Kløve, B. Fully integrated surface-subsurface flow modelling of groundwater–lake interaction in an esker aquifer: Model verification with stable isotopes and airborne thermal imaging. J. Hydrol. 2015, 522, 391–406. [Google Scholar] [CrossRef]
- Frei, S.; Fleckenstein, J.H. Representing effects of micro-topography on runoff generation and sub-surface flow patterns by using superficial rill/depression storage height variations. Environ. Model. Softw. 2014, 52, 5–18. [Google Scholar] [CrossRef]
- Li, Q.; Unger, A.J.A.; Sudicky, E.A.; Kassenaar, D.; Wexler, E.J.; Shikaze, S. Simulating the multi-seasonal response of a large-scale watershed with a 3D physically-based hydrologic model. J. Hydrol. 2008, 357, 317–336. [Google Scholar] [CrossRef]
- Voeckler, H.M.; Allen, D.M.; Alila, Y. Modeling coupled surface water—Groundwater processes in a small mountainous headwater catchment. J. Hydrol. 2014, 517, 1089–1106. [Google Scholar] [CrossRef]
- Weill, S.; Altissimo, M.; Cassiani, G.; Deiana, R.; Marani, M.; Putti, M. Saturated area dynamics and streamflow generation from coupled surface-subsurface simulations and field observations. Adv. Water Resour. 2013, 59, 196–208. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42, W03S04. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44, W09411. [Google Scholar] [CrossRef]
- Romano, N. Soil moisture at local scale: Measurements and simulations. J. Hydrol. 2014, 516, 6–20. [Google Scholar] [CrossRef]
- Graf, A.; Bogena, H.R.; Drüe, C.; Hardelauf, H.; Pütz, T.; Heinemann, G.; Vereecken, H. Spatiotemporal relations between water budget components and soil water content in a forested tributary catchment. Water Resour. Res. 2014, 50, 4837–4857. [Google Scholar] [CrossRef]
- Cornelissen, T.; Diekkrüger, B.; Bogena, H.R. Significance of scale and lower boundary condition in the 3D simulation of hydrological processes and soil moisture variability in a forested headwater catchment. J. Hydrol. 2014, 516, 140–153. [Google Scholar] [CrossRef]
- Goderniaux, P.; Brouyère, S.; Fowler, H.J.; Blenkinsop, S.; Therrien, R.; Orban, P.; Dassargues, A. Large scale surface-subsurface hydrological model to assess climate change impacts on groundwater reserves. J. Hydrol. 2009, 373, 122–138. [Google Scholar] [CrossRef]
- Rahman, M.; Sulis, M.; Kollet, S.J. The concept of dual-boundary forcing in land surface-subsurface interactions of the terrestrial hydrologic and energy cycles. Water Resour. Res. 2014, 50, 8531–8548. [Google Scholar] [CrossRef]
- Hauck, C.; Barthlott, C.; Krauss, L.; Kalthoff, N. Soil moisture variability and its influence on convective precipitation over complex terrain. Q. J. R. Meteorol. Soc. 2011, 137, 42–56. [Google Scholar] [CrossRef]
- Bogena, H.R.; Diekkrüger, B. Modelling solute and sediment transport at different spatial and temporal scales. Earth Surf. Process. Landf. 2002, 27, 1475–1489. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Stoltidis, I.; Krapp, L. Hydrological Map NRW. 1:25.000, Sheet 5404; State Agency for Water and Waste of North Rhine-Westfalia: Düsseldorf, Germany, 1980. [Google Scholar]
- Stockinger, M.P.; Bogena, H.R.; Lücke, A.; Diekkrüger, B.; Weiler, M.; Vereecken, H. Seasonal soil moisture patterns: Controlling transit time distributions in a forested headwater catchment. Water Resour. Res. 2014, 50, 5270–5289. [Google Scholar] [CrossRef]
- Bogena, H.R.; Herbst, M.; Huisman, J.A.; Rosenbaum, U.; Weuthen, A.; Vereecken, H. Potential of Wireless Sensor Networks for Measuring Soil Water Content Variability. Vadose Zone J. 2010, 9, 1002–1013. [Google Scholar] [CrossRef]
- Lehmkuhl, F.; Loibl, D.; Borchardt, H. Geomorphological map of the Wüstebach (Nationalpark Eifel, Germany)—An example of human impact on mid-European mountain areas. J. Maps 2010, 6, 520–530. [Google Scholar] [CrossRef]
- Bogena, H.R.; Bol, R.; Borchard, N.; Brüggemann, N.; Diekkrüger, B.; Drüe, C.; Groh, J.; Gottselig, N.; Huisman, J.A.; Lücke, A.; et al. A terrestrial observatory approach to the integrated investigation of the effects of deforestation on water, energy, and matter fluxes. Sci. China Earth Sci. 2015, 58, 61–75. [Google Scholar] [CrossRef]
- Aquanty. HGS 2013: HydroGeoSphere—User Manual; Aquanty: Waterloo, ON, Canada, 2013. [Google Scholar]
- Hwang, H.-T.; Park, Y.-J.; Sudicky, E.A.; Forsyth, P.A. A parallel computational framework to solve flow and transport in integrated surface–subsurface hydrologic systems. Environ. Model. Softw. 2014, 61, 39–58. [Google Scholar] [CrossRef]
- Kristensen, K.J.; Jensen, S.E. A model for estimating actual evapotranspiration form potential evapotranspiration. Nord. Hydrol. 1975, 6, 170–188. [Google Scholar]
- Partington, D.; Brunner, P.; Frei, S.; Simmons, C.T.; Werner, A.D.; Therrien, R.; Maier, H.R.; Dandy, G.C.; Fleckenstein, J.H. Interpreting streamflow generation mechanisms from integrated surface-subsurface flow models of a riparian wetland and catchment. Water Resour. Res. 2013, 49, 5501–5519. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Breuer, L.; Eckhardt, K.; Frede, H.-G. Plant parameter values for models in temperate climates. Ecol. Model. 2003, 169, 237–293. [Google Scholar] [CrossRef]
- Richter, D. Ergebnisse Methodischer Untersuchungen zur Korrektur des Systematischen Meßfehlers des Hellmann-Niederschlagsmessers. Berichte des Deutschen Wetterdienstes; German Weather Service: Offenbach am Main, Germany, 1995. [Google Scholar]
- Maidment, D. Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Waldhoff, G. Enhanced Land Use Classification of 2008 for the Rur Catchment; CRC/TR32 Database (TR32DB), doi:10.5880/TR32DB.1; University of Cologne: Cologne, Germany, 2012. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L. Prediction of soil water properties for hydrologic modeling. In Proceedings of the Symposium Watershed Management in the Eighties, Denver, CO, USA, 30 April–1 May 1985; pp. 293–399.
- Brakensiek, D.L.; Rawls, W.J. Soil containing rock fragments: Effects on infiltration. Catena 1994, 23, 99–110. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Baatz, R.; Hendricks Franssen, H.-J.; Vereecken, H. Accuracy of the cosmic-ray soil water content probe in humid forest ecosystems: The worst case scenario: Cosmic-Ray Probe in Humid Forested Ecosystems. Water Resour. Res. 2013, 49, 5778–5791. [Google Scholar] [CrossRef]
- Brakensiek, D.L.; Rawls, W.J.; Stephenson, G.R. Determining the Saturated Hydraulic Conductivity of a Soil Containing Rock Fragments. Soil Sci. Soc. Am. J. 1986, 50, 834–835. [Google Scholar] [CrossRef]
- Sciuto, G.; Diekkrüger, B. Influence of soil heterogeneity and spatial discretization on catchment water balance modeling. Vadose Zone J. 2010, 9, 955–969. [Google Scholar] [CrossRef]
- Meinen, C.; Hertel, D.; Leuschner, C. Biomass and morphology of fine roots in temperate broad-leaved forests differing in tree species diversity: Is there evidence of below-ground overyielding? Oecologia 2009, 161, 99–111. [Google Scholar] [CrossRef] [PubMed]
- Dannowski, M.; Wurbs, A. Spatial differentiated representation of maximum rooting depths of different plant communities on a field wood-area of the Northeast German Lowland. Bodenkultur 2003, 54, 93–108. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modelling—The Primer; Wiley: Chichester, UK, 2001. [Google Scholar]
- Rosenbaum, U.; Bogena, H.R.; Herbst, M.; Huisman, J.A.; Peterson, T.J.; Weuthen, A.; Western, A.W.; Vereecken, H. Seasonal and event dynamics of spatial soil moisture patterns at the small catchment scale. Water Resour. Res. 2012, 48, W10544. [Google Scholar] [CrossRef]
- Mendel, H. Elemente des Wasserkreislaufs: Eine Kommentierte Bibliographie zur Abflußbildung; Analytica: Berlin, Germany, 2000. [Google Scholar]
- Qu, W.; Bogena, H.R.; Huisman, J.A.; Vanderborght, J.; Schuh, M.; Priesack, E.; Vereecken, H. Predicting subgrid variability of soil water content from basic soil information: Predict soil water content variability. Geophys. Res. Lett. 2015, 42, 789–796. [Google Scholar] [CrossRef]
- Bormann, H.; Breuer, L.; Gräff, T.; Huisman, J.A. Analysing the effects of soil properties changes associated with land use changes on the simulated water balance: A comparison of three hydrological catchment models for scenario analysis. Ecol. Model. 2007, 209, 29–40. [Google Scholar] [CrossRef]
- Herbst, M.; Diekkrüger, B.; Vanderborght, J. Numerical experiments on the sensitivity of runoff generation to the spatial variation of soil hydraulic properties. J. Hydrol. 2006, 326, 43–58. [Google Scholar] [CrossRef]
- Kværnø, S.H.; Stolte, J. Effects of soil physical data sources on discharge and soil loss simulated by the LISEM model. CATENA 2012, 97, 137–149. [Google Scholar] [CrossRef]
- Harsch, N.; Brandenburg, M.; Klemm, O. Large-scale lysimeter site St. Arnold, Germany: Analysis of 40 years of precipitation, leachate and evapotranspiration. Hydrol. Earth Syst. Sci. 2009, 13, 305–317. [Google Scholar] [CrossRef]
- Oishi, A.C.; Oren, R.; Stoy, P.C. Estimating components of forest evapotranspiration: A footprint approach for scaling sap flux measurements. Agric. For. Meteorol. 2008, 148, 1719–1732. [Google Scholar] [CrossRef]
- Schuurmans, J.M.; Bierkens, M.F.P. Effect of spatial distribution of daily rainfall on interior catchment response of a distributed hydrological model. Hydrol. Earth Syst. Sci. Discuss. 2007, 11, 677–693. [Google Scholar] [CrossRef]
- Arnaud, P.; Bouvier, C.; Cisneros, L.; Dominguez, R. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 2002, 260, 216–230. [Google Scholar] [CrossRef]


| Data Type | Source | Spatial Resolution | Temporal Resolution | Availability | Measurement Location |
|---|---|---|---|---|---|
| Wüstebach and Erkensruhr simulations | |||||
| Digital Elevation | Land Surveying Office of North Rhine-Westphalia | 10 × 10 m2 | - | - | - |
| Climate | TERENO Observation Network | 1 Station | Hourly | Since 2009 | Schöneseiffen (3.4 km east to Wüstebach) |
| Wüstebach simulations | |||||
| Soil | Geological Survey of North Rhine-Westphalia | 1:2500 | - | - | - |
| Precipitation | German Weather Service | 1 Station | Hourly | Since 2001 | Kalterherberg (9.6 km west to Wüstebach) |
| Erkensruhr simulations | |||||
| Soil | Geological Survey of North Rhine-Westphalia | 1:50,000 | - | - | - |
| Precipitation (Radar Data) | Wasserverband Eifel-Rur | 1 × 1 km2 | 5 min | Since 2002 | - |
| Land Use | [34] | 15 × 15 m2 | - | Since 2008 | - |
| Land Use Class | Coniferous | Deciduous | Grassland | Agriculture | Urban | |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Fraction of land use type (%) | 40 | 19 | 38 | 2 | 1 | |
| Mean annual LAI (-) | 6.7 1 | 1.93 2 | 1.51 2 | 1.16 2 | 25.5 2 | |
| Evaporation depth (m) | 0.2 1 | Transferred | ||||
| Root depth (m) | 0.5 1 | 1.8 3 | 0.35 4 | 1.0 5 | Deactivation | |
| Root and evaporation distribution function (-) | Quadratic 1 | Quadratic 6 | Cubic 4 | Quadratic 5 | Deactivation | |
| Transpiration fitting parameters (-) | 0.3 1,0.2 1, 1.0 1 | Transferred | Deactivation | |||
| Transpiration limiting saturations (Wilting point, Field capacity, Oxic, Anoxic) (-) | 0.3 1, 0.4 1, 0.89 7, 0.97 7 | Transferred | 0.3 1, 0.4 1, 1.0, 1.0 | Transferred | ||
| Canopy storage (mm) | 0.8 | 0.83 8 | 1.0 8 | 2.5 8 | 15.0 5 | |
| Evaporation limiting saturations (min, max) (-) | 0.3 1, 0.4 1 | Transferred | ||||
| Simulation Scenarios | Soil Data | Land Use | Additional Information |
|---|---|---|---|
| Wüstebach Catchment | |||
| Wbach | Wüstebach | Coniferous | Reference scenario |
| WbachDeci | Wüstebach | Deciduous | |
| WbachGrass | Wüstebach | Grassland | |
| WbachEsoilConi | Erkensruhr | Coniferous | |
| WbachEsoilDeci | Erkensruhr | Deciduous | |
| WbachEsoilGrass | Erkensruhr | Grassland | |
| Erkensruhr Catchment | |||
| Erk | Erkensruhr | Coniferous | |
| Erk_LN | Erkensruhr | All | Distributed land use |
| Erk_LN_PET | Erkensruhr | All | Distributed land use and potential evapotranspiration |
| Erk_LN_PET_P | Erkensruhr | All | Distributed land use, potential evapotranspiration and precipitation |
| Simulation | 2010 | ||||||
|---|---|---|---|---|---|---|---|
| Water Balance Setup Component | Wbach | Wbach Deci | WbachGrass | Wbach Esoil Coni | Wbach Esoil Deci | Wbach Esoil Grass | |
| Rainfall (mm) | 1226 | ||||||
| Potential ET (mm) | 694 | ||||||
| Measured Discharge (mm) | 608 | ||||||
| Transpiration (mm) | 232 | 227 | 279 | 195 | 99 | 282 | |
| Evaporation (mm) | 247 | 254 | 289 | 247 | 256 | 293 | |
| Actual Evapotranspiration (mm) | 479 | 481 | 568 | 442 | 355 | 575 | |
| Discharge 1 (mm) | 611 | 657 | 591 | 647 | 764 | 587 | |
| Baseflow (%) | 76 | 76 | 75 | 64 | 62 | 63 | |
| Infiltration (mm) | 968 | 992 | 1011 | 891 | 879 | 954 | |
| 2011 | |||||||
| Rainfall (mm) | 1348 | ||||||
| Potential ET (mm) | 756 | ||||||
| Measured Discharge (mm) | 630 | ||||||
| Transpiration (mm) | 272 | 312 | 290 | 247 | 250 | 306 | |
| Evaporation (mm) | 273 | 283 | 314 | 273 | 289 | 325 | |
| Actual Evapotranspiration (mm) | 545 | 595 | 604 | 520 | 539 | 631 | |
| Discharge 1 (mm) | 637 | 640 | 626 | 652 | 673 | 594 | |
| Baseflow (%) | 62 | 64 | 60 | 56 | 58 | 53 | |
| Infiltration (mm) | 894 | 959 | 960 | 832 | 870 | 896 | |
| Simulation | Erk | Erk_LN | Erk_LN_PET | Erk_LN_PET_P | |||||
|---|---|---|---|---|---|---|---|---|---|
| Water Balance Setup Component | 2010 | 2011 | 2010 | 2011 | 2010 | 2011 | 2010 | 2011 | |
| Rainfall (mm) | 1226 | 1348 | 1226 | 1348 | 1226 | 1348 | 956 | 902 | |
| Potential ET (mm) | 694 | 756 | 694 | 756 | 694 | 757 | 694 | 757 | |
| Measured Discharge (mm) | 524 | 396 | 524 | 396 | 524 | 396 | 524 | 396 | |
| Transpiration (mm) | 226 | 272 | 268 | 286 | 260 | 305 | 283 | 332 | |
| Evaporation (mm) | 265 | 289 | 278 | 306 | 288 | 312 | 265 | 267 | |
| Actual Evapotranspiration (mm) | 491 | 561 | 546 | 592 | 548 | 617 | 548 | 599 | |
| Discharge (mm) | 721 | 654 | 696 | 623 | 692 | 619 | 391 | 245 | |
| Infiltration (mm) | 996 | 954 | 1024 | 980 | 1016 | 976 | 771 | 683 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornelissen, T.; Diekkrüger, B.; Bogena, H.R. Using High-Resolution Data to Test Parameter Sensitivity of the Distributed Hydrological Model HydroGeoSphere. Water 2016, 8, 202. https://doi.org/10.3390/w8050202
Cornelissen T, Diekkrüger B, Bogena HR. Using High-Resolution Data to Test Parameter Sensitivity of the Distributed Hydrological Model HydroGeoSphere. Water. 2016; 8(5):202. https://doi.org/10.3390/w8050202
Chicago/Turabian StyleCornelissen, Thomas, Bernd Diekkrüger, and Heye R. Bogena. 2016. "Using High-Resolution Data to Test Parameter Sensitivity of the Distributed Hydrological Model HydroGeoSphere" Water 8, no. 5: 202. https://doi.org/10.3390/w8050202
APA StyleCornelissen, T., Diekkrüger, B., & Bogena, H. R. (2016). Using High-Resolution Data to Test Parameter Sensitivity of the Distributed Hydrological Model HydroGeoSphere. Water, 8(5), 202. https://doi.org/10.3390/w8050202