Abstract
Most studies of input data used in hydrological models have focused on flow; however, point discharge data negligibly reflect deviations in spatial input data. To study the effects of different input data sources on hydrological processes at the catchment scale, eight MIKE SHE models driven by station-based data (SBD) and remote sensing data (RSD) were implemented. The significant influences of input variables on water components were examined using an analysis of the variance model (ANOVA) with the hydrologic catchment response quantified based on different water components. The results suggest that compared with SBD, RSD precipitation resulted in greater differences in snow storage in the different elevation bands and RSD temperatures led to more snowpack areas with thinner depths. These changes in snowpack provided an appropriate interpretation of precipitation and temperature distinctions between RSD and SBD. For potential evapotranspiration (PET), the larger RSD value caused less plant transpiration because parameters were adjusted to satisfy the outflow. At the catchment scale, the spatiotemporal distributions of sensitive water components, which can be defined by the ANOVA model, indicate that this approach is rational for assessing the impacts of input data on hydrological processes.
1. Introduction
Model simulation is a principal approach for studying hydrological processes at the catchment scale; however, the accuracy of modelling results is dwarfed owing to the uncertainties of model parameterizations, model structures and input data [1]. Most studies [2,3,4,5] have analysed the uncertainties of parameters using different methods and calibration focused on model’s parameters has determined the contributions from other sources of uncertainties [6]. Ajami et al. [7] confirmed the importance of input data and model structure to model output using the Integrated Bayesian Uncertainty Estimator (IBUNE). Kavetski et al. [8] demonstrated a multitude of distinctions in the predicted hydrographs and calibrated parameters, with or without consideration of the input uncertainty of precipitation data with similar conclusions drawn by Xu et al. [9]. In addition to the precipitation data, Thompson’s [10] research revealed that PET related uncertainty existed in high and low discharges. Furthermore, a number of studies have illustrated that input data may profoundly influence predicted river runoff [11,12,13,14]. However, little attention has been paid to the effect of different input data on the entire hydrological cycle at the catchment scale.
In mountainous catchments with scarce gauges, input data uncertainties are amplified due to the lack of observed data [15]. With the development of satellite technology, RSD provides a lot of information to drive, calibrate and validate hydrological models [16]. Some applications of RSD in hydrological models, even in semi-arid/arid watersheds, have attained promising performance [17,18,19]. RSD also supply a wealth of new observation types that can be applied to assess model uncertainty [20]. According to McMichael et al. [21], the prediction uncertainties of discharge among seven leaf area index (LAI) scenarios were less than 10% using the MIKE SHE simulation. Sun et al. [18] demonstrated that the uncertainties derived from RSD are smaller than those of model parameters. However, Knoche et al. [22] argued that high-resolution land surface temperature (LST) data did not yield a better result and that the simulated hydrographs could not explain the differences in input data. Due to satellite data limitations associated with the physical sensors, space-time coverage and spatial resolution [23], the application of raw RSD has been disputed and has resulted in some controversial results.
This paper characterizes the influence of different input data sources based on variations in distributed simulation outputs. Eight MIKE SHE models forced by SBD and RSD were calibrated separately to obtain optimal performance. The significant impact of input data on different water components was determined via the ANOVA model. Then the effects of the different input data on hydrological processes was studied based on the water components.
2. Study Area
Yarkant River basin (Figure 1) is located in the Xinjiang Uyghur autonomous region, an arid district in Northwest China. It is the longest source tributary of the Tarim River, the longest continental river in the world. The topography of this study catchment is very complex. Generally, the southern headwater region has a much higher elevation than that of the northern mountain outlet region. Mountains, gorges and basins are staggered throughout the watershed. The elevation ranges from 1450 m to 8611 m, averaging 4450 m. The average slope is approximately 30.8%.
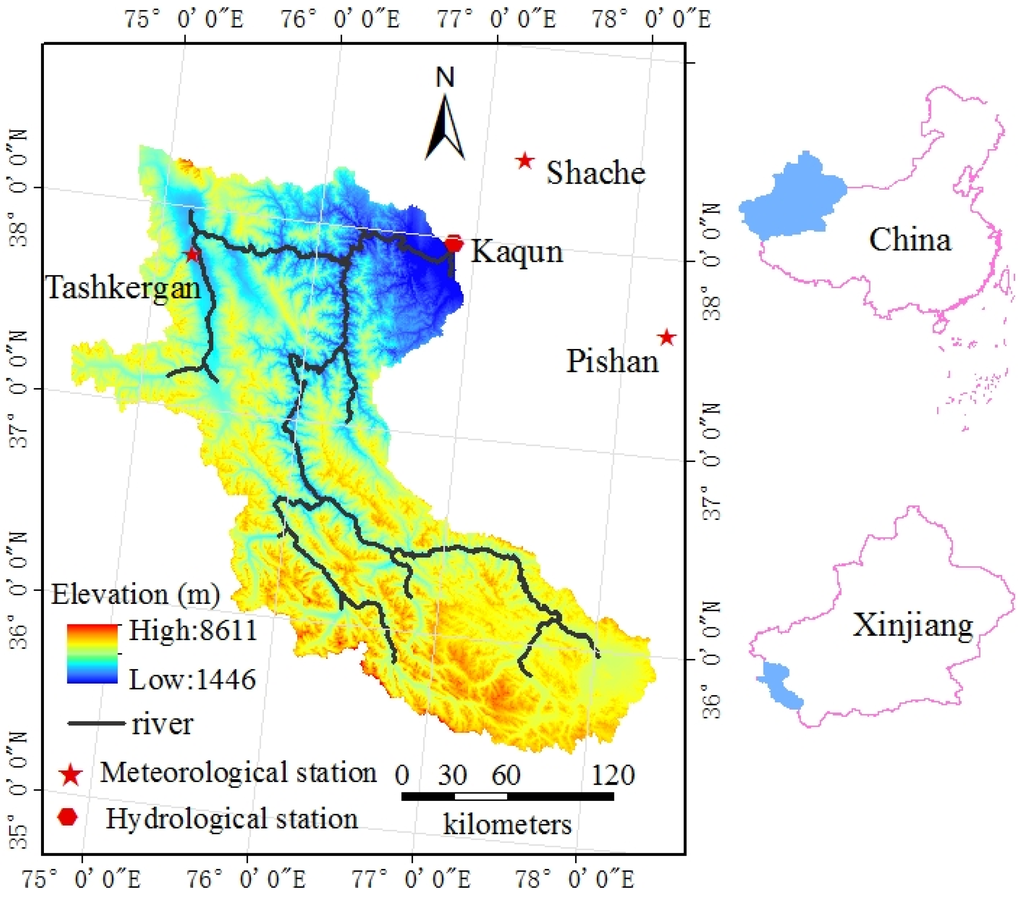
Figure 1.
The location, topography, gauging stations and river network of Yarkant River basin.
This catchment is situated on the northern slope of Karakoram, the largest area of mountain glaciers in the world. Based on the Landsat8 TM, land use data were generated and shows that the snowpack and glaciers cover 26.14% of this watershed (Figure 2a), situated mainly above 5000 m (Figure 2b). The total number of glaciers is 2698, including Insukati Valley, the largest glacier in China with a length of 40 km [24]. The other major land cover types are closed-open herbaceous, bare land and sparse herbaceous areas (Figure 2a) located below 5000 m (Figure 2b), contributing to 29%, 20% and 19.1% of the total area, respectively. The abundant snowpack and glaciers provide ample water resources to the Yarkant River irrigative oasis downstream below Kaqun, with an area of 2.5 × 104 km2. It is the largest irrigation region in Xinjiang and a major producer of grain and cotton [25]. Because of the seasonal snow and ice melt, the volume of river runoff in the flood season (from May to September) accounts for 80% of the annual runoff.
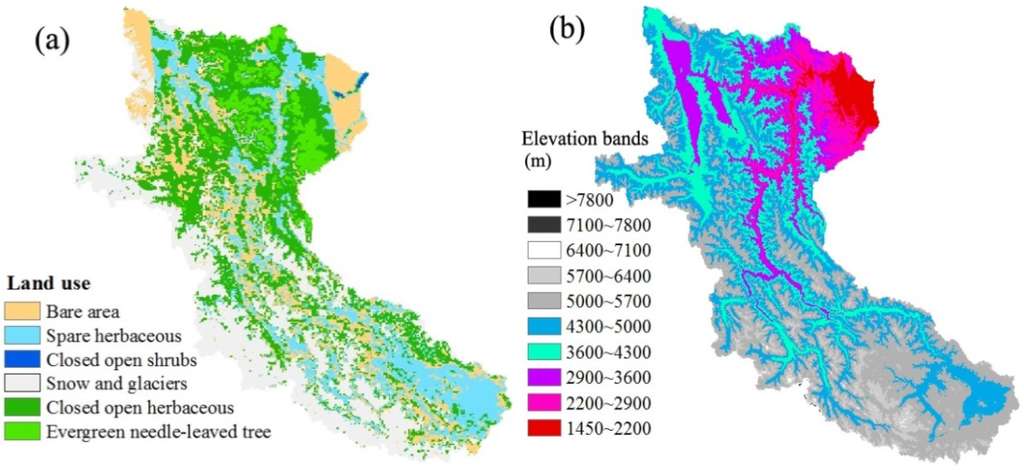
Figure 2.
The land use types. (a) In 2005 and elevation bands; (b) in Yarkant River basin.
The study area is a rarely studied catchment with only one internal meteorological station (Tashkurgan) and two adjacent stations (Shache and Pishan) (Figure 1). Based on the records from Tashkurgan station in 2000–2009, pan evaporation was much higher than precipitation, averaging 1500 mm compared to annual mean precipitation of 98 mm. Furthermore, because of the extreme topography variations, there are strong heterogeneities of precipitation and temperature in spatial distributions [26]. Annual precipitation is approximately 450 mm in high elevation areas (higher than 5000 m) and only 100 mm in lower regions (approximately 3000 m). The mean temperature around the snowline (approximately 5500 m) is approximately –10.5 °C. Therefore, the elevation lapse rate of precipitation (PCG) and air temperature (TCG) at different elevations can be determined, as shown in Table 1.

Table 1.
PCG and TCG at different elevations in Yarkant River basin.
3. Forcing Data
3.1. Station Data
The station meteorological data was obtained from the China Meteorological Data Sharing Service System (http://data.cma.cn/) and daily precipitation and mean air temperatures were collected from 2000 to 2009. Elevation is a central factor that significantly affects distributions of meteorological data, therefore the whole catchment was divided into 10 elevation bands at 700 m intervals (Figure 2b) to spatially distribute the SBD. The interpolated SBD are calculated as follows:
where Rband (Tband) and Rday (Tday) are the precipitation in mm (average temperature in °C) for the calculated elevation band and at the gauged station, the precipitation (mm H2O) and average temperature (°C) recorded at a gauging station, respectively; ELband and ELgage are the mean elevations (m) of the calculated elevation band and gauging station and days is the average number of rainy days in a year at the station. Based on a previous study [27], the same interpolations of precipitation and temperature were used in SWAT and MIKE SHE. SWAT calculates PET at a sub-basin scale using the Penman-Monteith equation based on station-interpolated data. This semi-distributed PET output from SWAT is chosen as input SBD PET in MIKE SHE.
3.2. TRMM
Remotely sensed precipitation data was obtained from the daily productions of the Tropical Rainfall Measuring Mission (TRMM) 3B42 V6 (http://trmm.gsfc.nasa.gov) at a spatial resolution of 0.25°, although the TRMM V6 data was calibrated on a global scale using rain gauge stations [28]. In mountainous regions such as the Yarkant River basin with arid climate conditions, extreme topography and few rain gauges, the accuracy is still unfavourable, especially at the daily temporal scale [29]. Thus, an analysis was conducted to determine whether the TRMM satellite detected the correct precipitation events (Equations (3) and (4)). In this analysis, TRMMdec is defined as the total days in which precipitation events were detected by TRMM but not recorded by SBD. SBDdec is defined as the total number of days in which precipitation events were recorded by SBD but not recorded by TRMM and TRSBdec is defined as the total number of days in which precipitation events were detected by both TRMM and SBD. In addition, Dr and Dw are the percentages of correct and incorrect precipitation events detected by TRMM for the satellite grids that the stations occupy.
The evaluation results are listed in Table 2. For the three stations, the Dw values are much larger than Dr, indicating that many precipitation events detected by TRMM are redundant. An in-depth analysis estimated the different intensity classes of precipitation using the same approach (Equations (3) and (4)). The results suggest that high values of Dw mainly correspond to low-intensity precipitation events (<0.3 mm) with a high probability of incorrect precipitation events (Dw_0.3) (Table 2).

Table 2.
Comparison between raw and corrected TRMM precipitation.
As can be concluded from Table 2, direct application of raw 3B42 V6 data in the Yarkant River basin is inappropriate for model simulation. Therefore, a correction was performed based on the local intensity scaling (LOCI) approach [30], which can correct the wet-day frequencies and intensities and effectively improve the overestimate of rainy days in the raw data. First, a wet-day threshold Pthres was determined from the raw TRMM data to ensure that the frequency matched the SBD. This value was set as 0.3 because TRMM detected too many redundant rainy days with precipitation amounts smaller than 0.3 mm (Table 2). A scaling factor sm was then calculated and used to determine that the mean of the corrected precipitation was equal to the observed precipitation, as follows:
where PSBD,m and PTRMM.raw,m are the SBD and raw TRMM precipitation respectively in the mth month, and PTRMM.cor,m is the corrected TRMM precipitation in the mth month. (.) represents the expectation operator (e.g., (PTRMM,.raw,m) and is the mean value of raw TRMM precipitation in given month m).
After correction, the raw TRMM data quality was much improved. Compared to the raw TRMM, the corrected TRMM was much closer to the SBD in the terms of the mean annual precipitation. In addition, the monthly correlation coefficient also displayed a remarkable improvement refer to rraw and rcor in Table 2. Eventually, this correction approach can be applied to the whole basin based on the ordinary Kriging method, with circular model interpolated sm using ArcGIS, providing revised TRMM data.
3.3. LST
As for temperature, Moderate Resolution Imaging Spectroradiometer (MODIS http://trmm.gsfc.nasa.gov/) MOD11C1 daily LST data was used with a spatial resolution of 0.05°. Version 4.1 was chosen because of its effectiveness in semi-arid and arid regions [31]. Daily mean air temperature data was needed as the MIKE SHE input. Previous research confirmed that there is a good linear relationship between LST and air temperature [32,33]. Because Shache station is missing LST data, only Tashkurgan and Pishan station data were plotted to verify this relationship (Figure 3).
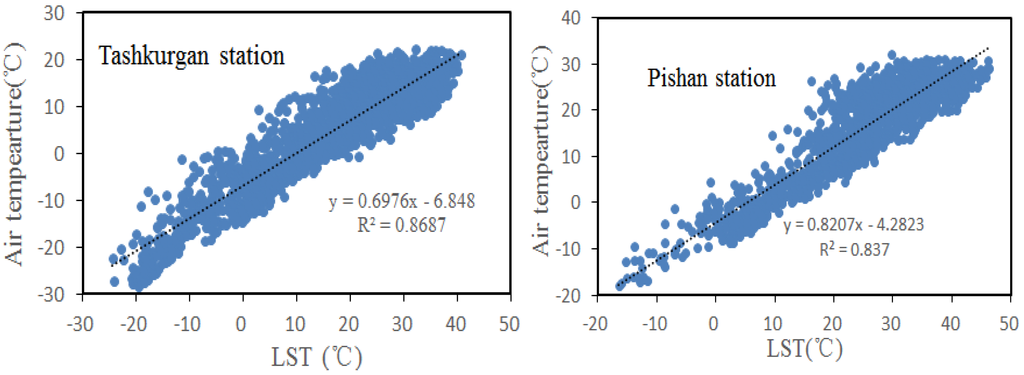
Figure 3.
Regression relationship between daily air temperature and LST at the Tashkurgan and Pishan stations in 2000–2009.
The mean values of the regression coefficients at Tashkurgan station and Pishan station were used in a simple transform Equation (7) to calculate air temperature for the Yarkant River basin. Daily mean air temperatures were acquired as input data for the MIKE SHE model.
3.4. PET
Daily global PET (GPET) data derived from the FEWS NET Data Portal (http://earlywarning.usgs.gov/fews/) was used in this study at a spatial resolution of 1°. This daily PET was calculated on a spatial basis using the Penman-Monteith equation and the formulation for reference crop evaporation [34]. GPET was directly applied in this research.
4. Methodology
4.1. Models
Because of the strong spatial heterogeneity associated with extreme topographical conditions, the fully distributed hydrological MIKE SHE model (European Hydrological System) [35] was employed in this study to reveal the spatial heterogeneity of the Yarkant River basin. MIKE SHE is a deterministic, dynamic, physically based hydrological model. In the MIKE SHE model, catchments are split into a number of square grids to reveal the spatial heterogeneity of the catchment. The input data and parameters in each grid are independent. Based on bilinear interpolation method, all input and output data possesses the same spatial resolution, as set in the model.
In this study, a spatial resolution of 2 km was set in the MIKE SHE model. SBD was applied as a benchmark and three types of RSD and their combinations were applied individually to replace the SBD. Finally, eight models were utilized based on different input data (Table 3). The entire simulated period was uniform from 2000 to 2009, including a warm-up period from 2000–2002, calibration period from 2003–2007 and verification period from 2008–2009.

Table 3.
The eight models in this study based on different input data.
4.2. Calibration
To obtain the optimal performance of each model, the same calibration procedures were executed separately. The auto calibration tool based on the Shuffled Complex Evolution (SCE) global optimization algorithm [36], which is a part of the MIKE SHE package, was chosen for calibration. The main significant parameters of snowmelt chosen for calibration include degree-day factor (DDF) and threshold melting temperature (TMT). Those of land surface flow include Manning values (MAN). Those of interflow include horizontal hydraulic conductivity (HHC) and vertical hydraulic conductivity (VHC). Those of evapotranspiration include LAI and root depth (RD). During the calibration, standard deviation (STD) was chosen as a statistical output measure and the weighted sum of STD was taken as the objective function. Additionally, three statistical coefficients were used as the performance judgement criteria: Nash-Sutcliffe [37] efficiency coefficient NSC, Pearson correlation coefficient r and root mean square error RMSE. Their expressions are written as follows:
where Qobs,i and Qsim,i are the measured and simulated discharges respectively, on day i (m3/s); and are the average measured and simulated discharges respectively, during the simulated period (m3/s); and n is the time step.
4.3. Hypothesis Test
The natural processes of hydrological cycles constitute complex systems with highly nonlinear relationships between the “affected” and the “caused”. To evaluate the effect of input data uncertainty on the hydrological process, it is necessary to define the sensitivities of the water components to the different input data. In this study, a statistical hypothesis test based on the ANOVA model, which is useful in comparing the statistical significance of three or more groups, was chosen to test different significant effect of the input data on water components.
Three types of input data (precipitation, temperature and PET) were used as effect factors A, B and C. They were investigated at two levels (SBD and RSD). When A is at level i (I = 1,2), B is at level j (j = 1,2) and C is at level k (k = 1,2), the resulting water component can be denoted by ui,j,k. The ANOVA model [38] for three factors with fixed effects is as follows:
where is the observation for the nth case or trial for the scenario based on the ith level of A, jth level of B and the kth level of C; is the grand mean of all dependent variables ui,j,k; , and are the main effects of factors A, B and C, respectively; , and are the main effects of the two-factor interaction is the main effect of the three-factor interaction; and is the independent random error which follows a normal distribution .
When factor A is tested, we assume that the null hypothesis H0, meaning that the influence of the factor on the result is not significant, is acceptable. Thus, . In this case, the probability p = P(F[(a-1),abc(n-1)]>FA) can be calculated. When the calculated p-value is larger than the significance level (α), set as 0.05 in this study, suggesting that the assumption is correct, the null hypothesis H0 will be accepted. Otherwise, the alternative hypothesis Ha should be accepted. Other hypotheses could be tested in the same way.
5. Results and Discussion
5.1. Simulated Discharges
After separate calibrations, the final values of chosen parameters were obtained. Among the eight models, MAN ranged from 25 to 60 based on different land use. For the different soil types, HHC and VHC ranged from 0.0003 to 0.001 and 0.0035 to 0.01, respectively. MAN, HHC and VHC showed insignificant changes between different models for the same land use or soil type. The calibrated values of other parameters are listed in Table 4. When temperature was replaced, the parameters of snow (DDF and TMT) were adjusted drastically. When PET was replaced, parameters of evapotranspiration (LAI and RD) changed remarkably. In the other cases, the variations were insignificant. These were revealed by comparing parameter values under STA to the three models setting with only one remote sensing input (i.e., the TRMM, LST and GPET) in table. Because of the periodic growth, LAI and RD in herbaceous areas exhibit distinct temporal variations [39] and not listed in Table 4.

Table 4.
The final values of calibration parameters in different models.
Based on the multiple evaluation coefficients (Table 5) in the verification period, the performances of most models were acceptable, except for the TRGP and RSD models. The NSC values of the other six models were higher than 0.5 and all r values exceeded 0.7. The STA model exhibited the best result, with the highest NSC and r value and the smallest RMSE, suggesting that the interpolation of meteorological data based on elevation intervals was feasible. The LOCI approach can correct only the magnitude and frequency of TRMM and not the probability distribution, possibly causing the relatively poor performance of the TRMM application. In general, the application of the corrected RSD in the Yarkant River basin was acceptable, although it could be improved.

Table 5.
Statistical coefficients of the performances of different models.
The boxplots of monthly mean simulated discharge (Figure 4) at the outlet station derived from the eight models indicate significant variations from April to September. The large differences suggest that even for simulated discharge at the outlet station, which are adjusted by the auto-calibration scheme, the eight models exhibit deviations, as clearly illustrated by the peak flow, which is influenced by mixed precipitation and snowmelt. If the input data is evaluated based on only the simulated runoff, this evaluation will affect the understanding of other water balance components negatively. Alternatively, variabilities in the distributed output are more available [40]. Accordingly, the distributed water components represent a better way to evaluate the effects of input data uncertainties on the simulation of hydrological processes.
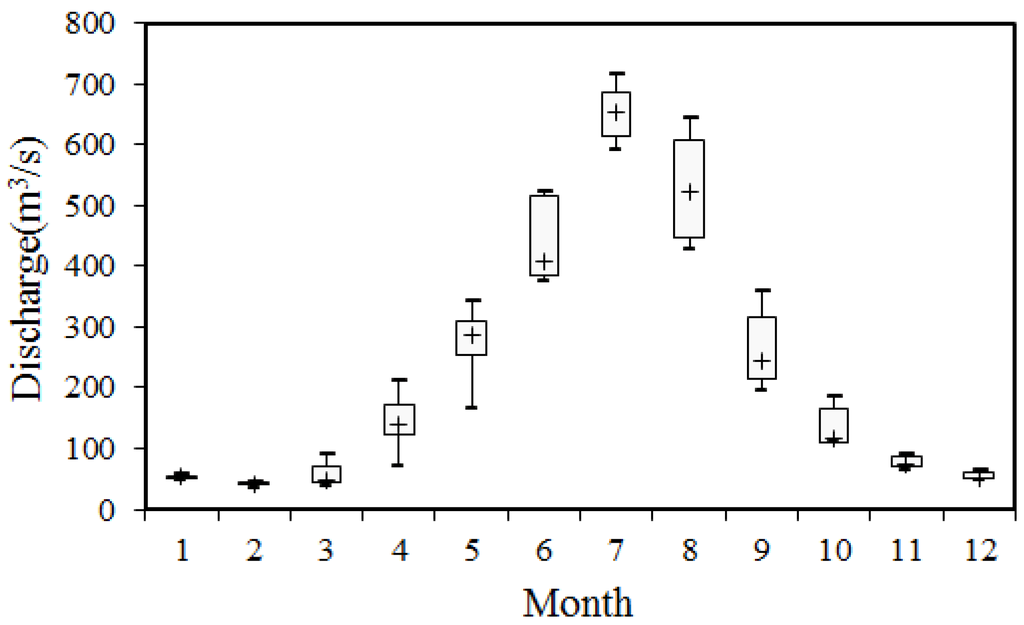
Figure 4.
Boxplots of monthly mean discharges at the outlet station derived from eight models from 2003 to 2009.
5.2. Sensitivities of Water Components
In this study, the hypothesis tests were aimed at differentiating water components based on their annual mean values and each group test dataset was first adopted by the normal distribution and variance homogeneity test. In the MIKE SHE model, ETa was divided into different categories: snow sublimation (SNOWS), canopy interception (CI), river and pond water evaporation (WE), soil evaporation (SOILE) and plant transpiration (PT). These five ETa sources, overland flow (OLF), base flow (BF) and snow storage (SS) were employed for the hypothesis test. The probability p value results are provided in Table 6.

Table 6.
The probability p values of the hypothesis H0 test.
Table 6 indicates that factor A, precipitation, had a significant effect on most hydrological components, except SNOWS, SOILE and PT. Factor B, temperature, plays a crucial role in the snow, PI and WE processes. All evapotranspiration sources except SNOWS were strongly sensitive to factor C, PET. Through the statistical hypothesis tests, the sensitivities of water components to different data types were illustrated intuitionally. Based on the results, the distributed output SS can be specified to analyse precipitation and temperature deviations from RSD and SBD. PT was employed in the PET deviation analysis.
5.3. Responses of Hydrological Processes
5.3.1. Snow Storage
Figure 5 illustrates the spatial distribution of the simulated annual mean snow storage depths from the STA, TRMM, LST and GPET models. When the significant impact factors, precipitation and temperature associated with snow storage (Table 5) were replaced by RSD in the TRMM and LST models, the spatial distribution of the snowpack underwent a huge change. In addition, the temporal distributions SS in different elevation bands (Figure 6) also exhibited significant variations among STA, TRMM and LST.
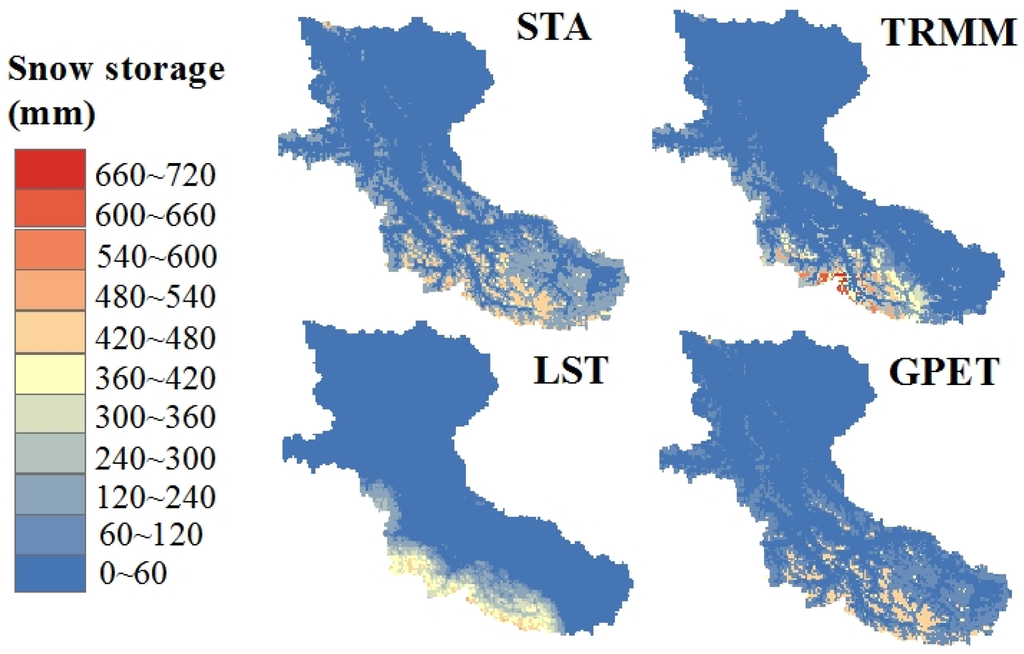
Figure 5.
Spatial distributions of simulated annual mean snow storage based on the STA, TRMM, LST and GPET models in the Yarkant River basin from 2003 to 2009.
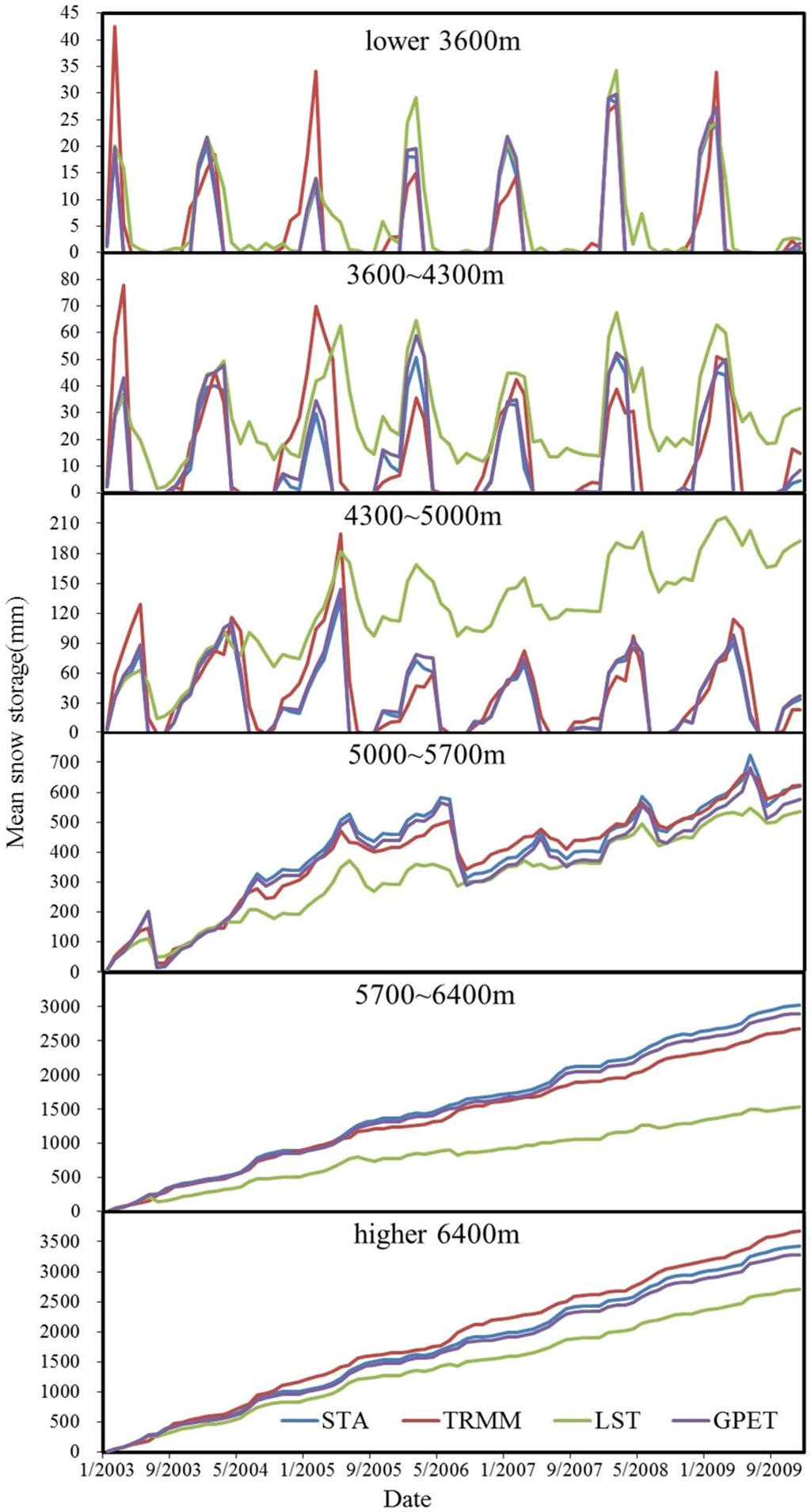
Figure 6.
The temporal distributions of snow storage in different elevation bands.
Compared to the STA model, the TRMM model resulted in significant variations in annual mean snow storage depth, with change proportions of −9.4% and 12.3% in the 5000 m–5700 m and higher than 6400 m zones, respectively. These differences may be interpreted based on the distribution of SBD and TRMM precipitation (Figure 7). However, the two data sets calculated similar average annual precipitation values of 309.86 mm and 323.14 mm. TRMM data resulted in a more reasonable spatial distribution characterized by a more reasonable isopluvial zone, which can reflect the influences of distance and elevation. For the interpolated station data, the spatial distribution was relatively fragmented. Compared with the average annual values of interpolated station data in the different elevation bands, TRMM precipitation was 12% larger in the higher than 6400 m zone. In the 5000–5700 m zone, underestimation of TRMM precipitation was remarkable, reaching 18%. These deviations matched snow storage variations well. In the region with elevations lower than 5000 m, because there is no permanent snowpack, the differences between SBD and TRMM precipitation cannot reflect snow storage.
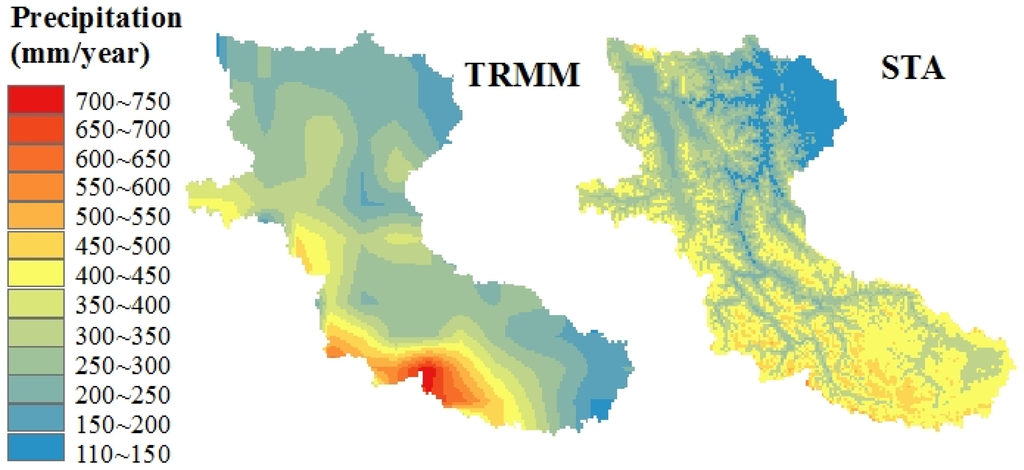
Figure 7.
Spatial distributions of the annual mean precipitation based on TRMM and SBD in Yarkant River basin from 2003–2009.
Another noteworthy change in Figure 5 is the snow coverage area in the STA and LST models. The areas of annual average snow storage depth higher than 5 mm (SS5), 10 mm (SS10) and 15 mm (SS15) in the LST model decreased by 37%, 46% and 47% relative to STA model, respectively. However, the area with snow depth less than 5 mm (SS0) was simulated to be 77% larger by the LST model. These changes could be caused by the distinct distributions of the SBD and LST data sets (Figure 8). For SBD, a piecemeal spatial distribution similar to that of precipitation was observed. Variation in the spatial distribution generally was not substantial. Compared with SBD in the zone with elevations lower than 3600 m, the LST data were lower by 3.2 °C. In the 5000–5700 m elevation band, the LST data were higher than SBD by 1.1 °C. In the 3600 m–5000 m region, there was little distinction between the data sets.
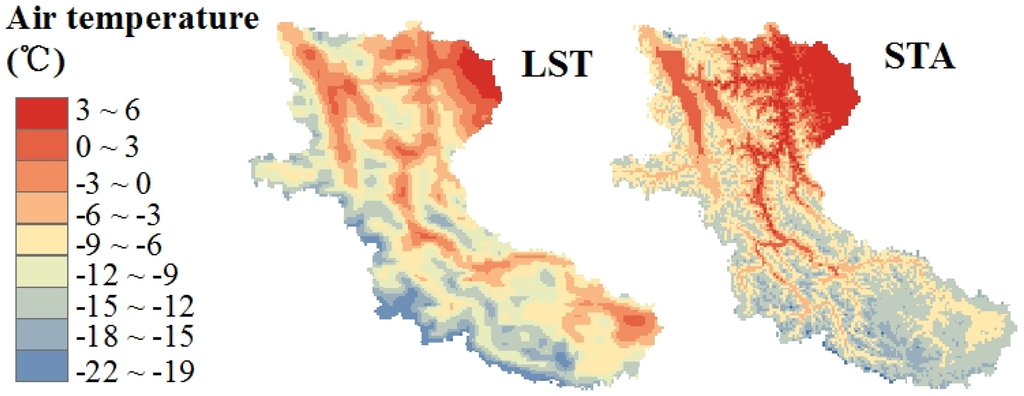
Figure 8.
Spatial distributions of the annual mean temperature between station and TRMM data in the Yarkant River basin from 2003–2009.
Based on Figure 6, in the 3600 m–5000 m region the temperatures from the two data sets were similar. Nevertheless, due to the smaller DDF and higher TMT in the LST model (Table 4), the speed of snowmelt decreased and a permanent snowpack appeared. In the 4300 m–5000 m region, the snow storage exhibited an increasing trend. Finally, the LST model simulated a 52.2% increase in snow storage compared with the estimate of the STA model in this region. However, the depth of the snowpack at 3600 m–4300 m was very thin, averaging 4.2 mm, which is why we detected the augmented SS0 in the LST model. In the higher 5000 m region where the dominant snowpack was located, the calculated higher air temperature in the LST model caused a 41.2% reduction in the annual snowpack. Figure 8 also shows a continuous increase in snow storage in the region higher than 5700 m, largely because there is little snowmelt in this region because of the very low temperature. Snowdrifts and snow slides become the primary movement methods. Unfortunately, these movements have not yet been included in MIKE SHE. Thus, this snow storage generally increased as snowfall accumulates.
5.3.2. Plant Transpiration
Based on Figure 5 and Figure 6, there is little or no variation between STA and GPET because PET does not significantly affect evapotranspiration (Table 6). Using plant transpiration (Table 6) as an example (Figure 9) to analyse the effect of PET, compared with the STA model the most significant variations occurred in the GPET model, with reductions in high transpiration regions covered by evergreen needle-leaved trees and closed-open herbaceous areas (Figure 2a), exhibiting change rates of 33.4% and 35.6%, respectively. These variations may be due to the different PET values in the two models because of the low resolution of the GPET data (1°). The spatial distribution features were not evident. Only the monthly temporal distributions of the two PET data sets are compared in Figure 10. The annual mean PET estimates in the Yarkant River basin were 256.5 mm and 309.2 mm, based on the two data sets. The higher PET estimated by the GPET model mainly occurred from May to August, increasing at a rate of 34.78%. Based on the MIKE SHE calculation, transpiration was closely related to land use parameters (i.e., LAI and RD). In the GPET model, the larger input PET values caused more evapotranspiration dissipation and decreased the simulation performance. To decrease evapotranspiration, the transpiration was reduced through adjusting LAI and RD, which were chosen as calibration parameters (Table 4).

Figure 9.
The spatial distributions of simulated annual mean transpiration based on the STA, TRMM, LST and GPET models in the Yarkant River basin from 2003–2009.
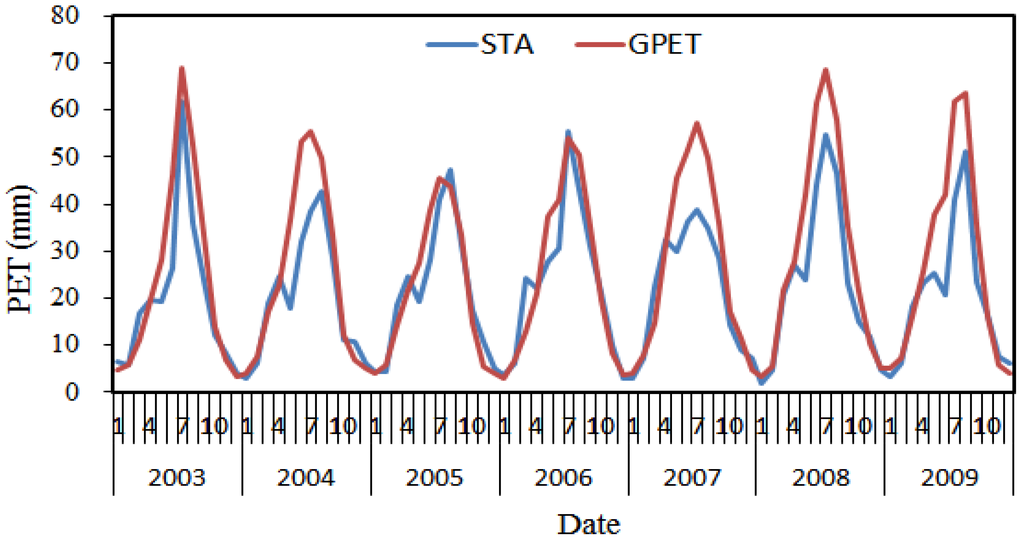
Figure 10.
The temporal distributions of mean monthly PET based on SBD and RSD in the entire Yarkant River basin from 2003–2009.
In addition, compared to STA, the reduction percentage of transpiration from GPET in different seasons was insignificant in evergreen needle-leaved tree zones. Due to seasonal variations of LAI and RD in closed-open herbaceous areas, the peak values appeared during the summer and variations mainly occurred from May to August, with a reduced proportion of 54.3%, compared with 23.1% during other months. Although the different ETa sources are calculated based on different parameters, all of these ETa sources are sensitive to PET and can yield clearer trends regarding the uncertainty of the input PET.
6. Conclusions
In the high and scarcely gauged alpine watershed of the Yarkant River basin, the MIKE SHE model using dissimilar data sources, demonstrated reasonable results and the simulated discharge barely explained deviations in input data reflected by flow hydrography peaks at the outlet station.
An ANOVA model indicated that precipitation, temperature and PET had significant effects on different water components in hydrological processes. Based on the ANOVA model, snow storage, a sensitive component, was chosen to analyse the effects of uncertainties in precipitation and temperature, including the plant transpiration associated with PET.
The application of TRMM made the differentiation of snow storage distribution more evident, resulting in large values in higher elevation regions. Corresponding to a TRMM precipitation overestimation of 12% higher than 6400 m and an underestimation of 18% at 5000 m–5700 m, the TRMM model resulted in snow storage changes of 12.3% and −9.4% compared with the STA model.
The application of LST caused a more extensive and continuous snow-covered area with a thinner depth. Because of the relatively smaller DDF and higher TMT, the LST model simulation obtained a larger snow storage area, with a rate of 52.2% and a lower snow line in the 3600 m–5000 m region than the STA results. In the 5000 m–5700 m region, the overestimation of temperature intensified snowmelt and decreased snow storage at a rate of 41.2%.
The application of GPET resulted in less plant transpiration, especially in areas of high vegetation coverage. Compared with the STA model, due to the larger GPET value, the GPET model reduced plant transpiration by adjusting the calibrated parameters RD and LAI to satisfy the water balance. The reductions primarily occurred in the lush vegetation regions characterized by evergreen needle-leaved trees and closed-open herbaceous areas, with proportions of 33.4% and 35.6%, respectively.
The different input data sources had significant effects on the hydrological process. These sources are marginally explained by the discharge hydrography. By examining the significant impact factors of the water components, the uncertainties associated with a certain type of input data can be determined by the spatiotemporal distributions of the responding water components. Furthermore, the proposed method in this study can be used to analyse changes in the hydrological processes and distributed patterns of water components caused by the different input data. In the hydrological cycle process, one type of input data can have a significant effect on several water components. In this study, each water component was analysed based on one certain type of input data. The hydrologic characteristics are quite different in different watersheds. Consequently, the more prominent components should be used for inter-comparison to define the uncertainties of input data associated with the entire cyclical process.
Acknowledgments
We gratefully acknowledge the valuable databases used in this study, including SRTM, TRMM, MODIS, FEWS NET Data Portal and the China meteorological data sharing service system. The authors are thankful for the assistance of the Xinjiang Tarim River Basin Management Bureau. This study was financially supported by the Thousand Youth Talents Plan of China (Xinjiang Project: 374231001), the Key Deployment Program of the Chinese Academy of Sciences (KZZD-EW-12-3) and the Project of Chinese Academy of Sciences (Y674122).
Author Contributions
Jiao Liu performed the major data processing and modelling and wrote manuscript. Tie Liu designed part of the MIKE SHE model and analysed the simulated results. Anming Bao chose the data and interpreted some results. Philippe De. Maeyer revised the manuscript’s structure and language and contributed to its professionalism. Alishir Kurban performed part of the data processing and helped improve the structure and language of the manuscript. Xi Chen evaluated the manuscript and made suggestions based on the study’s goals.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Jasper, A.V.; Hoshin, V.G.; Willem, B.; Soroosh, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model paremeters. Water Resour. Res. 2003, 39, 1–16. [Google Scholar]
- Misgana, K.M.; John, W.N. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar]
- Zhang, X.S.; Raghavan, S.; David, B. Calibration and uncertainty analysis of the SWAT model using Genetic Algorithm and Bayesian Model Averaging. J. Hydrol. 2009, 374, 307–317. [Google Scholar] [CrossRef]
- Jin, X.L.; Xu, C.Y.; Zhang, Q.; Singh, V.P. Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. J. Hydrol. 2010, 383, 147–155. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Gao, X.; Soroosh, S. Multimodel combination techniques for analysis of hydrological simulations application to distributed model intercomparison project results. J. Hydrometeorol. 2006, 4, 755–768. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43, 1–10. [Google Scholar]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 2. Application. Water Resour. Res. 2006, 42, 1–9. [Google Scholar] [CrossRef]
- Xu, C.Y.; Tunemar, L.; Chen, Y.D.; Singh, V.P. Evaluation of seasonal and spatial variations of lumped water balance model sensitivity to precipitation data errors. J. Hydrol. 2006, 324, 80–93. [Google Scholar] [CrossRef]
- Thompson, J.R.; Green, A.J.; Kingston, D.G. Potential evapotranspiration-related uncertainty in climate change impacts on river flow: An assessment for the Mekong River basin. J. Hydrol. 2014, 510, 259–279. [Google Scholar] [CrossRef]
- Dobler, C.; Bürger, G.; Stötter, J. Assessment of climate change impacts on flood hazard potential in the Alpine Lech watershed. J. Hydrol. 2012, 460, 29–39. [Google Scholar] [CrossRef]
- Chien, H.; Yeh, P.J.; Knouft, J.H. Modeling the potential impacts of climate change on streamflow in agricultural watersheds of the Midwestern United States. J. Hydrol. 2013, 491, 73–88. [Google Scholar] [CrossRef]
- Xu, Y.P.; Zhang, X.; Ran, Q.; Tian, Y. Impact of climate change on hydrology of upper reaches of Qiantang River Basin, East China. J. Hydrol. 2013, 483, 51–60. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.P.; Fu, G. Uncertainties in SWAT extreme flow simulation under climate change. J. Hydrol. 2014, 515, 205–222. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation for a catchment treated as ungauged (with uncertainty). Water Resour. Res. 2002, 38, 1411–1414. [Google Scholar] [CrossRef]
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- Liu, T.; Willems, P.; Feng, X.W.; Li, Q.; Huang, Y.; Bao, A.M.; Chen, X.; Veroustraete, F.; Dong, Q.H. On the usefulness of remote sensing input data for spatially distributed hydrological modelling: Case of the Tarim River basin in China. Hydrol. Process. 2012, 26, 335–344. [Google Scholar] [CrossRef]
- Sun, W.; Ishidaira, H.; Bastola, S. Calibration of hydrological models in ungauged basins based on satellite radar altimetry observations of river water level. Hydrol. Process. 2012, 26, 3524–3537. [Google Scholar] [CrossRef]
- Deus, D.; Gloaguen, R.; Krause, P. Water Balance Modeling in a Semi-Arid Environment with Limited in Situ Data Using Remote Sensing in Lake Manyara, East African Rift, Tanzania. Remote Sens. 2013, 5, 1651–1680. [Google Scholar] [CrossRef]
- Van, D.A. Model-data fusion: Using observations to understand and reduce uncertainty in hydrological models. In Proceedings of the 19th International Congress on Modelling and Simulation (MODSIM 2011), Perth, Australia, 12–16 December 2011.
- McMichael, C.E.; Hope, A.S.; Loaiciga, H.A. Distributed hydrological modelling in California semi-arid shrublands: MIKE SHE model calibration and uncertainty estimation. J. Hydrol. 2006, 317, 307–324. [Google Scholar]
- Knoche, M.; Fischer, C.; Pohl, E.; Krause, P.; Merz, R. Combined uncertainty of hydrological model complexity and satellite-based forcing data evaluated in two data-scarce semi-arid catchments in Ethiopia. J. Hydrol. 2014, 519, 2049–2066. [Google Scholar]
- Prigent, C. Precipitation retrieval from space: An overview. Comptes Rendus Geosci. 2010, 342, 380–389. [Google Scholar]
- Shi, Y.F. Brief of Glacier Inventory of China; Shanghai Popular Science Press: Shanghai, China, 2005. (In Chinese) [Google Scholar]
- Tang, H.; Yang, D.G.; Zhang, Y.F. Food security and agricultural structural adjustment in Yarkant River Basin, northwest China. J. Food Agricul. Environ. 2013, 11, 324–328. [Google Scholar]
- Gao, X.; Zhang, S.Q.; Ye, B.S.; Qiao, C.J. Glacier Runoff Change in the Upper Stream of Yarkant River and Its Impact on River Runoff during 1961–2006. J. Glaciol. Geocryol. 2010, 32, 445–453. (In Chinese) [Google Scholar]
- Liu, J.; Liu, T.; Bao, A.M.; Philippe, D.M.; Feng, X.W.; Scott, N.M.; Chen, X. Assessment of Different Modelling Studies on the Spitial Hydrological Processes in an Arid Alpine Catchment. Water Resour. Manag. 2016, 30, 1757–1770. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydeometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Xuan, J.; Luo, Y. Quality Assessment of the TRMM Precipitation Data in Mid Tianshan Mountains. Arid Land Geogr. 2013, 36, 253–262. (In Chinese) [Google Scholar]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. Intercomparison of versions 4, 4.1 and 5 of the MODIS Land Surface Temperature and Emissivity products and validation with laboratory measurements of sand samples from the Namib desert, Namibia. Remote Sens. Environ. 2009, 113, 1313–1318. [Google Scholar] [CrossRef]
- Vogt, J.V.; Viau, A.A.; Paquet, F. Mapping regional air temperature fields using satellite-derived surface skin temperatures. Int. J. Climato. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
- Cristóbal, J.; Ninyerola, M.; Pons, X. Modeling air temperature through a combination of remote sensing and GIS data. J. Geophy. Res. 2008, 113. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Abbott, M.; Bathurst, J.; Cunge, J.; O’connell, P.; Rasmussen, J. An introduction to the European Hydrological System-Systeme Hydrologique Europeen, “SHE”, 2: Structure of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Michael, H.K.; Christopher, J.N.; John, N.; William, L. Applied Linear Statistical Models; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Fabio, F.; Christian, R.; Tobias, J.; Gabriel, A.; Stefan, W. Alpine Grassland Phenology as Seen in AVHRR, VEGETATION, and MODIS NDVI Time Series-a Comparison with in Situ Measurement. Sensors 2008, 8, 2833–2853. [Google Scholar]
- Kristensen, K.J.; Jensen, S.E. A model for estimating actual evapotranspiration from potential evapotranspiration. Nordic Hydrol. 1975, 6, 170–188. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).