Next Article in Journal
Identification of Outlier Loci Responding to Anthropogenic and Natural Selection Pressure in Stream Insects Based on a Self-Organizing Map
Previous Article in Journal
Response of Hydrological Processes to Input Data in High Alpine Catchment: An Assessment of the Yarkant River basin in China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 8
Issue 5
10.3390/w8050186
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Rationalization of Altitudinal Precipitation Profiles in a Data-Scarce Glacierized Watershed Simulation in the Karakoram

by
Xiaolei Wang
1,2,
Lin Sun
1,
Yiqing Zhang
1,2 and
Yi Luo
1,2,3,*
1
Key Lab of Ecosystem Network Observation and Modeling, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences (CAS), 11A, Datun Road, Chaoyang District, Beijing 100101, China
2
University of Chinese Academy of Sciences, No. 19A, Yuquan Road, Shijingshan District, Beijing 100049, China
3
Xinjiang Institute of Ecology and Geography, CAS, Urumqi 830011, China
*
Author to whom correspondence should be addressed.
Water 2016, 8(5), 186; https://doi.org/10.3390/w8050186
Submission received: 25 February 2016 / Revised: 28 April 2016 / Accepted: 29 April 2016 / Published: 5 May 2016
Browse Figures
Versions Notes

Abstract

:
Due to the scarcity of field observations and geodetic measurements in catchments in the Karakoram Mountains in Western China, obtaining precipitation data for the high mountains involves large uncertainties and difficulties. In this study, we used a functional relationship between the annual glacier accumulation and summer temperature at the equilibrium line altitude (ELA) to derive precipitation lapse rates (PLAPSs) in a data-scarce watershed. These data were used in a modified Soil and Water Assessment Tool (SWAT) model with a glacier module to simulate glacio-hydrological processes in the Yarkant River basin in the Karakoram. The PLAPS based on the widely-used grid datasets considerably underestimated precipitation, yielding an unreasonable watershed water balance and inaccurate glacier changes. However, the ELA-based PLAPS improved the simulation significantly. In the Yarkant River basin, the annual precipitation reached a peak of 800–1000 mm at approximately 5300 m a.s.l. The model simulations indicated that the contributions of glacier melt and ice melt to total runoff were 52% and 31%, respectively. Moreover, a significant precipitation increase and a non-significant temperature increase during the melt season may be the major reasons for the decreased ice melt and slower glacier shrinkage on the northern slope of the Karakoram during the period of 1968–2007.

1. Introduction

The Karakoram Mountains are natural water towers for arid regions in Pakistan and Western China. In recent years, this region has been of interest to researchers due to its significance and the “Karakoram anomaly” [1]. This phenomenon deserves further investigation to clarify the relation between climate forcing and glacier responses in the region [2]. However, because of the complex terrain and high elevations of this area, sufficient hydrological and meteorological data are lacking in the high-elevation regions [3]. The lack of observed data is a major constraint for research studies.
Due to the scarcity of observed hydrological data, distributed hydrological models are considered useful tools for investigating the intra- and inter-annual dynamics of the hydrological process due to the high temporal resolutions over long time periods and the different spatial scales of the models [4]. Some hydrological models have been upgraded with glacial process modules and are widely used in snow- and glacier-dominated regions [5,6,7,8]. These models provide a solid foundation for studies in the Karakoram, in which a large area is covered by glaciers. However, as the availability of hydrometeorological data at high elevations is extremely limited, hydrological modeling is a challenging task in glacierized mountainous regions. To a large degree, the performance of a glacio-hydrological model depends on the forcing data for these catchments [9]. At high elevations, air temperature influences snow and glacier melting [9,10], and precipitation controls mass accumulation [3,11,12,13]. Therefore, the temperature and precipitation at high elevations have a large impact on the outputs of glacio-hydrological models. The temperature lapse rate (TLAPS) is one of the most important variables for modeling meltwater runoff using the T-index method [9,14]. Immerzeel et al. [9] proposed that larger TLAPS values in specific months led to an increase in glacier melt of 400%. However, relative to precipitation, temperature is more stable and less spatially variable [15]. Temperature and elevation exhibit a highly linear correlation with seasonal gradients [9,16,17]. Precipitation is generally more uncertain due to orographic effects in catchments and the fact that most rain gauges are located at lower elevations [18]. Bookhagen and Burbank [19] confirmed a strong relationship between topography and monsoon rainfall, illustrating two topography-related zones of high rainfall and an approximately exponentially-decreasing trend at higher elevations based on Tropical Rainfall Measuring Mission (TRMM) data in the Himalayas.
Currently, gridded precipitation products are generally used as forcing data in hydrological assessments [6,20], such as the Asian Precipitation Highly Resolved Observational Data Integration Towards Evaluation (APHRODITE) and National Centers for Environmental Prediction-National Center for Atmospheric Research (NCEP-NCAR) re-analyses. However, gridded data products always underestimate high-elevation precipitation in mountainous areas [4,20]. An underestimation of precipitation can be offset in a model by an overestimation of glacier melt [21,22]. In hydrological modeling, model performance is typically assessed using observed runoff data, and vertical precipitation gradients are generally derived based on the observed runoff [23]. If the precipitation is underestimated, good model performance can be achieved by increasing glacier melting. However, this process distorts the actual roles of glaciers and results in unrealistic losses of glacier area. The magnitude of precipitation required to sustain large glacier systems is much higher than that implied by gridded precipitation products [20]. Therefore, the similarity between observed and simulated glacier changes may be another potential way to correct mountain precipitation in addition to the traditional method based on observed streamflow. Long-term changes in glaciers indicate the relationship between glacier mass accumulation and ablation. In recent years, observed glacier mass balance changes were used to effectively quantify precipitation at high elevations in the Hunza and Indus River basins [13,20]. However, in glacierized regions with no observed glacier mass balance data, other quantification methods related to glacier change are necessary.
In our study, the Yarkant River basin on the northern slope of the Karakoram was chosen as the study area. We used a functional relationship between annual glacier accumulation and summer temperature at equilibrium line altitudes (ELAs) to derive the initial precipitation at high elevations. The precipitation lapse rates (PLAPSs) were calibrated based on both observed streamflow and glacier area changes using the glacier-enhanced Soil and Water Assessment Tool (SWAT). Once the observed streamflow and glacier area changes matched the simulated values, the PLAPSs were determined, and the high-elevation precipitation was inversely calculated based on the corrected PLAPSs. Finally, we explain the reason for the smaller loss of glacier area in this region based on the simulation results.

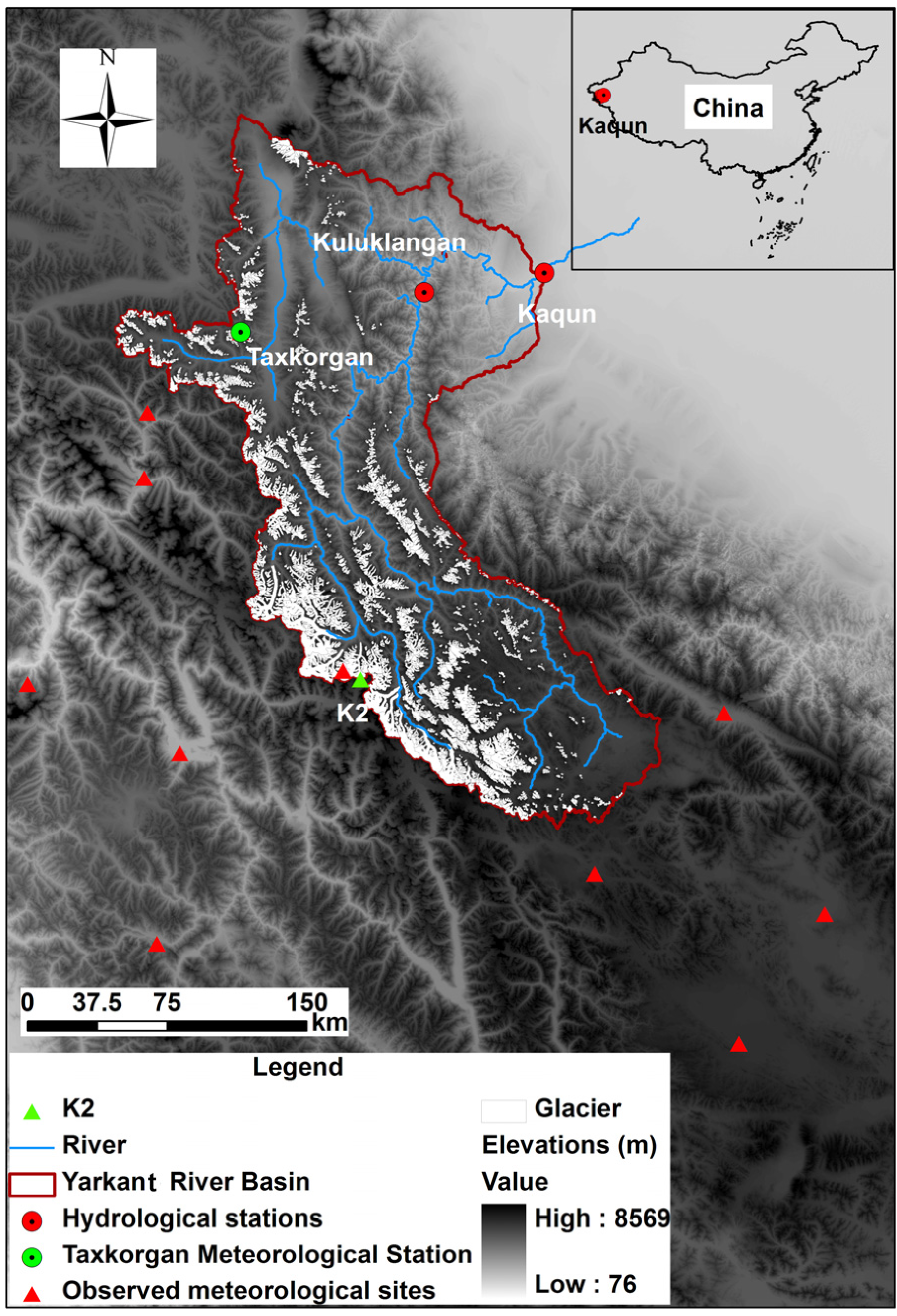
2. Study Area

The Yarkant River originates at the Karakoram Pass on the northern slope of the Karakoram Mountains. The source region of the Yarkant River above the Kaqun Hydrologic Station (KQHS) is 4.67 × 104 km2 (Figure 1). The Kuluklangan Hydrologic Station (KLKHS) is located upstream of KQHS and has a catchment area of 3.29 × 104 km2. There are 3064 glaciers in the basin, and 12% of the glacier coverage is estimated to be above KQHS. Among the glaciers, the Insukati Glacier is the largest in China, with an area of 359.09 km2. The K2 Glacier is extremely famous and is located on the mountain K2, the second highest mountain in the world. The catchment elevation ranges from 1446 to 8611 m a.s.l., with an average elevation of 4423 m a.s.l. Approximately 88% of the basin area is located between 3000 and 6000 m a.s.l. Due to the specific geographic conditions, the accumulation of ice and snow in high mountains is the primary source of runoff [24,25,26].
The climate in the source region is influenced primarily by mid-latitude westerlies and the summer southeastern monsoon from the Indian Ocean. The highest monthly temperature of 7.5 °C in the source region of the Yarkant River occurs in July, and the lowest monthly temperature of −20 °C occurs in January. The seasonal distribution of precipitation is highly uneven, with 67% of the annual precipitation concentrated between May and September.

3. Data and Methods

3.1. Description of the Data

3.1.1. Topography, Soil, Land Cover and Glacier Maps

The Shuttle Radar Topography Mission (SRTM3) digital elevation model (DEM), with a spatial resolution of 90 m, was used to delineate the source region of the Yarkant River into sub-basins and to generate the tributary and channel systems.
The First China Glacier Inventory (1960s) [27] and the Second China Glacier Inventory (2009) [28] were used in this study. The digital glacier vector data from the 1960s have inherent issues, such as georeferencing problems [29]. Therefore, the glacier outlines from the First China Glacier Inventory were adjusted manually based on topographic maps and aerial photographs. Based on the period of the First China Glacier Inventory, the simulation began in 1968. The observed glacier area of the Yarkant River basin has retreated by 9% from the 1960s–2009 based on the First and Second China Glacier Inventories. Land use/cover maps extracted from the European Space Agency GlobCover land cover maps (GlobCover 2009), which have a resolution of 300 m × 300 m, were used in this study. Soil data were obtained from the Harmonized World Soil Database of the Food and Agriculture Organization of the United Nations (HWSD Version 1.2), which was released in 2012. The data include some soil properties, such as the fractions of sand, silt and clay and the organic carbon content.

3.1.2. Precipitation and Temperature

Only the Taxkorgan Meteorological Station provides long-term climate monitoring data within the study area (see Figure 1). Therefore, the Asian Precipitation–High-Resolved Observed Data Integration Towards Evaluation version 1101 (APHRODITE) [30] and Princeton’s Global Meteorological Forcing Dataset (PGMFD) [31] were used as the precipitation and temperature inputs, respectively. The data from APHRODITE are long-term continental-scale daily gridded data from 1951 to 2007 based on a rain-gauge observation network with a spatial resolution of 0.25°. PGMFD was constructed by combining a suite of global observation-based datasets with the National Centers for Environmental Prediction-National Center for Atmospheric Research (NCEP-NCAR) reanalysis dataset. The data have a daily resolution and a spatial scale of 0.5°, including mean, minimum and maximum air temperatures from 1948 to 2010. The gridded daily air temperature data at a spatial resolution of 0.25° were obtained via bilinear interpolation from the grid cell centers in the PGMFD gridded temperature dataset. Each grid was regarded as a base station.

3.1.3. Observed Streamflow Data

The monthly discharge data spanning 1968–1989 from KQHS and KLKHS were used to calibrate and validate the model. They were obtained from the China Hydrological Almanac. The first two years were treated as the warm-up period for the simulation. The data segment from 1970 to 1979 was used for model calibration, and the data segment from 1980 to 1989 was used for model validation.

3.2. The Glacier-Enhanced SWAT Model

SWAT [32] is a public-domain, open-source, physically-based, long-term, basin-scale continuous model that enables users to modify the model code for their specific uses. It has been used widely in hydrological cycle and water resource management simulations [33,34].
The officially released versions of SWAT do not simulate glacier hydrology. Luo et al. [35] developed a glacier module that was incorporated into the SWAT model to simulate watershed glacio-hydrological processes. The module treats each individual glacier as a hydrological response unit (GHRU). Each GHRU is divided into ten elevation bands. The glacier mass balance is simulated in each band. The simulated glacier mass balance components include mass accumulation, sublimation, melting of ice and snow and refreezing of these meltwaters. The ice and snow melts are simulated using the degree-day factor approach [14,36]. The glacier volume is calculated based on the total glacier mass balance, and the glacier area is updated through the glacier volume-area scaling relation [37]. This relation is as follows:
A g l a = ( V g l a m ) 1 / n
where Agla (km2) and Vgla (m·km2) are the surface area and volume of the glacier, respectively. Based on Liu et al. [38], m is set at 40 and n at 1.35 in this study. These values were derived from measured glacier data in northwest China. This relation can also be used to calculate glacier water storage.
In this model, the Spatial Processes in Hydrology (SPHY) classification [6] was used to calculate the runoff in each hydrologic response unit (HRU/GHRU). This calculation consists of four possible contributing factors: rainfall runoff, snow melt, glacier melt and baseflow. Precipitation-based runoff consists of surface runoff and lateral flow released from soil water storage due to rainfall. Snow melt consists of snow meltwater released from snow storage. The runoff from glacier melt encompasses all of the melt generated in the glacierized area, including supraglacial snow melt, ice melt and rainfall runoff on the ice surface. Baseflow is released from shallow and deep groundwater storage. The total runoff in all HRUs is summed to determine the runoff for the entire watershed. The river discharge is routed to determine the loss via river channels. The glacier-enhanced SWAT model has been applied to several alpine watersheds in the Tianshan Mountains [35,39,40,41] and has proven to be a robust tool for glacio-hydrological simulations with a daily time step.

3.3. Method for Rationalizing High-Elevation Precipitation

In this study, APHRODITE precipitation at low elevations (usually including the non-glacierized area) can be assessed based on the observed data. However, at high elevations, there are no weather stations. Therefore, we assess the APHRODITE precipitation at high elevations based on the water balance and previous investigations. If APHRODITE precipitation is underestimated based on our assessment, we use the observed streamflow and glacier changes to estimate the precipitation at high elevations. The detailed procedures are as follows.

3.3.1. The Glacier Mass Accumulation-Summer Temperature Relationship

Because no observed glacier mass balance data are available for the study area, a relationship between glacier mass accumulation and summer temperature was used to obtain the initial high-elevation precipitation. Several authors have related annual accumulation (or ablation) at the ELA to the summer mean temperature using exponential or power-law functions [42,43,44]. Bookhagen and Burbank [19] and Salerno et al. [17] also showed an approximate exponentially-decreasing trend at higher elevations based on TRMM data and observed data in the Himalayas. Kotlyakov and Krenke [45] developed an empirical formula named the “global formula” based on 57 observation stations around the world and used it to calculate the annual ablation at the ELA. The relationship is formulated as follows:
A = 1.33 × ( 9.66 + T s ) 2.85
where A is the accumulation (or ablation) at the ELA per year (mm w.e., where w.e. = water equivalent) and Ts is the mean temperature in the summer (June–August) at the ELA (°C).
The summer season temperature-index method has been widely used to calculate ELA climates and glacial melt [46,47,48,49]. Here, Ts was calculated from the observed summer temperature at the Taxkorgan Meteorological Station via TLAPS. Because glacial accumulation at the ELA is equal to ablation, the amount of accumulation can be confirmed. Accounting for snowdrift, the accumulation is 1.3-times greater than the precipitation [19]. Thus, the annual precipitation at the ELA (PELA, in mm) can be expressed as follows:
P E L A = A / 1.3 = 1.02 × ( 9.66 + T s ) 2.85
For each glacier, the annual precipitation at the ELA was calculated using Equation (3) from 1968 to 1970, which is considered to have been a stable period for glaciers in the Karakoram Mountains [2]. Therefore, annual precipitation was determined at these different elevations in the glaciered zones. The APHRODITE precipitation at low elevations and simulated precipitation in glacierized regions were used to correct the annual PLAPSs in the high-elevation regions. Eventually, ELA-based PLAPS values with multiple rates were obtained over the entire basin.

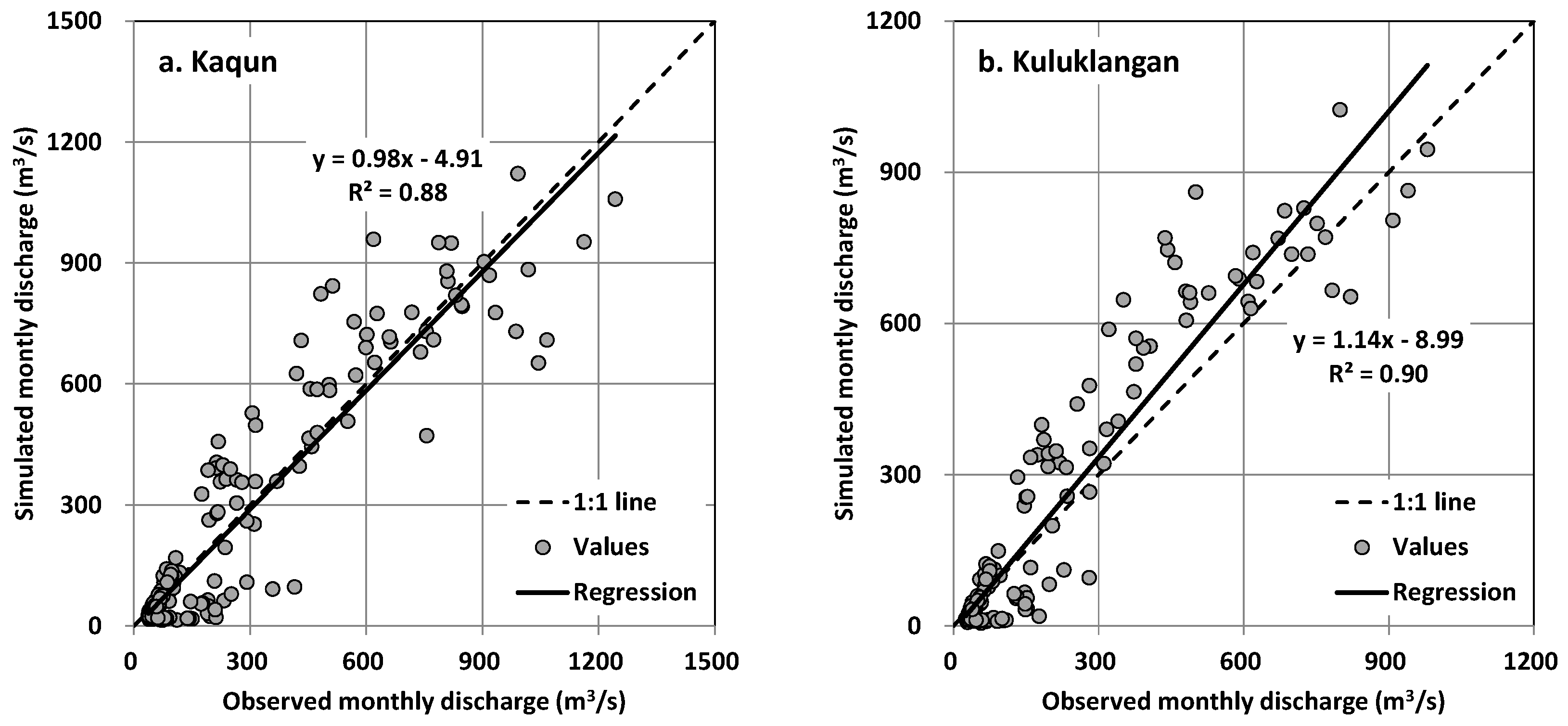
3.3.2. Calibration and Validation

In the SWAT model, the monthly discharges observed at KQHS and KLKHS and the observed glacier change data were used as the primary data for calibrating PLAPSs and other parameters. During calibration, the internal processes of the model were monitored to guarantee the rationality of the simulation. First, the model was calibrated and validated using the stream discharge data. The simulated monthly discharges at KQHS and KLKHS were compared to the observed values. The comparison was evaluated using the Nash–Sutcliffe efficiency (NSE) and the percent bias (PBIAS) indices. The performance of the model during the calibration and validation stages was rated according to the system proposed by Moriasi et al. [50].
Next, the model was run from 1968 to 1970. PLAPS values and other parameters related to glacier melt were adjusted to maintain glacier mass balance, especially for larger glaciers. Then, the model was run from 1968 to 2007. The simulated glacier area change during this period was compared to the change derived from the two phases of the China Glacier Inventory.
We repeated this process many times. Finally, the NSE, PBIAS and the comparison of the glacier area changes were evaluated comprehensively. When all of them were within an acceptable limit based on Moriasi et al. [50], the PLAPSs and other parameters were accepted.
Additionally, the water balance for the entire catchment was examined. The catchment water balance over a period can be expressed as follows:
R = P + Δ S - E T a
where R, P and ETa are the mean runoff, precipitation and evapotranspiration, respectively, for a given period. ∆S is the catchment water storage change, which includes changes in glacier water storage, snow water storage, soil water storage and aquifer water storage. As the snow, soil water and aquifer water storage values remained stable during the long period, the changes in water storage were mainly attributed to changes in the glacier reserves. The observed R can be acquired based on observed streamflow at KQHS. The changes in glacier water storage can be calculated based on the observed glacier area changes from the First and Second Chinese Glacier Inventories and Equation (1).
After the determination of the PLAPS, the precipitation at high elevations was acquired and rationalized, although some uncertainties existed.

3.4. Trend Analysis Method

Trend analyses of the temperature, precipitation and runoff were conducted using the Mann–Kendall test statistic [51,52,53], which is a non-parametric test. The Mann–Kendall test rejects the null hypothesis if Z ≥ |Zcr|, where Zcr is the critical value of the normal distribution at the 5% confidence level (Zcr = ±1.96). A positive value of Z indicates an increasing trend, while a negative value of Z indicates a decreasing trend. A robust estimate of the slope can be calculated using Sen’s non-parametric method [53,54]. In this case, Sen’s slope estimator is the median of the n(n − 1)/2 slopes of the pairs ( x j : x k ) , where j > k.

4. Results

4.1. Parameter Setting

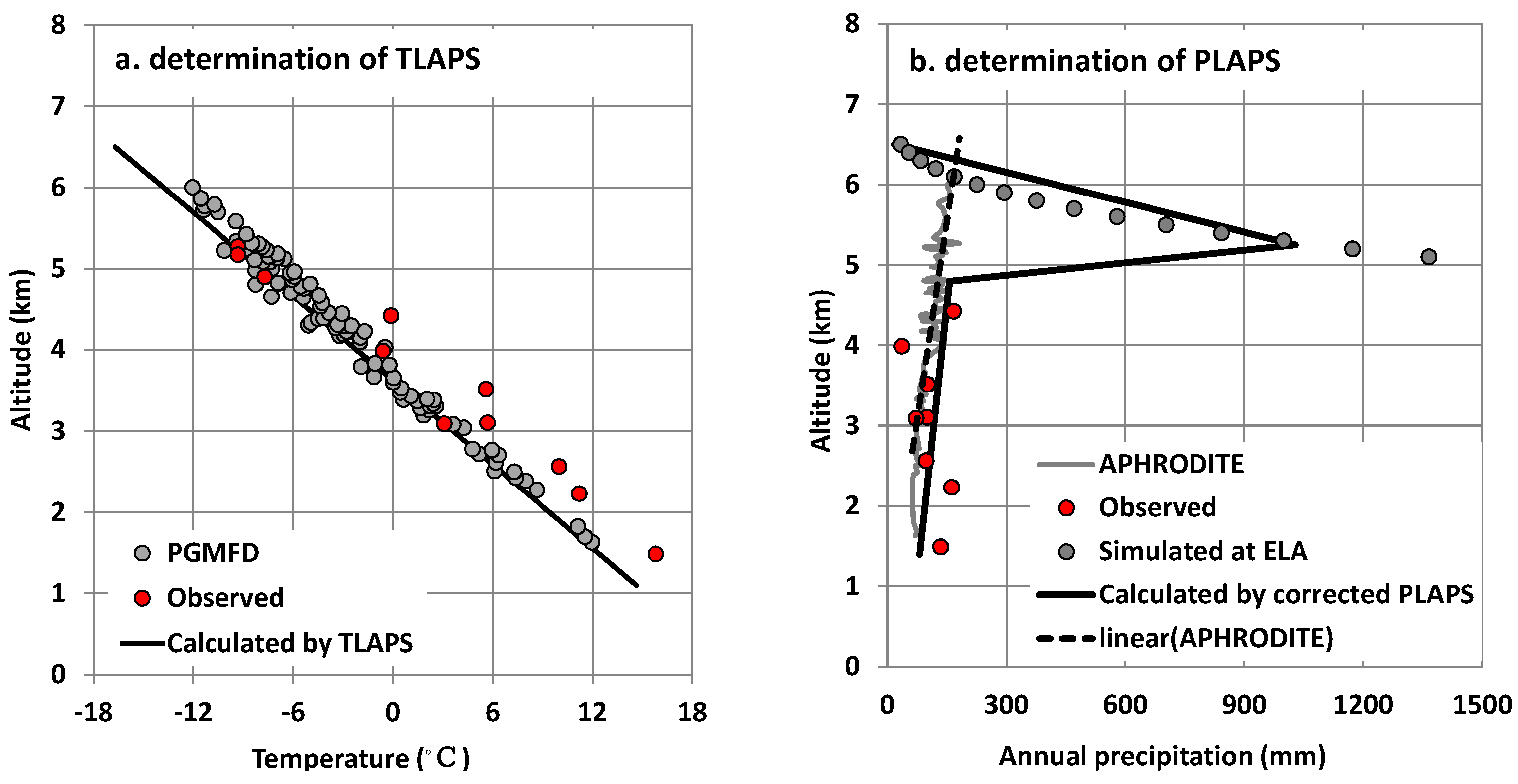
4.1.1. TLAPS

The TLAPS is generally linear and varies seasonally [9,16,17]. Therefore, monthly values were adopted based on the observed and PGMFD temperature data in this study. The initial TLAPS was determined using the gridded PGMFD temperatures. According to the linear regression analysis, the TLAPS from the annual PGMFD temperature was −6.1 °C·km−1. After calibration, the TLAPS based on the annual average temperature was determined to be −5.8 °C·km−1 (Figure 2a), and the TLAPS values for the spring, summer, autumn and winter were −5.3, −6.5, −5.8 and −5.3 °C·km−1, respectively. Moreover, most of the observed temperatures at the meteorological sites near the Yarkant River basin [55] were distributed around the TLAPS line. Only the observed temperatures of some sites below 3000 m a.s.l. were higher than the simulated values. Because less than 10% of the catchment area is located below 3000 m a.s.l., the underestimation may only slightly affect the modeling results. Similar TLAPS values were reported in previous studies in nearby glacierized catchments (e.g., −6.4 °C·km−1 in the Hunza River basin in Karakoram [56], −5.4 °C·km−1 in the upper Langtang catchment in the central Himalayas in Nepal [9], −6.0 and −6.5 °C·km−1 in the Baltoro and Langtang watersheds in the Himalayas [5] and −5.5 °C·km−1 in the Langtang valley [3]). Hence, the TLAPS used in this study is reliable.

4.1.2. Other Key Model Parameters

Except for TLAPS and PLAPS, the most sensitive parameters were adopted from similar studies [5,6,35,57,58]. The initial values were based on the default lower and upper bounds in the SWAT database and from the aforementioned studies. Calibration of these parameters was also performed based on the trial and error method with respect to the observed and simulated monthly streamflow at KQHS and KLKHS and the glacier area changes from 1968 to 2007. The parameterization results are listed in Table 1.

4.2. Reconciling High-Elevation Precipitation

4.2.1. Assessment of APHRODITE Precipitation

The water balance in the catchment was unbalanced based on the APHRODITE precipitation. The average annual observed streamflow (R) at KQHS from 1968 to 1989 was 137 mm, but the average annual APHRODITE precipitation (P) during the same period was only 98 mm. The decline in glacier water storage (∆S) was approximately 25 mm based on Equation (1) and the First and Second China Glacier Inventories. The sum of APHRODITE precipitation and glacier water storage changes was still smaller than the river discharge. Moreover, evapotranspiration in the arid region of northwestern China is intense. Based on Equation (4), APHRODITE substantially underestimates the actual precipitation in the Yarkant River basin.
In addition, when a linearly-fitted PLAPS based on APHRODITE (dotted line in Figure 2b and approximately 22 mm·km−1) was used to force the calibrated model, the simulated monthly average streamflow was underestimated by 60% at KQHS and 59% at KLKHS compared to the observed values. Additionally, the NSE values were only 0.42 and 0.51 at KQHS and KLKHS, respectively (Table 2). The simulated glacier area shrinkage rate based on the linear PLAPS was 15.6% from 1968–2007. This value is larger than the observed changes, highlighting the fact that underestimated precipitation may be offset in the model by overestimating melt [21,22]. If the model attempts to achieve an observed streamflow, a larger glacier area will retreat, disagreeing with the actual situation.
Overall, APHRODITE precipitation for the catchment is underestimated and cannot be directly used in the hydrological modeling. Figure 2b shows that APHRODITE precipitation below 4500 m is close to the observed values. Therefore, precipitation at high elevations must be corrected.

4.2.2. Determination of PLAPS

At high elevations, precipitation was calculated via Equation (3) and calibrated based on the observed monthly discharges at KQHS and KLKHS and glacier change data. For each glacier, the annual precipitation at the ELA was calculated using Equation (3) from 1968 to 1970, as shown in Figure 2b (the grey dots represent the average precipitation at the corresponding elevation and were derived from Equation (3) for each glacier). The precipitation exhibited a decreasing trend with increasing elevation. Bookhagen and Burbank [19] and Salerno et al. [17] used TRMM and observed precipitation data to confirm that precipitation at higher elevations exhibits a decreasing trend with increasing elevation in the Himalayas. Using APHRODITE precipitation data at low elevations, the PLAPS for the catchment is non-linear and can be divided into multiple rates. However, the turning points for the PLAPS are difficult to determine. As mentioned before, the Yarkant River basin contains 3064 glaciers. In the 1960s, the ELAs of 90% of the glaciers ranged from 5000 to 5800 m a.s.l., and the highest frequency occurred at approximately 5300 m a.s.l. based on data from the First China Glacier Inventory. After calibration, we selected 4800 m and 5300 m as the turning points for the multiple PLAPS values. The polyline in Figure 2b was thus determined based on the values at these points. After calibration, multiple PLAPSs were obtained for the entire basin.
This variable PLAPS was calibrated based on the observed and simulated monthly streamflow at KQHS and KLKHS and the glacier area changes. The results of the calibration and validation are as follows.
The performance of the SWAT model forced by the corrected PLAPS was assessed by comparing simulated and observed streamflows using calibration and validation analyses. During the calibration period, NSE values at KQHS and KLKHS were 0.87 and 0.85, respectively, and PBIAS values were 9.3% and −7.1% (Table 2). The model performance was rated as ‘very good’ based on Moriasi et al. [50]. For the validation analysis, NSE values were 0.87 and 0.83 for KQHS and KLKHS, respectively, and PBIAS values were −0.9% and −10.9%. The model performance was rated as ‘good’ and ‘very good’ based on NSE and PBIAS measures [50].
An assessment of the goodness-of-fit between the values simulated using corrected PLAPS and observed monthly streamflow at KQHS and KLKHS was performed based on linear regression analysis (Figure 3). It showed that the regression lines were very close to the 1:1 line, with a minor y-axis intercept, suggesting that the discharge at KQHS was slightly underestimated and that the discharge at KLKHS was slightly overestimated. The coefficients of determination (R2) were 0.88 and 0.9 for KQHS and KLKHS, respectively, suggesting that the simulated river discharge exhibited a good fit with the observed values in the Yarkant River basin.
However, using the change in the glacier area based on the different phases of glacier data as an additional criterion may help constrain the uncertainty of the high-elevation PLAPS. The observed glacier area retreated by 9% from the 1960s to 2009. The simulated glacier area shrinkage rate based on the corrected PLAPS was 8.9% from 1968 to 2007, which is extremely close to the observed value. Moreover, for different glacier size classes, the simulated area shrinkage rates were also close to the observed values (Figure 4), and the most obvious retreat occurred in glaciers with areas of less than 5 km2. The results may reveal that the precipitation in high-elevation regions calculated via ELA-based PLAPS effectively mimics the actual precipitation, thus providing sufficient accumulation for glaciers with low area shrinkage rates.
In addition, the precipitation calculated using the corrected PLAPS maintained the water balance. From 1968 to 1989, the simulated annual precipitation and evapotranspiration for the entire catchment were 207 mm and 98 mm, respectively. The changes in glacier water storage and other water storages (snow, soil water and aquifer storage) were −26.9 mm and 0.6 mm, respectively. The simulated annual average runoff for the same period was 135 mm, which was close to the observed streamflow. Based on Equation (4), the water balance error was almost zero, and the corrected PLAPS produced a close water balance for the glaciered watershed simulation.
Therefore, the model performance based on the corrected PLAPS, in terms of the simulated streamflow and glacier area change, was acceptable. Additionally, the PLAPS was able to simulate the precipitation, especially the high-elevation precipitation of the Yarkant catchment, with a relatively high accuracy.

4.2.3. Inversely Calculating Precipitation Using the Corrected PLAPS

The calibrated PLAPS controlled by streamflow and glacier area change was used to inversely calculate the high-elevation precipitation in the Yarkant River basin. Figure 2b shows that the precipitation simulated by the corrected PLAPS increased at elevations below 5300 m a.s.l. and decreased at elevations above this level. It peaked at 5300 m a.s.l., and the precipitation between 5100 and 5500 m a.s.l. was approximately 800–1000 mm, which was approximately five-times larger than the APHRODITE precipitation estimate. This result makes sense based on previous observations and studies. Field data indicate that the annual precipitation increases significantly between 4600 and 5150 m a.s.l. on the K2 glacier [11] and is 100 mm below 3000 m a.s.l. and 1300–1500 mm above 5000 m a.s.l. on the Batura glacier [11,59]. Some studies have reported a precipitation peak between 5000 and 6000 m a.s.l. in the Karakoram [13,60]. Combining time series analyses of the valley-based stations with short-term campaigns, Hijmans et al. [61] proposed that the annual precipitation in northwestern Karakoram increased from 150 to 500 mm at elevations of 1500–3000 m a.s.l. to greater than 1700 mm at 5500 m a.s.l. due to winter and occasional spring and summer rainfall. Based on conservative assumptions, Winiger et al. [62] suggested that rainfall in west Karakorum could reach 1500–1800 mm·y−1 at 5000 m a.s.l. Moreover, Shi [63] revealed that this region likely receives considerable precipitation, which leads to considerable accumulation, in turn supporting the development of famously large glaciers. Immerzeel et al. [5] also suggested that the observed glacier extents in the Karakoram can be explained by strong vertical precipitation lapse rates. Immerzeel et al. [20] unambiguously showed that high-elevation precipitation in this region was underestimated using gridded data and that the large glaciers here can only be sustained by much higher rates of accumulation. Therefore, the high precipitation rates at high elevations calculated using the corrected PLAPS are reasonable according to the aforementioned observations and investigations.

5. Discussion

5.1. Uncertainties of the PLAPS

With respect to data-scarce, high-alpine catchments, glacio-hydrological simulations are particularly limited by a lack of sufficient observation data. Despite the good simulation results in this study, uncertainties still exist. The PLAPS at high elevations was corrected by precipitation that was calculated via Equation (3). On the one hand, Equation (3) is an experimental formula based on observed glaciers from around the globe, and the calculated precipitation may represent large-scale values. On the other hand, the multiple PLAPS in this study used four points to determine the lapse rates in the three sections (Figure 2b). Among the points, the precipitation values and elevations of the second and third points (P_2, P_3 and EL_2, EL_3; numbered from low to high) were more difficult to determine and were more uncertain. Figure 5 shows that streamflow is sensitive to the precipitation and elevation values of the two points, whereas the glacier area changes are more sensitive to precipitation at the third point. Based on Moriasi et al. [50], to reach a “satisfactory” rate, the elevations at the two points can range from 4600 to 5050 m a.s.l. and 5000 to 5800 m a.s.l., and the precipitation values can range from 56 to 330 mm and 800 to 1300 mm. Note that the uncertainty interval is not small. As shown in Figure 5, NSE first increases and then decreases, and the absolute PBIAS increases for every 100-m increase of EL_2 and EL_3. The NSE changes from 0.77 to 0.89 when EL_2 or EL_3 varies by 500 m, but PBIAS can range from −15% to 30% for the same elevation changes (Figure 5a,b). With increases in P_2 (56–330 mm) and P_3 (800–1300 mm), NSE decreases and ranges from 0.72 to 0.89, while PBIAS changes from −26% to 18% (Figure 5c,d). The glacier area shrinkage rates can range from 8.3% to 10.5% based on the elevation changes and from 6.2% to 11.5% based on the precipitation variations (Figure 5e,f). Thus, P_2 is more sensitive to glacier area changes. Combining the NSE and PBIAS values with the glacier area changes, the PLAPS values shown in Figure 2b achieve the optimal model performance.
In general, land surface hydrology model simulations are highly sensitive to the accuracy of the precipitation input. Reliable precipitation inputs are necessary for producing reasonable model parameters and simulations [64]. Therefore, the PLAPS has a significant impact on the outputs of the glacio-hydrological model used [9]. Studies on the impact of climate change in similar regions [6,65,66] have also revealed that precipitation differences in mountainous areas can significantly affect the temporal and spatial distributions of runoff and changes in glacier areas, mass balances and meltwater. As a result, accurately determining PLAPS is a key process in hydrological modeling. The combined use of NSE, PBIAS and glacier area changes may provide a more reliable assessment of model performance. Additional information regarding glacier area change and mass balance may enhance model parameterization and reduce the uncertainty to some extent [67,68,69].

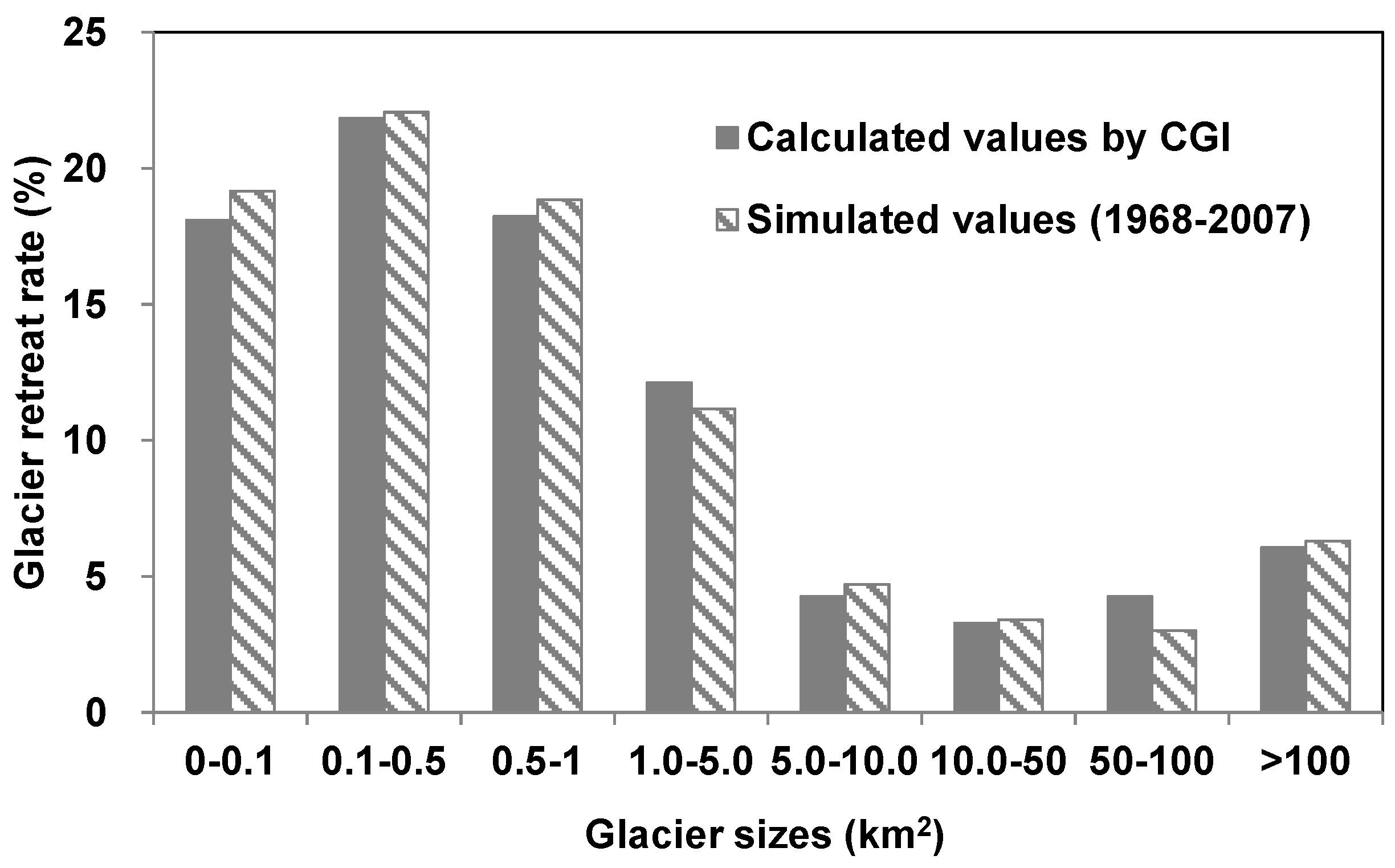
5.2. Explanation of Current Glacier Changes

The loss of glacier area in the Yarkant River basin located on the north slope of the Karakoram was 9% from the 1960s to 2009. This rate was less rapid than those in most Himalayan basins [70]. We use the calibrated SWAT model to simulate the glacio-hydrological regimes, especially glacier melt in the Yarkant River basin from 1968 to 2007, and try to explain the reasons for the glacier response.

5.2.1. Intra-Annual Distribution

Figure 6a shows that approximately 60% of the precipitation fell during the summer months (June–September) and that only 10% fell during the winter months (December–February). Furthermore, rain and heat occurred during the same period, and the highest temperature was recorded in July and August.
The average annual flow volume for the catchment was 6.44 km3 from 1968 to 2007, with the monthly flow peaking in August. The runoff pattern was similar to that for precipitation, with 88% of the total annual runoff occurring from July–September and only 5% during winter months (Figure 6b). However, the proportion of runoff in summer months was higher than that for precipitation. The good correlation between the runoff and precipitation patterns suggests that monsoon precipitation plays a dominant role in runoff generation in this region. Additionally, the higher proportion of runoff implies that there are other important sources of runoff. Averaged from 1968 to 2007, the contributions of glacier melt, snow melt, rainfall runoff and baseflow to total runoff were 52%, 17%, 16% and 15%, respectively. Glacier meltwater was the most significant component of the water balance, and the contribution of glacier meltwater was close to that simulated by Yang [30] using glacier meltwater runoff modules. The hydrograph associated with glacier meltwater started to rise in July, peaked in August and then decreased through October (Figure 6b). From June–September, meltwater constituted the major component of the water balance in the Yarkant River basin, contributing to 63%–83% of the total runoff in each month (Figure 6c).
In this study, glacier melt is defined as the total runoff generated on glaciers, including ice melt, supraglacial snow melt and rainfall runoff [4]. Figure 6d shows that the contributions of these three components to glacier melt were 61%, 28% and 11%, respectively, for the Yarkant catchment from 1968 to 2007. Moreover, ice melt contributed to 31% of the total runoff. This indicates that glaciers played a crucial role in the water supply of the Yarkant River basin. Moreover, approximately 98% of ice melt occurred from June–September, peaking in August.

5.2.2. Trend Analysis

We analyzed annually-averaged flow records of total runoff, glacier melt and ice melt separately to detect temporal trends based on the Mann–Kendall test statistic at the 5% confidence level (p < 0.05). The Z statistics of climatic variables, runoff components and glacier melt components at p < 0.05 are shown in Figure 7. The annual average temperature and precipitation values all showed significant increasing trends from 1968 to 2007. The minimum temperature increased by 0.38 °C/decade, which was more significant than that of the maximum temperature (0.15 °C/decade). The total runoff increased by 0.09 km3/decade, with a non-significant level due to the increase in precipitation in recent years. The glacier melt decreased non-significantly by 0.09 km3/decade. Ice melt, the major component of glacier melt, also non-significantly decreased at p < 0.05. The decline in ice melt may be the reason for the slow glacier area retreat. However, based on the temperature increase, why did ice melt exhibit a decreasing trend from 1968 to 2007? This issue must be carefully studied and discussed.
Figure 8 shows that the mean temperatures in January, February, March and September significantly increased by 0.3–0.8 °C/decade from 1968 to 2007 and increased non-significantly (at p < 0.05) at a low rate in other months. Especially in the months from June–August, the temperature only increased by 0.03–0.17 °C/decade. However, for precipitation, the largest increases occurred in June–August due to abundant precipitation (Figure 8b). To investigate the main factor controlling the ice melt decline, a regression analysis was performed between seasonal ice melt and temperature and precipitation in the Yarkant River basin. The periods used in this analysis were the same as those of significant changes in temperature and precipitation. The correlation coefficients are shown, and the results that pass the significance tests (p < 0.01) are highlighted in bold in Table 3. The analysis shows that runoff, glacier melt and ice melt during the summer were significantly and positively correlated with summer temperature. However, a significant negative correlation was found between ice melt and summer precipitation. This relation is called the “glacier compensation effect” [71]. Runoff and ice melt exhibited no significant correlations with temperature or precipitation in the winter. Hence, the increasing precipitation from June–August led to less ice melt and more accumulation. Moreover, the significantly increased temperatures from January–March were not associated with ice melt. During this period, ice melt exhibited a decreasing trend, and the glacier area shrinkage rate was less severe throughout the Yarkant River basin in more recent years. We suggest that the significant precipitation increase and the slight temperature increase during the melt season were the major reasons for the “Karakoram anomaly” on the northern slope of the Karakoram range.

5.2.3. Regional Differentiation in the Karakoram

With the influences of the westerlies and monsoons, the climate characteristics of the southern slope of the Karakoram Mountains are different from those on the northern slope. The Indus River basin, a large river originating from the southern slope of Karakoram, has cold climates and substantial precipitation during the boreal winter [5]. The precipitation pattern in the Upper Indus River is characterized by a peak in the winter months (approximately 37% of the annual total) and a peak in the summer months (44% of the annual total) [64], with the largest peaks occurring in the months of March and April [72]. Thus, ablation occurs during summer, and most accumulation occurs during the winter months on the southern slope of the Karakoram [5].
Although the seasonal distributions of precipitation are different, the flow patterns are similar among the Karakoram regions. Based on long-term recorded hydrological data, more than 70% of the annual runoff occurs in the summer months (June–September), with nearly 50% in July and August and less than 10% in the winter months in the Upper Indus River basin [64,73,74]. Meltwater is also a significant component of the water balance and represents more than 70% of the runoff in the Upper Indus River [6,64,73,75,76]. Based on distributed cryospheric-hydrological SPHY and Variable Infiltration Capacity (VIC) models, the contributions of glacier melt to total runoff in the Upper Indus River are 40.6% and 48%, respectively, based on simulations by Lutz et al. [6] and Zhang et al. [64]. The calculated glacier melt generally occurs from June–September and accounts for 54% of the annual runoff, peaking in August. These glacier melt results are similar to the previous analysis related to the Yarkant River basin.
However, the reason for larger glacier areas on the southern slope of the Karakoram in recent years [2,30,77,78] is different from that affecting the northern slope. Most studies have focused on the relationship between climate forcing and glacier responses. Based on observed hydrometeorological data, significant increases in winter, summer and annual precipitation have been found; significant warming has occurred in winter; and summer has exhibited a cooling trend since 1961 in the Indus River basin [72,79,80]. Increased winter precipitation potentially increased glacier accumulation, and the decreased mean summer temperature probably resulted in decreased glacier melting [78,79]. Bocchiola and Diolaiuti [81] explained that increased winter precipitation and decreased summer temperatures likely increased the snow-covered area and resulted in the advance of glaciers. The “Karakoram anomaly” also occurred due to increasing snowfall during winter months, offsetting snowfall reductions during the summer in the southern Karakoram, which is dominated by non-monsoonal winter precipitation [82]. This phenomenon also coincides with a period of increased precipitation and a positive glacier mass balance in this region [77]. Although these reasons are different from those on the northern slope of Karakoram, changes in the glacier mass balance are the major reason. Mass balance has an important control on the frequency of glacier surging.

6. Conclusions

In this study, we used the relationship between glacier mass accumulation and summer temperature at the ELA to rationalize the altitudinal precipitation profiles in data-scarce glacierized watershed simulations. An ELA-based PLAPS was calibrated based on observed streamflow and glacier area changes that more accurately control hydrological processes and glacier changes. High-elevation precipitation was inversely calculated using the calibrated PLAPS. Finally, the calibrated, distributed, glacier-enhanced SWAT model forced by the PLAPS was used to simulate the glacio-hydrological processes and to explain the small loss of glacier area in the Yarkant River basin on the northern slope of the Karakoram Mountains from 1968 to 2007.
The PLAPS based on the widely-used APHRODITE data considerably underestimated precipitation, resulting in an unreasonable watershed water balance and inaccurate glacier area changes. However, the ELA-based precipitation improved the simulation significantly. In this scenario, PLAPS was based on multiple rates. At low elevations, it was determined using APHRODITE precipitation and observation data from the meteorological stations yielding a value of 22 mm·km−1. At high elevations, PLAPS was corrected using precipitation at the ELA based on Equation (3). The precipitation simulated using the calibrated, ELA-based PLAPS increased below 5300 m a.s.l. and decreased above this elevation, while the annual precipitation between 5000 and 5500 m a.s.l. reached 800–1000 mm, which was approximately five-times larger than the APHRODITE precipitation. We conclude that the high-elevation precipitation is much greater than the gridded data estimate and observed data at low-elevation rain gages.
Based on the simulations of the calibrated model, averaged from 1968 to 2007, we conclude that glaciers play a crucial role in the water supply of the Yarkant River basin. The contributions of glacier melt and ice melt to the total runoff were 52% and 31%, respectively, and meltwater mainly occurred from June–September, supplying important water for irrigation. However, based on the Mann–Kendall test statistic at the 5% confidence level, glacier melt and ice melt exhibited a non-significant decreasing trend from 1968 to 2007. The decline in ice melt may result in less severe glacier area retreat. The increased precipitation in summer may have recently caused decreased ice melt and weak glacier recession on the northern slope of Karakoram. The significant temperature increase during the cold season had almost no effect on accelerating the shrinkage of glaciers.
Although some uncertainties exist in the simulation, the precipitation at high elevations is demonstrably abundant, and the APHRODITE and the observed data from low-elevation weather stations are not effective proxies. The APHRODITE precipitation data at high elevations is effectively rationalized based on the methods used in this study. Moreover, the hydrological regimes simulated using SWAT and a corrected PLAPS in glacierized regions with scarce observation data may provide more in-depth and effective information associated with the slow rates of glacier area shrinkage. Furthermore, more precise precipitation data should be obtained and used to improve the accuracies of the hydrological models.

Acknowledgments

This study was funded by the Natural Science Foundation of China (Grant 41130641; Grant 41371115) and the Ministry of Science and Technology of China (Grant 2010DFA92720; Grant 2012BAC19B07).

Author Contributions

This study was designed by Yi Luo. The modeling was conducted by Lin Sun. Xiaolei Wang performed the simulations and composed the manuscript. Some data in the manuscript were analyzed by Yiqing Zhang.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hewitt, K. The Karakoram anomaly? Glacier expansion and the ‘elevation effect’, Karakoram Himalaya. Mt. Res. Dev. 2005, 25, 332–340. [Google Scholar] [CrossRef]
  2. Bolch, T.; Kulkarni, A.; Kaab, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Baral, P.; Kayastha, R.B.; Immerzeel, W.W.; Pradhananga, N.S.; Bhattarai, B.C.; Shahi, S.; Galos, S.; Springer, C.; Joshi, S.P.; Mool, P.K. Preliminary results of mass-balance observations of Yala glacier and analysis of temperature and precipitation gradients in Langtang valley, Nepal. Ann. Glaciol. 2014, 55, 9–14. [Google Scholar] [CrossRef]
  4. Unger-Shayesteh, K.; Vorogushyn, S.; Farinotti, D.; Gafurov, A.; Duethmann, D.; Mandychev, A.; Merz, B. What do we know about past changes in the water cycle of central Asian headwaters? A review. Glob. Planet. Chang. 2013, 110, 4–25. [Google Scholar] [CrossRef]
  5. Immerzeel, W.W.; Pellicciotti, F.; Bierkens, M.F.P. Rising river flows throughout the twenty-first century in two Himalayan Glacierized watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
  6. Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in high Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar] [CrossRef]
  7. Hagg, W.; Mayer, C.; Lambrecht, A.; Kriegel, D.; Azizov, E. Glacier changes in the big Naryn basin, central Tian Shan. Glob. Planet. Chang. 2013, 110, 40–50. [Google Scholar] [CrossRef]
  8. Hagg, W.; Hoelzle, M.; Wagner, S.; Mayr, E.; Klose, Z. Glacier and runoff changes in the Rukhk catchment, upper Amu-Darya basin until 2050. Glob. Planet. Chang. 2013, 110, 62–73. [Google Scholar] [CrossRef]
  9. Immerzeel, W.W.; Petersen, L.; Ragettli, S.; Pellicciotti, F. The importance of observed gradients of air temperature and precipitation for modeling runoff from a glacierized watershed in the Nepalese Himalayas. Water Resour. Res. 2014, 50, 2212–2226. [Google Scholar] [CrossRef]
  10. Yang, K.; Ye, B.S.; Zhou, D.G.; Wu, B.Y.; Foken, T.; Qin, J.; Zhou, Z.Y. Response of hydrological cycle to recent climate changes in the Tibetan plateau. Clim. Chang. 2011, 109, 517–534. [Google Scholar] [CrossRef]
  11. Richard, C.; Gratton, D.J. The importance of the air temperature variable for the snowmelt runoff modelling using the SRM. Hydrol. Process. 2001, 15, 3357–3370. [Google Scholar] [CrossRef]
  12. Petersen, L.; Pellicciotti, F. Spatial and temporal variability of air temperature on a melting glacier: Atmospheric controls, extrapolation methods and their effect on melt modeling, Juncal Norte glacier, Chile. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
  13. Immerzeel, W.W.; Pellicciotti, F.; Shrestha, A.B. Glaciers as a proxy to quantify the spatial distribution of precipitation in the Hunza basin. Mt. Res. Dev. 2012, 32, 30–38. [Google Scholar] [CrossRef]
  14. Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
  15. Garen, D.C.; Marks, D. Spatially distributed energy balance snowmelt modelling in a mountainous river basin: Estimation of meteorological inputs and verification of model results. J. Hydrol. 2005, 315, 126–153. [Google Scholar] [CrossRef]
  16. Kattel, D.B.; Yao, T.; Yang, K.; Tian, L.; Yang, G.; Joswiak, D. Temperature lapse rate in complex mountain terrain on the southern slope of the central Himalayas. Theor. Appl. Climatol. 2013, 113, 671–682. [Google Scholar] [CrossRef]
  17. Salerno, F.; Guyennon, N.; Thakuri, S.; Viviano, G.; Romano, E.; Vuillermoz, E.; Cristofanelli, P.; Stocchi, P.; Agrillo, G.; Ma, Y. Weak precipitation, warm winters and springs impact glaciers of south slopes of MT. Everest (central Himalaya) in the last 2 decades (1994–2013). Cryosphere 2015, 9, 5911–5959. [Google Scholar] [CrossRef]
  18. Tustison, B.; Harris, D.; Foufoula-Georgiou, E. Scale issues in verification of precipitation forecasts. J. Geophys. Res. Atmos. 2001, 106, 11775–11784. [Google Scholar] [CrossRef]
  19. Bookhagen, B.; Burbank, D.W. Topography, relief, and trmm-derived rainfall variations along the Himalaya. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
  20. Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
  21. Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and uncertainties in hydrological modeling of remote Hindu kush-karakoram-himalayan (HKH) basins: Suggestions for calibration strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
  22. Schaefli, B.; Hingray, B.; Niggli, M.; Musy, A. A conceptual glacio-hydrological model for high mountainous catchments. Hydrol. Earth Syst. Sci. 2005, 9, 95–109. [Google Scholar] [CrossRef]
  23. Valéry, A.; Andréassian, V.; Perrin, C. Regionalization of precipitation and air temperature over high-altitude catchments—Learning from outliers. Hydrol. Sci. J. 2010, 55, 928–940. [Google Scholar] [CrossRef]
  24. Yang, Z. Glacier Water Resources in China; Gansu Science and Technology Press: Lanzhou, China, 1991. (In Chinese) [Google Scholar]
  25. Chen, Y.N.; Xu, C.C.; Chen, Y.P.; Li, W.H.; Liu, J.S. Response of glacial-lake outburst floods to climate change in the Yarkant river basin on northern slope of Karakoram mountains, China. Quat. Int. 2010, 226, 75–81. [Google Scholar] [CrossRef]
  26. Zhang, S.Q.; Gao, X.; Ye, B.S.; Zhang, X.W.; Hagemann, S. A modified monthly degree-day model for evaluating glacier runoff changes in China. Part II: Application. Hydrol. Process. 2012, 26, 1697–1706. [Google Scholar] [CrossRef]
  27. Wu, L.; Li, X. Dataset of the first glacier inventory in China. Cold Arid Reg. Sci. Data Center Lanzhou 2004. [Google Scholar] [CrossRef]
  28. Guo, W.Q.; Xu, J.L.; Liu, S.Y.; Shangguan, D.H.; Wu, L.Z.; Yao, X.J.; Zhao, J.D.; Liu, Q.; Jiang, Z.L.; Li, P.; et al. The second glacier inventory dataset of China (version 1.0). Cold Arid Reg. Sci. Data Center Lanzhou 2014. [Google Scholar] [CrossRef]
  29. Frauenfelder, R.; Kääb, A. Glacier mapping from multitemporal optical remote sensing data within the Brahmaputra river basin. In Proceedings of the 33rd International Symposium on Remote Sensing of Environment, Stresa, Italy, 4–8 May 2009; p. 4.
  30. Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. Aphrodite: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
  31. Sheffield, J.; Goteti, G.; Eric, F. Development of a 50-year high-resolution data set of meteorological forcings for land surface modeling. J. Clim. 2006. [Google Scholar] [CrossRef]
  32. Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part i: Model development1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
  33. Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. Swat: Model use, calibration, and validation. Trans. Asabe 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
  34. Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. Asabe 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
  35. Luo, Y.; Arnold, J.; Liu, S.; Wang, X.; Chen, X. Inclusion of glacier processes for distributed hydrological modeling at basin scale with application to a watershed in Tianshan mountains, northwest China. J. Hydrol. 2013, 477, 72–85. [Google Scholar] [CrossRef]
  36. Hock, R.; Jansson, P.; Braun, L.N. Modelling the response of mountain glacier discharge to climate warming. In Global Change and Mountain Regions: An Overview of Current Knowledge; Huber, U.M., Bugmann, H.K.M., Reasoner, M.A., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2005; pp. 243–252. [Google Scholar]
  37. Chen, J.; Ohmura, A. Estimation of alpine glacier water resources and their change since the 1870s. In Hydrology in Mountainous Regions—I. Hydrologic Measurements, the Water Cycle, In Proceedings of the two international symposia, Lausanne, Switzerland, 24–25 August 1990; IAHS Publication: Wallingford, UK, 1990; Volume 193, pp. 127–135. [Google Scholar]
  38. Liu, S.Y.; Sun, W.X.; Shen, Y.P.; Li, G. Glacier changes since the little ice age maximum in the western Qilian Shan, northwest China, and consequences of glacier runoff for water supply. J. Glaciol. 2003, 49, 117–124. [Google Scholar]
  39. Gan, R.; Luo, Y.; Zuo, Q.; Sun, L. Effects of projected climate change on the glacier and runoff generation in the Naryn river basin, central Asia. J. Hydrol. 2015, 523, 240–251. [Google Scholar] [CrossRef]
  40. Ma, C.; Sun, L.; Liu, S.; Shao, M.A.; Luo, Y. Impact of climate change on the streamflow in the glacierized Chu River Basin, Central Asia. J. Arid Land 2015, 7, 501–513. [Google Scholar] [CrossRef]
  41. Wang, X.L.; Luo, Y.; Sun, L.; Zhang, Y.Q. Assessing the effects of precipitation and temperature changes on hydrological processes in a glacier-dominated catchment. Hydrol. Process. 2015, 29, 4830–4845. [Google Scholar] [CrossRef]
  42. Hans, W.S.A. Le niveau de glaciation comme fonction de l’accumulation d’humidité sous forme solide. Méthode pour le calcul de l’humidité condensée dans la haute montagne et pour l'étude de la fréquence des glaciers. Geografiska Annaler 1924, 6, 223–272. [Google Scholar]
  43. Ohmura, A.; Kasser, P.; Funk, M. Climate at the equilibrium line of glaciers. J. Glaciol. 1992, 38, 397–411. [Google Scholar]
  44. Leonard, E.M. Climatic change in the Colorado Rocky Mountains: Estimates based on modern climate at late Pleistocene equilibrium lines. Arct. Alp. Res. 1989, 21, 245–255. [Google Scholar] [CrossRef]
  45. Kotlyakov, V.M.; Krenke, A.N. Investigations of the hydrological conditions of alpine regions by glaciological methods. Hydrol. Asp. Alp. High Mt. Areas 1982, 27, 251–252. [Google Scholar]
  46. Allen, R.; Siegert, M.J.; Payne, A.J. Reconstructing glacier-based climates of LGM Europe and Russia—Part 3: Comparison with previous climate reconstructions. Clim. Past. 2008, 4, 265–280. [Google Scholar] [CrossRef]
  47. Munroe, J.S.; Mickelson, D.M. Last Glacial Maximum equilibrium-line altitudes and paleoclimate, northern Uinta Mountains, northeastern Utah, U.S.A. J. Glaciol. 2002, 48, 257–266. [Google Scholar] [CrossRef]
  48. Kang, E.; Liu, C.H.; Xie, Z.C.; Li, X.; Shen, Y.P. Assessment of glacier water resources based on the glacier inventory of China. Ann. Glaciol. 2009, 50, 104–110. [Google Scholar]
  49. Schaper, J.; Seidel, K.; Martinec, J. Precision snow cover and glacier mapping for runoff modelling in a high alpine basin. In Remote Sensing and Hydrology 2000, In Proceedings of a symposium, Santa Fe, NM, USA, April 2000; IAHS Publication: Wallingford, UK, 2001; Volume 267, pp. 1–8. [Google Scholar]
  50. Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
  51. Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
  52. Hirsch, R.M.; Alexander, R.B.; Smith, R.A. Selection of methods for the detection and estimation of trends in water quality. Water Resour. Res. 1991, 27, 803–813. [Google Scholar] [CrossRef]
  53. Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
  54. Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
  55. Zhang, B.P. Physical features and vertical zones of the Karakoram and Ali-Karakoram Mountains. J. Arid Land Resour. Environ. 1990, 4, 49–63. [Google Scholar]
  56. Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza river basin, Karakoram range, northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
  57. Immerzeel, W.W.; van Beek, L.P.H.; Konz, M.; Shrestha, A.B.; Bierkens, M.F.P. Hydrological response to climate change in a glacierized catchment in the Himalayas. Clim. Chang. 2012, 110, 721–736. [Google Scholar] [CrossRef] [PubMed]
  58. Luo, Y.; Arnold, J.; Allen, P.; Chen, X. Baseflow simulation using swat model in an inland river basin in Tianshan Mountains, northwest China. Hydrol. Earth Syst. Sci. 2012, 16, 1259–1267. [Google Scholar] [CrossRef]
  59. The Batura Glacier Investigation Group. The Batura glacier in the Karakoram mountains and its variations. Sci. China Ser. A 1979, 958–974. [Google Scholar]
  60. Hewitt, K. Glacier change, concentration, and elevation effects in the Karakoram Himalaya, upper Indus basin. Mt. Res. Dev. 2011, 31, 188–200. [Google Scholar] [CrossRef]
  61. Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
  62. Winiger, M.; Gumpert, M.; Yamout, H. Karakorum-Hindukush-western Himalaya: Assessing high-altitude water resources. Hydrol. Process. 2005, 19, 2329–2338. [Google Scholar] [CrossRef]
  63. Shi, Y.F. The glaciers of k2 were the left of late pleistocene glaciers? Xinjiang Geogr. 1984, 3, 1–4. [Google Scholar]
  64. Zhang, L.; Su, F.; Yang, D.; Hao, Z.; Tong, K. Discharge regime and simulation for the upstream of major rivers over Tibetan plateau. J. Geophys. Res. Atmos. 2013, 118, 8500–8518. [Google Scholar] [CrossRef]
  65. Kezer, K.; Matsuyama, H. Decrease of river runoff in the lake Balkhash basin in central Asia. Hydrol. Process. 2006, 20, 1407–1423. [Google Scholar] [CrossRef]
  66. Li, Z.Q.; Wang, W.B.; Zhang, M.J.; Wang, F.T.; Li, H.L. Observed changes in streamflow at the headwaters of the Urumqi river, eastern Tianshan, central Asia. Hydrol. Process. 2010, 24, 217–224. [Google Scholar] [CrossRef]
  67. Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Glob. Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
  68. Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.P.; de Jong, S.M. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
  69. Sorg, A.; Huss, M.; Rohrer, M.; Stoffel, M. The days of plenty might soon be over in glacierized central Asian catchments. Environ. Res. Lett. 2014, 9, 104018. [Google Scholar] [CrossRef]
  70. Liu, S.Y.; Ding, Y.J.; Shangguan, D.H.; Zhang, Y.; Li, J.; Han, H.D.; Wang, J.; Xie, C.W. Glacier retreat as a result of climate warming and increased precipitation in the Tarim river basin, northwest China. Ann. Glaciol. 2006, 43, 91–96. [Google Scholar] [CrossRef]
  71. Lang, H. Forecasting meltwater runoff from snow-covered areas and from glacier basins. In River Flow Modelling and Forecasting; Kraijenhoff, D.A., Moll, J.R., Eds.; Springer Netherlands: Berlin, Germany, 1986; Volume 3, pp. 99–127. [Google Scholar]
  72. Ahmad, Z.; Hafeez, M.; Ahmad, I. Hydrology of mountainous areas in the upper Indus basin, Northern Pakistan with the perspective of climate change. Environ. Monit. Assess. 2012, 184, 5255–5274. [Google Scholar] [CrossRef] [PubMed]
  73. Mukhopadhyay, B.; Khan, A. Rising river flows and glacial mass balance in central karakoram. J. Hydrol. 2014, 513, 192–203. [Google Scholar] [CrossRef]
  74. Archer, D. Contrasting hydrological regimes in the upper Indus basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
  75. Mukhopadhyay, B.; Khan, A. A quantitative assessment of the genetic sources of the hydrologic flow regimes in upper Indus basin and its significance in a changing climate. J. Hydrol. 2014, 509, 549–572. [Google Scholar] [CrossRef]
  76. Immerzeel, W.W.; Droogers, P.; de Jong, S.M.; Bierkens, M.F.P. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
  77. Copland, L.; Sylvestre, T.; Bishop, M.P.; Shroder, J.F.; Seong, Y.B.; Owen, L.A.; Bush, A.; Kamp, U. Expanded and recently increased glacier surging in the Karakoram. Arct. Antarct. Alp. Res. 2011, 43, 503–516. [Google Scholar] [CrossRef]
  78. Gardelle, J.; Berthier, E.; Arnaud, Y. Slight mass gain of Karakoram glaciers in the early twenty-first century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
  79. Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the upper Indus basin, global teleconnections and hydrological implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef]
  80. Fowler, H.J.; Archer, D.R. Conflicting signals of climatic change in the upper Indus basin. J. Clim. 2006, 19, 4276–4293. [Google Scholar] [CrossRef]
  81. Bocchiola, D.; Diolaiuti, G. Recent (1980–2009) evidence of climate change in the upper Karakoram, Pakistan. Theor. Appl. Climatol. 2013, 113, 611–641. [Google Scholar] [CrossRef]
  82. Kapnick, S.B.; Delworth, T.L.; Ashfaq, M.; Malyshev, S.; Milly, P.C.D. Snowfall less sensitive to warming in Karakoram than in Himalayas due to a unique seasonal cycle. Nat. Geosci. 2014, 7, 834–840. [Google Scholar] [CrossRef]
Water 08 00186 g001 1024
Figure 1. Map of the source region of the Yarkant River basin in the Karakoram Mountains.
Figure 1. Map of the source region of the Yarkant River basin in the Karakoram Mountains.
Water 08 00186 g001
Water 08 00186 g002 1024
Figure 2. Comparison between the altitudinal distributions of the average annual temperatures based on observed values, Princeton’s Global Meteorological Forcing Dataset (PGMFD) values and temperature lapse rate (TLAPS) (a); and the annual precipitation based on the observed values, Asian Precipitation Highly Resolved Observational Data Integration Towards Evaluation (APHRODITE) values, Equation (3) results and corrected precipitation lapse rate (PLAPS) (b).
Figure 2. Comparison between the altitudinal distributions of the average annual temperatures based on observed values, Princeton’s Global Meteorological Forcing Dataset (PGMFD) values and temperature lapse rate (TLAPS) (a); and the annual precipitation based on the observed values, Asian Precipitation Highly Resolved Observational Data Integration Towards Evaluation (APHRODITE) values, Equation (3) results and corrected precipitation lapse rate (PLAPS) (b).
Water 08 00186 g002
Water 08 00186 g003 1024
Figure 3. Comparisons between observed and simulated monthly streamflows at the Kaqun (a) and Kuluklangan (b) hydrological stations in the Yarkant River Basin from 1968 to 1989.
Figure 3. Comparisons between observed and simulated monthly streamflows at the Kaqun (a) and Kuluklangan (b) hydrological stations in the Yarkant River Basin from 1968 to 1989.
Water 08 00186 g003
Water 08 00186 g004 1024
Figure 4. Comparison between the observed and simulated glacier shrinkage rates for different glacier size classes in the Yarkant River basin (CGI stands for the China Glacier Inventory).
Figure 4. Comparison between the observed and simulated glacier shrinkage rates for different glacier size classes in the Yarkant River basin (CGI stands for the China Glacier Inventory).
Water 08 00186 g004
Water 08 00186 g005 1024
Figure 5. Plots of precipitation and elevation sensitivities at the second and third points using the variable PLAPS to simulate streamflow at KQHS and glacier area change in the Yarkant River basin. EL_2 and EL_3 represent the elevations of the second and third points, respectively; P_2 and P_3 represent the precipitation values of the second and third points, respectively. (a–d) the NSE and PBIAS values for scenarios in which EL_2, EL_3, P_2 and P_3 varied; (e,f) the glacier area shrinkage rates when one of EL_2, EL_3, P_2 or P_3 varied.
Figure 5. Plots of precipitation and elevation sensitivities at the second and third points using the variable PLAPS to simulate streamflow at KQHS and glacier area change in the Yarkant River basin. EL_2 and EL_3 represent the elevations of the second and third points, respectively; P_2 and P_3 represent the precipitation values of the second and third points, respectively. (a–d) the NSE and PBIAS values for scenarios in which EL_2, EL_3, P_2 and P_3 varied; (e,f) the glacier area shrinkage rates when one of EL_2, EL_3, P_2 or P_3 varied.
Water 08 00186 g005
Water 08 00186 g006 1024
Figure 6. Monthly average temperature and precipitation (a); separated annual hydrographs for total runoff and the four major components of river flows from 1968 to 2007 (b); histograms showing the monthly contributions of the four components of flows in terms of the percentage of contributions to the total runoff (c); area diagrams for monthly ice melt, supraglacial snow melt and rain, which form the glacier melt (d).
Figure 6. Monthly average temperature and precipitation (a); separated annual hydrographs for total runoff and the four major components of river flows from 1968 to 2007 (b); histograms showing the monthly contributions of the four components of flows in terms of the percentage of contributions to the total runoff (c); area diagrams for monthly ice melt, supraglacial snow melt and rain, which form the glacier melt (d).
Water 08 00186 g006
Water 08 00186 g007 1024
Figure 7. Z statistics for annual temperature, precipitation, runoff, glacier melt and ice melt from 1968 to 2007 in the Yarkant River basin. Tavg, Tmx and Tmn represent average, maximum and minimum temperatures, respectively. P represents precipitation. TR, GM and GIM represent total runoff, glacier melt and ice melt, respectively. The grey dotted lines represent the critical values of the normal distribution at the 5% confidence level (Z = ±1.96).
Figure 7. Z statistics for annual temperature, precipitation, runoff, glacier melt and ice melt from 1968 to 2007 in the Yarkant River basin. Tavg, Tmx and Tmn represent average, maximum and minimum temperatures, respectively. P represents precipitation. TR, GM and GIM represent total runoff, glacier melt and ice melt, respectively. The grey dotted lines represent the critical values of the normal distribution at the 5% confidence level (Z = ±1.96).
Water 08 00186 g007
Water 08 00186 g008 1024
Figure 8. Z statistics (a) and rates of change (b) for monthly average temperature and precipitation from 1968 to 2007 in the Yarkant River basin at p < 0.05. The grey dotted lines in (a) represent the critical values of the normal distribution at p < 0.05 (Z = ±1.96).
Figure 8. Z statistics (a) and rates of change (b) for monthly average temperature and precipitation from 1968 to 2007 in the Yarkant River basin at p < 0.05. The grey dotted lines in (a) represent the critical values of the normal distribution at p < 0.05 (Z = ±1.96).
Water 08 00186 g008
Table
Table 1. The most sensitive parameters and the final calibrated values or ranges of values for the glacier-enhanced SWAT model in the Yarkant River basin
Table 1. The most sensitive parameters and the final calibrated values or ranges of values for the glacier-enhanced SWAT model in the Yarkant River basin
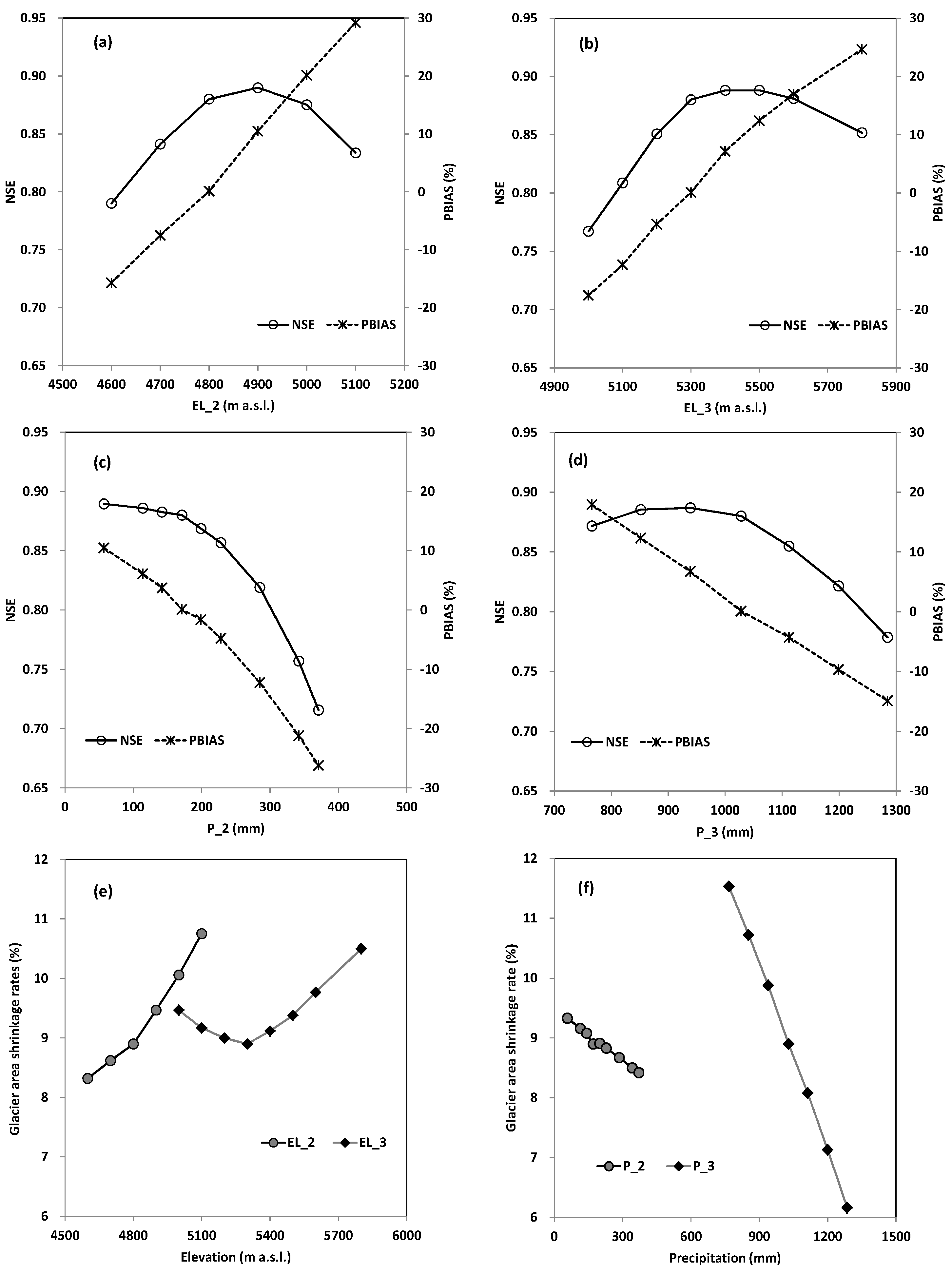
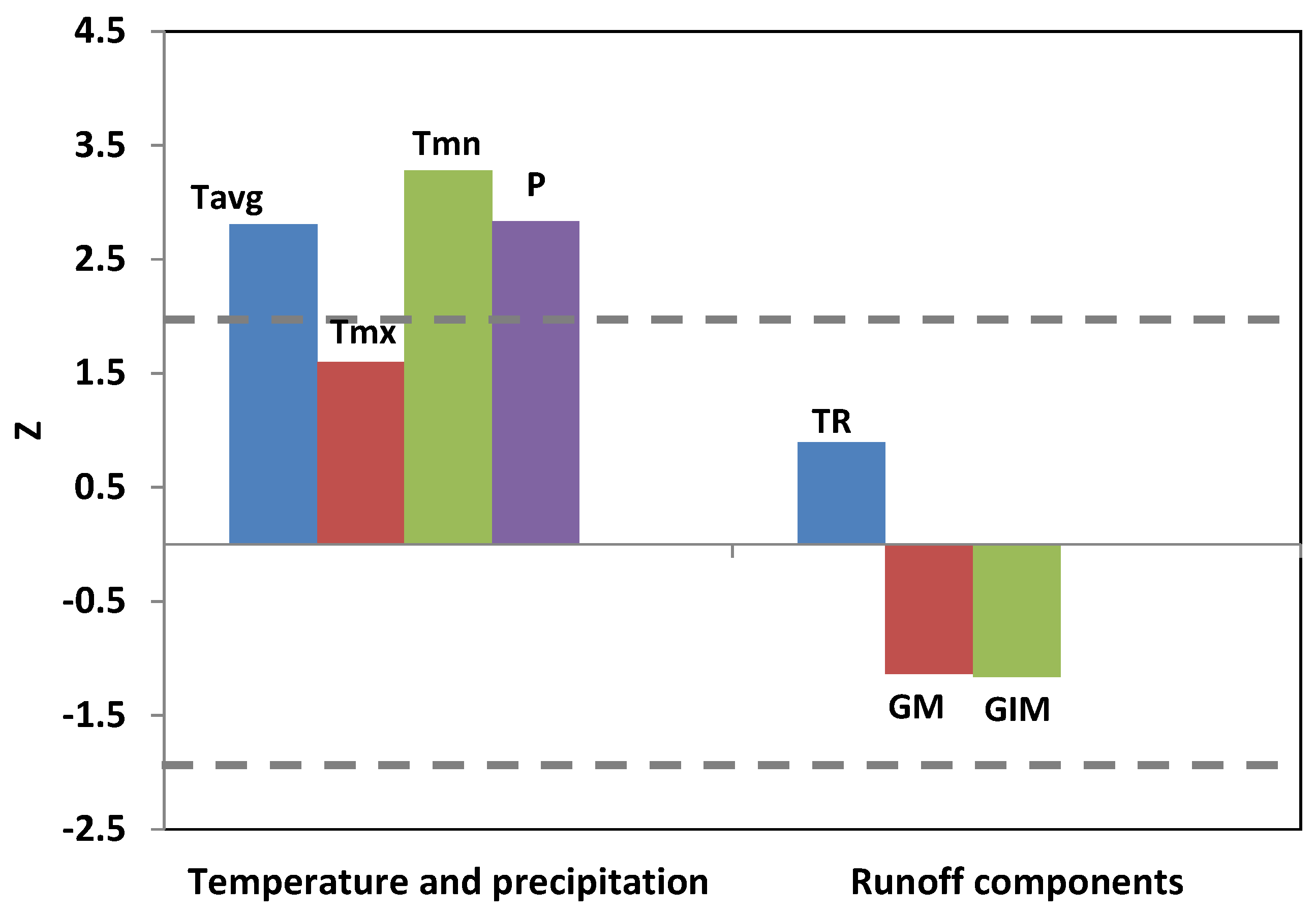
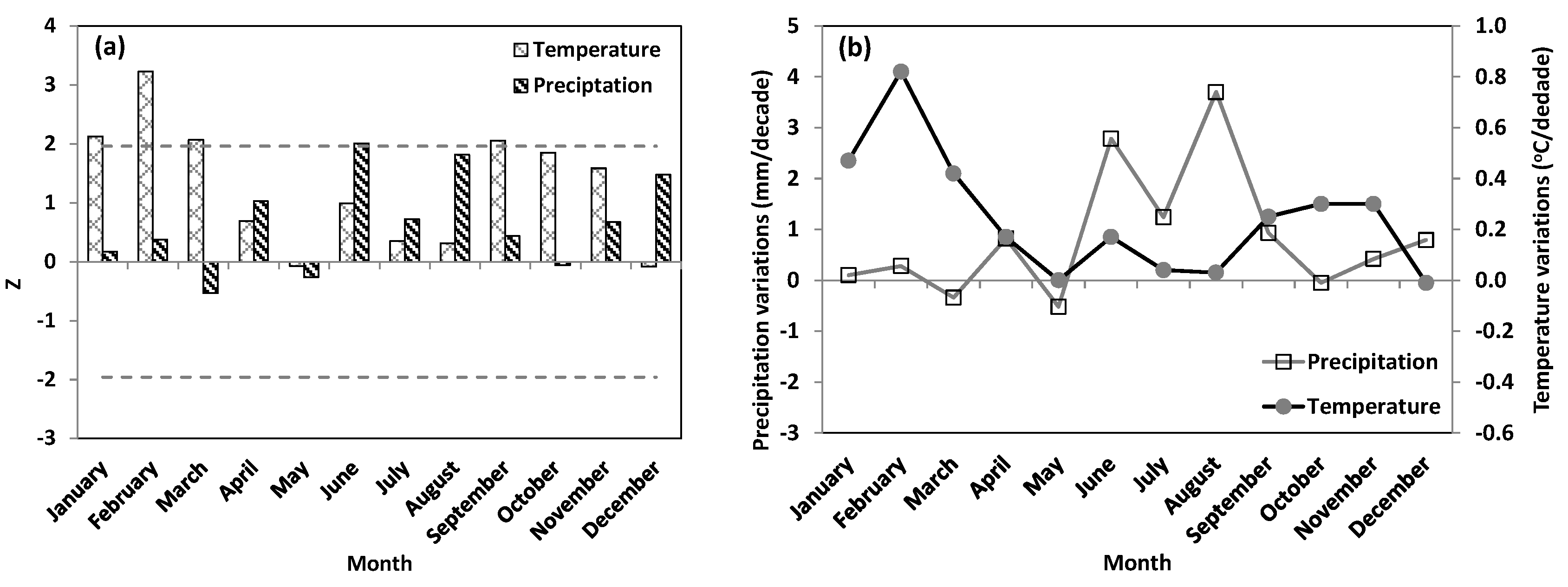
Sensitive ParametersParameter DefinitionParameter Change RangeFinal Parameter Value Range
ALPHA_BFBaseflow alpha factor0–10.02–0.8
RCHRG_DPDeep aquifer percolation factor0–10.4
CH_K2Channel effective hydraulic conductivity (mm/h)0–30010–50
gmfmxDegree-day factor for ice melt on 21 June (mm·°C−1·day−1)1.4–16.03–14.5
gmfmnDegree-day factor for ice melt on 21 December (mm·°C−1·day−1)1.4–16.01.0–8.8
SMFMXDegree-day factor for snow melt on 21 June (mm·°C−1·day−1)1.4–6.71.8–4.5
SMFMNDegree-day factor for snow melt on 21 December (mm·°C−1·day−1)1.4–6.70.5–3.5
Table
Table 2. NSE and PBIAS results for the simulated monthly streamflow at the Kaqun and Kuluklangan hydrological stations (KQHS and KLKHS) based on corrected and linear PLAPSs from 1968 to 1989 in the Yarkant River basin using the glacier-enhanced SWAT model.
Table 2. NSE and PBIAS results for the simulated monthly streamflow at the Kaqun and Kuluklangan hydrological stations (KQHS and KLKHS) based on corrected and linear PLAPSs from 1968 to 1989 in the Yarkant River basin using the glacier-enhanced SWAT model.
ScenariosAnalysisKQHSKLKHS
NSEPBIAS (%)NSEPBIAS (%)
Simulated using corrected PLAPSCalibration0.879.30.85−7.1
Validation0.87−0.90.83−10.9
Simulated using linear PLAPS1968–19890.42600.5159
Table
Table 3. Seasonal correlation between total runoff, glacier melt and ice melt and temperature and precipitation in the Yarkant River basin from 1968 to 2007.
Table 3. Seasonal correlation between total runoff, glacier melt and ice melt and temperature and precipitation in the Yarkant River basin from 1968 to 2007.
Climate VariablesClimate PeriodJune–September
Total RunoffGlacier MeltIce Melt
TemperatureJJA0.72 **0.90 **0.91 **
JFM−0.010.090.09
PrecipitationJJA−0.07−0.47 **−0.59 **
JFM0.07−0.11−0.17
Notes: ** Significance at 0.01. JJA represents months from June–August. JFM represents January–March.

Share and Cite

MDPI and ACS Style

Wang, X.; Sun, L.; Zhang, Y.; Luo, Y. Rationalization of Altitudinal Precipitation Profiles in a Data-Scarce Glacierized Watershed Simulation in the Karakoram. Water 2016, 8, 186. https://doi.org/10.3390/w8050186

AMA Style

Wang X, Sun L, Zhang Y, Luo Y. Rationalization of Altitudinal Precipitation Profiles in a Data-Scarce Glacierized Watershed Simulation in the Karakoram. Water. 2016; 8(5):186. https://doi.org/10.3390/w8050186

Chicago/Turabian Style

Wang, Xiaolei, Lin Sun, Yiqing Zhang, and Yi Luo. 2016. "Rationalization of Altitudinal Precipitation Profiles in a Data-Scarce Glacierized Watershed Simulation in the Karakoram" Water 8, no. 5: 186. https://doi.org/10.3390/w8050186

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop