Adaptive Kalman Filter Based on Adjustable Sampling Interval in Burst Detection for Water Distribution System
Abstract
:1. Introduction
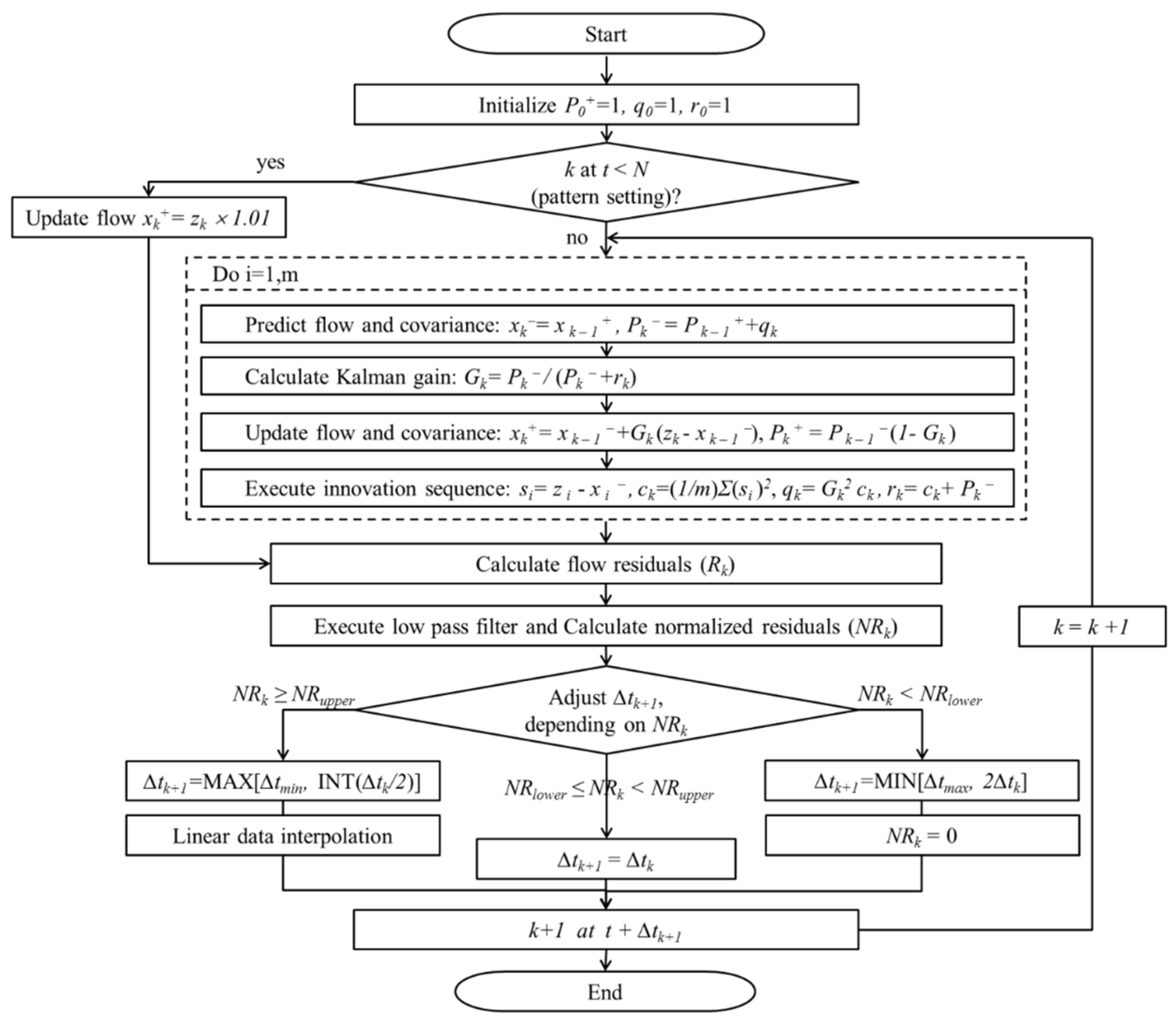
2. Proposed Methodology
2.1. Kalman Filtering
2.2. Adaptive Method with Adjustable Sampling Interval
3. Results and Discussion
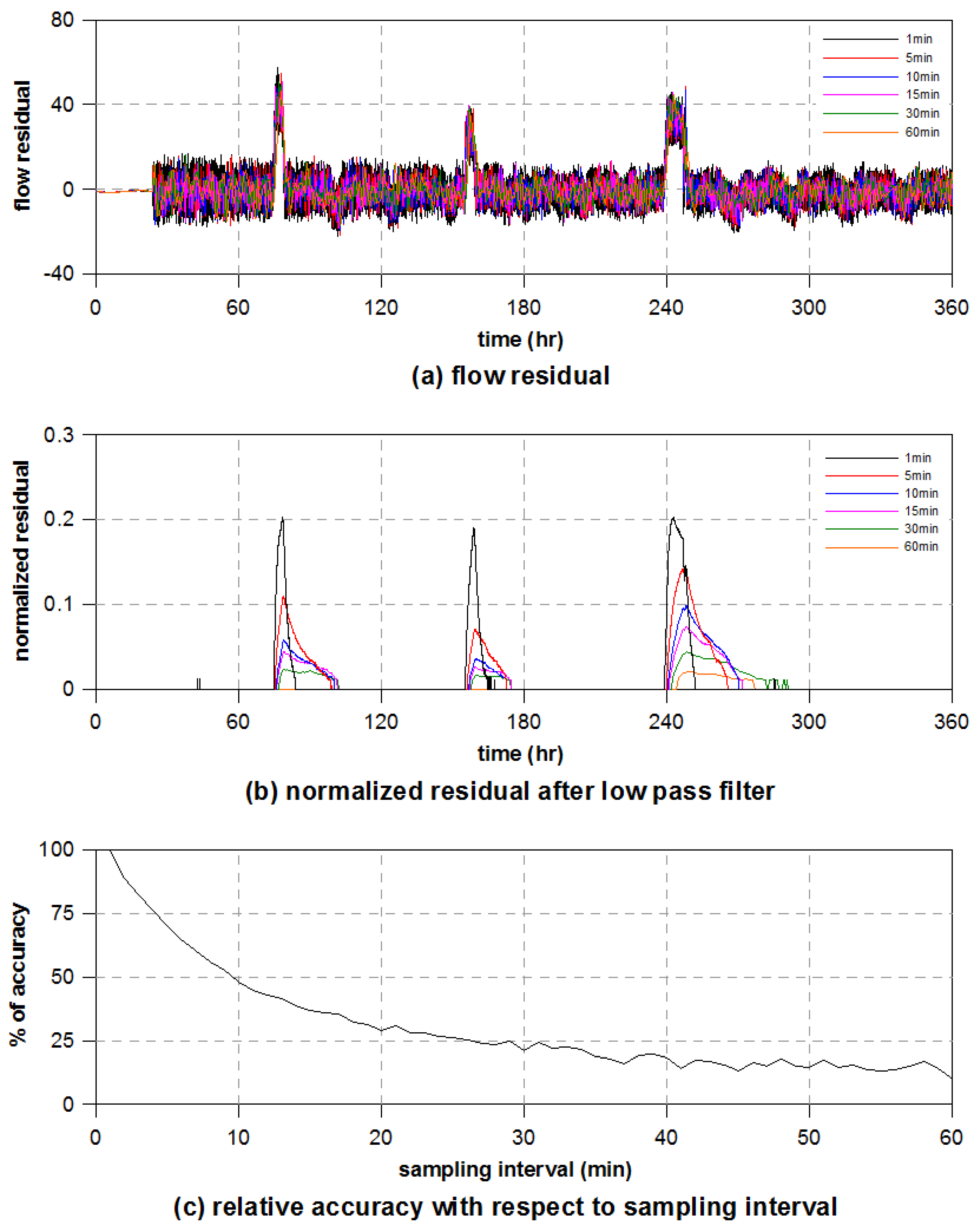
3.1. Effect of Sampling Interval
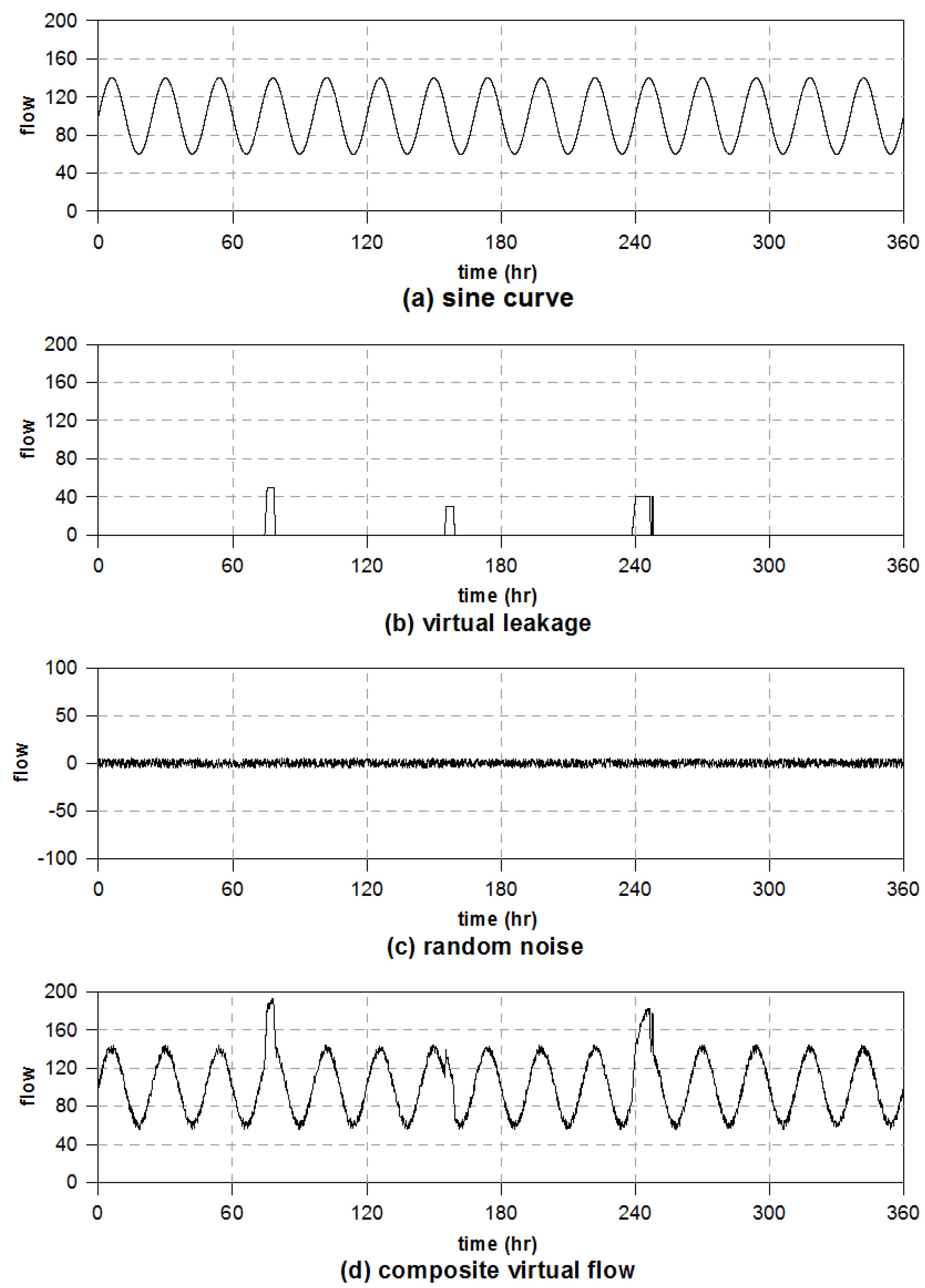
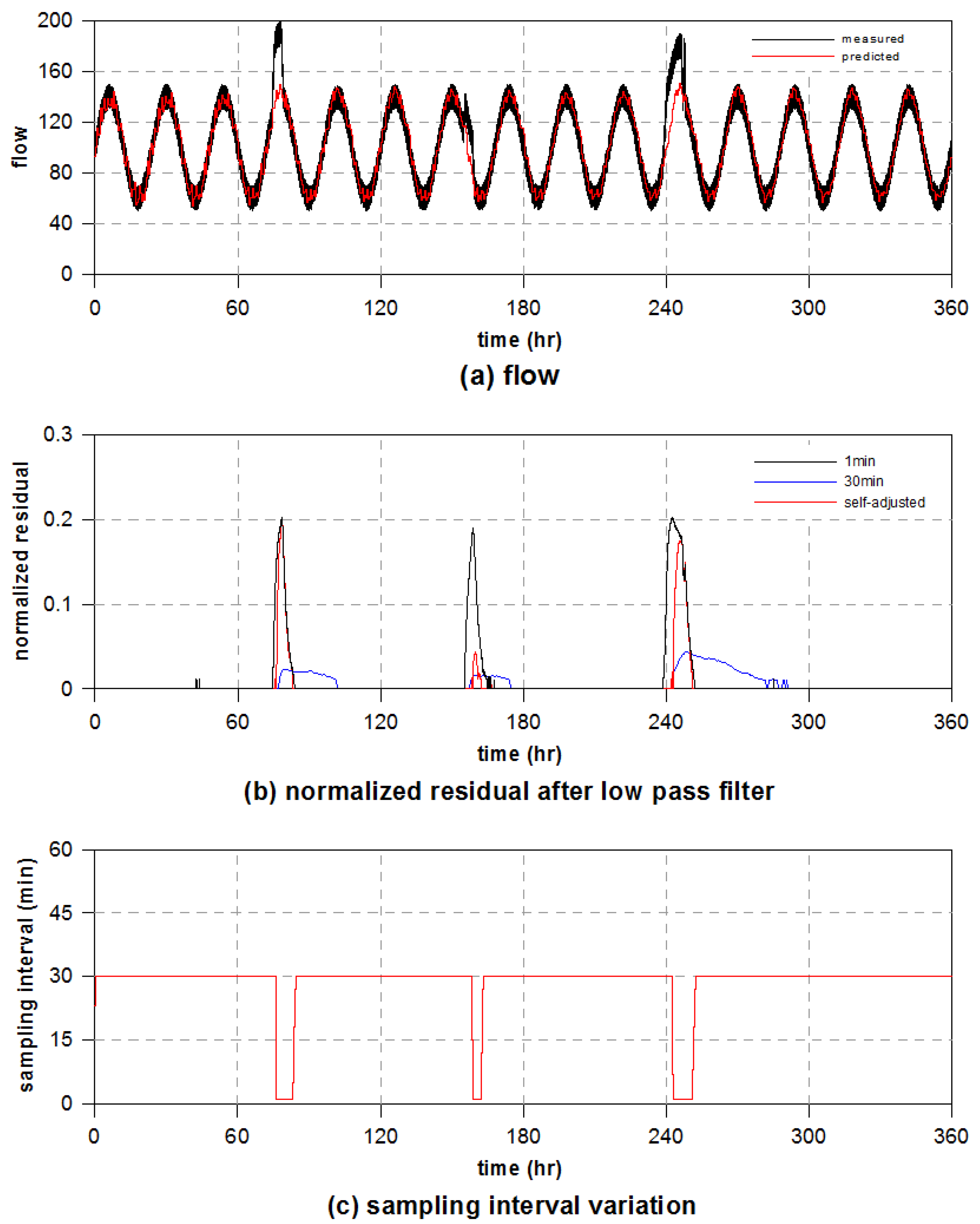
3.2. Application of Self-Adjusting Method to Virtual Flow Data
3.3. Application of Self-Adjusting Method to Real DMA Flow Data
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Farley, B.; Mounce, S.R.; Boxall, J.B. Field testing of an optimal sensor placement methodology for event detection in an urban water distribution network. Urban Water J. 2010, 7, 345–356. [Google Scholar] [CrossRef]
- Lambert, A. Accounting for losses: the bursts and background concept. Water Environ. J. 1994, 8, 205–214. [Google Scholar] [CrossRef]
- Giurco, D.P.; White, S.B.; Stewart, R.A. Smart metering and water end-use data: Conservation benefits and privacy risks. Water 2010, 2, 461–467. [Google Scholar] [CrossRef]
- Liggett, J.A.; Chen, L.C. Inverse transient analysis in pipe networks. J. Hydraul. Eng. 1994, 120, 934–955. [Google Scholar] [CrossRef]
- Covas, D.; Ramos, H.; de Almeida, A.B. Standing wave difference method for leak detection in pipeline systems. J. Hydraulic Eng. 2005, 131, 1106–1116. [Google Scholar] [CrossRef]
- Anderson, J.H.; Powell, R.S. Implicit state-estimation technique for water network monitoring. Urban Water 2000, 2, 123–130. [Google Scholar] [CrossRef]
- Poulakis, Z.; Valougeorgis, D.; Papadimitriou, C. Leakage detection in water pipe networks using a Bayesian probabilistic framework. Probabilistic Eng. Manag. 2003, 18, 315–327. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. Probabilistic leak detection in pipe networks using the SCEM-UA algorithm. In Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006.
- Palau, C.V.; Arregui, F.J.; Carlos, M. Burst detection in water networks using principal component analysis. J. Water Resour. Plan. Manag. 2012, 138, 47–54. [Google Scholar] [CrossRef]
- Mounce, S.R.; Machell, J. Burst detection using hydraulic data from water distribution systems with artificial neural networks. Urban Water J. 2006, 3, 21–31. [Google Scholar] [CrossRef]
- Aksela, K.; Aksela, M.; Vahala, R. Leakage detection in a real distribution network using a SOM. Urban Water J. 2009, 6, 279–289. [Google Scholar] [CrossRef]
- Mounce, S.R.; Boxall, J.B.; Machell, J. Development and verification of an online artificial intelligence system for detection of bursts and other abnormal flows. J. Water Resour. Plan. Manag. 2012, 136, 309–318. [Google Scholar] [CrossRef]
- Ye, G.; Fenner, R.A. Kalman filtering of hydraulic measurements for burst detection in water distribution systems. J. Pipeline Syst. Eng. Pract. 2011, 2, 14–22. [Google Scholar] [CrossRef]
- Ye, G.; Fenner, R.A. Study of burst alarming and sampling frequency in water distribution networks. J. Water Resour. Plan. Manag. 2014, 140, 06014001. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Mehra, R.K. On the identification of variances and adaptive Kalman filtering. Automatic Control 1970, 15, 175–184. [Google Scholar] [CrossRef]
- Berthouex, P.M.; Brown, L.C. Statistics for Environmental Engineers, 2nd ed.; Lewis Publishers: Boca Raton, FL, USA, 2002. [Google Scholar]
- US Environmental Protection Agency (US EPA). Data Quality Assessment: Statistical Methods for Practitioners; Report No. EPA QA/G-9S; US EPA: Washington, DC, USA, 2006.
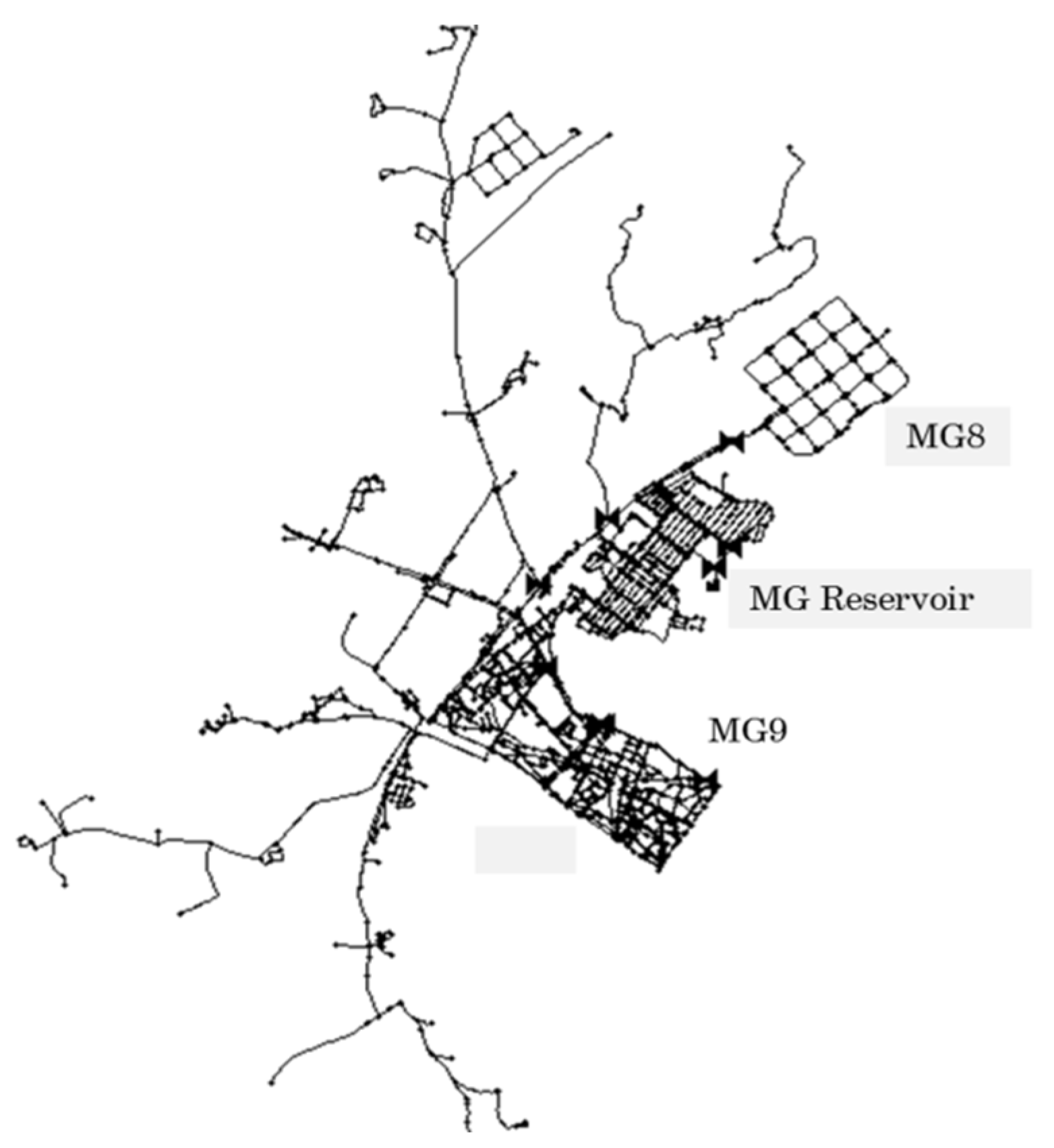
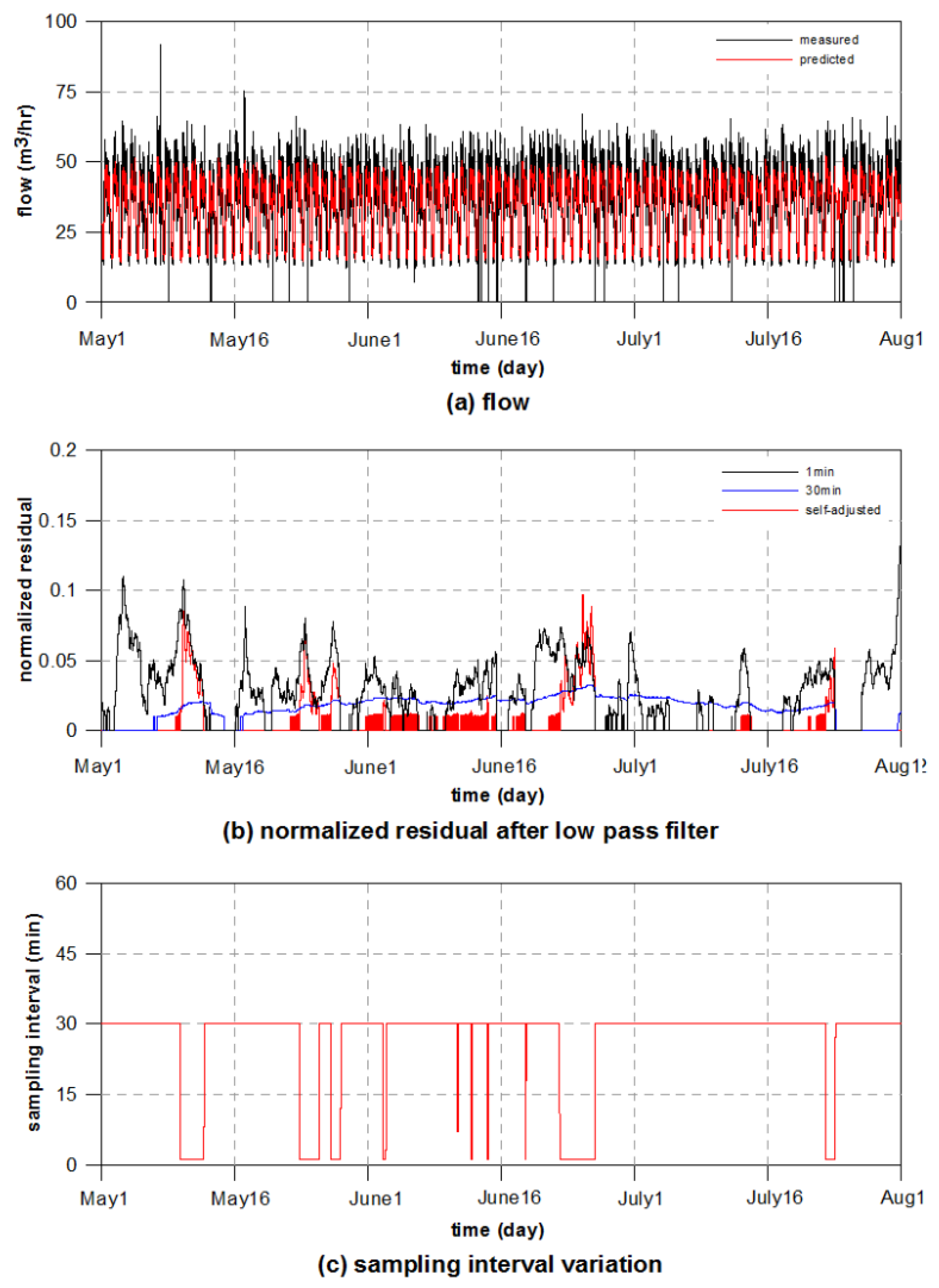
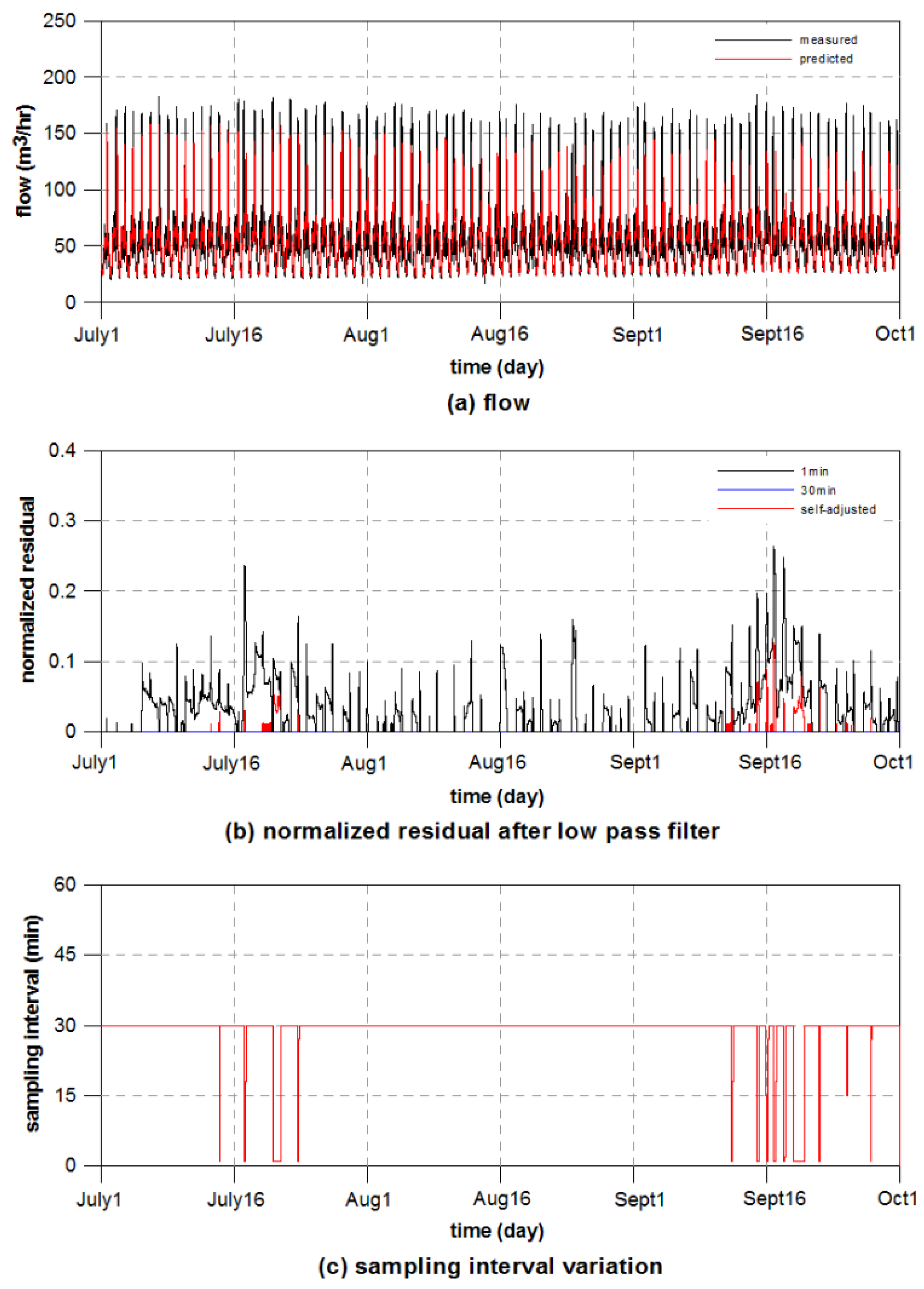
| DMA | Alarms | Samples | ||||
|---|---|---|---|---|---|---|
| 1 min | 30 min | Self-Adjusted | 1 min | 30 min | Self-Adjusted | |
| MG8 | 38 | 5 | 19 | 132,481 | 4416 | 21,003 |
| MG9 | 73 | 0 | 20 | 132,481 | 4416 | 9486 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.Y.; Kim, S.-W.; Choi, M.-A.; Geem, Z.W. Adaptive Kalman Filter Based on Adjustable Sampling Interval in Burst Detection for Water Distribution System. Water 2016, 8, 142. https://doi.org/10.3390/w8040142
Choi DY, Kim S-W, Choi M-A, Geem ZW. Adaptive Kalman Filter Based on Adjustable Sampling Interval in Burst Detection for Water Distribution System. Water. 2016; 8(4):142. https://doi.org/10.3390/w8040142
Chicago/Turabian StyleChoi, Doo Yong, Seong-Won Kim, Min-Ah Choi, and Zong Woo Geem. 2016. "Adaptive Kalman Filter Based on Adjustable Sampling Interval in Burst Detection for Water Distribution System" Water 8, no. 4: 142. https://doi.org/10.3390/w8040142
APA StyleChoi, D. Y., Kim, S.-W., Choi, M.-A., & Geem, Z. W. (2016). Adaptive Kalman Filter Based on Adjustable Sampling Interval in Burst Detection for Water Distribution System. Water, 8(4), 142. https://doi.org/10.3390/w8040142







