Investigation of Temperature Dynamics in Small and Shallow Reservoirs, Case Study: Lake Binaba, Upper East Region of Ghana
Abstract
:1. Introduction
2. Water Bodies Modeling
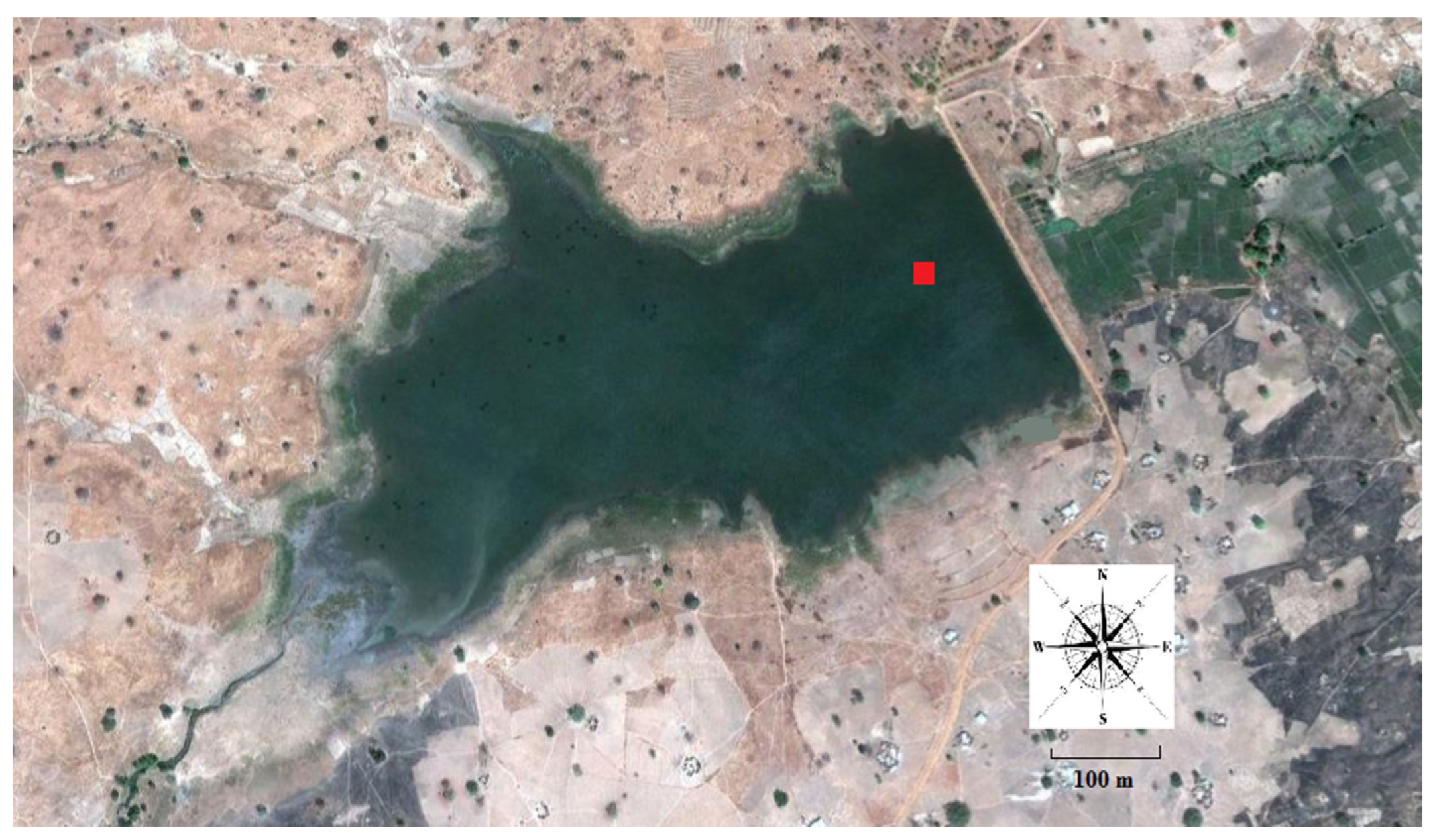
3. Description of Study Site and Data Collection
4. Mathematical Model
4.1. Governing Equations
4.2. Turbulence Modelling
5. Numerical Simulation
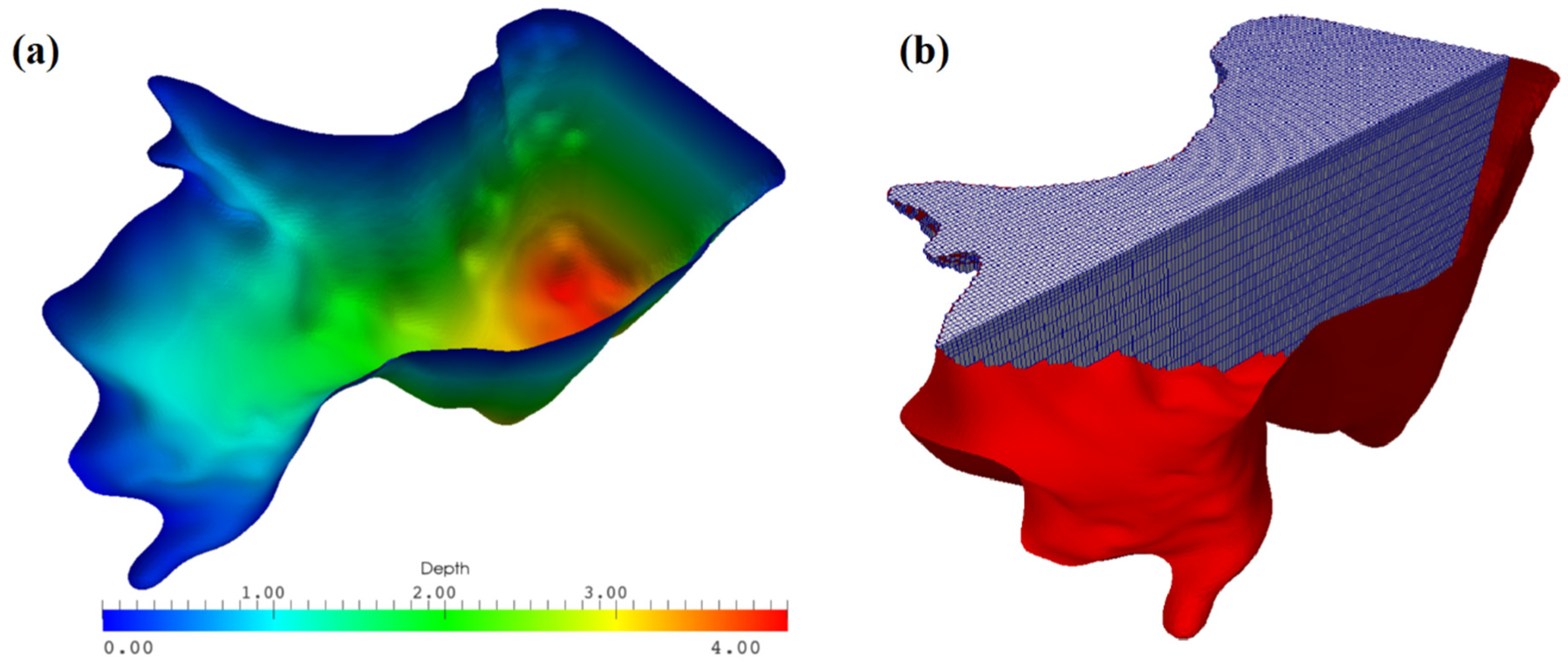
5.1. Numerical Grid
5.2. Numerical Setup
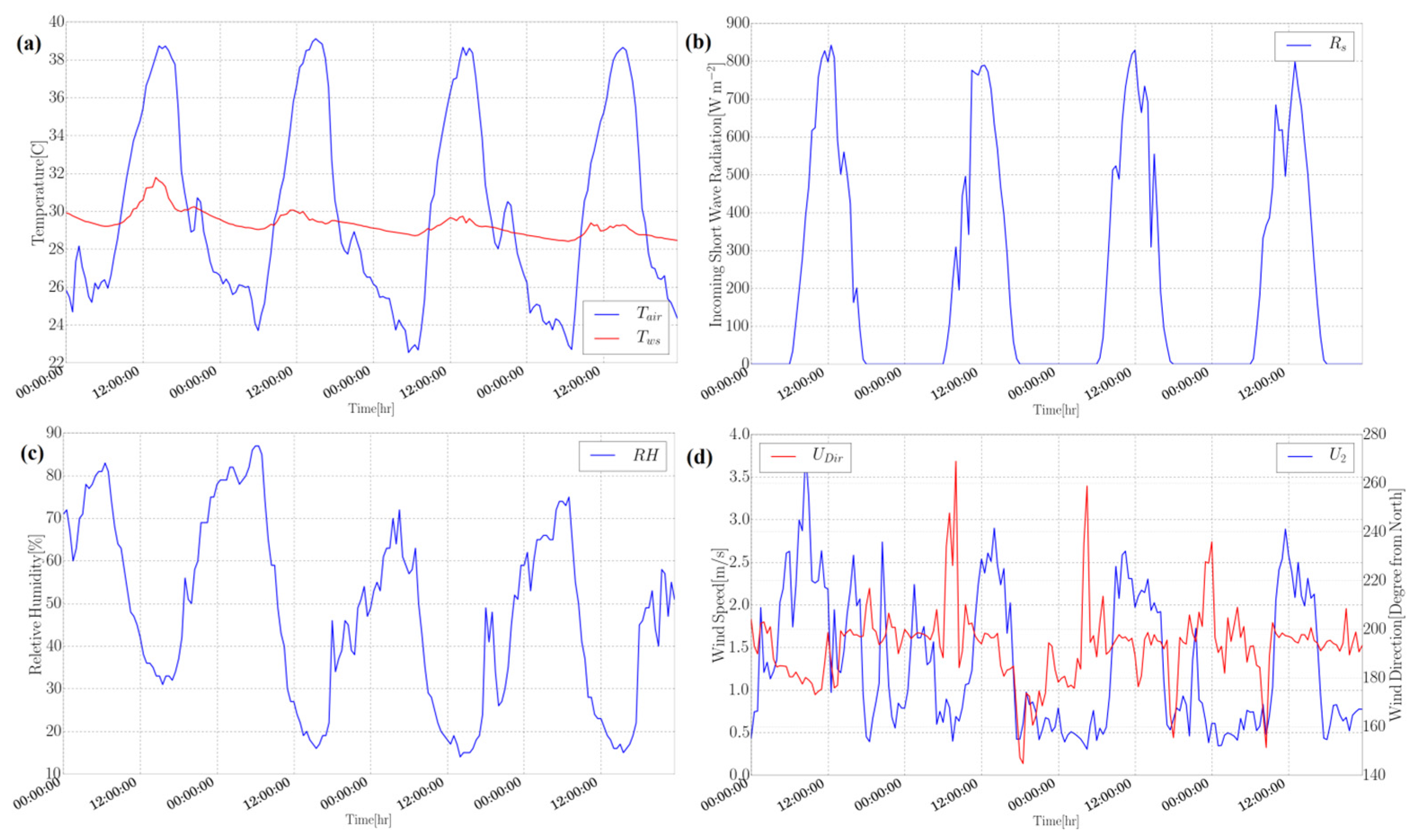
6. Boundary Conditions
6.1. Temperature
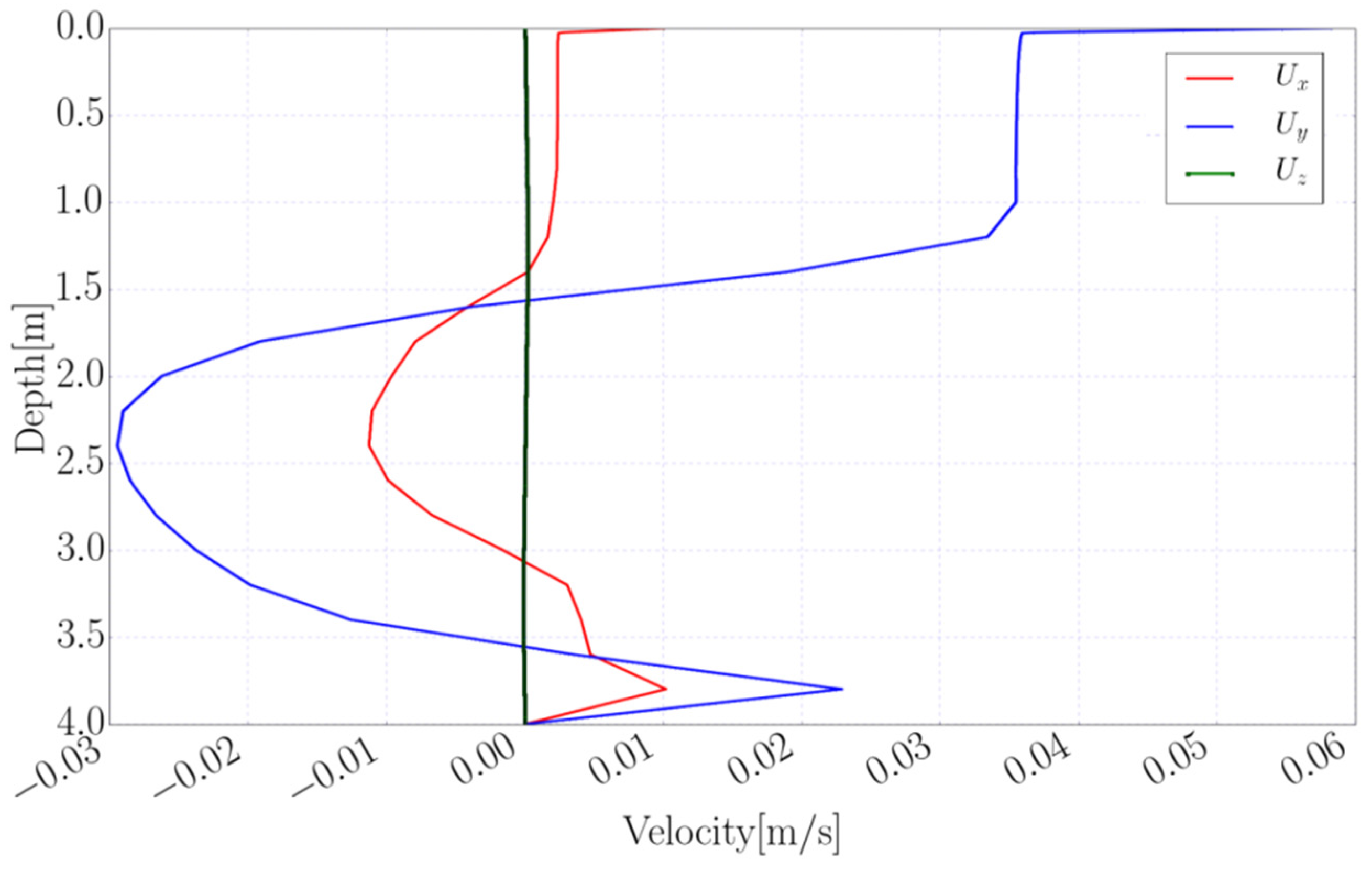
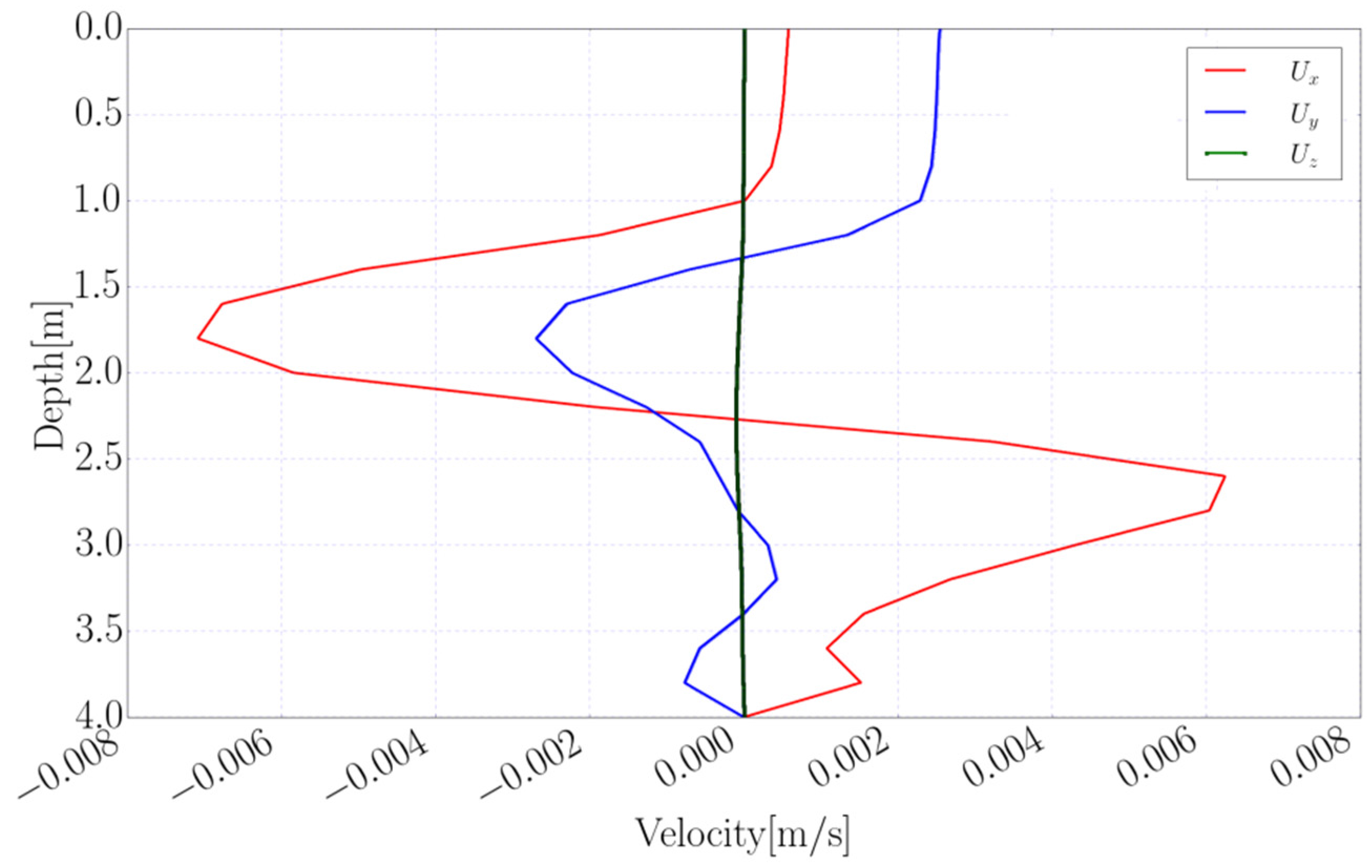
6.2. Velocity
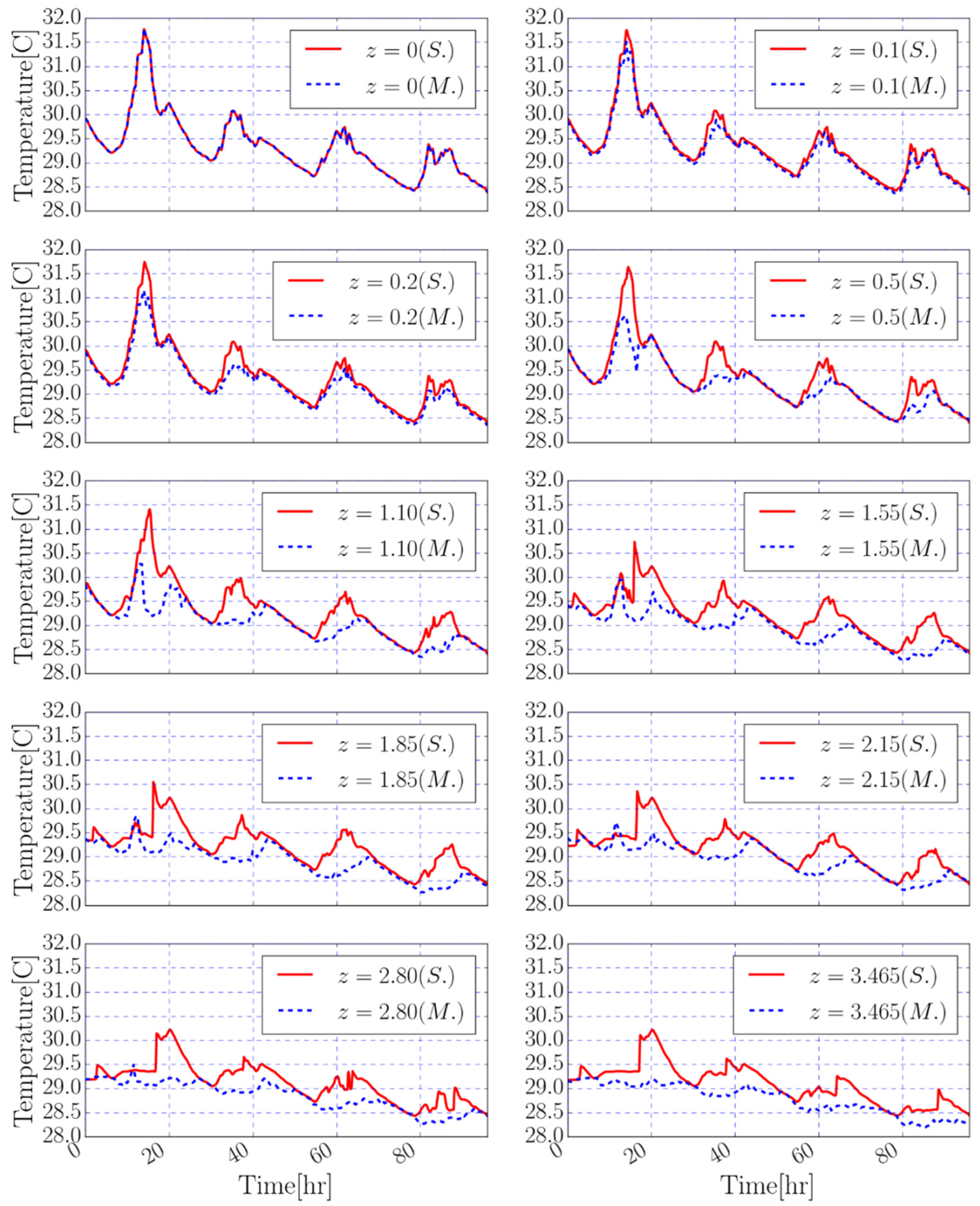
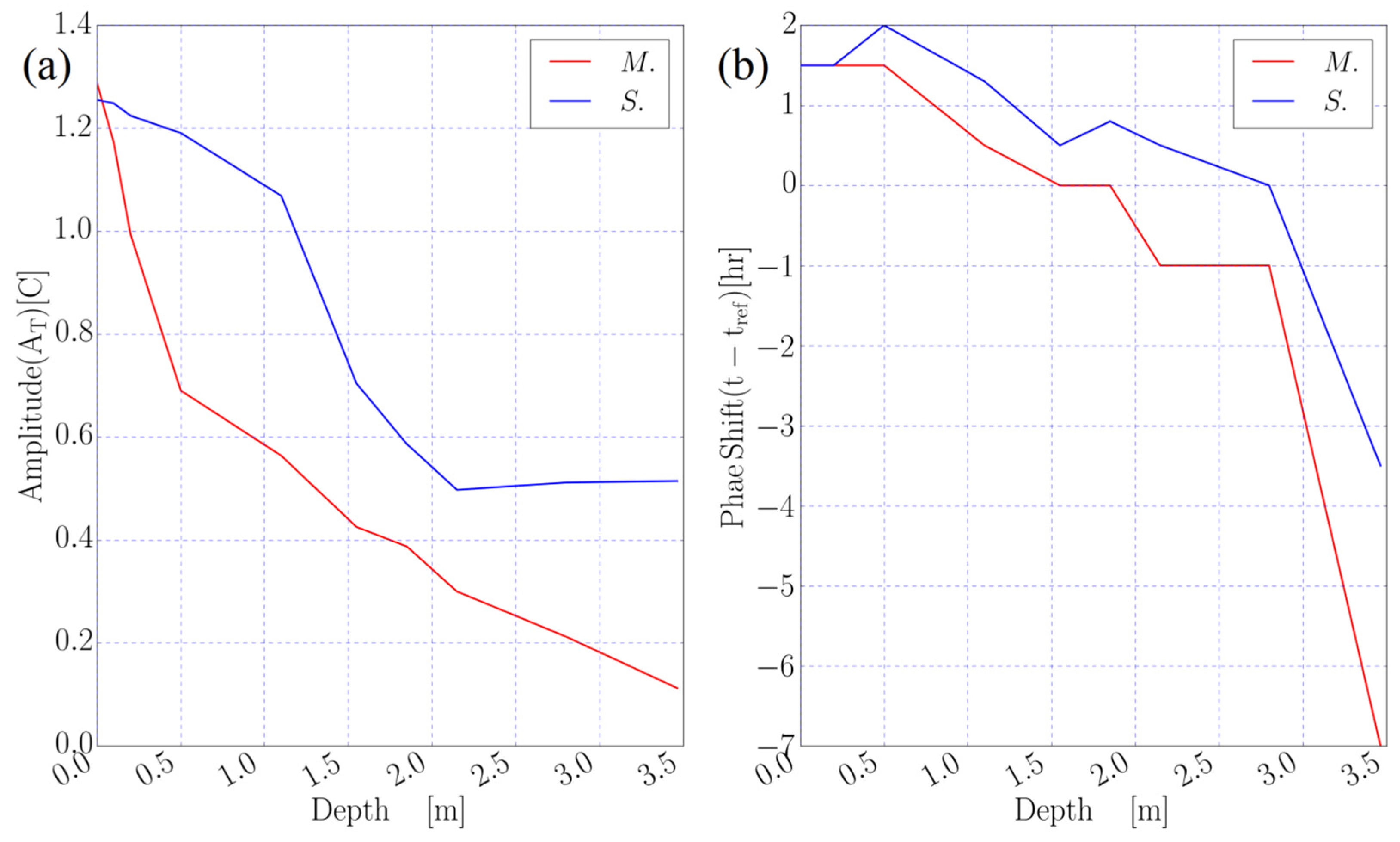
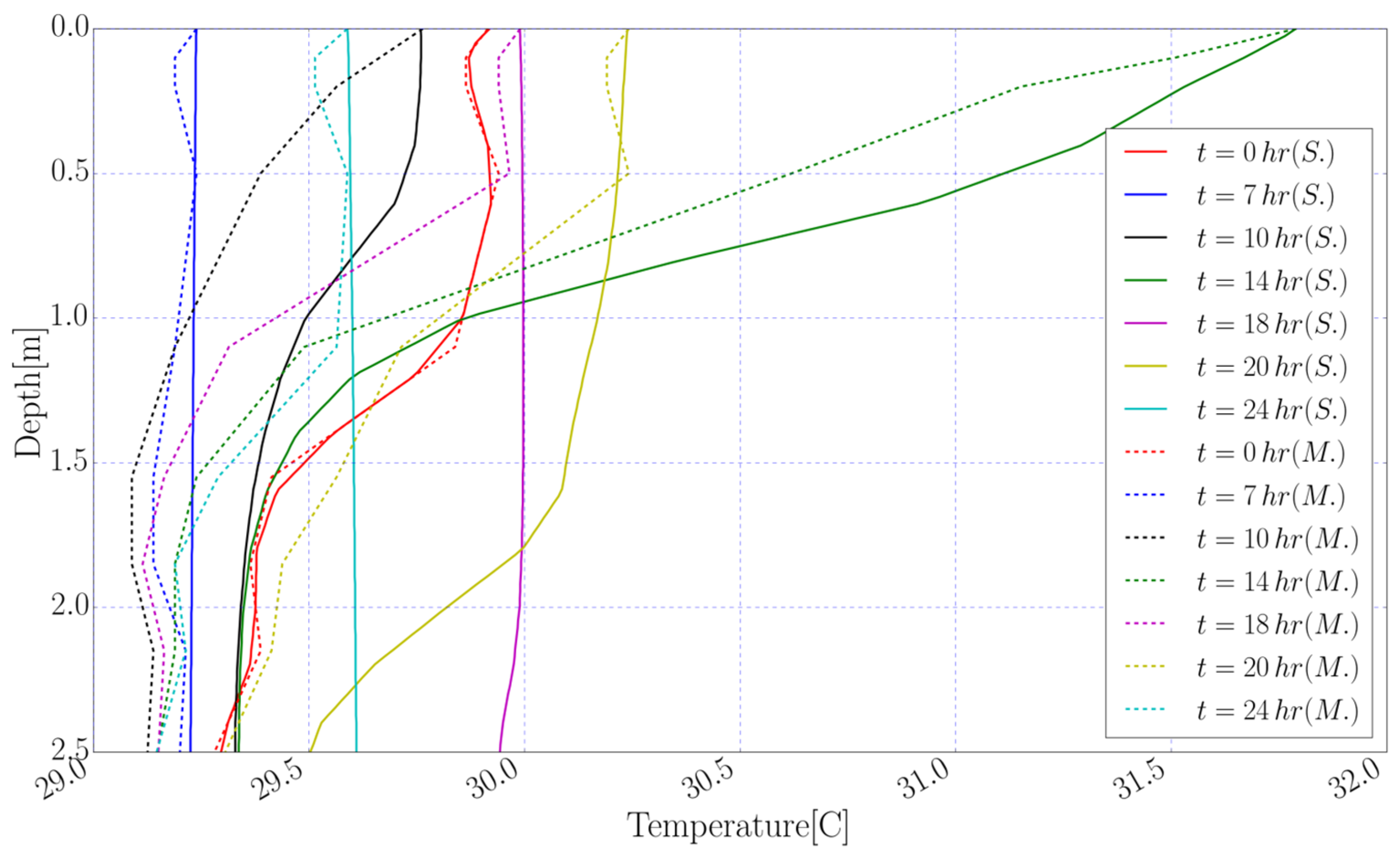
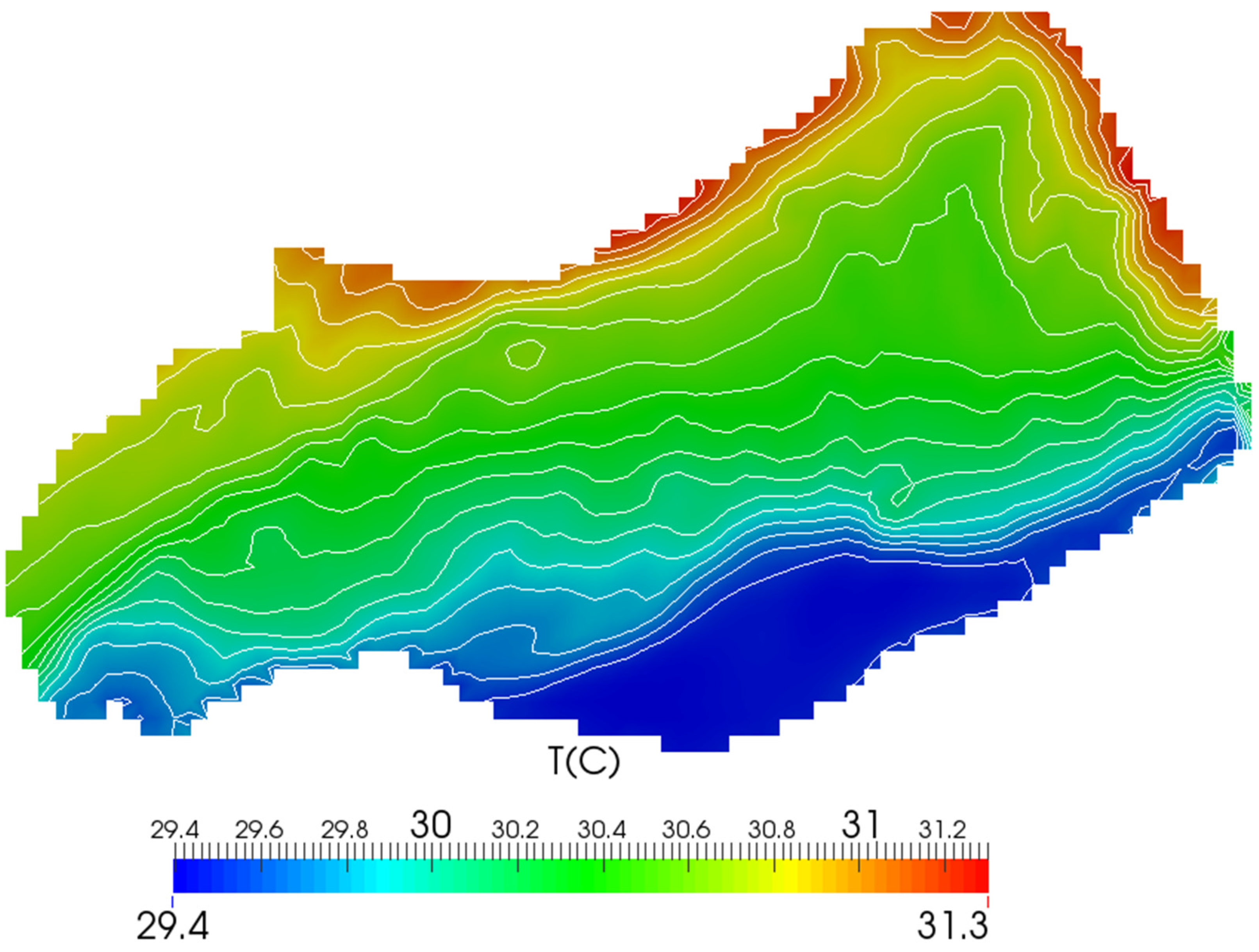
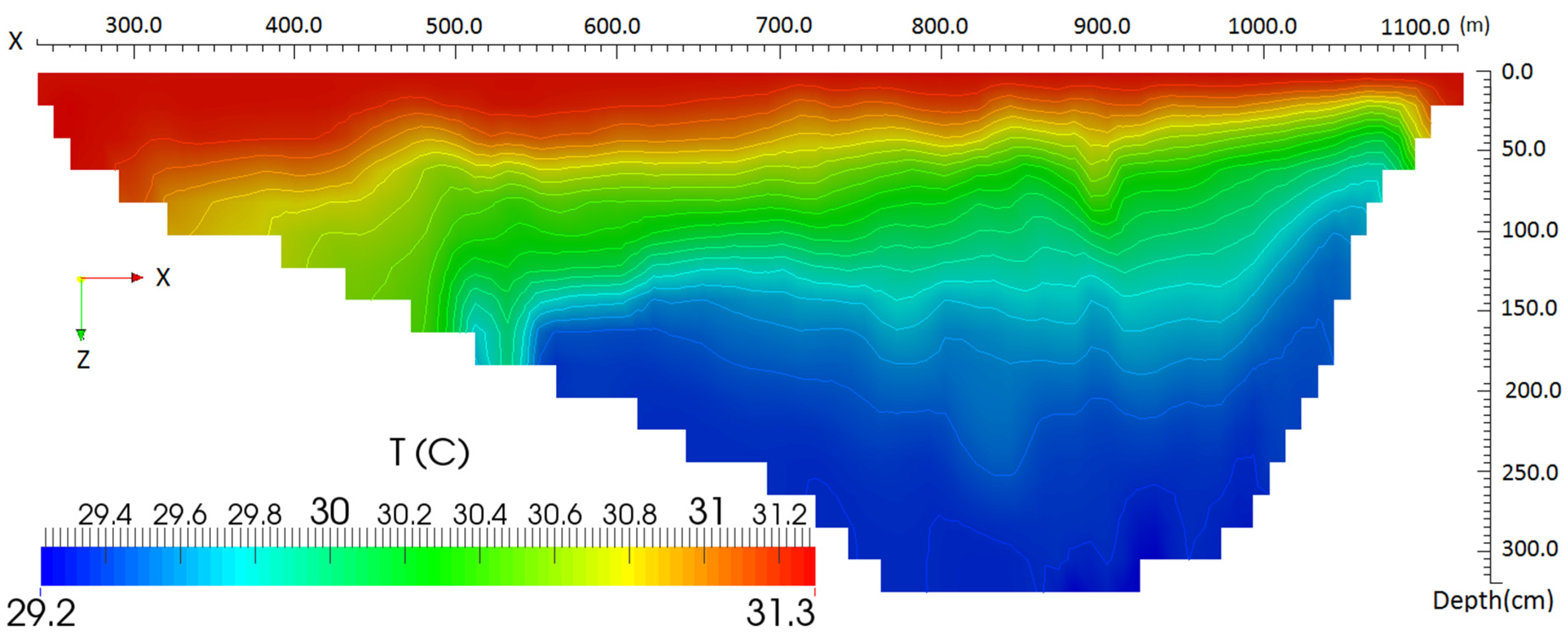
7. Numerical Results and Discussion
- 1)
- Estimating heat fluxes over the water surface as boundary condition is very uncertain especially for latent heat flux. The location, climate, shape, depth, bathymetry, atmospheric stability conditions, etc. make it difficult to estimate evaporation accurately from the water surface.
- 2)
- There are no measurements for some important parameters that can affect the flow field and temperature in the water body, such as turbidity, and heat fluxes at the bottom and side walls where using simplified temperature boundary conditions could be considered as a source of error.
- 3)
- The measurements were taken only at one point. This means that the distribution of parameters over the water surface was assumed homogeneous. For shallow and small lakes with limited fetch, this assumption could produce a large error in the results.
- 4)
- Coupling the turbulent flow and heat transfer in a shallow water body is complex and computational issues such as numerical errors, mesh dependency and residuals control should be considered.
- 5)
- Errors in field measurements on the water surface especially for water surface temperature or heat fluxes.
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shufen, S.; Jinfeng, Y.; Nan, X.; Changhai, S. Development of a Model for Water and Heat Exchange Between the Atmosphere and a Water Body. Adv. Atmos. Sci. 2007, 24, 927–938. [Google Scholar]
- Casamitjana, X.; Serra, T.; Colomer, J.; Baserba, C.; Pérez-Losada, J. Effects of the water withdrawal in the stratification patterns of a reservoir. Hydrobiologia 2003, 504, 21–28. [Google Scholar] [CrossRef]
- Falconer, R.A.; George, D.G.; Hall, P. Three-dimensional numerical modelling of wind-driven circulation in a shallow homogeneous lake. J. Hydrol. 1991, 124, 59–79. [Google Scholar] [CrossRef]
- Elo, A. The energy balance and vertical thermal structure of two small boreal lakes in summer. Boreal Environ. Res. 2007, 12, 585–600. [Google Scholar]
- Antonopoulos, V.; Gianniou, S.K. Simulation of water temperature and dissolved oxygen distribution in Lake Vegoritis, Greece. Ecol. Model. 2003, 160, 39–53. [Google Scholar] [CrossRef]
- Babajimopoulos, C.; Papadopoulos, F. Mathematical Prediction of Thermal Stratification of Lake Ostrove(Vegorities), Greece. Water Resour. Res. 1986, 22, 1590–1596. [Google Scholar] [CrossRef]
- Vercauteren, N.; Huwald, H.; Bou-Zeid, E.; Selker, J.S.; Lemmin, U.; Parlange, M.B.; Lunati, I. Evolution of superficial lake water temperature profile under diurnal radiative forcing. Water Resour. Res. 2011, 47, 1–10. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology—An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Katul, G.G.; Parlange, M.B. A Penman-Brutsaert model for wet surface evaporation. Water Resour. Res. 1992, 28, 121–126. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Ahsan, A.K.M.Q.; Blumberg, A.F. Three-dimensional hydrothermal model of Onondaga Lake, New York. J. Hydraul. Eng. 1999, 125, 912–923. [Google Scholar] [CrossRef]
- Koçyigit, M.; Falconer, R. Modelling of wind-induced currents in water basins. Proc. ICE-Water 2004, 197–210. [Google Scholar] [CrossRef]
- Hodges, B.R.; Imberger, J.; Laval, B.; Appt, J. Modeling the Hydrodynamics of Stratified Lakes. In Proceedings of the 4th International Conference Hydroinformatics 2000, Iowa Institute of Hydraulic Research, Iowa City, Iowa, USA, 23–27 July 2000; pp. 1–14.
- Hostetler, S.W.; Bartlein, P. Simulation of lake evaporation with application to modeling lake level variations of Harney-Malheur Lake, Oregon. Water Resour. Res. 1990, 26, 2603–2612. [Google Scholar] [CrossRef]
- Dake, J.M.K.; Harleman, D.R.F. Thermal stratification in lakes: Analytical and laboratory studies. Water Resour. Res. 1969, 5, 484–495. [Google Scholar] [CrossRef]
- Politano, M.; Haque, M.M.; Weber, L.J. A numerical study of the temperature dynamics at McNary Dam. Ecol. Model. 2008, 212, 408–421. [Google Scholar] [CrossRef]
- MacKay, M.D.; Neale, P.J.; Arp, C.D.; Domis, L.N.S.; Fang, X.; Gal, G.; Jöhnk, K.D.; Kirillin, G.; Lenters, J.D.; Litchman, E.; et al. Modeling lakes and reservoirs in the climate system. Limnol. Oceanogr. 2009, 54, 2315–2329. [Google Scholar] [CrossRef]
- Ferrarin, C.; Umgiesser, G. Hydrodynamic modeling of a coastal lagoon: The Cabras lagoon in Sardinia, Italy. Ecol. Modell. 2005, 188, 340–357. [Google Scholar] [CrossRef]
- Lei, C.; Patterson, J.C. Natural Convection in a Reservoir Sidearm Subject To Solar Radiation: A Two-Dimensional Simulation. Numer. Heat Transf. Part A 2002, 42, 13–32. [Google Scholar] [CrossRef]
- Debolsky, V.K.; Neymark, R.V. Thermally non-uniform flow in water reservoir: Numerical investigation. J. Hydraul. Res. 1994, 32, 25–40. [Google Scholar] [CrossRef]
- Liu, W.-C.; Chen, W.-B.; Chiu, C.-Y. Numerical modeling of hydrodynamic and hydrothermal characteristics in subtropical alpine lake. Appl. Math. Model. 2012, 36, 2094–2109. [Google Scholar] [CrossRef]
- Haque, M.M.; Constantinescu, G.; Weber, L. Validation of a 3D RANS model to predict flow and stratification effects related to fish passage at hydropower dams. J. Hydraul. Res. 2007, 45, 787–796. [Google Scholar] [CrossRef]
- Kennedy, M.G.; Ahlfeld, D.P.; Schmidt, D.P.; Tobiason, J.E. Three-Dimensional Modeling for Estimation of Hydraulic Retention Time in a Reservoir. J. Environ. Eng. 2006, 132, 976–984. [Google Scholar] [CrossRef]
- Rueda, F.J.; Schladow, S.G. Dynamics of large polymictic lake. II: Numerical simulations. J. Hydraul. Eng. 2003, 129, 92–101. [Google Scholar] [CrossRef]
- Jin, K.-R.; Ji, Z.-G.; Hamrick, J.H. Modeling Winter Circulation in Lake Okeechobee, Florida. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 114–125. [Google Scholar] [CrossRef]
- Davies, A.M. On computing the three dimensional flow in a stratified sea using the Galerkin method. Appl. Math. Model. 1982, 6, 347–362. [Google Scholar] [CrossRef]
- Leon, L.; Lam, D.; Schertzer, W.; Swayne, D.; Imberger, J. Towards coupling a 3D hydrodynamic lake model with the Canadian Regional Climate Model: Simulation on Great Slave Lake. Environ. Model. Softw. 2007, 22, 787–796. [Google Scholar] [CrossRef]
- Wang, Y.-S.; Politano, M.; Laughery, R. Towards full predictions of temperature dynamics in McNary Dam forebay using OpenFOAM. Water Sci. Eng. 2013, 6, 317–330. [Google Scholar]
- Abbasi, A.; Annor, F.O.; van de Giesen, N. A Framework to Simulate Small and Shallow Inland Water Bodies. Comput. Methods Appl. Mech. Eng. (Manuscript Submitt. Publ.) 2015, in press. [Google Scholar]
- Annor, F.O.; van de Giesen, N.; Liebe, J.; van de Zaag, P.; Tilmant, A.; Odai, S.N. Delineation of small reservoirs using radar imagery in a semi-arid environment: A case study in the upper east region of Ghana. Phys. Chem. Earth 2009, 34, 309–315. [Google Scholar] [CrossRef]
- Keller, A.; Sakthivadivel, R.; Seckler, D. Water Scarcity and the Role of Storage in Development; International Water Management Institute: Colombo, 2000. [Google Scholar]
- Van Emmerik, T.H.M.; Rimmer, A.; Lechinsky, Y.; Wenker, K.J.R.; Nussboim, S.; van de Giesen, N.C. Measuring heat balance residual at lake surface using Distributed Temperature Sensing. Limnol. Oceanogr. Methods 2013, 11, 79–90. [Google Scholar] [CrossRef]
- HOBO TidbiT v2 Water Temperature Data Logger- Specifications. Available online: http:// www.onsetcomp.com/products/data-loggers/utbi-001 (accessed on 20 November 2015).
- Tsanis, I.; Wu, J.; Shen, H.; Valeo, C. Environmental Hydraulics: Hydrodynamic and Pollutant Transport Modelling of Lakes and Coastal Waters; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Fredriksson, S. A Buoyantboussinesqsurfactantfoam Tutorial—An Introduction to FAM; Technical Report; Chalmers University of Technology: Gothenburg, Sweden, 2011. [Google Scholar]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- White, F.M. Viscous fluid flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Wood, T.M.; Cheng, R.T.; Gartner, J.W.; Hoilman, G.R.; Lindenberg, M.K.; Wellman, R.E. Modeling Hydrodynamics and Heat Transport in Upper Klamath Lake, Oregon, and Implications for Water Quality; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2008. [Google Scholar]
- Branco, B.F.; Torgersen, T. Predicting the onset of thermal stratification in shallow inland waterbodies. Aquat. Sci. 2009, 71, 65–79. [Google Scholar] [CrossRef]
- Momii, K.; Ito, Y. Heat budget estimates for Lake Ikeda, Japan. J. Hydrol. 2008, 361, 362–370. [Google Scholar] [CrossRef]
- Losordo, T.M.; Piedrahita, R.H. Modelling temperature variation and thermal stratification in shallow aquaculture ponds. Ecol. Model. 1991, 54, 189–226. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Goudsmit, G.-H.; Burchard, H.; Peeters, F.; Wuest, A. Application of k-ε turbulence models to enclosed basins: The role of internal seiches. J. Geophys. Res. 2002, 107, 1–13. [Google Scholar]
- Bigham Stephens, D.L.; Carlson, R.E.; Horsburgh, C.A.; Hoyer, M.V.; Bachmann, R.W.; Canfield, D.E. Regional distribution of Secchi disk transparency in waters of the United States. Lake Reserv. Manag. 2015, 31, 55–63. [Google Scholar] [CrossRef]
- Idso, S.B.; Gilbert, R.G. On the universality of the Poole and Atkins Secchi disk-light extinction equation. J. Appl. Ecol. 1974, 11, 399–401. [Google Scholar] [CrossRef]
- Williams, D.T.; Drummond, G.R.; Ford, D.E.; Robey, D.L. Determination of Light Extinction Coefficients in Lakes and Reservoirs. In Proceedings of the Symposium on Surface Water Impoundments (ASCE), Minnesota, USA, 2–5 June 1981; pp. 1329–1335.
- Subin, Z.M.; Riley, W.J.; Mironov, D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Syst. 2012, 4, 1–27. [Google Scholar] [CrossRef]
- Weinberger, S.; Vetter, M. Using the hydrodynamic model DYRESM based on results of a regional climate model to estimate water temperature changes at Lake Ammersee. Ecol. Model. 2012, 244, 38–48. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Joubert, E.C.; Harms, T.M.; Muller, A.; Hipondoka, M.; Henschel, J.R. A CFD study of wind patterns over a desert dune and the effect on seed dispersion. Environ. Fluid Mech. 2012, 12, 23–44. [Google Scholar] [CrossRef]
- Wang, Y. Development of A Numerical Tool To Predict Hydrodynamics, Temperature And TDG in Hydropower Flows. Ph.D Thesis, University of Iowa, Iowa City, IA, USA, 2013. [Google Scholar]
- Rohdin, P.; Moshfegh, B. Numerical predictions of indoor climate in large industrial premises. A comparison between different k-ε models supported by field measurements. Build. Environ. 2007, 42, 3872–3882. [Google Scholar] [CrossRef]
- Lee, J.W. Numerical Modelling of Temperature-Induced Circulation in Shallow Water Bodies and Application to Torrens Lake, South Australia. Ph.D Thesis, The University of Adelaide Applied Mathematics, Adelaide, Austrilia, 2007. [Google Scholar]
- Stepanenko, V.; Johnk, K.D.; Machulskaya, E.; Perroud, M.; Subin, Z.; Nordbo, A.; Mammarella, I.; Mironov, D. Simulation of surface energy fluxes and stratification of a small boreal lake by a set of one-dimensional models. Tellus A 2014, 66, 1–18. [Google Scholar] [CrossRef]
- OpenFOAM User Guide: Mesh Generation with snappyHexMesh. Available online: http://cfd.direct/ openfoam/user-guide/snappyhexmesh/ (accessed on 20 November 2015).
- CFD Direct: The Architects of OpenFOAM. Available online: http://cfd.direct/ (accessed on 20 November 2015).
- Brockhaus, G.T. Hydrodynamic Design of Ship Bulbous Bows Considering Seaway and Operational Conditions. Ph.D Thesis, Berlin Technischen Universit, Berlin, Germany, 2011. [Google Scholar]
- Martinez, B. Wind Resource in Complex Terrain with OpenFOAM. Master’s Thesis, National Laboratory for Sustainable Energy, Technical University of Denmark, Copenhagen, Denmark, 2011. [Google Scholar]
- Bechmann, A. Large-Eddy Simulation of Atmospheric Flow over Complex Terrain, Ph.D Thesis, Risø National Laboratory, Technical University of Denmark, Copenhagen, Denmark, 2006. [Google Scholar]
- Perroud, M.; Goyette, S. Impact of warmer climate on Lake Geneva water-temperature profiles. Boreal Environ. Res. 2010, 15, 255–278. [Google Scholar]
- Lap, B.Q.; Mori, K. A two-dimensional numerical model of wind-induced flow and water quality in closed water bodies. Paddy Water Environ. 2007, 5, 29–40. [Google Scholar] [CrossRef]
- Henderson-Sellers, B. Sensitivity of thermal stratification models to changing boundary conditions. Appl. Math. Model. 1988, 12, 31–43. [Google Scholar] [CrossRef]
- Yao, H. Long-Term Study of Lake Evaporation and Evaluation of Seven Estimation Methods: Results from Dickie Lake, South-Central Ontario, Canada. J. Water Resour. Prot. 2009, 01, 59–77. [Google Scholar] [CrossRef]
- Abbasi, A.; Annor, F.O.; van de Giesen, N. Developing a CFD-based Approach to Estimate Evaporation from Water Surfaces in (Semi-)Arid Regions. Hydrol. Process. (Manuscript Submitt. Publ. 2015. [Google Scholar]
- Goff, J.A. Saturation pressure of water on the new Kelvin temperature scale. In Transactions of the American society of heating and ventilating engineers; American Society of Heating and Ventilating Engineers: New York, NY, 1957; pp. 347–354. [Google Scholar]
- Livingstone, D.M.; Imboden, D.M. Annual heat balance and equilibrium temperature of Lake Aegeri, Switzerland. Aquat. Sci. 1989, 51, 351–369. [Google Scholar] [CrossRef]
- groovyBC Boundary Condition. Available online: https://openfoamwiki.net/index.php/Contrib/groovyBC (accessed on 20 November 2015).
- Wüest, A.; Lorke, A. Small-scale hydrodynamics in lakes. Annu. Rev. Fluid Mech. 2003, 35, 373–412. [Google Scholar] [CrossRef]
- Markfort, C.D.; Perez, A.L.S.; Thill, J.W.; Jaster, D.A.; Porté-Agel, F.; Stefan, H.G. Wind sheltering of a lake by a tree canopy or bluff topography. Water Resour. Res. 2010, 46, 1–13. [Google Scholar] [CrossRef]
- Suárez, F.; Tyler, S.W.; Childress, A.E. A fully coupled, transient double-diffusive convective model for salt-gradient solar ponds. Int. J. Heat Mass Transf. 2010, 53, 1718–1730. [Google Scholar] [CrossRef]
- Jacobs, A.F.G.; Jetten, T.H.; Lucassen, D.; Heusinkveld, B.G.; Joost, P.N. Diurnal temperature fluctuations in a natural shallow water body. Agric. For. Meteorol. 1997, 88, 269–277. [Google Scholar] [CrossRef]
- Collaborative Organisation for ICT in Dutch Higher Education and Research. Available online: https://www.surf.nl/en/services-and-products/hpc-cloud/technical-specifications/index.html (accessed on 20 November 2015).



| Wavelength (nm) | [m−1] | |
|---|---|---|
| <400 (UV) | 0.046 | assume same as VIS |
| 400–700 (VIS) | 0.430 | 3.0 (assumed) |
| 700–910 | 0.214 | 2.92 |
| 910–950 | 0.020 | 20.4 |
| 950–1090 | 0.089 | 29.5 |
| 1090–1350 | 0.092 | 98.4 |
| >1350 | 0.109 | 2880 |
| Depth (m) | MAE (°C) | RMSE (°C) | Mean Error (°C) | RME(%) | ||||
|---|---|---|---|---|---|---|---|---|
| max | min | ave | max | min | ave | |||
| 0.0 | 0.029 | 0.043 | 0.2053 | −0.1985 | 0.0032 | 0.6556 | 0.0017 | 0.0969 |
| 0.1 | 0.079 | 0.110 | 0.0650 | −0.4645 | −0.0773 | 1.4922 | 0.0000 | 0.2659 |
| 0.2 | 0.117 | 0.172 | 0.0023 | −0.7523 | −0.1166 | 2.4385 | 0.0076 | 0.3960 |
| 0.5 | 0.169 | 0.297 | 0.0760 | −1.4065 | −0.1402 | 4.6780 | 0.1038 | 0.5764 |
| 1.10 | 0.258 | 0.442 | 0.0335 | −1.6010 | −0.2541 | 5.4021 | 0.0009 | 0.8870 |
| 1.55 | 0.282 | 0.407 | 0.0340 | −1.5325 | −0.2816 | 5.2681 | 0.0075 | 0.9770 |
| 1.85 | 0.298 | 0.415 | 0.1960 | −1.2730 | −0.2931 | 4.3723 | 0.0094 | 1.0320 |
| 2.15 | 0.253 | 0.360 | 0.2560 | −1.0185 | −0.2277 | 3.4922 | 0.0009 | 0.8750 |
| 2.80 | 0.283 | 0.374 | 0.1123 | −1.0593 | −0.2780 | 3.6444 | 0.0009 | 0.9800 |
| 3.465 | 0.308 | 0.385 | 0.0425 | −1.0400 | −0.3057 | 3.5659 | 0.0043 | 1.0690 |
| Total | 0.208 | 0.329 | 0.2560 | −1.6010 | −0.1972 | 5.4021 | 0.0000 | 0.7162 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbasi, A.; Annor, F.O.; Van de Giesen, N. Investigation of Temperature Dynamics in Small and Shallow Reservoirs, Case Study: Lake Binaba, Upper East Region of Ghana. Water 2016, 8, 84. https://doi.org/10.3390/w8030084
Abbasi A, Annor FO, Van de Giesen N. Investigation of Temperature Dynamics in Small and Shallow Reservoirs, Case Study: Lake Binaba, Upper East Region of Ghana. Water. 2016; 8(3):84. https://doi.org/10.3390/w8030084
Chicago/Turabian StyleAbbasi, Ali, Frank Ohene Annor, and Nick Van de Giesen. 2016. "Investigation of Temperature Dynamics in Small and Shallow Reservoirs, Case Study: Lake Binaba, Upper East Region of Ghana" Water 8, no. 3: 84. https://doi.org/10.3390/w8030084
APA StyleAbbasi, A., Annor, F. O., & Van de Giesen, N. (2016). Investigation of Temperature Dynamics in Small and Shallow Reservoirs, Case Study: Lake Binaba, Upper East Region of Ghana. Water, 8(3), 84. https://doi.org/10.3390/w8030084






