Estimating Sediment Discharge Using Sediment Rating Curves and Artificial Neural Networks in the Shiwen River, Taiwan
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
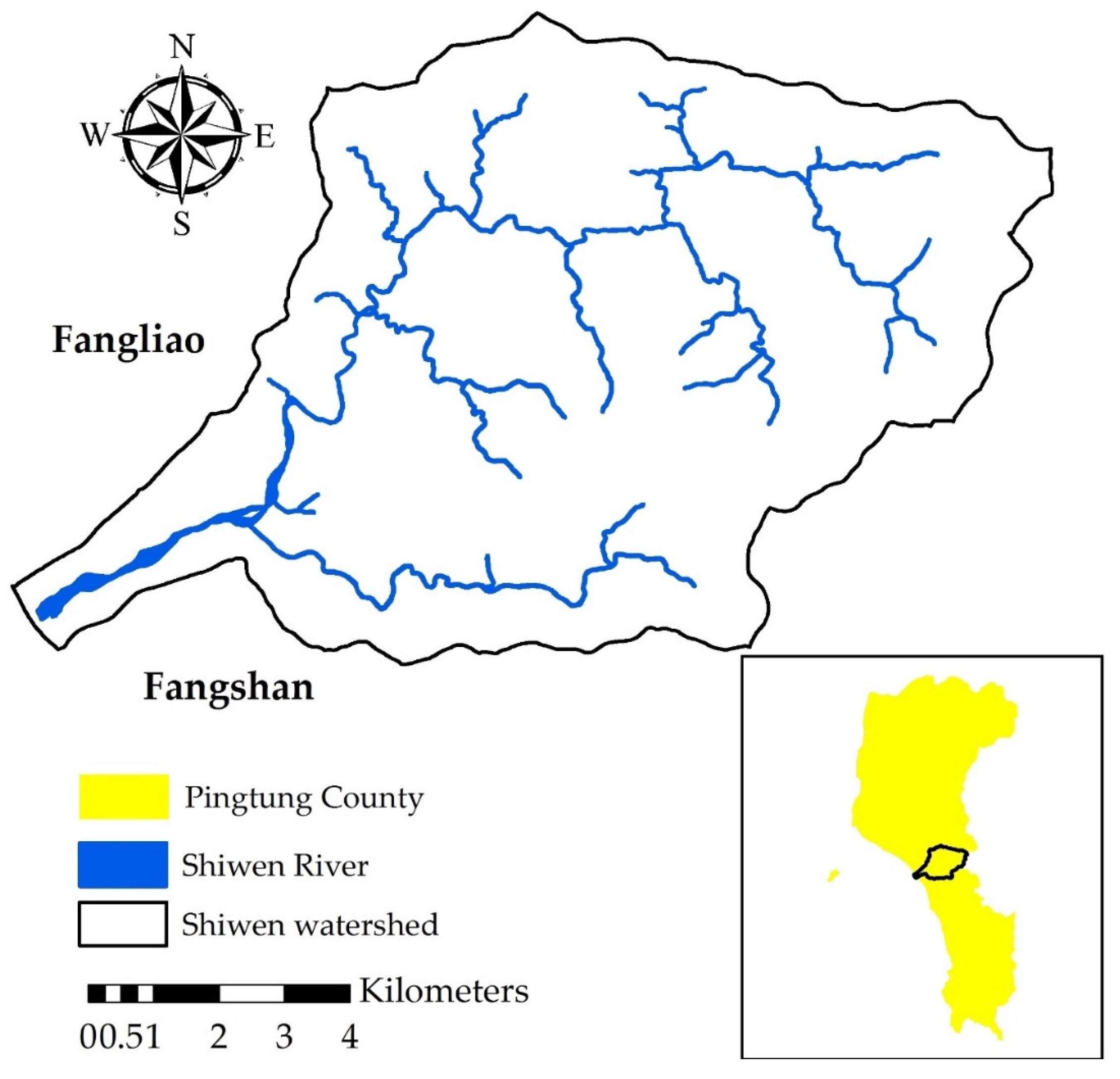

2.2. Sediment Rating Curve
2.3. Artificial Neural Networks
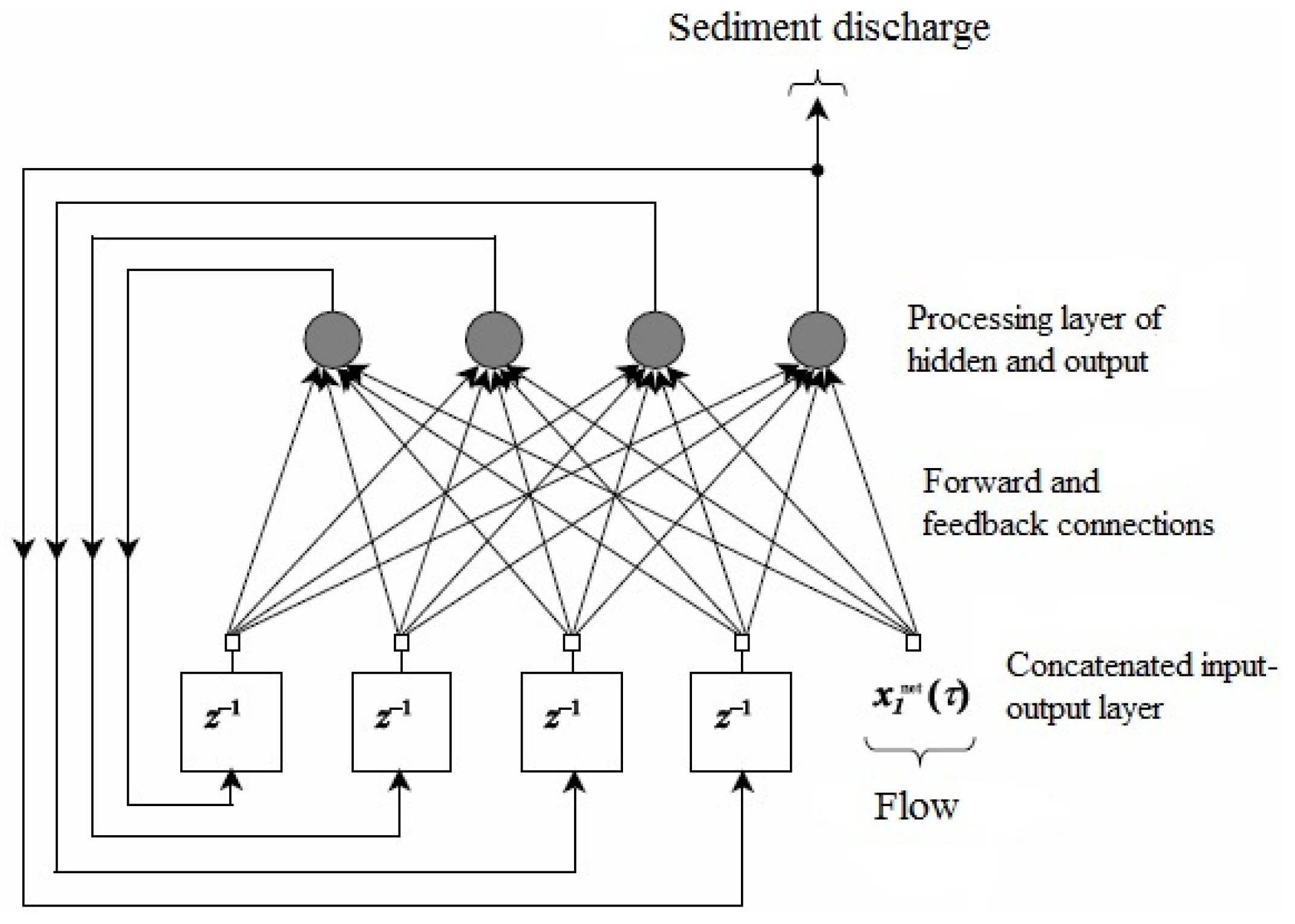
2.3.1. Fully Recurrent Neural Networks (FRNNs)
| Training Variables | Assigned Value |
|---|---|
| Step size | 1 |
| Momentum | 0.7 |
| Iterations | 1000 |
| Training threshold | 0.001 |
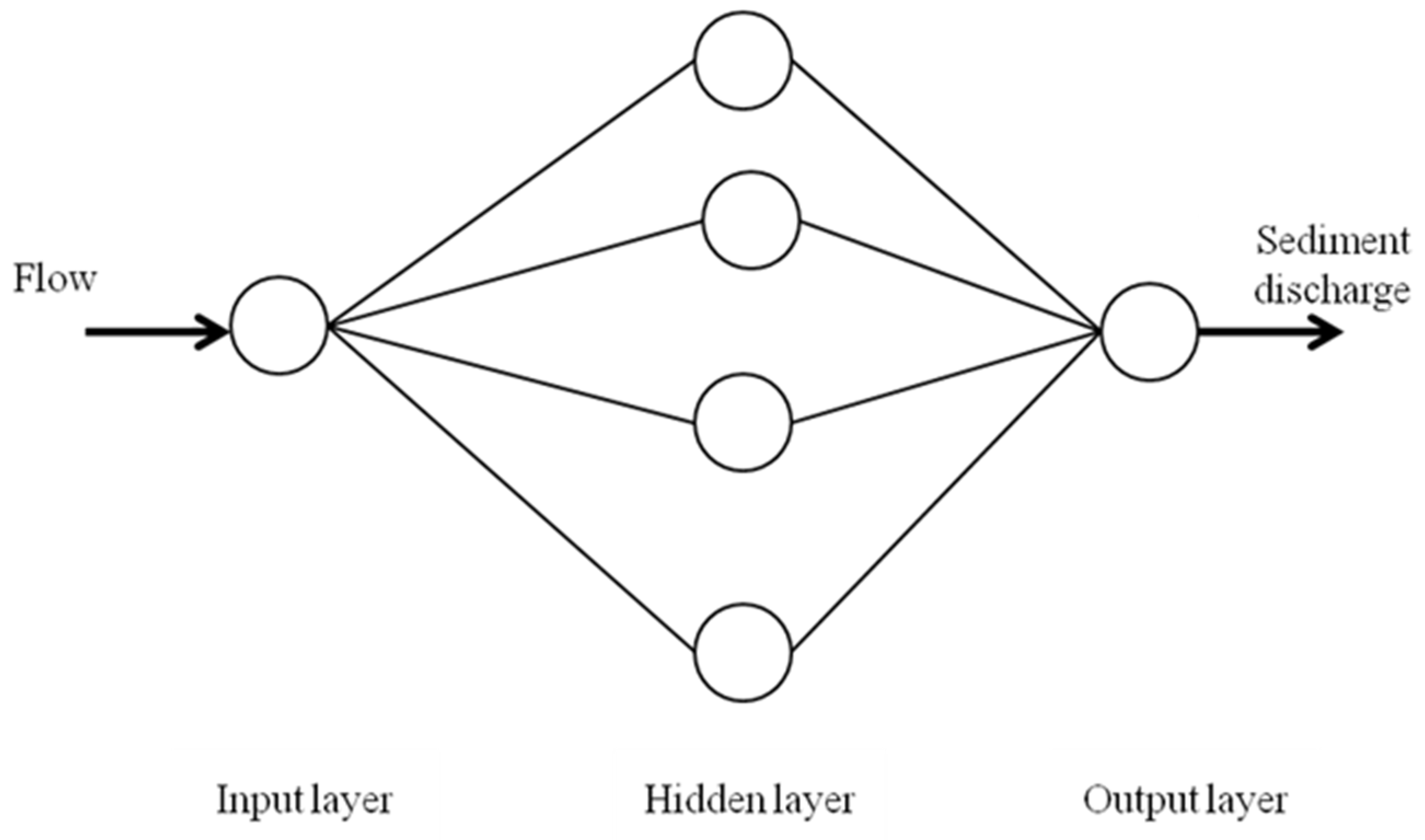
2.3.2. Multilayer Perceptron (MLP)
| Training Variables | Assigned Value |
|---|---|
| Step size | 1 |
| Momentum | 0.7 |
| Iterations | 5000 |
| Training threshold | 0.001 |
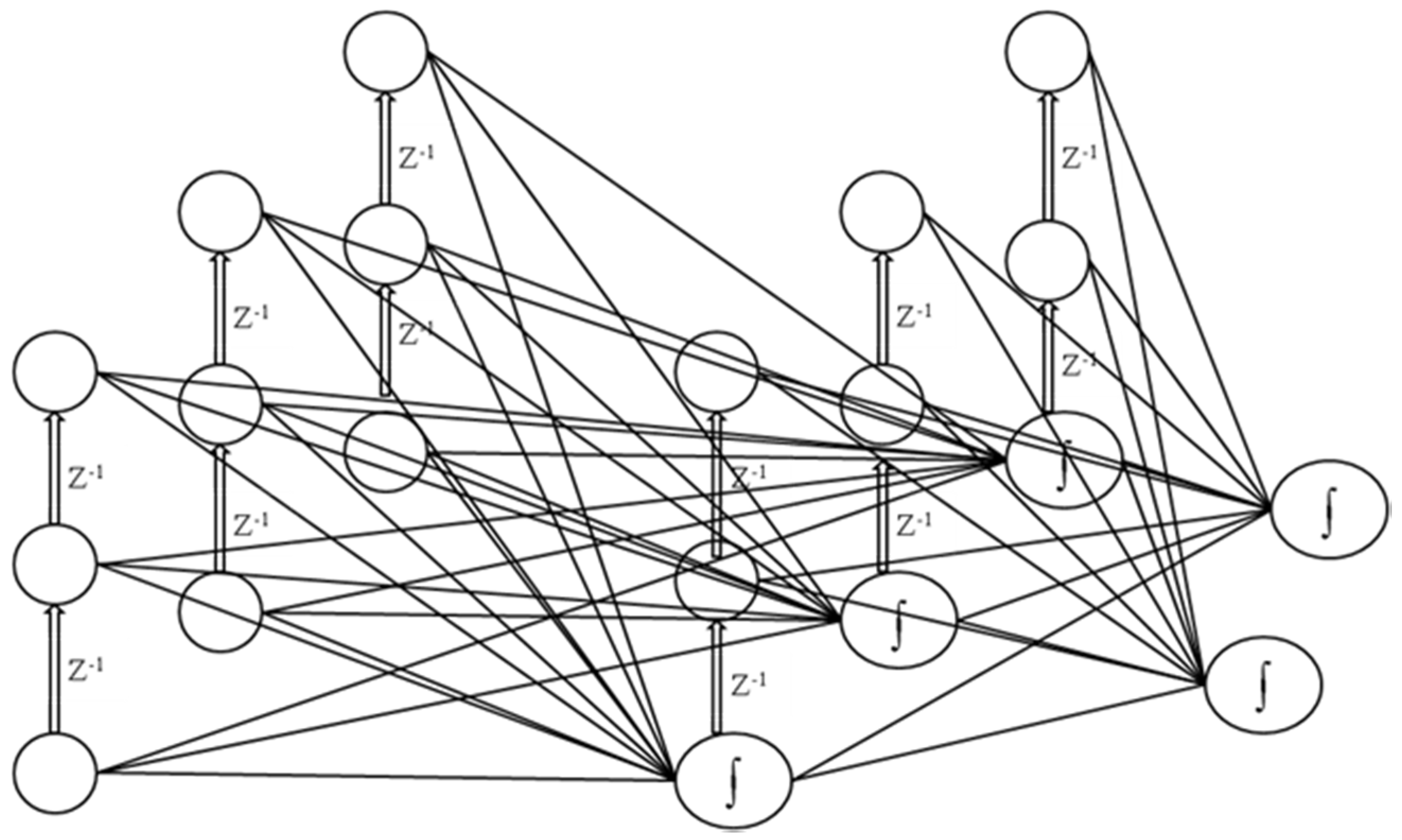
2.3.3. Time Lagged Recurrent Networks (TLRNs)
| Training Variables | Assigned Value |
|---|---|
| Depth in samples | 10 |
| Trajectory length | 50 |
| Momentum | 0.7 |
| Iterations | 1000 |
| Training threshold | 0.001 |
2.3.4. Radial Basis Function (RBF)
2.3.5. Coactive Neurofuzzy Inference System Model (CANFISM)
| Training Variables | Assigned Value |
|---|---|
| Membership function | Gaussian |
| MFs per input | 2 |
| Fuzzy model | TSK |
| Step size | 1 |
| Momentum | 0.7 |
| Iterations | 1000 |
| Training threshold | 0.001 |
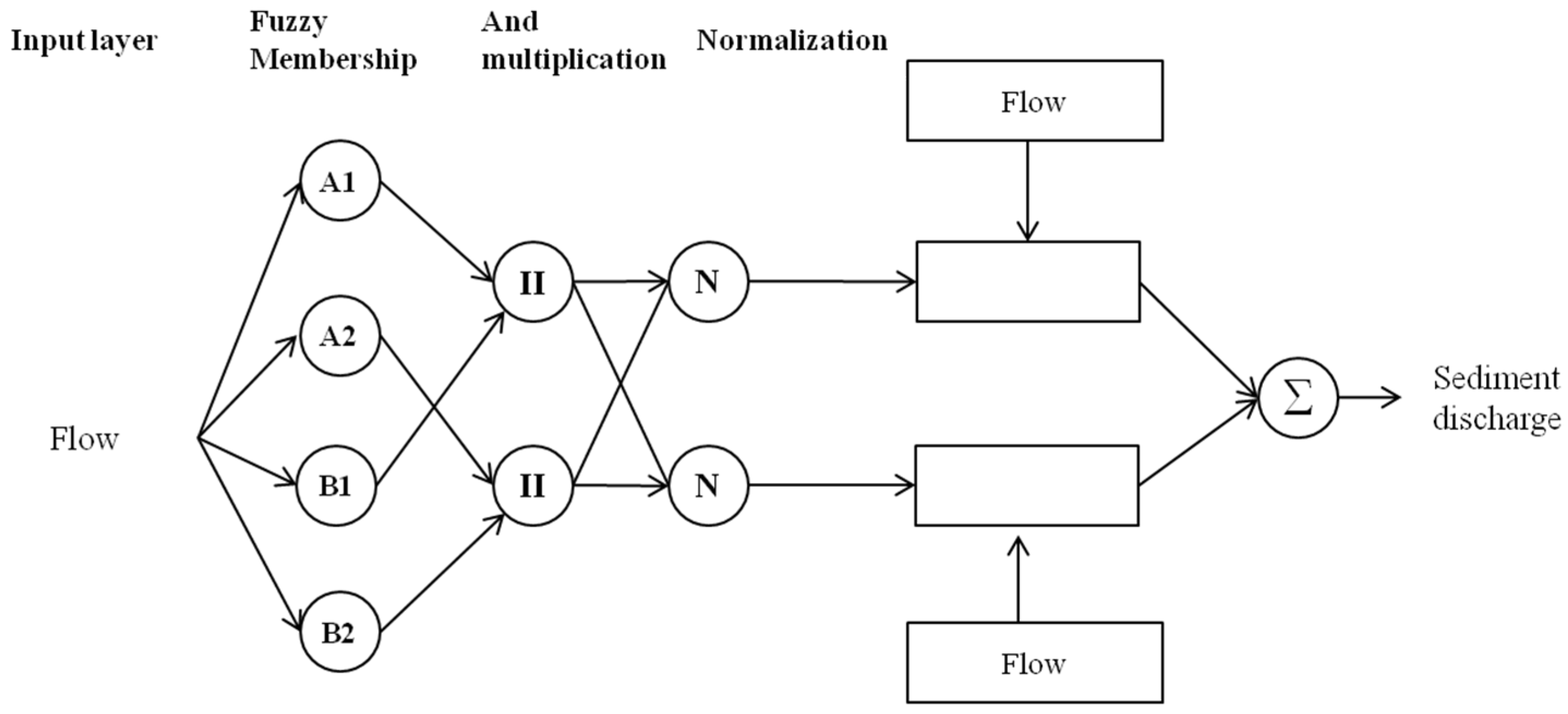
2.4. Data Normalization
2.5. Models Evaluation
3. Results and Discussion
3.1. Sediment Discharge—Based on Rating Curve
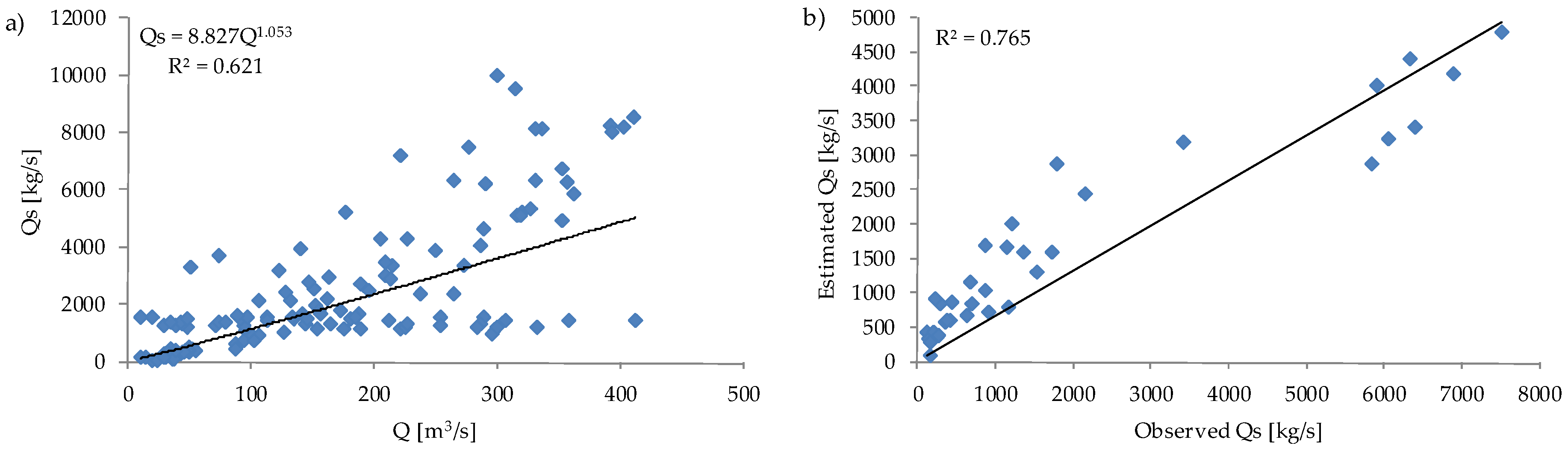
3.2. Sediment Discharge—Based on ANNs
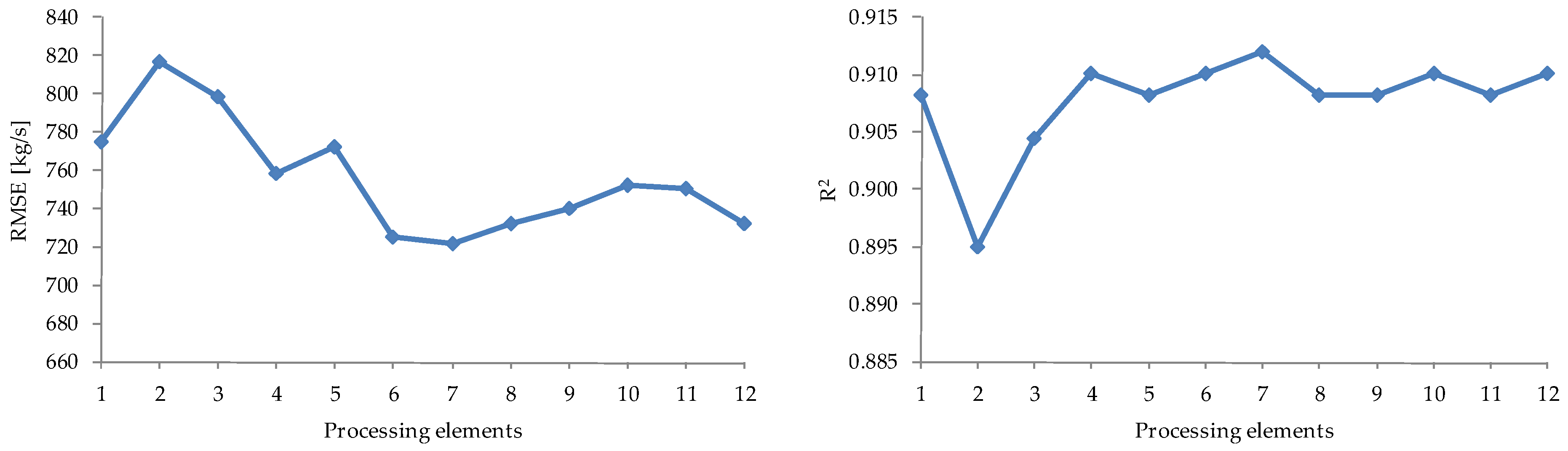
| Model | Stage | RMSE (m3/s) | MAE (m3/s) | R2 |
|---|---|---|---|---|
| MLP | Training | 1431.536 | 893.700 | 0.709 |
| Cross validation | 1091.186 | 706.003 | 0.823 | |
| Testing | 721.175 | 509.584 | 0.912 | |
| CANFISM | Training | 1380.483 | 890.829 | 0.721 |
| Cross validation | 1122.562 | 758.043 | 0.826 | |
| Testing | 775.401 | 591.837 | 0.906 | |
| TLRN | Training | 1329.052 | 900.685 | 0.743 |
| Cross validation | 1187.290 | 786.072 | 0.801 | |
| Testing | 860.803 | 649.805 | 0.878 | |
| FRNN | Training | 1400.275 | 931.110 | 0.716 |
| Cross validation | 1142.759 | 775.643 | 0.823 | |
| Testing | 782.847 | 588.648 | 0.906 | |
| RBF | Training | 1359.194 | 844.964 | 0.729 |
| Cross validation | 1124.365 | 730.110 | 0.828 | |
| Testing | 859.805 | 615.986 | 0.876 |
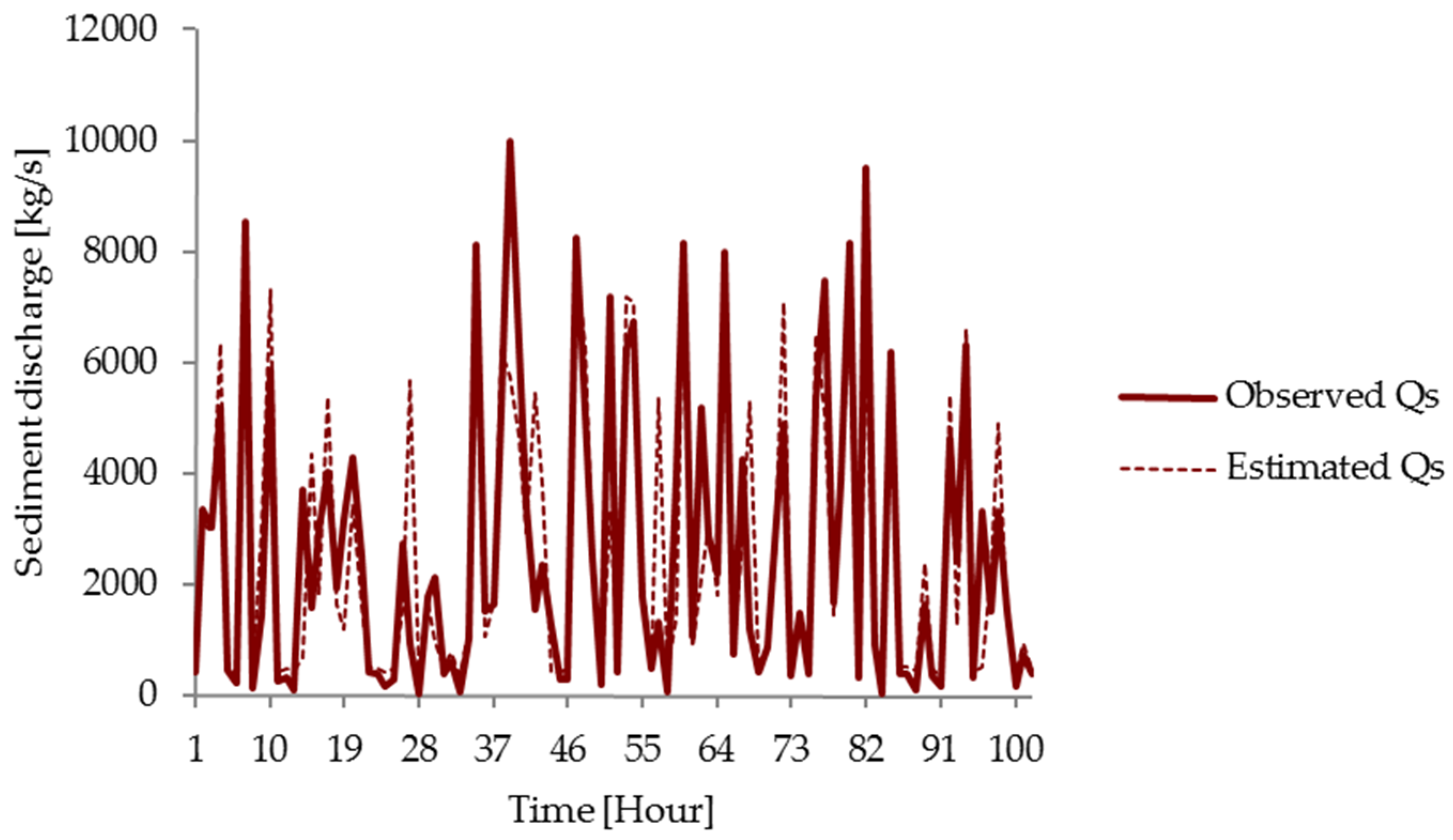
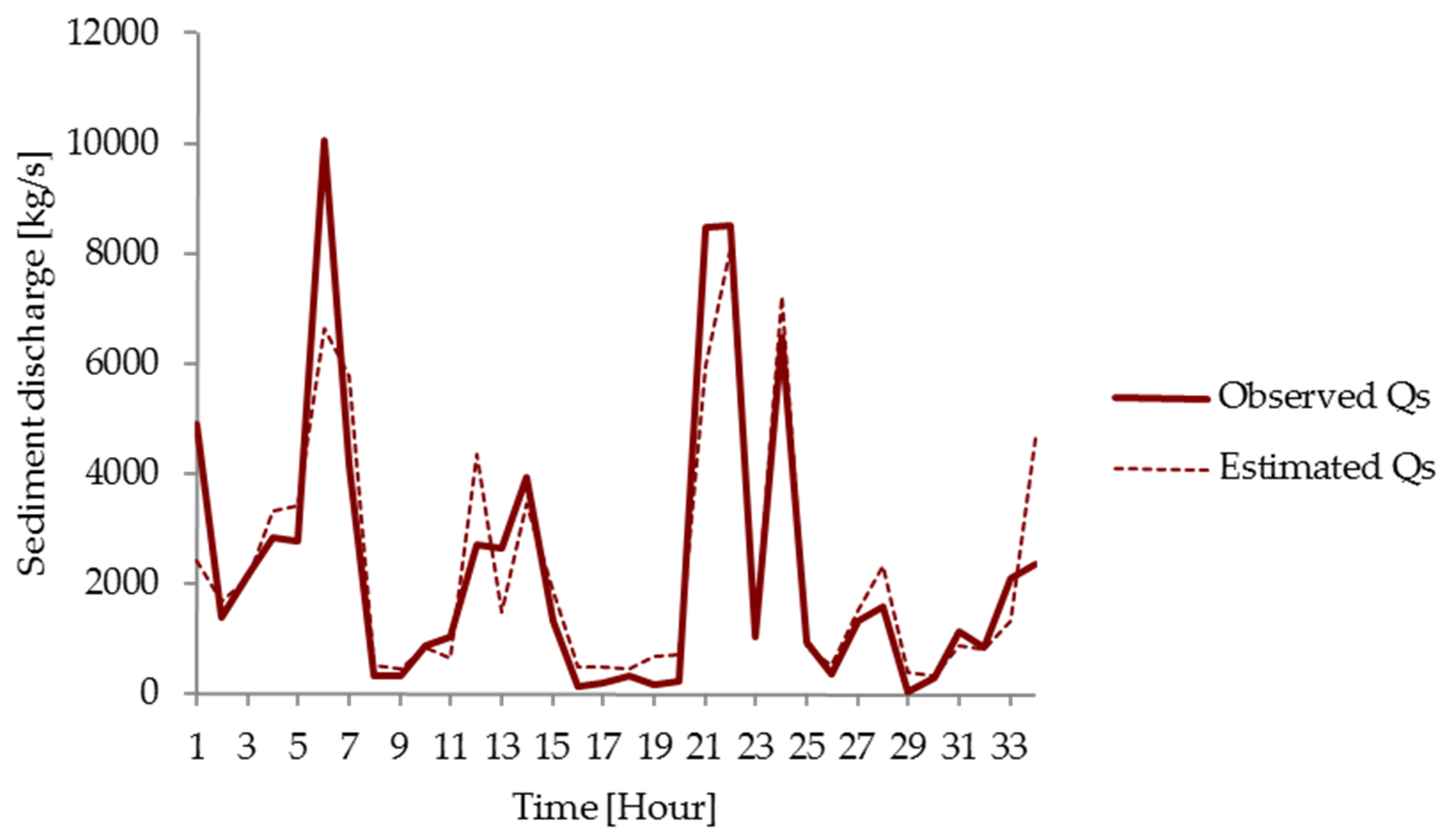
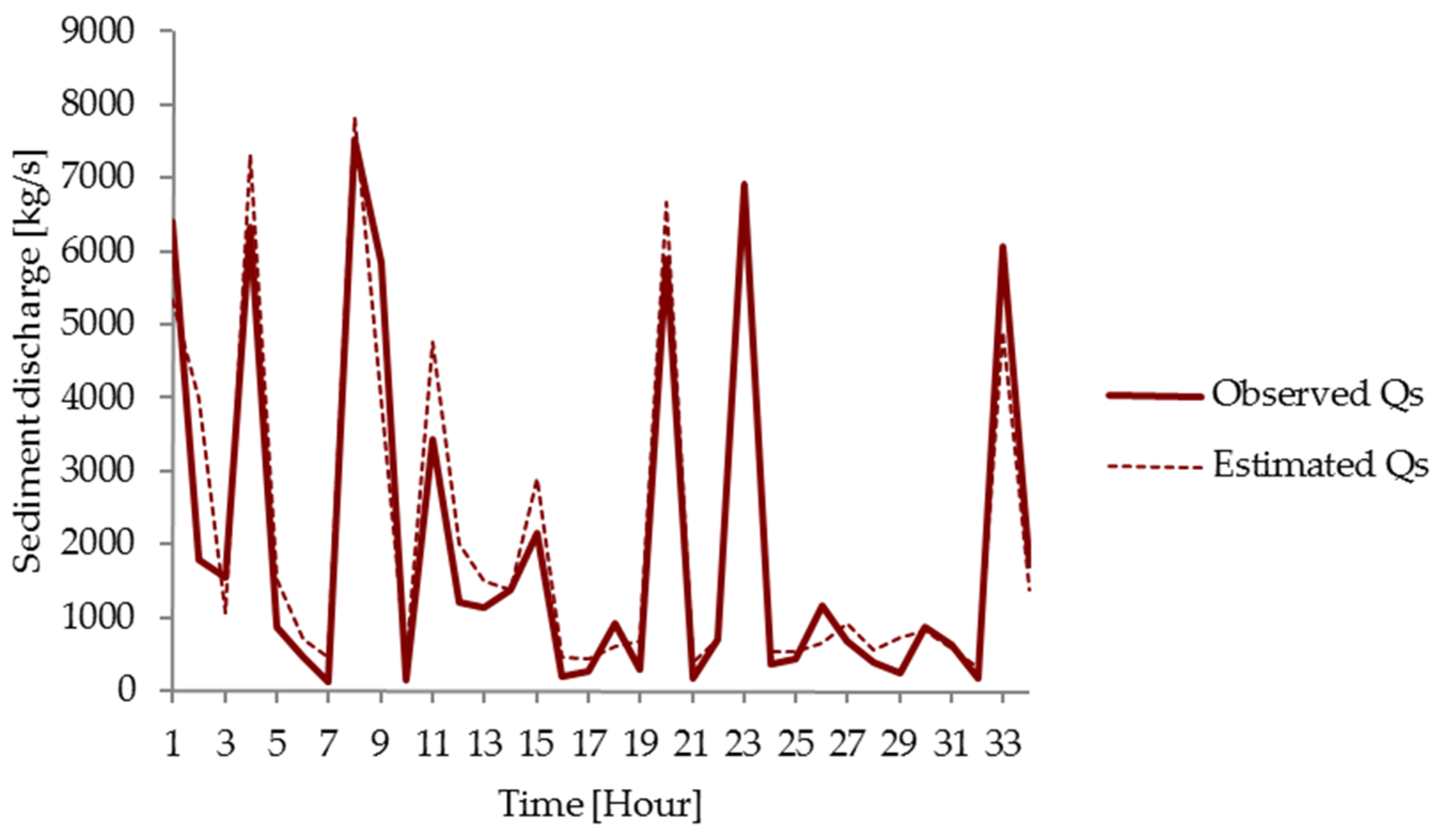
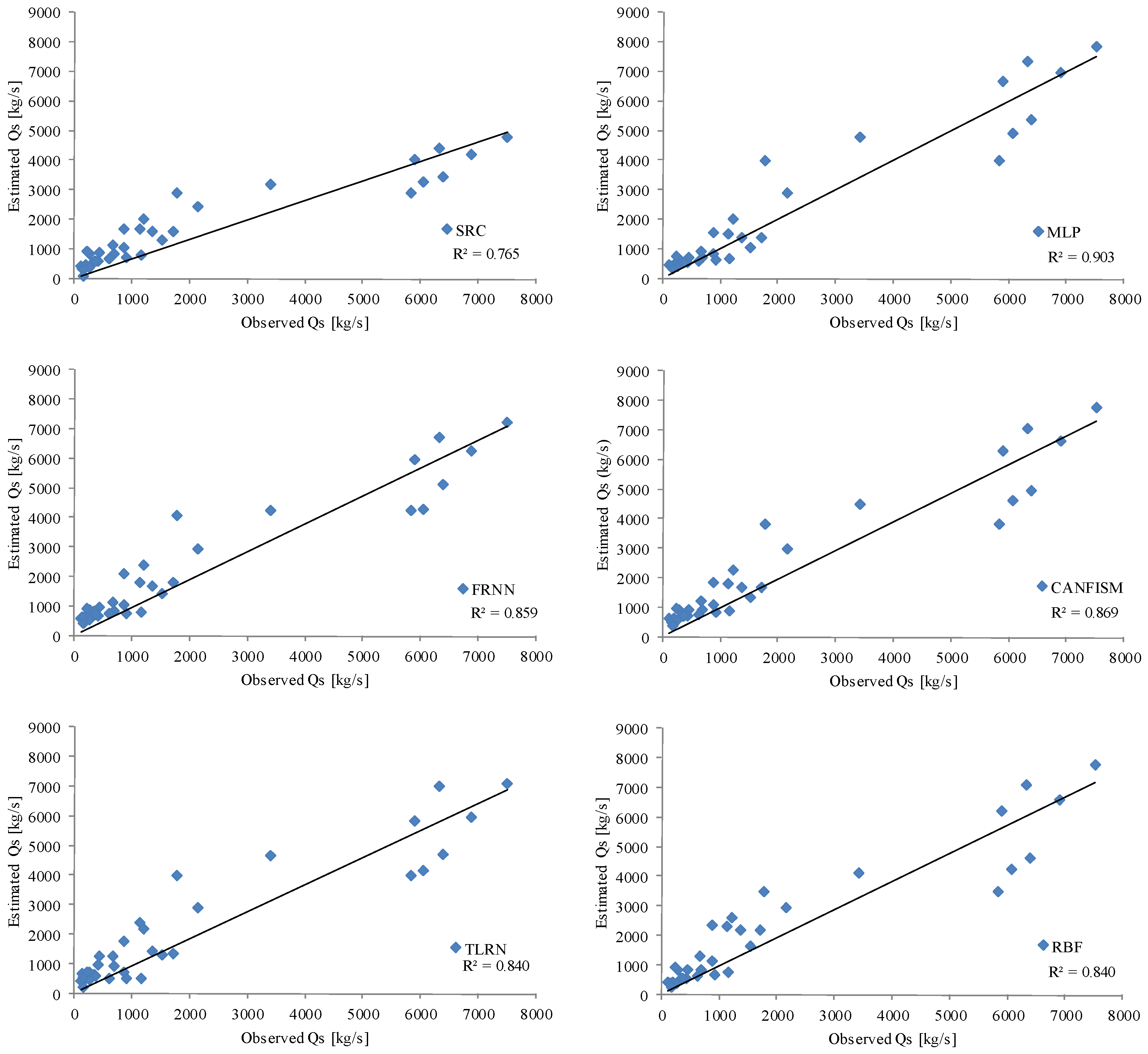
3.3. Comparison of Models
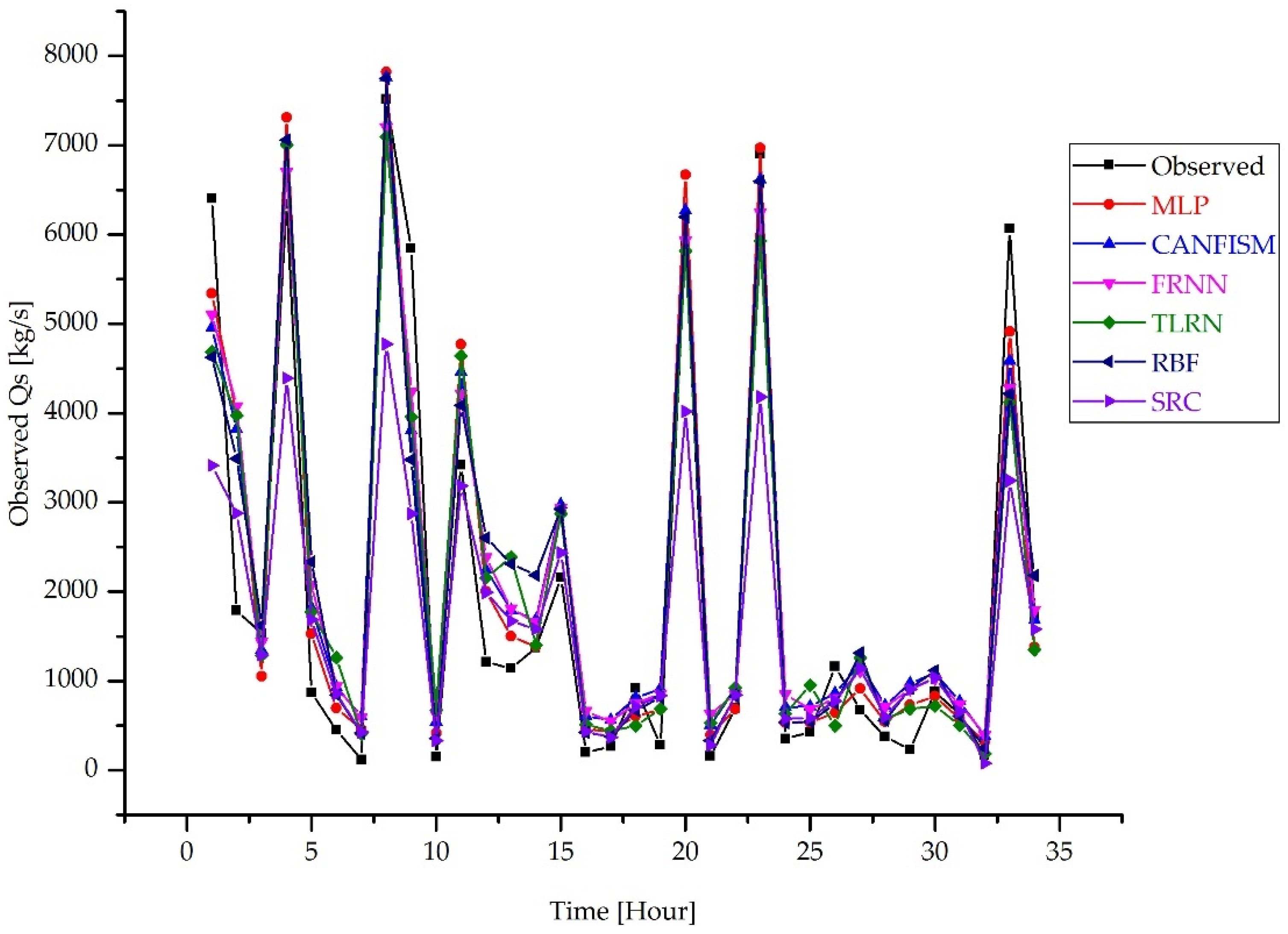
| Observed | MLP | CANFISM | FRNN | TLRN | RBF | SRC | Relative Error (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Kg/s) | MLP | CANFISM | FRNN | TLRN | RBF | SRC | ||||||
| 6402 | 5341 | 4954 | 5104 | 4689 | 4625 | 3414 | −17 | −23 | −20 | −27 | −28 | −47 |
| 6339 | 7312 | 7046 | 6701 | 7002 | 7062 | 4392 | 15 | 11 | 6 | 10 | 11 | −31 |
| 7520 | 7822 | 7760 | 7202 | 7095 | 7749 | 4775 | 4 | 3 | −4 | −6 | 3 | −37 |
| 3418 | 4768 | 4461 | 4218 | 4641 | 4087 | 3186 | 39 | 31 | 23 | 36 | 20 | −7 |
| 2160 | 2901 | 2977 | 2932 | 2872 | 2923 | 2437 | 34 | 38 | 36 | 33 | 35 | 13 |
| 5904 | 6671 | 6271 | 5936 | 5815 | 6197 | 4017 | 13 | 6 | 1 | -2 | 5 | −32 |
| 6904 | 6969 | 6616 | 6243 | 5927 | 6595 | 4180 | 1 | −4 | −10 | −14 | −4 | −39 |
| 6065 | 4915 | 4584 | 4280 | 4123 | 4216 | 3244 | −19 | −24 | −29 | −32 | −30 | −47 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, S.L.; Zhang, G.A.; Young, S.L.; Shi, J.Z. Temporal variations of fine suspended sediment concentration in the Changjiang River estuary and adjacent coastal waters, China. J. Hydrol. 2006, 331, 137–145. [Google Scholar] [CrossRef]
- Wang, Y.M.; Tfwala, S.S.; Chan, H.C.; Lin, Y.C. The effects of sporadic torrential rainfall events on suspended sediments. Arch. Sci. J. 2013, 66, 211–224. [Google Scholar]
- Teng, W.-H.; Hsu, M.-H.; Wu, C.-H.; Chen, A.S. Impact of flood disasters on taiwan in the last quarter century. Nat. Hazards 2006, 37, 191–207. [Google Scholar] [CrossRef]
- Milliman, J.D.; Syvitski, J.P. Geomorphic/tectonic control of sediment discharge to the ocean: The importance of small mountainous rivers. J. Geol. 1992, 525–544. [Google Scholar] [CrossRef]
- Horowitz, A.J. An evaluation of sediment rating curves for estimating suspended sediment concentrations for subsequent flux calculations. Hydrol. Process. 2003, 17, 3387–3409. [Google Scholar] [CrossRef]
- Thomas, R.B. Estimating total suspended sediment yield with probability sampling. Water Resour. Res. 1985, 21, 1381–1388. [Google Scholar] [CrossRef]
- Wang, Y.M.; Traore, S. Time-lagged recurrent network for forecasting episodic event suspended sediment load in typhoon prone area. Int. J. Phys. Sci. 2009, 4, 519–528. [Google Scholar]
- Chen, S.M.; Wang, Y.M.; Tsou, I. Using artificial neural network approach for modelling rainfall–runoff due to typhoon. J. Earth Syst. Sci. 2013, 122, 399–405. [Google Scholar] [CrossRef]
- Tfwala, S.S.; Wang, Y.M.; Lin, Y.C. Prediction of missing flow records using multilayer perceptron and coactive neurofuzzy inference system. Sci. World J. 2013, 2013, 584516. [Google Scholar] [CrossRef] [PubMed]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Kisi, O. Generalized regression neural networks for evapotranspiration modelling. Hydrol. Sci. J. 2006, 51, 1092–1105. [Google Scholar] [CrossRef]
- Wang, Y.M.; Traore, S.; Kerh, T. Computing and modelling for crop yields in burkina faso based on climatic data information. WSEAS Trans. Inf. Sci. Appl. 2008, 5, 832–842. [Google Scholar]
- Lin, J.Y.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Leahy, P.; Kiely, G.; Corcoran, G. Structural optimisation and input selection of an artificial neural network for river level prediction. J. Hydrol. 2008, 355, 192–201. [Google Scholar] [CrossRef]
- Martens, J.; Sutskever, I. Learning recurrent neural networks with hessian free optimization. In Proceedings of the 28th International Conference on Machine Learning, Belluvue, WA, USA, 28 June–2 July 2011.
- Wang, Y.M.; Kerh, T.; Traore, S. Neural network approach for modelling river suspended sediment concentration due to tropical storms. Glob. NEST J. 2009, 11, 457–466. [Google Scholar]
- Maraqa, M.; Abu-Zaiter, R. Recognition of Arabic Sign Language (ArSL) using recurrent neural networks. In Proceedings of the First International Conference on the Applications of Digital Information and Web Technologies, 2008—ICADIWT 2008, 4–6 August 2008; pp. 478–481.
- Feyzolahpour, M. Estimating suspended sediment concentration using neural differential evolution (NDE), multi layer perceptron (MLP) and radial basis function (RBF) models. Int. J. Phys. Sci. 2012, 7, 5106–5177. [Google Scholar] [CrossRef]
- Wang, Y.M.; Traore, S.; Kerh, T.; Leu, J.-M. Modelling reference evapotranspiration using feed forward backpropagation algorithm in arid regions of Africa. Irrig. Drain. 2011, 60, 404–417. [Google Scholar] [CrossRef]
- Kim, S.; Park, K.B.; Seo, Y.M. Estimation of pan evaporation using neural networks and climate-based models. Disaster Adv. 2012, 5, 34–43. [Google Scholar]
- Suditu, G.D.; Piuleac, C.G.; Bulgariu, L.; Curteanu, S. Application of a neuro-genetic technique in the optimization of heavy metals removal from wastewaters for environmental risk reduction. Environ. Eng. Manag. J. 2013, 12, 167–174. [Google Scholar]
- Charaniya, N.A.; Dudul, S.V. Time lag recurrent neural network model for rainfall prediction using El Niño indices. Int. J. Sci. Res. Publ. 2013, 3, 1–5. [Google Scholar]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Sandberg, I. Universal approximation using radial-basis-function networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef]
- Coulibaly, P.; Evora, N.D. Comparison of neural network methods for infilling missing daily weather records. J. Hydrol. 2007, 341, 27–41. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Abghari, H. Utility of coactive neuro-fuzzy inference system for pan evaporation modeling in comparison with multilayer perceptron. Meteorol. Atmos. Phys. 2012, 116, 147–154. [Google Scholar] [CrossRef]
- Wang, Y.M.; Lin, C.P.; Tfwala, S.S.; Chen, C.N.; Chi, T.H. Predicting airport visibility using back propagation neural network. Jokull 2014, 64, 77–90. [Google Scholar]
- Lin, C.C. Partitioning capabilities of multilayer perceptions on nested rectangular decision regions part I: Algorithm. WSEAS Trans. Inf. Sci. Appl. 2006, 3, 1674–1681. [Google Scholar]
- Boukhrissa, Z.A.; Khanchoul, K.; Le Bissonnais, Y.; Tourki, M. Prediction of sediment load by sediment rating curve and neural network (ANN) in El Kebir catchment, Algeria. J. Earth Syst. Sci. 2013, 122, 1303–1312. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tfwala, S.S.; Wang, Y.-M. Estimating Sediment Discharge Using Sediment Rating Curves and Artificial Neural Networks in the Shiwen River, Taiwan. Water 2016, 8, 53. https://doi.org/10.3390/w8020053
Tfwala SS, Wang Y-M. Estimating Sediment Discharge Using Sediment Rating Curves and Artificial Neural Networks in the Shiwen River, Taiwan. Water. 2016; 8(2):53. https://doi.org/10.3390/w8020053
Chicago/Turabian StyleTfwala, Samkele S., and Yu-Min Wang. 2016. "Estimating Sediment Discharge Using Sediment Rating Curves and Artificial Neural Networks in the Shiwen River, Taiwan" Water 8, no. 2: 53. https://doi.org/10.3390/w8020053
APA StyleTfwala, S. S., & Wang, Y.-M. (2016). Estimating Sediment Discharge Using Sediment Rating Curves and Artificial Neural Networks in the Shiwen River, Taiwan. Water, 8(2), 53. https://doi.org/10.3390/w8020053







