A Two-Step Approach for Analytical Optimal Hedging with Two Triggers
Abstract
:1. Introduction
2. Methods
2.1. Analytical Optimal Hedging Rule with Two Triggers (AOHR-TT)
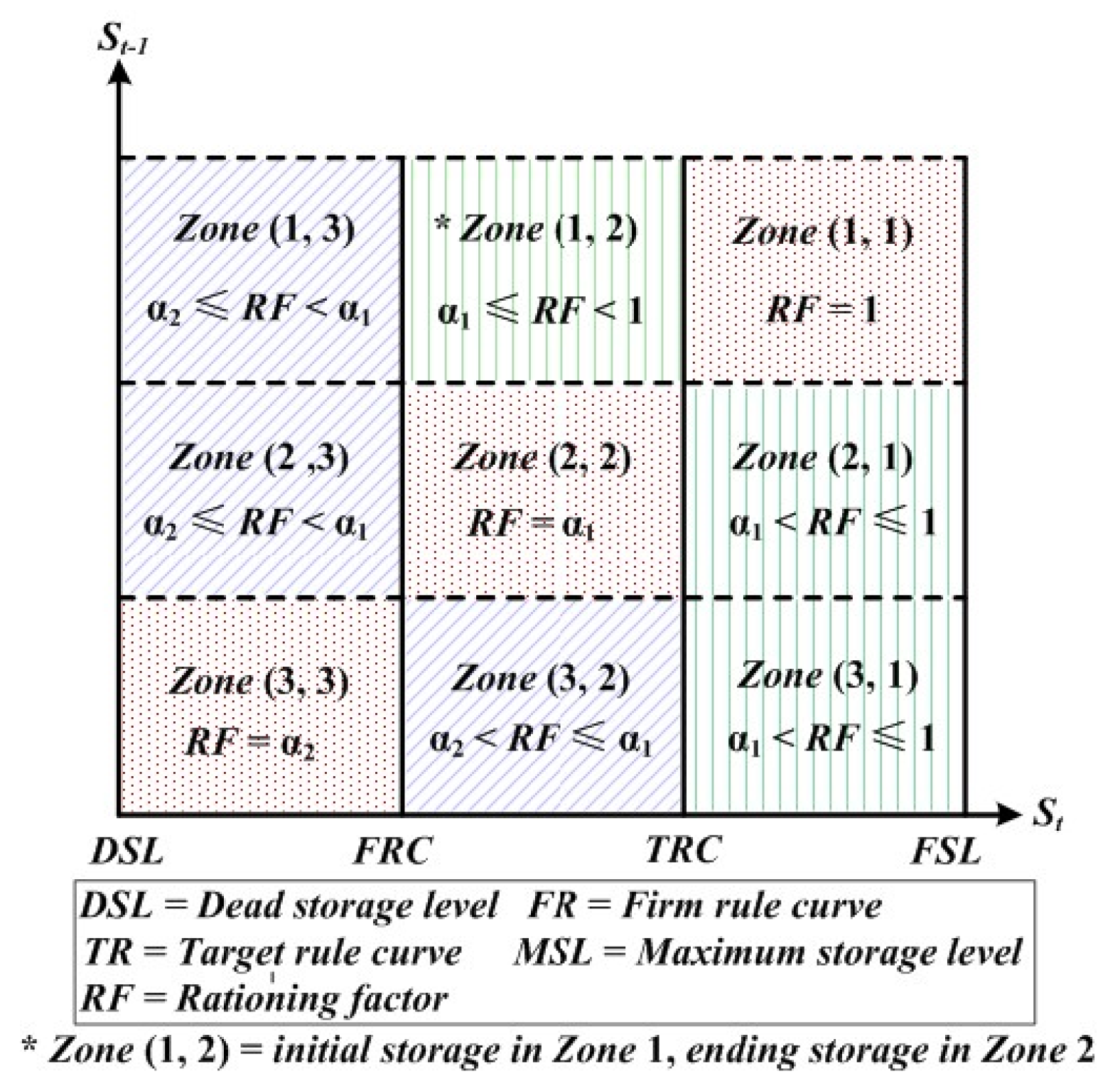
2.1.1. Mathematical Programming Model for the AOHR-TT
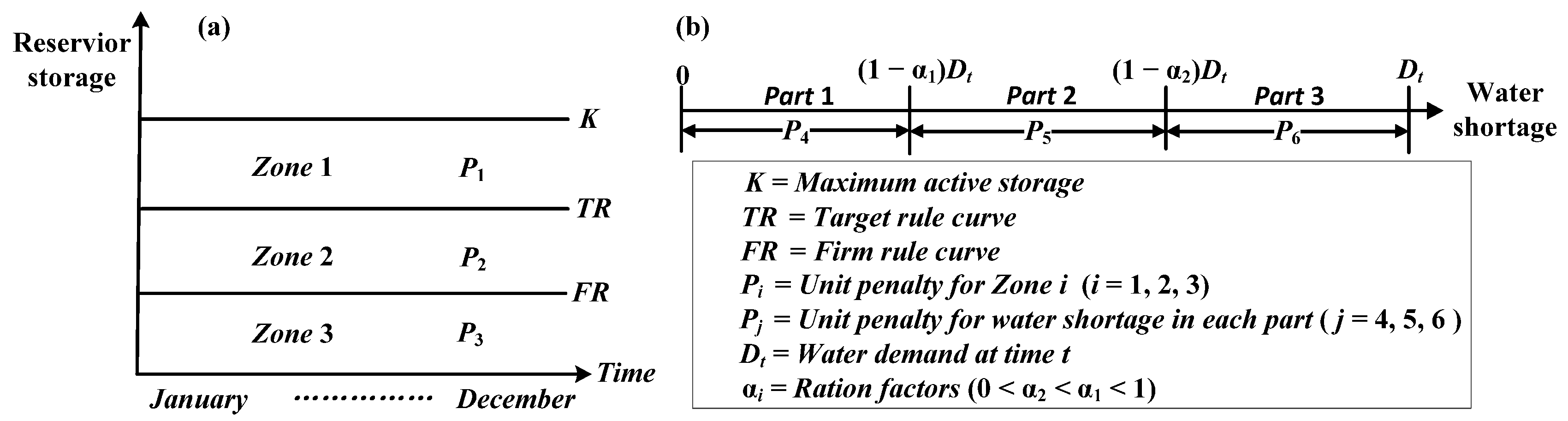
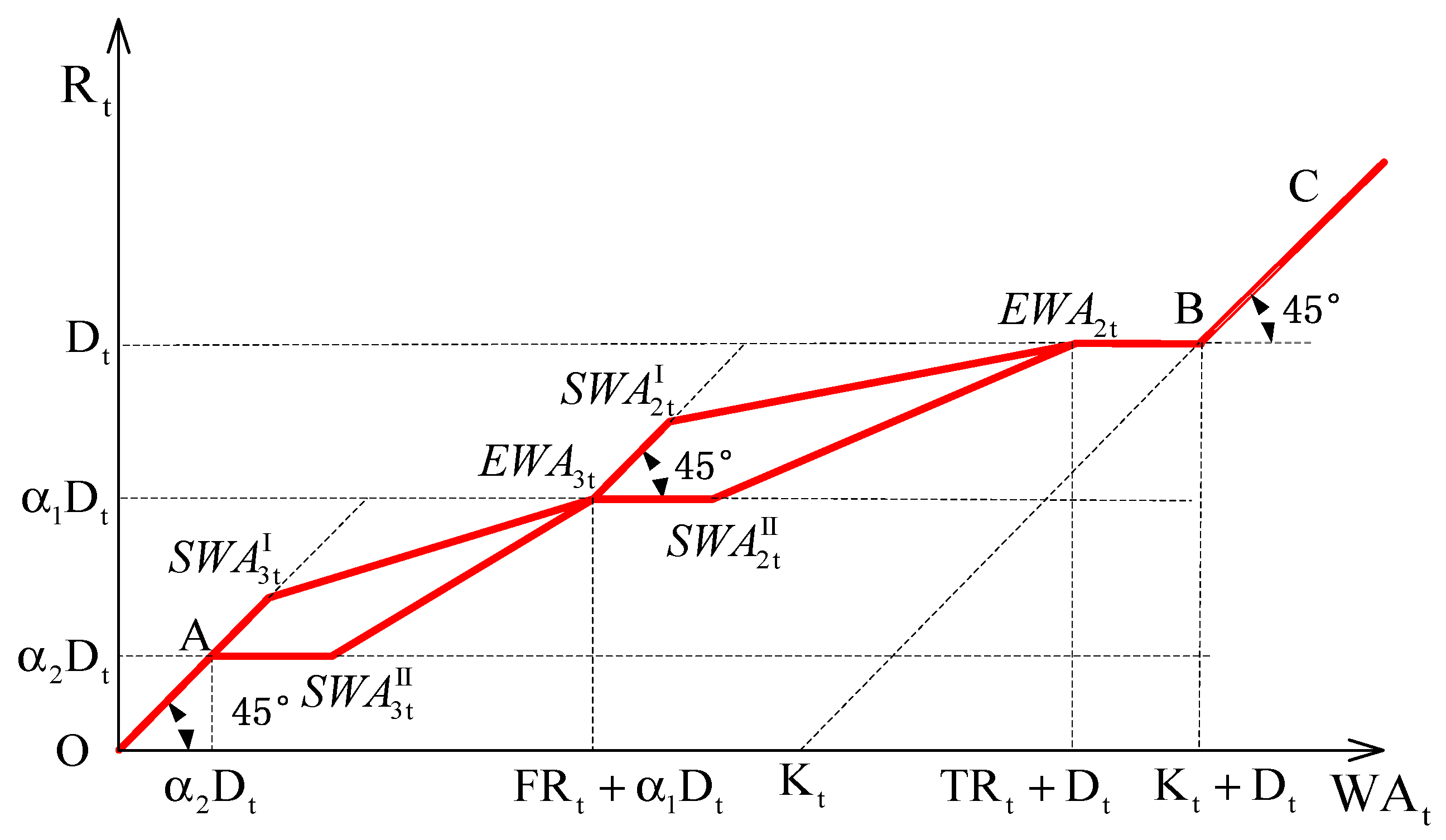
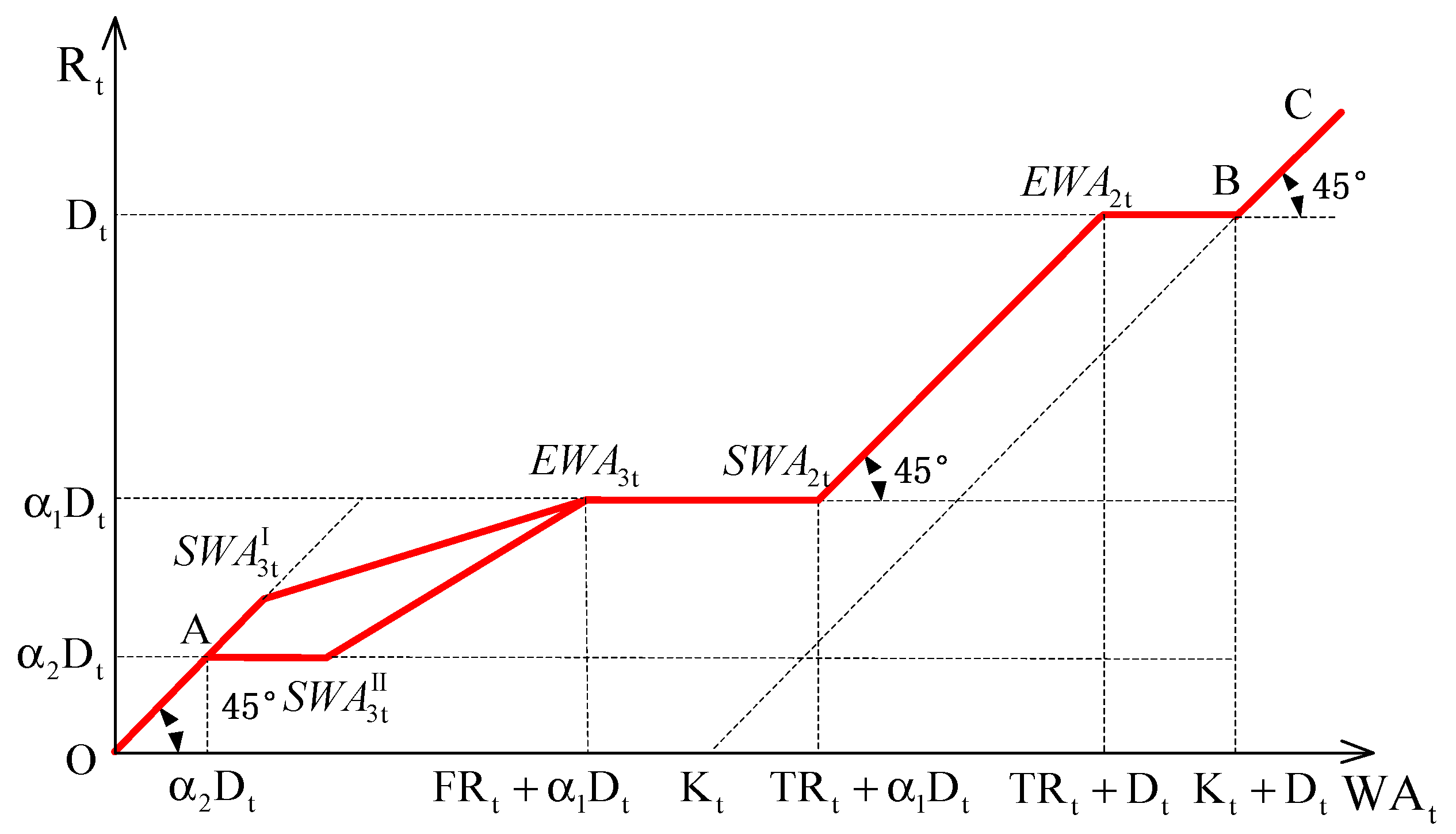
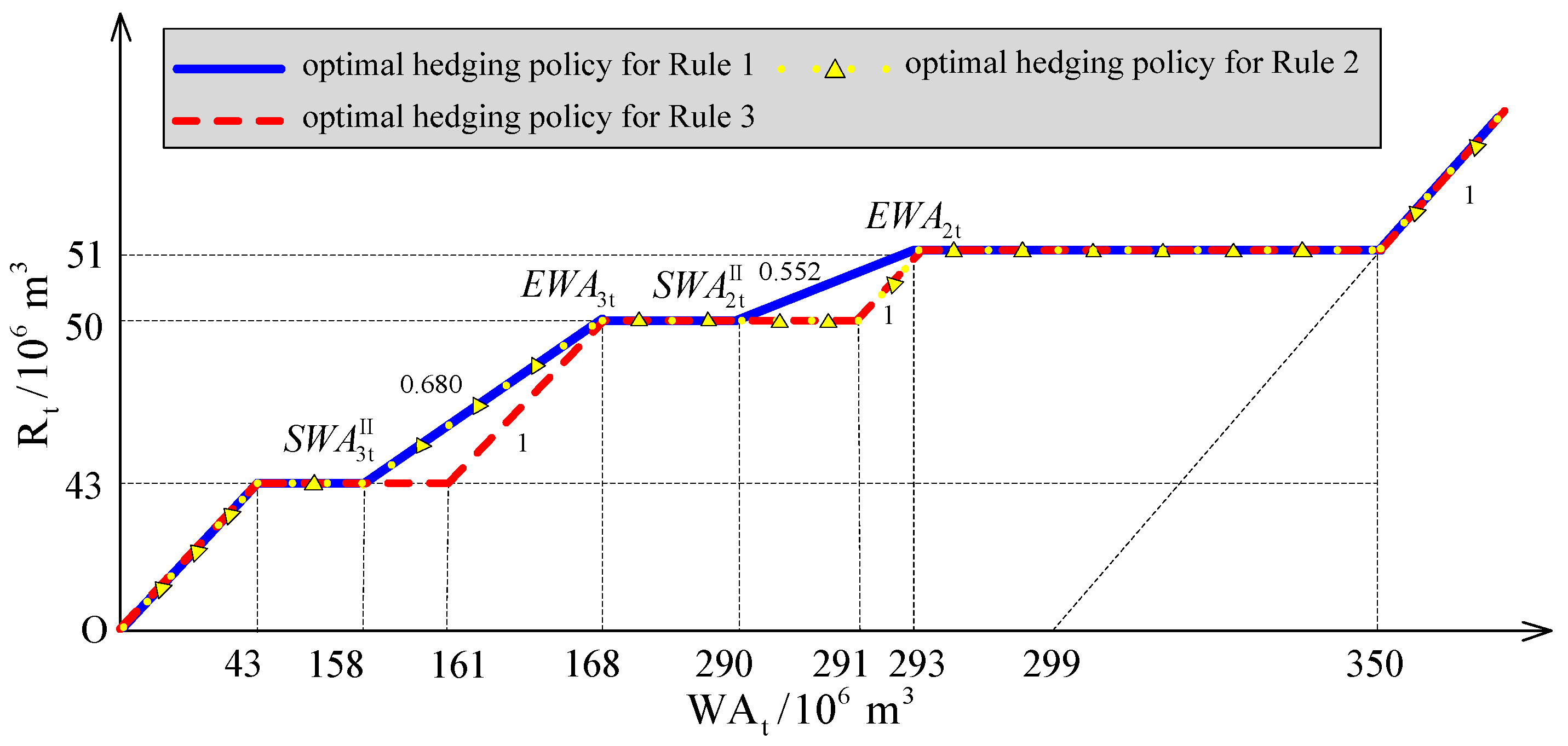
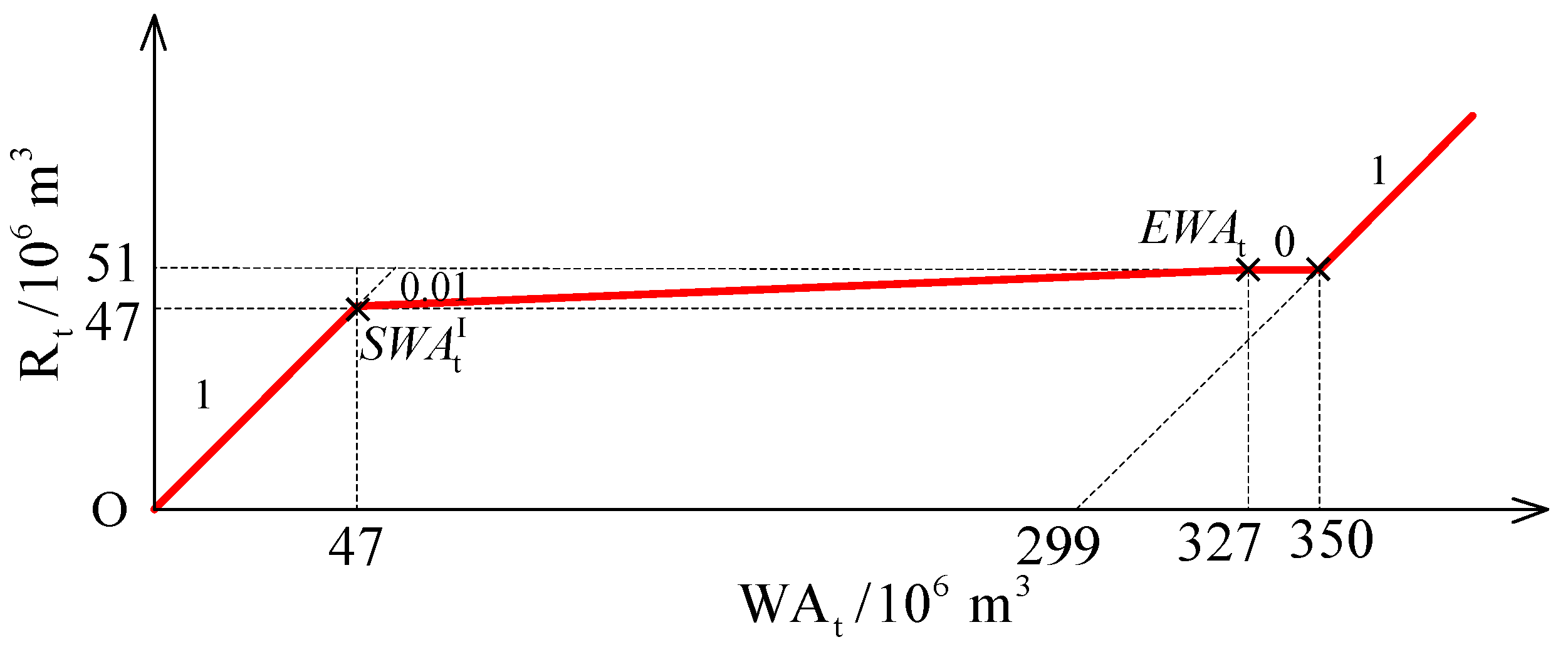
2.1.2. Model Solution and Analysis
- (1)
- Rule 1: is located in Zone 1, which corresponds to normal conditions, i.e.,
- (2)
- Rule 2: is located in Zone 2, which corresponds to drought conditions, i.e.,
- (3)
- Rule 3: is located in Zone 3, which corresponds to severe drought conditions, i.e.,
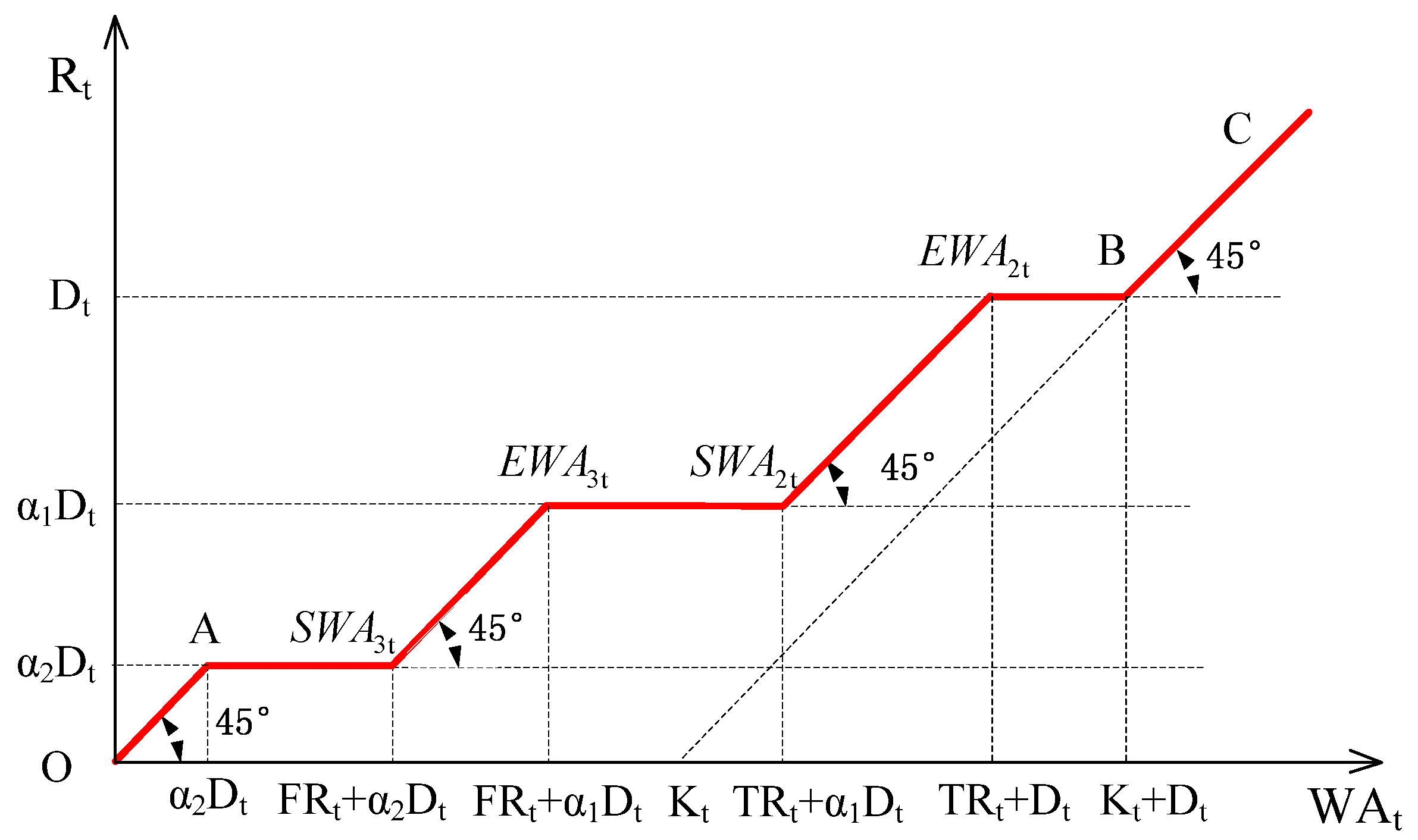
2.2. Formulation of the Optimization-Simulation Model for the AOHR-TT
2.2.1. Optimization Model
Optimization Objective
System Constraints
Method of Solution
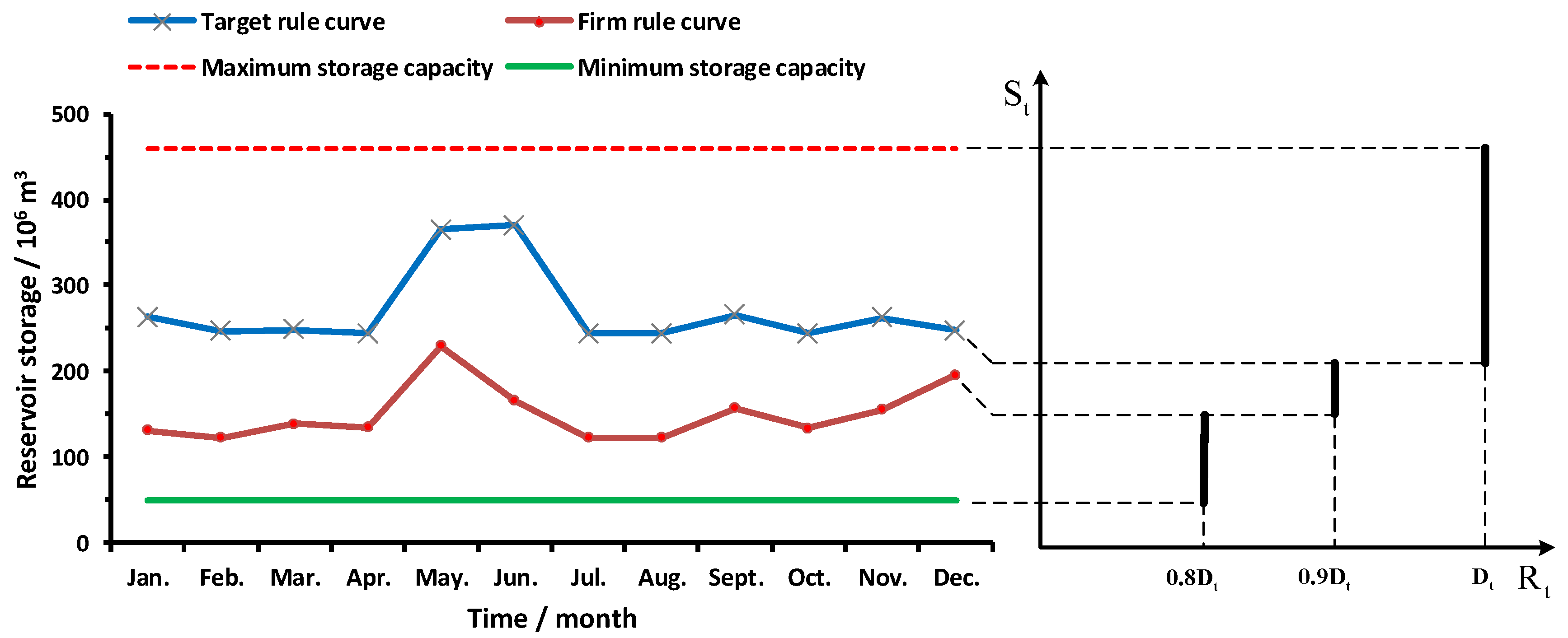
2.2.2. Simulation Model
- (1)
- According to the relationship between the initial storage level and the present level of the rule curves, the hedging sub-rule in the AOHR-TT is triggered first. Then, the current release is obtained based on the current water availability.
- (2)
- The ending reservoir storage level in the current period is then obtained by the water balance equation, and it is used to determine which hedging sub-rule is triggered in the next period. At the end of this step, the simulation procedure returns to step (1).
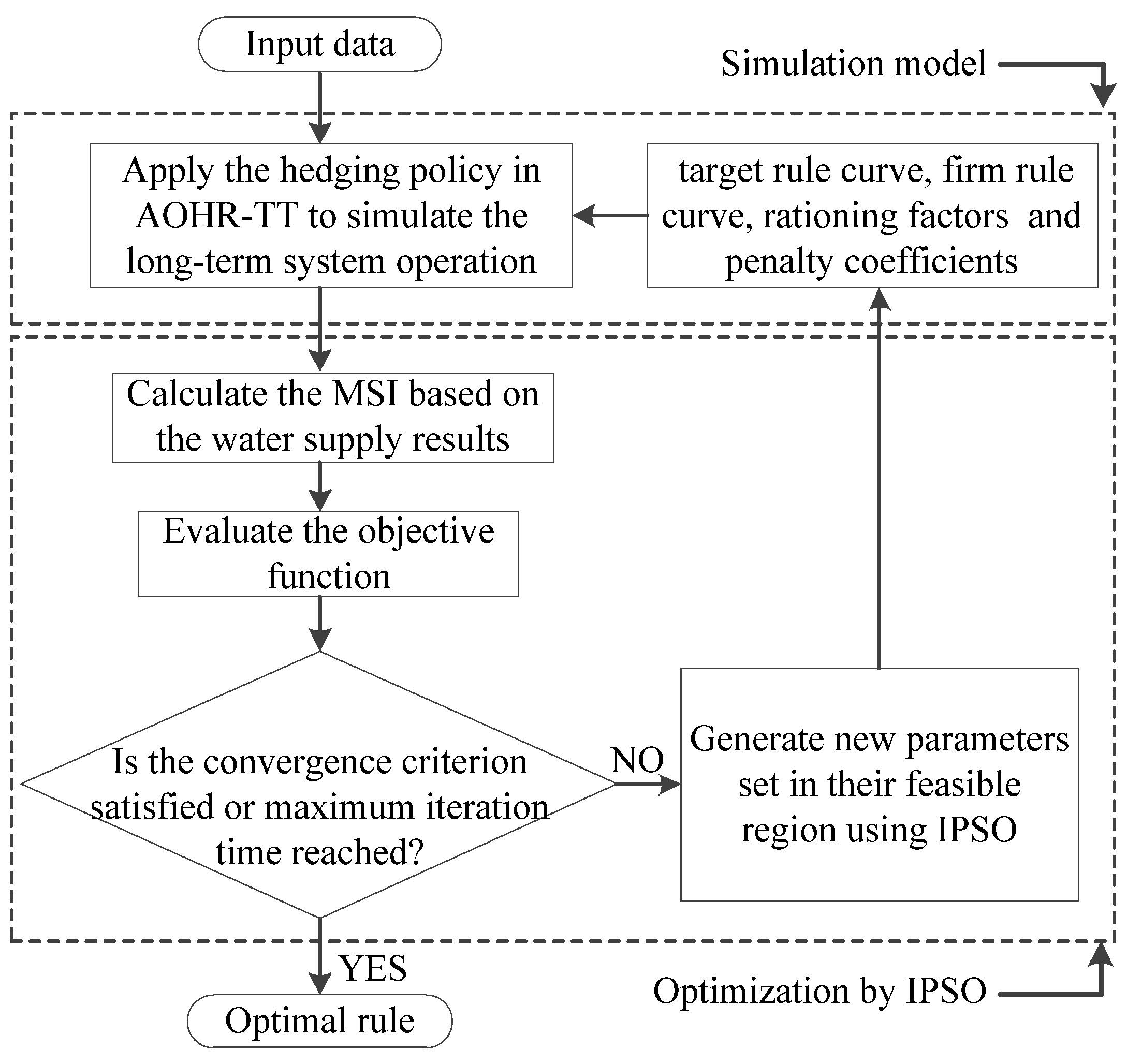
3. Study Area and Scenario Design
3.1. Study Area
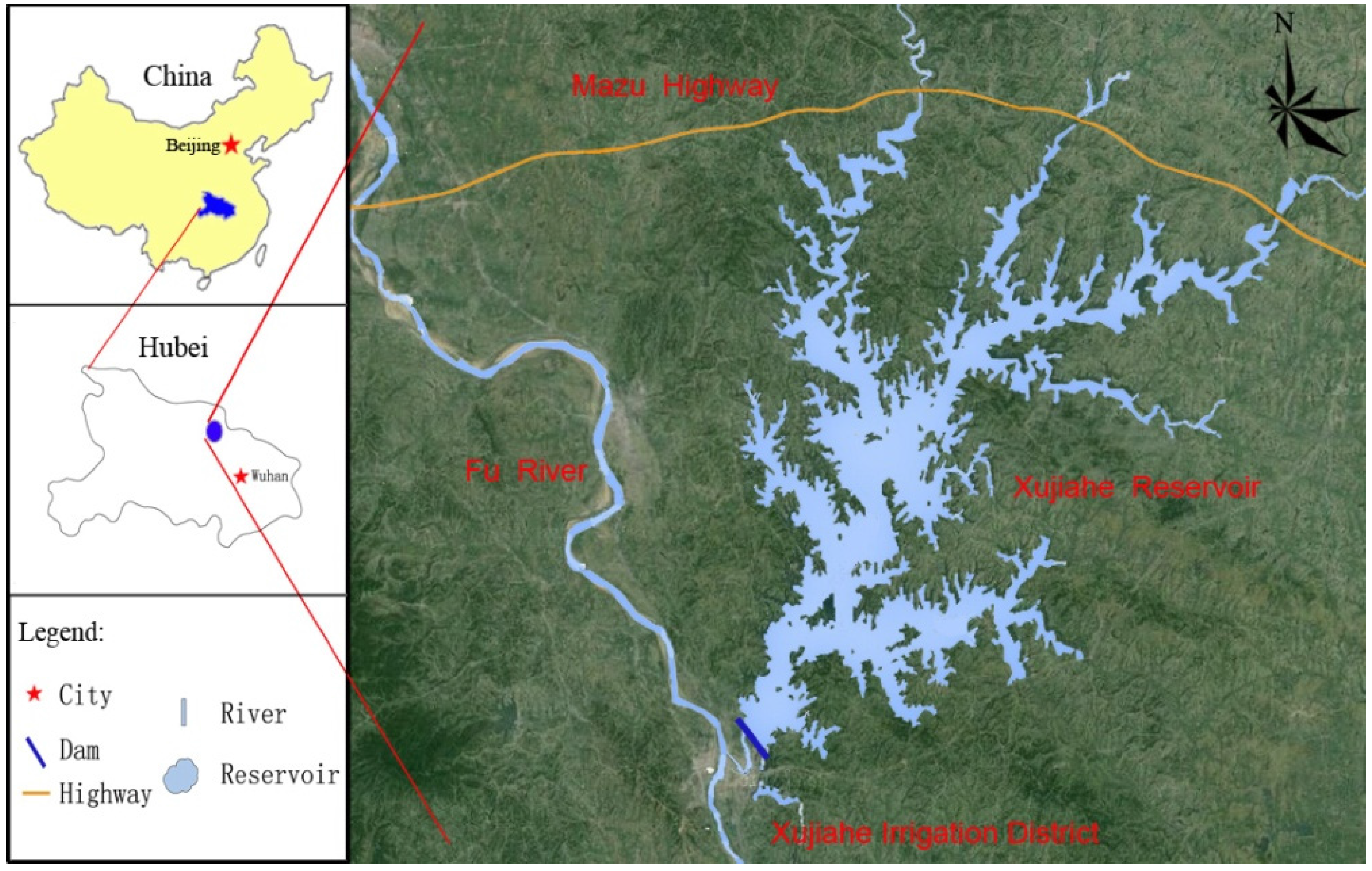
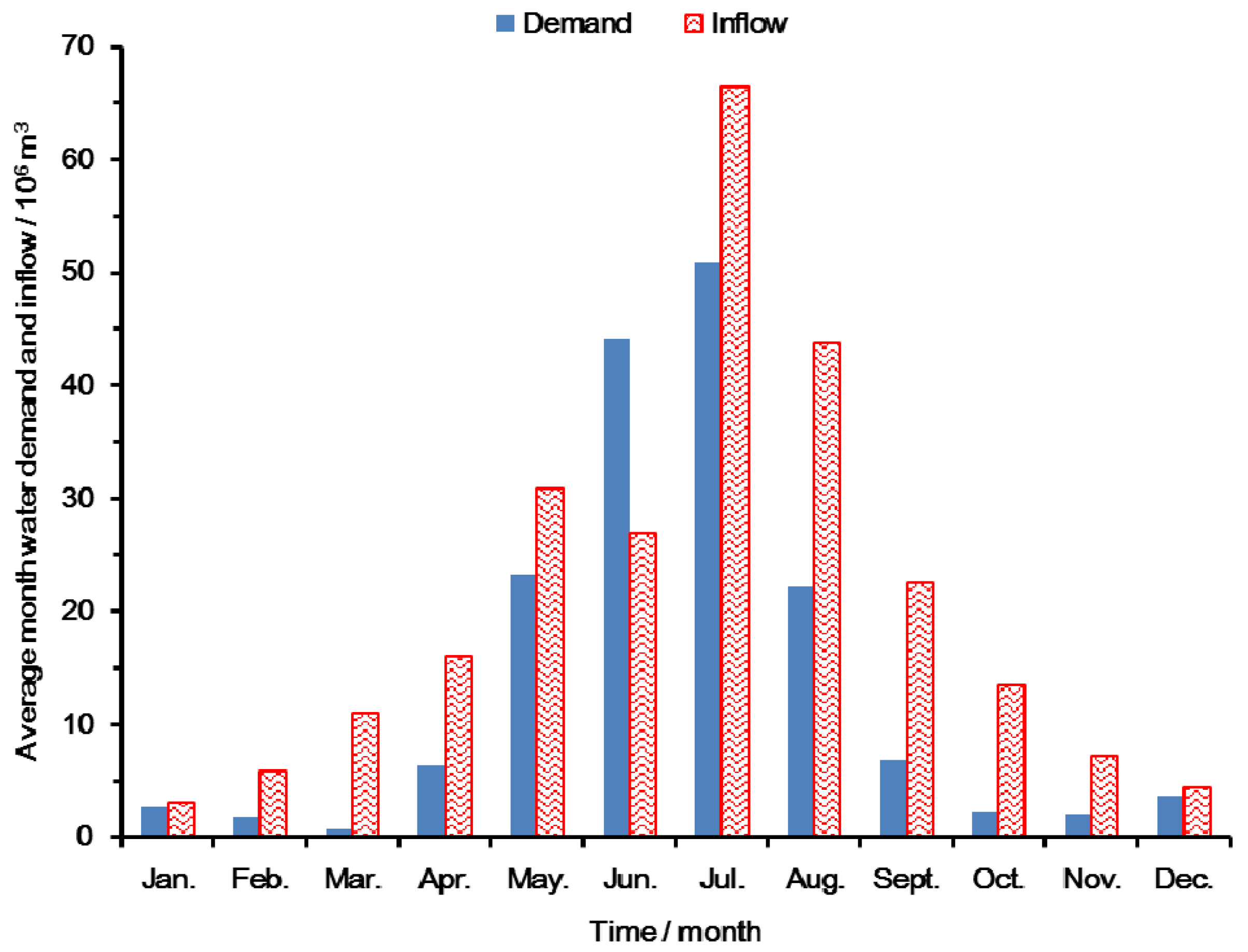
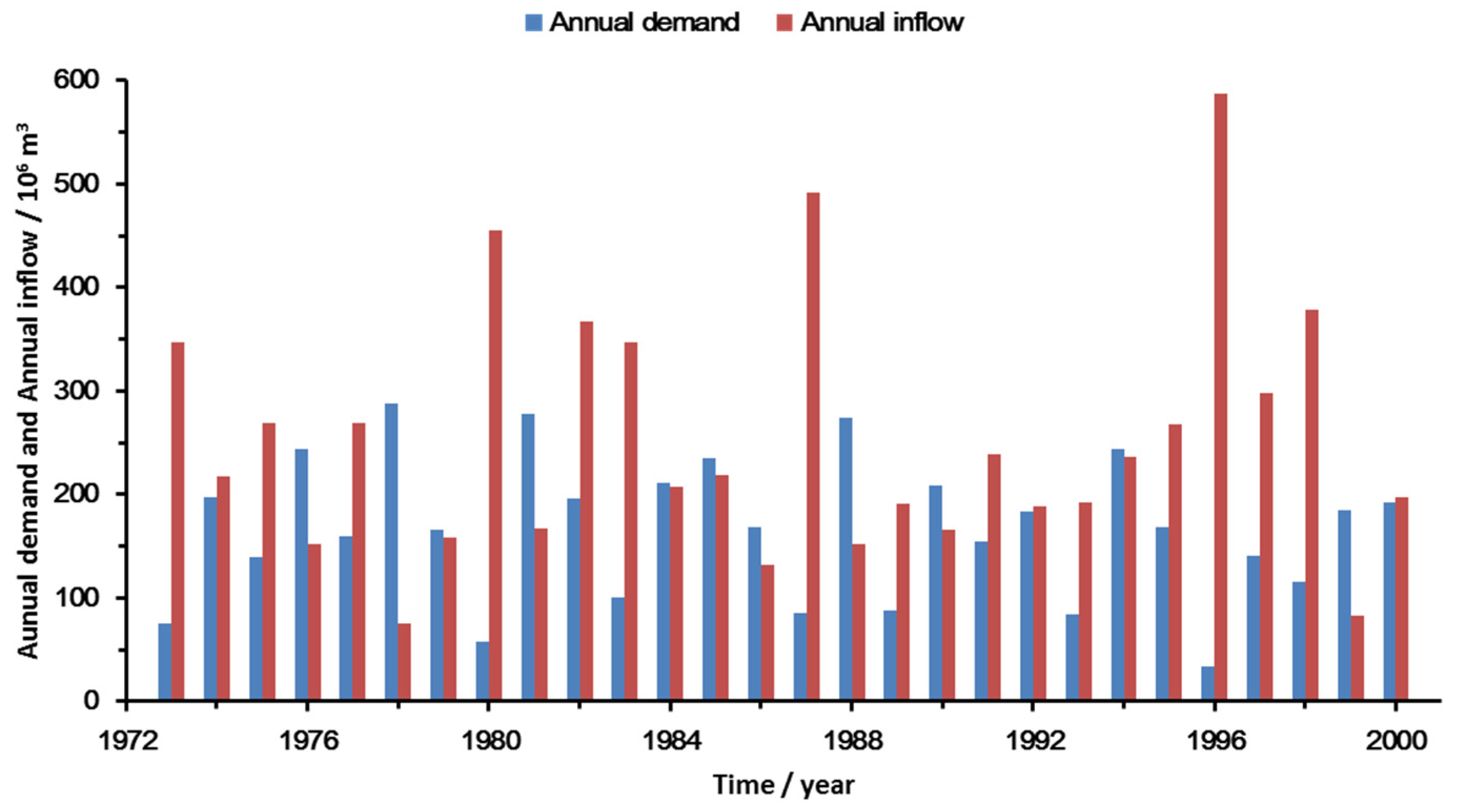
3.2. Scenario Design
3.3. Evaluation Criteria
4. Results and Discussion
4.1. Analysis of Rule Curves in the Proposed Rule
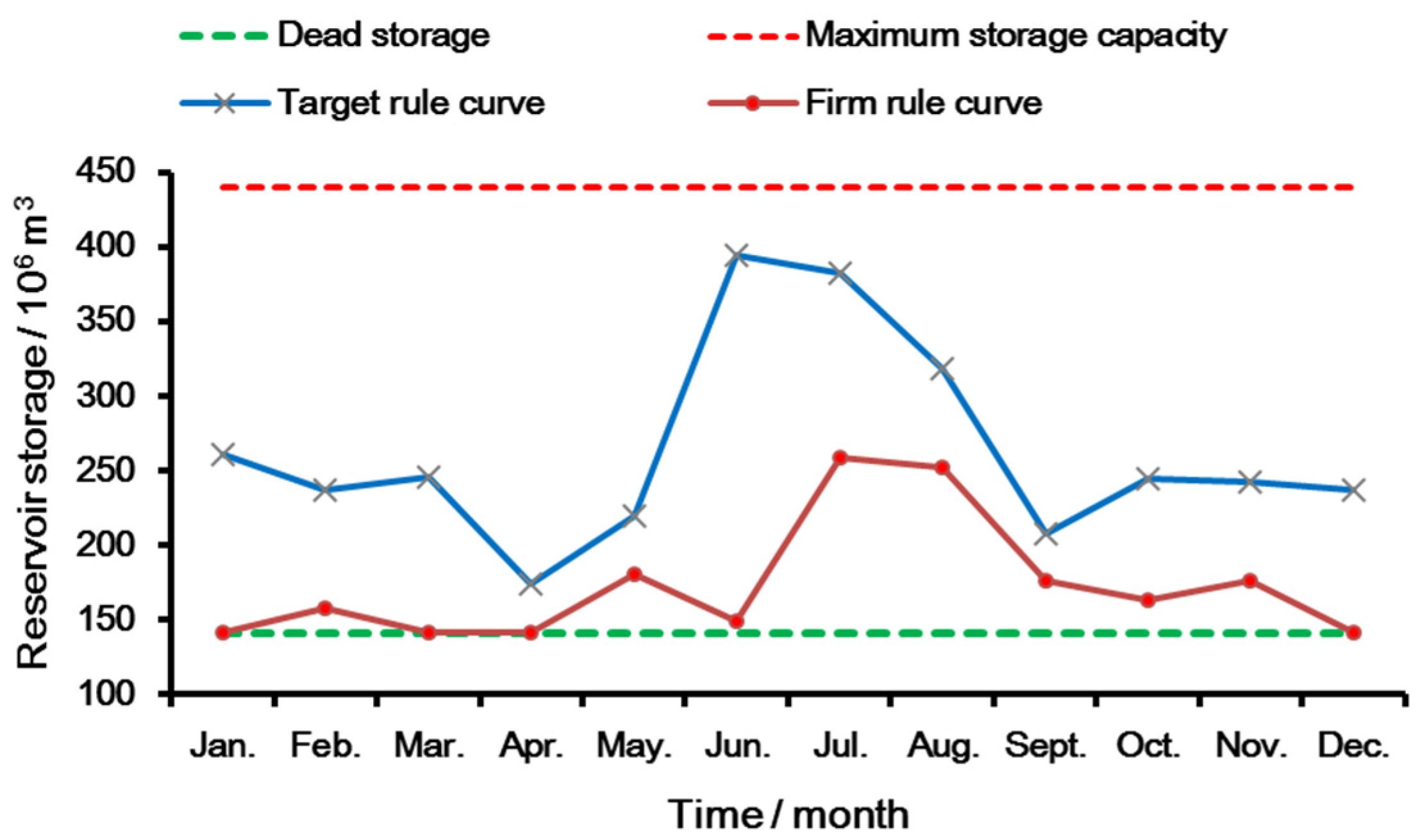
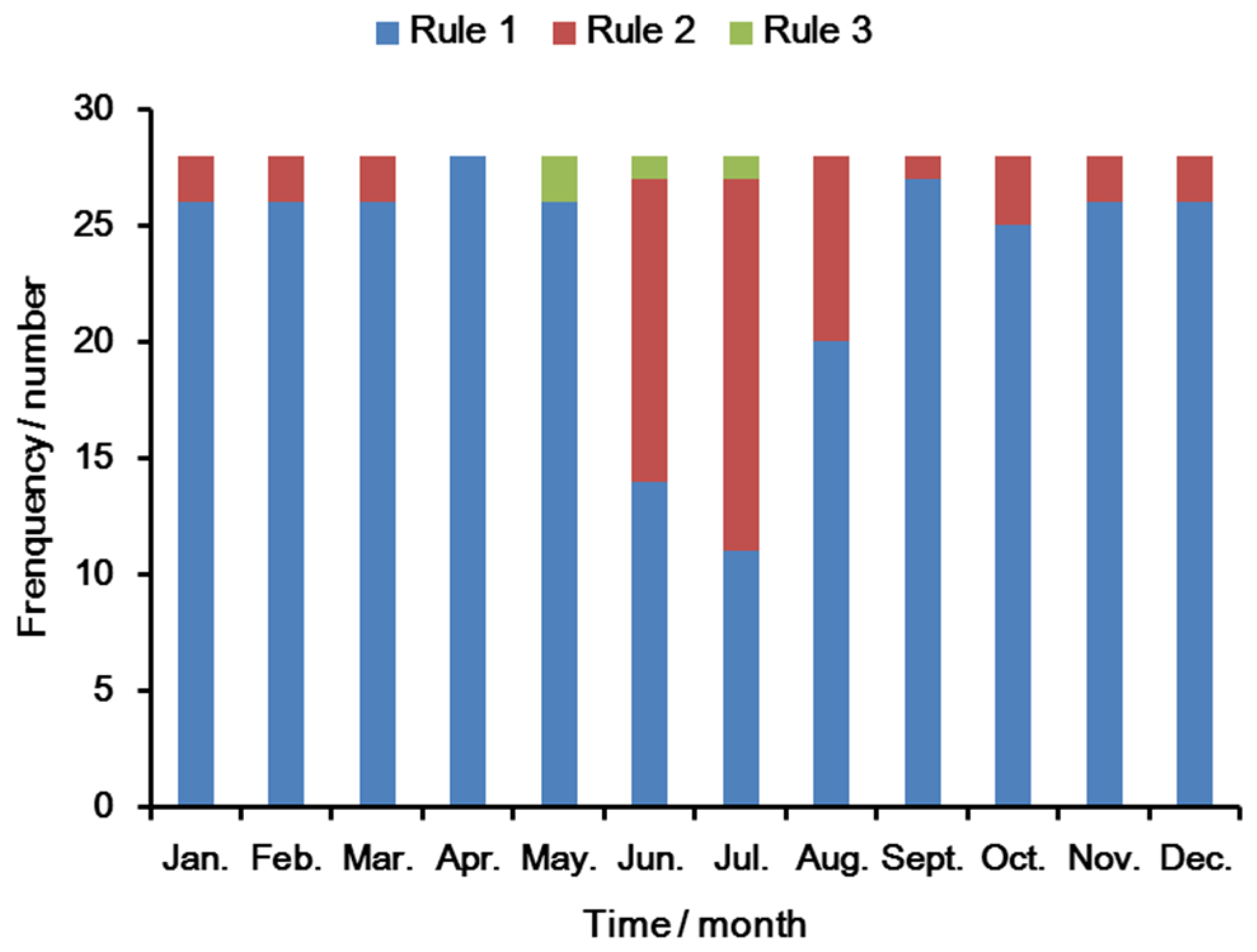
4.2. Comparison and Analysis of Operation Scenarios
4.2.1. Comparison and Analysis of the Operation Types
| Parameters | ||||||
|---|---|---|---|---|---|---|
| α1 | α2 | P1 | P2 | P3 | P4 | P5 |
| 0.973 | 0.838 | 50.0 | 67.9 | 144.9 | 55.1 | 68.1 |
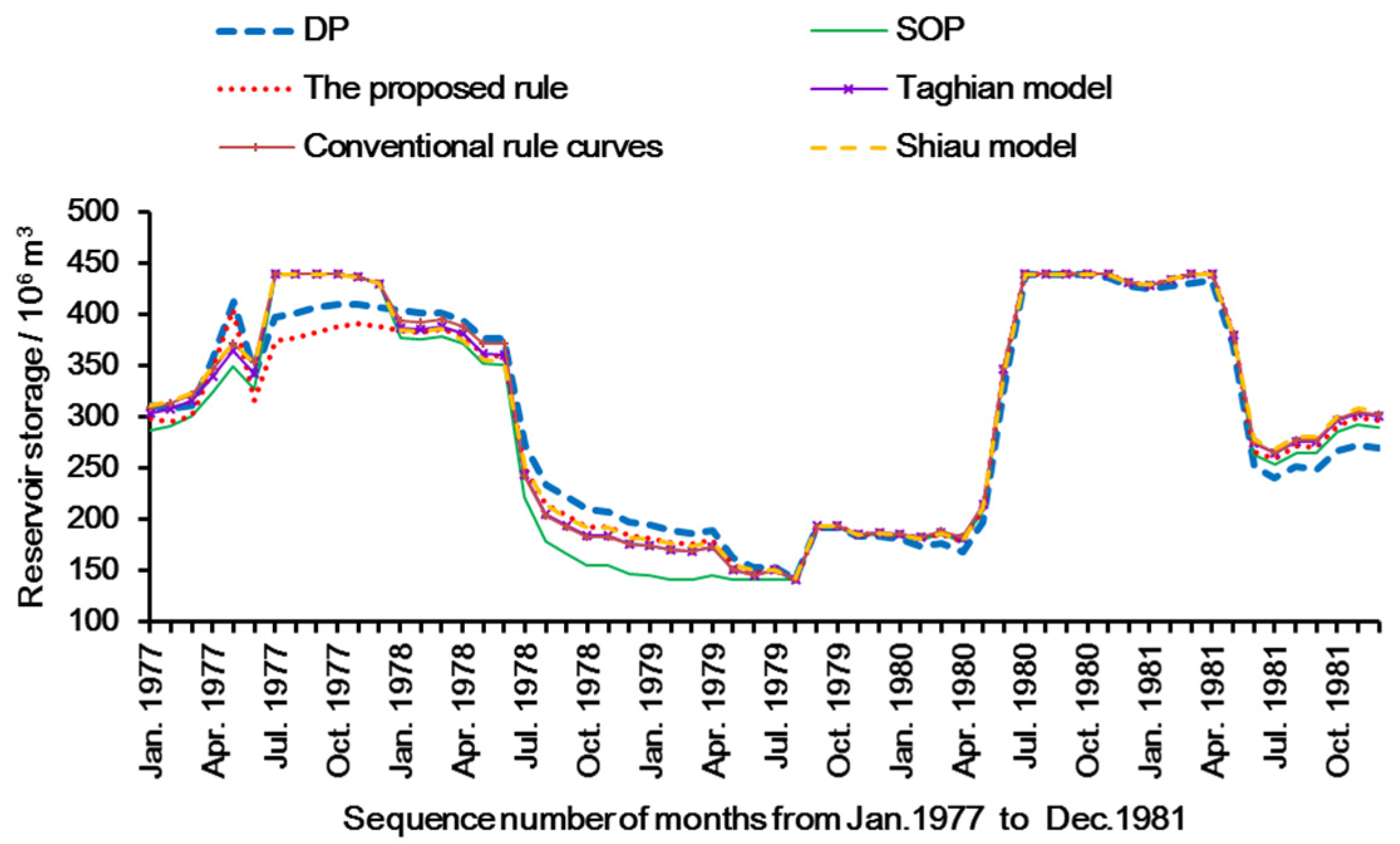
4.2.2. Comparison and Analysis of Long-Term Operation Results
| Indices | Scenarios | |||||
|---|---|---|---|---|---|---|
| SOP | Conventional Rule Curves | Shiau’s Method | Taghian’s Method | DP Model | Proposed Rule | |
| MSI | 0.5340 | 0.2470 | 0.0840 | 0.1563 | 0.0533 | 0.0695 |
| MSR | 100.00% | 20.00% | 19.94% | 20.00% | 19.68% | 16.22% |
| Reliability | 98.50% | 82.44% | 82.74% | 87.20% | 93.40% | 81.85% |
| Scenarios | Rationing Factors (RF) of the Scenarios | ||||
|---|---|---|---|---|---|
| RF = 0.8 | 0.8 < RF < 0.9 | RF = 0.9 | 0.9 < RF < 1 | RF = 1 | |
| Conventional Rule Curves | 2.38% | 0 | 15.18% | 0 | 82.44% |
| Shiau’s Method | 0 | 2.68% | 0 | 14.58% | 82.74% |
| Taghian’s Method | 1.49% | 0 | 0 | 11.31% | 87.20% |
| Proposed Rule | 0 | 2.08% | 0 | 15.77% | 81.85% |
4.2.3. Comparison and Analysis of Critical-Period Operation Results
| Years | Indices | Scenarios | ||||
|---|---|---|---|---|---|---|
| SOP | Conventional Rule Curves | Shiau’s Method | Taghian’s Method | Proposed Rule | ||
| 1977 | MSI | 0.0000 | 0.1667 | 0.0014 | 0.1464 | 0.0125 |
| MSR | 0.00% | 10.00% | 1.29% | 9.37% | 2.74% | |
| Reliability | 100.00% | 83.33% | 91.67% | 83.33% | 83.33% | |
| 1978 | MSI | 0.0000 | 1.0833 | 0.4698 | 0.4393 | 0.4591 |
| MSR | 0.00% | 20.00% | 19.94% | 9.37% | 16.04% | |
| Reliability | 100% | 41.67% | 50.00% | 50.00% | 41.67% | |
| 1979 | MSI | 14.9586 | 2.1667 | 0.9523 | 1.8459 | 0.7874 |
| MSR | 100.00% | 20.00% | 19.80% | 20.00% | 16.22% | |
| Reliability | 58.33% | 8.33% | 8.33% | 8.33% | 16.67% | |
| 1980 | MSI | 0.0000 | 0.5833 | 0.0375 | 0.5530 | 0.0188 |
| MSR | 0.00% | 20.00% | 6.20% | 20.00% | 2.74% | |
| Reliability | 100.00% | 66.67% | 66.67% | 66.67% | 75.00% | |
| 1981 | MSI | 0.0000 | 0.0833 | 0.0431 | 0.0732 | 0.0313 |
| MSR | 0.00% | 10.00% | 7.17% | 9.37% | 4.74% | |
| Reliability | 100.00% | 91.67% | 75.00% | 91.67% | 75% | |
| 5 years | MSI | 2.9917 | 0.8167 | 0.3008 | 0.6116 | 0.2618 |
| MSR | 100.00% | 20.00% | 19.94% | 20.00% | 16.22% | |
| Reliability | 91.67% | 58.33% | 58.33% | 60.00% | 58.33% | |
| Evaluation Criteria | Scenarios | ||||
|---|---|---|---|---|---|
| SOP | Conventional Rule Curves | Shiau’s Method | Taghian’s Method | Proposed Rule | |
| R2 | 0.974 | 0.985 | 0.987 | 0.984 | 0.990 |
| NSE | 0.917 | 0.960 | 0.967 | 0.959 | 0.982 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cancelliere, A.; Ancarani, A.; Rossi, G. Susceptibility of Water Supply Reservoirs to Drought Conditions. J. Hydrol. Eng. 1998, 3, 140–148. [Google Scholar] [CrossRef]
- Bayazit, M.; Ünal, N.E. Effects of Hedging on Reservoir Performance. Water Resour. Res. 1990, 26, 713–719. [Google Scholar] [CrossRef]
- Bower, B.T.; Hufschmidt, M.M.; Reedy, W.W. Operating Procedures: Their Role in the Design of Water-Resource Systems by Simulation Analyses; Harvard University Press: Cambridge, MA, USA, 1962; pp. 443–458. [Google Scholar]
- Draper, A.; Lund, J. Optimal Hedging and Carryover Storage Value. J. Water Resour. Plan. Manag. 2003, 130, 83–87. [Google Scholar] [CrossRef]
- Shiau, J.-T. Analytical Optimal Hedging with Explicit Incorporation of Reservoir Release and Carryover Storage Targets. Water Resour. Res. 2011, 47, W01515. [Google Scholar] [CrossRef]
- Srinivasan, K.; Philipose, M.C. Evaluation and Selection of Hedging Policies Using Stochastic Reservoir Simulation. Water Resour. Manag. 1996, 10, 163–188. [Google Scholar] [CrossRef]
- Srinivasan, K.; Philipose, M.C. Effect of Hedging on over-Year Reservoir Performance. Water Resour. Manag. 1998, 12, 95–120. [Google Scholar] [CrossRef]
- You, J.-Y.; Cai, X. Hedging Rule for Reservoir Operations: 1. A Theoretical Analysis. Water Resour. Res. 2008, 44, W01415. [Google Scholar] [CrossRef]
- Shiau, J.T.; Lee, H.C. Derivation of Optimal Hedging Rules for a Water-Supply Reservoir through Compromise Programming. Water Resour. Manag. 2005, 19, 111–132. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, X.; Wang, Z. Optimality Conditions for a Two-Stage Reservoir Operation Problem. Water Resour. Res. 2011, 47, W08503. [Google Scholar] [CrossRef]
- Revelle, C.; Joeres, E.; Kirby, W. The Linear Decision Rule in Reservoir Management and Design: 1, Development of the Stochastic Model. Water Resour. Res. 1969, 5, 767–777. [Google Scholar] [CrossRef]
- Houck, M.H.; Cohon, J.L.; ReVelle, C.S. Linear Decision Rule in Reservoir Design and Management: 6. Incorporation of Economic Efficiency Benefits and Hydroelectric Energy Generation. Water Resour. Res. 1980, 16, 196–200. [Google Scholar] [CrossRef]
- Neelakantan, T.R.; Pundarikanthan, N.V. Hedging Rule Optimisation for Water Supply Reservoirs System. Water Resour. Manag. 1999, 13, 409–426. [Google Scholar] [CrossRef]
- Ilich, N.; Simonovic, S.P.; Amron, M. The Benefits of Computerized Real-Time River Basin Management in the Malahayu Reservoir System. Can. J. Civ. Eng. 2000, 27, 55–64. [Google Scholar] [CrossRef]
- Neelakantan, T.; Pundarikanthan, N. Neural Network-Based Simulation-Optimization Model for Reservoir Operation. J. Water Resour. Plan. Manag. 2000, 126, 57–64. [Google Scholar] [CrossRef]
- Tu, M.; Hsu, N.; Yeh, W. Optimization of Reservoir Management and Operation with Hedging Rules. J. Water Resour. Plan. Manag. 2003, 129, 86–97. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, Resiliency, and Vulnerability Criteria for Water Resource System Performance Evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Shih, J.; ReVelle, C. Water-Supply Operations During Drought: Continuous Hedging Rule. J. Water Resour. Plan. Manag. 1994, 120, 613–629. [Google Scholar] [CrossRef]
- Shih, J.-S.; ReVelle, C. Water Supply Operations During Drought: A Discrete Hedging Rule. Eur. J. Oper. Res. 1995, 82, 163–175. [Google Scholar] [CrossRef]
- Taghian, M.; Rosbjerg, D.; Haghighi, A.; Madsen, H. Optimization of Conventional Rule Curves Coupled with Hedging Rules for Reservoir Operation. J. Water Resour. Plan. Manag. 2014, 140, 693–698. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.; Xiong, L.; Cao, Z.; Xu, C. Derivation of Operation Rules for Reservoirs in Parallel with Joint Water Demand. Water Resour. Res. 2015, 51, 9539–9563. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Sherali, H.D.; Shetty, C.M. Nonlinear Programming: Theory and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 188–199. [Google Scholar]
- Koutsoyiannis, D.; Economou, A. Evaluation of the Parameterization-Simulation-Optimization Approach for the Control of Reservoir Systems. Water Resour. Res. 2003, 39, 1170. [Google Scholar] [CrossRef]
- Hydraulic Engineering Center (US). Reservoir Yield, Generalized Computer Program 23-J2-L245; U.S. Army Corps of Engineers: Sacramento, CA, USA, 1966. [Google Scholar]
- Hydraulic Engineering Center (US). Reservoir Yield. In Hydrologic Engineering Methods for Water Resources Development; U.S. Army Corps of Engineers: Davis, CA, USA, 1975. [Google Scholar]
- Hsu, N.; Cheng, K. Network Flow Optimization Model for Basin-Scale Water Supply Planning. J. Water Resour. Plan. Manag. 2002, 128, 102–112. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, USA, 27 November–1 December 1995.
- Jiang, Y.; Hu, T.; Huang, C.; Wu, X. An Improved Particle Swarm Optimization Algorithm. Appl. Math. Comput. 2007, 193, 231–239. [Google Scholar] [CrossRef]
- Guo, X.; Hu, T.; Zhang, T.; Lv, Y. Bilevel Model for Multi-Reservoir Operating Policy in Inter-Basin Water Transfer-Supply Project. J. Hydrol. 2012, 424–425, 252–263. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.; Guo, X.; Li, X. Water Transfer Triggering Mechanism for Multi-Reservoir Operation in Inter-Basin Water Transfer-Supply Project. Water Resour. Manag. 2014, 28, 1293–1308. [Google Scholar] [CrossRef]
- Guo, X.; Hu, T.; Zeng, X.; Li, X. Extension of Parametric Rule with the Hedging Rule for Managing Multireservoir System During Droughts. J. Water Resour. Plan. Manag. 2012, 139, 139–148. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer, IEEE World Congress on Computational Intelligence. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998.
- Zhao, T.; Cai, X.; Lei, X.; Wang, H. Improved Dynamic Programming for Reservoir Operation Optimization with a Concave Objective Function. J. Water Resour. Plan. Manag. 2011, 138, 590–596. [Google Scholar] [CrossRef]
- Loucks, D.P.; Stedinger, J.R.; Haith, D.A. Water Resource Systems Planning and Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- Yeh, W.W.G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Labadie, J. Optimal Operation of Multireservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Faber, B.A.; Stedinger, J.R. Reservoir Optimization Using Sampling SDP with Ensemble Streamflow Prediction (ESP) Forecasts. J. Hydrol. 2001, 249, 113–133. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating Rules for Multireservoir Systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, T.; Zhang, X.-Z.; Zeng, X.; Wang, J. A Two-Step Approach for Analytical Optimal Hedging with Two Triggers. Water 2016, 8, 52. https://doi.org/10.3390/w8020052
Hu T, Zhang X-Z, Zeng X, Wang J. A Two-Step Approach for Analytical Optimal Hedging with Two Triggers. Water. 2016; 8(2):52. https://doi.org/10.3390/w8020052
Chicago/Turabian StyleHu, Tiesong, Xu-Zhao Zhang, Xiang Zeng, and Jing Wang. 2016. "A Two-Step Approach for Analytical Optimal Hedging with Two Triggers" Water 8, no. 2: 52. https://doi.org/10.3390/w8020052
APA StyleHu, T., Zhang, X.-Z., Zeng, X., & Wang, J. (2016). A Two-Step Approach for Analytical Optimal Hedging with Two Triggers. Water, 8(2), 52. https://doi.org/10.3390/w8020052







