Exploration of an Optimal Policy for Water Resources Management Including the Introduction of Advanced Sewage Treatment Technologies in Zaozhuang City, China
Abstract
:1. Introduction
2. Study Area and Methods
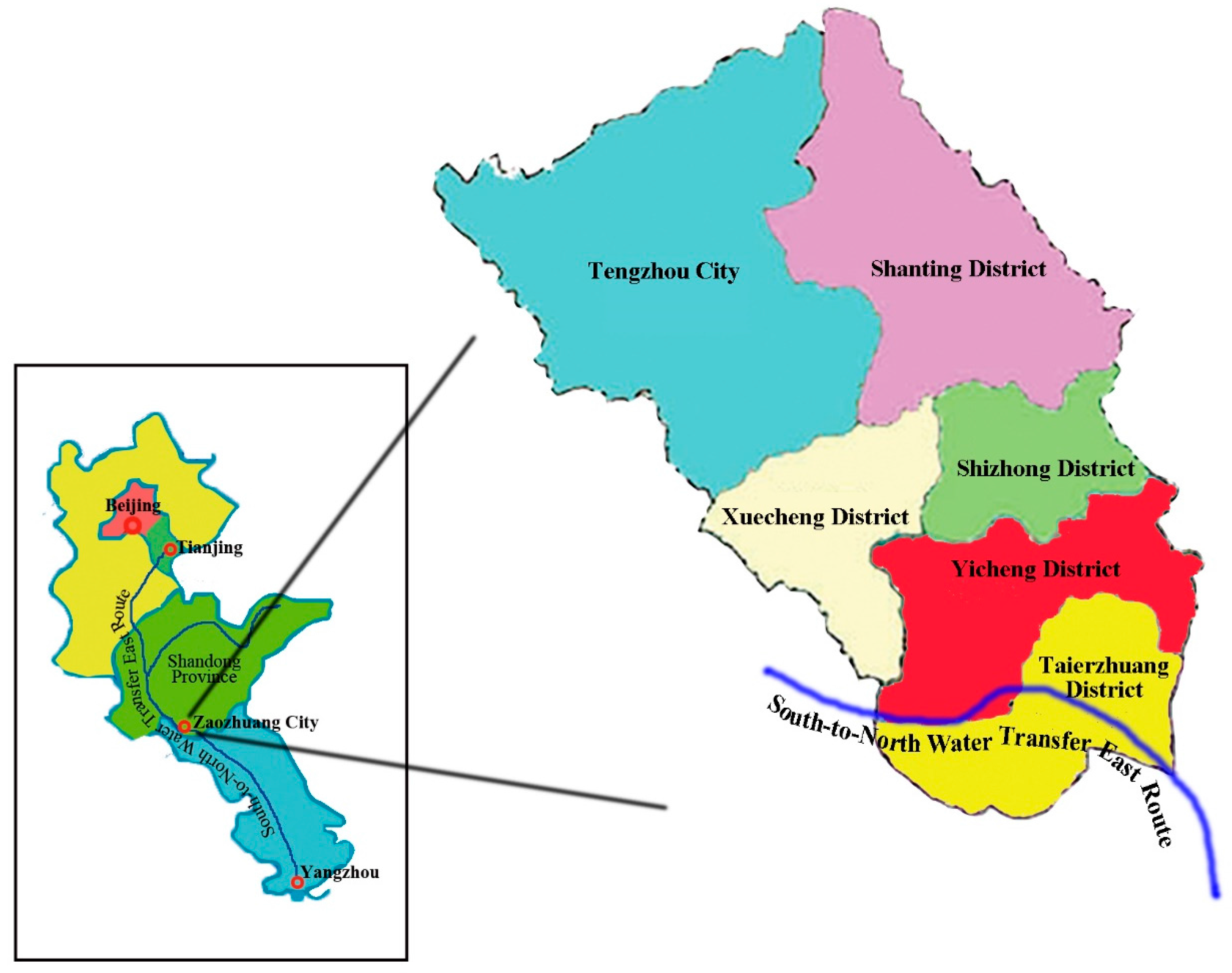
2.1. Study Area
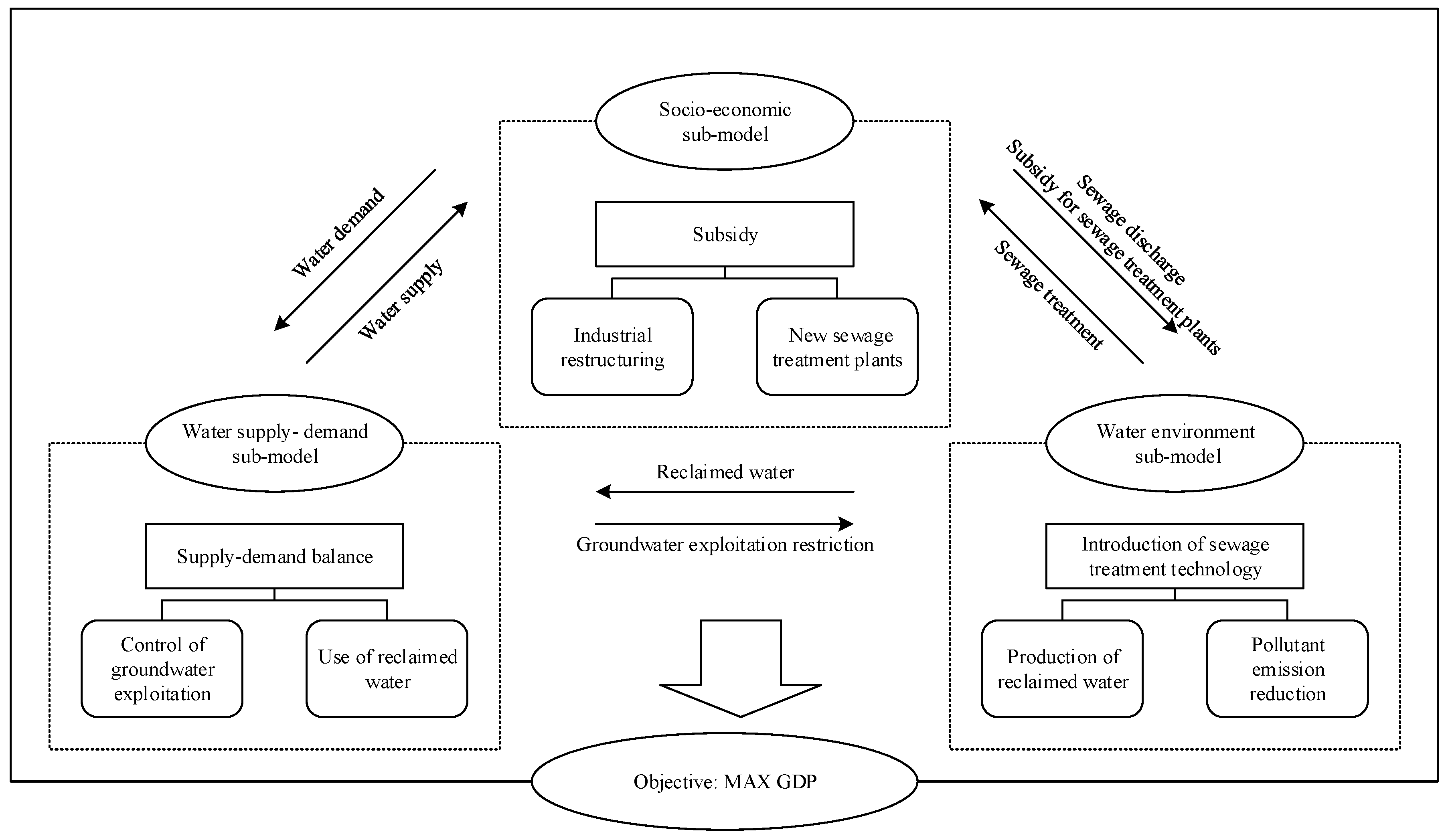
2.2. Research Method
2.3. Data
3. Modeling and Simulation
3.1. Objective Function
3.2. Socio-Economic Sub-Model
3.2.1. Population and Urban Land System
3.2.2. Market Equilibrium System
3.2.3. Financial Subsidy System
3.3. Water Environment Sub-Model
3.3.1. Production of Reclaimed Water
3.3.2. Water Quality Control System
3.4. Water Supply–Demand Sub-Model
3.4.1. Water Supply
3.4.2. Water Demand
4. Results
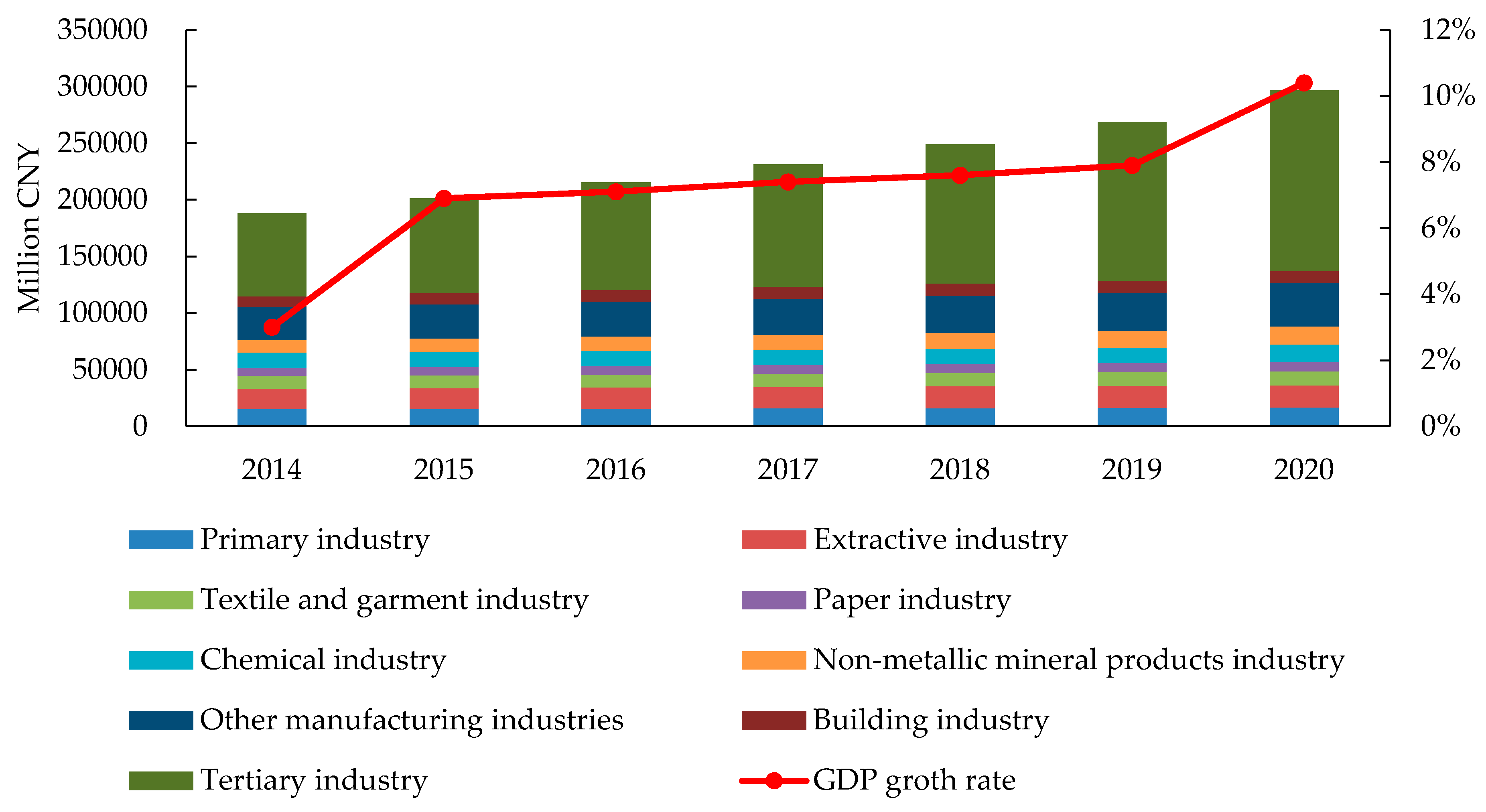
4.1. Economic Development
4.2. Technology Selection
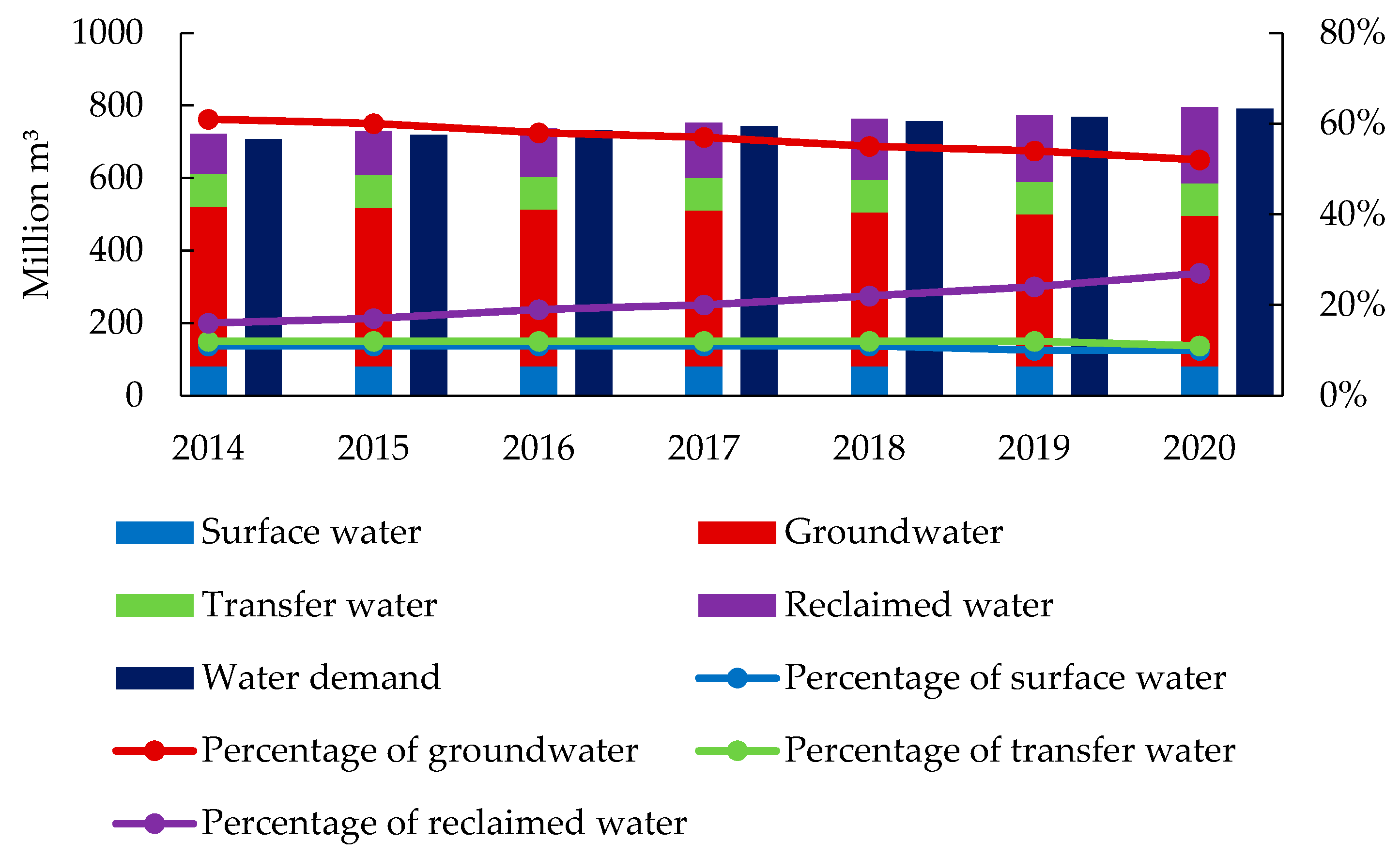
4.3. Water Supply and Water Environment
4.3.1. Water Supply
4.3.2. Water Environment
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Superscripts and Subscripts | |
|---|---|
| the -th year of the target term, = 1,2,3,4,5,6,7 | |
| the -th industry, = 1,2,3,4,5,6,7,8,9 | |
| the -th region, = 1,2,3,4,5,6 | |
| the -th land type, = 1,2,3,4 | |
| the -th overdraft source area, = 1,2,3,4,5 | |
| the -th normal source area, = 1,2,3,4,5 | |
| Variables | Units | |
|---|---|---|
| sewage discharge coefficient per urban/rural resident | kt/104 people | |
| sewage discharge coefficient of industry | kt/million CNY | |
| COD emission coefficient per urban/rural resident | t/104 people | |
| COD emission coefficient of industry | t/million CNY | |
| COD emission coefficient per unit area of land type | t/km2 | |
| water requirement coefficient per urban/rural resident | kt/104 people | |
| water requirement coefficient of industry | kt/million CNY | |
| // | reclaimed water production coefficient of advanced technology A/B/C | % |
| // | COD removal rates of advanced technology A/B/C | t/million m3 |
| the production of industry | million CNY | |
| the production of industry in region | million CNY | |
| capital stock of industry | million CNY | |
| industrial subsidies of industry | million CNY | |
| investment of industry | million CNY | |
| the upper limit of the financial budget | million CNY | |
| the investment for construction of new sewage treatment plants | million CNY | |
| the investment for operation of sewage treatment plants | million CNY | |
| urban populations in region | 104 people | |
| rural populations in region | 104 people | |
| the area of land type in region | km2 | |
| the total amount of sewage discharge | million m3 | |
| the total amount of treated sewage | million m3 | |
| the total amount of water supply | million m3 | |
| the total amount of water demand | million m3 | |
| surface water supply | million m3 | |
| groundwater supply | million m3 | |
| transfer water supply | million m3 | |
| reclaimed water supply | million m3 | |
| household water demand | million m3 | |
| industrial water demand | million m3 | |
| ecological water demand | million m3 | |
| groundwater supply from overdraft source area | million m3 | |
| groundwater supply from normal source area | million m3 | |
| exploitation from overdraft source area in base year | million m3 | |
| exploitation from normal source area in base year | million m3 | |
| the exploitation limit of normal source area | million m3 | |
| the maximum/minimum decreasing amount from overdraft source area | million m3 | |
| treatment capacity of new sewage treatment plants with advanced technology A/B/C in region | million m3 | |
| existing sewage treatment capacity in region | million m3 | |
| the amount of existing reclaimed water in region | million m3 | |
| the total emissions of COD | ton | |
| COD emissions from households | ton | |
| COD emissions from industries | ton | |
| COD emissions from nonpoint sources | ton | |
| the existing COD treatment amount in region | ton | |
| urban population growth rate in region | % | |
| rural population growth rate in region | % | |
| the change rate of land type in region | % | |
| value-added rate of industry | % | |
| the social discount rate | % | |
| the ratio of capital to output of industry | % | |
| the depreciation rate of industry | % | |
| the column vector of total production | ||
| the column vector of total consumption | ||
| the column vector of total investment | ||
| the column vector of net exports | ||
| the column vector of investment for construction of sewage treatment plants | ||
| the input–output coefficient matrix (nine-order) | ||
| the diagonal matrix (nine-order) of coefficient associated with the production induced by the construction investment | ||
| Industry Sector | Added Value (Million CNY) | Value-Added Rate (%) |
|---|---|---|
| Primary Industry | 149.80 | 53% |
| Extractive Industry | 178.79 | 32% |
| Textile and Garment Industry | 111.26 | 29% |
| Paper Industry | 70.97 | 31% |
| Chemical Industry | 133.81 | 25% |
| Non-Metallic Mineral Products Industry | 103.77 | 27% |
| Other Manufacturing Industries | 344.55 | 26% |
| Building Industry | 94.59 | 34% |
| Tertiary Industry | 643.27 | 53% |
| Industry Sector | Water Demand Coefficient (kt/Million CNY) | Sewage Discharge Coefficient (kt/Million CNY) | COD Emission Coefficient (t/Million CNY) |
|---|---|---|---|
| Primary Industry | 14.831 | - | - |
| Extractive Industry | 0.328 | 0.668 | 0.132 |
| Textile and Garment Industry | 0.259 | 0.209 | 0.302 |
| Paper Industry | 0.929 | 0.754 | 2.244 |
| Chemical Industry | 0.597 | 0.379 | 0.266 |
| Non-Metallic Mineral Products Industry | 0.161 | 0.003 | 0.002 |
| Other Manufacturing Industries | 0.292 | 0.091 | 0.217 |
| Building Industry | 0.544 | 0.264 | 0.311 |
| Tertiary Industry | 0 | 0 | 0 |
| Region | Average Population Growth Rates (%) | |
|---|---|---|
| Urban Area | Rural Area | |
| Shizhong District | 0.92 | 0.93 |
| Xuecheng District | −1.23 | 2.99 |
| Yicheng District | 0.33 | 1.51 |
| Taierzhuang District | −1.02 | 1.03 |
| Shanting District | 0.79 | 0.59 |
| Tengzhou City | 4.95 | −0.54 |
| Land Type | COD Emission Coefficient |
|---|---|
| Residential Land | 61.25 |
| Commercial Land | 61.25 |
| Industrial Land | 61.25 |
| Traffic Land | 36.75 |
| 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|---|---|
| Ecological water demand | 22.74 | 23.68 | 24.67 | 25.70 | 26.77 | 27.88 | 29.04 | 30.25 |
References
- Nandalal, K.D.W.; Simonovic, S.P. Resolving conflicts in water sharing: A systemic approach. Water Resour. Res. 2013, 39. [Google Scholar] [CrossRef]
- Luckman, J.; Grethe, H.; McDonald, S.; Orlov, A.; Siddig, S. An integrated economic model of multiple types and uses of water. Water Resour. Res. 2014, 50, 3875–3892. [Google Scholar] [CrossRef]
- Davidsen, C.; Pereira-Cardenal, S.J.; Liu, S.X.; Mo, X.G.; Rosbjerg, D.; Bauer-Gottwein, P. Using stochastic dynamic programming to support water resources management in the Ziya River Basin, China. J. Water Resour. Plan. Manag. ASCE 2015, 141. [Google Scholar] [CrossRef]
- Peng, J.; Yuan, X.M.; Qi, L.; Li, Q.L. A study of multi-objective dynamic water resources allocation modeling of Huai River. Water Sci. Technol. Water Supply 2015, 15, 817–824. [Google Scholar] [CrossRef]
- Viaggi, D.; Zanni, G.; Raggi, M. Changing perspectives on the economics of Water. Water 2014, 6, 2969–2977. [Google Scholar] [CrossRef]
- Rogers, P. A game theory approach to the problems of international river basin. Water Resour. Res. 1969, 5, 749–760. [Google Scholar] [CrossRef]
- Safari, N.; Zarghami, M.; Szidarovszky, F. Nash bargaining and leader-follower models in water allocation: Application to the Zarrinehrud River basin, Iran. Appl. Math. Model. 2014, 38, 1959–1968. [Google Scholar] [CrossRef]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Huang, C.H.; Chang, C.T.; Ling, H.C.; Chang, C.C. A mathematical programming model for water usage and treatment network design. Ind. Eng. Chem. Res. 1999, 38, 2666–2679. [Google Scholar] [CrossRef]
- Karterakis, S.M.; Karatzas, G.P.; Nikolos, L.K.; Papadopoulou, M.P. Application of linear programming and differential evolutionary optimization methodologies for the solution of coastal subsurface water management problems subject to environmental criteria. J. Hydrol. 2007, 342, 270–282. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. Genetic algorithms for least-cost design of water distribution networks. J. Water Resour. Plan. Manag. ASCE 1997, 123, 67–77. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Nie, S.L. An interval-parameter multi-stage stochastic programming model for water resources management under uncertainty. Adv. Water Resour. 2006, 29, 776–789. [Google Scholar] [CrossRef]
- Abrishamchi, A.; Ebrahimian, A.; Tajrishi, M. Case study: Application of multicriteria decision making to urban water supply. J. Water Resour. Plan. Manag. ASCE 2005, 131, 326–335. [Google Scholar] [CrossRef]
- Fattahi, P.; Fayyaz, S. A compromise programming model to integrated urban water management. Water Resour. Manag. 2010, 24, 1211–1227. [Google Scholar] [CrossRef]
- Lotze-Campen, H.; Müller, C.; Bondeau, A.; Rost, S.; Popp, A.; Lucht, W. Global food demand, productivity growth, and the scarcity of land and water resources: A spatially explicit mathematical programming approach. Agric. Econ. 2008, 39, 325–338. [Google Scholar] [CrossRef]
- Liu, X.M.; Huang, G.H.; Wang, S.; Fan, Y.R. Water resources management under uncertainty: Factorial multi-stage stochastic program with chance constraints. Stoch. Environ. Res. Risk Assess. 2016, 30, 945–957. [Google Scholar] [CrossRef]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S.R. Multi-objective optimization model for the allocation of water resources in arid regions based on the maximization of socioeconomic efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Higano, Y.; Sawada, T. The dynamic optimal policy to improve the water quality of Lake Kasumigaura. Study Reg. Sci. 1995, 26, 75–86. [Google Scholar] [CrossRef]
- Higano, Y.; Yoneta, A. Economical policies to relieve contamination of Lake Kasumigaura. Study Reg. Sci. 1998, 29, 205–218. [Google Scholar] [CrossRef]
- Yan, J.J.; Sha, J.H.; Chu, X.; Xu, F.; Higano, Y. Endogenous derivation of optimal environmental policies for proper treatment of stockbreeding wastes in the upstream region of the Miyun Reservoir, Beijing. Pap. Reg. Sci. 2014, 93, 477–500. [Google Scholar] [CrossRef]
- Xiang, N.; Sha, J.H.; Yan, J.J.; Xu, F. Dynamic modeling and simulation of water environment management with a focus on a water recycling. Water 2014, 6, 17–31. [Google Scholar] [CrossRef]
- Yang, W.; Song, J.; Higano, Y.; Tang, J. Exploration and assessment of optimal policy combination for total water pollution control with a dynamic simulation model. J. Clean. Prod. 2015, 102, 342–352. [Google Scholar] [CrossRef]
- He, K.Q.; Wang, B.; Zhou, D.Y. Mechanism and mechanical model of karst collapse in an over-pumping area. Environ. Geol. 2004, 46, 1102–1107. [Google Scholar]
- Wang, X.P.; Mauzerall, D.L. Evaluating impacts of air pollution in China on public health: Implication for future air pollution and energy policies. Atmos. Environ. 2006, 40, 1706–1721. [Google Scholar] [CrossRef]
- He, K.Q.; Jia, Y.Y.; Chen, W.G.; Wang, R.L.; Luo, H.L. Evaluation of karst collapse risks induced by over-pumping and karst groundwater resource protection in Zaozhuang City, China. Environ. Earth. Sci. 2014, 71, 3443–3454. [Google Scholar] [CrossRef]
- Zaozhuang Planning Bureau. Zaozhuang City Master Plan (2010–2020). Available online: http://www.zzsghj.gov.cn/article.asp?id=1914 (accessed on 21 November 2015).
- Zaozhuang Statistical Bureau. Zaozhuang. Statistical Year Book 2014; China Statistics Press: Beijing, China, 2014.
- Zaozhuang Environmental Monitoring Station. Zaozhuang City Environmental Quality Report 2014. Available online: http://test.zzhb.gov.cn/index.php?m=content&c=index&a=show&catid=60&id=4926 (accessed on 21 November 2015).
- People’s Government of Zaozhuang City. Zaozhuang City Planning of Resource City Transformation and Sustainable Development (2010–2020); People’s Government of Zaozhuang City: Zaozhuang, China, 2011.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Classification of Urban. Land Use and Planning Standards of Development Land; China Architecture & Building Press: Beijing, China, 2011. [Google Scholar]
- Ministry of Environmental Protection of People’s Republic of China. List of National Urban Sewage Treatment Facilities. Available online: http://www.zhb.gov.cn/gkml/hbb/bgg/201404/t20140415_270550.htm (accessed on 15 November 2015).
- Ministry of Environmental Protection of People’s Republic of China. The National Environmental Protection Standards of China. Available online: http://kjs.mep.gov.cn/hjbhbz/ (accessed on 15 November 2015).
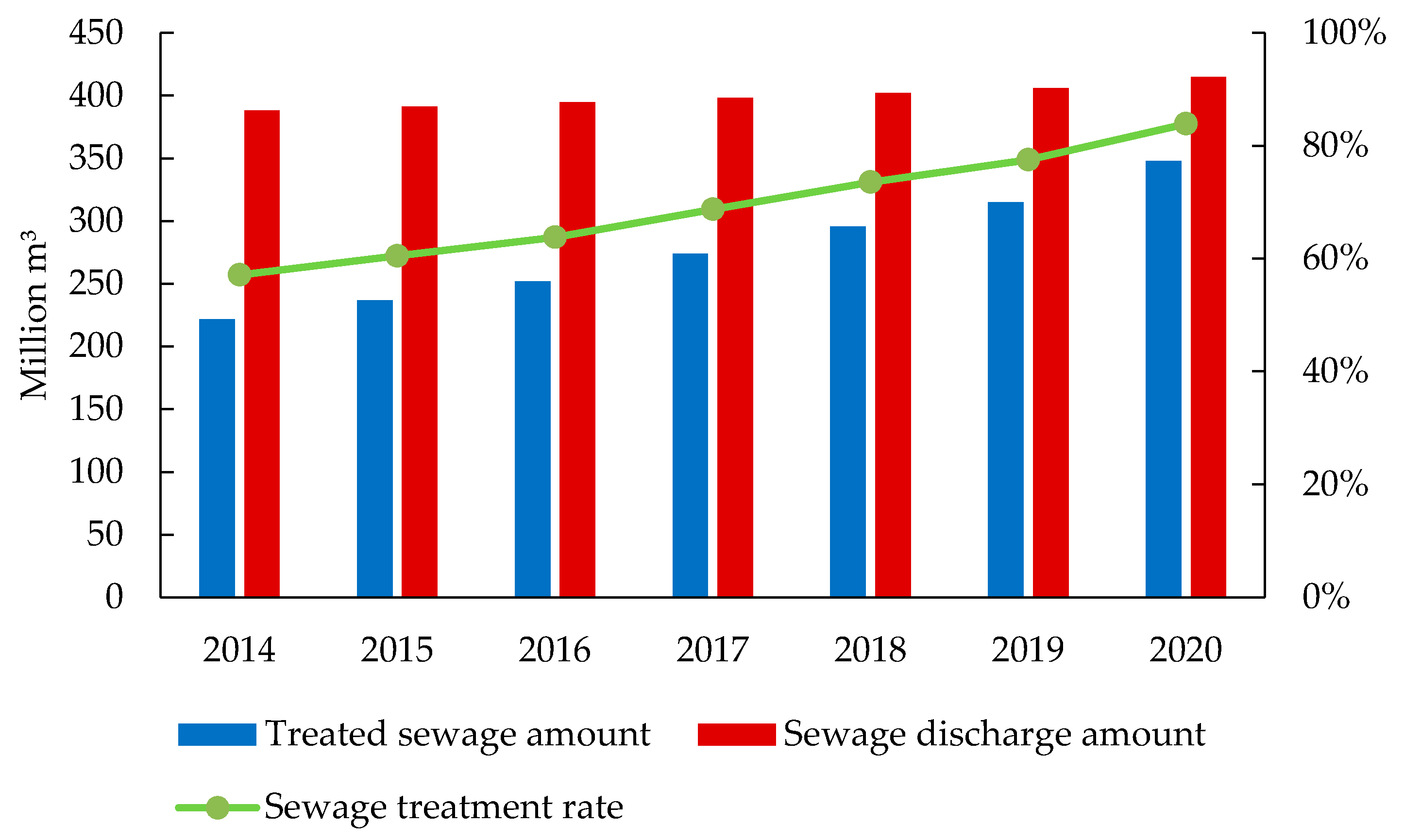
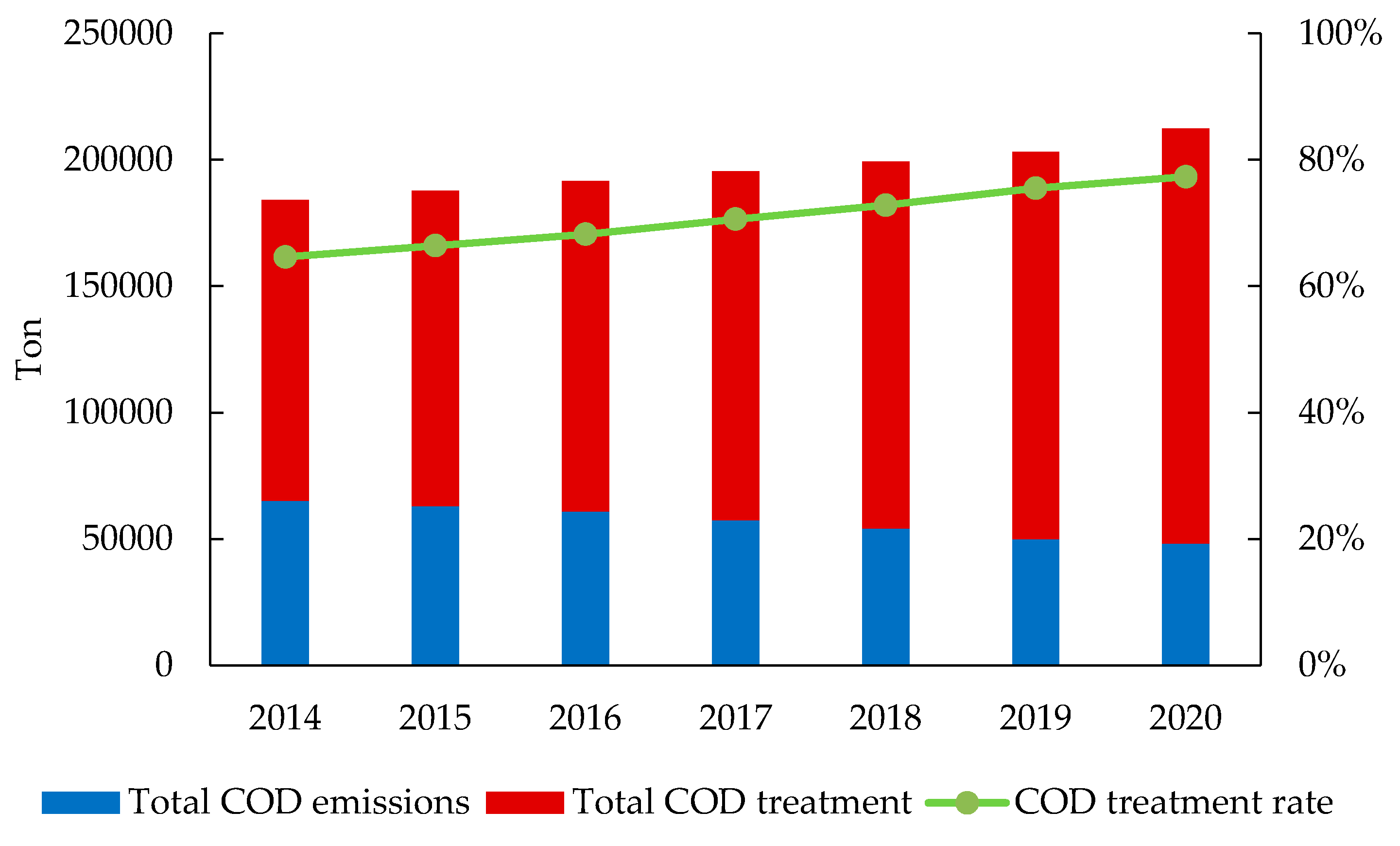
| Policy | Measures |
|---|---|
| Water environment control | Industrial restructuring |
| Water pollutant emission reduction | |
| Water supply plan | Sewage treatment technology selection |
| Groundwater exploitation restriction |
| No. | Technologies | Construction Cost (Million CNY) | Operation Cost (CNY/m3) | Treatment Capacity (Million m3/Year) | Reclaimed Water Production Capacity (Million m3/Year) | COD Removal Amount (mg/L) |
|---|---|---|---|---|---|---|
| A | EMBR | 30 | 1.4 | 4 | 3.8 | 560 |
| B | MBR | 60 | 1.0 | 11 | 8.5 | 330 |
| C | DMBR | 160 | 2.0 | 36.5 | 30 | 345 |
| No. | Overdraft Groundwater Source Area | No. | Normal Groundwater Source Area |
|---|---|---|---|
| 1 | Dongwangzhuang | 1 | South Area of Jin River |
| 2 | Shili Spring | 2 | Yicheng Basin |
| 3 | Kekou | 3 | Houzhangzhuang |
| 4 | Qingliang Spring | 4 | Yangzhuang Spring |
| 5 | Tengxi Plain | 5 | South of Jin Spring |
| No. | Shizhong District | Xuecheng District | Yicheng District | Taierzhuang District | Shanting District | Tengzhou City |
|---|---|---|---|---|---|---|
| A | 0 | 0 | 1 | 1 | 3 | 1 |
| B | 0 | 2 | 1 | 1 | 2 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 0 |
| No. | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|
| A | 2 | 1 | 1 | 0 | 0 | 2 | 0 |
| B | 0 | 1 | 1 | 2 | 2 | 1 | 3 |
| C | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Exploitation Amount (Million m3) | Limit Amount (Million m3) | ||
|---|---|---|---|
| 2013 | 2020 | ||
| Dongwangzhuang | 30 | 29.3 | 29.5 |
| Shili Spring | 18 | 16.4 | 17 |
| Kekou | 7 | 4.9 | 6.4 |
| Qingliang Spring | 21 | 18.9 | 21 |
| Tengxi Plain | 190 | 184.4 | 185.2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, G.; Yan, J.; Sha, J.; Song, C.; Zhong, S. Exploration of an Optimal Policy for Water Resources Management Including the Introduction of Advanced Sewage Treatment Technologies in Zaozhuang City, China. Water 2016, 8, 608. https://doi.org/10.3390/w8120608
He G, Yan J, Sha J, Song C, Zhong S. Exploration of an Optimal Policy for Water Resources Management Including the Introduction of Advanced Sewage Treatment Technologies in Zaozhuang City, China. Water. 2016; 8(12):608. https://doi.org/10.3390/w8120608
Chicago/Turabian StyleHe, Gengyu, Jingjing Yan, Jinghua Sha, Ci Song, and Shuai Zhong. 2016. "Exploration of an Optimal Policy for Water Resources Management Including the Introduction of Advanced Sewage Treatment Technologies in Zaozhuang City, China" Water 8, no. 12: 608. https://doi.org/10.3390/w8120608
APA StyleHe, G., Yan, J., Sha, J., Song, C., & Zhong, S. (2016). Exploration of an Optimal Policy for Water Resources Management Including the Introduction of Advanced Sewage Treatment Technologies in Zaozhuang City, China. Water, 8(12), 608. https://doi.org/10.3390/w8120608








