Groundwater Modeling in Support of Water Resources Management and Planning under Complex Climate, Regulatory, and Economic Stresses
Abstract
:1. Introduction
2. Materials and Methods
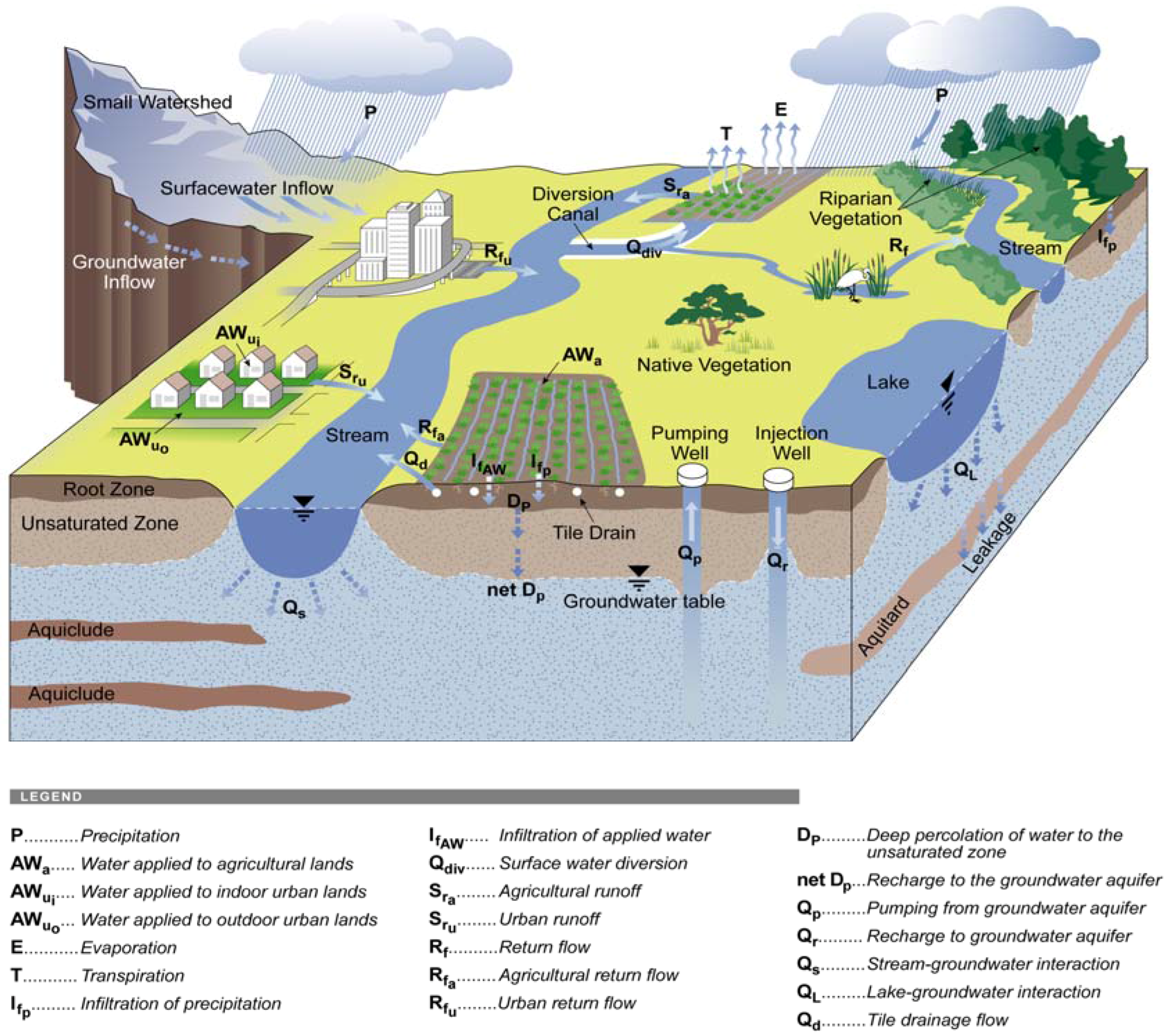
2.1. General Description of IWFM
2.1.1. Groundwater
2.1.2. Streams
2.1.3. Lakes
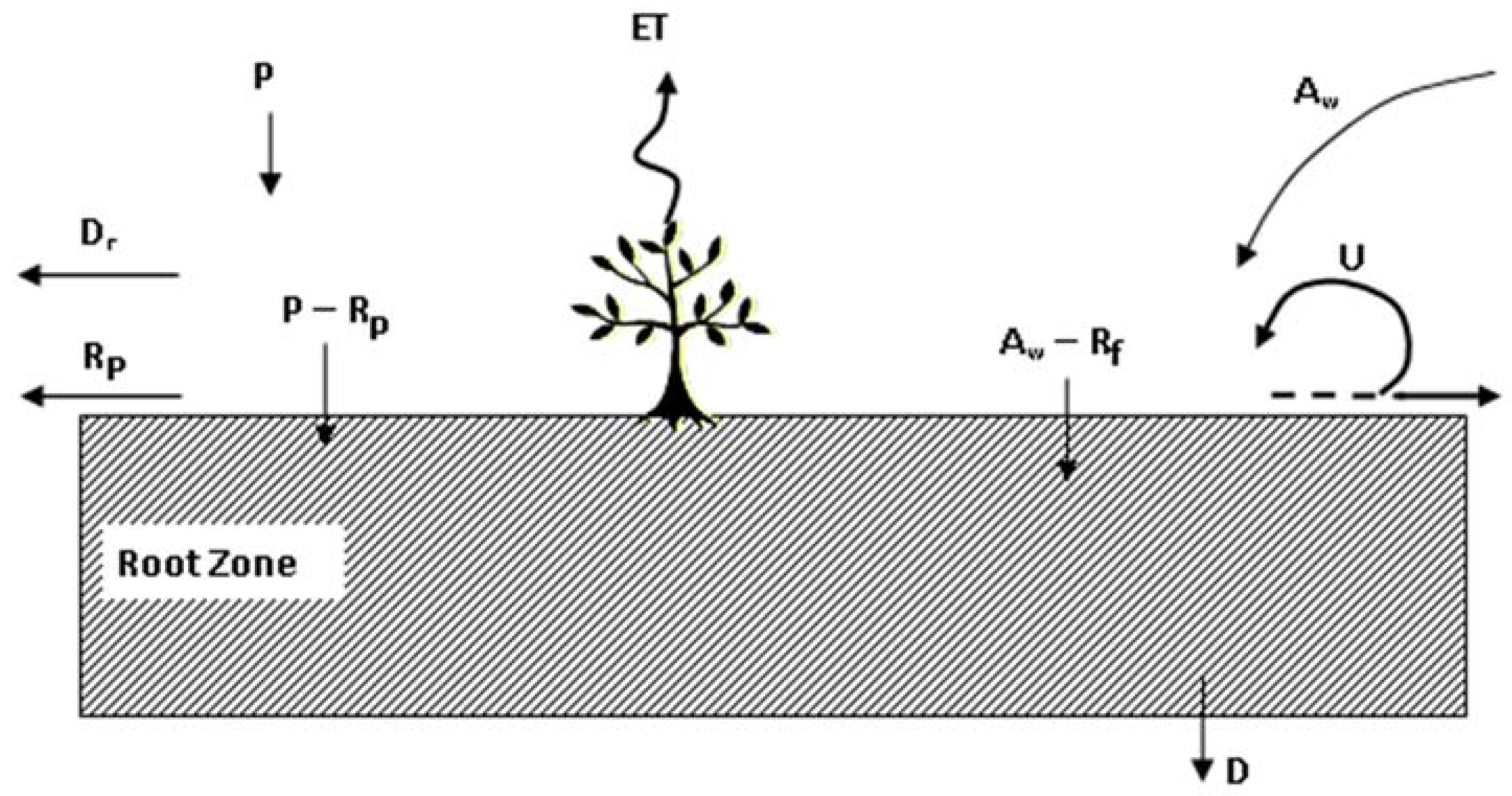
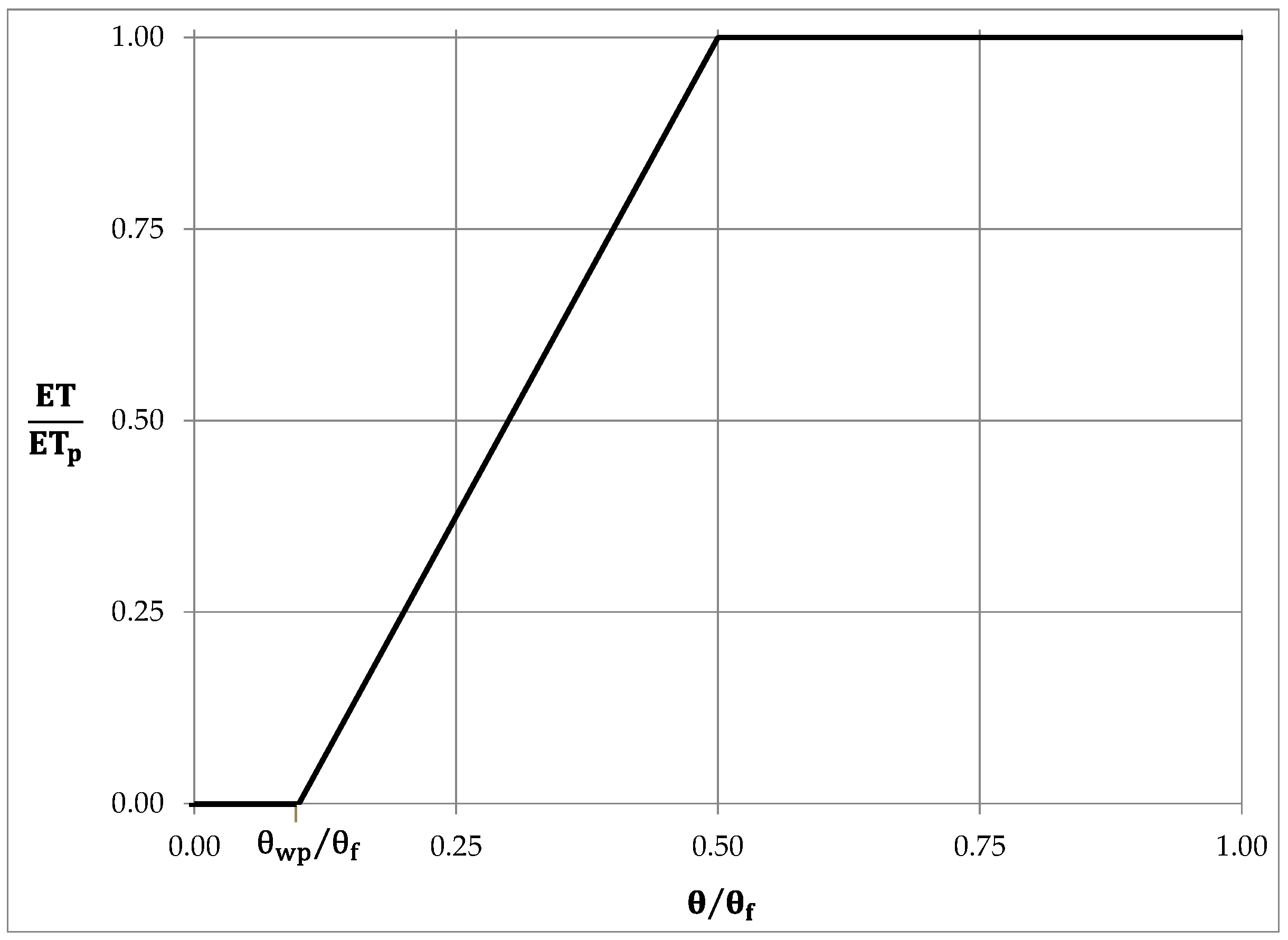
2.1.4. Land Surface and Root Zone
2.1.5. Unsaturated Zone
2.1.6. Water Demand and Automatic Supply Adjustment
2.2. Software Design of IWFM
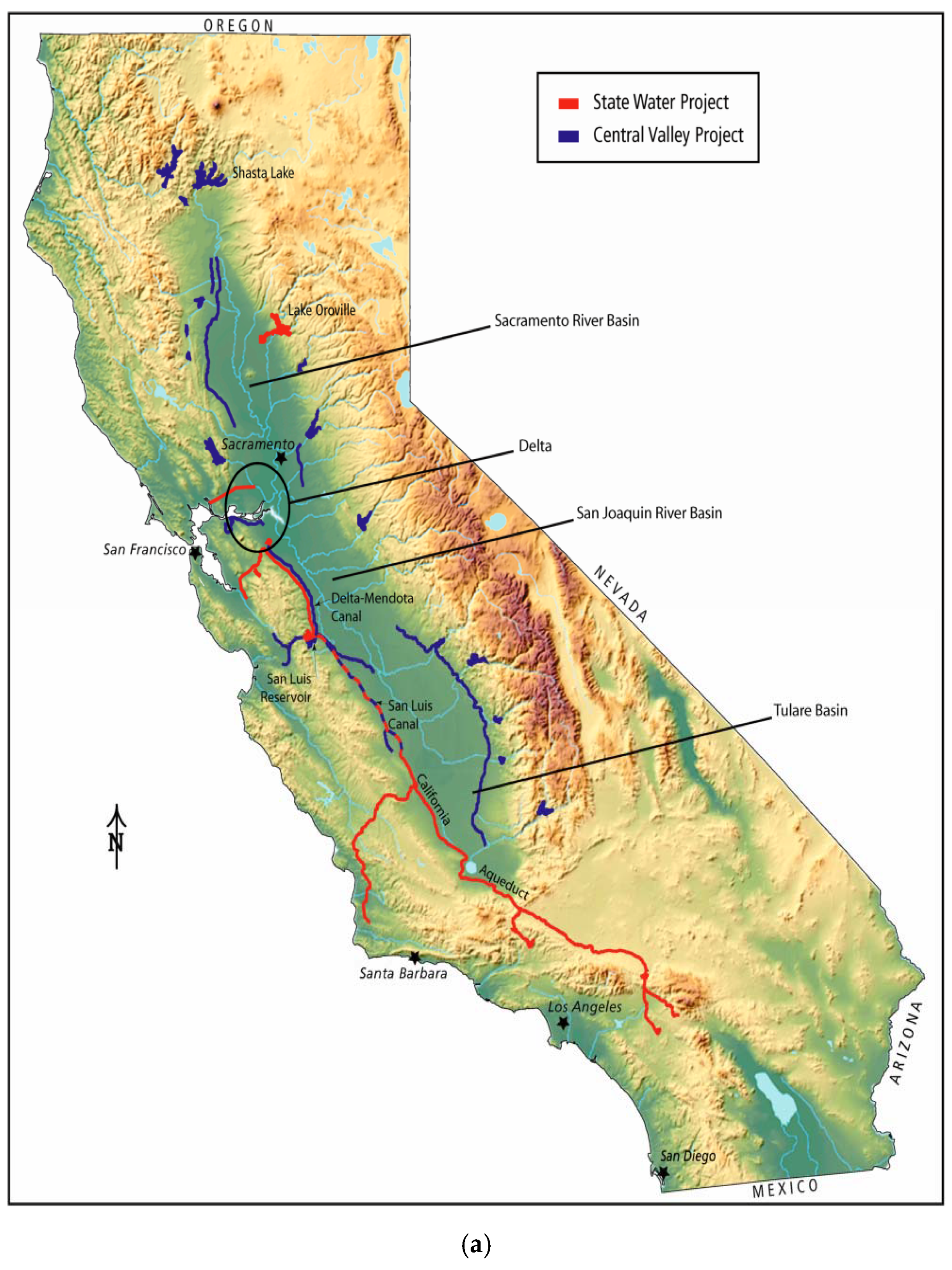
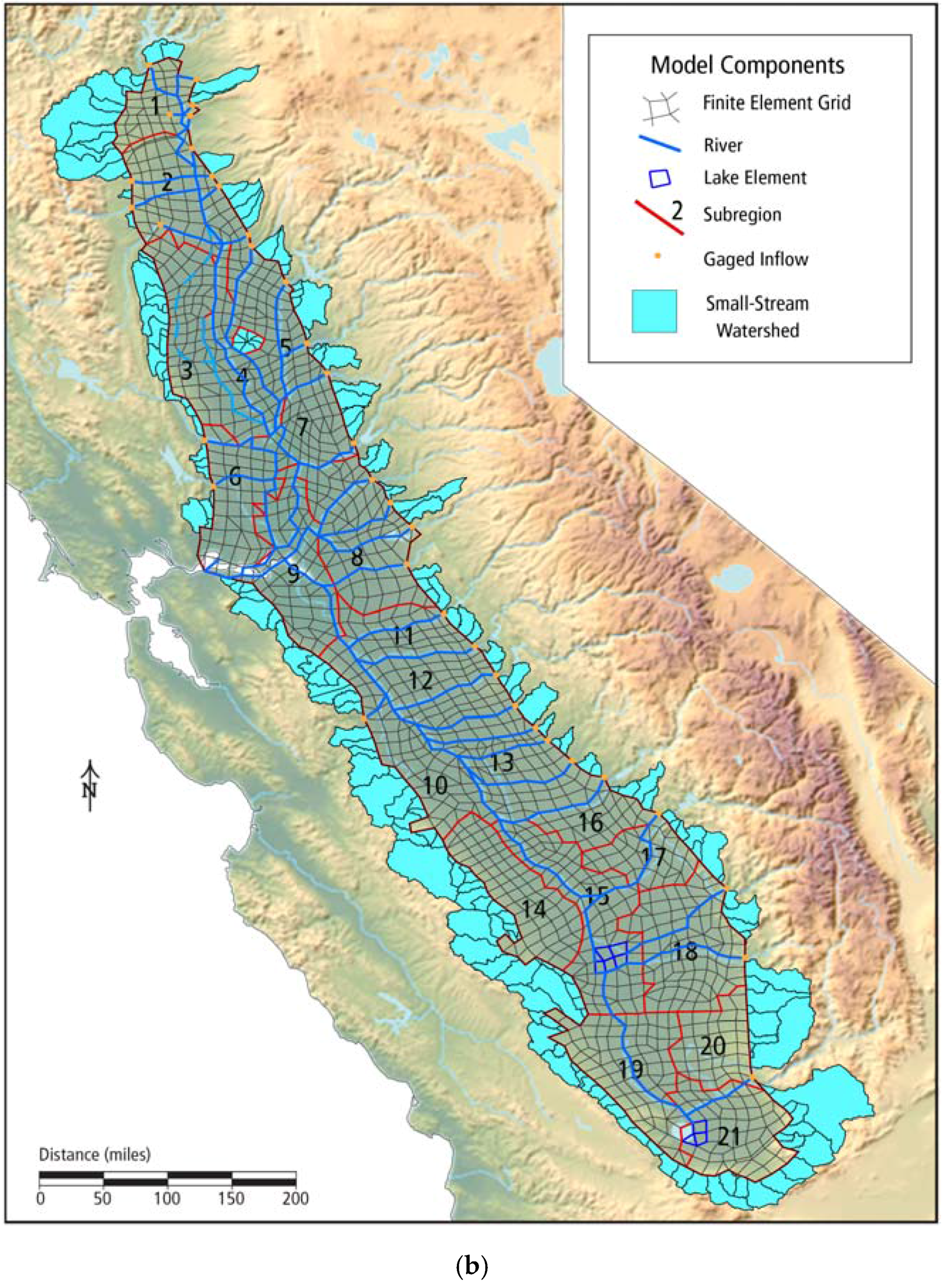
2.3. California Central Valley Groundwater–Surface Water Simulation Model (C2VSim)
3. Results and Discussion
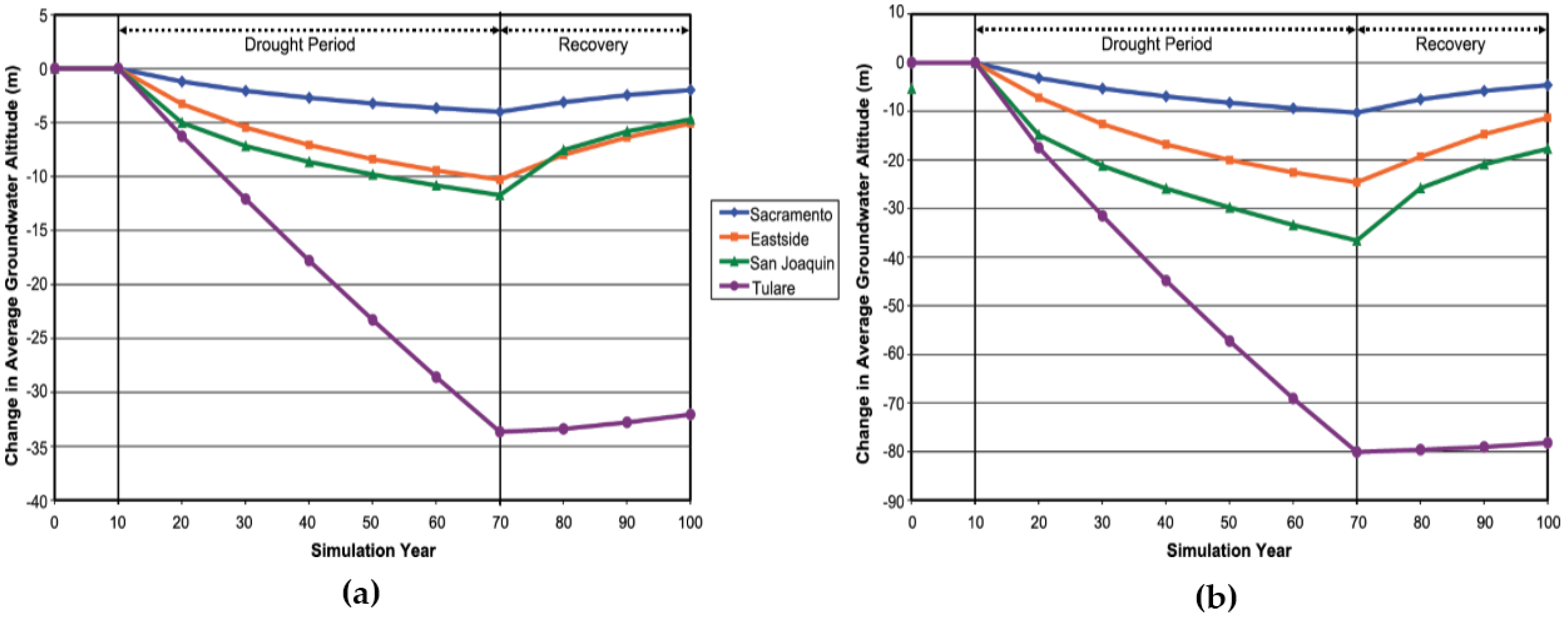
3.1. Effect of Long-Term Droughts on Groundwater in the Valley under Constant Land Use
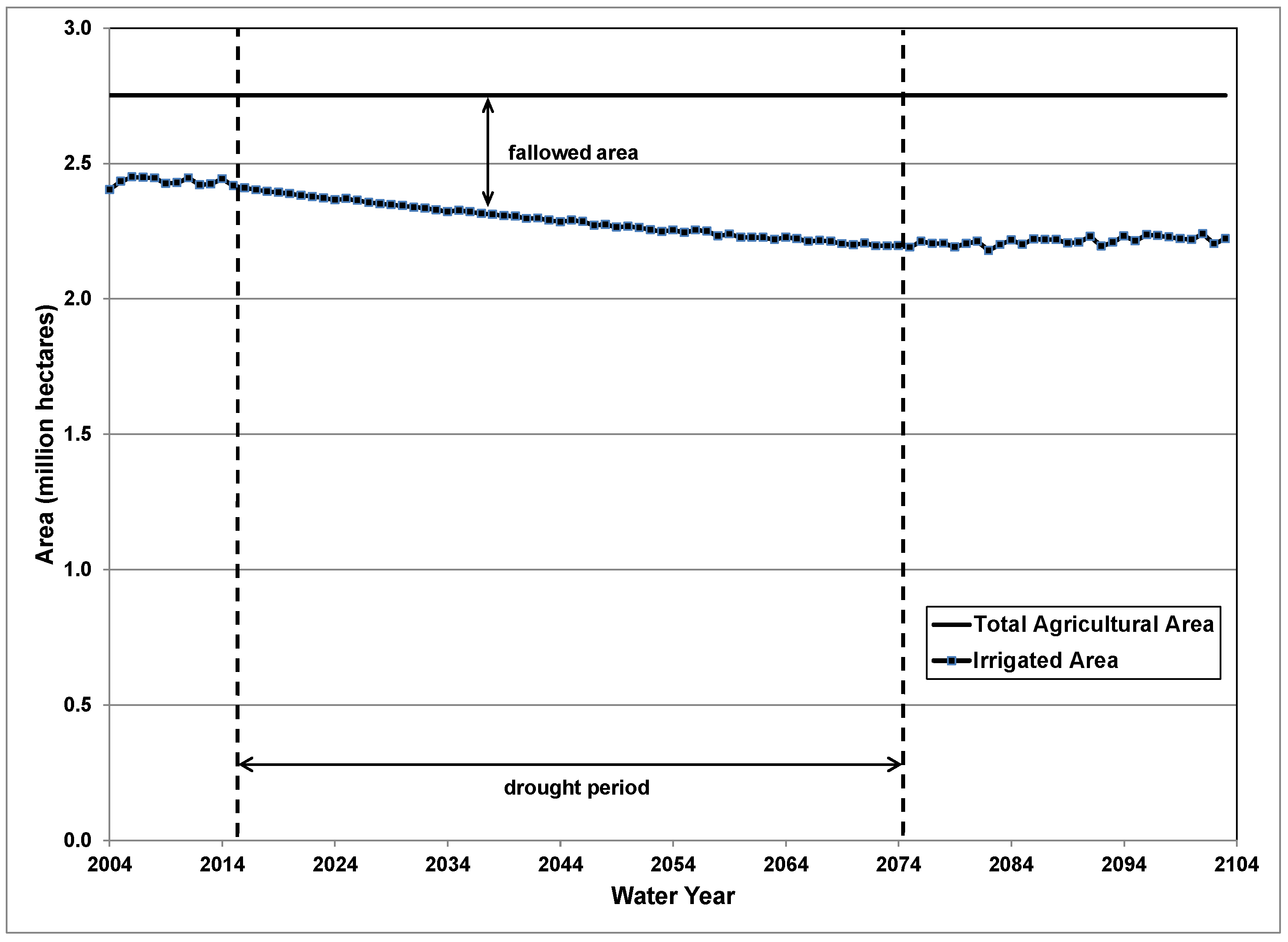
3.2. Effect of Long-Term Droughts on Groundwater in the Valley under Varying Land Use
3.3. Impact of 2012–2016 Drought on California’s Agricultural Economy
3.4. Linking a Groundwater Simulation Model to a Reservoir System Analysis Model
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Jyrkama, M.I.; Sykes, J.F. The impact of climate change on spatially varying groundwater recharge in the grand river watershed (Ontario). J. Hydrol. 2007, 338, 237–250. [Google Scholar] [CrossRef]
- Karamouz, M.; Kerachian, R.; Zahraie, B. Monthly water resources and irrigation planning: Case study of conjunctive use of surface and groundwater resources. J. Irrig. Drain. E 2004, 130, 391–402. [Google Scholar] [CrossRef]
- Swartjes, F.A. Risk-based assessment of soil and groundwater quality in the Netherlands: Standards and remediation urgency. Risk Anal. 1999, 19, 1235–1249. [Google Scholar] [CrossRef] [PubMed]
- MicroFEM. Available online: http://www.microfem.com (accessed on 13 October 2016).
- Hsieh, P.A.; Matott, S. SVFlux and ChemFlux: Software for two-dimensional/three-dimensional finite element variably saturated flow and transport modeling. Ground Water 2004, 42, 804–808. [Google Scholar]
- Voss, C.I.; Provost, A.M. SUTRA, A Model for Saturated-Unsaturated Variable-Density Ground-Water Flow with Solute or Energy Transport; Water-Resources Investigations Report 02–4231; US Geologic Survey: Reston, VA, USA, 2002.
- Brunner, P.; Simmons, C.T. HydroGeoSphere: A fully integrated, physically based hydrological model. Ground Water 2012, 50, 170–176. [Google Scholar] [CrossRef]
- Qu, Y.; Duffy, C.J. A semidiscrete finite volume formulation for multiprocess watershed simulation. Water Resources Res. 2007, 43. [Google Scholar] [CrossRef]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, the US Geological Survey Modular Ground-Water Model: User Guide to Modularization Concepts and the Ground-Water Flow Process; US Geological Survey: Reston, VA, USA, 2000.
- Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW-Coupled Ground-water and Surface-water flow model based on the integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model. (MODFLOW-2005); US Geologic Survey: Reston, VA, USA, 2008; Volume 6, p. 240.
- Kavvas, M.L.; Chen, Z.Q.; Dogrul, C.; Yoon, J.Y.; Ohara, N.; Liang, L.; Aksoy, H.; Anderson, M.L.; Yoshitani, J.; Fukami, K.; Matsuura, T. Watershed Environmental Hydrology (WEHY) model based on upscaled conservation equations: Hydrologic module. J. Hydrol. Eng. 2004, 9, 450–464. [Google Scholar] [CrossRef]
- IWFM: Integrated Water Flow Model. Available online: http://baydeltaoffice.water.ca.gov/modeling/hydrology/IWFM/ (accessed on 13 October 2016).
- Dogrul, E.C. Integrated Water Flow Model. (IWFM–2015): Theoretical documentation. Modeling Support Branch, Bay-Delta Office, Department of Water Resources: Sacramento, CA, USA, 2016. Available online: http://baydeltaoffice.water.ca.gov/modeling/hydrology/IWFM/IWFM2015/v2015_0_475/downloadables/IWFM-2015.0.475_TheoreticalDocumentation.pdf (accessed on 28 September 2016). [Google Scholar]
- Wang, H.F.; Anderson, M.P. Introduction to Groundwater Modeling: Finite Difference and Finite Element Methods; Academic Press: San Diego, CA, USA, 1995; p. 237. [Google Scholar]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer; Taylor & Francis: USA, 1984; p. 599. [Google Scholar]
- Mehl, S.W.; Hill, M.C. MODFLOW-2005, The US Geological Survey modular ground-water model–Documentation of shared node local grid refinement (LGR) and the boundary flow and head (BFH) package, 2006. Available online: http://pubs.usgs.gov/tm/2006/tm6a12/pdf/TM6-A12.pdf (accessed on 28 September 2016).
- Chaudhry, M.H. Open-Channel Flow; Springer Science & Business Media: Englewood Cliffs, NJ, USA, 2007; p. 523. [Google Scholar]
- Dogrul, E.C. IWFM Demand Calculator—IDC–2015: Theoretical documentation and user’s manual. Modeling Support Branch, Bay-Delta Office, Department of Water Resources: Sacramento, CA, USA, 2016. Available online: http://baydeltaoffice.water.ca.gov/modeling/hydrology/IDC/IDC-2015/v2015_0_42/downloadables/IDC-2015.0.42_Documentation.pdf (accessed on 30 September 2016). [Google Scholar]
- Dogrul, E.C.; Kadir, T.N.; Chung, F.I. Root Zone Moisture Routing and Water Demand Calculations in the Context of Integrated Hydrology. J. Irrig. Drain. E 2011, 137, 359–366. [Google Scholar] [CrossRef]
- Schroeder, P.R.; Aziz, N.; Lloyd, C.; Zappi, P. The Hydrologic Evaluation of Landfill Performance (HELP) Model: User’s Guide for Version 3; Report. No. EPA/600/R-94/168a; US Environmental Protection Agency: Cincinnati, OH, USA, 1994.
- NRCS. National Engineering Handbook: Part. 630—Hydrology; USDA Soil Conservation Service: Washington, DC, USA, 2004.
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Campbell, G.S. A simple method for determining unsaturated conductivity from moisture retention data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop. evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Brush, C.F.; Dogrul, E.C.; Kadir, T.N. DWR Technical Memorandum: Development and Calibration the California Central Valley Groundwater–Surface Water Simulation Model. (C2VSim), Version 3. Bay-Delta Office, California Dept. Water Resources: Sacramento, CA, USA, 2013. Available online: http://baydeltaoffice.water.ca.gov/modeling/hydrology/c2vsim/index_c2vsim.cfm (accessed on 4 October 2016). [Google Scholar]
- Scherberg, J.; Baker, T.; Selker, J.; Henry, R. Design of managed aquifer recharge for agricultural and ecological water supply assessed through numerical modeling. Water Resour. Manag. 2014, 28, 4971–4984. [Google Scholar] [CrossRef]
- HydroMetrics. County of Ventura 2013 water supply and demand, 2015. Available online: http://www.farmbureauvc.com/new/assets/pdf-forms/water-issues/2013-vent-co-water.pdf (accessed on 3 October 2016).
- YCWA. Yuba County Water Agency agricultural water management plan, 2015. Available online: http://www.water.ca.gov/wateruseefficiency/sb7/docs/2016/Yuba%20Co%20WA%202015%20AWMP.pdf (accessed on 3 October 2016).
- Treasure Valley future water demand, 2010. Idaho Water Resources Board (IWRB). Available online: http://www.idwr.idaho.gov/WaterBoard/WaterPlanning/CAMP/TV_CAMP/PDF/2010/09–29–2010_Water_Demand.pdf (accessed on 31 August 2016).
- WRIME. Task 3.3—Numerical model: Riverside/Arlington basins numerical groundwater model and GWMPs development project. 2009, p. 7. Available online: project.wrime.com/Riverside-Arlington_GW_Model/downloads/TM3–3.DOC (accessed on 3 October 2016).
- WRIME. Technical memorandum: Peer review of Sacramento Valley Finite Element Groundwater Model. (SACFEM). 2011; p. 60. Available online: http://www.waterboards.ca.gov/waterrights/water_issues/programs/bay_delta/california_waterfix/exhibits/docs/CSPA%20et%20al/aqua_65.pdf (accessed on 3 October 2016). [Google Scholar]
- USDA. 2010 State Agriculture Overview; U.S. Department of Agriculture, U.S. National Agricultural Statistics Service: Washington, DC, USA, 2011; p. 102.
- California’s Central Valley. Available online: http://ca.water.usgs.gov/projects/central-valley/about-central-valley.html (accessed on 5 October 2016).
- CDOF. 1850–2010 historical U.S. census populations of counties and unincorporated cities/towns in California. California Department of Finance: Sacramento, CA, USA, 2011. Available online: http://www.dof.ca.gov/Reports/Demographic_Reports/documents/2010–1850_STCO_IncCities-FINAL.xls (accessed on 6 October 2016). [Google Scholar]
- California State Water Project Overview. Available online: http://www.water.ca.gov/swp/ (accessed on 6 October 2016).
- Central Valley Project. Available online: http://www.usbr.gov/mp/cvp/about-cvp.html (accessed on 6 October 2016).
- CADWR. California Water Plan: Update 2005. California Dept. Water Resources: Sacramento, CA, USA, 2005. Available online: http://www.waterplan.water.ca.gov/previous/cwpu2005/index.cfm (accessed on 6 October 2016). [Google Scholar]
- Kenny, J.F.; Barber, N.L.; Hutson, S.S.; Linsey, K.S.; Lovelace, J.K.; Maupin, M.A. Estimated use of water in the United States in 2005. US Geological Survey, 2009; p. 60. Available online: https://pubs.er.usgs.gov/publication/cir1344 (accessed on 6 October 2016). [Google Scholar]
- Reilly, T.E.; Dennehy, K.F.; Alley, W.M.; Cunningham, W.L. Ground-water availability in the United States. Geological Survey (US), 2008; p. 70. Available online: http://pubs.usgs.gov/circ/1323/ (accessed on 6 October 2016). [Google Scholar]
- C2VSim: California Central Valley Groundwater-Surface Water Simulation Model. Available online: http://baydeltaoffice.water.ca.gov/modeling/hydrology/C2VSim/index_C2VSIM.cfm (accessed on 7 October 2016).
- Miller, N.L.; Dale, L.L.; Brush, C.F.; Vicuna, S.D.; Kadir, T.N.; Dogrul, E.C.; Chung, F.I. Drought Resilience of the California Central Valley Surface-Ground-Water-Conveyance System. J. Am. Water Resour. As. 2009, 45, 857–866. [Google Scholar] [CrossRef]
- Dale, L.L.; Dogrul, E.C.; Brush, C.F.; Kadir, T.N.; Chung, F.I.; Miller, N.L.; Vicuna, S.D. Simulating the impact of drought on California’s central valley hydrology, groundwater and cropping. Br. J. Environ. Clim. Chang. 2013, 3, 271–291. [Google Scholar] [CrossRef]
- Medellín-Azuara, J.; MacEwan, D.; Howitt, R.; Koruakos, G.; Dogrul, E.; Brush, C.; Kadir, T.; Harter, T.; Melton, F.; Lund, J. Hydro-economic analysis of groundwater pumping for irrigated agriculture in California’s Central Valley, USA. Hydrogeol. J. 2015, 23, 1205–1216. [Google Scholar] [CrossRef]
- Dogrul, E.C.; Kadir, T.N.; Brush, C.F.; Chung, F.I. Linking groundwater simulation and reservoir system analysis models: The case for California’s Central Valley. Environ. Model. Softw. 2016, 77, 168–182. [Google Scholar] [CrossRef]
- RMC. Transitioning to sustainability: Modeling groundwater sustainability in the Kings-Tulare Lake region. RMC Water and Environment. M. Cubed. ERA Economics. 2015, p. 23. Available online: http://californiawaterfoundation.org/wp-content/uploads/CWF-Transitioning-to-Sustainability-Final-Report_11_09_2015.pdf (accessed on 7 October 2016).
- RMC. RMC Water and Environment; The Nature Conservancy. Groundwater and stream interaction in California’s Central Valley: Insights for sustainable groundwater management. 2016, p. 140. Available online: http://scienceforconservation.org/dl/GroundwaterStreamInteraction_2016.pdf (accessed on 7 October 2016).
- Howitt, R.; Medellin-Azuara, J.; MacEwan, D.; Lund, J.; Sumner, D.; Howitt, R.; Medellin-Azuara, J.; MacEwan, D.; Lund, J.; Sumner, D. Economic analysis of the 2014 drought for California agriculture. 2014, p. 16. Available online: http://www.circleofblue.org/wp-content/uploads/2014/07/Economic_Impact_of_the_2014_California_Water_Drought_0.pdf (accessed on 7 October 2016).
- Howitt, R.; MacEwan, D.; Medellin-Azuara, J.; Lund, J.; Sumner, D.; Howitt, R.; MacEwan, D.; Medellin-Azuara, J.; Lund, J.; Sumner, D. Economic analysis of the 2015 drought for California agriculture. 2015, p. 16. Available online: https://watershed.ucdavis.edu/files/biblio/Economic_Analysis_2015_California_Drought__Main_Report.pdf (accessed on 11 October 2016).
- Draper, A.J.; Munevar, A.; Arora, S.K.; Reyes, E.; Parker, N.L.; Chung, F.I.; Peterson, L.E. CalSim: Generalized model for reservoir system analysis. J. Water Res. Pl. 2004, 130, 480–489. [Google Scholar] [CrossRef]
- Farnam, F. Irrigation Technology Adoption in Agriculture. Ph.D. Thesis, University of California, Davis, CA, USA, 1994. [Google Scholar]
- Howitt, R.E. Positive Mathematical Programming. Am. J. Agric. Econ. 1995, 77, 329–342. [Google Scholar] [CrossRef]
- Howitt, R.E.; Medellín-Azuara, J.; MacEwan, D.; Lund, J.R. Calibrating disaggregate economic models of agricultural production and water management. Environ. Model. Softw. 2012, 38, 244–258. [Google Scholar] [CrossRef]
- Yates, D.; Sieber, J.; Purkey, D.; Huber-Lee, A. WEAP21—A demand-, priority-, and preference-driven water planning model: Part 1: Model characteristics. Water Int. 2005, 30, 487–500. [Google Scholar] [CrossRef]
- Cai, X.M.; McKinney, D.C.; Lasdon, L.S. Integrated hydrologic-agronomic-economic model for river basin management. J. Water Res. Pl. 2003, 129, 4–17. [Google Scholar] [CrossRef]
- Fredericks, J.W.; Labadie, J.W.; Altenhofen, J.M. Decision support system for conjunctive stream-aquifer management. J. Water Res. Pl. 1998, 124, 69–78. [Google Scholar] [CrossRef]
- MODSIM 8.1: River basin management decision support system: User manual and documentation. Available online: http://modsim.engr.colostate.edu/modsim.php (accessed on 2 September 2016).
- Belaineh, G.; Peralta, R.C.; Hughes, T.C. Simulation/optimization modeling for water resources management. J. Water Res. Pl. 1999, 125, 154–161. [Google Scholar] [CrossRef]
- Illangasekare, T.H.; Morel-Seytoux, H.J. Algorithm for Surface/Ground-Water Allocation under Appropriation Doctrine. Groundwater 1986, 24, 199–206. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Ahlfeld, D.; Andreu, J.; Sahuquillo, A. Reducing the computational cost of unconfined groundwater flow in conjunctive-use models at basin scale assuming linear behaviour: The case of Adra-Campo de Dalias. J. Hydrol. 2008, 353, 159–174. [Google Scholar] [CrossRef]
- Triana, E.; Labadie, J.W.; Gates, T.K.; Anderson, C.W. Neural network approach to stream-aquifer modeling for improved river basin management. J. Hydrol. 2010, 391, 235–247. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dogrul, E.C.; Brush, C.F.; Kadir, T.N. Groundwater Modeling in Support of Water Resources Management and Planning under Complex Climate, Regulatory, and Economic Stresses. Water 2016, 8, 592. https://doi.org/10.3390/w8120592
Dogrul EC, Brush CF, Kadir TN. Groundwater Modeling in Support of Water Resources Management and Planning under Complex Climate, Regulatory, and Economic Stresses. Water. 2016; 8(12):592. https://doi.org/10.3390/w8120592
Chicago/Turabian StyleDogrul, Emin C., Charles F. Brush, and Tariq N. Kadir. 2016. "Groundwater Modeling in Support of Water Resources Management and Planning under Complex Climate, Regulatory, and Economic Stresses" Water 8, no. 12: 592. https://doi.org/10.3390/w8120592
APA StyleDogrul, E. C., Brush, C. F., & Kadir, T. N. (2016). Groundwater Modeling in Support of Water Resources Management and Planning under Complex Climate, Regulatory, and Economic Stresses. Water, 8(12), 592. https://doi.org/10.3390/w8120592





