Hydrological Responses to Land Use/Cover Changes in the Olifants Basin, South Africa
Abstract
:1. Introduction
2. Materials and Methods
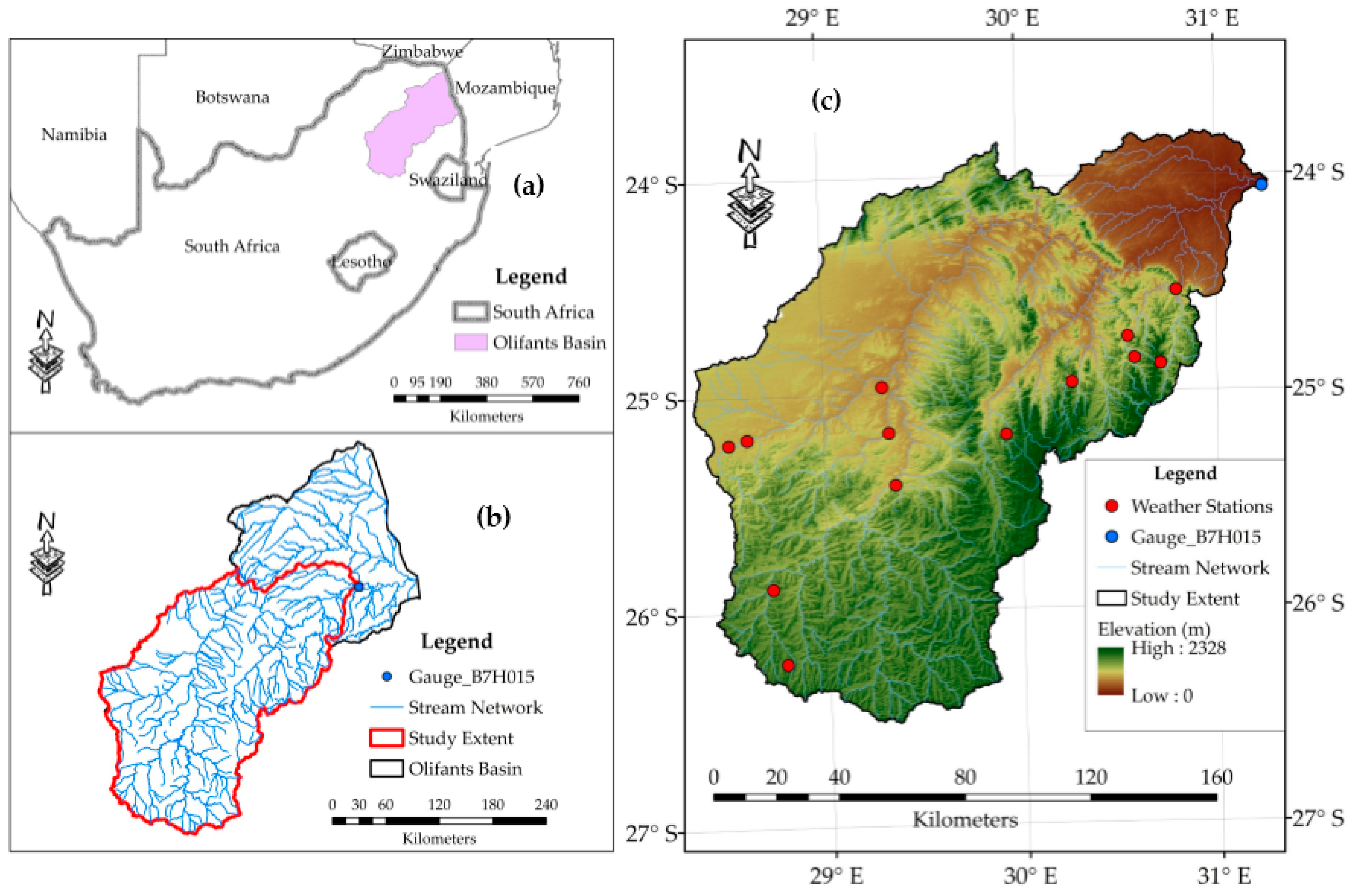
2.1. Study Location
2.2. Model Selection and Description
2.3. Model Inputs
2.4. Model Calibration and Validation
- Coefficient of determination (R2): It measures the proportional variation in the simulated variable explainable by the observed variable and gives an indication of the linear relationship between the simulated and observed variables. R2 is calculated as follows:
- Nash–Sutcliffe efficiency (NSE): This statistic determines the relative magnitude of the residual variance compared to the observed data variance. NSE ranges from − to 1, where 1 denotes perfect agreement between simulated and observed variables. NSE is formulated as:
- RMSE observations standard deviation ratio (RSR): RSR standardizes the root mean square error (RMSE) using the observation standard deviations. It is calculated as:
- Percent Bias (PBIAS): PBIAS is a measure of how much (in percentage) the observed variable is either underestimated or overestimated. It is calculated as shown:where is the observed variable, is the simulated variable, is the mean of the observed variable, is the mean of the simulated variable, n is the number of observations under consideration, RMSE is the root mean square error, is the standard deviation of the observed variable.
2.5. Model Application
2.6. Statistical Analysis
3. Results and Discussion
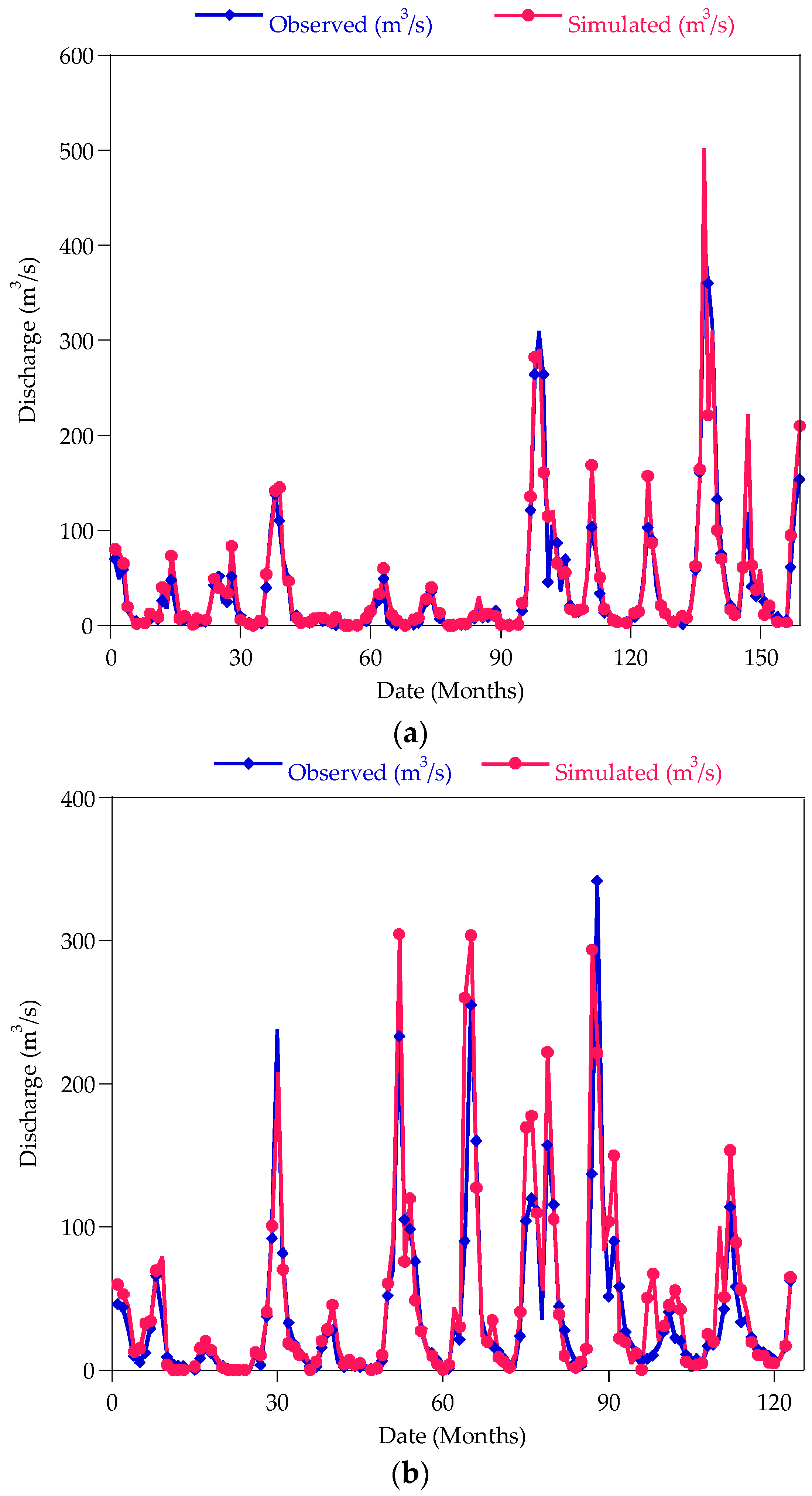
3.1. Calibration and Validation of the SWAT Model
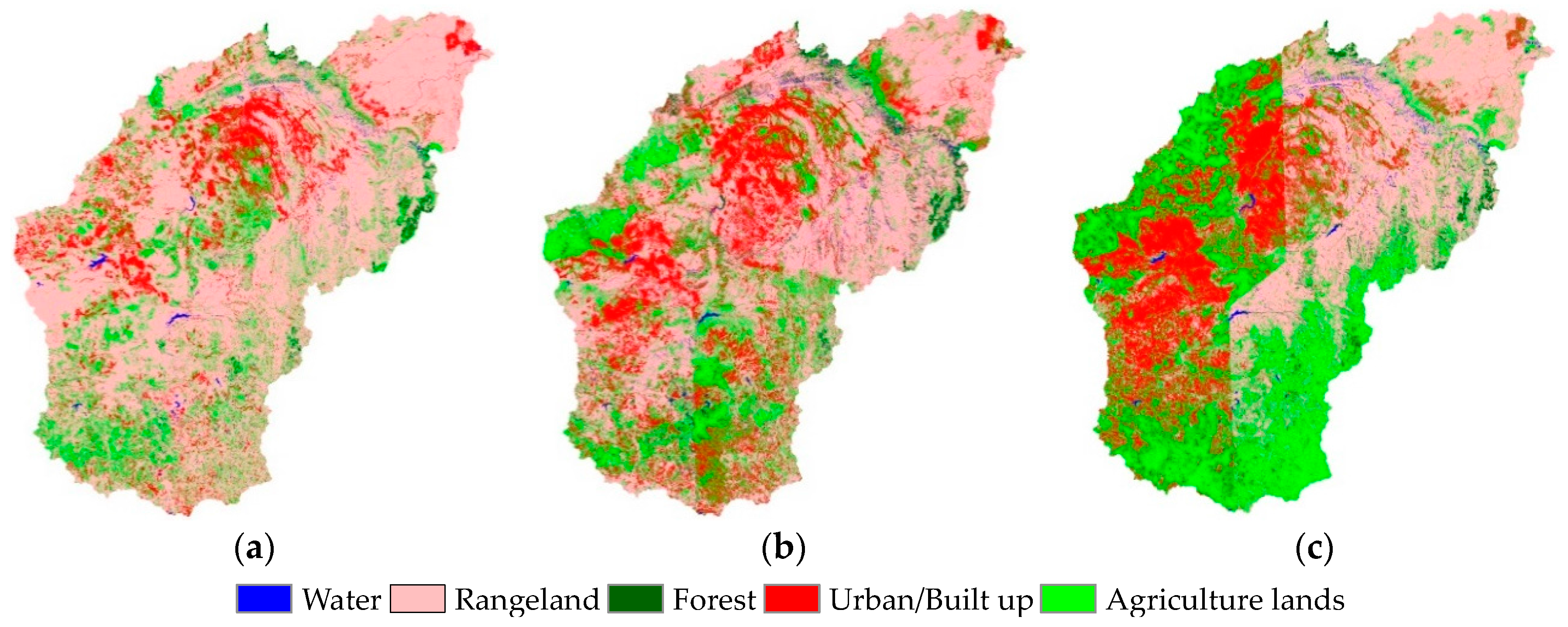
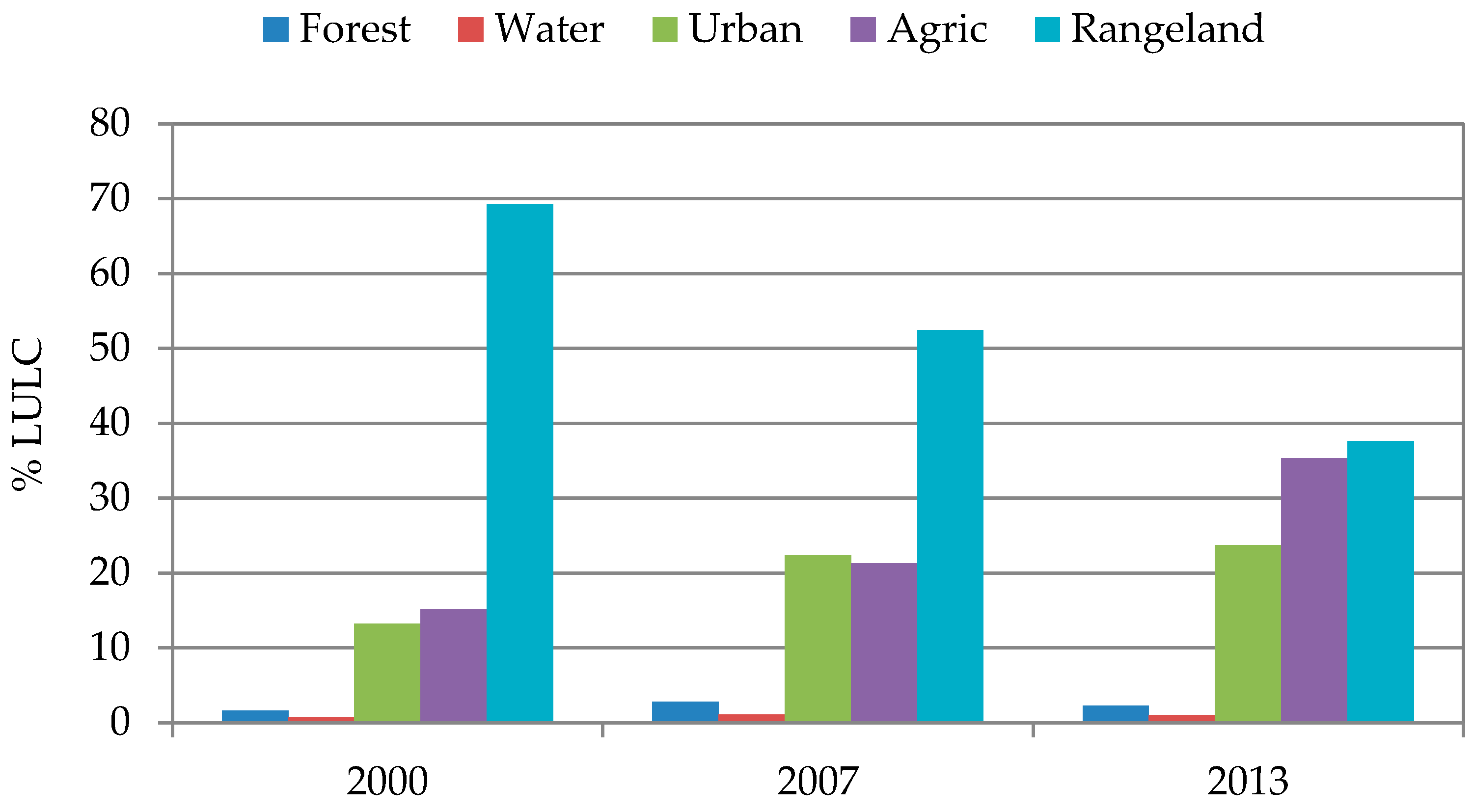
3.2. Land Use Change Detection
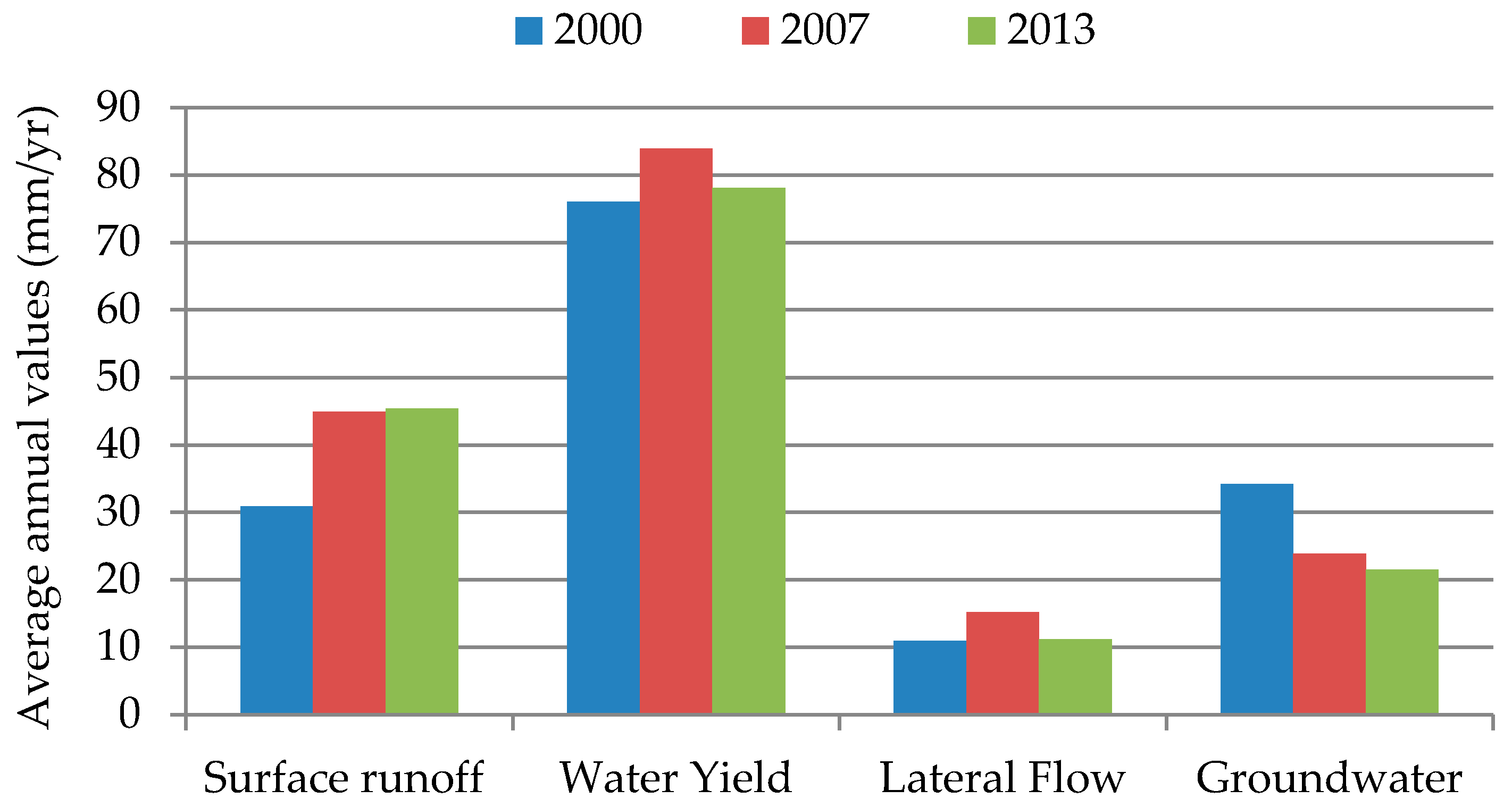
3.3. Hydrological Responses to Different Land Use Scenarios at the Basinal Scale
3.4. Alterations in Water Balance Ratios
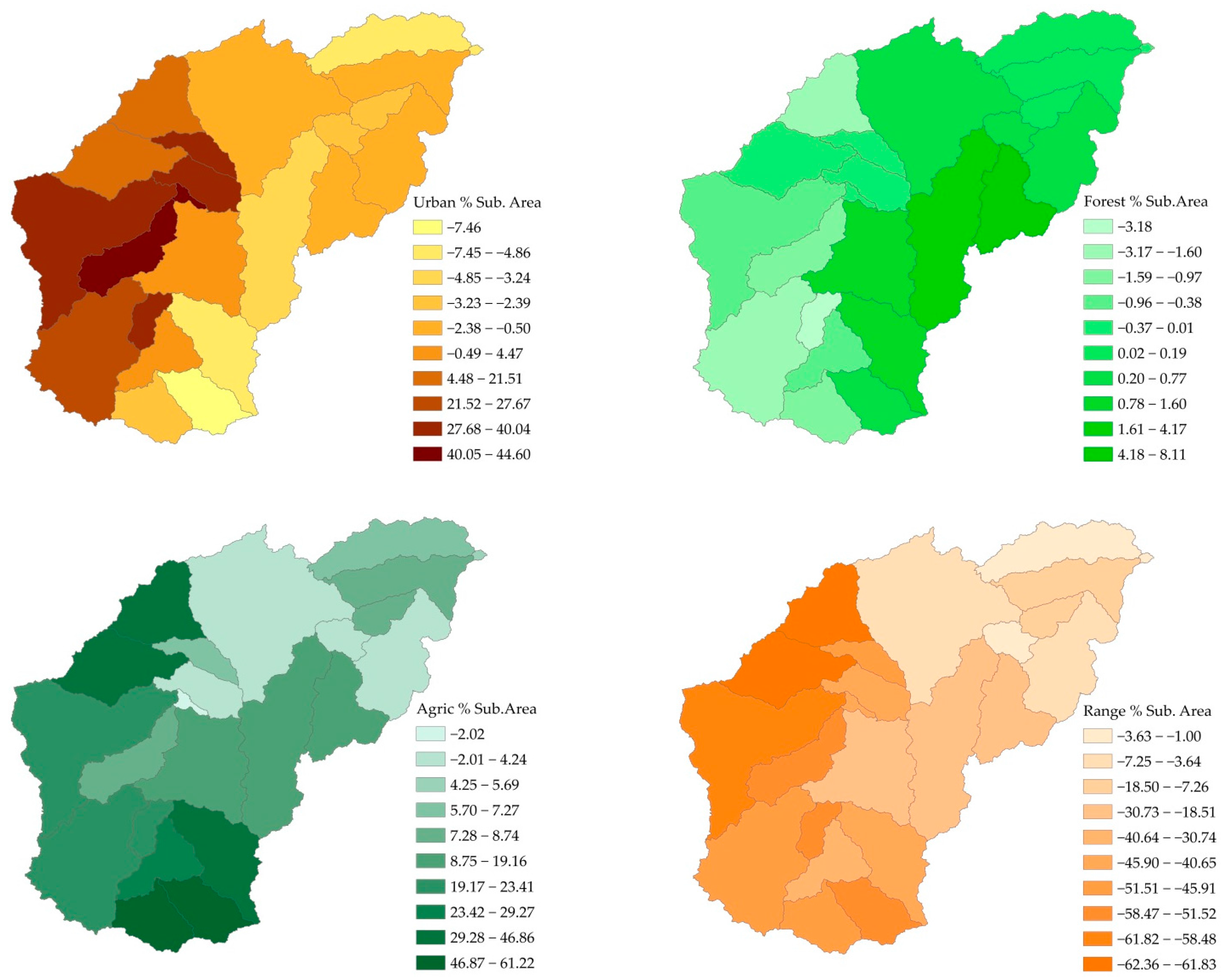
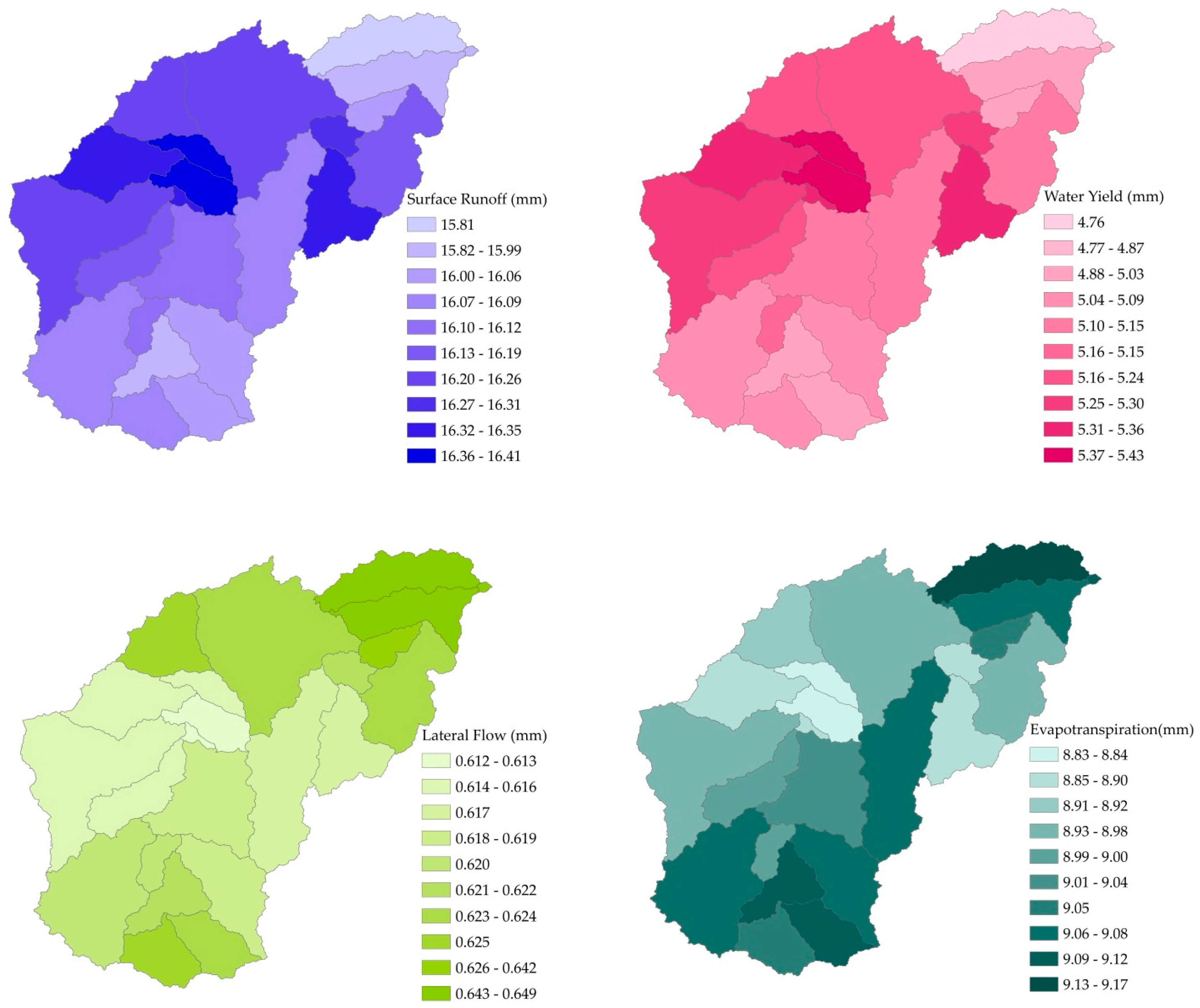
3.5. Contributions of Changes in Individual LULCs on Hydrological Components at the Sub-Basinal Scale
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Githui, F.; Mutua, F.; Bauwens, W. Estimating the impacts of land cover change on runoff using the soil and water assessment tool (SWAT): Case study of Nzoia catchment, Kenya. Hydrol. Sci. J. 2010, 54, 899–908. [Google Scholar] [CrossRef]
- Cai, T.; Li, Q.; Yu, M.; Lu, G.; Cheng, L.; Wei, X. Investigation into the impacts of land use change on sediment yield characteristics in the upper Huaihe River basin, China. Phys. Chem. Earth B 2012, 53–54, 1–9. [Google Scholar] [CrossRef]
- Baker, T.J.; Miller, S.N. Using the Soil and Water Assessmnent Tool (SWAT) to assess land use impact on water resources in an East African watershed. J. Hydrol. 2013, 486, 100–111. [Google Scholar] [CrossRef]
- Yan, B.; Fang, N.F.; Zhang, P.C.; Shi, Z.H. Impacts of land use change on watershed streamflow and sediment yield: An assessment using hydrologic modelling and partial least squares regression. J. Hydrol. 2013, 484, 26–37. [Google Scholar] [CrossRef]
- Woldesenbet, T.A.; Elagib, N.A.; Ribbe, L.; Heinrich, J. Hydrological responses to land use/cover changes in the source region of the Upper Blue Nile Basin, Ethiopia. Sci. Total Environ. 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Van Werkhoven, K.; Wagener, T. Hydrological impacts of climate change in gauged and ungauged watersheds of the Olifants basin: A trading-space-for-time approach. Hydrol. Sci. J. 2014, 59, 29–55. [Google Scholar] [CrossRef]
- Uhlenbrook, S.; McDonnell, J.; Leibundgut, C. Run-off generation and implications for river basin modelling special issue. Hydrol. Process. 2003, 17, 197–198. [Google Scholar] [CrossRef]
- Wang, S.; Kang, S.; Zhang, L.; Li, F. Modelling hydrological response to different land use and climate change scenarios in the Zamu River basin of the northwest China. Hydrol. Process. 2008, 22, 2502–2510. [Google Scholar] [CrossRef]
- Ghaffari, G.; Keesstra, S.; Ghodousi, J.; Ahmadi, H. SWAT–Simulated hydrological impact of land use change in the Zanjanrood Basin, Northwest Iran. Hydrol. Process. 2010, 24, 892–903. [Google Scholar] [CrossRef]
- Karvonen, T.; Koivusalo, H.; Jauhiainen, M. A hydrological model for predicting runoff from different land use areas. J. Hydrol. 1999, 217, 253–265. [Google Scholar] [CrossRef]
- Fohrer, N.; Haverkamp, S.; Eckhardt, K.; Frede, H.G. Hydrologic response to land use changes on the catchment scale. Phys. Chem. Earth B 2001, 26, 577–582. [Google Scholar] [CrossRef]
- Felix, N.; Simon, S.; Markus, W.A. Process based assessment of the potential to reduce flood runoff by land use change. J. Hydrol. 2002, 267, 74–79. [Google Scholar]
- Niraula, R.; Meixner, T.; Norman, L. Determining the importance of model calibration for forecasting absolute/relative changes in streamflow from LULC and climate changes. J. Hydrol. 2015, 522, 439–451. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Qiu, L.; Sun, Y. SWAT-DayCent coupler: An integration tool for simultaneous hydro-biogeochemical modeling using SWAT and DayCent. Environ. Model. Softw. 2016, 86, 81–90. [Google Scholar] [CrossRef]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in Alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef] [PubMed]
- Muenich, R.L.; Chaubey, I.; Pyron, M. Evaluating potential water quality of a fish regime shift in the Wabash River using the SWAT model. Ecol. Model. 2016, 340, 116–125. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, L.; Kong, X. Estimating spatiotemporal varaibility and sustainability of shallow groundwater in a well-irrigated plain of the Haihe River basin uisng SWAT model. J. Hydrol. 2016, 541, 1221–1240. [Google Scholar] [CrossRef]
- Briak, H.; Moussadek, R.; Aboumaria, K.; Mrabet, R. Assessing sediment yield in Kalaya gauged watershed (Northern Morocco) using GIS and SWAT model. Int. Soil Water Conserv. Res. 2016, 4, 177–185. [Google Scholar] [CrossRef]
- Stoll, S.; Franssen, H.; Butts, M.; Kinzelbach, W. Analysis of the impact of climate change on groundwater related hydrologicalfluxes: A multi-model approach including different downscaling methods. Hydrol. Earth Syst. Sci. 2011, 15, 21–38. [Google Scholar] [CrossRef]
- Cuo, L.; Lettenmaier, D.P.; Mattheussen, B.V.; Storck, P.; Wiley, M. Hydrological prediction for urban watersheds with the distributed hydrology soil vegetation model. Hydrol. Process. 2008, 22, 4205–4213. [Google Scholar] [CrossRef]
- Qi, S.; Sun, G.; Wang, Y.; McNulty, S.G.; Myers, J.A.M. Streamflow response to climate and landuse changes in a coastal watershed in North Carolina. Trans. ASABE 2009, 52, 739–749. [Google Scholar] [CrossRef]
- Stathis, D.; Sapountzis, M.; Myronidis, D. Assessment of land use change effect on a design storm hydrograph using the SCS curve number method. Fresenius Environ. Bull. 2010, 19, 1928–1934. [Google Scholar]
- Nie, W.; Yuan, Y.; Kepner, W.; Nash, M.S.; Jackson, M.; Erickson, C. Assessing impacts of land use and land cover changes on hydrology for the upper San Pedro watershed. J. Hydrol. 2011, 407, 105–114. [Google Scholar] [CrossRef]
- Department of Water Affairs. Draft National Water Resource Strategy 2 (NWRS 2): Managing Water for an Equitable and Sustainable Future; DWA: Pretoria, South Africa, 2012.
- Gyamfi, C.; Ndambuki, J.M.; Salim, R.W. A historical analysis of rainfall trend in the Olifants Basin in South Africa. Earth Sci. Res. 2016, 5, 129–142. [Google Scholar] [CrossRef]
- Food and Agriculture Organization. Digital Soil Map of the World and Derived Soil Properties of the World; Food and Agricultural Organization of the United Nations: Rome, Italy, 2005. [Google Scholar]
- McCartney, M.P.; Yawson, D.K.; Magagula, T.F.; Seshoka, J. Hydrology and Water Resources Development in the Olifants River Catchment: Working Paper 76; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2004. [Google Scholar]
- Arnold, J.G.; Fohrer, N. Current capabilities and research opportunities in applied watershed modeling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Res. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, W.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; USGS (United States Geological Survey): Washington, VI, USA, 1976; Volume 964, pp. 138–145.
- Di Luzio, M.; Johnson, G.L.; Daly, C.; Eischeid, J.K.; Arnold, J.G. Constructing retrospective gridded daily precipitation and temperature datasets for the conterminous United States. J. Appl. Meteorol. Clim. 2008, 47, 475–497. [Google Scholar] [CrossRef]
- Gyamfi, C.; Ndambuki, J.M.; Salim, R.W. Application of SWAT Model to the Olifants Basin: Calibration, Validation and Uncertainty Analysis. J. Water Res. Prot. 2016, 8, 397–410. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wang, G.; Xia, J.; Chen, J. Quantification of the effects of climate variations and human activities on runoff by a monthly water balance model: A case study of the Chaobai River Basin in Northern China. Water Res. 2009, 45, W00A11. [Google Scholar] [CrossRef]
- Tang, L.H.; Yang, D.W.; Hu, H.P.; Gao, B. Detecting the effect of land use change on streamflow, sediment and nutrient losses by distributed hydrological simulation. J. Hydrol. 2011, 409, 172–182. [Google Scholar] [CrossRef]
- Lin, B.; Chen, X.; Yao, H.; Chen, Y.; Liu, M.; Gao, L.; James, A. Analysis of landuse change impacts on catchment runoff using different time indicators based on SWAT model. Ecol. Indic. 2015, 58, 55–63. [Google Scholar] [CrossRef]
- Viera, A.J.; Garrett, J.M. Understanding inter-observer agreement: The Kappa statistic. Fam. Med. 2005, 37, 360–363. [Google Scholar] [PubMed]
- Department of Water Affairs. Development of a Reconciliation Strategy for the Olifants River Water Supply System: Summary Report; Report No. P WMA 04/B50/00/8310/2; DWA: Pretoria, South Africa, 2010.
- Tripathi, M.P.; Panda, R.K.; Raghuwanshi, N.S. Development of effective management plan for critical subwatersheds using SWAT model. Hydrol. Process. 2005, 19, 809–826. [Google Scholar] [CrossRef]
- De Lange, M.; Merrey, D.J.; Levite, H.; Svendsen, M. Water Resources Planning and Management in the Olifants Basin of South Africa: Past, Present and Future; IWMI: Pretoria, South Africa, 2003. [Google Scholar]
- Department of Water Affairs. Development of a Reconciliation Strategy for the Olifants River Water Supply System. Groundwater Options Report; Report no. PWMA 04/B50/00/8310/10; DWA: Pretoria, South Africa, 2011.
- Calow, R.C.; Macdonald, A.M. What Will Climate Change Mean for Groundwater Supply in Africa? Background Note; Overseas Development Institute (ODI): London, UK, 2009. [Google Scholar]
- Calow, R.C.; Robins, N.S.; Macdonald, A.M.; Macdonald, D.M.J.; Gibbs, B.R.; Orpen, W.R.G.; Mtembezeka, P.; Andrews, A.J.; Appiah, S.O. Groundwater management in drought-prone areas of Africa. Int. J. Water Res. Dev. 1997, 13, 241–262. [Google Scholar] [CrossRef]
- Paul, M.J.; Meyer, J.L. Streams in the urban landscape. Ann. Rev. Ecol. Evol. Syst. 2001, 32, 333–365. [Google Scholar] [CrossRef]
- Poff, N.L.; Bledsoe, B.P.; Cuhaciyan, C.O. Hydrologic variation with land use across the contiguous United States: Geomorphic and ecological consequences for stream ecosystems. Geomorphology 2006, 79, 264–285. [Google Scholar] [CrossRef]
- Roy, A.H.; Freeman, M.C.; Freeman, B.J.; Wenger, S.J.; Ensign, W.E.; Meyer, J.L. Investigating hydrologic alterations as a mechanism of fish asssemblages shifts in urbanizing streams. J. N. Am. Benthol. Soc. 2005, 24, 656–678. [Google Scholar] [CrossRef]
- Walsh, C.J.; Roy, A.H.; Feminella, J.W.; Cottingham, P.D.; Groffman, P.M.; Morgan, R.P. The urban stream syndrome: Current knowledge and the search for a cure. J. N. Am. Benthol. Soc. 2005, 24, 706–723. [Google Scholar] [CrossRef]
- Schulze, R.E.; Maharaj, M.; Lynch, S.D.; Howe, B.J.; Melvil-Thomson, B. South African Atlas for Agrohydrology and Climatology; University of Natal: Pietermaritzburg, South Africa, 1997. [Google Scholar]
- Department of Water Affairs. Water Resources Planning of the Olifants River Basin—Study of Development Potential and Management of the Water Resources; DWA: Pretoria, South Africa, 1991.
- Gyamfi, C.; Ndambuki, J.M.; Salim, R.W. Simulation of Sediment Yield in a Semi-Arid River Basin under Changing Land Use: An integrated approach of hydrologic modelling and principal component analysis. Sustainability 2016, 8, 1133. [Google Scholar] [CrossRef]
| Acquisition Date | Path | Row | Image ID |
|---|---|---|---|
| 3 June 2000 | 169 | 077 | LE71690772000155SGS00 |
| 3 June 2000 | 169 | 078 | LE71690782000155SGS00 |
| 23 April 2000 | 170 | 077 | LE71700772000114SGS01 |
| 23 April 2000 | 170 | 078 | LE71700782000114SGS01 |
| 22 May 2007 | 169 | 077 | LE71690772007142ASN00 |
| 23 June 2007 | 169 | 078 | LE71690782007174ASN00 |
| 13 May 2007 | 170 | 077 | LE71700772007133ASN00 |
| 18 September 2007 | 170 | 078 | LE71700782007261ASN00 |
| 7 June 2013 | 169 | 077 | LE71690772013158ASN00 |
| 6 May 2013 | 169 | 078 | LE71690782013126ASN00 |
| 14 June 2013 | 170 | 077 | LE71700772013165ASN00 |
| 14 June 2013 | 170 | 078 | LE71700782013165ASN00 |
| Land Cover Class | Description |
|---|---|
| Rangeland | Herbaceous, shrub and brush and mixed rangeland |
| Water | Lakes, reservoirs, stream |
| Agricultural lands | Crop fields and pastures |
| Forest | Deciduous, evergreen and mixed forest |
| Urban/Built up | Residential, commercial services, industrial, transportation, communications, mixed urban or built up lands |
| Parameter | Description | Range | Fitted Value | t-Stat (Absolute Values) |
|---|---|---|---|---|
| CN2 | Runoff curve number | 35–98 | 65 * | 37.72 |
| ALPHA_BNK | Base flow alpha factor for bank storage | 0–1 | 0.39 | 6.97 |
| ESCO | Soil evaporation compensation factor | 0–1 | 0.67 | 5.57 |
| SOIL_AWC | Soil available water capacity | 0–1 | 0.2 | 4.13 |
| GW_DELAY | Groundwater delay (days) | 0–500 | 345 | 3.02 |
| GW_REVAP | Groundwater “revap” coefficient | 0.02–0.2 | 0.15 | 2.34 |
| Performance Rating | PBIAS (%) | RSR | NSE |
|---|---|---|---|
| Very good | 0.00 | 0.75 | |
| Good | 0.50 | 0.65 | |
| Satisfactory | 0.60 | 0.50 | |
| Unsatisfactory |
| Model Stage | Evaluation Statistics * | |||
|---|---|---|---|---|
| R2 | NSE | RSR | PBIAS (%) | |
| Calibration (1988–2001) | 0.89 | 0.88 | 0.34 | −11.49 |
| Validation (2002–2013) | 0.78 | 0.67 | 0.57 | −20.69 |
| Land Cover Class | 2000 | 2007 | 2013 | |||
|---|---|---|---|---|---|---|
| Producers’ | Users’ | Producers’ | Users’ | Producers’ | Users’ | |
| Urban/Built up | 65.63 | 80.77 | 87.50 | 94.23 | 84.00 | 84.00 |
| Rangeland | 97.50 | 89.14 | 97.69 | 88.81 | 89.01 | 82.65 |
| Water | 100.0 | 100.00 | 100.00 | 100.00 | 100.00 | 85.71 |
| Agriculture | 76.36 | 87.50 | 86.27 | 86.27 | 88.54 | 88.54 |
| Forest | 71.43 | 100.00 | 41.18 | 87.50 | 30.77 | 80.00 |
| Overall accuracy | 88.28 | 89.45 | 85.16 | |||
| Kappa | 77.43 | 83.00 | 78.28 | |||
| Hydrologic Component | LULC Scenario | ||
|---|---|---|---|
| 2000 | 2007 | 2013 | |
| Surface runoff (mm) | 30.91 | 44.91 | 45.43 |
| Water yield (mm) | 76.04 | 83.92 | 78.11 |
| Lateral flow (mm) | 10.92 | 15.18 | 11.18 |
| Groundwater (mm) | 34.21 | 23.84 | 21.5 |
| Evapotranspiration (mm) | 518.40 | 546.60 | 531.40 |
| LULC Scenario | Water Balance Ratios * | |||||
|---|---|---|---|---|---|---|
| B/TF | SR/TF | SF/P | PC/P | DR/P | ET/P | |
| 2000 | 0.26 | 0.74 | 0.07 | 0.1 | 0.05 | 0.78 |
| 2007 | 0.25 | 0.75 | 0.09 | 0.05 | 0.04 | 0.82 |
| 2013 | 0.24 | 0.76 | 0.09 | 0.08 | 0.03 | 0.80 |
| SURQ | WYLD | ET | LAT Q | FRST | URHD | AGRL | RNGB | |
|---|---|---|---|---|---|---|---|---|
| SURQ | 1.00 | |||||||
| WYLD | 0.98 | 1.00 | ||||||
| ET | −0.99 | −0.96 | 1.00 | |||||
| LAT Q | −0.72 | 0.81 | 0.65 | 1.00 | ||||
| FRST | 0.09 | 0.13 | 0.05 | −0.15 | 1.00 | |||
| URHD | 0.88 | 0.82 | −0.24 | 0.36 | −0.44 | 1.00 | ||
| AGRL | 0.61 | 0.54 | 0.15 | −0.31 | 0.00 | 0.43 | 1.00 | |
| RNGB | −0.15 | −0.22 | 0.08 | 0.42 | 0.21 | −0.85 | −0.83 | 1.00 |
| Responses | Predictors | R2 | |||
|---|---|---|---|---|---|
| Urban | Agric | Forest | Rangeland | ||
| Surface runoff | 0.48(+) | 0.13(+) | 0.61 | ||
| Water yield | 0.54(+) | 0.13(+) | 0.08(−) | 0.75 | |
| Lateral flow | 0.14(+) | 0.53(+) | 0.67 | ||
| ET | 0.48(+) | 0.15(+) | 0.63 | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyamfi, C.; Ndambuki, J.M.; Salim, R.W. Hydrological Responses to Land Use/Cover Changes in the Olifants Basin, South Africa. Water 2016, 8, 588. https://doi.org/10.3390/w8120588
Gyamfi C, Ndambuki JM, Salim RW. Hydrological Responses to Land Use/Cover Changes in the Olifants Basin, South Africa. Water. 2016; 8(12):588. https://doi.org/10.3390/w8120588
Chicago/Turabian StyleGyamfi, Charles, Julius M. Ndambuki, and Ramadhan W. Salim. 2016. "Hydrological Responses to Land Use/Cover Changes in the Olifants Basin, South Africa" Water 8, no. 12: 588. https://doi.org/10.3390/w8120588
APA StyleGyamfi, C., Ndambuki, J. M., & Salim, R. W. (2016). Hydrological Responses to Land Use/Cover Changes in the Olifants Basin, South Africa. Water, 8(12), 588. https://doi.org/10.3390/w8120588





