Experimental and Numerical Analysis of Egg-Shaped Sewer Pipes Flow Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Egg-Shaped Section Definition
2.2. Experimental Set-Up
2.3. CFD Model
3. Results
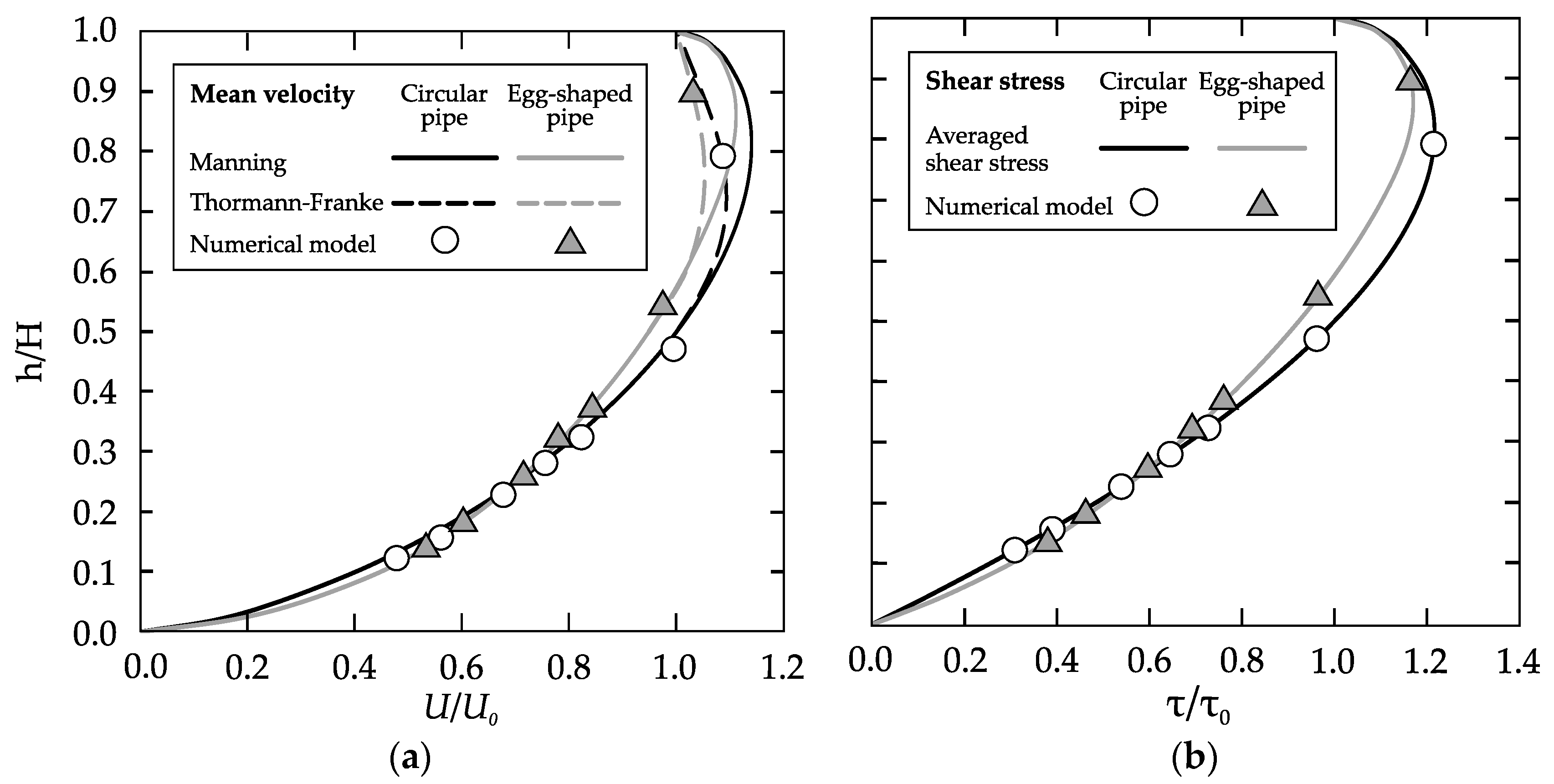
3.1. Boundary Shear Stress and Centreline Velocity Profiles
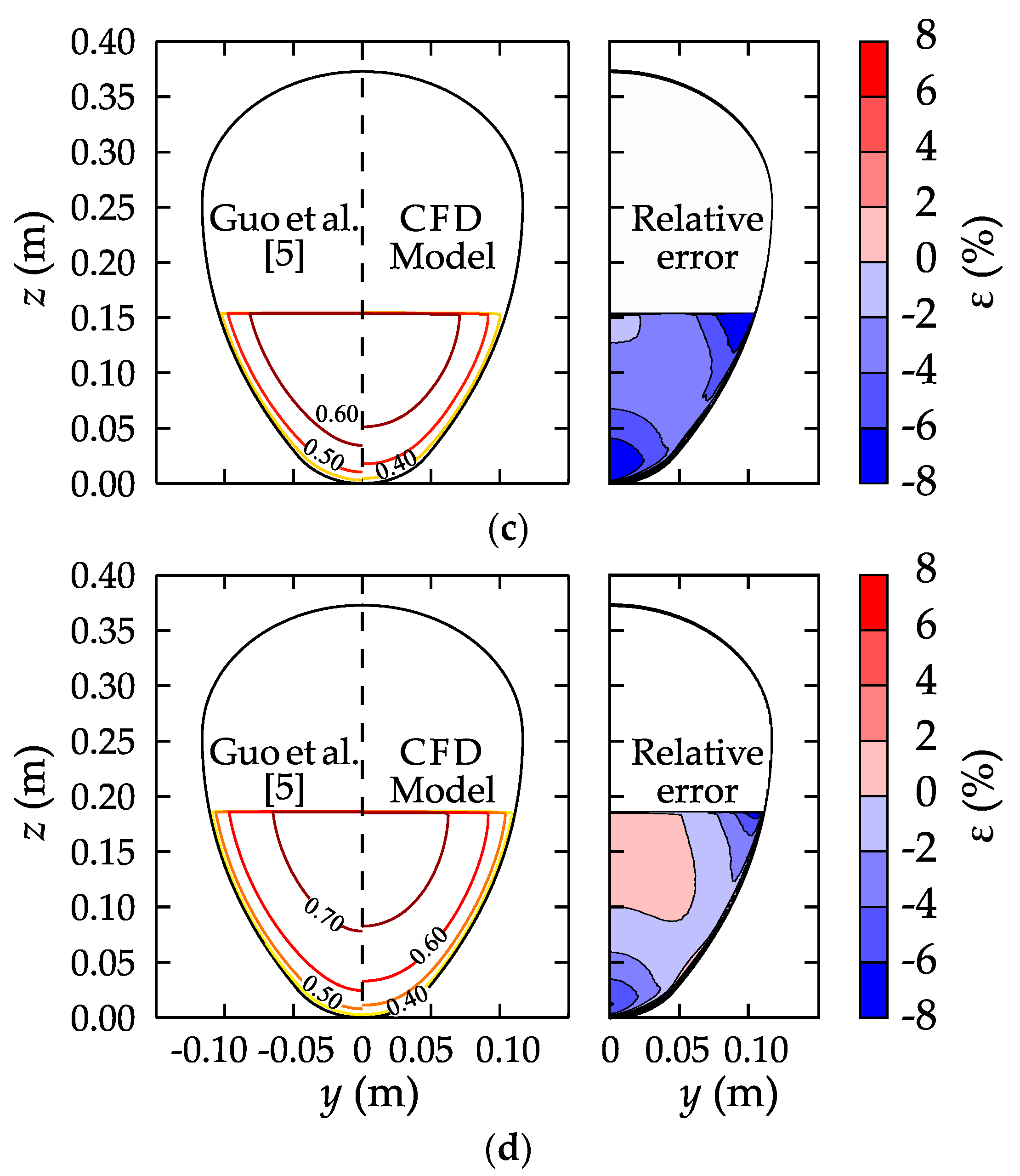
3.2. Cross-Sectional Velocity Distributions
3.3. Numerical Comparison of Circular and Egg-Shaped Mean Flow Behavior
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Butler, D.; Davies, J. Urban Drainage, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Suarez, J.; Puertas, J. Determination of COD, BOD, and suspended solids loads during combined sewer overflow (CSO) events in some combined catchments in Spain. Ecol. Eng. 2005, 24, 199–217. [Google Scholar] [CrossRef]
- Suarez, J.; Puertas, J.; Anta, J.; Jacome, A.; Alvarez-Campana, J.M. Gestión integrada de los recursos hídricos en el sistema agua urbana: Desarrollo Urbano Sensible al Agua como enfoque estratégico. Ingeniería Agua 2014, 18, 111–123. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; A.A. Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Guo, J.; Mohebbi, A.; Zhai, Y.; Clark, S.P. Turbulent velocity distribution with dip phenomenon in conic open channels. J. Hydraul. Res. 2015, 53, 73–82. [Google Scholar] [CrossRef]
- Yoon, J.I.; Sung, J.; Ho Lee, M. Velocity profiles and friction coefficients in circular open channels. J. Hydraul. Res. 2012, 50, 304–311. [Google Scholar] [CrossRef]
- Newton, C.H.; Behnia, M. Numerical calculation of turbulent stratified gas–liquid pipe flows. Int. J. Multiph. Flow 2000, 26, 327–337. [Google Scholar] [CrossRef]
- Ghorai, S.; Nigam, K.D.P. CFD modeling of flow profiles and interfacial phenomena in two-phase flow pipes. Chem. Eng. Process. 2006, 45, 55–65. [Google Scholar] [CrossRef]
- De Schepper, S.C.K.; Heynderickx, G.J.; Marin, G.B. CFD modeling of all gas-liquid and vapor-liquid flow regimes predicted by Baker chart. Chem. Eng. J. 2008, 138, 349–357. [Google Scholar] [CrossRef]
- Bhramara, P.; Rao, V.D.; Sharma, K.V.; Reddy, T.K.K. CFD Analysis of Two Phase Flow in a Horizontal Pipe–Prediction of Pressure Drop. Momentum 2009, 10, 476–482. [Google Scholar]
- Berlamont, J.E.; Trouw, K.; Luyckx, G. Shear stress distribution in partially filled pipes. J. Hydraul. Eng. 2003, 129, 697–705. [Google Scholar] [CrossRef]
- Hager, W.H. Wastewater Hydraulics: Theory and Practice; Springer: Berlin, Germany, 2010. [Google Scholar]
- Goring, D.G.; Nikora, V.I. Despiking Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Cea, L.; Puertas, J.; Pena, L. Velocity measurements on highly turbulent free surface flow using ADV. Exp. Fluids 2007, 42, 333–348. [Google Scholar] [CrossRef]
- ANSYS CFX. ANSYS CFX-Solver Theory Guide; ANSYS CFX Release: Canonsburg, PA, USA, 2012; Volume 11, pp. 69–118. [Google Scholar]
- Lun, I.; Calay, R.K.; Holdo, A.E. Modelling two-phase flows using CFD. Appl. Energy 1996, 53, 299–314. [Google Scholar] [CrossRef]
- Vallée, C.; Höhne, T.; Prasser, H.M.; Sühnel, T. Experimental investigation and CFD simulation of horizontal stratified two-phase flow phenomena. Nucl. Eng. Des. 2008, 238, 637–646. [Google Scholar]
- Ashley, R.; Bertrand-Krajewski, J.L.; Hvitved-Jacobsen, T.; Verbanck, M. Solids in Sewers; Scientific & Technical Report 14; IWA Publishing: London, UK, 2004. [Google Scholar]
- Fresenius, W.; Schneider, W.; Böhnke, B.; Pöppinghaus, K.M. Manual de Disposición de Aguas Residuales: Origen, Descarga, Tratamiento y Análisis de las Aguas Residuales; CEPIS: Lima, Peru, 1991. [Google Scholar]
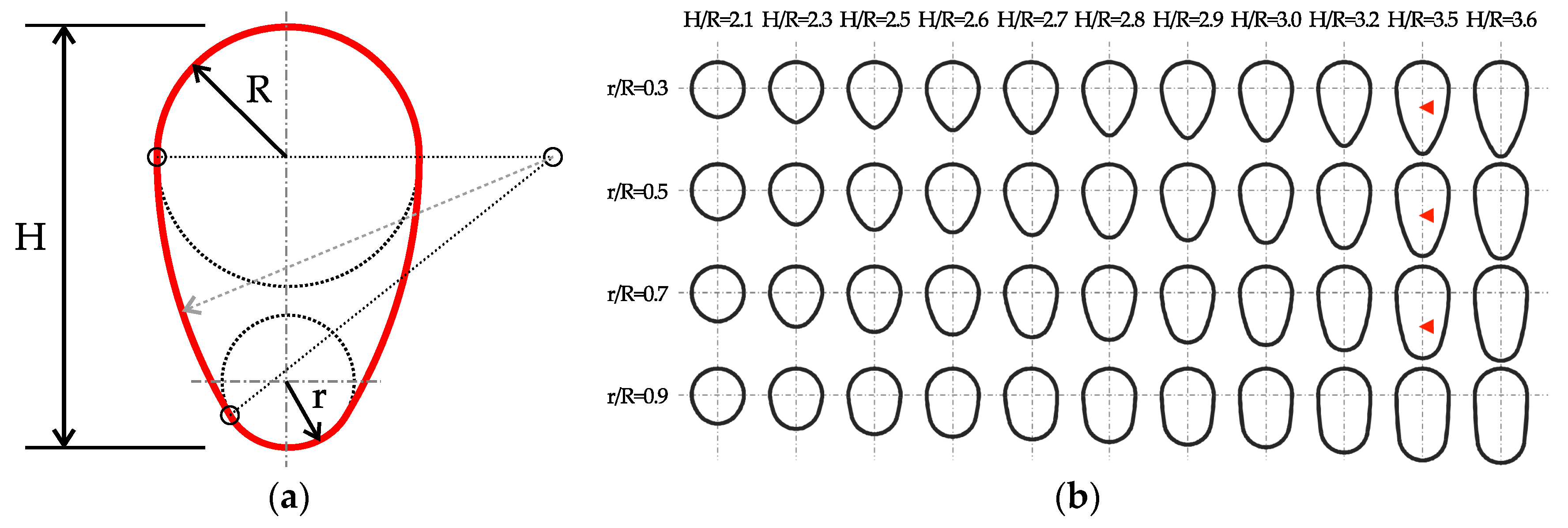
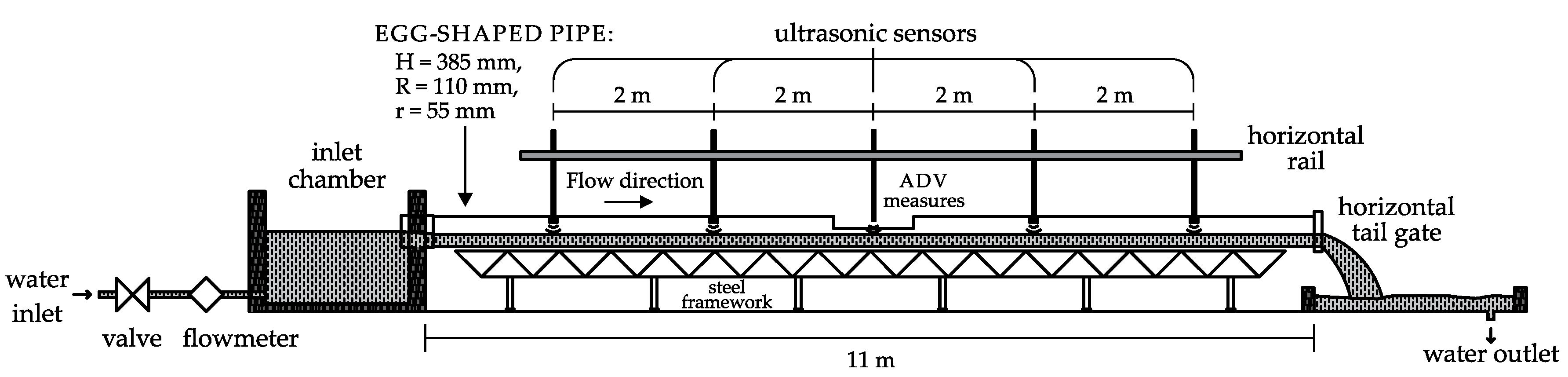
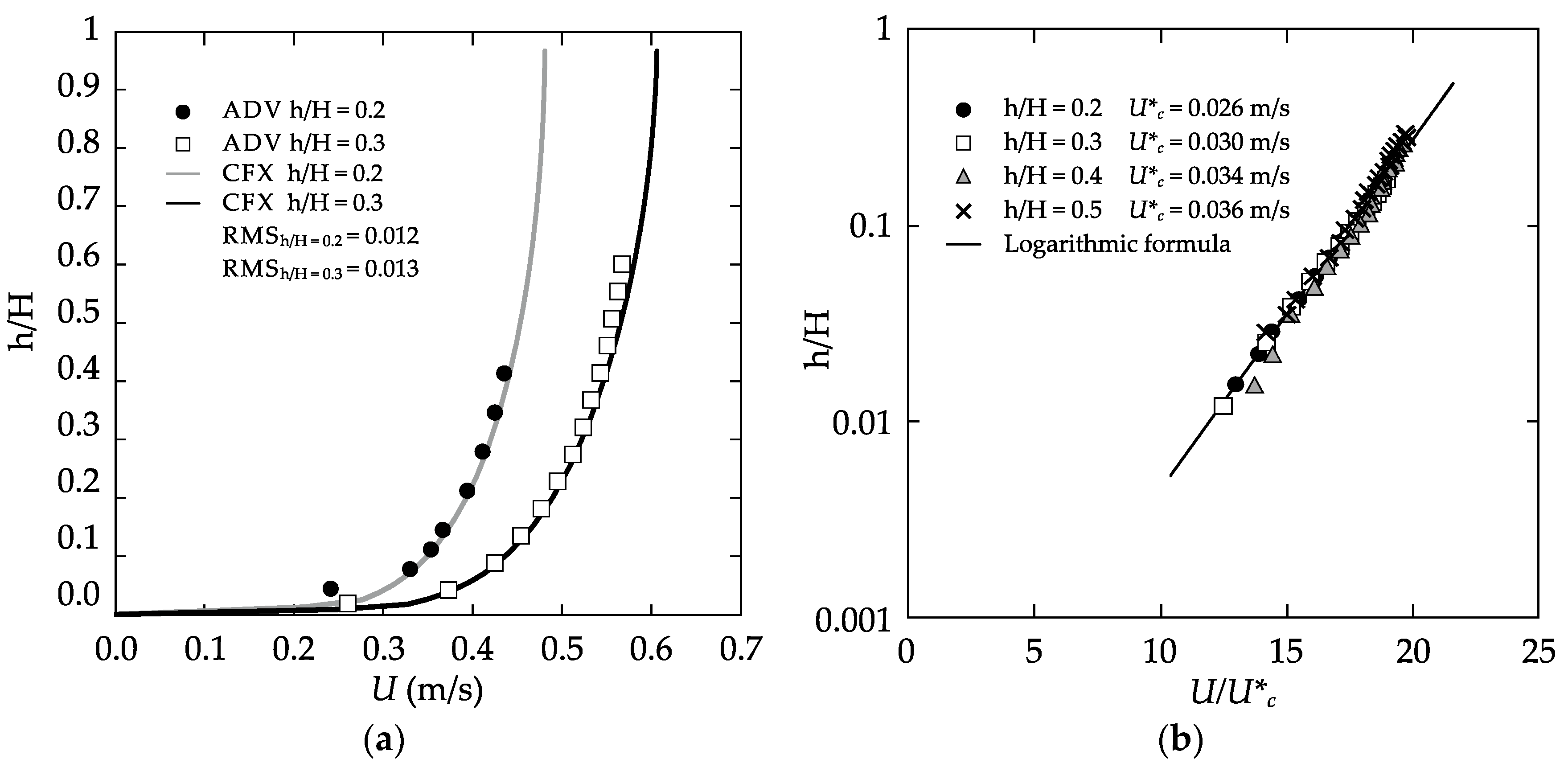
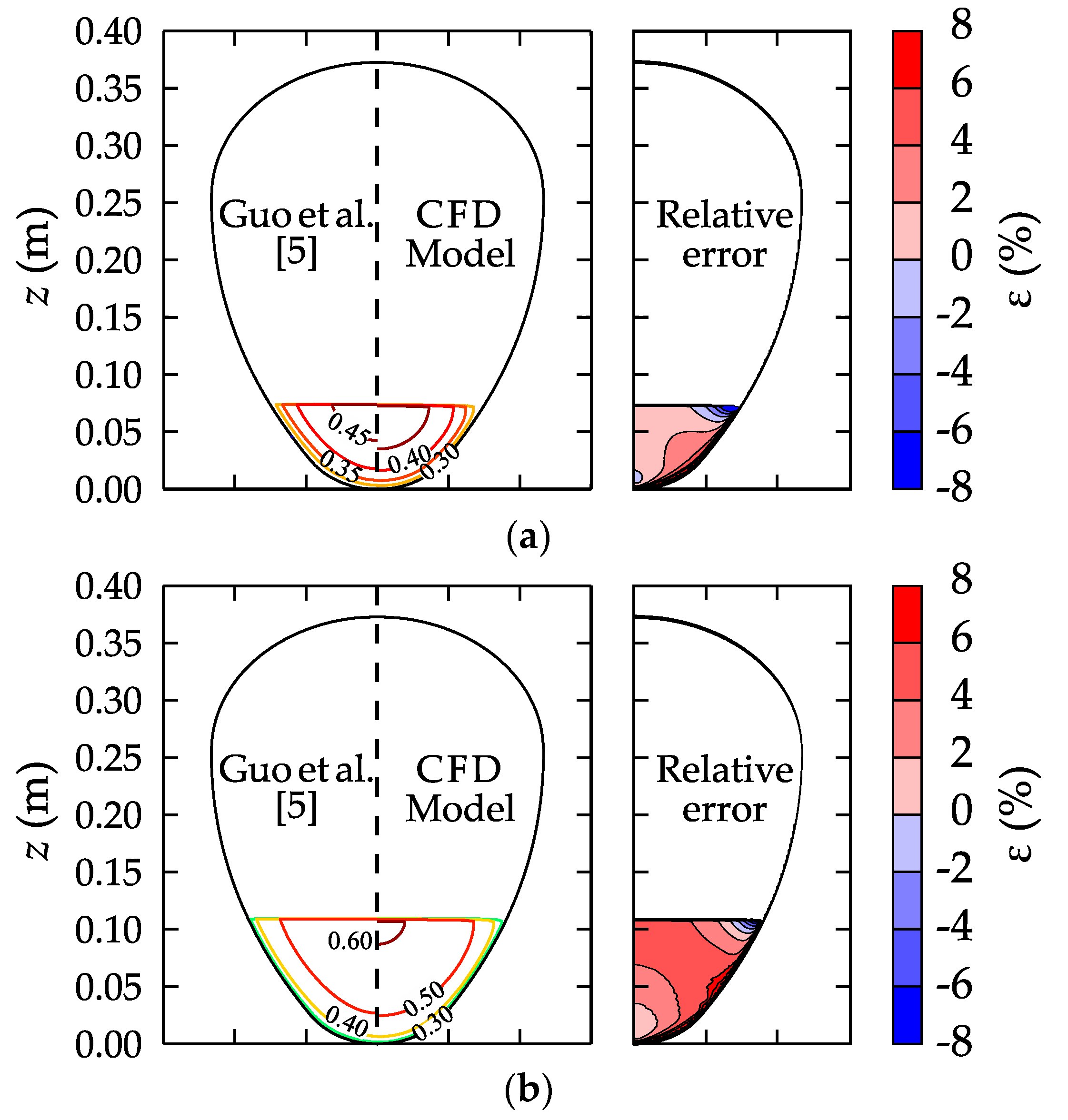
| H/R | r/R | Rh 1:10 | Rh 1:20 | Rh 1:50 | Rh Q0 | Q0 |
|---|---|---|---|---|---|---|
| 3.5 | 0.3 | 1.038 | 1.103 | 1.193 | 0.905 | 0.934 |
| 3.5 | 0.5 | 1.064 | 1.125 | 1.187 | 0.897 | 0.930 |
| 3.5 | 0.7 | 1.078 | 1.114 | 1.132 | 0.925 | 0.949 |
| Test | Experimental Conditions | CFD Model | ||||||
|---|---|---|---|---|---|---|---|---|
| Q (L/s) | Uav (m/s) | h/H (-) | Rh (m) | Re (×103) | τ = ρU*av2 (N/m2) | τCFD (N/m2) | ||
| 1 | 3.20 | 0.410 | 0.2 | 0.034 | 5.7 | 0.684 | 0.664 | (−2.9%) |
| 2 | 7.04 | 0.528 | 0.3 | 0.045 | 9.5 | 0.883 | 0.964 | (9.2%) |
| 3 | 13.08 | 0.582 | 0.4 | 0.057 | 13.3 | 1.121 | 1.159 | (3.4%) |
| 4 | 19.03 | 0.658 | 0.5 | 0.064 | 16.8 | 1.254 | 1.374 | (9.6%) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Regueiro-Picallo, M.; Naves, J.; Anta, J.; Puertas, J.; Suárez, J. Experimental and Numerical Analysis of Egg-Shaped Sewer Pipes Flow Performance. Water 2016, 8, 587. https://doi.org/10.3390/w8120587
Regueiro-Picallo M, Naves J, Anta J, Puertas J, Suárez J. Experimental and Numerical Analysis of Egg-Shaped Sewer Pipes Flow Performance. Water. 2016; 8(12):587. https://doi.org/10.3390/w8120587
Chicago/Turabian StyleRegueiro-Picallo, Manuel, Juan Naves, Jose Anta, Jerónimo Puertas, and Joaquín Suárez. 2016. "Experimental and Numerical Analysis of Egg-Shaped Sewer Pipes Flow Performance" Water 8, no. 12: 587. https://doi.org/10.3390/w8120587
APA StyleRegueiro-Picallo, M., Naves, J., Anta, J., Puertas, J., & Suárez, J. (2016). Experimental and Numerical Analysis of Egg-Shaped Sewer Pipes Flow Performance. Water, 8(12), 587. https://doi.org/10.3390/w8120587








