Estimation of Variability Characteristics of Regional Drought during 1964–2013 in Horqin Sandy Land, China
Abstract
:1. Introduction
2. Materials and Methods
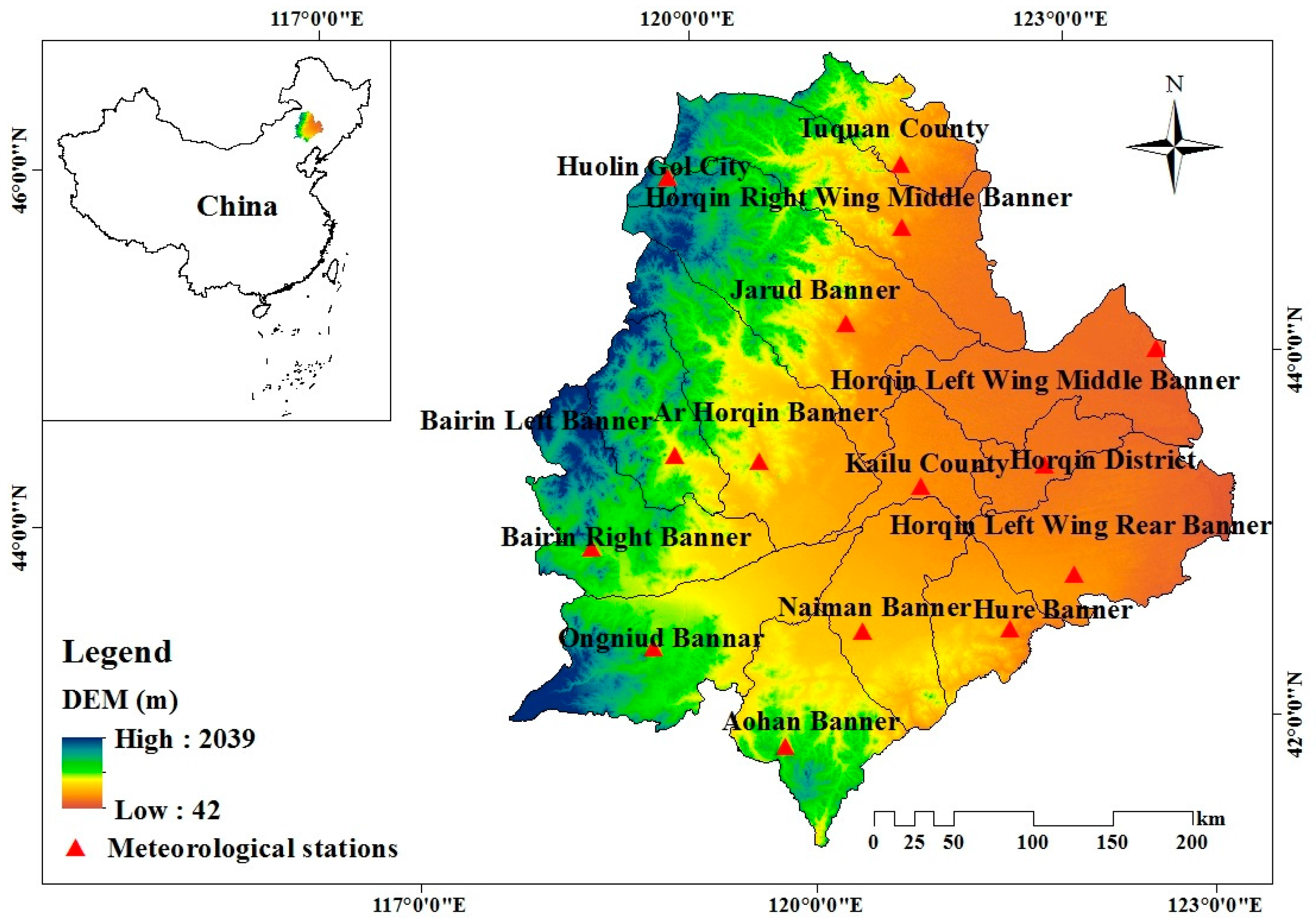
2.1. Study Area and Data
2.2. Methodology
2.2.1. Standardized Precipitation Evapotranspiration Index
2.2.2. Extreme Climate Indices
2.2.3. Statistical Method
1. Sen’s Slope Estimator
2. Cross Wavelet Transform
3. Results
3.1. Temporal Variability Characteristics of Drought in Horqin Sandy Land
3.2. Spatial Variability Characteristics of Drought in Horqin Sandy Land
3.2.1. Spatial Distribution of the Drought Frequency
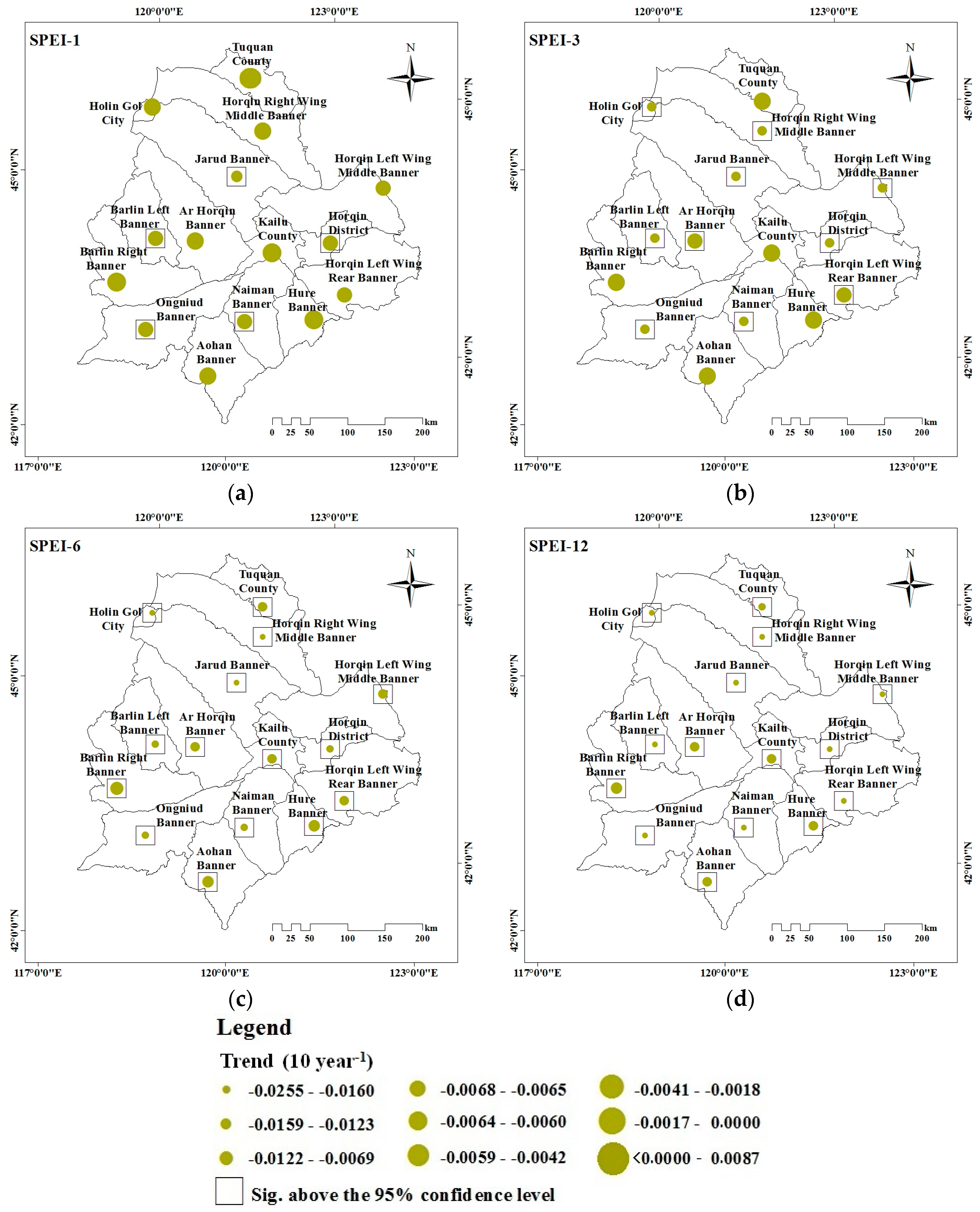
3.2.2. Spatial Trends of the Multi-Timescale SPEI
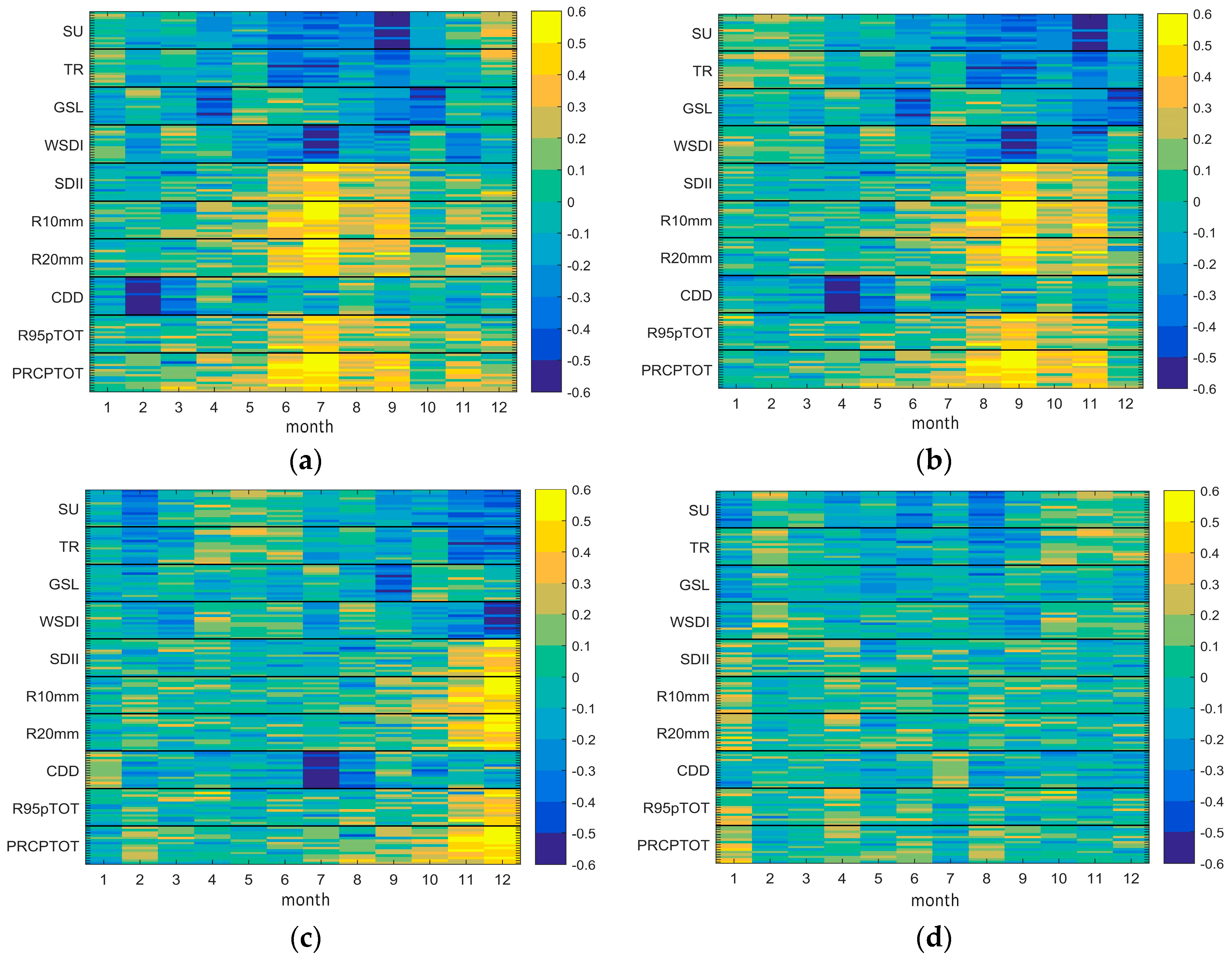
3.3. Relationships between the Multi-Timescale SPEI and Extreme Climate Indices
3.4. Relationships between Multi-Timescale SPEI-12 and Large Scale Atmosphereindices
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Homdee, T.; Pongput, K.; Kanae, S. A Comparative Performance Analysis of Three Standardized Climatic Drought Indices in the Chi River Basin, Thailand. Agric. Nat. Resour. 2016, 50, 211–219. [Google Scholar] [CrossRef]
- Hao, Z.C.; Hao, F.H.; Singh, V.P. A General Framework for Multivariate Multi-Index Drought Prediction Based on Multivariate Ensemble Streamflow Prediction (MESP). J. Hydrol. 2016, 539, 1–10. [Google Scholar] [CrossRef]
- Wang, Q.F.; Wu, J.J.; Lei, T.J.; He, B.; Wu, Z.T.; Liu, M.; Mo, X.Y.; Geng, G.P.; Li, X.H.; Zhou, H.K.; et al. Temporal-spatial Characteristics of Severe Drought Events and Their Impact on Agriculture on a Global Scale. Quat. Int. 2014, 349, 10–21. [Google Scholar] [CrossRef]
- Duan, H.C.; Wang, T.; Xue, X.; Liu, S.L.; Guo, J. Dynamics of Aeolian Desertification and Its Driving Forces in the Horqin Sandy Land, Northern China. Environ. Monit. Assess. 2014, 186, 6083–6096. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Wang, W.; Singh, V.P.; Liu, Y. Combined Use of Meteorological Drought Indices at Multi-time Scales for Improving Hydrological Drought Detection. Sci. Total Environ. 2016, 571, 1058–1068. [Google Scholar] [CrossRef] [PubMed]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- American Meteorological Society (AMS). Statement on Meteorological Drought. Bull. Am. Meteorol. Soc. 2004, 85, 771–773. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Masud, M.B.; Khaliq, M.N.; Wheater, H.S. Analysis of Meteorological Droughts for the Saskatchewan River Basin using Univariate and Bivariate Approaches. J. Hydrol. 2015, 522, 452–466. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological Drought Explained. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; García-Ruiz, J.M.; Cuadrat, J.M. The Impact of Droughts and Water Management on Various Hydrological Systems in the Headwaters of the Tagus River (central Spain). J. Hydrol. 2010, 386, 13–26. [Google Scholar] [CrossRef]
- Zou, X.K.; Ren, G.Y.; Zhang, Q. Drought Variations in China Based on Compound Index of Meteorological Drought. Clim. Environ. Res. 2010, 15, 371–378. (In Chinese) [Google Scholar]
- Liu, X.L.; Yu, M.X. Investigation into Drought Evolution Characteristics of China in 60 Years. J. Arid Land Resour. Environ. 2015, 29, 177–183. (In Chinese) [Google Scholar]
- Farahmand, A.; AghaKouchak, A. A Generalized Framework for Deriving Nonparametric Standardized Drought Indicators. Adv. Water Resour. 2015, 76, 140–145. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A Review of Water Scarcity and Drought Indexes in Water Resources Planning and Management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef]
- Huang, J.; Sun, S.; Zhang, J. Detection of Trends in Precipitation during 1960–2008 in Jiangxi Province, Southeast China. Theor. Appl. Climatol. 2013, 114, 237–251. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Cabello, D.; Tomás-Burguera, M.; Martín-Hernández, N.; Beguería, S.; Azorin-Molina, C.; Kenawy, A.E. Drought Variability and Land Degradation in Semiarid Regions: Assessment Using Remote Sensing Data and Drought Indices (1982–2011). Remote Sen. 2015, 7, 4391–4423. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; Wang, J.B.; Lu, H.Q.; Guo, A.H.; Zhu, Z.C.; Myneni, R.B.; Shugart, H.H. Assessing Spatiotemporal Variation of Drought in China and Its Impact on Agriculture during 1982–2011 by using PDSI Indices and Agriculture Drought Survey Data. J. Geophys. Res. Atmos. 2016, 121, 2283–2298. [Google Scholar] [CrossRef]
- Stagge, J.H.; Kohn, I.; Tallaksen, L.M.; Stahl, K. Modeling Drought Impact Occurrence based on Meteorological Drought Indices in Europe. J. Hydrol. 2015, 530, 37–50. [Google Scholar] [CrossRef]
- Abramopoulos, F.; Rosenzweig, C.; Choudhury, B. Improved Ground Hydrology Calculations for Global Climate Models (GCMs): Soil Water Movement and Evapotranspiration. J. Clim. 1988, 1, 921–941. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Kumar, K.N.; Rajeevan, M.; Pai, D.S.; Srivastava, A.K.; Preethi, B. On the Observed Variability of Monsoon Droughts over India. Weather Clim. Extrem. 2013, 1, 42–50. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized Precipitation Evapotranspiration Index (SPEI) Revisited: Parameter Fitting, Evapotranspiration Models, Tools, Datasets and Drought Monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Potopová, V.; Štěpánek, P.; Možný, M.; Türkott, L.; Soukup, J. Performance of the Standardised Precipitation Evapotranspiration Index at Various Lags for Agricultural Drought Risk Assessment in the Czech Republic. Agric. For. Meteorol. 2015, 202, 26–38. [Google Scholar] [CrossRef]
- Li, B.Q.; Zhou, W.; Zhao, Y.Y.; Ju, Q.; Yu, Z.B.; Liang, Z.M.; Acharya, K. Using the SPEI to Assess Recent Climate Change in the Yarlung Zangbo River Basin, South Tibet. Water 2015, 7, 5474–5486. [Google Scholar] [CrossRef]
- Meza, F.J. Recent Trends and ENSO Influence on Droughts in Northern Chile: An Application of the Standardized Precipitation Evapotranspiration Index. Weather Clim. Extrem. 2013, 1, 51–58. [Google Scholar] [CrossRef]
- You, L.; Wang, G.Q.; Yan, J.; Li, F. Impact of Climate Warming on Agriculture and Animal Husbandry in Horqin Sandy Land, Inner Mongolia. Meteorology 2007, 33, 31–40. (In Chinese) [Google Scholar]
- Zhang, M.J.; Chun, X.; Liang, A.R.N.; Liu, M.P.; Liu, Y. Climate Changes in Horqin Sandy Land in Recent 60 Years. J. Arid Land Resour. Environ. 2012, 26, 8–16. (In Chinese) [Google Scholar]
- Qu, C.P.; Guan, D.X.; Wang, A.Z.; Jin, C.J.; Yuan, F.H.; Wu, J.B.; Ni, P. Characteristics of Climate Change in Horqin Sandy Land in Past 56 Years. Chin. J. Ecol. 2009, 28, 2326–2332. (In Chinese) [Google Scholar]
- Wang, J.R.; Ma, L.; Liu, T.X.; Huang, X.; Liu, D.H.; Li, H.Y. Comparative Analysis of Temperature Before and after Abrupt Changes in Horqin Sandy Land from 1951 to 2012. Resour. Sci. 2016, 38, 690–703. (In Chinese) [Google Scholar]
- Seager, R.; Ting, M.; Li, C.; Naik, N.; Cook, B.; Nakamura, J.; Liu, H. Projections of Declining Surface-Water Availability for the Southwestern United States. Nat. Clim. Chang. 2013, 35, 482–486. [Google Scholar] [CrossRef]
- Wu, R.; Hu, Z.Z.; Kirtman, B.P. Evolution of ENSO-related Rainfall Anomalies in East Asia. J. Clim. 2003, 16, 3742–3758. [Google Scholar] [CrossRef]
- Su, M.; Wang, H. Relationship and Its Instability of ENSO—Chinese Variations in Droughts and Wet Spells. Sci. China Ser. D 2007, 50, 145–152. [Google Scholar] [CrossRef]
- Ma, Z.; Shao, L. Relationship between Dry/Wet Variation and the Pacific Decade Oscillation (PDO) in Northern China during the Last 100 Years. Chin. J. Atmos. Sci. 2006, 30, 464–474. (In Chinese) [Google Scholar]
- Gong, D.Y.; Wang, S.W. Influence of Arctic Oscillation on Winter Climate over China. J. Geogr. Sci. 2003, 13, 208–216. [Google Scholar]
- Park, T.; Jang, C.J.; Kwon, M.; Na, H.; Kim, K.Y. An Effect of ENSO on Summer Surface Salinity in the Yellow and East China Seas. J. Mar. Syst. 2015, 141, 122–127. [Google Scholar] [CrossRef]
- Wolter, K. Multivariate ENSO Index (MEI). Climate Diagnostics Center Report. Available online: www.cdc.noaa.gov (accessed on 15 November 2016).
- Earth System Research Laboratory. Available online: http://www.esrl.noaa.gov/psd/enso/mei/table.html (accessed on 6 July 2016).
- Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like interdecadal variability: 1900–1993. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Q.; Singh, V.P. Influences of ENSO, NAO, IOD and PDO on Seasonal Precipitation Regimes in the Yangtze River Basin, China. Int. J. Climatol. 2015, 35, 3556–3567. [Google Scholar] [CrossRef]
- College of the Environment, University of Washington. Available online: http://research.jisao.washington.edu/pdo/PDO.latest (accessed on 10 June 2016).
- Zhu, J.; Liao, H.; Li, J. Increases in aerosol Concentrations over Eastern China due to the Decadal-Scale Weakening of the East Asian Summer Monsoon. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Jianping Li’s Home Page. Available online: http://ljp.gcess.cn/dct/page/1 (accessed on 28 May 2016).
- Zhang, Q.; Zhang, J.Q.; Wang, C.Y. Risk Assessment of Drought Disaster in Typical Area of Corn Cultivation in China. Theor. Appl. Climatol. 2016, 25, 1–8. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J. Drought Hazard Assessment in Typical Corn Cultivated Areas of China at Present and Potential Climate Change. Nat. Hazards 2016, 81, 1323–1331. [Google Scholar] [CrossRef]
- Wang, K.Y.; Li, Q.F.; Yang, Y.; Zeng, M.; Li, P.C.; Zhang, J.X. Analysis of Spatio-Temporal Evolution of Droughts in Luanhe River Basin Using Different Drought Indices. Water Sci. Eng. 2015, 8, 282–290. [Google Scholar] [CrossRef]
- Zhang, Q.; Gemmer, M.; Chen, J. Climate Changes and Flood/Drought Risk in the Yangtze Delta, China, during the Past Millennium. Quat. Int. 2008, 176–177, 62–69. [Google Scholar] [CrossRef]
- Dai, A.G.; Trenberth, K.E.; Qian, T.T. A Global Data Set of Palmer Drought Severity Index for 1870–2002: Relationship with Soil Moisture and Effects of Surface Warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Können, G.P. Trends in Indices of Daily Temperature and Precipitation Extremes in Europe, 1946–1999. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- Bartholy, J.; Pongrácz, R.; Kis, A. Projected Changes of Extreme Precipitation using Multi-model Approach. Q. J. Hung. Meteorol. Serv. 2015, 119, 129–142. [Google Scholar]
- Fang, S.; Qi, Y.; Han, G.; Zhou, G. Changing Trends and Abrupt Features of Extreme Temperature in Mainland China during 1960 to 2010. Earth Syst. Dyn. Discuss. 2015, 6, 979–1000. [Google Scholar] [CrossRef]
- Zhang, D.D.; Yan, D.H.; Wang, Y.C.; Lu, F.; Wu, D. Changes in Extreme Precipitation in the Huang-Huai-Hai River Basin of China during 1960–2010. Theor. Appl. Climatol. 2015, 120, 195–209. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1955. [Google Scholar]
- Axelson, J.N.; Sauchyn, D.J.; Barichivich, J. New Reconstructions of Streamflow Variability in the South Saskatchewan River Basin from a Network of Tree Ring Chronologies, Alberta, Canada. Water Resour. Res. 2009, 45, 318–326. [Google Scholar] [CrossRef]
- Zanchettin, D.; Rubino, A.; Matei, D.; Bothe, O.; Jungclaus, J.H. Multidecadal-to-centennial SST Variability in the MPI-ESM Simulation Ensemble for the Last Millennium. Clim. Dyn. 2012, 40, 1–18. [Google Scholar] [CrossRef]
- Solomon, S.; Qin, D.; Manning, M.; Marquis, M.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. (Eds.) Climate Change 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2007; p. 996.
- Dai, A.G.; Trenberth, K.E.; Karl, T.R. Global Variations in Droughts and Wet Spells: 1900–1995. Geophys. Res. Lett. 1998, 25, 3367–3370. [Google Scholar] [CrossRef]
- Wang, H.L.; Chen, A.F.; Wang, Q.F.; He, B. Drought Dynamics and Impacts on Vegetation in China from 1982 to 2011. Ecol. Eng. 2015, 75, 303–307. [Google Scholar] [CrossRef]
- Zou, X.; Zhai, P.; Zhang, Q. Variations in Droughts over China: 1951–2003. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Wang, C.M.; Bian, R.J.; Qu, X.J.; Yang, X.M. The Climate Change Analysis of Most Typical Region in Horqin Sandy Area for Nearly 50 Years. Chin. Agric. Sci. Bull. 2012, 28, 287–290. (In Chinese) [Google Scholar]
- Bao, H.H.; Bao, Y.W. Characteristics of Drought/Flood Spatial and Temporal Distribution in Horqin Sandy Land during the Last 300 Years. J. Arid Land Resour. Environ. 2008, 4, 100–107. (In Chinese) [Google Scholar]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal Variation of Drought in China during 1961–2012: A Climatic Perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.; He, H.; Wang, F.; Du, H.; Zong, S. Changes in summer extreme precipitation in Northeast Asia and their relationships with the East Asian summer monsoon during 1961–2009. Int. J. Climatol. 2016. [Google Scholar] [CrossRef]




| Grade | Type | SPEI Value |
|---|---|---|
| 0 | Normal | >−0.5 |
| 1 | Mild drought | (−1.00, −0.5] |
| 2 | Moderate drought | (−1.50, −1.00] |
| 3 | Severe drought | (−2.00, −1.50] |
| 4 | Extreme drought | ≤−2.00 |
| Abbreviation | Full Name | Definitions | Unit |
|---|---|---|---|
| SU | Summer days | Annual count when TX (daily maximum) > 25 °C | Days |
| TR | Tropical nights | Annual count when TN (daily minimum) > 20 °C | Days |
| GSL | Growing season length | Annual (1 January to 31 December in NH, 1 July to 30 June in SH) count between first span of at least 6 days with TG > 5 °C and first span after July 1 (1 January in SH) of 6 days with TG < 5 °C | Days |
| WSDI | Warm spell duration indicator | Annual count of days with at least 6 consecutive days when TX > 90th percentile | Days |
| SDII | Simple daily intensity index | Annual total precipitation divided by the number of wet days (defined as PRCP ≥ 1.0 mm) in the year | mm/day |
| R 10mm | Number of heavy precipitation days | Annual count of days when PRCP ≥ 10 mm | Days |
| R 20mm | Number of very heavy precipitation days | Annual count of days when PRCP ≥ 20 mm | Days |
| CDD | Consecutive dry days | Maximum number of consecutive days with RR < 1 mm | Days |
| R95pTOT | Very wet days | Annual total PRCP when RR > 95th percentile | mm |
| PRCPTOT | Annual total wet-day precipitation | Annual total PRCP in wet days (RR ≥ 1 mm) | mm |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, J.; Guo, E.; Dong, Z.; Quan, L. Estimation of Variability Characteristics of Regional Drought during 1964–2013 in Horqin Sandy Land, China. Water 2016, 8, 543. https://doi.org/10.3390/w8110543
Wang Y, Zhang J, Guo E, Dong Z, Quan L. Estimation of Variability Characteristics of Regional Drought during 1964–2013 in Horqin Sandy Land, China. Water. 2016; 8(11):543. https://doi.org/10.3390/w8110543
Chicago/Turabian StyleWang, Yongfang, Jiquan Zhang, Enliang Guo, Zhenhua Dong, and Lai Quan. 2016. "Estimation of Variability Characteristics of Regional Drought during 1964–2013 in Horqin Sandy Land, China" Water 8, no. 11: 543. https://doi.org/10.3390/w8110543
APA StyleWang, Y., Zhang, J., Guo, E., Dong, Z., & Quan, L. (2016). Estimation of Variability Characteristics of Regional Drought during 1964–2013 in Horqin Sandy Land, China. Water, 8(11), 543. https://doi.org/10.3390/w8110543







