Effect of Slope, Rainfall Intensity and Mulch on Erosion and Infiltration under Simulated Rain on Purple Soil of South-Western Sichuan Province, China
Abstract
:1. Introduction
2. Materials and Methods
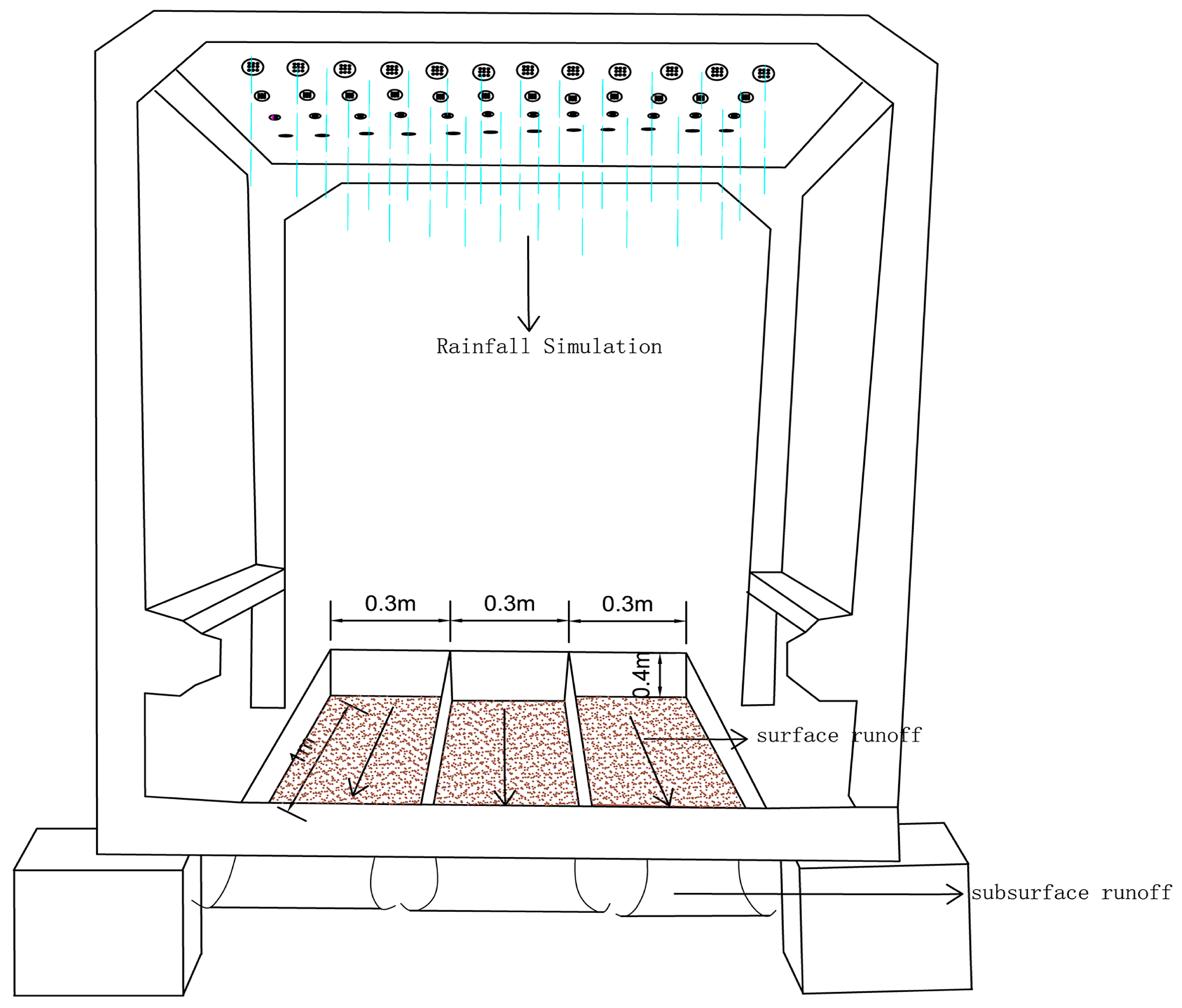
2.1. Experimental Equipment
2.2. Experimental Treatments and Measurements
2.3. Calculations and Data Analysis
- ei = runoff or sediment losses under different rainfall intensities when the slope steepness remains unchanged (5° or 15°).
- Ei = runoff or sediment losses at a higher slope under different rainfall intensities when the slope steepness changed from 5° to 15° or 15° to 25°.
- eo = values of runoff or sediment losses during rainfall intensity of 33 mm·h−1 at 5° and 15° slopes during an increase in steepness from 5° to 15° and 15° to 25°, respectively.
3. Results and Discussions
3.1. Surface Runoff
3.2. Sediment Losses
3.3. Water Infiltration
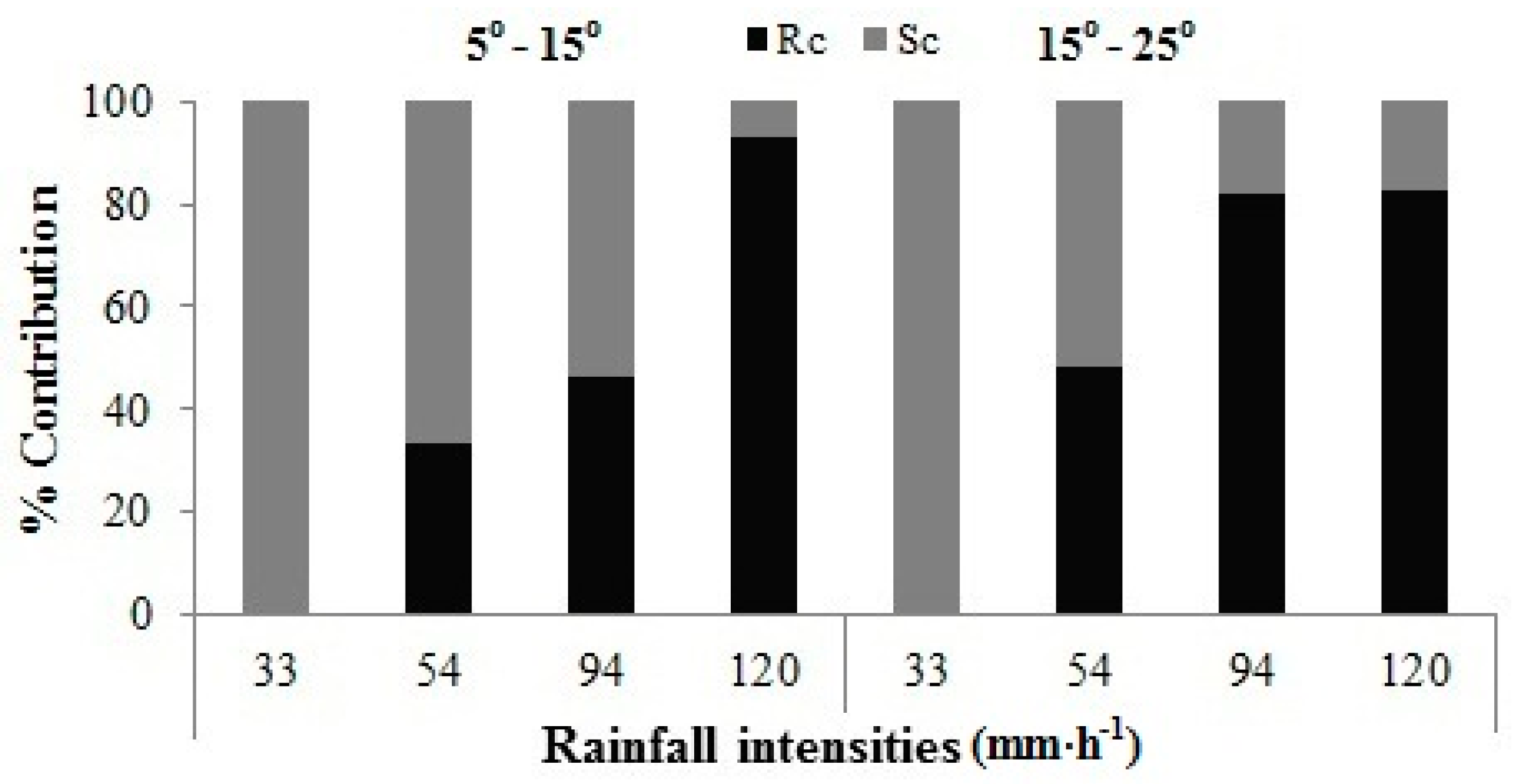
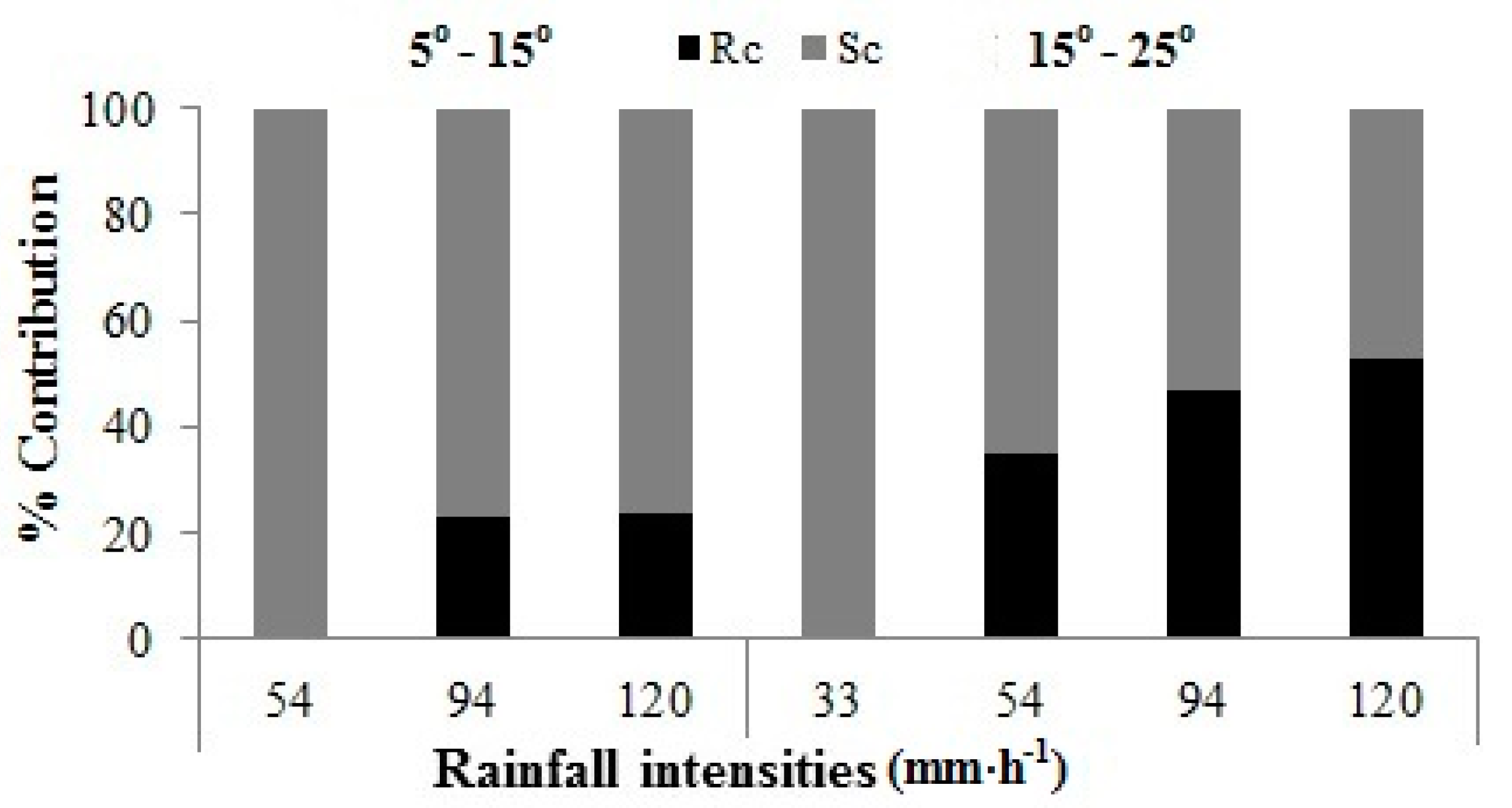
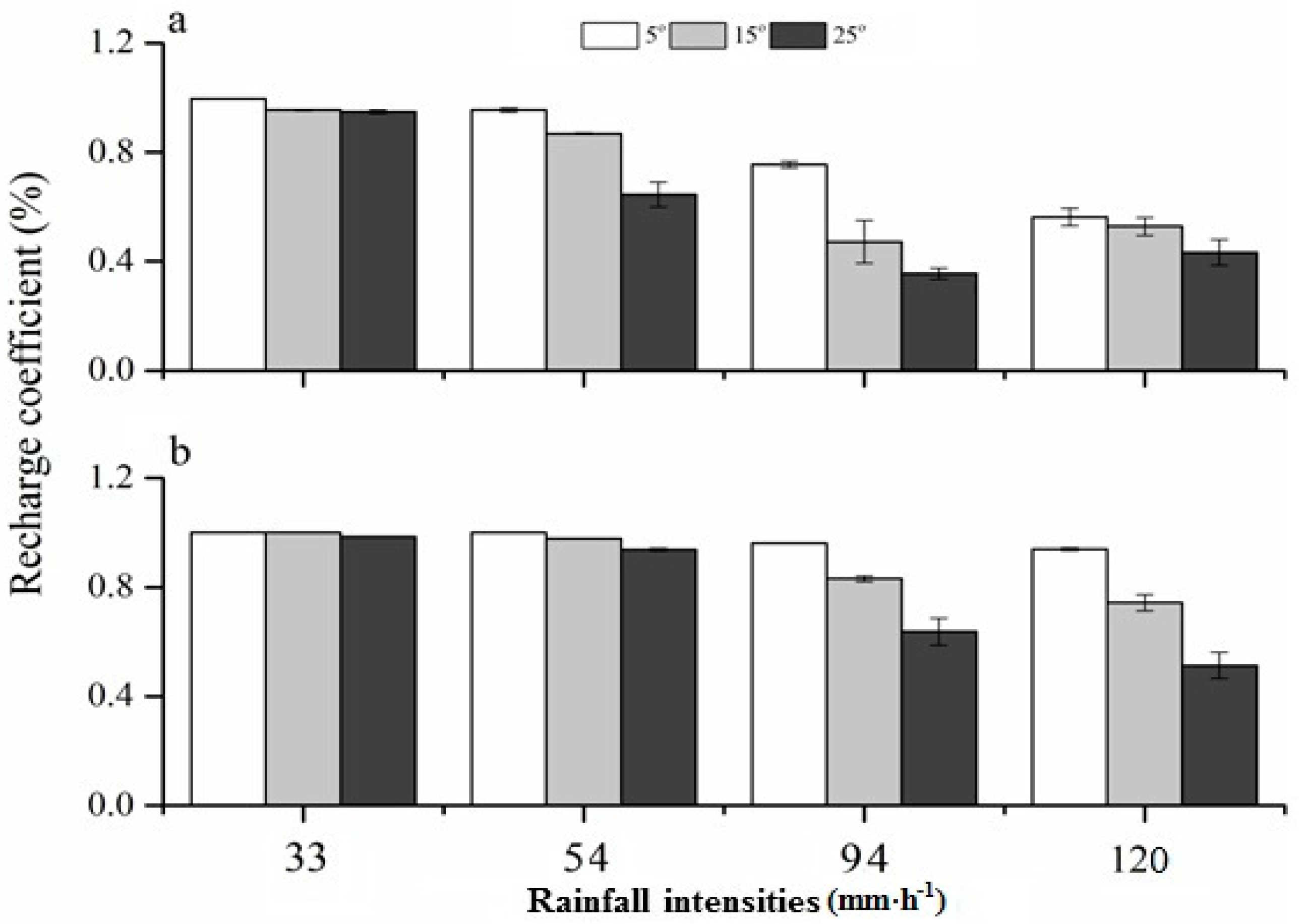
3.4. Recharge Coefficient
4. Conclusions
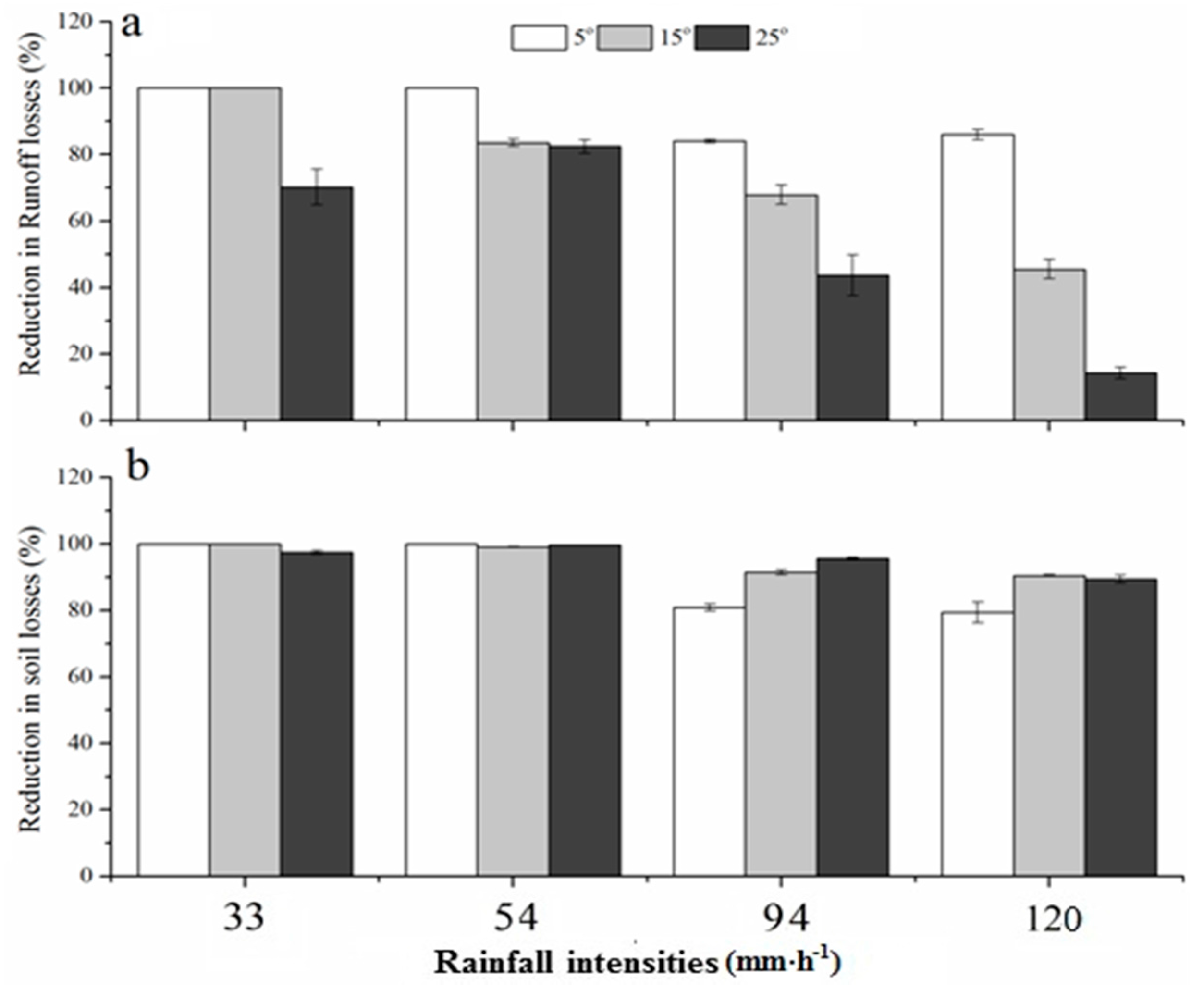
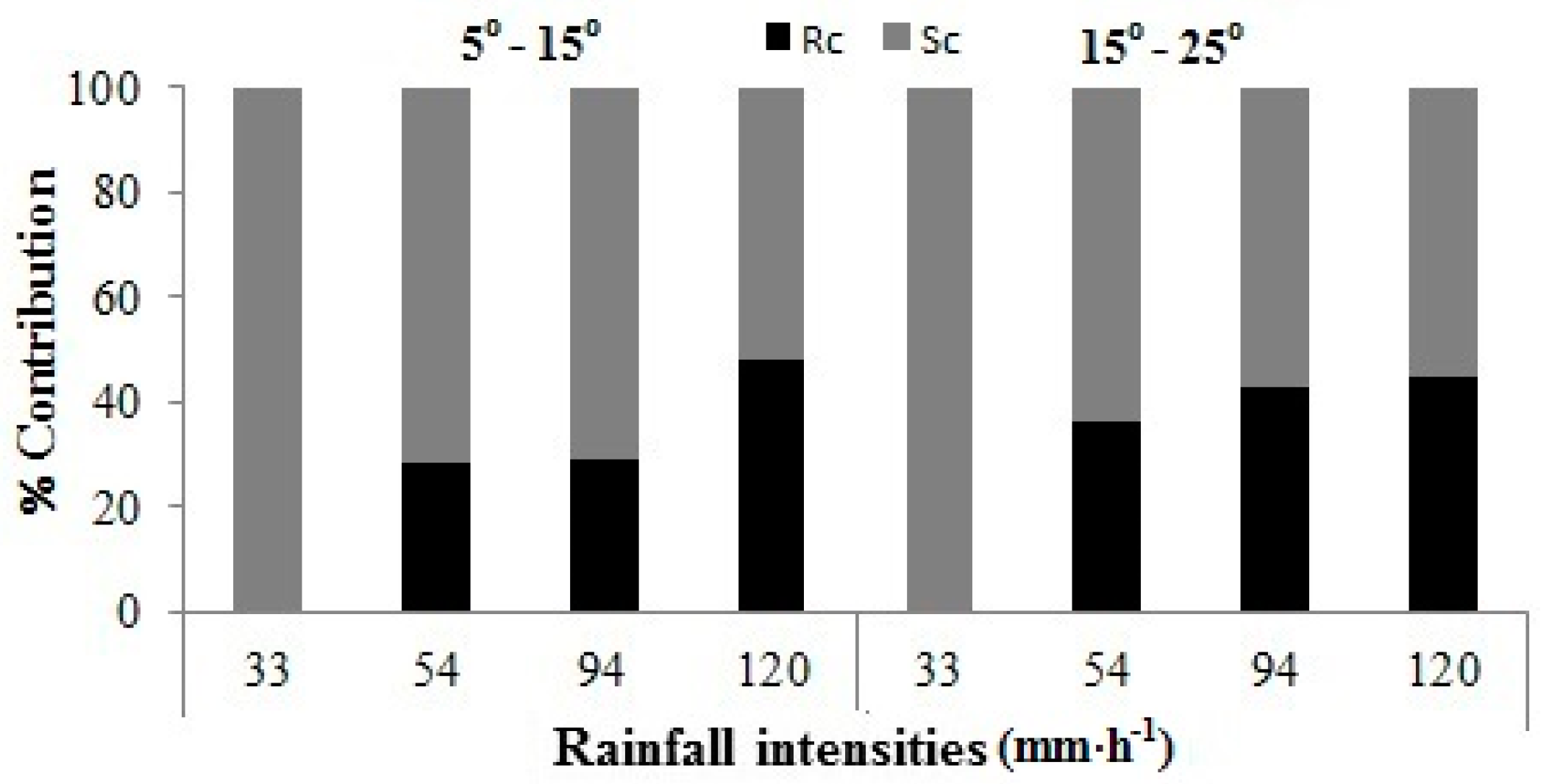
- In un-mulched treatments for all rainfall intensities, slope was the dominant factor in sediment loss, while the runoff process was independent of slope steepness for rainfall of high intensities.
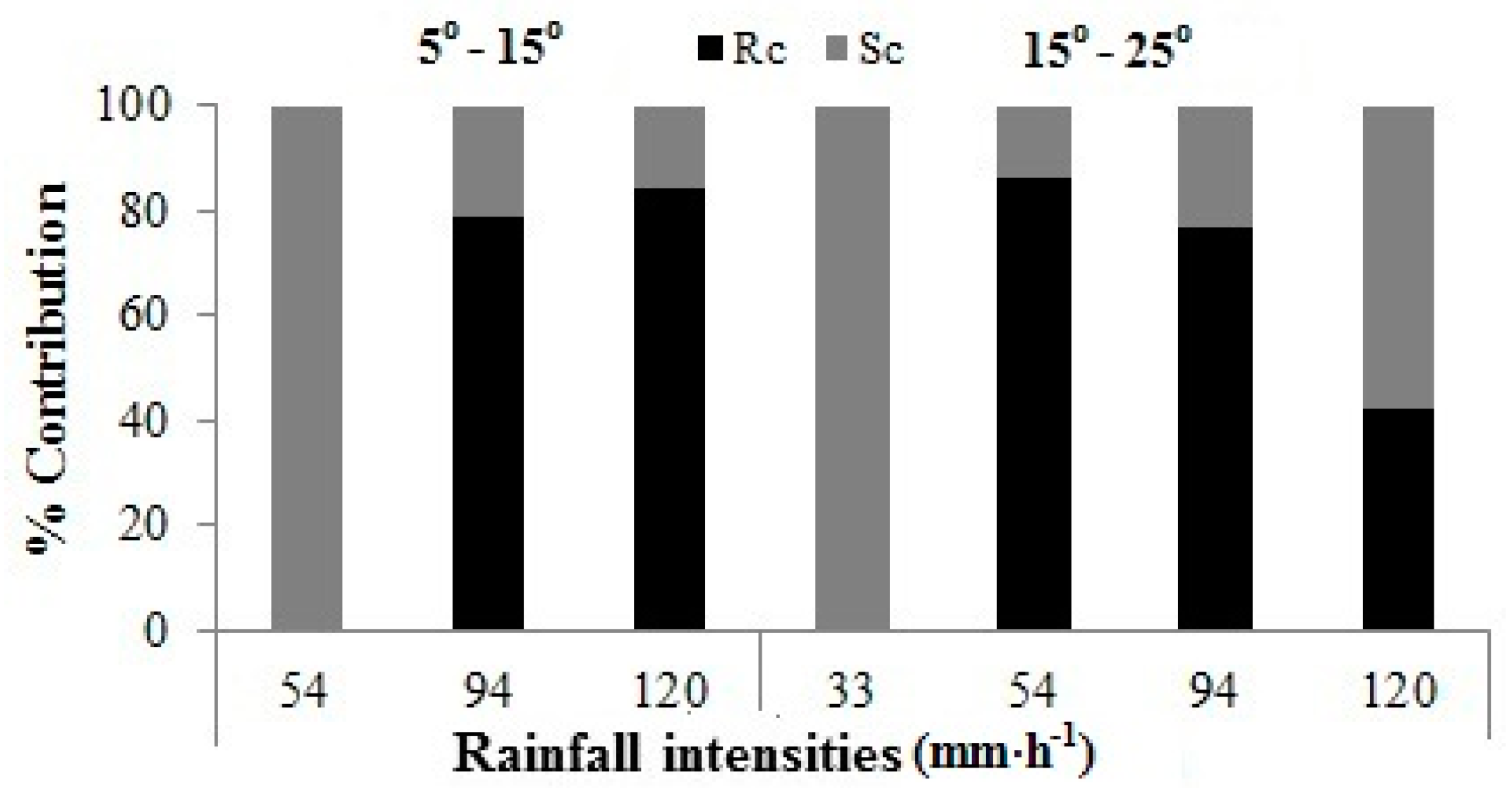
- In mulched soil, the contribution of rainfall intensity was >50% in producing sediment loss, and controlled by the wash flow under mulch cover. However, the mulch cover reduced the flow rate, and the slope steepness controlled the magnitude of water runoff.
- Straw mulch significantly reduced sediment and water losses. Under high rainfall intensity, the conservation effectiveness of mulch increased with increasing slope steepness. On the contrary, the magnitude of reduction in water loss decreased with an increase in slope steepness at higher rainfall intensities.
- The infiltration rate decreased with an increase in slope and increased with an increase in rainfall intensity. The effect of rainfall intensity on the infiltration rate changed with the slope angle due to the creation of different micro-relief features. In mulched soil, however, the water infiltration rate significantly increased with an increase in rainfall intensity at all slopes because of the uniform surface conditions under the mulch layers. The recharge coefficient decreased with an increase in rainfall intensity and an increase in slope steepness in all treatments, whereas the mulch maintained a higher infiltration rate and RC compared with un-mulched treatments.
- The short slope length in this experimental setup resulted in less surface area availability for water recharge into the soil during intense rainfalls. Due to a smaller quantity of runoff and lower velocities during low rainfall intensity, the slope effect could be generalized to field conditions. However, for intense rainfalls, the slope effect could be different under field conditions in that; the steeper and the longer slopes would have a higher infiltration rate with increasing rainfall intensities because of the availability of a large area for water infiltration with increasing slope length. Therefore, additional field research is needed to study the effects of longer and steeper slopes on the water infiltration rate and runoff loss under intense rain storms.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhu, B.; Wang, T.; You, X.; Gao, M.R. Nutrient release from weathering of purplish rocks in the Sichuan Basin, China. Pedosphere 2008, 18, 257–264. [Google Scholar] [CrossRef]
- Fu, B.; Wang, Y.; Xu, P.; Wang, D. Changes in overland flow and sediment during simulated rainfall events on cropland in hilly areas of the Sichuan Basin, China. Prog. Natl. Sci. 2009, 19, 1613–1618. [Google Scholar] [CrossRef]
- Stolte, J.; Shi, X.; Ritsema, C.J. Introduction: Soil erosion and nutrient losses in the hilly purple soil area in China. Soil Tillage Res. 2009, 105, 283–284. [Google Scholar] [CrossRef]
- Bracken, L.J.; Croke, J. The concept of hydrological connectivity and its contribution to understanding runoff-dominated geomorphic systems. Hydrol. Process. 2007, 21, 1749–1763. [Google Scholar] [CrossRef]
- Mu, W.; Yu, F.; Li, C.; Xie, Y.; Tian, J.; Liu, J.; Zhao, N. Effects of rainfall intensity and slope gradient on runoff and soil moisture content on different growing stages of spring maize. Water 2015, 7, 2990–3008. [Google Scholar] [CrossRef]
- Mouzai, L.; Bouhadef, M. Water drop erosivity: Effects on soil splash. J. Hydraul. Res. 2003, 41, 61–68. [Google Scholar] [CrossRef]
- Aksoy, H.; Kavvas, M.L. A review of hillslope and watershed scale erosion and sediment transport models. Catena 2005, 64, 247–271. [Google Scholar] [CrossRef]
- Cuomo, S.; Della Sala, M.; Novità, A. Physically based modelling of soil erosion induced by rainfall in small mountain basins. Geomorphology 2015, 243, 106–115. [Google Scholar] [CrossRef]
- Fox, D.M.; Bryan, R.B. The relationship of soil loss by interrill erosion to slope gradient. Catena 2000, 38, 211–222. [Google Scholar] [CrossRef]
- Kinnell, P. Comment on “A new splash and sheet erosion equation for rangelands”. Soil Sci. Soc. Am. J. 2010, 74, 340–341. [Google Scholar] [CrossRef]
- Meyles, E.; Williams, A.; Ternan, L.; Dowd, J. Runoff generation in relation to soil moisture patterns in a small Dartmoor catchment, Southwest England. Hydrol. Process. 2003, 17, 251–264. [Google Scholar] [CrossRef]
- Seeger, M.; Errea, M.P.; Beguerı́a, S.; Arnáez, J.; Martı́, C.; Garcı́a-Ruiz, J.M. Catchment soil moisture and rainfall characteristics as determinant factors for discharge/suspended sediment hysteretic loops in a small headwater catchment in the Spanish pyrenees. J. Hydrol. 2004, 288, 299–311. [Google Scholar] [CrossRef]
- Castillo, V.M.; Gómez-Plaza, A.; Martı́nez-Mena, M. The role of antecedent soil water content in the runoff response of semiarid catchments: A simulation approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Poesen, J.; Vandaele, K.; van Wesemael, B. Gully erosion: Importance and model implications. In Modelling Soil Erosion by Water; Boardman, J., Favis-Mortlock, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 285–311. [Google Scholar]
- Gholami, L.; Sadeghi, S.H.; Homaee, M. Straw mulching effect on splash erosion, runoff, and sediment yield from eroded plots. Soil Sci. Soc. Am. J. 2013, 77, 268–278. [Google Scholar] [CrossRef]
- Shi, Z.; Yue, B.; Wang, L.; Fang, N.; Wang, D.; Wu, F. Effects of mulch cover rate on interrill erosion processes and the size selectivity of eroded sediment on steep slopes. Soil Sci. Soc. Am. J. 2013, 77, 257–267. [Google Scholar] [CrossRef]
- Smets, T.; Poesen, J.; Knapen, A. Spatial scale effects on the effectiveness of organic mulches in reducing soil erosion by water. Earth Sci. Rev. 2008, 89, 1–12. [Google Scholar] [CrossRef]
- Poesen, J.; Lavee, H. Effects of size and incorporation of synthetic mulch on runoff and sediment yield from interrils in a laboratory study with simulated rainfall. Soil Tillage Res. 1991, 21, 209–223. [Google Scholar] [CrossRef]
- Adekalu, K.; Olorunfemi, I.; Osunbitan, J. Grass mulching effect on infiltration, surface runoff and soil loss of three agricultural soils in Nigeria. Bioresour. Technol. Biol. 2007, 98, 912–917. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Tarchitzky, J.; Brouwer, J.; Morin, J.; Banin, A. Scanning electron microscope observations on soil crusts and their formation. Soil Sci. 1980, 130, 49–55. [Google Scholar] [CrossRef]
- Bu, C.F.; Gale, W.J.; Cai, Q.G.; Wu, S.F. Process and mechanism for the development of physical crusts in three typical Chinese soils. Pedosphere 2013, 23, 321–332. [Google Scholar] [CrossRef]
- Cheng, Q.; Cai, Q.; Ma, W. Comparative study on rain splash erosion of representative soils in China. Chin. Geogr. Sci. 2008, 18, 155–161. [Google Scholar] [CrossRef]
- Mills, A.J.; Fey, M.V. Effects of vegetation cover on the tendency of soil to crust in South Africa. Soil Use Manag. 2004, 20, 308–317. [Google Scholar] [CrossRef]
- Rees, H.; Chow, T.; Loro, P.; Lavoie, J.; Monteith, J.; Blaauw, A. Hay mulching to reduce runoff and soil loss under intensive potato production in Northwestern New Brunswick, Canada. Can. J. Soil Sci. 2002, 82, 249–258. [Google Scholar] [CrossRef]
- García-Orenes, F.; Cerdà, A.; Mataix-Solera, J.; Guerrero, C.; Bodí, M.; Arcenegui, V.; Zornoza, R.; Sempere, J. Effects of agricultural management on surface soil properties and soil–water losses in Eastern Spain. Soil Tillage Res. 2009, 106, 117–123. [Google Scholar] [CrossRef]
- Findeling, A.; Ruy, S.; Scopel, E. Modeling the effects of a partial residue mulch on runoff using a physically based approach. J. Hydrol. 2003, 275, 49–66. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, B.; Zhou, P.; Tang, J.L.; Wang, T.; Miao, C.Y. Effects of vegetation cover on phosphorus loss from a hillslope cropland of purple soil under simulated rainfall: A case study in China. Nutr. Cycl. Agroecosyst. 2009, 85, 263–273. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, D.; Zhuo, M.; Guo, T.; Liao, Y.; Xie, Z. Effects of rainfall intensity and slope gradient on erosion characteristics of the red soil slope. Stoch. Environ. Res. Risk Assess. 2015, 29, 609–621. [Google Scholar] [CrossRef]
- Geng, X.D.; Zheng, F.L.; Liu, L. Effect of rainfall intensity and slope gradient on soil erosion process on purple soil hill slopes. J. Sediment Res. 2010, 6, 48–53. (In Chinese) [Google Scholar]
- Onstad, C. Depressional storage on tilled soil surfaces. Trans. ASAE 1984, 27, 729–732. [Google Scholar] [CrossRef]
- Kamphorst, E.; Jetten, V.; Guérif, J.; Iversen, B.; Douglas, J.; Paz, A. Predicting depressional storage from soil surface roughness. Soil Sci. Soc. Am. J. 2000, 64, 1749–1758. [Google Scholar] [CrossRef]
- Cao, L.; Liang, Y.; Wang, Y.; Lu, H. Runoff and soil loss from pinus massoniana forest in Southern China after simulated rainfall. Catena 2015, 129, 1–8. [Google Scholar] [CrossRef]
- Darboux, F.; Davy, P.; Gascuel-Odoux, C.; Huang, C. Evolution of soil surface roughness and flowpath connectivity in overland flow experiments. Catena 2002, 46, 125–139. [Google Scholar] [CrossRef]
- Antoine, M.; Javaux, M.; Bielders, C.L. Integrating subgrid connectivity properties of the micro-topography in distributed runoff models, at the interrill scale. J. Hydrol. 2011, 403, 213–223. [Google Scholar] [CrossRef]
- Yang, J.; Chu, X. Quantification of the spatio-temporal variations in hydrologic connectivity of small-scale topographic surfaces under various rainfall conditions. J. Hydrol. 2013, 505, 65–77. [Google Scholar] [CrossRef]
- Penuela Fernandez, A.; Javaux, M.; Bielders, C. Scale effect on overland flow connectivity at the plot scale. Hydrol. Earth Syst. Sci. 2013, 17, 1–15. [Google Scholar]
- Zhong, R.L.; Zhang, P.C. Experimental research on runoff and sediment yield characteristics on purple soil slope. Zhejiang Hydrotech. 2011, 2. (In Chinese) [Google Scholar] [CrossRef]
- Xiang, H.; Liu, Q.Q.; Li, J.C. Influences of slope surface conditions on the runoff generation. J. Hydrodyn. Ser. B 2004, 19, 774–782. (In Chinese) [Google Scholar]
- Xu, P.; Fu, B. The runoff characteristics under simulated rainfall on purple soil sloping cropland. Chin. J. Geochem. 2011, 30, 317–322. [Google Scholar] [CrossRef]
- Sharma, K.; Singh, H.; Pareek, O. Rainwater infiltration into a bare loamy sand. Hydrol. Sci. J. 1983, 28, 417–424. [Google Scholar] [CrossRef]
- Wu, C.C.; Chen, C.; Tsou, C. Effects of different mulching materials on soil moisture variation and erosion control for steep sloping lands. J. Chin. Soil Water Conserv. 1995, 26, 121–133. (In Chinese) [Google Scholar]
- Won, C.H.; Choi, Y.H.; Shin, M.H.; Lim, K.J.; Choi, J.D. Effects of rice straw mats on runoff and sediment discharge in a laboratory rainfall simulation. Geoderma 2012, 189, 164–169. [Google Scholar] [CrossRef]
- Li, X.Y.; Shi, P.J.; Liu, L.Y.; Gao, S.Y.; Wang, X.S.; Cheng, L.S. Influence of pebble size and cover on rainfall interception by gravel mulch. J. Hydrol. 2005, 312, 70–78. [Google Scholar] [CrossRef]
- Pérez, F.L. The influence of surface volcaniclastic layers from Haleakala (Maui, Hawaii) on soil water conservation. Catena 2000, 38, 301–332. [Google Scholar] [CrossRef]
- Sirjani, E.; Mahmoodabadi, M. Effects of sheet flow rate and slope gradient on sediment load. Arab. J. Geosci. 2014, 7, 203–210. [Google Scholar] [CrossRef]
- Kinnell, P. Raindrop-impact-induced erosion processes and prediction: A review. Hydrol. Process. 2005, 19, 2815–2844. [Google Scholar] [CrossRef]
- Renard, K.; Foster, G.; Weesies, G.; McCool, D.; Yoder, D. A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Department of Agriculture, Agricultural Research Service (USDA-ARS) Handbook No. 703; United States Government Printing Office: Washington, DC, USA, 1997; pp. 1–385.
- Zhang, G.H.; Liu, B.Y.; Nearing, M.; Huang, C.H.; Zhang, K.L. Soil detachment by shallow flow. Trans. ASAE 2002, 45, 351. [Google Scholar]
- Fu, S.; Liu, B.; Liu, H.; Xu, L. The effect of slope on interrill erosion at short slopes. Catena 2011, 84, 29–34. [Google Scholar] [CrossRef]
- Ekwue, E.; Harrilal, A. Effect of soil type, peat, slope, compaction effort and their interactions on infiltration, runoff and raindrop erosion of some trinidadian soils. Biosyst. Eng. 2010, 105, 112–118. [Google Scholar] [CrossRef]
- Lu, K.X.; Li, Z.B.; Zhang, X.; Yu, G.Q. Experimental study on law of runoff-erosion-sediment yield under indoor simulated rainfall condition. J. Soil Water Conserv. 2011, 25. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, H.; Peng, X.; Darboux, F. Effect of rainfall kinetic energy on crust formation and interrill erosion of an ultisol in subtropical China. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Lal, R. Soil erosion on alfisols in western Nigeria: II. Effects of mulch rates. Geoderma 1976, 16, 377–387. [Google Scholar] [CrossRef]
- Gómez, J.; Nearing, M. Runoff and sediment losses from rough and smooth soil surfaces in a laboratory experiment. Catena 2005, 59, 253–266. [Google Scholar] [CrossRef]
- Prats, S.A.; Martins, M.A.D.S.; Malvar, M.C.; Ben-Hur, M.; Keizer, J.J. Polyacrylamide application versus forest residue mulching for reducing post-fire runoff and soil erosion. Sci. Total Environ. 2014, 468, 464–474. [Google Scholar] [CrossRef] [PubMed]
- Vega, J.A.; Fernández, C.; Fonturbel, T.; González-Prieto, S.; Jiménez, E. Testing the effects of straw mulching and herb seeding on soil erosion after fire in a gorse shrubland. Geoderma 2014, 223, 79–87. [Google Scholar] [CrossRef]
- Wang, G.; Fang, Q.; Wu, B.; Yang, H.; Xu, Z. Relationship between soil erodibility and modeled infiltration rate in different soils. J. Hydrol. 2015, 528, 408–418. [Google Scholar] [CrossRef]
- Essig, E.T.; Corradini, C.; Morbidelli, R.; Govindaraju, R.S. Infiltration and deep flow over sloping surfaces: Comparison of numerical and experimental results. J. Hydrol. 2009, 374, 30–42. [Google Scholar] [CrossRef]
- Fox, D.; Bryan, R.; Price, A. The influence of slope angle on final infiltration rate for interrill conditions. Geoderma 1997, 80, 181–194. [Google Scholar] [CrossRef]
- Rudolph, A.; Helming, K.; Diestel, H. Effect of antecedent soil water content and rainfall regime on microrelief changes. Soil Technol. 1997, 10, 69–81. [Google Scholar] [CrossRef]
- Poesen, J. The influence of slope angle on infiltration rate and hortonian overland flow. Z. Geomorphol. Suppl. Band 1984, 49, 117–131. [Google Scholar]
- Janeau, J.-L.; Bricquet, J.-P.; Planchon, O.; Valentin, C. Soil crusting and infiltration on steep slopes in northern Thailand. Eur. J. Soil Sci. 2003, 54, 543–554. [Google Scholar] [CrossRef]
- Chaplot, V.; Le Bissonnais, Y. Field measurements of interrill erosion under-different slopes and plot sizes. Earth Surf. Process. Landf. 2000, 25, 145–153. [Google Scholar] [CrossRef]
- Jiang, D.; Huang, G. Simulated experiment on the influence of slope gradient on rainfall infiltration. Bull. Soil Water Conserv. 1984, 4, 10–13. (In Chinese) [Google Scholar]
- Jin, C.; Cai, Q.G.; Wang, Z.K. An experimental study of infiltration and erosion under slope gradients and vegetal covers. J. Geogr. Sci. 1995, 4, 62–73. (In Chinese) [Google Scholar]
- Yuan, J.; Lei, T.; Guo, S.; Jiang, D. Study on spatial variation of infiltration rates for small watershed in loess plateau. J. Hydraul. Eng. 2001, 10, 88–92. (In Chinese) [Google Scholar]
- Levy, G.; Mamedov, A. High-energy-moisture-characteristic aggregate stability as a predictor for seal formation. Soil Sci. Soc. Am. J. 2002, 66, 1603–1609. [Google Scholar] [CrossRef]
- Warrington, D.; Mamedov, A.; Bhardwaj, A.; Levy, G. Primary particle size distribution of eroded material affected by degree of aggregate slaking and seal development. Eur. J. Soil Sci. 2009, 60, 84–93. [Google Scholar] [CrossRef]
- Assouline, S.; Mualem, Y. Modeling the dynamics of seal formation and its effect on infiltration as related to soil and rainfall characteristics. Water Resour. Res. 1997, 33, 1527–1536. [Google Scholar] [CrossRef]
- Foley, J.; Silburn, D. Hydraulic properties of rain impact surface seals on three clay soils—Influence of raindrop impact frequency and rainfall intensity during steady state. Soil Res. 2002, 40, 1069–1083. [Google Scholar] [CrossRef]
- Hawke, R.; Price, A.; Bryan, R. The effect of initial soil water content and rainfall intensity on near-surface soil hydrologic conductivity: A laboratory investigation. Catena 2006, 65, 237–246. [Google Scholar] [CrossRef]
- Morin, J.; Benyamini, Y. Rainfall infiltration into bare soils. Water Resour. Res. 1977, 13, 813–817. [Google Scholar] [CrossRef]
- McIntyre, D. Permeability measurements of soil crusts formed by raindrop impact. Soil Sci. 1958, 85, 185–189. [Google Scholar] [CrossRef]
- Ribolzi, O.; Patin, J.; Bresson, L.-M.; Latsachack, K.; Mouche, E.; Sengtaheuanghoung, O.; Silvera, N.; Thiébaux, J.-P.; Valentin, C. Impact of slope gradient on soil surface features and infiltration on steep slopes in northern Laos. Geomorphology 2011, 127, 53–63. [Google Scholar] [CrossRef]
- Liu, H.; Lei, T.; Zhao, J.; Yuan, C.; Fan, Y.; Qu, L. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- De Souza, E.R.; de Assunção Montenegro, A.A.; Montenegro, S.M.G.; de Matos, J.D.A. Temporal stability of soil moisture in irrigated carrot crops in northeast Brazil. Agric. Water Manag. 2011, 99, 26–32. [Google Scholar] [CrossRef]
- Mannering, J.; Meyer, L. The effects of various rates of surface mulch on infiltration and erosion. Soil Sci. Soc. Am. J. 1963, 27, 84–86. [Google Scholar] [CrossRef]
- Huang, J.; Wu, P.; Zhao, X. Effects of rainfall intensity, underlying surface and slope gradient on soil infiltration under simulated rainfall experiments. Catena 2013, 104, 93–102. [Google Scholar] [CrossRef]
- Xiaoan, C.; Qiangguo, C.; Mingguo, Z.; Junlan, L. Empirical soil erosion model for single rainstorm in Chabagou Drainage Basin. Prog. Geogr. 2011, 30, 325–329. [Google Scholar]
- Abu-Awwad, A. Water infiltration and redistribution within soils affected by a surface crust. J. Arid Environ. 1997, 37, 231–242. [Google Scholar] [CrossRef]
- Chen, H.; Cai, Q. Experimental study on the effect of slope on runoff and infiltration. In Experimental Research on Soil Erosion Law in Loess Plateau Region of Western Shanxi Province; Water Power Press: Beijing, China, 1990. (In Chinese) [Google Scholar]
- Schmidt, J. Effects of Soil Slaking and Sealing on Infiltration—Experiments and Model Approach. In Proceedings of the 19th World Congress of Soil Science: Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010.
- Dourte, D.; Shukla, S.; Singh, P.; Haman, D. Rainfall intensity-duration-frequency relationships for Andhra Pradesh, India: Changing rainfall patterns and implications for runoff and groundwater recharge. J. Hydrol. Eng. 2012, 18, 324–330. [Google Scholar] [CrossRef]
- Stone, J.J.; Paige, G.B.; Hawkins, R.H. Rainfall intensity-dependent infiltration rates on rangeland rainfall simulator plots. Trans. ASABE 2008, 51, 45–53. [Google Scholar] [CrossRef]
| Treatments | Slope (°) | Rainfall Intensity (mm·h−1) Runoff | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 33 | 54 | 94 | 120 | ANOVA | ||||||
| Mean | S.D | Mean | S.D | Mean | S.D | Mean | S.D | |||
| Un-mulched | 5 | 0.2 b,C | 0.02 | 2.5 c,C | 0.40 | 23.0 c,B | 1.05 | 52.4 b,A | 3.84 | p < 0.01 |
| 15 | 1.5 a,B | 0.09 | 7.1 b,B | 0.13 | 49.6 b,A | 7.30 | 56.6 b,A | 4.01 | p < 0.01 | |
| 25 | 1.7 a,D | 0.21 | 19.2 a,C | 2.44 | 60.5 a,B | 1.90 | 68.1 a,A | 5.73 | p < 0.01 | |
| ANOVA | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.05 | ||||||
| Mulched | 5 | 0.00 b,C | 0.00 | 0.00 c,C | 0.00 | 3.7 c,B | 0.13 | 7.3 c,A | 0.57 | p < 0.01 |
| 15 | 0.00 b,C | 0.00 | 1.17 b,C | 0.07 | 15.9 b,B | 1.07 | 30.9 b,A | 3.62 | p < 0.01 | |
| 25 | 0.50 a,C | 0.03 | 3.38 a,C | 0.28 | 34.1 a,B | 4.70 | 58.4 a,A | 5.81 | p < 0.01 | |
| ANOVA | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | ||||||
| Treatments | Slope (°) | Rainfall Intensity (mm·h−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 33 | 54 | 94 | 120 | ANOVA | ||||||
| Mean | S.D | Mean | S.D | Mean | S.D | Mean | S.D | |||
| Un-mulched | 5 | 0.43 c,C | 0.10 | 23.5 c,C | 4.8 | 111.2 c,B | 6.60 | 184.5 b,A | 24.7 | p < 0.01 |
| 15 | 3.60 b,C | 0.60 | 84.6 b,B | 5.1 | 382.1 b,A | 37.8 | 387.0 b,A | 76.8 | p < 0.01 | |
| 25 | 5.79 a,C | 1.50 | 220.0 a,B | 35.0 | 876.2 a,A | 76.3 | 849.4 a,A | 162.4 | p < 0.01 | |
| ANOVA | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | ||||||
| Mulched | 5 | 0.00 b,C | 0.00 | 0.00 b,C | 0.00 | 21.26 c,B | 0.17 | 31.03 b,A | 3.19 | p < 0.01 |
| 15 | 0.00 b,C | 0.00 | 0.73 a,C | 0.08 | 26.88 b,B | 0.95 | 36.84 b,A | 7.57 | p < 0.01 | |
| 25 | 0.43 a,C | 0.03 | 0.85 a,C | 0.07 | 34.69 a,B | 2.35 | 88.63 a,A | 8.75 | p < 0.01 | |
| ANOVA | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | ||||||
| Treatments | Slope (°) | Rainfall Intensity (mm·h−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 33 | 54 | 94 | 120 | ANOVA | ||||||
| Mean | S.D | Mean | S.D | Mean | S.D | Mean | S.D | |||
| Un-mulched | 5 | 32.8 a,C | 0.02 | 51.5 a,B | 0.40 | 70.9 a,A | 1.05 | 67.6 a,A | 3.84 | p < 0.01 |
| 15 | 31.5 b,C | 0.09 | 46.9 b,B | 0.13 | 44.4 b,B | 7.30 | 63.4 a,A | 4.01 | p < 0.01 | |
| 25 | 31.3 b,B | 0.21 | 34.8 c,B | 2.44 | 33.5 c,B | 1.90 | 51.9 b,A | 5.73 | p < 0.01 | |
| ANOVA | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.05 | ||||||
| Mulched | 5 | 33.0 a,D | 0.00 | 54.0 a,C | 0.00 | 90.3 a,B | 0.13 | 112.7 a,A | 0.57 | p < 0.01 |
| 15 | 33.0 a,D | 0.00 | 52.8 b,C | 0.07 | 78.1 b,B | 1.07 | 89.1 b,A | 3.62 | p < 0.01 | |
| 25 | 32.5 b,C | 0.03 | 50.6 c,B | 0.28 | 59.9 c,A | 4.70 | 61.6 c,A | 5.81 | p < 0.01 | |
| ANOVA | p < 0.01 | p < 0.01 | p < 0.01 | p < 0.01 | ||||||
| Source | DF | SS | MS | F | p |
|---|---|---|---|---|---|
| Regression | 3 | 2.626 | 0.875 | 106.95 | 0.000 |
| Residual | 68 | 0.557 | 0.008 | ||
| Total | 71 | 3.248 |
| Variables | Coefficient | Std. Error | T | p |
|---|---|---|---|---|
| Constant | 1.027 | 0.046 | 22.51 | <0.000 |
| RI | −0.044 | 0.003 | −13.86 | <0.000 |
| S | −0.011 | 0.001 | −8.11 | <0.000 |
| M | 0.171 | 0.022 | 7.94 | <0.000 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.N.; Gong, Y.; Hu, T.; Lal, R.; Zheng, J.; Justine, M.F.; Azhar, M.; Che, M.; Zhang, H. Effect of Slope, Rainfall Intensity and Mulch on Erosion and Infiltration under Simulated Rain on Purple Soil of South-Western Sichuan Province, China. Water 2016, 8, 528. https://doi.org/10.3390/w8110528
Khan MN, Gong Y, Hu T, Lal R, Zheng J, Justine MF, Azhar M, Che M, Zhang H. Effect of Slope, Rainfall Intensity and Mulch on Erosion and Infiltration under Simulated Rain on Purple Soil of South-Western Sichuan Province, China. Water. 2016; 8(11):528. https://doi.org/10.3390/w8110528
Chicago/Turabian StyleKhan, Muhammad Naeem, Yuanbo Gong, Tingxing Hu, Rattan Lal, Jiangkun Zheng, Meta Francis Justine, Muhammad Azhar, Mingxuan Che, and Haitao Zhang. 2016. "Effect of Slope, Rainfall Intensity and Mulch on Erosion and Infiltration under Simulated Rain on Purple Soil of South-Western Sichuan Province, China" Water 8, no. 11: 528. https://doi.org/10.3390/w8110528
APA StyleKhan, M. N., Gong, Y., Hu, T., Lal, R., Zheng, J., Justine, M. F., Azhar, M., Che, M., & Zhang, H. (2016). Effect of Slope, Rainfall Intensity and Mulch on Erosion and Infiltration under Simulated Rain on Purple Soil of South-Western Sichuan Province, China. Water, 8(11), 528. https://doi.org/10.3390/w8110528







