Interannual Variability in Global Mean Sea Level Estimated from the CESM Large and Last Millennium Ensembles
Abstract
:1. Introduction
2. Materials and Methods
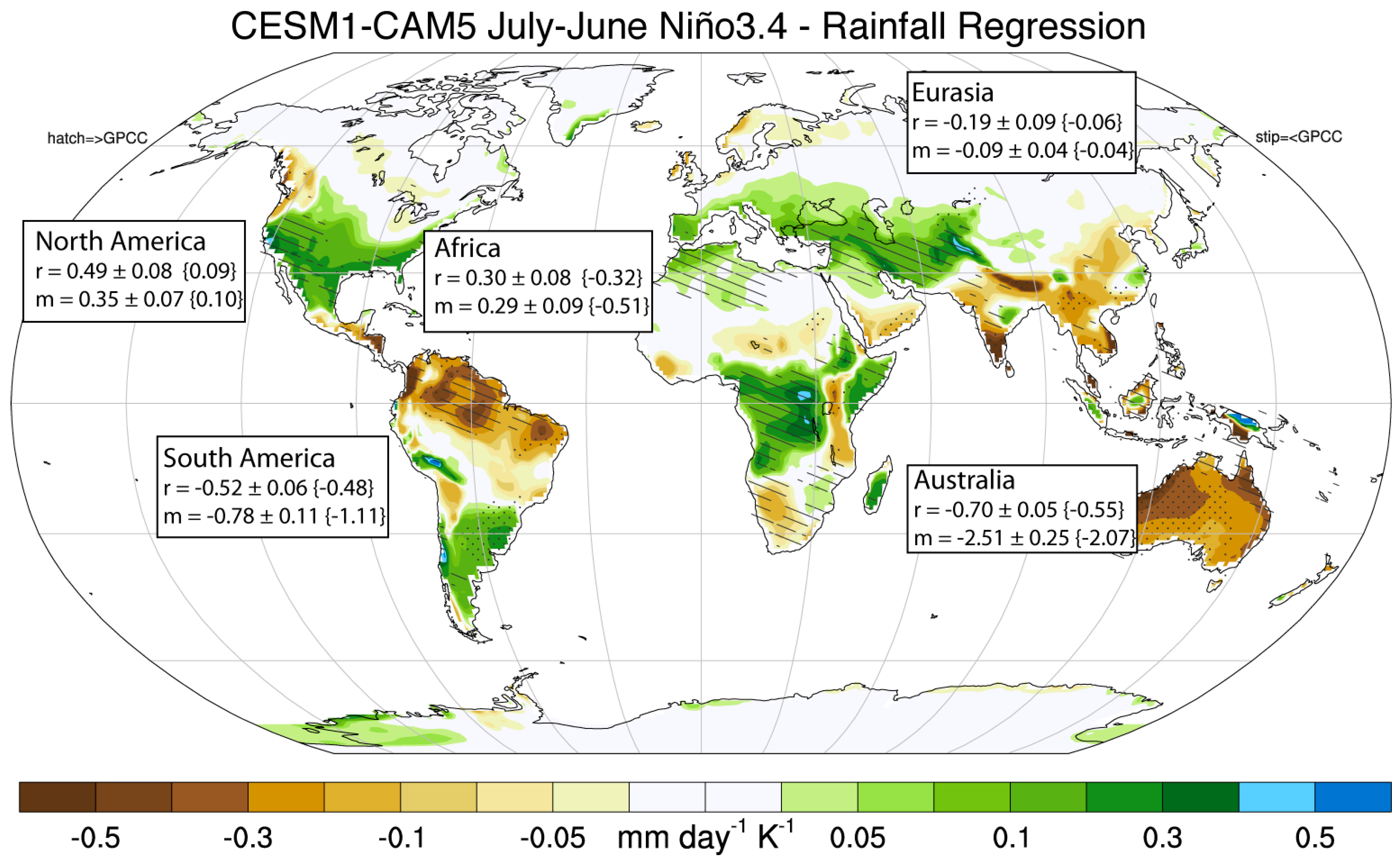
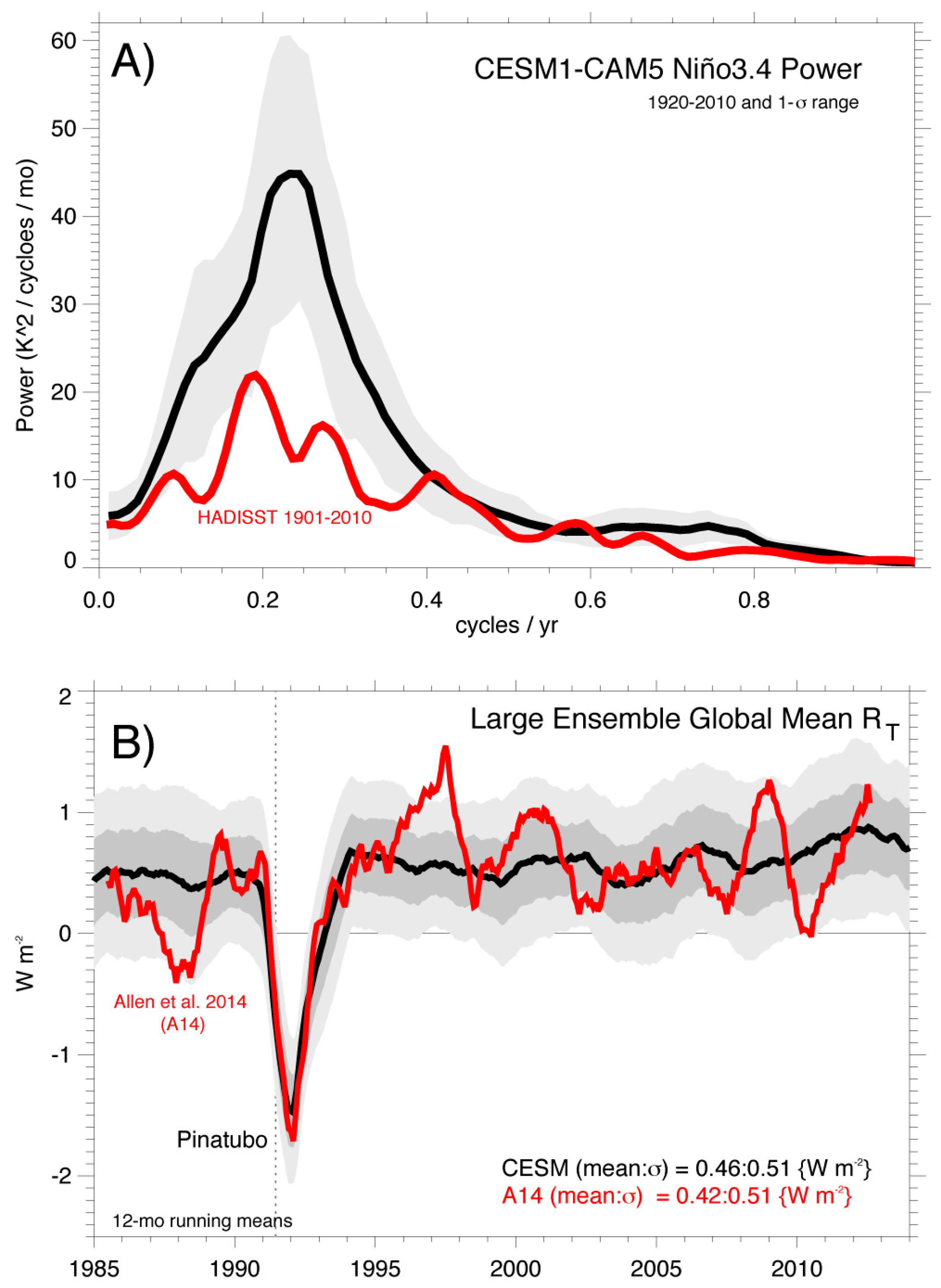
Model Evaluation
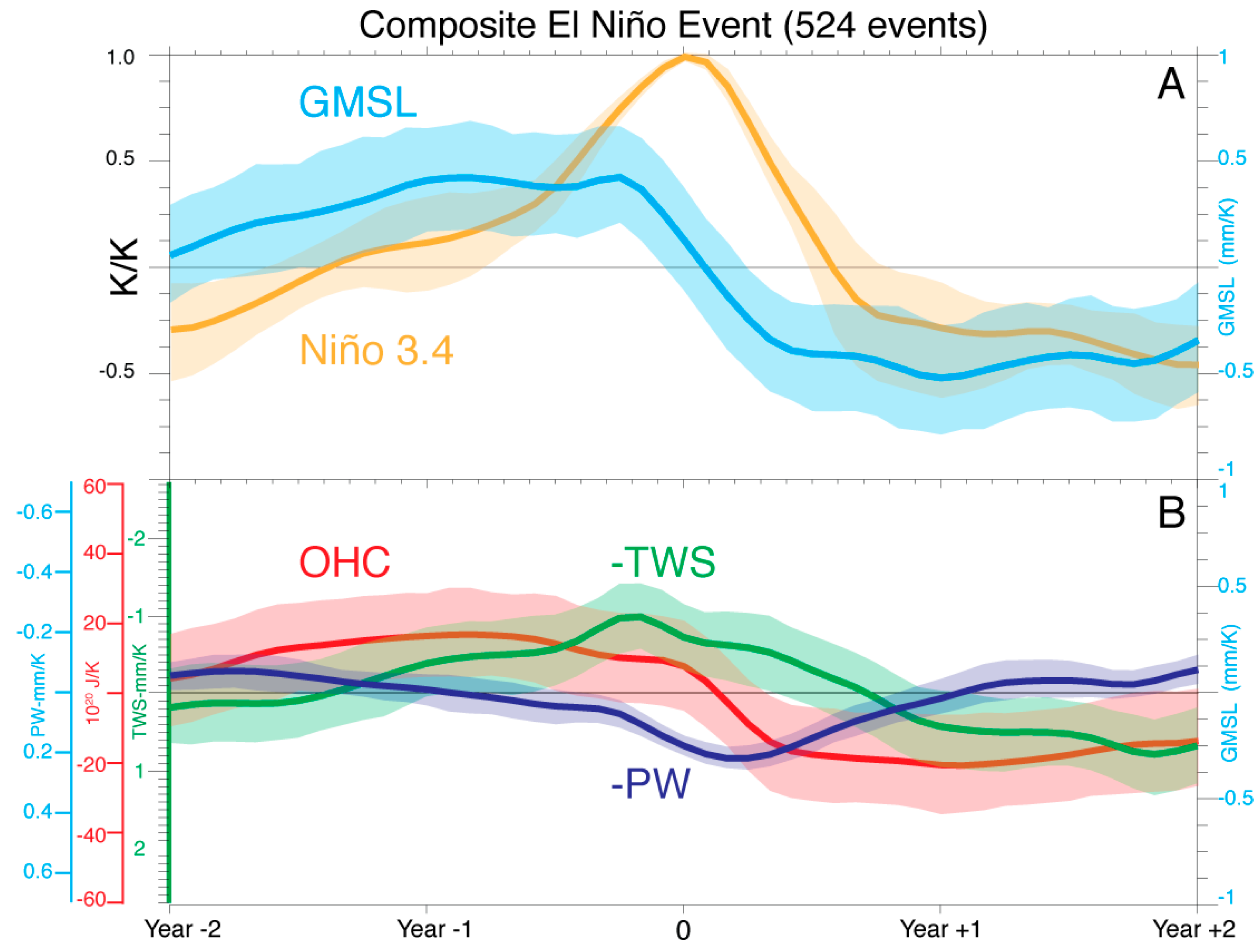
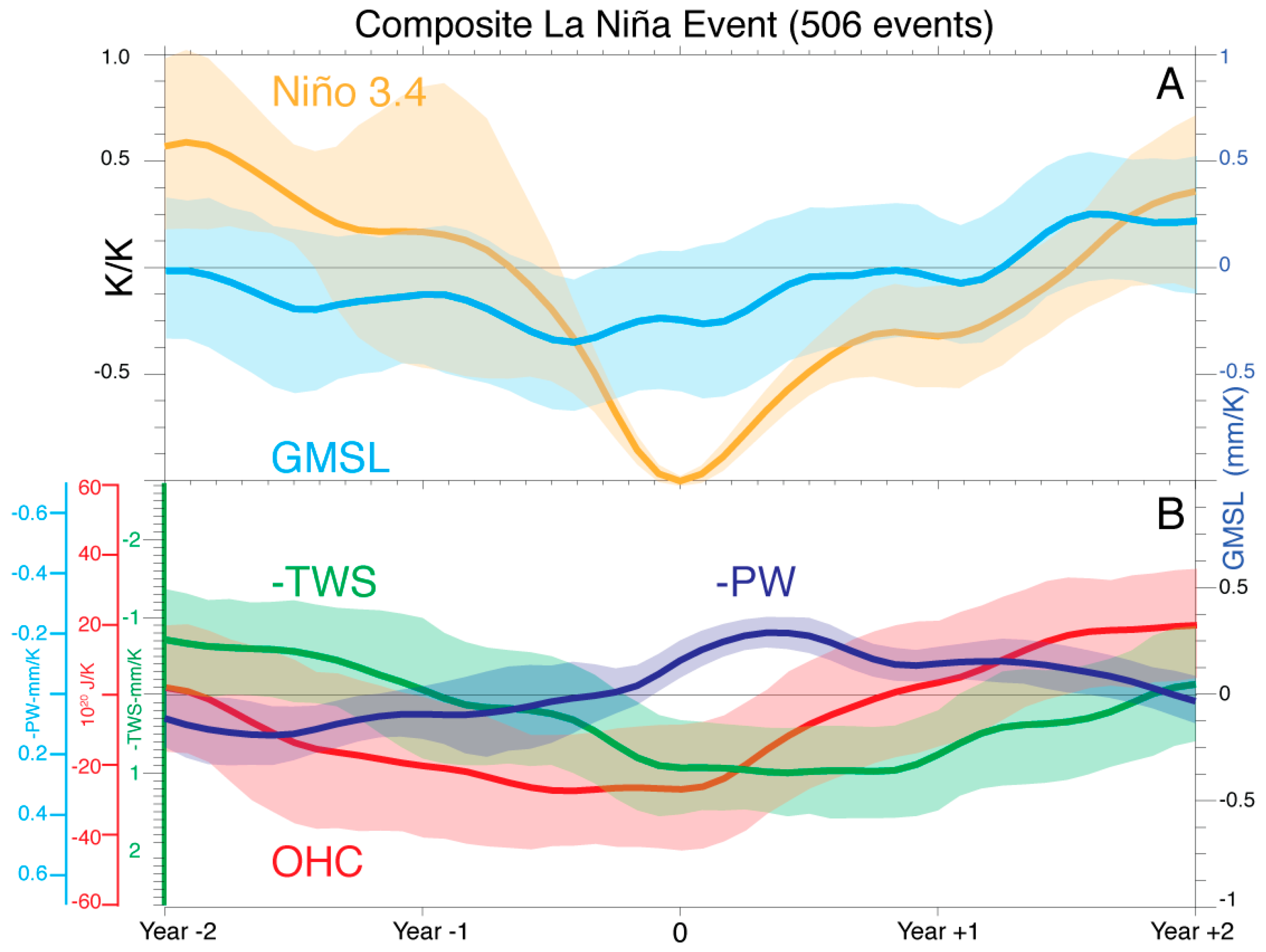
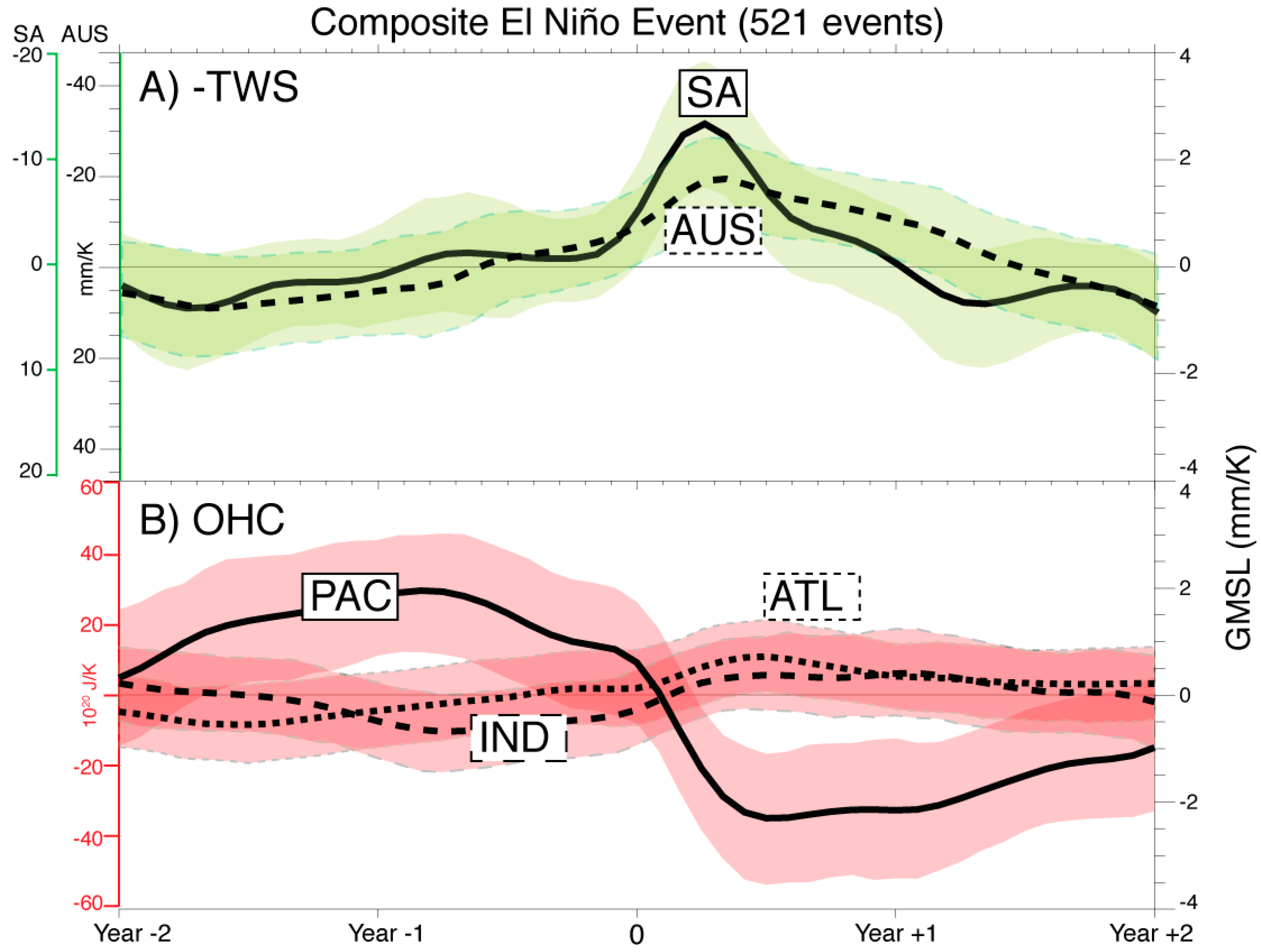
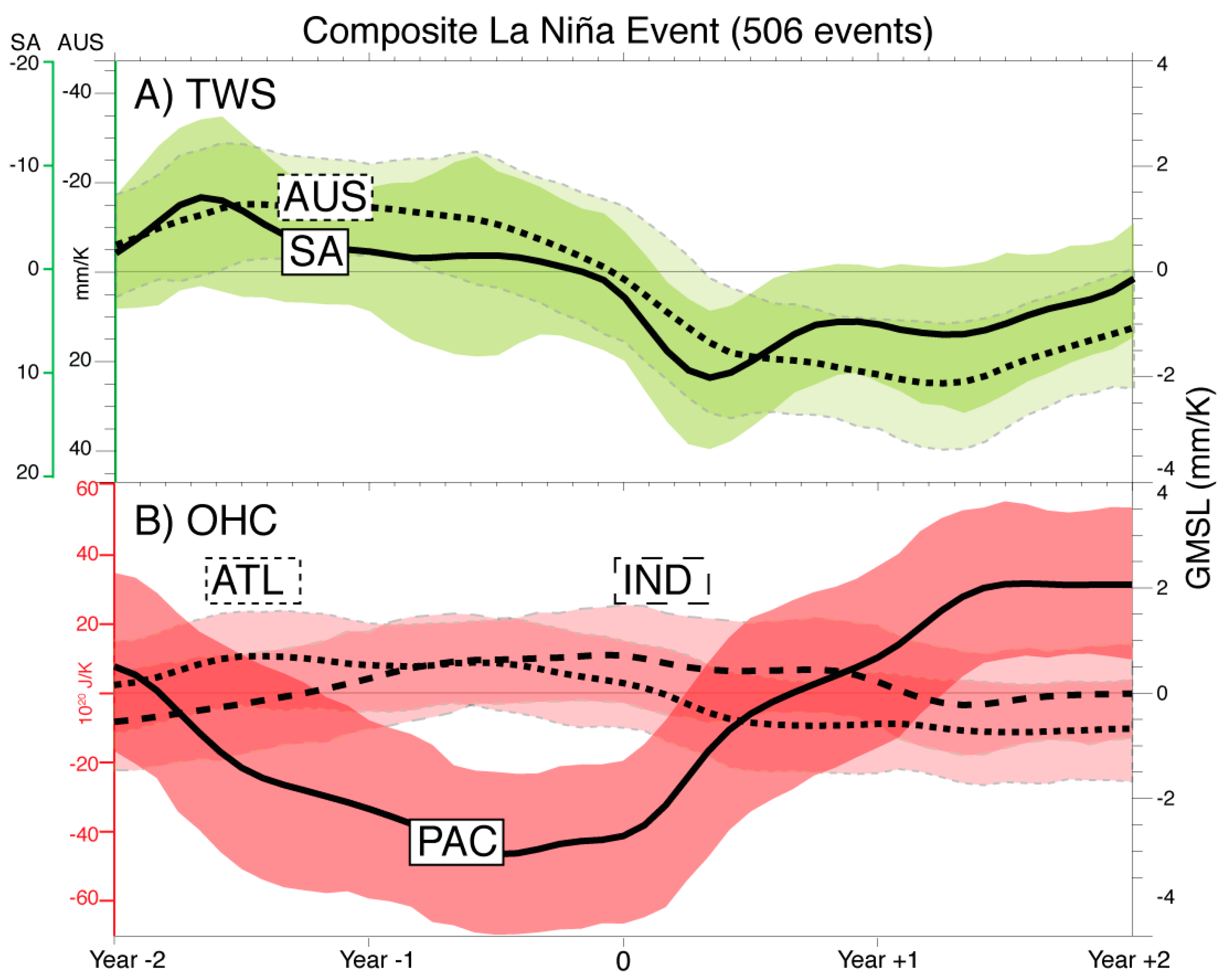
3. GMSL Variability during ENSO
4. Regional Sources of GMSL Variability
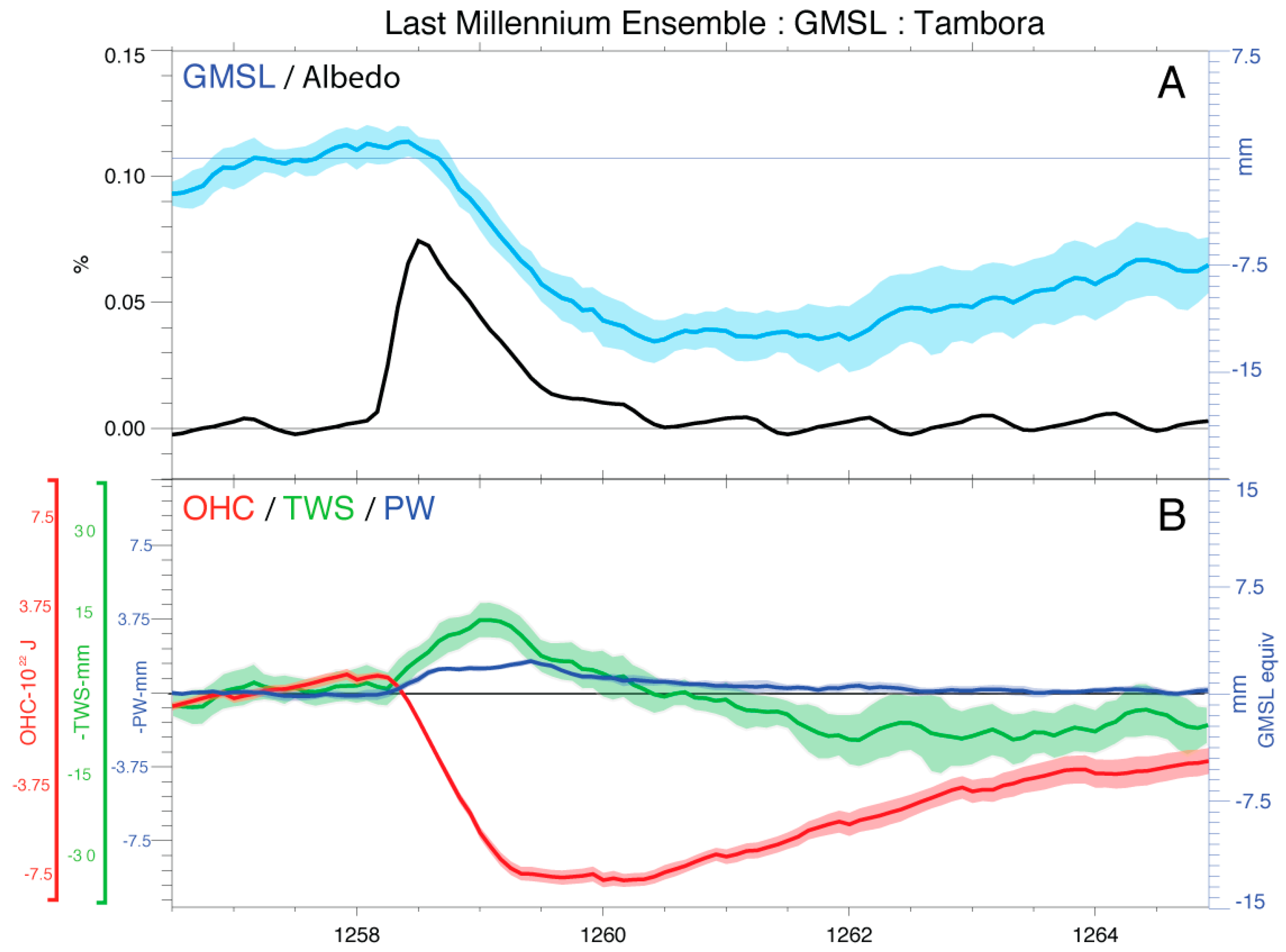
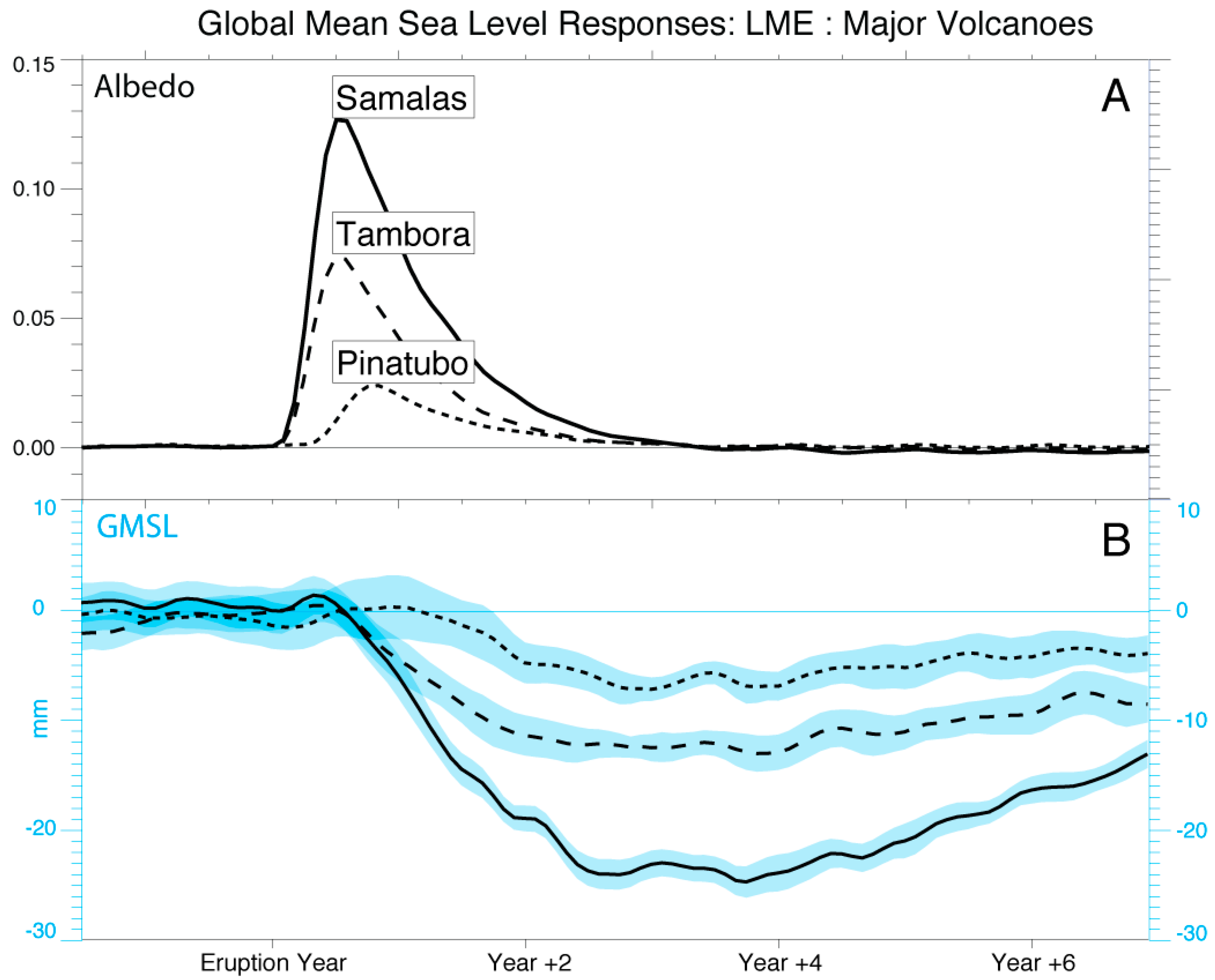
5. GMSL Variability Following Volcanic Eruptions
6. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nerem, R.S.; Haines, B.J.; Hendricks, J.; Minster, J.F.; Mitchum, G.T.; White, W.B. Improved determination of global mean sea level variations using TOPEX/POSEIDON altimeter data. Geophys. Res. Lett. 1997, 24, 1331–1334. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Matthews, A.P.; Spada, G. Trends and acceleration in global and regional sea levels since 1807. Glob. Planet. Chang. 2014, 113, 11–22. [Google Scholar] [CrossRef]
- Church, J.A.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifeld, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; Payne, A.J.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, B., Midgley, B.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 1137–1216. [Google Scholar]
- Landerer, F.W.; Jungclaus, J.H.; Marotzke, J. El Niño–Southern Oscillation signals in sea level, surface mass redistribution, and degree-two geoid coefficients. J. Geophys. Res. 2008, 113, C08014. [Google Scholar] [CrossRef]
- Adhikari, S.; Ivins, E.R. Climate-driven polar motion: 2003–2015. Sci. Adv. 2016, 2, e1501693. [Google Scholar] [CrossRef] [PubMed]
- Carson, M.; KöhlD, A.; Stammer, D.; Slangen, A.B.A.; Katsman, C.A.; van de Wal, R.S.W.; Church, J.; White, N. Coastal sea level changes, observed and projected during the 20th and 21st century. Clim. Chang. 2016, 134, 269–281. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Leuliette, E.W.; Nerem, R.S.; Mitchum, G.T. Calibration of TOPEX/Poseidon and Jason altimeter data to construct a continuous record of mean sea level change. Mar. Geod. 2004, 27, 79–94. [Google Scholar] [CrossRef]
- Nerem, R.S.; Chambers, D.P.; Leuliette, E.W.; Mitchum, G.T.; Giese, B.S. Variations in global mean sea level associated with the 1997–1998 ENSO event: Implications for measuring long term sea level change. Geophys. Res. Lett. 1999, 26, 3005–3008. [Google Scholar] [CrossRef]
- Ngo-Duc, T.; Laval, K.; Polcher, J.; Cazenave, A. Contribution of continental water to sea level variations during the 1997–1998 El Niño–Southern Oscillation event: Comparison between Atmospheric Model Intercomparison Project simulations and TOPEX/Poseidon satellite data. J. Geophys. Res. 2005, 110, D09103. [Google Scholar] [CrossRef]
- Gu, G.; Adler, R.F.; Huffman, G.J.; Curtis, S. Tropical rainfall variability on interannual-to-interdecadal and longer time scales derived from the GPCP monthly product. J. Clim. 2007, 20, 4033–4046. [Google Scholar] [CrossRef]
- Nerem, R.S.; Chambers, D.; Choe, C.; Mitchum, G.T. Estimating mean sea level change from the TOPEX and Jason altimeter missions. Mar. Geod. 2010, 33, 435–446. [Google Scholar] [CrossRef]
- Boening, C.; Willis, J.K.; Landerer, F.W.; Nerem, R.S.; Fasullo, J.T. The 2011 La Niña: So strong, the oceans fell. Geophys. Res. Lett. 2012, 39, L19602. [Google Scholar] [CrossRef]
- Cazenave, A.; Henry, O.; Munier, S.; Delcroix, T.; Gordon, A.L.; Meyssignac, B.; Llovel, W.; Palanisamy, H.; Becker, M. Estimating ENSO influence on the global mean sea level, 1993–2010. Mar. Geod. 2012, 35, 82–97. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Boening, C.; Landerer, F.W.; Nerem, R.S. Australia’s unique influence on global sea level in 2010–2011. Geophys. Res. Lett. 2013, 40, 4368–4373. [Google Scholar] [CrossRef]
- Llovel, W.; Becker, M.; Cazenave, A.; Jevrejeva, S.; Alkama, R.; Decharme, B.; Douville, H.; Ablain, M.; Beckley, B. Terrestrial waters and sea level variations on interannual time scale. Glob. Planet. Chang. 2011, 75, 76–82. [Google Scholar] [CrossRef]
- Gu, G.; Adler, R.F. Precipitation and temperature variations on the interannual time scale: Assessing the impact of ENSO and volcanic eruptions. J. Clim. 2011, 24, 2258–2270. [Google Scholar] [CrossRef]
- Balmaseda, M.A.; Trenberth, K.E.; Källén, E. Distinctive climate signals in reanalysis of global ocean heat content. Geophys. Res. Lett. 2013, 40, 1754–1759. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J.; Arblaster, J.M. Significant decadal-scale impact of volcanic eruptions on sea level and ocean heat content. Nature 2005, 438, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Gleckler, P.J.; Wigley, T.M.L.; Santer, B.D.; Gregory, J.M.; AchutaRao, K.M.; Taylor, K.E. Volcanoes and climate: Krakatoa’s signature persists in the ocean. Nature 2006, 439, 675. [Google Scholar] [CrossRef] [PubMed]
- Gleckler, P.J.; AchutaRao, K.; Gregory, J.M.; Santer, B.D.; Taylor, K.E.; Wigley, T.M.L. Krakatoa lives: The effect of volcanic eruptions on ocean heat content and thermal expansion. Geophys. Res. Lett. 2006, 33, L17702. [Google Scholar] [CrossRef]
- Gregory, J.M.; Lowe, J.A.; Tett, S.F.B. Simulated global-mean sea level changes over the last half-millennium. J. Clim. 2006, 19, 4576–4591. [Google Scholar] [CrossRef]
- Slangen, A.; Church, J.; Zhang, X.; Monselesan, D. Detection and attribution of global mean thermosteric sea level change. Geophys. Res. Lett. 2014, 41, 5951–5959. [Google Scholar] [CrossRef]
- Slangen, A.; Church, J.; Zhang, X.; Monselesan, D. The sea level response to external forcings in historical simulations of CMIP5 climate models*. J. Clim. 2015, 28, 8521–8539. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Nerem, R.S.; Hamlington, B. Is the detection of accelerated sea level rise imminent? Sci. Rep. 2016, 6, 31245. [Google Scholar] [CrossRef] [PubMed]
- Knutti, R.; Masson, D.; Gettelman, A. Climate model genealogy: Generation CMIP5 and how we got there. Geophys. Res. Lett. 2013, 40, 1194–1199. [Google Scholar] [CrossRef]
- Kay, J.E.; Deser, C.; Phillips, A.; Mai, A.; Hannay, C.; Strand, G.; Arblaster, J.; Bates, S.S.; Danabasoglu, G.; Edwards, J.; et al. The Community Earth System Model (CESM) large ensemble project: A community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meterol. Soc. 2015, 119, 1333–1349. [Google Scholar] [CrossRef]
- Otto-Bliesner, B.L.; Brady, E.C.; Fasullo, J.T.; Jahn, A.; Landrum, L.; Stevenson, S.; Rosenbloom, N.; Mai, A.; Strand, G. Climate Variability and Change since 850 C.E.: An Ensemble Approach with the Community Earth System Model (CESM). Bull. Am. Meterol. Soc. 2015, 119, 735–754. [Google Scholar]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3, M03001. [Google Scholar]
- Lawrence, D.M.; Oleson, K.; Flanner, M.G.; Fletcher, C.G.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Bonan, G.B. The CCSM4 land simulation, 1850–2005: Assessment of surface climate and new capabilities. J. Clim. 2012, 25, 2240–2260. [Google Scholar] [CrossRef]
- Smith, R.D.; Jones, P.; Briegleb, B.; Bryan, F.; Danabasoglu, G.; Dennis, J.; Dukowicz, J.; Eden, C.; Fox-Kemper, B.; Gent, P.; et al. The Parallel Ocean Program (POP) Reference Manual: Ocean Component of the Community Climate System Model (CCSM) and Community Earth System Model (CESM); Technical Report LAUR-10-01853; Los Alamos National Laboratory: Boulder, CO, USA, 23 March 2010; p. 141. [Google Scholar]
- Gent, P.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, L19503. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Holland, M.M.; Gent, P.R.; Ghan, S.; Kay, J.; Kushner, P.; Lamarque, J.-F.; Large, W.G.; Lawrence, D.; Lindsay, K.; et al. The community earth system model: A framework for collaborative research. Bull. Am. Meterol. Soc. 2013, 94, 1339–1360. [Google Scholar] [CrossRef]
- Church, J.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901-present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Rayner, N.A.; Brohan, P.; Parker, D.E.; Folland, C.F.; Kennedy, J.J.; Vanicek, M.; Ansell, T.; Tett, S.F.B. Improved analyses of changes and uncertainties in sea surface temperature measured In Situ since the mid-nineteenth century: The HadSST2 data set. J. Clim. 2006, 19, 446–469. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Balmaseda, M.A. Earth’s Energy Imbalance. J. Clim. 2014, 27, 3129–3144. [Google Scholar] [CrossRef]
- Allan, R.P.; Liu, C.; Loeb, N.G.; Palmer, M.D.; Roberts, M.; Smith, D.; Vidale, P.-L. Changes in global net radiative imbalance 1985–2012. Geophys. Res. Lett. 2014, 41, 5588–5597. [Google Scholar] [CrossRef] [PubMed]
- Mayer, M.; Haimberger, L.; Balmaseda, M.A. On the energy exchange between tropical ocean basins related to ENSO. J. Clim. 2014, 27, 6393–6403. [Google Scholar] [CrossRef]
- Raible, C.C.; Brönnimann, S.; Auchmann, R.; Brohan, P.; Frölicher, T.L.; Graf, H.-F.; Jones, P.; Luterbacher, J.; Muthers, S.; Neukom, R.; et al. Tambora 1815 as a test case for high impact volcanic eruptions: Earth system effects. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 569–589. [Google Scholar] [CrossRef]
- Stevenson, S.; Otto-Bliesner, B.; Fasullo, J.T.; Brady, E. “El Niño Like” hydroclimate responses to last millennium volcanic eruptions. J. Clim. 2016, 29, 2907–2921. [Google Scholar] [CrossRef]
- Lavigne, F.; Degeai, J.-P.; Komorowski, J.-C.; Guillet, S.; Robert, V.; Lahittee, P.; Oppenheimer, C.; Stoffel, M.; Vidal, C.M.; Surono, C.M.; et al. Source of the great AD 1257 mystery eruption unveiled, Samalas volcano, Rinjani Volcanic Complex, Indonesia. Proc. Nat. Acad. Sci. USA 2013, 110, 16742–16747. [Google Scholar] [CrossRef] [PubMed]
- Cazenave, A.; Dieng, H.B.; Meyssignac, B.; von Schuckmann, K.; Decharme, B.; Berthier, E. The rate of sea-level rise. Nat. Clim. Chang. 2014, 4, 358–361. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Chen, J.; Robertson, F.R.; Adler, R.F. Evaluation of global precipitation in reanalyses. J. Appl. Meteorol. Climatol. 2008, 47, 2279–2299. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fasullo, J.T.; Nerem, R.S. Interannual Variability in Global Mean Sea Level Estimated from the CESM Large and Last Millennium Ensembles. Water 2016, 8, 491. https://doi.org/10.3390/w8110491
Fasullo JT, Nerem RS. Interannual Variability in Global Mean Sea Level Estimated from the CESM Large and Last Millennium Ensembles. Water. 2016; 8(11):491. https://doi.org/10.3390/w8110491
Chicago/Turabian StyleFasullo, John T., and Robert S. Nerem. 2016. "Interannual Variability in Global Mean Sea Level Estimated from the CESM Large and Last Millennium Ensembles" Water 8, no. 11: 491. https://doi.org/10.3390/w8110491
APA StyleFasullo, J. T., & Nerem, R. S. (2016). Interannual Variability in Global Mean Sea Level Estimated from the CESM Large and Last Millennium Ensembles. Water, 8(11), 491. https://doi.org/10.3390/w8110491





