Residential Water Demand in a Mexican Biosphere Reserve: Evidence of the Effects of Perceived Price
Abstract
:1. Introduction
2. Materials and Methods
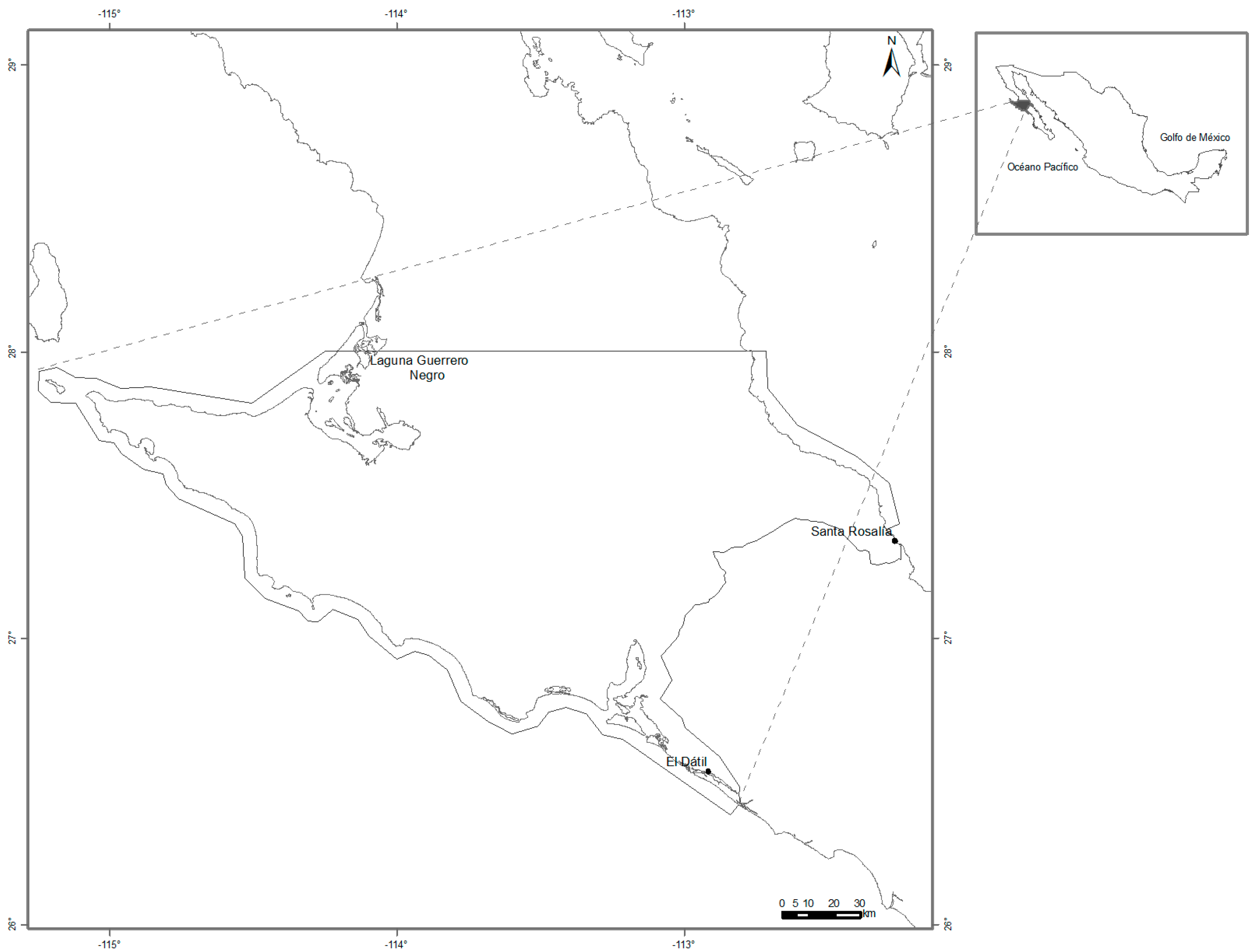
2.1. Study Area
2.2. Specification of Water Demand Dynamics
2.3. Method of Estimating Water Demand Dynamics
2.4. Description of the Database
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AP | Average price |
| m3 | Cubic meters |
| MP | Marginal price |
| p | Precipitation |
| t | Temperature |
| w | Water consumption average per capita residential use |
References
- Gleick, P.H. Water in the 21st century. In Water in Crisis; Gleick, P.H., Ed.; Oxford University Press: Oxford, UK, 1993; pp. 105–113. [Google Scholar]
- The Food and Agriculture Organization of the United Nations (FAO). El Riego en América Latina y el Caribe en Cifras; FAO: Roma, Italy, 2000; p. 348. [Google Scholar]
- The Secretariat of Environment and Natural Resources (SEMARNAT). El Medio Ambiente en México 2005; SEMARNAT: Mexico City, Mexico, 2005. [Google Scholar]
- Foro Consultivo Científico y Tecnológico (FCCyT). Diagnóstico del Agua en las Américas; FCCyT: Mexico City, Mexico, 2012. [Google Scholar]
- Comisión Nacional del Agua (CNA). Estadísticas del Agua en México; CNA: Metepec, Mexico, 2008. [Google Scholar]
- Barkin, D.; Klooster, D. Estrategias de la Gestión del Agua Urbana. En la Gestión del Agua Urbana en México: Retos, Debates y Bienestar; Barkin, D., Ed.; Universidad de Guadalajara: Guadalajara, Mexico, 2006. [Google Scholar]
- Beltrán-Morales, L.F.; Borgues-Conterras, J.; Lagunas-Vazquéz, M.; Beltrán-Morales, J.; García-Rodríguez, F. Volúmenes de consume de agua por localidad en la Reserva de La Biosfera del Vizcaíno, B.C.S. México. In Valoración Hidrosocial en la Reserva de la Biosfera del Vizcaíno; Beltrán-Morales, L.F., Chávez López, S., Ortega-Rubio, A., Eds.; CIBNOR: La Paz, Mexico, 2010; pp. 113–128. [Google Scholar]
- Almendarez-Hernández, M.A.; Avilés-Polanco, G.; Beltrán-Morales, L.F. Demanda de agua de uso comercial en la Reserva de la Biosfera El Vizcaíno, México: Una estimación con datos de panel. Nova Sci. 2015, 7, 553–576. [Google Scholar] [CrossRef]
- Rogers, P.; de Silva, R.; Bhatia, R. Water is an economic good: How to use prices to promote equity, efficiency, and sustainability. Water Policy 2002, 4, 1–17. [Google Scholar] [CrossRef]
- PRI Project. Economic Instruments for Water Demand Management in an Integrated Water Resources Management Framework; Policy Research Initiative, The Walter and Duncan Gordon Foundation, Agriculture and Agri-Food Canada, Environment Canada the Canadian Water Network: Edmonton, AB, Canada, 2004. [Google Scholar]
- Arbués, F.; Villanúa, I. Potential for pricing policies in water resource management: Estimation of urban residential water demand in Zaragoza, Spain. Urban Stud. 2006, 43, 2421–2442. [Google Scholar] [CrossRef]
- Arbués, F.; García-Valiñas, M.; Martínez-Espiñeira, R. Estimation of residential water demand: A state of the art review. J. Socio-Econ. 2003, 32, 81–102. [Google Scholar] [CrossRef]
- Worthington, A.C.; Hoffman, M. An empirical survey of residential water demand modelling. J. Econ. Surv. 2008, 22, 842–871. [Google Scholar] [CrossRef]
- Billings, R.; Agthe, D. Price elasticities for water: A case of increasing block rates. Land Econ. 1980, 56, 73–84. [Google Scholar] [CrossRef]
- Bachrach, M.; Vaughan, W. Household Water Demand Estimation; Working Paper ENP 106; Inter-American Development Bank: Washington, DC, USA, 1994. [Google Scholar]
- Charney, A.H.; Woodard, G.C. A test of consumer demand response to water prices: Comment. In Land Economics; University of Wisconsin Press: Madison, WI, USA, 1984; Volume 60, pp. 414–416. [Google Scholar]
- Opaluch, J. A test of consumer demand response to water prices: Reply. In Land Economics; University of Wisconsin Press: Madison, WI, USA, 1984; Volume 60, pp. 417–421. [Google Scholar]
- Stavins, R.N. Managing Water Demand: Price vs. Non-Price Conservation Programs; A Pioneer Institute White Paper; Pioneer Institute: Boston, MA, USA, 2007. [Google Scholar]
- Tracy Mehan, G., III; Kline, I. Pricing as a demand-side management tool: Implications for water policy and governance, Unites States: American Water Works Association. J. Am. Water Works Assoc. 2012, 104, 61–66. [Google Scholar]
- Boland, J.; Whittington, D. The Political Economy of Water Tariff Design in Developing Countries: Increasing Block Tariffs versus Uniform Price with Rebate. In The Political Economy of Water Pricing Reforms; Dinar, A., Ed.; Oxford University Press: New York, NY, USA, 2000; pp. 215–235. [Google Scholar]
- Shin, J.-S. Perception of Price when Price Information is Costly: Evidence from Residential Electricity Demand. Rev. Econ. Stat. 1985, 67, 591–598. [Google Scholar] [CrossRef]
- The Secretariat of Environment and Natural Resources (SEMARNAT); Comisión Nacional del Agua (CNA). Estadísticas del Agua en México; SEMARNAT and CNA: Mexico City, Mexico, 2004. [Google Scholar]
- Nauges, C.; Thomas, A. Long-run study of residential water consumption. Environ. Resour. Econ. 2003, 26, 25–43. [Google Scholar] [CrossRef]
- García, M. Fijación de precios para el servicio municipal de suministro de agua: Un ejercicio de análisis de bienestar. Hacienda Pública Española/Revista Economía Pública 2005, 172, 119–142. [Google Scholar]
- Chang, H.; House-Peters, L. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47, 1–15. [Google Scholar]
- Arbués, F.; Barberán, R. Price impact on urban residential water demand: A dynamic panel data approach. Water Resour. Res. 2004, 40, 1–9. [Google Scholar] [CrossRef]
- Ito, K. Do Consumers Respond to Marginal or Average Price? Evidence from Nonlinear Electricity Price. Am. Econ. Rev. 2014, 104, 537–563. [Google Scholar] [CrossRef]
- Wichman, C. Perceived price in residential water demand: Evidence from a natural experiment. J. Econ. Behav. Organ. 2014, 107, 308–323. [Google Scholar] [CrossRef]
- Baltagi, B. Econometric Analysis of Panel Data, 3rd ed.; John Wiley and Sons: New York, NY, USA, 2005. [Google Scholar]
- Kiviet, J. On Bias, Inconsistency, and Efficiency of Various Estimators in Dynamic Panel Data Models. J. Econom. 1995, 68, 53–78. [Google Scholar] [CrossRef]
- Judson, R.; Owen, A. Estimating Dynamic Panel Data Models: A Practical Guide for Macroeconomists. Econ. Lett. 1999, 65, 9–15. [Google Scholar] [CrossRef]
- Anderson, T.; Cheng, H. Estimation of Dynamic Models with Error Components. J. Am. Stat. Assoc. 1981, 76, 598–606. [Google Scholar] [CrossRef]
- Arellano, M.; Bond, S. Some tests of Specification for Panel Data: Monte Carlo Evidence and Application to Employment Equations. Rev. Econ. Stud. 1991, 58, 277–297. [Google Scholar] [CrossRef]
- Bruno, G. Approximating the bias of the LSDV estimator for dynamic unbalanced panel data models. Econ. Lett. 2005, 87, 361–366. [Google Scholar] [CrossRef]
- Cermeño, R. Median-Unbiased Estimation in Fixed-Effects Dynamic Panels. Ann. D’Econ. Stat. 1999, 55, 351–368. [Google Scholar] [CrossRef]
- Breitung, J. The Local Power of Some Unit Root Tests for Panel Data. In Advances in Econometrics; Baltagi, B., Ed.; Elsevier: New York, NY, USA, 2000; Volume 15. [Google Scholar]
- Levin, A.; Lin, C.-F.; Chu, C.-S.J. Unit root tests in panel data: Asymptotic and finite-sample properties. J. Econom. 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Harris, R.D.F.; Tzavalis, E. Inference for unit roots in dynamic panels where the time dimension is fixed. J. Econom. 1999, 91, 201–226. [Google Scholar] [CrossRef]
- Im, K.; Pesaran, M.; Shin, Y. Testing for unit roots in heterogeneous panels. J. Econom. 2003, 115, 53–74. [Google Scholar] [CrossRef]
- Baltagi, B.; Chihwa, K. Nonstationary panels, cointegration in panels and dynamic panels: A survey. In Advances in Econometrics; Baltagi, B., Ed.; Elsevier: New York, NY, USA, 2001; Volume 15. [Google Scholar]
- Schleich, J.; Hillenbrand, T. Determinants of residential water demand in Germany. Ecol. Econ. 2008, 68, 1756–1769. [Google Scholar] [CrossRef]
- Angrist, J.; Pischke, J.-S. Mostly Harmless Econometrics: An Empiricist’s Companion; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Shin, J.-S. Aggregation and the Endogeneity Problem. Int. Econ. J. 1987, 1, 57–65. [Google Scholar] [CrossRef]
- Hausman, J. Specification tests in econometrics. Econometrica 1978, 46, 1251–1271. [Google Scholar] [CrossRef]
- Almendarez-Hernández, M.A.; Jaramaillo-Mosqueira, L.; Áviles-Polanco, G.; Beltrán-Morales, L.F.; Hernández-Trejo, V.; Ortega-Rubio, A. Economic Valuation of Water in a Natural Protected Area of an Emerging Economy: Recommendations for El Vizcaino Biosphere Reserve, Mexico. Interciencia 2013, 38, 245–252. [Google Scholar]
- Musolesi, A.; Nosvelli, M. Dynamics of residential water consumption in a panel of Italian municipalities. Appl. Econ. Lett. 2007, 14, 441–444. [Google Scholar] [CrossRef]
- Fullerton, T.M., Jr.; Katherine, C.W.; Wm, D.S.; Adam, G.W. An empirical analysis of Halifax municipal water consumption. Canadian Water Resources Association. Can. Water Resour. J. 2013, 38, 148–158. [Google Scholar] [CrossRef]
- Younes, B.Z. A long-run analysis of residential water consumption. Econ. Bull. 2013, 33, 536–544. [Google Scholar]
- Nieswiadomy, M.; Molina, D. A note on Price Perception in Water Demand Models. Land Econ. 1991, 67, 352–359. [Google Scholar] [CrossRef]
- Kavezeri-Karuaihe, S.; Wandschneider, P.R.; Yoder, J.K. Perceived Water Prices and Estimated Water Demand in the Residential Sector of Windhoek, Namibia; Food and Agriculture Organization of the United Nations: Rome, Italy, 2005. [Google Scholar]
- Binet, M.-E.; Carlevaro, F.; Paul, M. Estimation of residential water demand with imprecise price perception. Environ. Resour. Econ. 2014, 59, 561–581. [Google Scholar] [CrossRef]
- Wichman, C.; Taylor, L.; von Haefen, R. Conservation policies: Who responds to price and who responds to prescription? J. Environ. Econ. Manag. 2016, 79, 114–134. [Google Scholar] [CrossRef]
- Jaramillo-Mosqueira, L. Evaluación econométrica de la demanda de agua de uso residencial en México. Trimestre Económico 2005, 72, 367–390. [Google Scholar]
- García-Salazar, J.A.; Mora-Flores, J.S. Tarifas y consumo de agua en el sector residencial de la Comarca Lagunera. Región Sociedad 2008, 20, 119–132. [Google Scholar]
- Adams, A.S.; Pablos, N.P. Factores que afectan la demanda de agua para uso doméstico en México. Región Sociedad 2010, 22, 3–16. [Google Scholar]
- Avilés-Polanco, G.; Almendarez-Hernández, M.; Hernández-Trejo, V.; Beltrán-Morales, L. Elasticidad-precio de corto y largo plazos de la demanda de agua residencial de una zona árida. Caso de estudio: La Paz, B.C.S., México. Tecnología Ciencias Agua 2015, 4, 85–99. [Google Scholar]
- Avilés-Polanco, G.; Huato, L.; Troy-Diéguez, E.; Murillo, B.; García, J.; Beltrán-Morales, L. Valoración económica del servicio hidrológico del acuífero de La Paz, B.C.S.: Una valoración contingente del uso de agua municipal. Frontera Norte 2010, 22, 103–128. [Google Scholar]
- Sánchez-Brito, I.; Almendarez-Hernández, M.A.; Morales-Zárate, M.V.; Salinas-Zavala, C.A. Valor de Existencia del Servicio Ecosistémico Hidrológico en la Reserva de la Biosfera Sierra La Laguna, Baja California Sur México. Frontera Norte 2013, 25, 97–129. [Google Scholar]
| Variable | Description | Source |
|---|---|---|
| Symbolizes average water consumption per capita in residential use. The variable is measured in cubic meters (m3). | System Operator Agency Water Supply and Sewerage (OOMSAPA). | |
| AP | Average price, obtained by dividing the water bill paid by the consumer living in one housing unit and the volume of water consumed. Additionally, the measurement of price was deflated using the National Consumer Price Index (NCPI), base 2010 = 100, where 2010 is the bases year for the estimation, obtained from the Bank of Mexico (BM). | System Operator Agency Water Supply and Sewerage (OOMSAPA). |
| MP | Marginal price, representing the amount that the consumer must pay, according to the fee structure for final consumption units associated with the average amount. The price was deflated using the CPI, base 2010 = 100. | System Operator Agency Water Supply and Sewerage (OOMSAPA). |
| Income | Defined as the average daily wage by state according to the Mexican Social Security Institute (IMSS). In the regression analysis it is used as a proxy for income, representing an indicator of household income. For purposes of inclusion in the dynamic equations, we calculated monthly wage. This variable was deflated with CPI base 2010 = 100 and weighted with the working population. | National Commission for Minimum Wage in the State of Baja California Sur. |
| t | Monthly maximum temperature, measured in degrees Celsius (°C). | National Water Commission (CONAGUA). |
| P | Total monthly precipitation, measured in millimetres (mm). | National Water Commission (CONAGUA). |
| Variable | Mean | Standar Devation | Minimun | Maximun |
|---|---|---|---|---|
| Natural Logarithm of Water Consumption | 3.08 | 0.39 | 1.27 | 3.92 |
| Natural Logarithm of Average Price | 1.59 | 0.37 | 1.22 | 3.22 |
| Natural Logarithm of Income | 8.44 | 0.04 | 8.33 | 8.5 |
| Natural Logarithm of Temperature | 3.48 | 0.18 | 2.89 | 3.78 |
| Natural Logarithm of Precipitation | 9.5 | 25.15 | 0 | 218 |
| Natural Logarithm of Marginal Price | 1.49 | 0.19 | 1.12 | 2.88 |
| Test | Variable | ||||||
|---|---|---|---|---|---|---|---|
| Natural Logarithm Water Consumption | Natural Logarithm Average Price | Natural Logarithm of Income | Natural Logarithm Temperature | Natural Logarithm Marginal Price | Precipitation | ||
| Levin, Lin and Chu t-stat 1 | No trend | −3.5058 * | −2.9591 * | −4.7032 * | −3.3096 * | −5.3825 * | −14.8757 * |
| Trend | −3.7844 * | −3.6753 * | −4.5454 * | −2.9802 * | −7.1843 * | −16.4279 * | |
| Breitung t-stat 1 | No trend | −2.016 ** | 0.8364 | −2.8989 * | −3.8967 * | −3.8093 * | −11.1172 * |
| Trend | −2.9742 * | −1.7696 ** | −1.6902 ** | −3.1495 * | −1.5693 | −11.1841 * | |
| Harris-Tzavalis 1 | No trend | −12.4917 * | −9.9615 * | −39.8499 * | −14.5436 * | −29.5214 * | −39.8661 * |
| Trend | −8.4543 * | −8.6226 * | −30.2714 * | −7.3701 * | −24.2629 * | −24.5517 * | |
| Im, Pesaran and Shin W-stat 2 | No trend | −4.7914 * | −5.1862 * | −6.9979 * | −9.5987 * | −7.1840 * | −13.172 * |
| Trend | −4.9233 * | −3.7272 * | −13.1415 * | −8.9286 * | −9.8964 * | −13.7871 * | |
| ADF-Fisher Chi-square 2 | No trend | 61.273 * | 24.9921 ** | 76.8509 * | 117.714 * | 87.2638 * | 170.723 * |
| Trend | 55.8855 * | 36.2216 * | 158.721* | 98.8576 * | 112.370 * | 161.536 * | |
| PP-Fisher Chi-square 2 | No trend | 61.0525 * | 42.2184 * | 209.668 * | 81.1587 * | 83.0181 * | 183.702 * |
| Trend | 54.2991 * | 59.9753 * | 234.038 * | 57.8068 * | 105.175 * | 156.455 * | |
| Variable | Model 1 | Model 2 | Model 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Coefficient | t-Ratio | Probability | Coefficient | t-Ratio | Probability | Coefficient | t-Ratio | Probability | |
| Constant | 0.6426 | 1.4173 | 0.1572 | 0.5768 | 1.2110 | 0.2940 | 1.0790 | 1.3621 | 0.1739 |
| Lagged consumption | 0.6171 | 13.2977 * | 0.0000 | 0.6116 | 12.2336 * | 0.0000 | - | - | - |
| AP | −0.2735 | −5.9151 * | 0.0000 | - | - | - | - | - | - |
| MP | - | - | - | −0.2587 | −4.3048 * | 0.0000 | −0.2830 | −5.5984 * | 0.0000 |
| AP/MP | - | - | - | −0.2803 | −5.6858 * | 0.0000 | −0.3123 | −7.5952 * | 0.0000 |
| Income | 0.1047 | 1.7747 *** | 0.0767 | 0.1127 | 1.8093 *** | 0.0712 | 0.1329 | 1.8579 *** | 0.0639 |
| Temperature | 0.0259 | 1.3592 | 0.1748 | 0.0245 | 1.2785 | 0.2018 | 0.0557 | 1.1124 | 0.2666 |
| Precipitation | −0.00015 | −2.5679 ** | 0.0106 | −0.00015 | −2.4170 ** | 0.0161 | −0.00017 | −2.8669 * | 0.0043 |
| k | - | - | - | 1.0832 | 4.8567 * | 0.0000 | - | - | - |
| R2 | 0.9253 | 0.9251 | - | ||||||
| F Test of fixed effects | 13.1292 *, 0.0000 | 13.0892 *, 0.0000 | - | ||||||
| DURBIN-WATSON | 2.1497 | 2.1507 | - | ||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almendarez-Hernández, M.A.; Avilés Polanco, G.; Hernández Trejo, V.; Ortega-Rubio, A.; Beltrán Morales, L.F. Residential Water Demand in a Mexican Biosphere Reserve: Evidence of the Effects of Perceived Price. Water 2016, 8, 428. https://doi.org/10.3390/w8100428
Almendarez-Hernández MA, Avilés Polanco G, Hernández Trejo V, Ortega-Rubio A, Beltrán Morales LF. Residential Water Demand in a Mexican Biosphere Reserve: Evidence of the Effects of Perceived Price. Water. 2016; 8(10):428. https://doi.org/10.3390/w8100428
Chicago/Turabian StyleAlmendarez-Hernández, Marco Antonio, Gerzaín Avilés Polanco, Víctor Hernández Trejo, Alfredo Ortega-Rubio, and Luis Felipe Beltrán Morales. 2016. "Residential Water Demand in a Mexican Biosphere Reserve: Evidence of the Effects of Perceived Price" Water 8, no. 10: 428. https://doi.org/10.3390/w8100428
APA StyleAlmendarez-Hernández, M. A., Avilés Polanco, G., Hernández Trejo, V., Ortega-Rubio, A., & Beltrán Morales, L. F. (2016). Residential Water Demand in a Mexican Biosphere Reserve: Evidence of the Effects of Perceived Price. Water, 8(10), 428. https://doi.org/10.3390/w8100428






