To control hydraulic jump and enhance hydraulic jump efficiency, sills such as sharp-crested weirs, broad-crested weirs or end sills at the bottoms of waterways are frequently used. The force acting upon such a sill in the hydraulic jump rapidly decreases to the minimum as the end point of roller at downstream of the hydraulic jump moves upward at a point where it almost overflows a sill. This impact of sills can make the length of the scour risk zone shorter than a normal hydraulic jump phenomenon. Then, as the hydraulic jump becomes shorter and moves further upstream, the force upon a sill gradually increases to reach a certain level. Since such a rapidly varying flow is characterized as having an uneven velocity distribution, the changes in force upon a sill seem to be because of the changes in velocity distribution occurring between the starting points of the hydraulic jump to its end point. Consequently, in a cross-section with unequal velocities, the momentum surges greatly. Theoretically, hydraulic jump controlled by sills can be interpreted using the momentum theory. However, in the absence of a precise theory of velocity distribution, an accurate quantification can hardly be made by just relying on theoretic interpretation. An experiment for simulating the behavior of a sluice gate and an associated hydraulic jump experiment have been carried out in different conditions to enable an investigation of the characteristics of hydraulic jump, and to analyze energy dissipation, the physical experiment collects data that are afterwards used to define relations, which are used as guidelines for design operations.
2.1. Experiment Equipment and Method
The open-channel system used in this experiment is a channel installed in a hydraulic experiment lab of Incheon University, Korea.
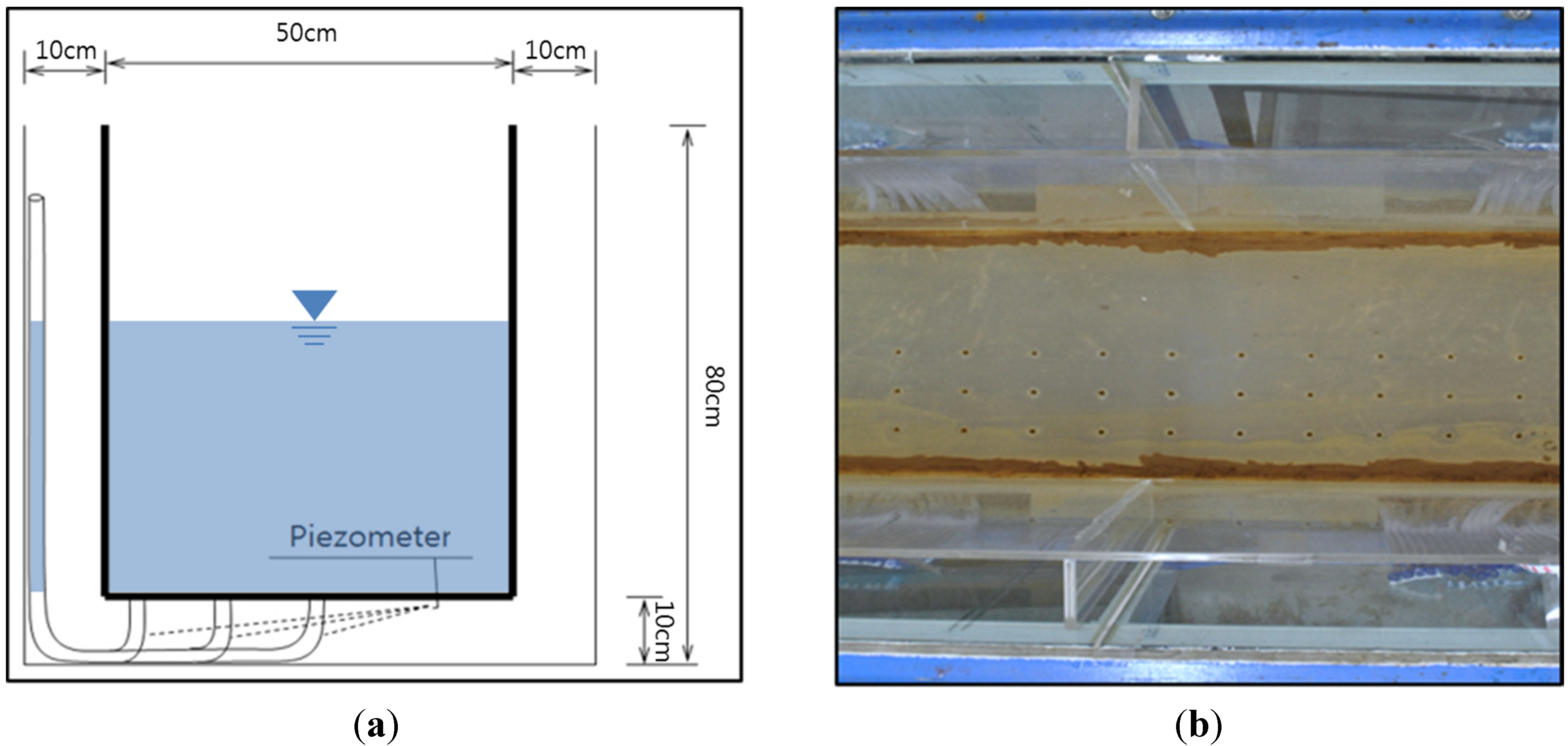
The straight-line channel is 11.0 m in total length, 0.7 m in width, and 0.8 m in height and has reinforced glass walls for flow observation. It has three distribution plates at the inlet to induce steady-state inflow. Although inflow passes through the distribution plates to become steady, in order to minimize the inlet contraction effect, a fixed weir and sluice gate weir were installed at points 2.0 m away from the inlet. Vertical grooves were made on the left and right sides of the channel to install weirs at the same height and adjust movable weir heights. Since it is occasionally hard to measure the variation of flow surface created by the hydraulic jump, besides using a velocimetry and a point gauge, piezometers were installed on the bottom of the channel to monitor water pressure to estimate hydraulic characteristics. The installed piezometers were attached to the walls for the purpose of observation.
In order to install and adjust the weirs and piezometers, an acrylic-plate channel was made by distancing each 0.10 m inward from the left side, right side and bottom.
Figure 1 shows the channel cross section. The piezometers were installed in three rows at 0.08 m intervals toward the channel center on the left side from a point approximately 0.20 m away from the weir installation. The installation intervals were 10 cm long, and a total of 60 piezometers were installed. The maximum water supply of the installed pump was 0.056 m
3/s. However, given the channel size and to ensure constant flow maintenance, 0.026 m
3/s was supplied as the maximum. The variation of the pressure head caused by the installation of the weir could be observed through the piezometers. In order to measure detailed hydraulic characteristics, the 2-D velocity meter (VP1200, KENEK Corp., Tokyo, Japan), which uses very thin sensor needle, was used to minimize flow interference.
Figure 1.
Structure diagram of channel. (a) Cross-sectional view with piezometer; (b) Floor plan showing the piezometer hole in the channel; and (c) weir and the channel.
Figure 1.
Structure diagram of channel. (a) Cross-sectional view with piezometer; (b) Floor plan showing the piezometer hole in the channel; and (c) weir and the channel.
As the fixed weir and sluice gate-type weir have different shapes, the centers of the two different weirs were made sure to be in the same position for installation consistency.
The fixed weir was 0.1 m in height, 0.05 m in upper width, 0.11 m in lower width and had a 1:0.7 ratio for the overflow slope. The sluice gate-type weir was 0.3 m in height and 0.01 m in thickness.
Figure 2 shows the overflow-type weir.
Figure 2.
Overflow-type fixed weir (a) plan of fixed weir installation; (b) photo of weir installed in the channel.
Figure 2.
Overflow-type fixed weir (a) plan of fixed weir installation; (b) photo of weir installed in the channel.
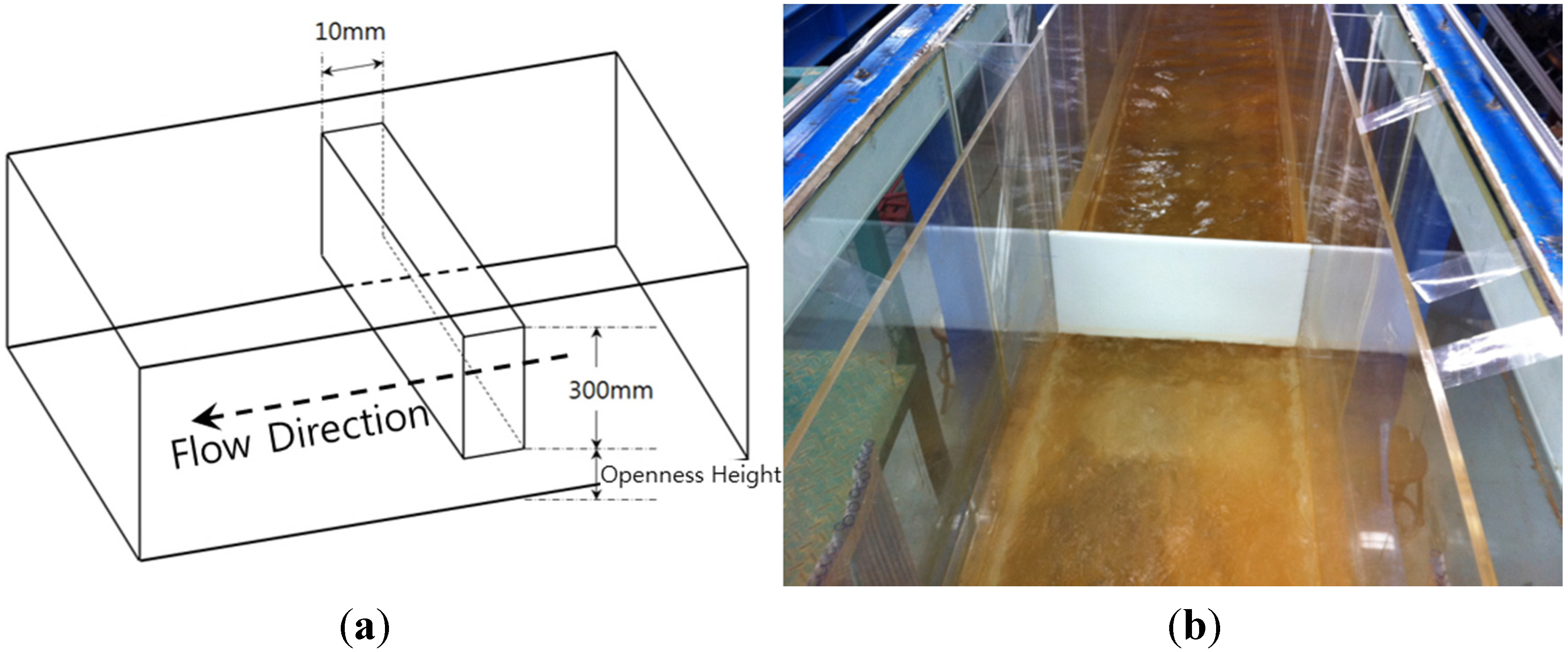
As the sluice gate movable weir changes its openness heights, the experiment devices should be structured to accept such changes. Therefore, after fixing the weir, grooves of 0.01 m width and 0.005 m depth were made on the left and right walls of the channel for the free height change. To prevent possible leakage through the weir bottom when the sluice gate is completely closed, the same 0.01 m wide and 0.005 m deep grooves were made and the back wall of the fixed weir was elongated by 0.005 m to fit in, as shown in
Figure 3.
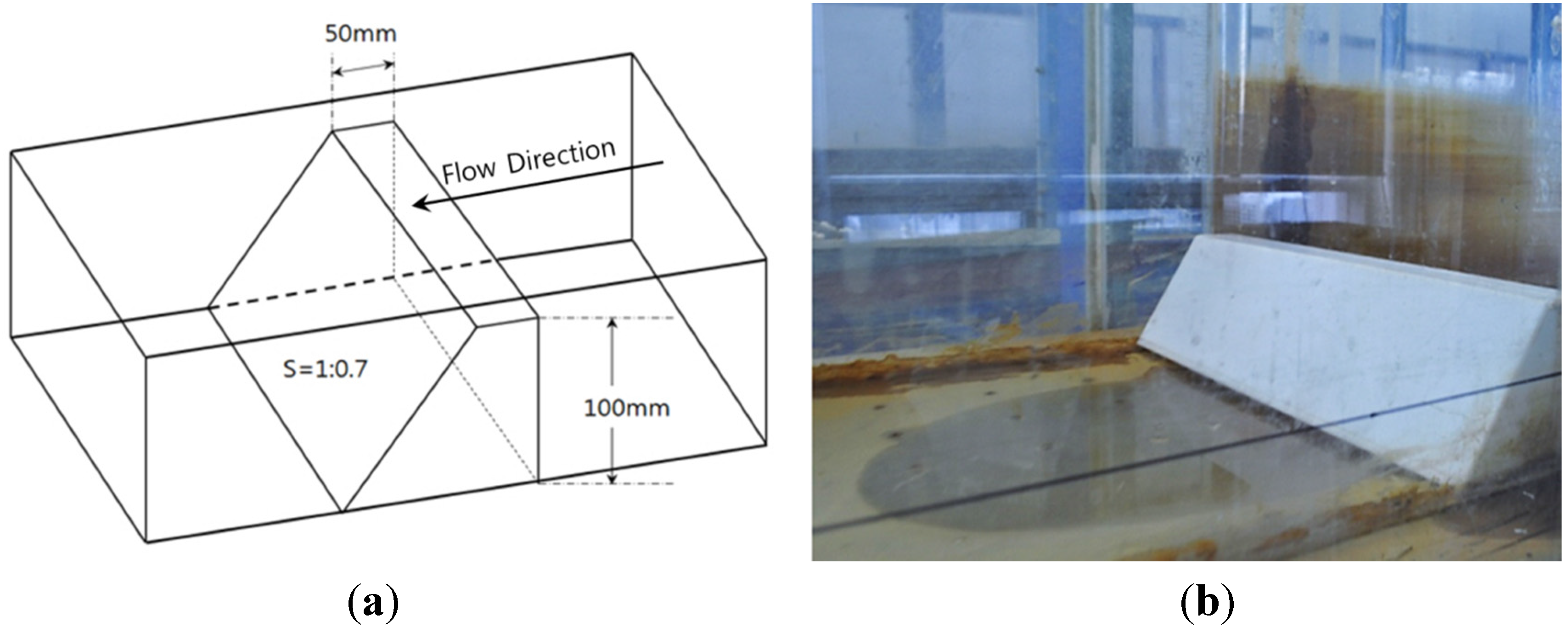
As mentioned in the introduction on the effectiveness of energy dissipators in the use of a conventional fixed weir, it was found that tooth-formed blocks were more effective than total cross-section installation. However, as the present study does not aim to examine certain targeted rivers, but rather to produce experiment results based on unit width, the authors tried to install the whole widths of the experiment channel throughout, as shown in
Figure 4.
Figure 3.
Sluice gate-type movable weir (a) plan of sluice gate installation; (b) photo of sluice gate installed in the channel.
Figure 3.
Sluice gate-type movable weir (a) plan of sluice gate installation; (b) photo of sluice gate installed in the channel.
Figure 4.
Installation diagram of energy dissipator: (a) Horizontal plan; (b) Longitudinal plan.
Figure 4.
Installation diagram of energy dissipator: (a) Horizontal plan; (b) Longitudinal plan.
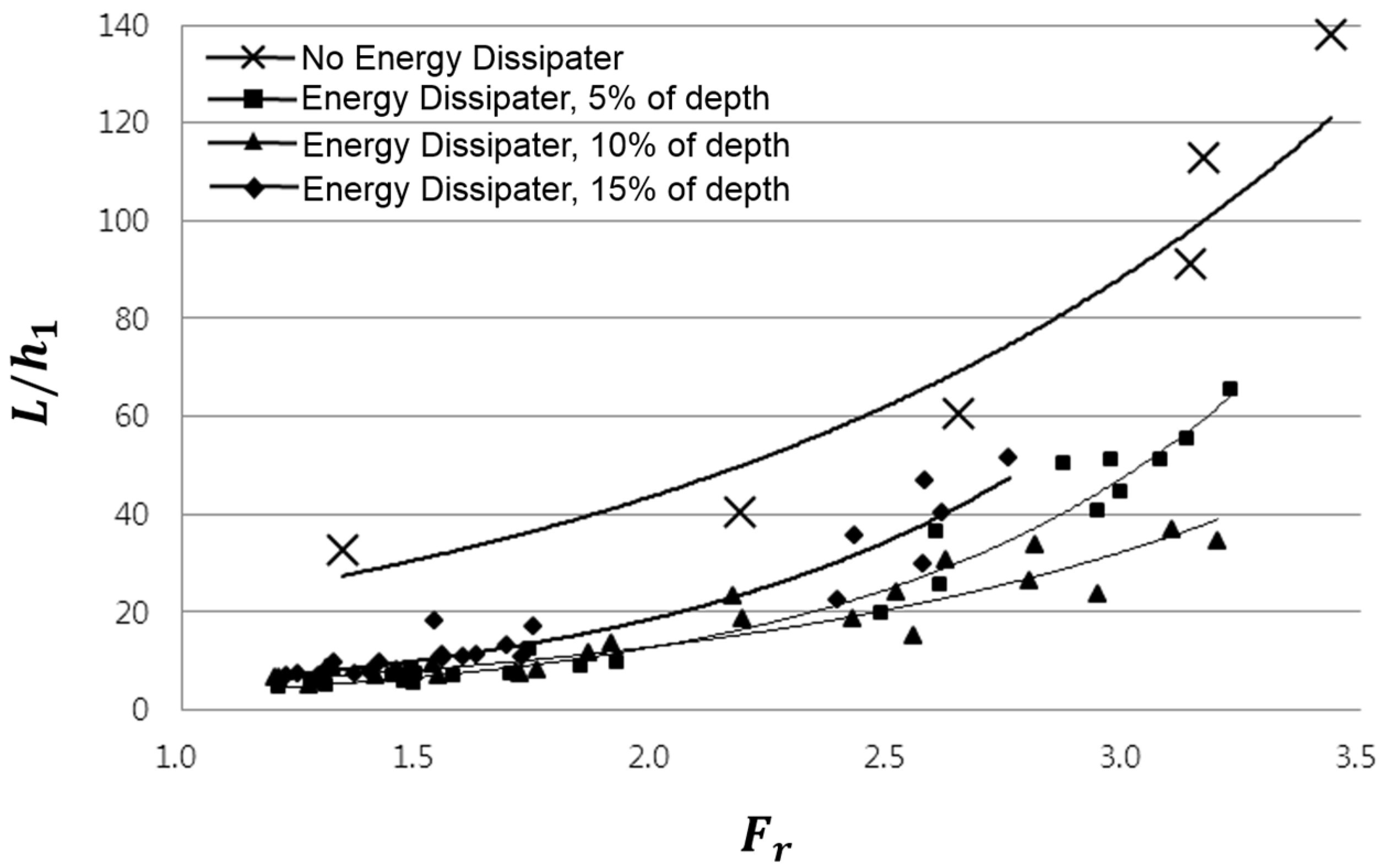
The dissipators used herein were 500 mm long to fit into the whole width of the channel. The width of the dissipators was set at 10% of the average downstream water depth measured in a preliminary experiment. The heights of the dissipators were set at 5%, 10% and 15% of the average downstream water depth in order to compare diverse cases, as in
Table 1, which shows the height of the model.
Table 1.
Height of energy dissipator.
Table 1.
Height of energy dissipator.
| Mean Downstream Depth | Height of Energy Dissipator (Hb) |
|---|
| 5% | 10% | 15% |
|---|
| 100 mm | 5 mm | 10 mm | 15 mm |
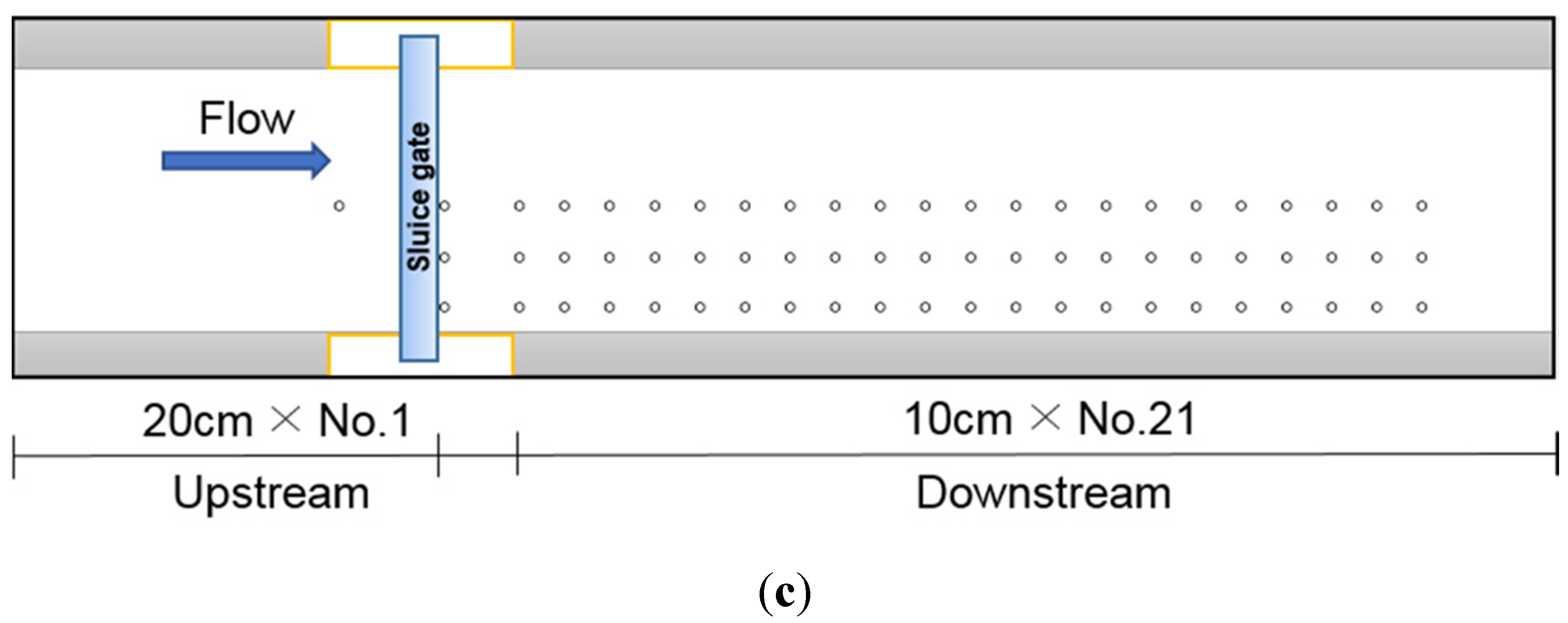
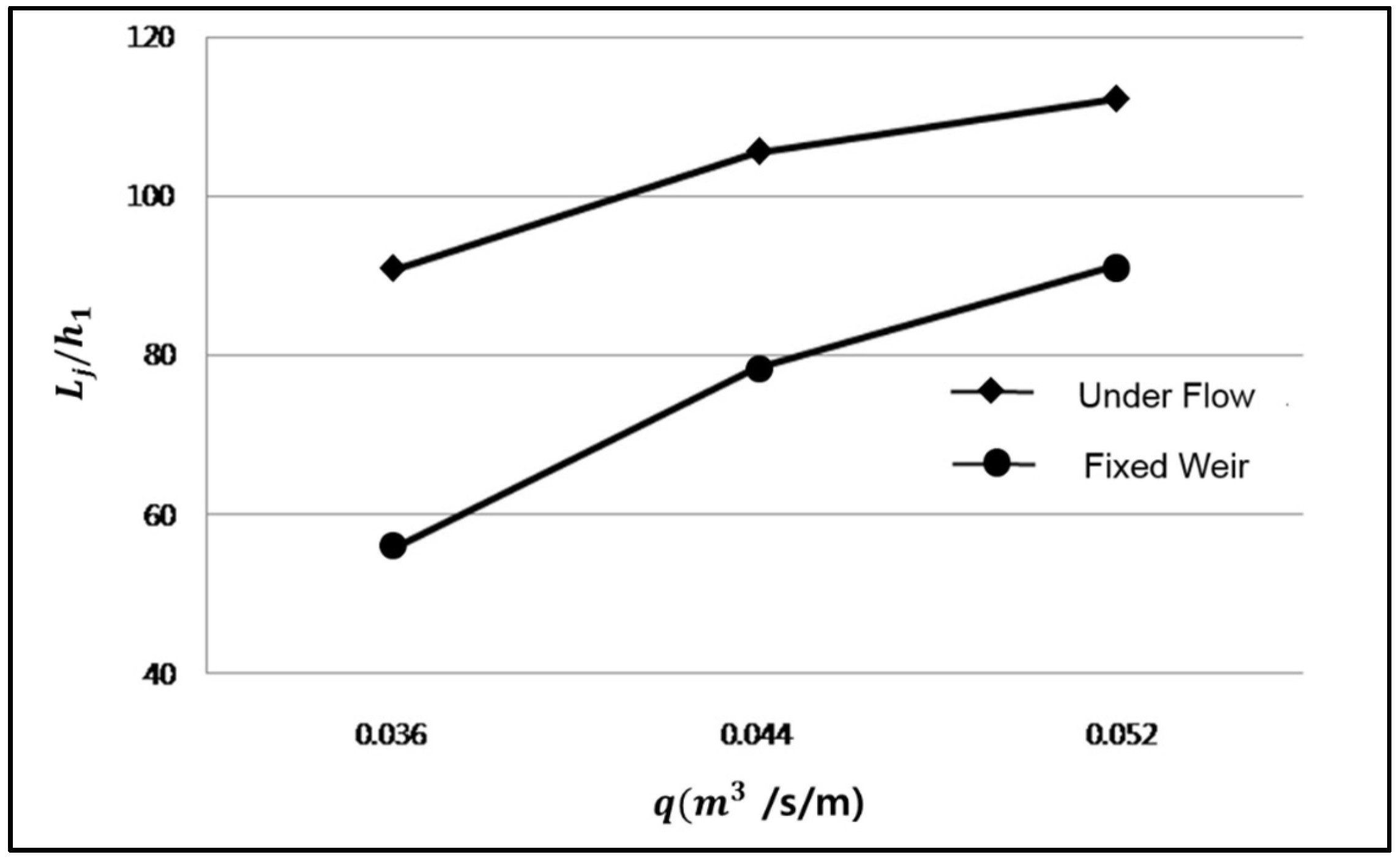
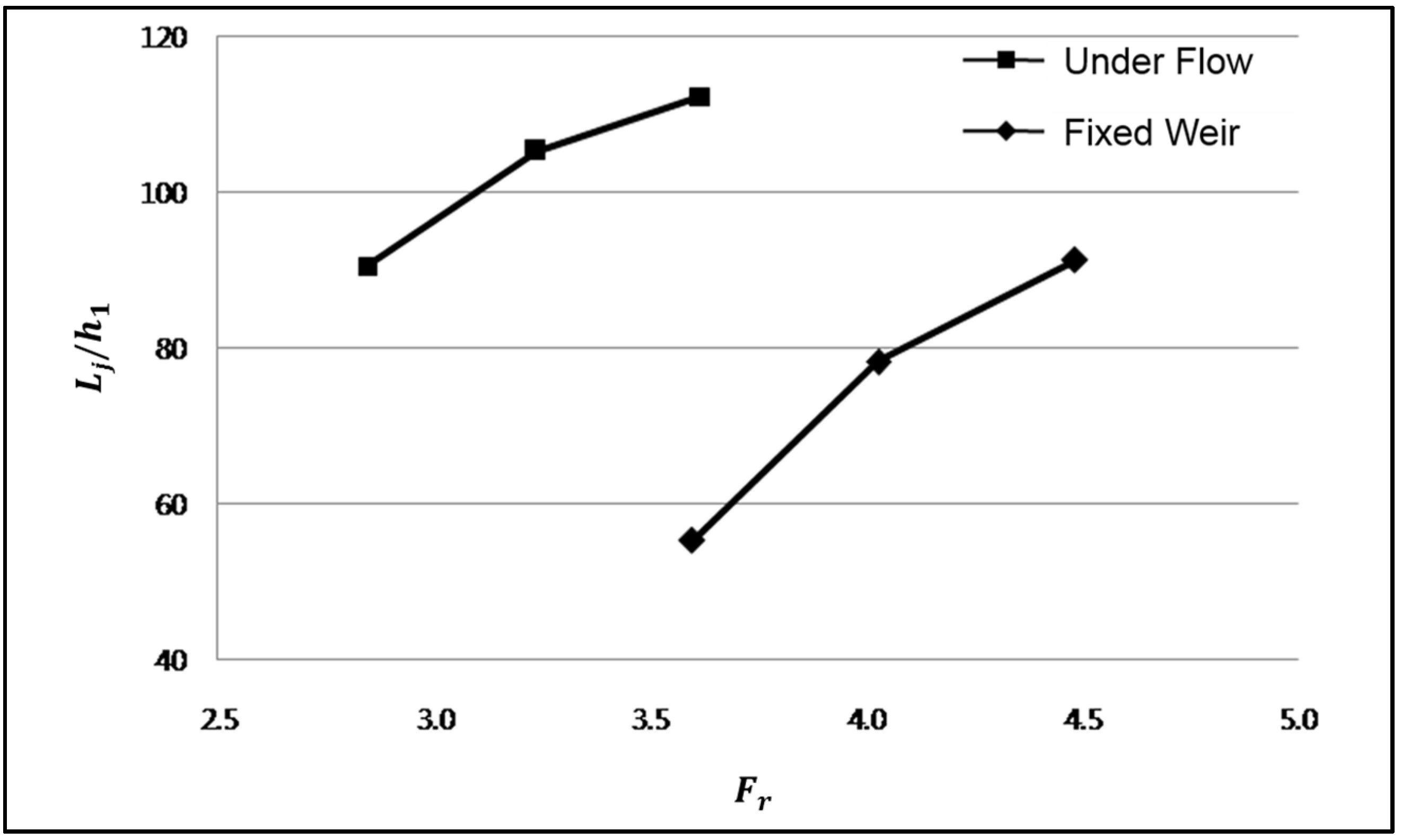
In this research, different flow patterns were investigated according to weir installation types and hydraulic jump starting points and their lengths were measured. To compare the flow patterns of fixed weir and sluice gate-type movable weirs, the constant upstream water level of the fixed weir was measured and applied to the movable weir case, since the fixed-weir upstream water levels were constant at each different flow rate. In order to keep the upstream water level constant in the movable weir case, its opening rate was adjusted.
In the movable weir experiment herein, the openness height was changed to produce Froude numbers to measure and compare the velocities and water levels at the discharge point from the gate. The measurement points were marked on the upper part of the experiment channel to ensure the measurement was performed at the same point. The main measurement points are shown in
Figure 5.
Figure 5.
Measurement regions of fixed weir and movable weir (a) Measurement point of fixed weir and (b) Measurement point of movable weir.
Figure 5.
Measurement regions of fixed weir and movable weir (a) Measurement point of fixed weir and (b) Measurement point of movable weir.
Figure 5 shows the following region-specific characteristics:
- (1)
Region 1: A supercritical flow region formed when water is discharged by the sluice gate-type movable weir. The flow conditions in Region 1 and associated Froude number are used to describe each experiment.
- (2)
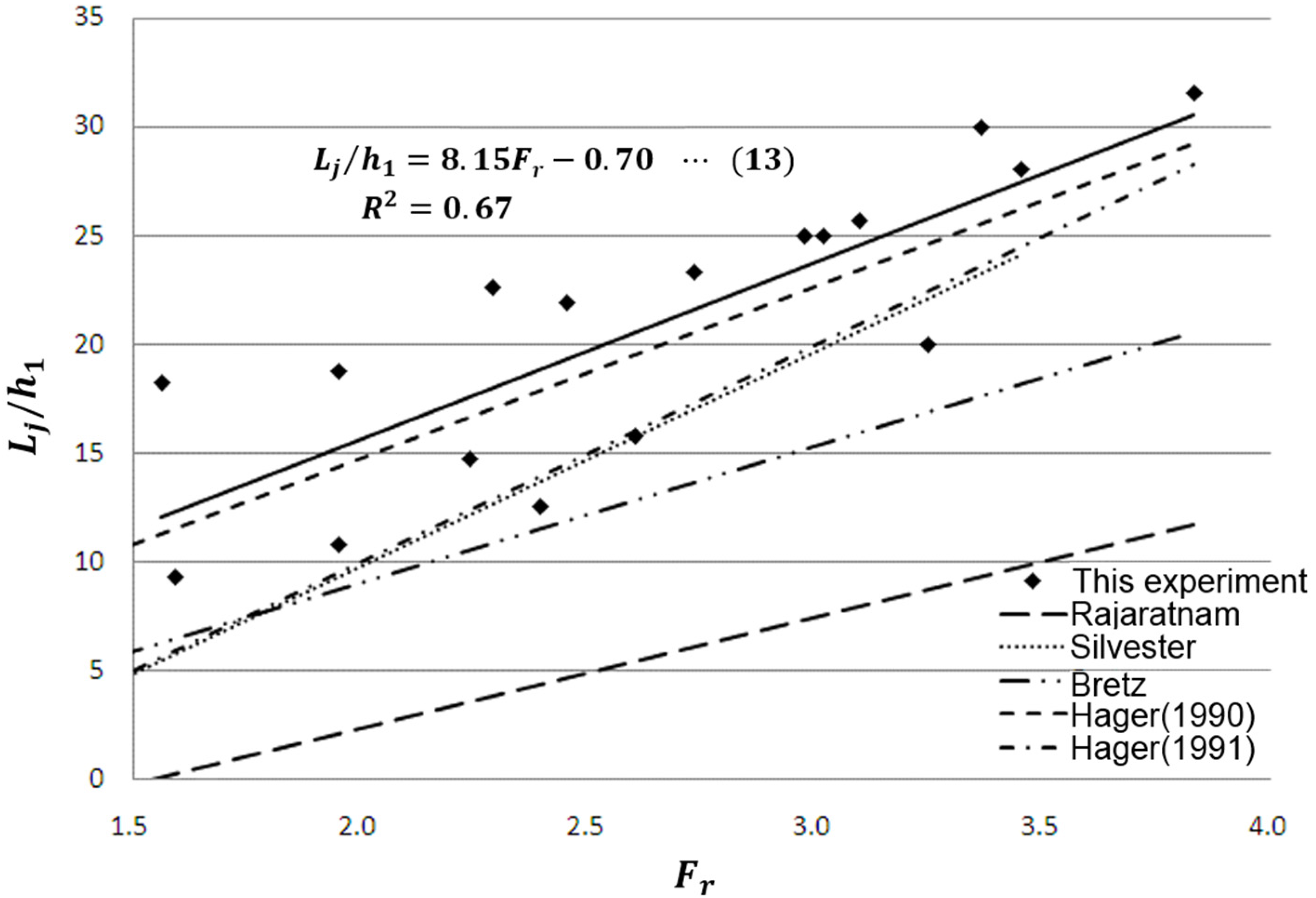
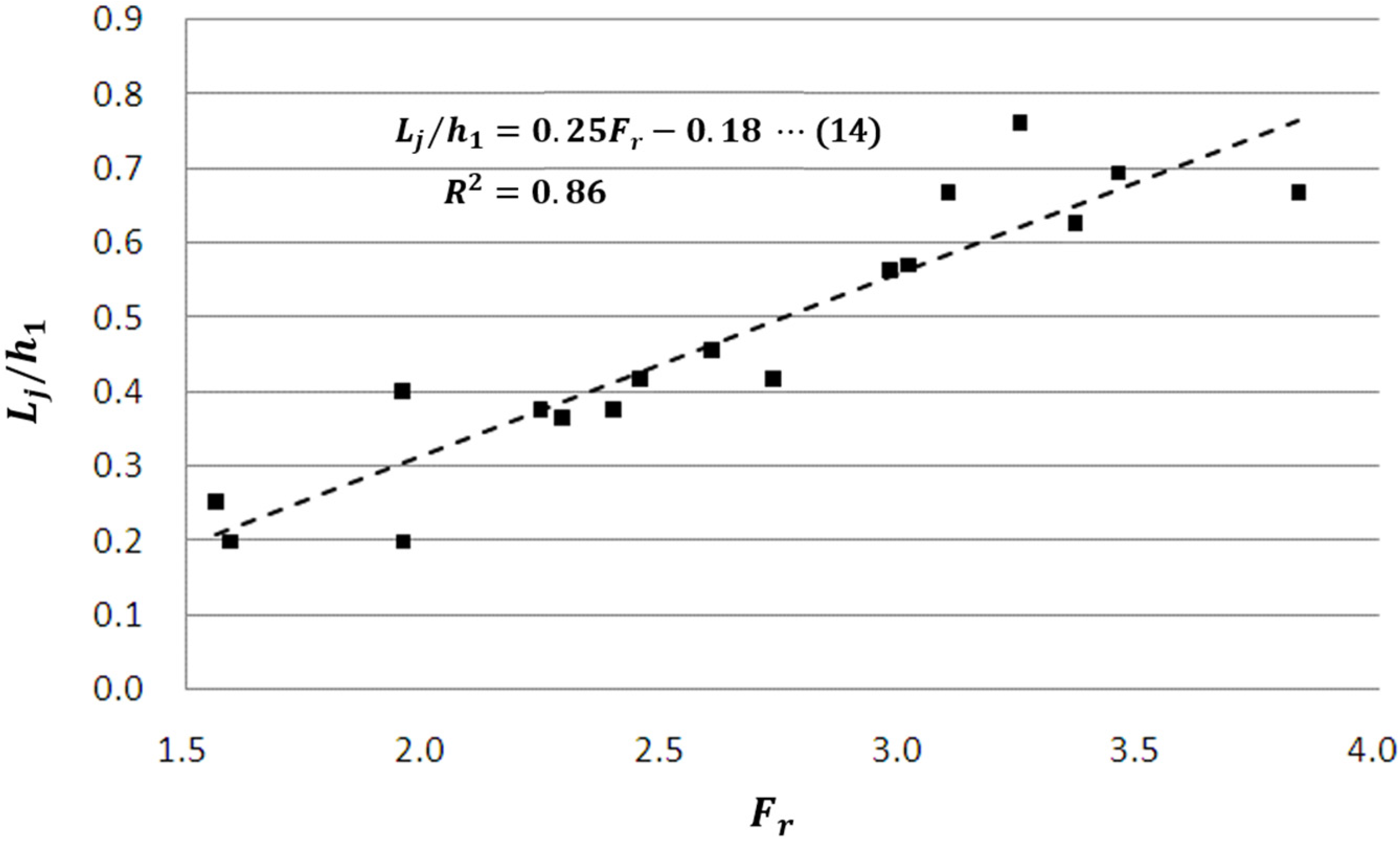
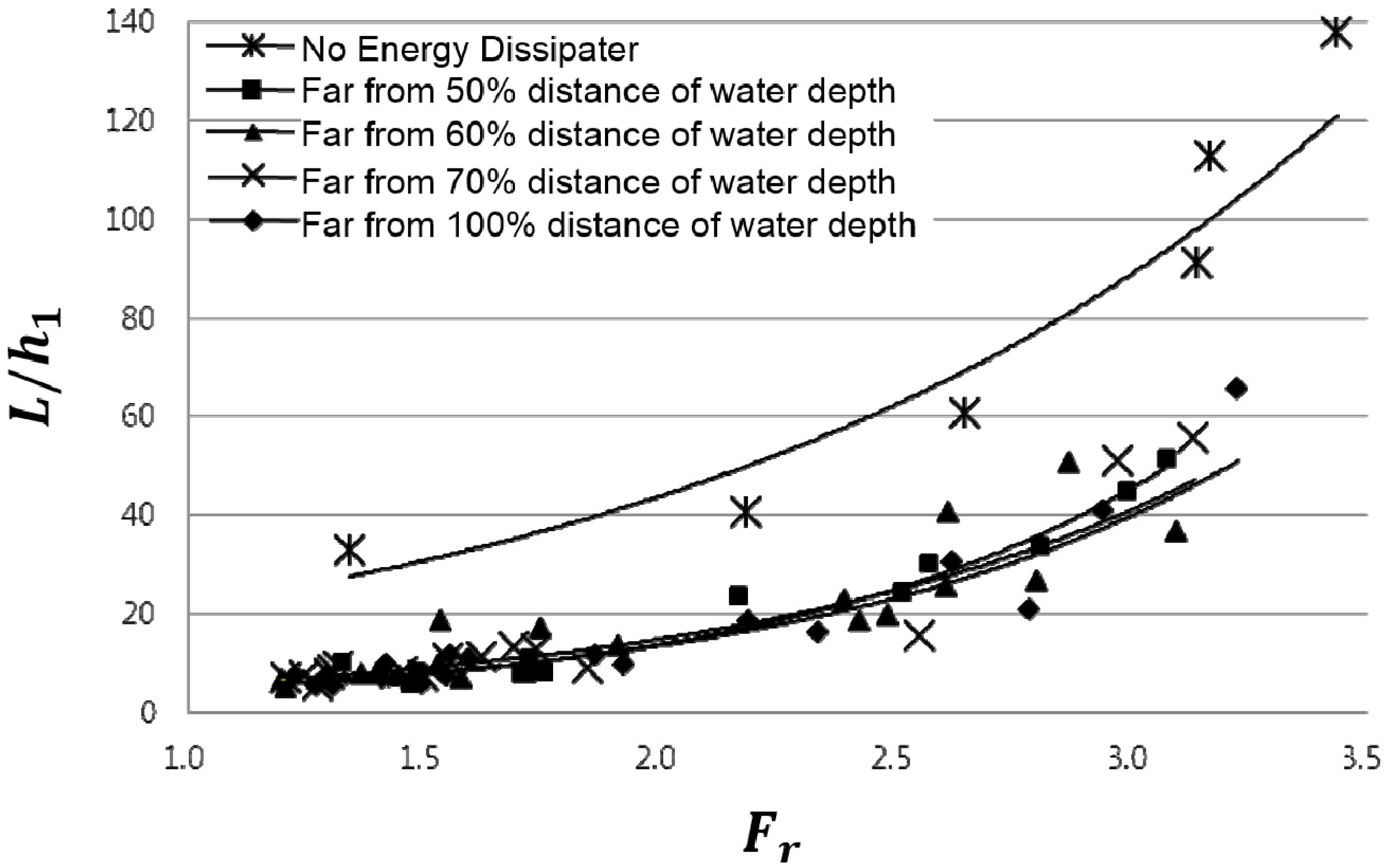
Region 2: Hydraulic jumps appear in this region in the discharged water flow of the sluice gate-type movable weir. The hydraulic jump lengths are calculated from the existing equations.
- (3)
Region 3: The discharged flow stabilizes after the hydraulic jumps in this region to show a similar flow to that of the fixed weirs.
- (4)
Region 4: The upstream domain of the weir region.
Each region was separated based on distinguished flow characteristics. Region 1 with supercritical flow, especially, showed different patterns from those of the fixed weir dependent upon flow rates. To avoid the effect of the channel walls, the central part of the channel was measured in this experiment. As fixed-weir flow and movable-weir flow are slightly different, the measurement locations were determined as shown in
Figure 5 to ensure identical factors were compared.
The supercritical flow region was recognized as Region 1; the hydraulic jump region as Region 2; and the post-hydraulic jump flow identical to that of the weir-free open channel as Region 3. Additionally, the upstream weir section elevated by the weir installation was recognized as Region 4. To ensure the same upstream conditions, the movable weir openness heights were adjusted to meet the equal water depth.
This study examined the flow characteristics variation according to sluice gate-type movable weir operation and downstream water level conditions as well as hydraulic jump, changes in their lengths and energy variation. To examine flow changes dependent upon the openness height of the movable weir, the movable weir openness height was changed to help generate diversified flow patterns in the channel after passing through the sluice gate. That is, the water flow moving through the sluice gate movable weir showed a similar pattern to the flow through the orifice. Orifice flow was also diversified dependent upon the submerged level, including the completely submerged orifice and partially submerged orifice. Therefore, the opening rate of the sluice gate-type movable weir was determined to show diverse patterns in this experiment. For each flow, the minimum movable weir openness height was determined by opening the movable weir until supercritical flow and all upstream flows appeared in the experiment channel. The openness height of sluice gate was then determined to make a similar condition to the fixed weir under the same flow rate, as shown in
Table 2.
Table 2.
Condition of flow rate and openness height of sluice gate.
Table 2.
Condition of flow rate and openness height of sluice gate.
| Flow Rate (m3/s/m) | Openness Height (m) | Remarks |
|---|
| 0.036 | 0.026 | There are additional openness heights (m) of extended cases for Chapter 5 (Energy dissipation) (0.036, 0.039, 0.042 and 0.045) |
| 0.044 | 0.036 |
| 0.052 | 0.036 |
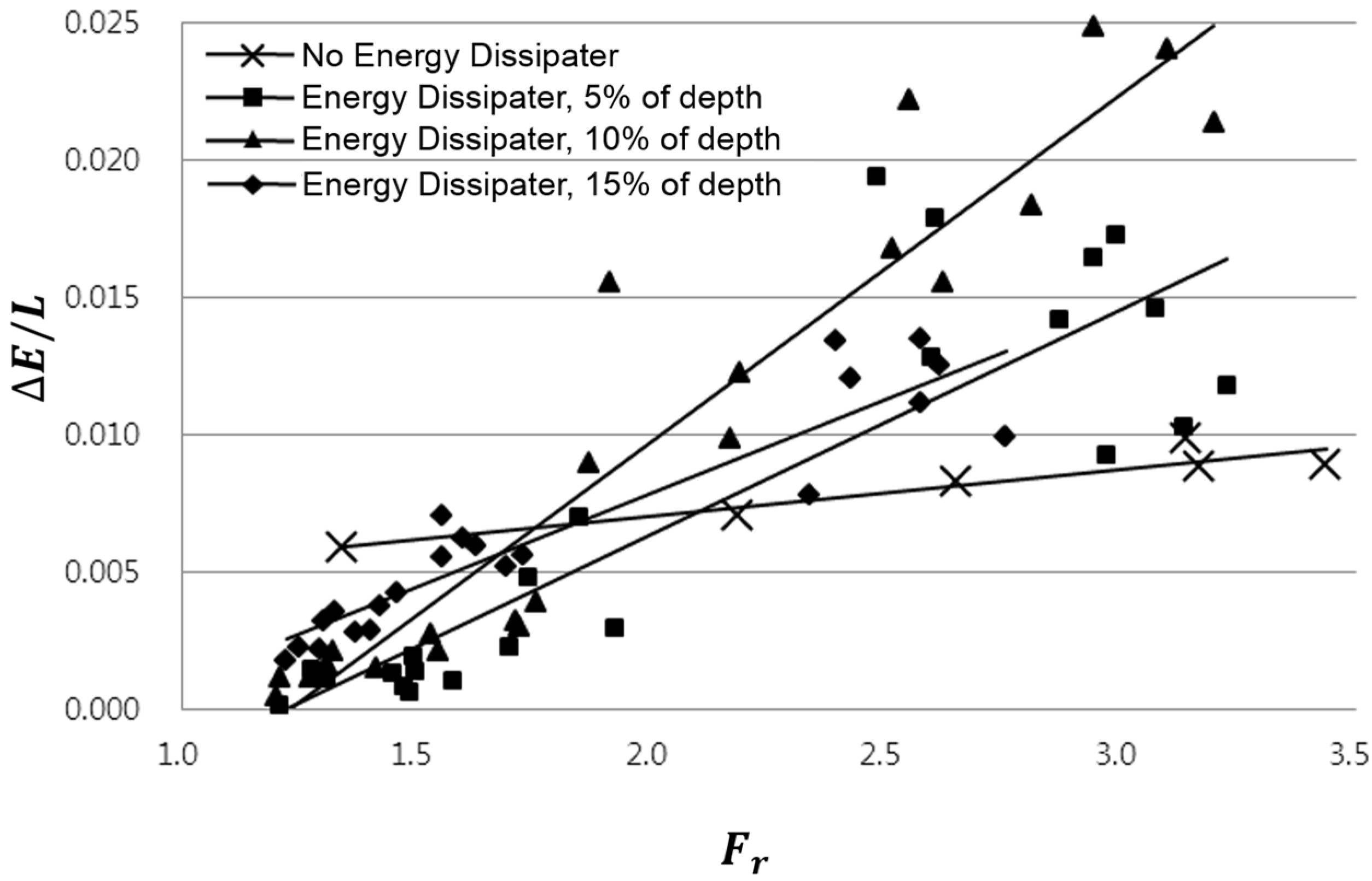
2.2. Changes in Energy after Weir Installation
Regarding the energy loss other than the water depth fluctuation before and after the hydraulic jump,
is the amount of pre-hydraulic jump energy,
, less than the post-hydraulic jump energy,
,
where
(m) is a water depth before the hydraulic jump,
(m) is a water depth after the hydraulic jump as a conjugate depth,
and
(m/s) are the flow velocity of the pre/post-hydraulic jump, respectively, and
(m
3/s/m) is a unit of water flow rate in the channel.
However, based on the momentum equation:
If Equation (3) is substituted into Equation (2),
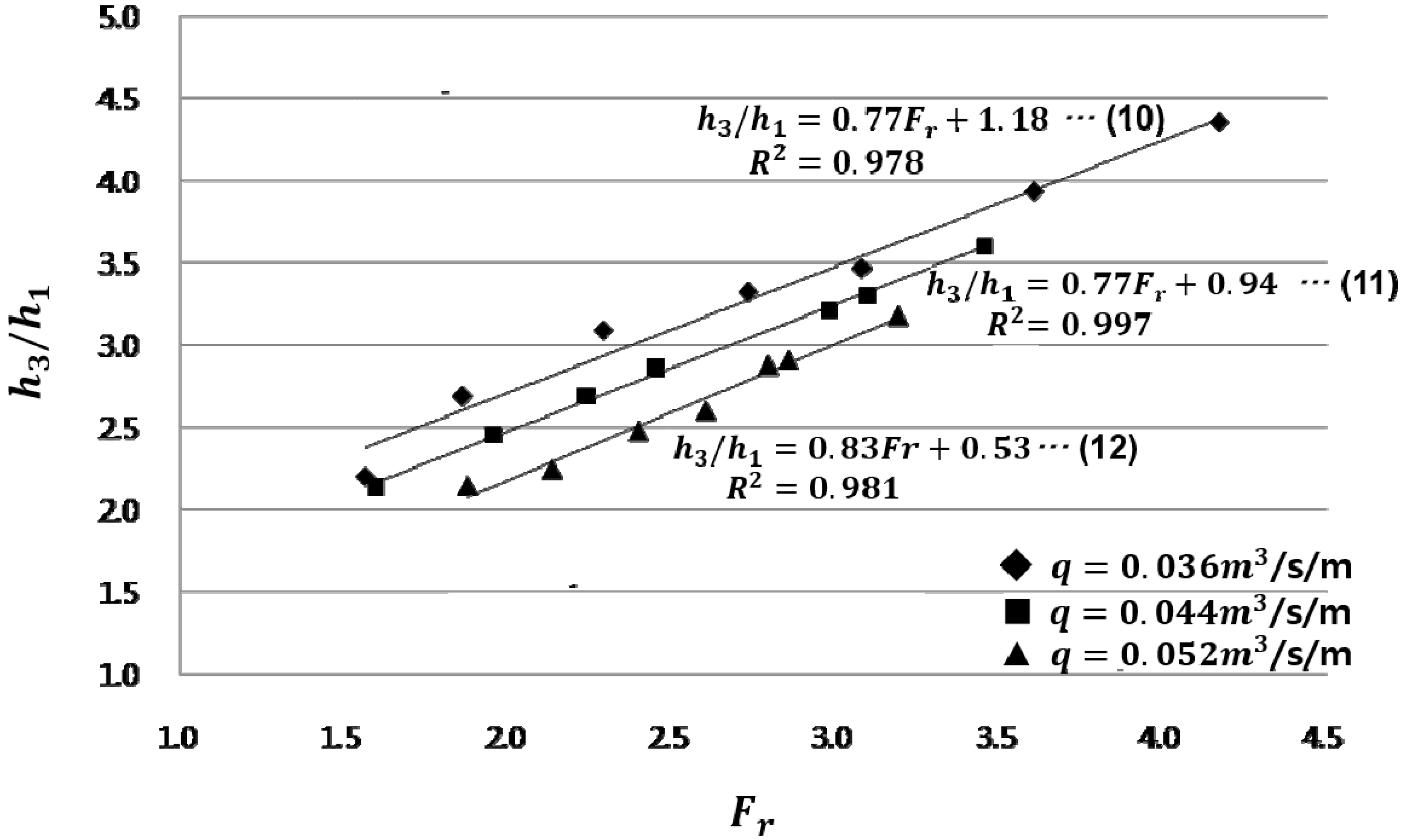
The hydraulic jump-caused energy loss can be calculated simply with the pre/post-hydraulic jump water depths. The specific forces for the pre/post-hydraulic jump water depths h1 and h2 are the same. However, the specific energy curve shows that the specific energy of h2, E2, is smaller than the specific energy of h1, E1, by . This is the energy loss due to the hydraulic jump.
If both sides of Equation (4) are divided by
h1 and expressed by the post-hydraulic jump Froude Numbers as
Fr1,
Equation (5) can be expressed solely by the function of the Froude Number Fr1 regarding the pre-hydraulic jump water level and hydraulic jump-caused energy loss.
The pre-hydraulic jump specific energy,
E1, is,
If both sides of Equation (6) are divided by
h1,
If Equation (5) is divided by Equation (7),
The
expressed by Equation (8) is called a relative loss.
In Equation (9), the ratio of pre/post-hydraulic jump specific energies (
is called the hydraulic jump efficiency. The hydraulic jump height refers to the difference between the pre/post-hydraulic jump water depths or
, and the following relation formula can be proven.
where
,
and
are called the relative hydraulic jump heights, pre-hydraulic jump and post-hydraulic jump relative water depth, respectively.