Impact Analysis of Lakefront Land Use Changes on Lake Area in Wuhan, China
Abstract
:1. Introduction
2. Materials and Methods
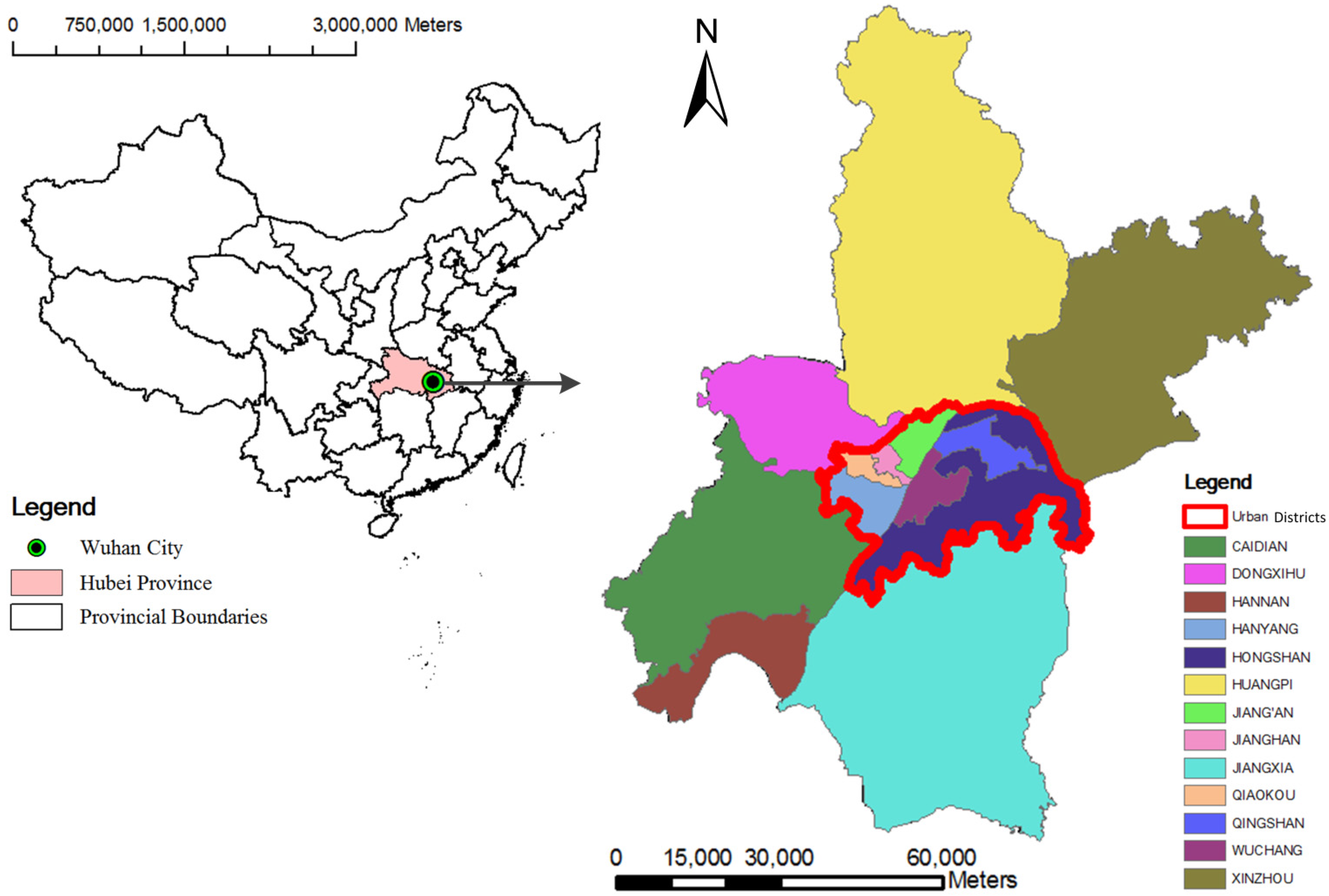
2.1. Study Area
| Date | Sensor | Spatial Resolution |
|---|---|---|
| 19 July 1991 | TM | Bands 1–5 and 7: 30 m |
| Band 6: 120 m | ||
| 11 September 2005 | ETM+ | Bands 1–5 and 7: 30 m |
| Band 6: 120 m | ||
| Band 8: 15 m |
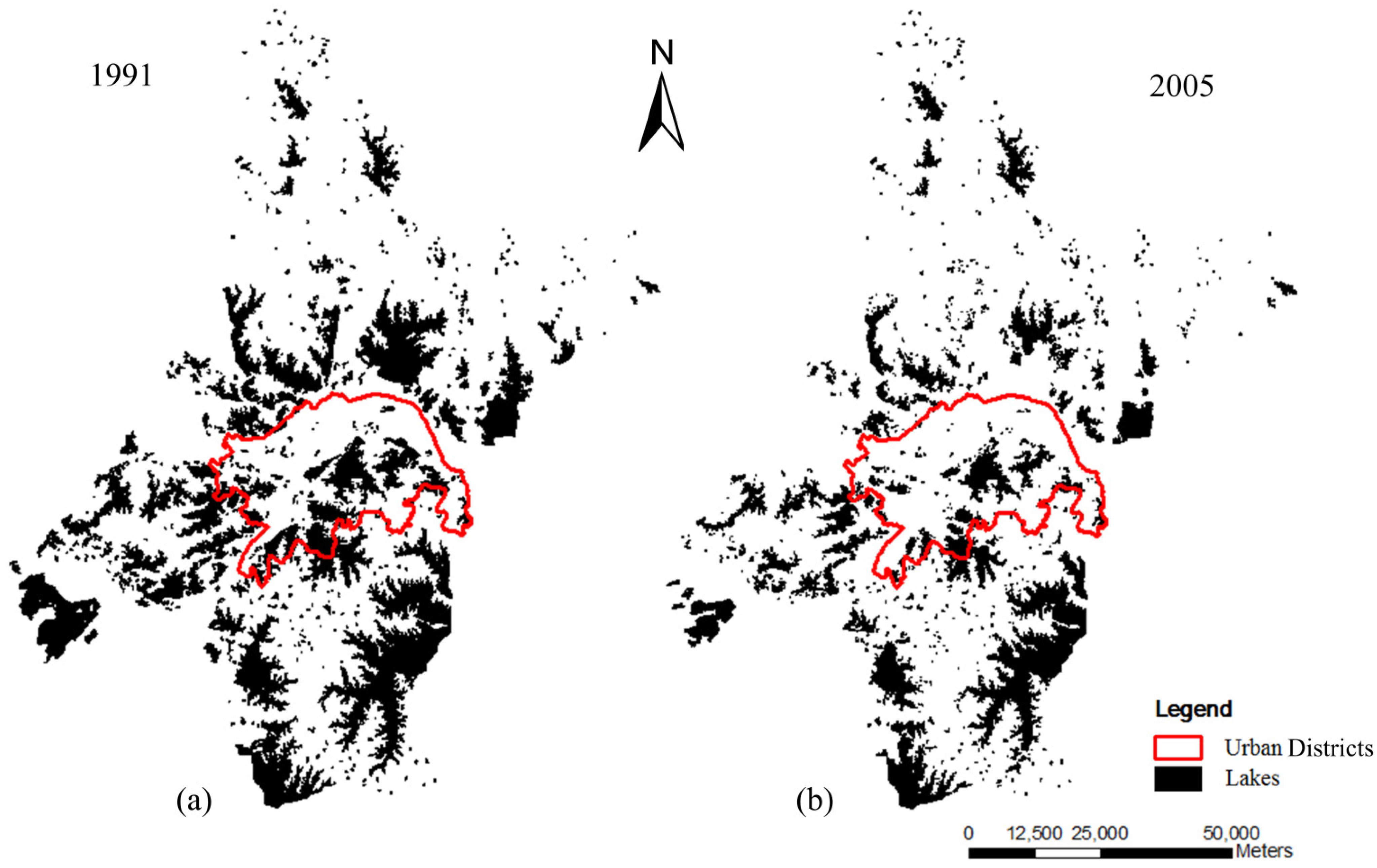
2.2. Extraction of Lake Areal Extent and Land Use Classification
| ID | Category | Remarks |
|---|---|---|
| 1 | Water body | Surface water bodies: rivers, lakes, and ponds |
| 2 | Shallow water | Edge of water bodies: wetlands |
| 3 | Agricultural | Dry land and paddy fields |
| 4 | Vegetated | Nature forests and grasslands |
| 5 | Developed | Artificial areas: residential, commercial, and industrial areas |
| 6 | Bare | Bare surfaces: bare lands and construction sites |

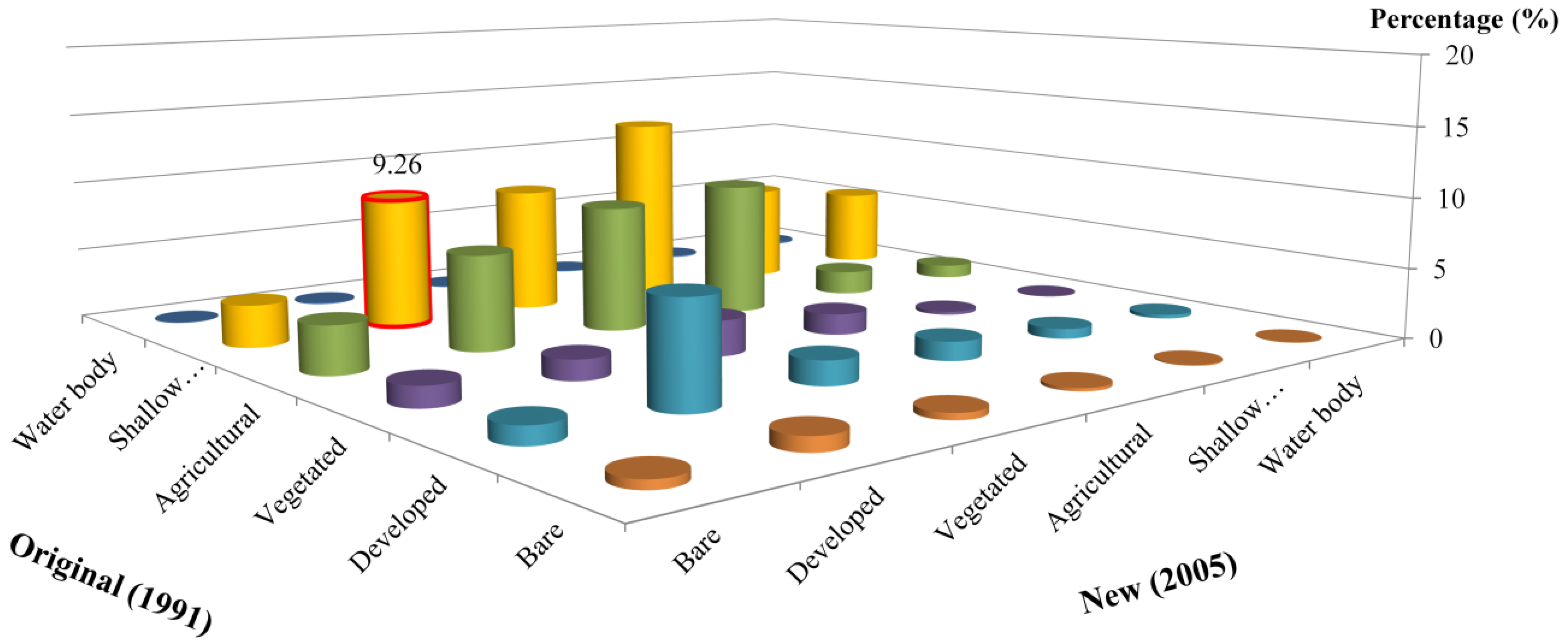
2.3. Expression of Lake Area and Land Use Changes
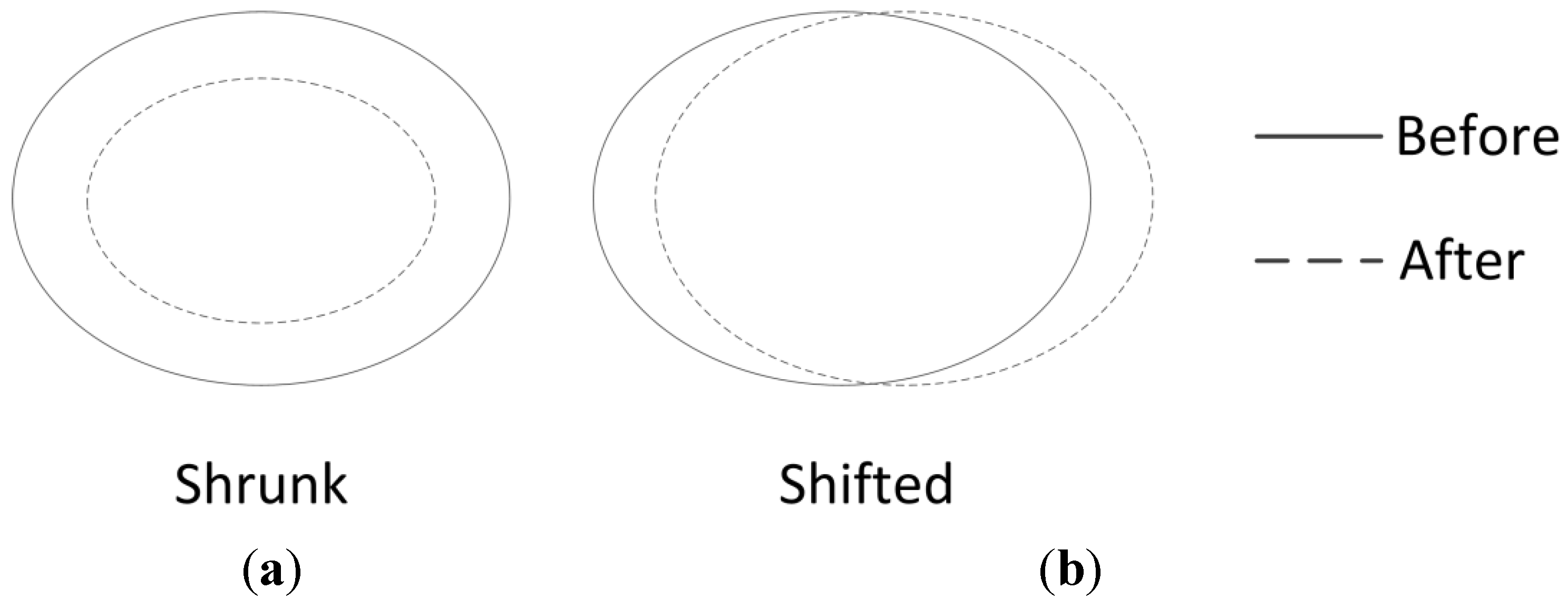
2.4. Relationships between Lake Area and Lakefront Land Use Change
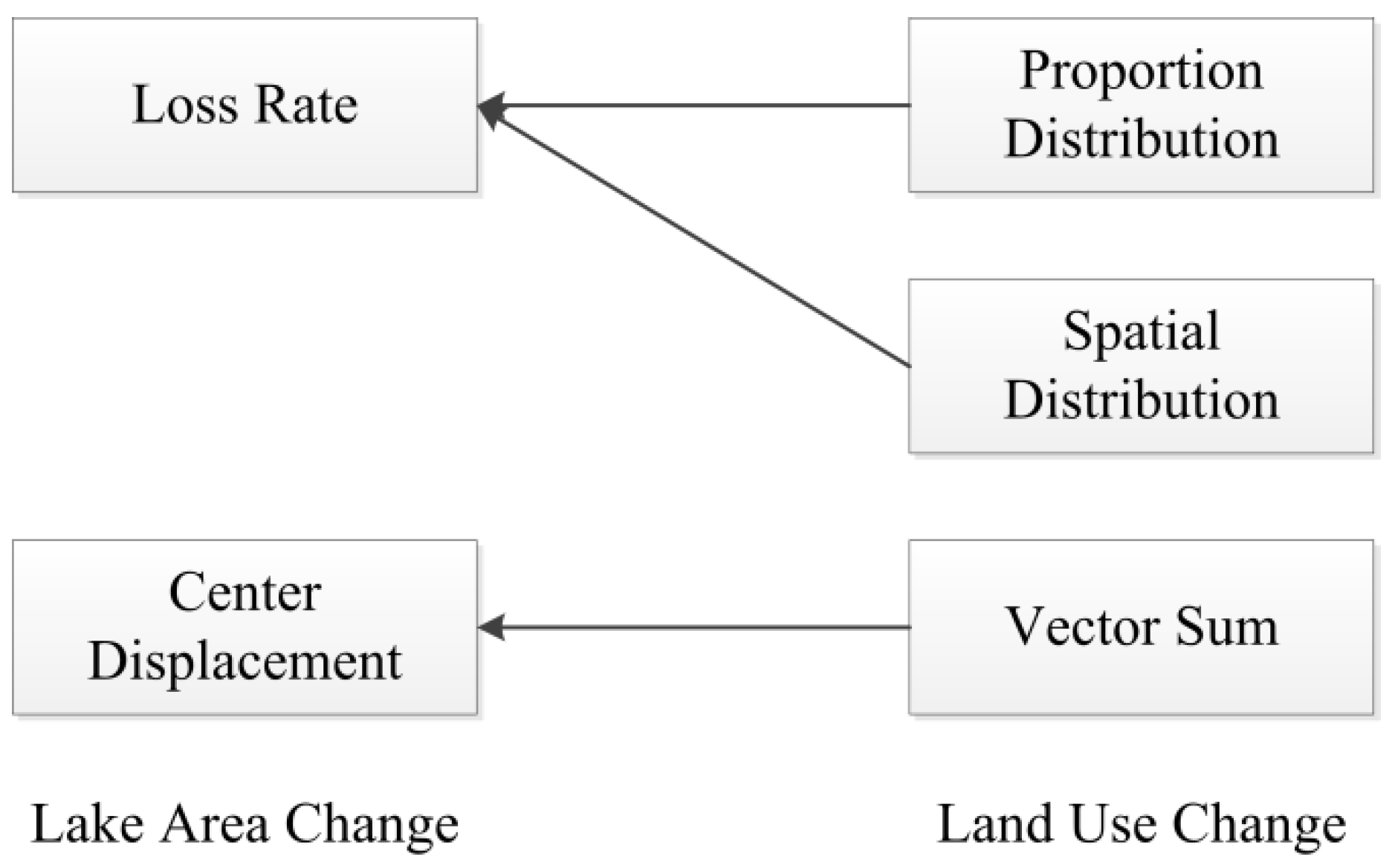
2.4.1. Measuring Loss Rate with Proportion of Lakefront Land Use Change
- (1)
- If 0 < ρij ≤ 1 there is a positive correlation between R and Pij, which shows that an increasing Pij is most likely to lead to the lake being filled in.
- (2)
- If ρij = 0, tij cannot be correlated with the loss rate, this shows that the loss rate has nothing to do with the lakefront land use change.
- (3)
- If −1 ≤ ρij < 0, there is a negative correlation between R and Pij, which indicates that the higher the proportion of tij, the lower the loss rate.
2.4.2. Measuring Spatial Autocorrelation of Lakefront Land Use
2.4.3. Measuring Center Displacement with Lakefront Land Use Change
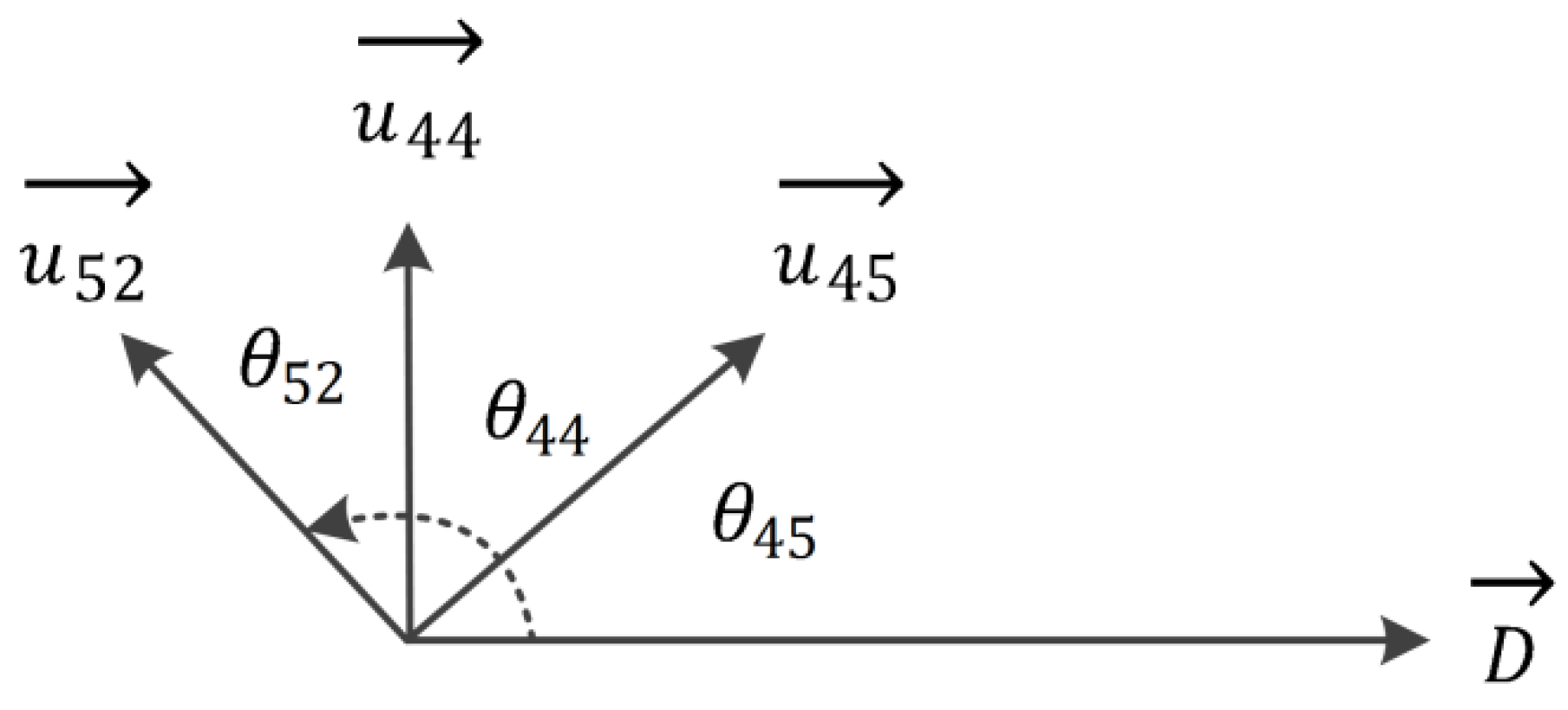
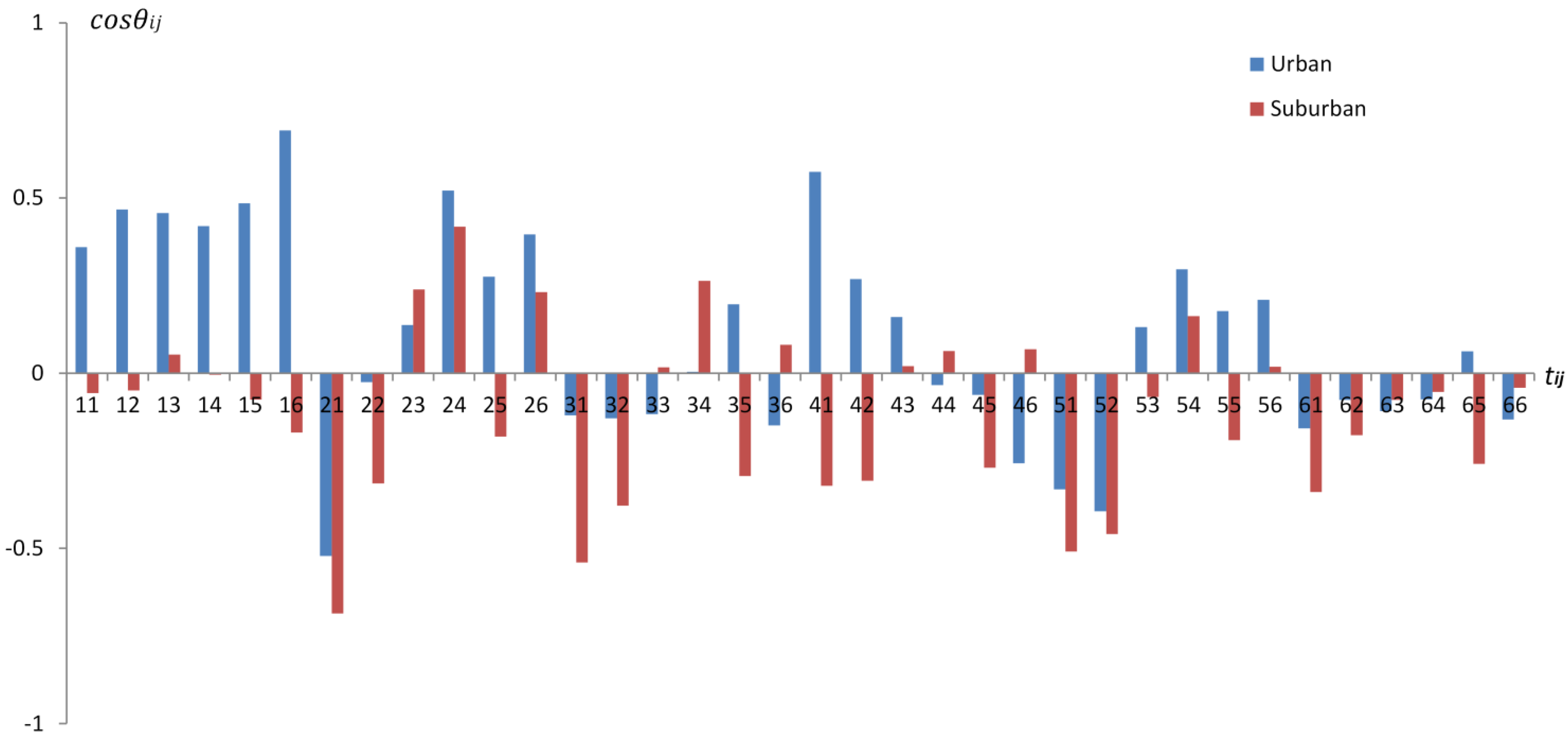
- (1)
- If cos θij > 0, such as θ45, uij has a correlation with D, there is a pushing effect of land use change tij on the lake area. In other words, there are some reductions in lake area due to land use change tij.
- (2)
- If cos θij ≤ 0, such as θ52 and θ44, uij has no correlation with D, there is no reduction in lake area due to land use change tij.
3. Results and Discussions
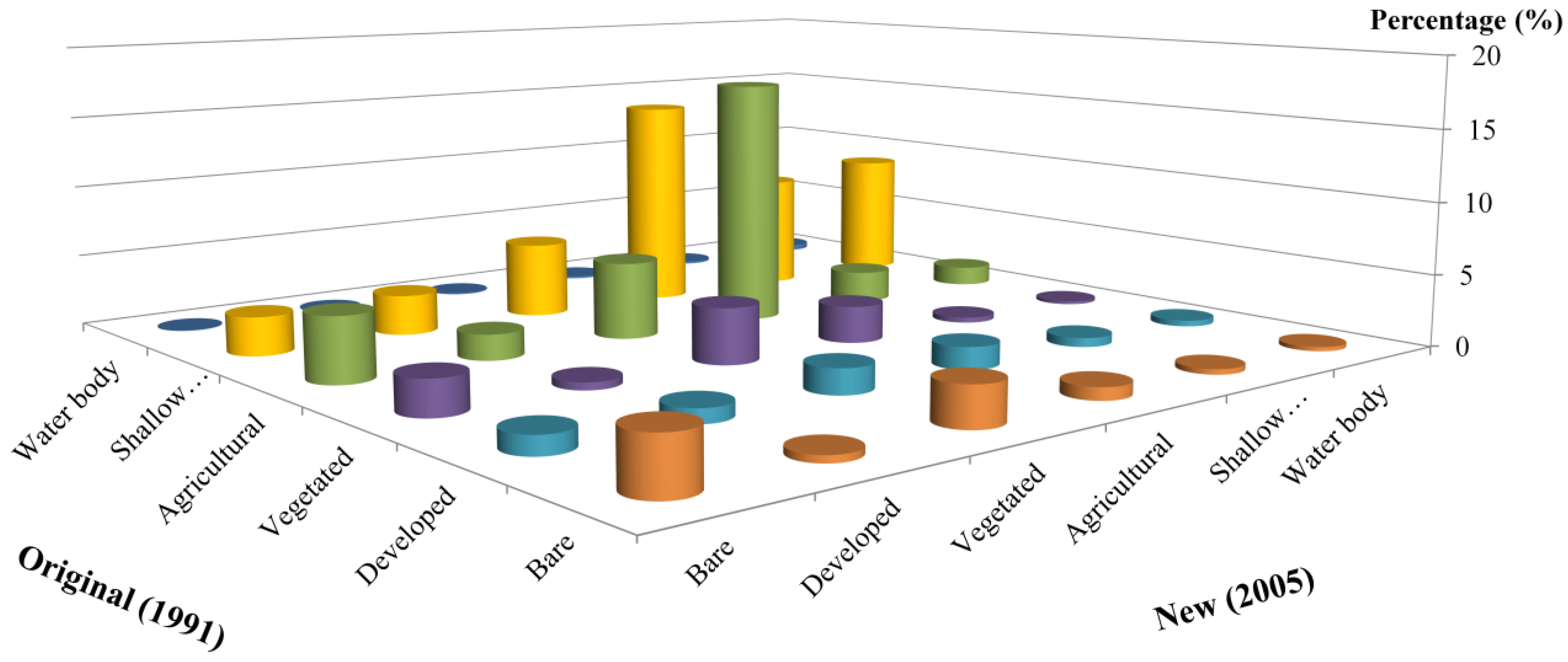
3.1. Loss Rate of Lake Area with Proportion of Lakefront Land Use Change
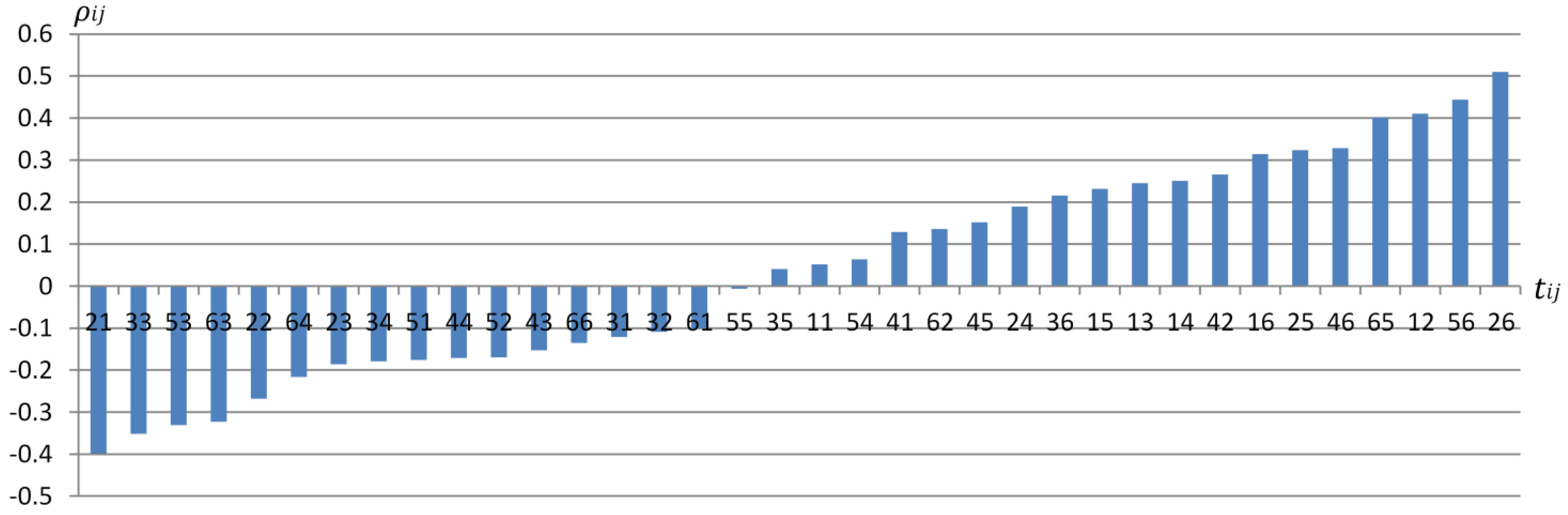
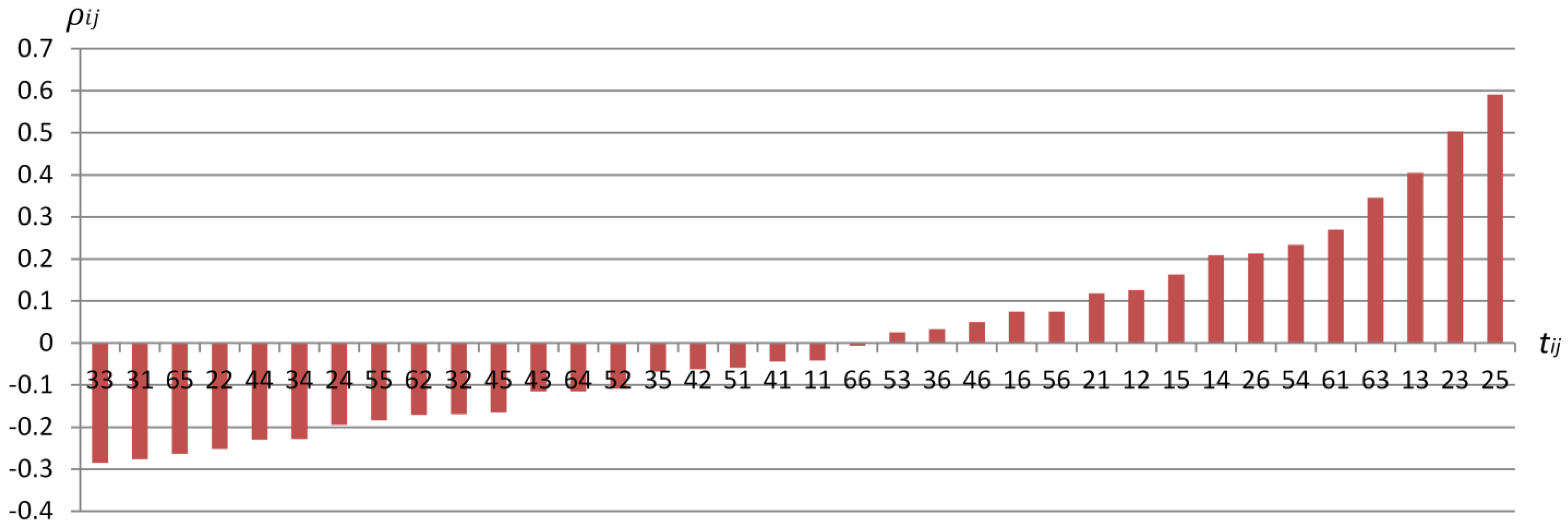
3.2. Loss Rate of Lake Area with Spatial Autocorrelation of Lakefront Land Use
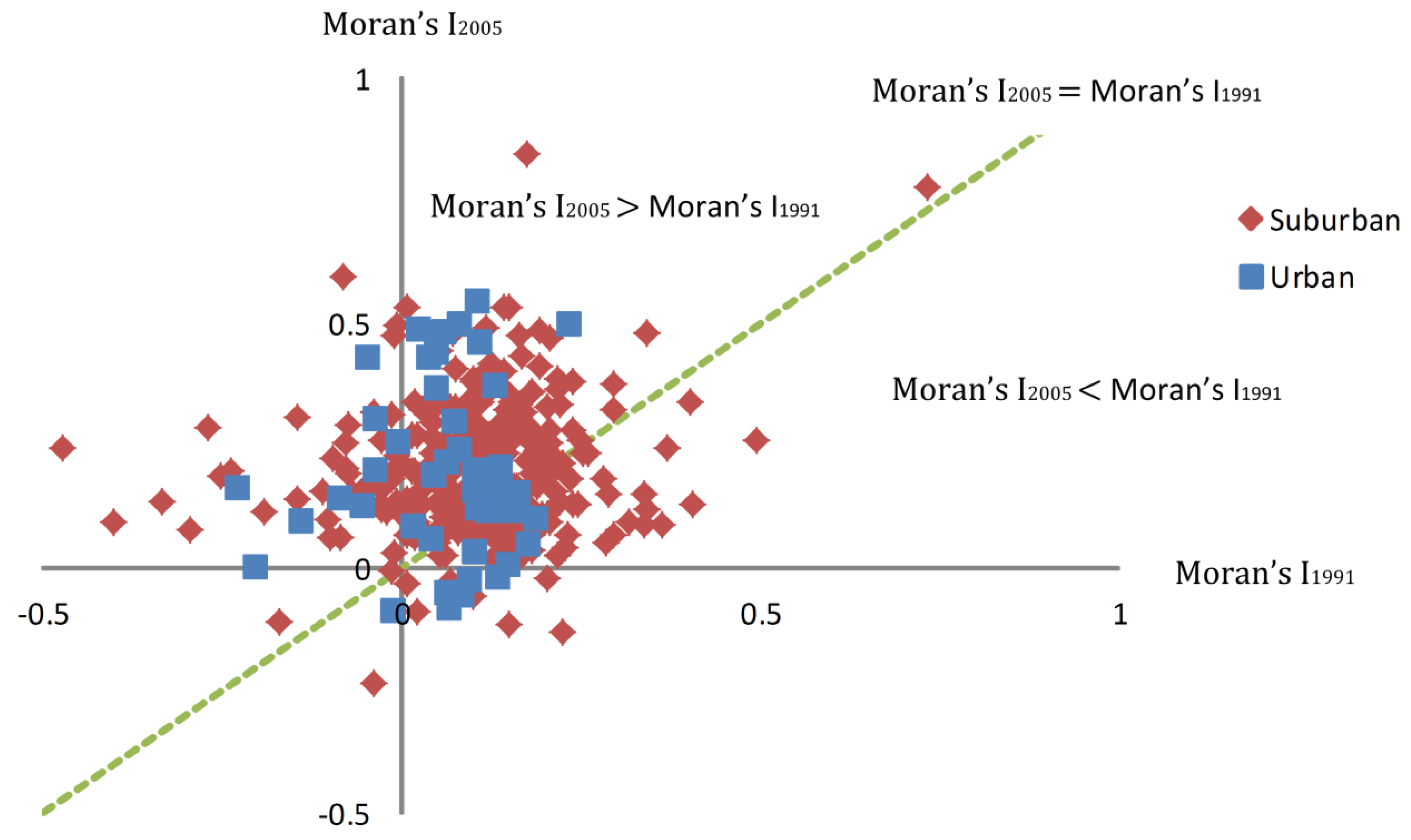

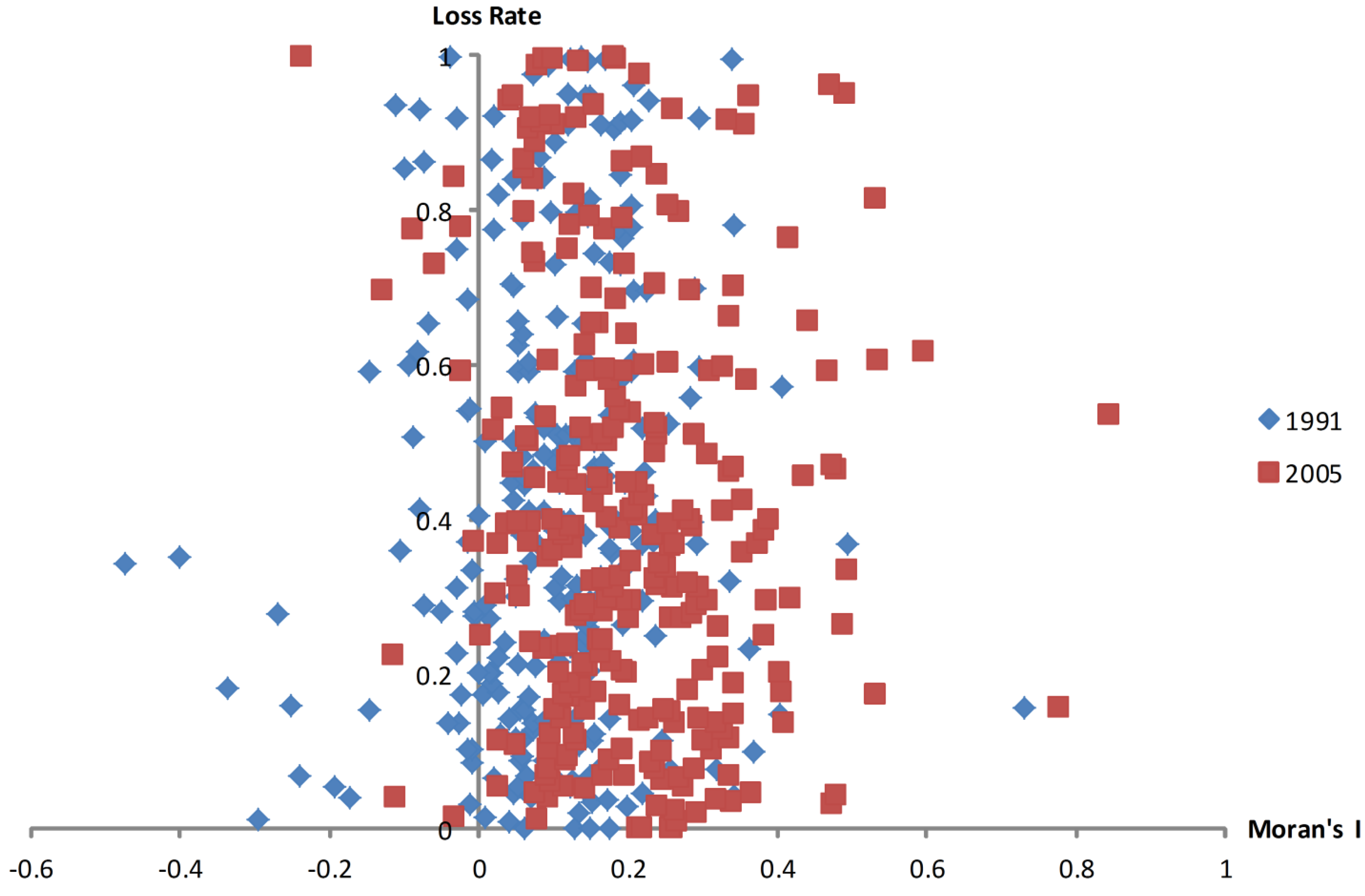
3.3. Center Displacement of Lake Area with Lakefront Land Use Change
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Birch, S.; McCaskie, J. Shallow urban lakes: A challenge for lake management. Hydrobiologia 1999, 395, 365–378. [Google Scholar] [CrossRef]
- Martínez-Arroyo, A.; Jáuregui, E. On the environmental role of urban lakes in Mexico City. Urban Ecosyst. 2000, 4, 145–166. [Google Scholar] [CrossRef]
- Naselli-Flores, L. Urban lakes: Ecosystems at risk, worthy of the best care. In Proceedings of Taal2007: The 12th World Lake Conference, Jaipur, India, 28 October–2 November 2007; pp. 1333–1337.
- Schuler, T.; Simpson, J. Introduction: Why urban lakes are different. Urban Lake Manag. Watershed Prot. Tech. 2001, 3, 747–750. [Google Scholar]
- Snehal, P.; Unnati, P. Challenges faced and solutions towards conservation of ecology of urban lakes. Inter. J. Sci. Eng. Res. 2012, 3, 170–183. [Google Scholar]
- Nakayama, T.; Watanabe, M. Role of flood storage ability of lakes in the Changjiang River catchment. Glob. Planet. Chang. 2008, 63, 9–22. [Google Scholar] [CrossRef]
- Liu, Y. Modelling the lake water environment impact on urban system expansion. Inf. Int. Insterdiscip. J. 2012, 15, 2351–2356. [Google Scholar]
- Henny, C.; Meutia, A.A. Urban lakes in megacity Jakarta: Risk and management plan for future sustainability. In Proceedings of 4th International Conference on Sustainable Future for Human Security Sustain, Kyoto, Japan, 18–21 October 2013; pp. 737–746.
- Lemoalle, J.; Bader, J.C.; Leblanc, M.; Sedick, A. Recent changes in Lake Chad: Observations, simulations and management options (1973–2011). Glob. Planet. Chang. 2012, 80–81, 247–254. [Google Scholar] [CrossRef]
- Noges, T. Relationships between morphometry, geographic location and water quality parameters of European lakes. Hydrobiologia 2009, 633, 33–43. [Google Scholar] [CrossRef]
- Morais, J.; Martins, A.; Vale, M.; Vasconcelos, V. Assessment of cyanobacterial toxinogenic genotypes and estimation of toxin content in urban lakes. Fresenius Environ. Bull. 2014, 23, 1867–1873. [Google Scholar]
- Stahl, L.L.; Snyder, B.D.; Olsen, A.R.; Kincaid, T.M.; Wathen, J.B.; McCarty, H.B. Perfluorinated compounds in fish from US urban rivers and the Great Lakes. Sci. Total Environ. 2014, 499, 185–195. [Google Scholar] [CrossRef]
- Leavitt, P.R.; Brock, C.S.; Ebel, C.; Patoine, A. Landscape-scale effects of urban nitrogen on a chain of freshwater lakes in central North America. Limnol. Oceanogr. 2006, 51, 2262–2277. [Google Scholar] [CrossRef]
- Bogard, M.J.; Donald, D.B.; Finlay, K.; Leavitt, P.R. Distribution and regulation of urea in lakes of central North America. Freshw. Biol. 2012, 57, 1277–1292. [Google Scholar] [CrossRef]
- Wu, J.; Xie, H. Research on characteristics of changes of lakes in Wuhan’s main urban area. In Proceedings of International Conference on Green Buildings and Sustainable Cities, Bologna, Italy, 15–16 September 2011; pp. 395–404.
- Xu, K.; Kong, C.; Liu, G.; Wu, C.; Deng, H.; Zhang, Y.; Zhuang, Q. Changes of urban wetlands in Wuhan, China, from 1987 to 2005. Prog. Phys. Geogr. 2010, 34, 207–220. [Google Scholar]
- Huang, P.; Liu, Y.; Liu, C.; Jiang, Q. Study on evolution of urban lakes in Wuhan based on RS/GIS. Ecol. Environ. Sci. 2012, 21, 1588–1593. [Google Scholar]
- Cao, B.; Kang, L.; Yang, S.; Tan, D.; Wen, X. Monitoring the Dynamic Changes in Urban Lakes Based on Multi-source Remote Sensing Images. In Geo-Informatics in Resource Management and Sustainable Ecosystem; Springer: Berlin, Germany, 2015; pp. 68–78. [Google Scholar]
- Si, H.; Liwei, C. Influence of the development in Wuhan city on lake resource. In Proceedings of International Conference on Environmental Science and Information Application Technology (ESIAT) 2009, Wuhan, China, 4–5 July 2009; IEEE; pp. 221–224.
- Du, N.; Ottens, H.; Sliuzas, R. Spatial impact of urban expansion on surface water bodies—A case study of Wuhan, China. Landsc. Urban Plan. 2010, 94, 175–185. [Google Scholar] [CrossRef]
- Zhongping, Z.; Xinhai, L. Spatial-temporal evolution of urban lakes in Wuhan City based on remote sensing images. J. Lake Sci. 2008, 20, 648–654. [Google Scholar] [CrossRef]
- Sanchez, A.; Medina, N.; Vojinovic, Z.; Price, R. An integrated cellular automata evolutionary-based approach for evaluating future scenarios and the expansion of urban drainage networks. J. Hydroinformatics 2014, 16, 319–340. [Google Scholar] [CrossRef]
- Razavi, B.S. Predicting the trend of land use changes using artificial neural network and markov chain model (case study: Kermanshah City). Res. J. Environ. Earth Sci. 2014, 6, 215–226. [Google Scholar]
- Fichera, C.R.; Modica, G.; Pollino, M. Land cover classification and change-detection analysis using multi-temporal remote sensed imagery and landscape metrics. Eur. J. Remote Sens. 2012, 45, 1–18. [Google Scholar] [CrossRef]
- Jat, M.K.; Khare, D.; Garg, P.K.; Shankar, V. Remote sensing and GIS-based assessment of urbanisation and degradation of watershed health. Urban Water J. 2009, 6, 251–263. [Google Scholar] [CrossRef]
- Radhi, H.; Fikry, F.; Sharples, S. Impacts of urbanisation on the thermal behaviour of new built up environments: A scoping study of the urban heat island in Bahrain. Landsc. Urban Plan. 2013, 113, 47–61. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, X.; Fu, G.; Zhou, H.; Wang, H. The impacts of climate change on water diversion strategies for a water deficit reservoir. J. Hydroinformatics 2014, 16, 872–889. [Google Scholar] [CrossRef]
- Shi, P.J.; Yuan, Y.; Zheng, J.; Wang, J.A.; Ge, Y.; Qiu, G.Y. The effect of land use/cover change on surface runoff in Shenzhen region, China. Catena 2007, 69, 31–35. [Google Scholar] [CrossRef]
- Peterson, H.M.; Nieber, J.L.; Kanivetsky, R.; Shmagin, B. Regionalization of landscape characteristics to map hydrologic variables. J. Hydroinformatics 2014, 16, 971–972. [Google Scholar] [CrossRef]
- Suriya, S.; Mudgal, B. Impact of urbanization on flooding: The Thirusoolam sub watershed—A case study. J. Hydrol. 2012, 412, 210–219. [Google Scholar] [CrossRef]
- Wang, J.; Da, L.; Song, K.; Li, B.L. Temporal variations of surface water quality in urban, suburban and rural areas during rapid urbanization in Shanghai, China. Environ. Pollut. 2008, 152, 387–393. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Ludwig, D.; Brock, W.A. Management of eutrophication for lakes subject to potentially irreversible change. Ecol. Appl. 1999, 9, 751–771. [Google Scholar] [CrossRef]
- Choiński, A.; Ptak, M. Lake infill as the main factor leading to lake’s disappearance. Pol. J. Environ. Stud. 2009, 18, 347–352. [Google Scholar]
- Wasige, J.E.; Groen, T.A.; Smaling, E.; Jetten, V. Monitoring basin-scale land cover changes in Kagera Basin of Lake Victoria using ancillary data and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 32–42. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, S.; Zhao, K.; Xie, P.; Fang, J. Land-cover changes in an urban lake watershed in a mega-city, Central China. Environ. Monit. Assess. 2006, 115, 349–359. [Google Scholar] [CrossRef]
- Liu, Y.; Lv, X.; Qin, X.; Guo, H.; Yu, Y.; Wang, J.; Mao, G. An integrated GIS-based analysis system for land-use management of lake areas in urban fringe. Landsc. Urban Plan. 2007, 82, 233–246. [Google Scholar] [CrossRef]
- Xiang, W.N. GIS-based riparian buffer analysis: Injecting geographic information into landscape planning. Landsc. Urban Plan. 1996, 34, 1–10. [Google Scholar] [CrossRef]
- Wuhan Bureau of Statistics. Wuhan Statistical Yearbook 2006; China Statistics Press: Beijing, China, 2006.
- Wang, Z. Study on protection and utilization of Wuhan City lake since 1990s. Environ. Sci. Manag. 2013, 38, 38–45. [Google Scholar]
- National Climate Center. Available online: http://ncc.cma.gov.cn/Website/index.php?ChannelID=43&WCHID=5 (accessed on 26 July 2015).
- Xu, H.Q. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Waldhör, T. The spatial autocorrelation coefficient Moran’s I under heteroscedasticity. Stat. Med. 1996, 15, 887–892. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Zhang, Q.; Tong, Z. Impact Analysis of Lakefront Land Use Changes on Lake Area in Wuhan, China. Water 2015, 7, 4869-4886. https://doi.org/10.3390/w7094869
Zhu J, Zhang Q, Tong Z. Impact Analysis of Lakefront Land Use Changes on Lake Area in Wuhan, China. Water. 2015; 7(9):4869-4886. https://doi.org/10.3390/w7094869
Chicago/Turabian StyleZhu, Jianfeng, Qiuwen Zhang, and Zhong Tong. 2015. "Impact Analysis of Lakefront Land Use Changes on Lake Area in Wuhan, China" Water 7, no. 9: 4869-4886. https://doi.org/10.3390/w7094869
APA StyleZhu, J., Zhang, Q., & Tong, Z. (2015). Impact Analysis of Lakefront Land Use Changes on Lake Area in Wuhan, China. Water, 7(9), 4869-4886. https://doi.org/10.3390/w7094869






