Integrated River and Coastal Flow, Sediment and Escherichia coli Modelling for Bathing Water Quality
Abstract
:1. Introduction
1.1. Background
1.2. Key Physical, Chemical and Ecological Processes
1.3. Brief Review of Methods and Models
2. Model Details
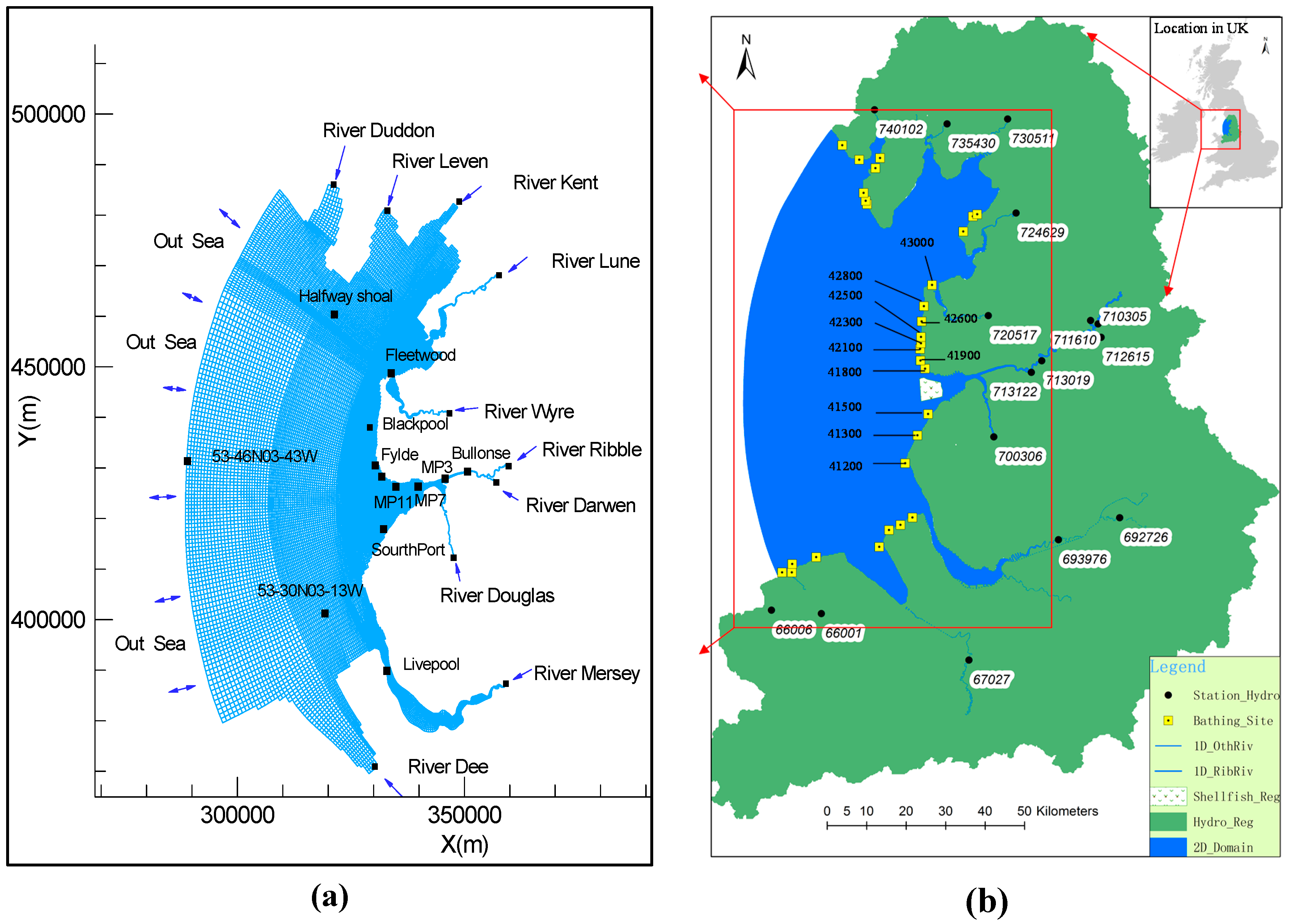
2.1. Model Grid System
2.2. Catchment Hydrological Model
2.2.1. Hydrological Model in Catchment Cells
2.2.2. Sediment Processes in Streams and River Channels
2.2.3. Distributed Bathing Water Quality Model
2.3. River Networks and EFDC 2D Coastal Model
3. Model Application
3.1. Study Site
3.2. Data Source and Processing
| Database | Purpose | Note (Content and Source) |
|---|---|---|
| Geographic Data | Model boundaries | Catchment: [67] River and Ocean: OS1 to 10,000, OS1 to 50,000 |
| Catchment DTM, River networks | Cell slope, flow direction, river generation | (I) 50 m Integrated Hydrological Digital Terrain Model (IHDTM) [68] (II) 1:50,000 Watercourses, River centreline network [69] |
| Coastal Bathymetry | Grid topography for coastal model | The bathymetric data in the estuary and riverine are merged from 6 data sources and interpolated to the model nodes [64] |
| Land and river coastal bed sediments | Estuary and riverine bed grain gradation and spatial distribution | (I) Offshore region: Surface sediment distribution data (BGS 1:250,000 V3) ([70]); (II) Riverine: OS maps for the bed sediment type; (III) Nearshore: Sand grain gradation along sandy beach and south part of sea region by Kenneth Pye Associates Ltd [71] with 1566 sampling; (IV) Land: 1000 × 1000 m HWSD soil DEM [65] |
| Land cover map | Catchment model input | LCM 1990, 2000 and 2007 from Edina: [72] |
| Climate and meteorological | Meteorological inputs into catchment and coastal model | (I) BADC hourly weather (1989–2013) data including: rainfall, radiation, wind, moisture, temperature and etc. [73] (II) 15 Min rainfall data from EA and Natural Resources Wales (NRW), 68 stations across the model domain. |
| Discharge data | Model validation and calibration | (I) 15 Min Data from EA and NRW with 30 stations at Ribble catchment and the main 8 controlled stations in the other rivers (II) Daily averaged discharge: [67] |
| Hydrodynamic | Model lower boundary and verification | Tidal level and current velocity data in 2012 and 2013 measured by the Centre for Research into Environment and Health (CREH), University of Aberystwyth, as part of the Cloud to Coast (C2C) Project |
| Sediment | Suspended sediment concentrations (SSCs) | (I) SSC measurement in catchment (EA water quality database); (II) SSC in the river Ribble and estuary by CREH in 2012, University of Aberystwyth, as part of C2C, relationship between turbidity (NTU) and SSC(mg/L) is: SSC = 0.51 × NTU (III) SSC data 1997–1999 in the river and estuary from the NERC database |
| Population and livestock | Population and livestock | (I) Population in 2011 obtained from Office of National Statistics. [74] (II) Livestock and crop areas in 2000 and 2010 across England and Wales. Defra statistics. [75] |
| CSO, tanks, WwTPs flow and FIO data | Flow and FIO fluxes in urban region, used as point source | From the Infoworks model using results from Pennine Water Group, Dept of Civil and Structural Engineering, University of Sheffield as part of C2C |
| FIO data | FIO data in River Ribble and estuary and Bathing region | (I) 1999 sample data invested by EA and North West Water Ltd. (II) 2012 sampling, CREH, University of Aberystwyth as part of the C2C. (III) FIO and E. coli in the bathing region (1988–2013) [76] |
3.3. Key Parameters Related to Hydrological, Hydrodynamic and FIO Transport Processes
3.4. Model Validation
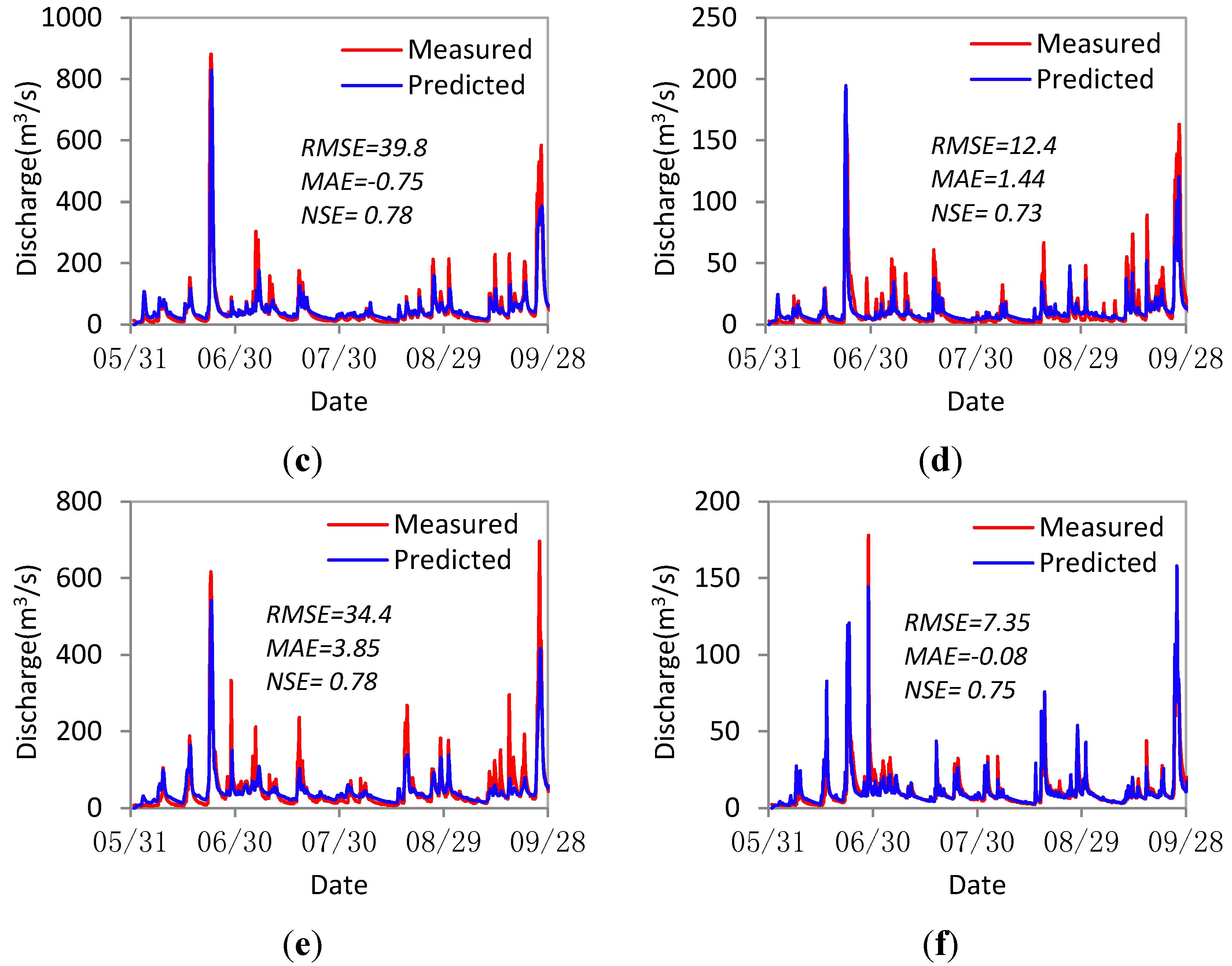
3.4.1. Discharge Verification at Control Gauging Stations
| Parameter | Label | Value | Note |
|---|---|---|---|
| Time step in catchment, 1D river and 2D coastal model | 300, 30, 2 | Time steps for different model(s) | |
| Infiltration rate | IHoton | 0.02–0.13 | Soil type and land use (m/s) |
| Impervious area ratio | AlfaIm | 0.0–1.0 | Land use |
| Top Soil layer thickness | Um | 5–20 | HWSD and land use (cm) |
| Mid soil layer | Lm | 20–40 | HWSD and land use (cm) |
| Bottom soil layer | Dm | 30–50 | HWSD and land use (cm) |
| Soil particle diameter | Dsed(i) | 0.05–1.0 | HWSD (mm) |
| Surface roughness | N | 0.03–0.06 | HWSD and land use (cm) |
| Transport time at surface | Ls | 0.1–1.0 | DEM, HWSD, land use (Hour) |
| Time in mid soil layer | Li | 0.5–10.0 | DEM, HWSD, land use (Hour) |
| Time in bottom soil layer | Lg | 3–24.0 | DEM, HWSD, land use (Hour) |
| Time in sub-channel | Lr | 0.08–1.0 | DEM, HWSD, land use (Hour) |
| River Bed thickness | ThkBed | 0.1, 0.5 | Estimation value |
| Bed sediment composition | DsedBed | 50, 100, 200, 300, 500, 1000 | Same with closest grid cell (µm) |
| Manure ratio in surface | αLMN | 0.1–0.3 | Empirical value varied with manure mode |
| Grazing feces ratio in surface | αLGZ | 0.8–0.9 | Empirical value varied with land use |
| Washing coefficient for soil water | k1 | 0.1–0.5 | Empirical value with different soil |
| dimensionless fitting parameters | k3 | 0.2 | Washing coefficient in the surface |
| dimensionless fitting parameters | β | 0.5~2.0 | Washing coefficient in the surface |
| Natural die-off rate | Kn | 0.5~10 | Variation for different habitat |
| radiation coefficient | KS | 1.5 | Constant |
| Moisture coefficient | αm | 0.4–0.8 | Variation with land use above |
| Temperature coefficient | θ | 1.047 | Constant |
| Sediment partition coefficient | Kd | 10~70 | Variation with diameter, clay ratio and temperature (mL/g) |
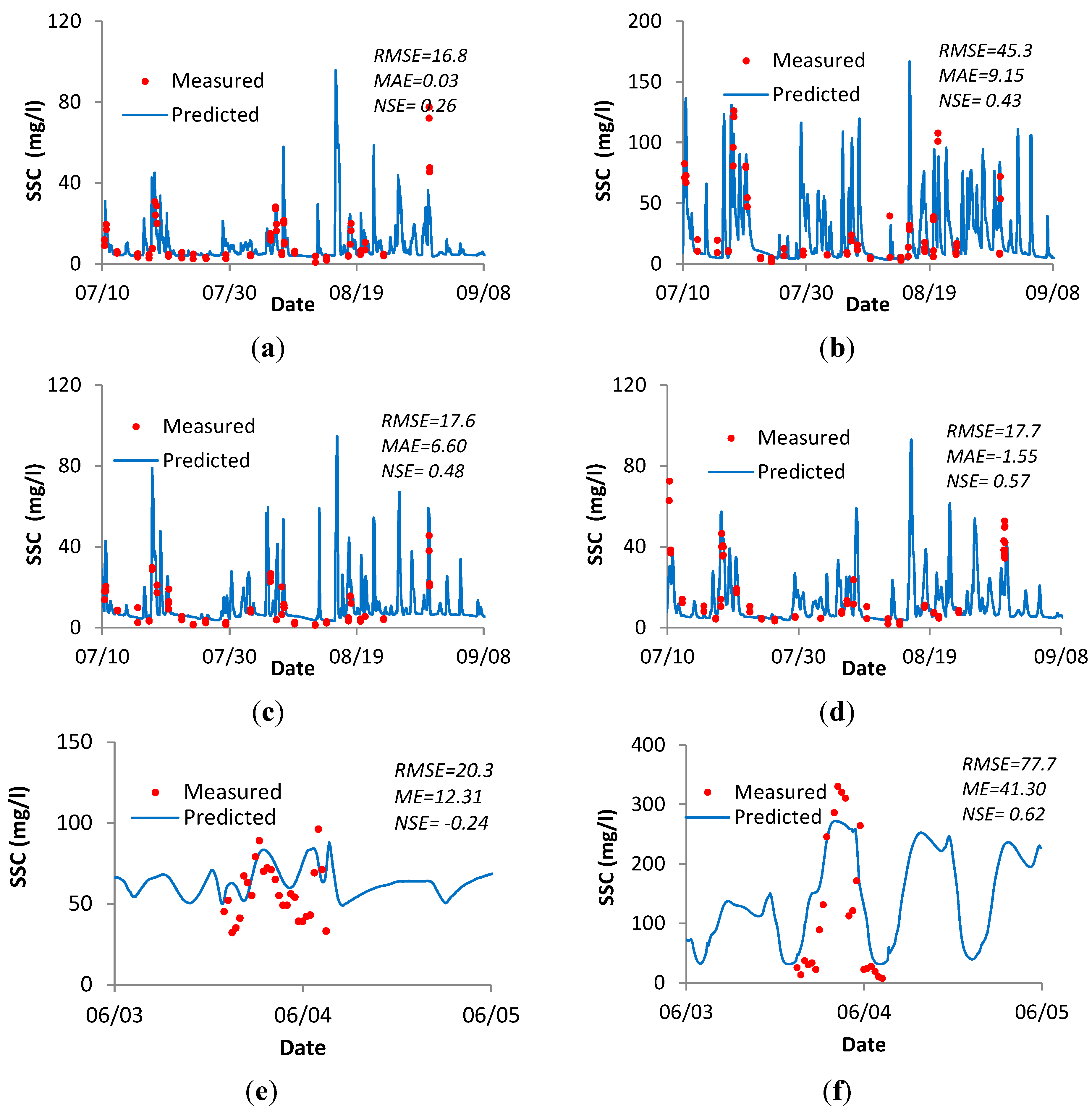
3.4.2. Verification of Sediment Concentration for the River Ribble
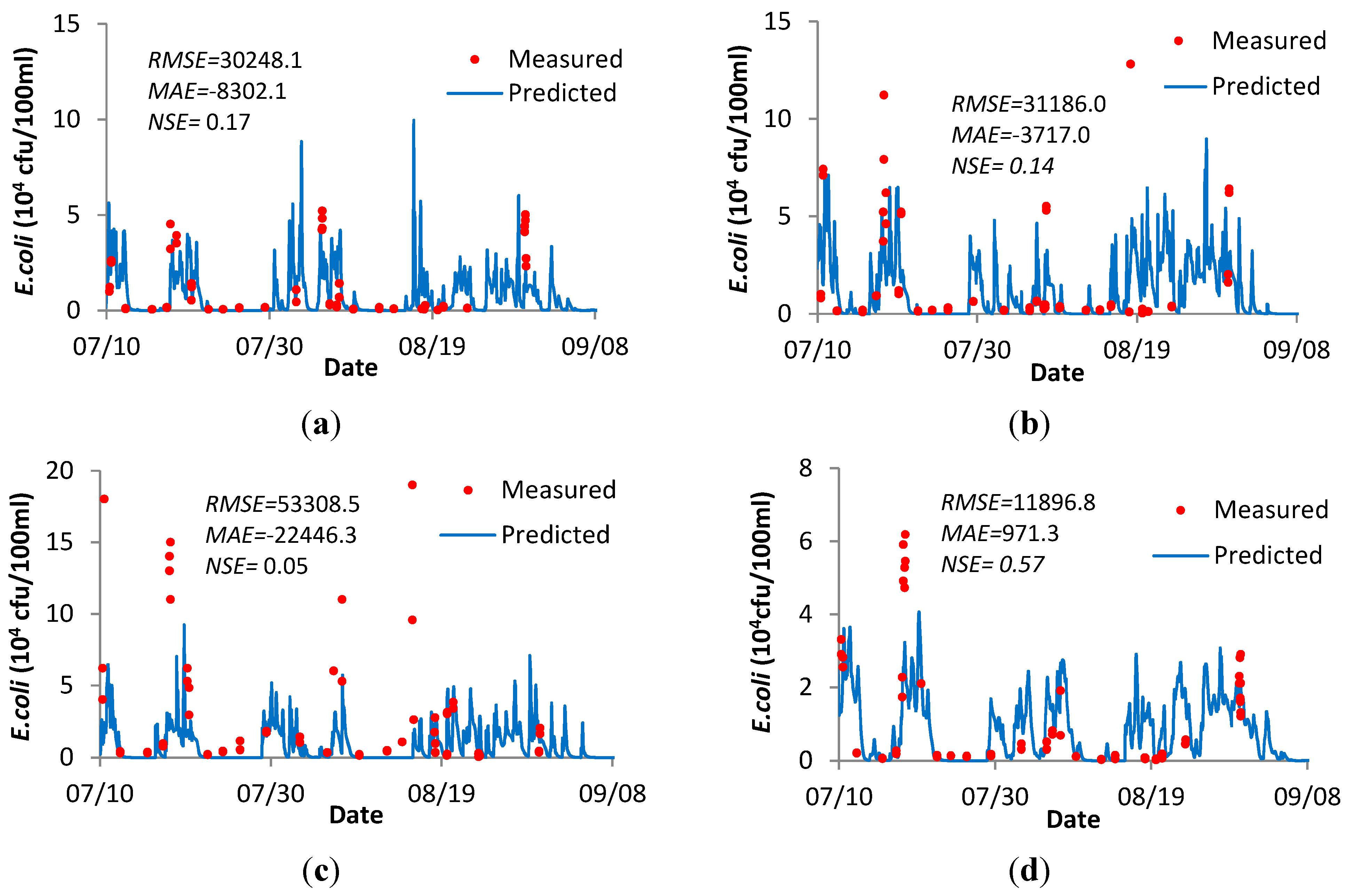
3.4.3. E. coli Verification for the River Ribble and Bathing Region
4. Discussion
4.1. Key Processes, Methods and Model Performance
4.2. Factors Influencing the High FIO Concentration Events at Bathing Sites in 2012
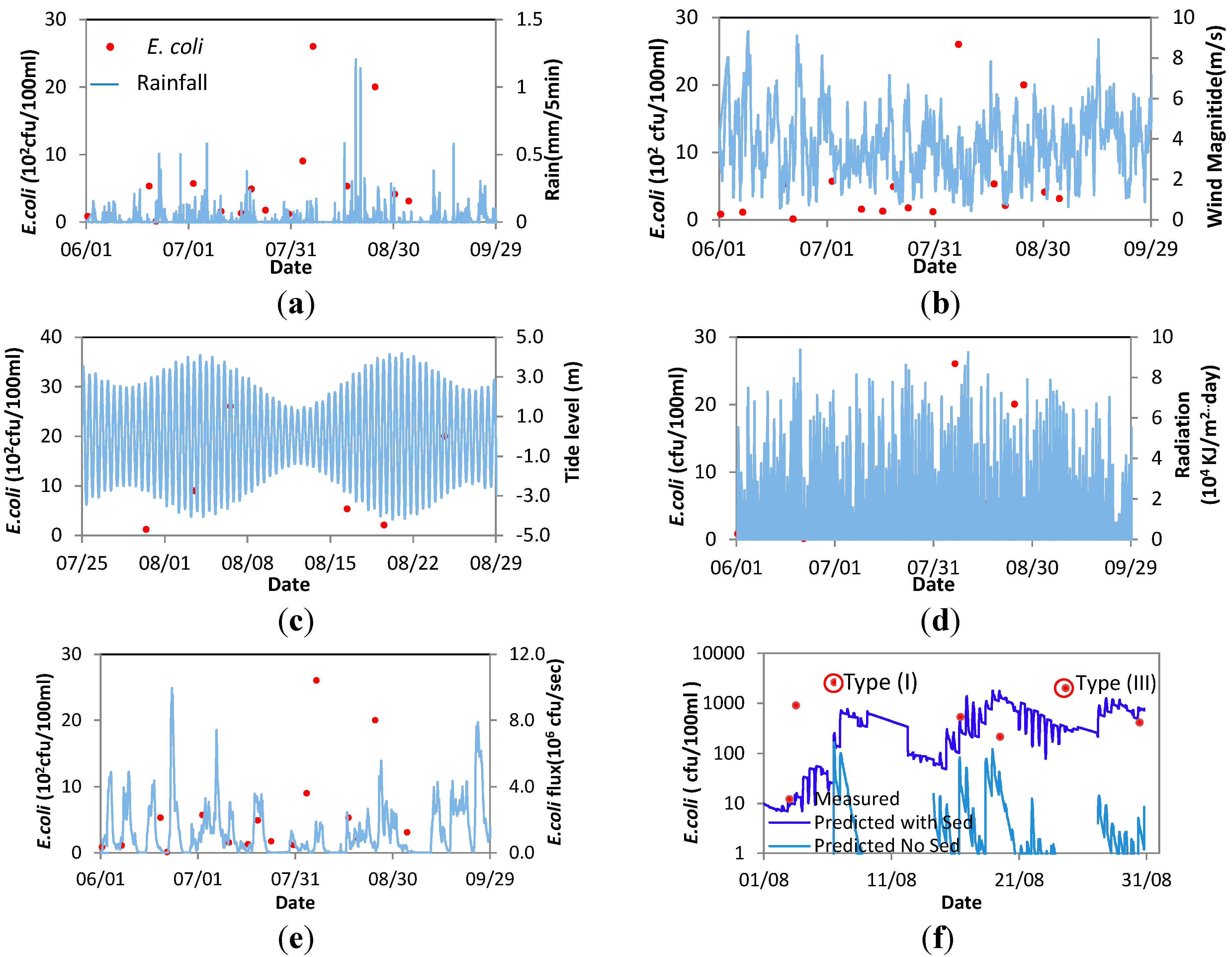
| BWR No. | 1976/EC | 2006/EC | Peak and Time (cfu/100 mL) | Key Driving Factor | Event Type |
|---|---|---|---|---|---|
| 41200 | LC | HC | 827 (17 August) | Rainfall and Ribble flux | & (III) |
| 41300 | HC | HC | 1100 (25 June) | Rainfall and Ribble flux | (I) & (III) |
| 41500 | HC | HC | 1300 (25 June) | Rainfall and Ribble flux | (I) & (III) |
| LC | HC | 750 (5 August) | Local rain or transport | (I) and (II) | |
| 41800 | HC | HC | 2600 (6 August) | Antecedent dry weather before | (II) |
| HC | HC | 2000 (24 August) | Local large rainfall | & (III) | |
| 41900 | HC | HC | 4800 (6 August) | Antecedent dry weather before | (II) |
| HC | HC | 2000 (24 August) | Local large rainfall | (I) | |
| 42100 | HC | HC | 6500 (24 June) | Rainfall and Wind | (IV) |
| HC | HC | 2600 (28 August) | Local large rainfall | (III) | |
| 42300 | HC | HC | 7000 (24 June) | rainfall and strong Wind | (IV) |
| HC | HC | 1900 (28 August) | Local middle rainfall | (III) | |
| 42500 | HC | HC | 5000 (24 June) | Intense rainfall and strong Wind | (IV) |
| HC | HC | 1100 (28 August) | Ribble middle rainfall | (III) | |
| 42600 | HC | HC | 4600 (24 June) | Intense rainfall and strong Wind | (III) & (I) |
| LC | HC | 900 (28 August) | Ribble middle rainfall | (III) | |
| 42800 | HC | HC | 4800 (24 June) | Intense rainfall and strong Wind | (III) & (I) |
| HC | HC | 3200 (6 August) | Small radiation | (III) | |
| 43000 | HC | HC | 3200 (6 August) | High tide | (III) |
| HC | HC | 1400 (16 August) | Local middle rainfall | (I) |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kay, D.; Edwards, A.C.; Ferrier, R.; Francis, C.; Kay, C.; Rushby, L.; Watkins, J.; McDonald, A.T.; Wyer, M.; Crowther, J. Catchment Microbial Dynamics: The Emergence of a Research Agenda. Prog. Phys. Geogr. 2007, 31, 59–76. [Google Scholar]
- Figueras, M.; Borrego, J.J. New perspectives in monitoring drinking water microbial quality. Int. J. Environ. Res. Public Health 2010, 7, 4179–4202. [Google Scholar]
- European Environment Agency (EEA). European Bathing Water Quality in 2013; European Environment Agency (EEA) Report No 1/2014; EEA: Copenhagen, Denmark, 2014; pp. 1–32. [Google Scholar]
- Pompepuy, M.; Catherine, M.; Le Saux, J.C.; Joanny, M.; Camus, P. Impacts of Microbiological Contamination on the Marine Environment of the North-East Atlantic; OSPAR Commission: London, UK, 2009; pp. 1–23. [Google Scholar]
- European Union (EU). Directive 2006/7/EC of the European Parliament and of the Council of 15 February 2006 Concerning the Management of Bathing Water Quality and Repealing Directive 76/160/EE. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:32006L0007 (accessed on 31 August 2015).
- Stapleton, C.M.; Wyer, M.D.; Crowther, J.; McDonald, A.T.; Kay, D.; Greaves, J.; Wither, A.; Watkins, J.; Francis, C.; Humphrey, N.; et al. Quantitative catchment profiling to apportion faecal indicator organism budgets for the Ribble system, the UK’s sentinel drainage basin for Water Framework Directive research. J. Environ. Manag. 2008, 87, 535–550. [Google Scholar]
- Kay, D.; Crowther, J.; Stapleton, C.M.; Wyer, M.D.; Fewtrell, L.; Anthony, S.; Bradford, M.; Edwards, A.; Francis, C.A.; Hopkins, M.; et al. Faecal indicator organism concentrations and catchment export coefficients in the UK. Water Res. 2008, 42, 2649–2661. [Google Scholar]
- Lin, B.; Syed, M.; Falconer, R.A. Predicting faecal indicator levels in estuarine receiving waters—An integrated hydrodynamic and ANN modelling approach. Environ. Model. Softw. 2008, 23, 729–740. [Google Scholar]
- Kashefipour, S.M.; Lin, B.; Falconer, R.A. Modelling the fate of faecal indicators in a coastal basin. Water Res. 2006, 40, 1413–1425. [Google Scholar] [CrossRef] [PubMed]
- De Brauwere, A.; Gourgue, O.; de Brye, B.; Servais, P.; Ouattara, N.K.; Deleersnijder, E. Integrated modelling of faecal contamination in a densely populated river–sea continuum (Scheldt River and Estuary). Sci. Total Environ. 2014, 468–469, 31–45. [Google Scholar] [CrossRef] [PubMed]
- Tetzlaff, D.; Capell, R.; Soulsby, C. Land use and hydroclimatic influences on Faecal Indicator Organisms in two large Scottish catchments: Towards land use-based models as screening tools. Sci. Total Environ. 2012, 434, 110–122. [Google Scholar]
- Solvi, A.-M. Modelling the Sewer-Treatment-Urban River System in View of the EU Water Framework Directive. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2007. [Google Scholar]
- Benham, B.; Baffaut, C.; Zeckoski, R.; Mankin, K.; Pachepsky, Y.; Sadeghi, A.; Brannan, K.; Soupir, M.; Habersack, M. Modeling bacteria fate and transport in watersheds to support TMDLs. Trans. ASAE 2006, 49, 987–1002. [Google Scholar]
- Crane, B.S.; Moore, J. Modeling enteric bacterial die-off: A review. Water Air Soil Pollut. 1986, 27, 411–439. [Google Scholar]
- Medema, G.; Bahar, M.; Schets, F. Survival of Cryptosporidium parvum, Escherichia coli, faecal enterococci and Clostridium perfringens in river water: Influence of temperature and autochthonous microorganisms. Water Sci. Technol. 1997, 35, 249–252. [Google Scholar]
- Thupaki, P.; Phanikumar, M.S.; Schwab, D.J.; Nevers, M.B.; Whitman, R.L. Evaluating the role of sediment-bacteria interactions on Escherichia coli concentrations at beaches in southern Lake Michigan. J. Geophys. Res.: Oceans 2013, 118, 7049–7065. [Google Scholar]
- Gao, G.; Falconer, R.A.; Lin, B. Modelling importance of sediment effects on fate and transport of enterococci in the Severn Estuary, UK. Mar. Pollut. Bull. 2013, 67, 45–54. [Google Scholar]
- Bai, S.; Lung, W.-S. Modeling Sediment Impact on the Transport of Fecal Bacteria. Water Res. 2005, 39, 5232–5240. [Google Scholar]
- American Society of Agricultural Engineers (ASAE). American Society of Agricultural Engineers (ASAE) Standards D384.1: Manure Production and Characteristics; ASAE: St Joseph, MI, USA, 1998. [Google Scholar]
- Coffey, R.; Cummins, E.; Bhreathnach, N.; Flaherty, V.O.; Cormican, M. Development of a pathogen transport model for Irish catchments using SWAT. Agric. Water Manag. 2010, 97, 101–111. [Google Scholar]
- USEPA. Bacterial Indicator Tool User’s Guide; EPA-832-B-01-003; USEPA: Washington, DC, USA, 2000.
- Zeckoski, R.; Benham, B.; Shah, S.; Wolfe, M.; Brannan, K.; Al-Smadi, M.; Dillaha, T.; Mostaghimi, S.; Heatwole, C. BSLC: A tool for bacteria source characterization for watershed management. Appl. Eng. Agric. 2005, 21, 879–892. [Google Scholar]
- Faust, M.A. Relationship between land-use practices and fecal bacteria in soils. J. Environ. Qual. 1982, 11, 141–146. [Google Scholar]
- Hutchison, M.; Walters, L.; Moore, A.; Crookes, K.; Avery, S. Effect of length of time before incorporation on survival of pathogenic bacteria present in livestock wastes applied to agricultural soil. Appl. Environ. Microbiol. 2004, 70, 5111–5118. [Google Scholar]
- Vadas, P.; Kleinman, P.; Sharpley, A. A simple method to predict dissolved phosphorus in runoff from surface-applied manures. J. Environ. Qual. 2004, 33, 749–756. [Google Scholar]
- Chick, H. An investigation of the laws of disinfection. J. Hyg. 1908, 8, 92–158. [Google Scholar]
- Brookes, J.D.; Antenucci, J.; Hipsey, M.; Burch, M.D.; Ashbolt, N.J.; Ferguson, C. Fate and transport of pathogens in lakes and reservoirs. Environ. Int. 2004, 30, 741–759. [Google Scholar]
- Cho, K.H.; Pachepsky, Y.A.; Kim, J.H.; Kim, J.-W.; Park, M.-H. The modified SWAT model for predicting fecal coliforms in the Wachusett Reservoir Watershed, USA. Water Res. 2012, 46, 4750–4760. [Google Scholar]
- Reddy, K.; Khaleel, R.; Overcash, M. Behavior and transport of microbial pathogens and indicator organisms in soils treated with organic wastes. J. Environ. Qual. 1981, 10, 255–266. [Google Scholar]
- Gerba, C.P.; Melnick, J.L.; Wallis, C. Fate of wastewater bacteria and viruses in soil. J. Irrig. Drain. Div. 1975, 101, 157–174. [Google Scholar]
- Tian, Y.Q.; Gong, P.; Radke, J.D.; Scarborough, J. Spatial and temporal modeling of microbial contaminants on grazing farmlands. J. Environ. Qual. 2002, 31, 860–869. [Google Scholar]
- Nagels, J.; Davies-Colley, R.; Donnison, A.; Muirhead, R. Faecal contamination over flood events in a pastoral agricultural stream in New Zealand. Water Sci. Technol. 2002, 45, 45–52. [Google Scholar]
- Muirhead, R.W.; Davies-Colley, R.J.; Donnison, A.M.; Nagels, J.W. Faecal bacteria yields in artificial flood events: Quantifying in-stream stores. Water Res. 2004, 38, 1215–1224. [Google Scholar]
- Wheeler Alm, E.; Burke, J.; Spain, A. Fecal indicator bacteria are abundant in wet sand at freshwater beaches. 2003, 37, 3978–3982. [Google Scholar] [CrossRef]
- Passerat, J.; Ouattara, N.K.; Mouchel, J.-M.; Vincent, R.; Servais, P. Impact of an intense combined sewer overflow event on the microbiological water quality of the Seine River. Water Res. 2011, 45, 893–903. [Google Scholar]
- Even, S.; Mouchel, J.-M.; Servais, P.; Flipo, N.; Poulin, M.; Blanc, S.; Chabanel, M.; Paffoni, C. Modelling the impacts of Combined Sewer Overflows on the river Seine water quality. Sci. Total Environ. 2007, 375, 140–151. [Google Scholar]
- Chapra, S. Surface Water-Quality Modeling; WCB McGraw-Hill: Boston, MA, USA, 1997. [Google Scholar]
- Ling, T.; Achberger, E.; Drapcho, C.; Bengtson, R. Quantifying adsorption of an indicator bacteria in a soil-water system. Trans. Asae 2002, 45, 669–674. [Google Scholar]
- Chin, D.; Sakura-Lemessy, D.; Bosch, D.; Gay, P. Watershed-scale fate and transport of bacteria. Trans. ASABE 2009, 52, 145–154. [Google Scholar]
- Kay, D.; Wyer, M.; Crowther, J.; Stapleton, C.; Bradford, M.; McDonald, A.; Greaves, J.; Francis, C.; Watkins, J. Predicting faecal indicator fluxes using digital land use data in the UK’s sentinel Water Framework Directive catchment: The Ribble study. Water Res. 2005, 39, 3967–3981. [Google Scholar]
- Servais, P.; Garcia-Armisen, T.; George, I.; Billen, G. Fecal bacteria in the rivers of the Seine drainage network (France): Sources, fate and modelling. Sci. Total Environ. 2007, 375, 152–167. [Google Scholar]
- Borah, D.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. Trans. ASAE 2003, 46, 1553–1566. [Google Scholar]
- Papanicolaou, A.; Bdour, A.; Wicklein, E. One-dimensional hydrodynamic sediment transport model applicable to steep mountain streams. J. Hydraul. Res. 2004, 42, 357–375. [Google Scholar]
- Papanicolaou, A.N.; Sanford, J.T.; Dermisis, D.C.; Mancilla, G.A. A 1-D Morphodynamic Model for Rill Erosion. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. Simulation of rapidly varying flow using an efficient TVD-MacCormack scheme. Int. J. Numer. Methods Fluids 2007, 53, 811–826. [Google Scholar]
- Garcia-Navarro, P.; Alcrudo, F.; Saviron, J. 1-D open-channel flow simulation using TVD-McCormack scheme. J. Hydraul. Eng. 1992, 118, 1359–1372. [Google Scholar]
- Ji, Z. General hydrodynamic model for sewer/channel network systems. J. Hydraul. Eng. 1998, 124, 307–315. [Google Scholar]
- Garcia-Navarro, P.; Alcrudo, F.; Priestley, A. An implicit method for water flow modelling in channels and pipes. J. Hydraul. Res. 1994, 32, 721–742. [Google Scholar]
- Djordjevic, S.; Prodanovic, D.; Walters, G.A. Simulation of transcritical flow in pipe/channel networks. J. Hydraul. Eng. 2004, 130, 1167–1178. [Google Scholar]
- Kashefipour, S.M.; Lin, B.; Harris, E.; Falconer, R.A. Hydro-Environmental Modelling for Bathing Water Compliance of an Estuarine Basin. Water Res. 2002, 36, 1854–1868. [Google Scholar]
- De Brauwere, A.; de Brye, B.; Servais, P.; Passerat, J.; Deleersnijder, E. Modelling Escherichia coli concentrations in the tidal Scheldt river and estuary. Water Res. 2011, 45, 2724–2738. [Google Scholar] [CrossRef] [PubMed]
- Bedri, Z.; Corkery, A.; O’Sullivan, J.J.; Alvarez, M.X.; Erichsen, A.C.; Deering, L.A.; Demeter, K.; O’Hare, G.M.; Meijer, W.G.; Masterson, B. An integrated catchment-coastal modelling system for real-time water quality forecasts. Environ. Model. Softw. 2014, 61, 458–476. [Google Scholar]
- Shrestha, N.K.; Leta, O.T.; de Fraine, B.; van Griensven, A.; Bauwens, W. OpenMI-based integrated sediment transport modelling of the river Zenne, Belgium. Environ. Model. Softw. 2013, 47, 193–206. [Google Scholar]
- Amaguchi, H.; Kawamura, A.; Olsson, J.; Takasaki, T. Development and testing of a distributed urban storm runoff event model with a vector-based catchment delineation. J. Hydrol. 2012, 420–421, 205–215. [Google Scholar] [CrossRef]
- Zhao, R. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Lu, M.; Li, X. Time scale dependent sensitivities of the XinAnJiang model parameters. Hydrol. Res. Lett. 2014, 8, 51–56. [Google Scholar]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Visi. Graph. Image Process. 1984, 28, 323–344. [Google Scholar]
- Alam, M.J.; Dutta, D. A process-based and distributed model for nutrient dynamics in river basin: Development, testing and applications. Ecol. Model. 2012, 247, 112–124. [Google Scholar]
- Wu, W. Computational River Dynamics; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Jamieson, R.; Gordon, R.; Joy, D.; Lee, H. Assessing microbial pollution of rural surface waters: A review of current watershed scale modeling approaches. Agric. Water Manag. 2004, 70, 1–17. [Google Scholar]
- Pachepsky, Y.A.; Sadeghi, A.; Bradford, S.; Shelton, D.; Guber, A.; Dao, T. Transport and fate of manure-borne pathogens: Modeling perspective. Agric. Water Manag. 2006, 86, 81–92. [Google Scholar]
- Meselhe, E.A.; Holly, F.M., Jr. Simulation of Unsteady Flow in Irrigation Canals with Dry Bed. J. Hydraul. Eng. 1993, 119, 1021–1039. [Google Scholar]
- Hamrick, J.M. A Three-Dimensional Environmental Fluid Dynamics Computer Code: Theoretical and Computational Aspects; Virginia Institute of Marine Science, College of William and Mary: Gloucester Point, VA, USA, 1992. [Google Scholar]
- Huang, G.; Falconer, R.A.; Boye, B.A.; Lin, B. Cloud to coast: Integrated assessment of environmental exposure, health impacts and risk perceptions of faecal organisms in coastal waters. Int. J. River Basin Manag. 2015, 13, 73–86. [Google Scholar]
- Nachtergaele, F.; van Velthuizen, H.; Verelst, L.; Batjes, N.; Dijkshoorn, K.; van Engelen, V.; Fischer, G.; Jones, A.; Montanarella, L.; Petri, M. Harmonized World Soil Database; Food and Agriculture Organization of the United Nations: Rome, Italy, 2008. [Google Scholar]
- The British Atmospheric Date Centre. Available online: http://badc.nerc.ac.uk/home/ (accessed on 31 August 2015).
- Center for Ecology and Hydrology. Available online: http://www.ceh.ac.uk/data/nrfa/data/search.html (accessed on 31 August 2015).
- Morris, D.; Flavin, R. Sub-set of the UK 50 m by 50 m Hydrological Digital Terrain Model Grids; NERC, Institute of Hydrology: Wallingford, UK, 1994. [Google Scholar]
- Moore, R.; Morris, D.; Flavin, R. Sub-set of UK Digital 1: 50,000 Scale River Centre-Line Network; NERC, Institute of Hydrology: Wallingford, UK, 1994. [Google Scholar]
- British Geological Survey. Available online: http://www.bgs.ac.uk/products/offshore/DigSBS250.html (accessed on 31 August 2015).
- Pye, K.; Blott, S.J.; Witton, S.J.; Pye, A.L. Cell 11 Regional Monitoring Strategy Results of Sediment Particle Size Analysis; Report (Kenneth Pye Associates Ltd.); Kenneth Pye Associates Ltd.: Solihull, UK, 2010; p. 1. [Google Scholar]
- Digimap Home Page. Available online: http://digimap.edina.ac.uk/digimap/home (accessed on 31 August 2015).
- Weather and Climate Met Office. Available online: http://www.metoffice.gov.uk/ (accessed on 31 August 2015).
- Office for National Statistics. Available online: http://www.ons.gov.uk/ons/index.html (accessed on 31 August 2015).
- Welcome to GOV.UK. Available online: https://www.gov.uk (accessed on 31 August 2015).
- Bathing Water Quality. Available online: http://environment.data.gov.uk/bwq/profiles/ (accessed on 31 August 2015).
- Frey, S.K.; Topp, E.; Edge, T.; Fall, C.; Gannon, V.; Jokinen, C.; Marti, R.; Neumann, N.; Ruecker, N.; Wilkes, G.; Lapen, D.R. Using SWAT, Bacteroidales microbial source tracking markers, and fecal indicator bacteria to predict waterborne pathogen occurrence in an agricultural watershed. Water Res. 2013, 47, 6326–6337. [Google Scholar]
- Kim, J.-W.; Pachepsky, Y.A.; Shelton, D.R.; Coppock, C. Effect of streambed bacteria release on E. coli concentrations: Monitoring and modeling with the modified SWAT. Ecol. Model. 2010, 221, 1592–1604. [Google Scholar]
- Ouattara, N.K.; de Brauwere, A.; Billen, G.; Servais, P. Modelling faecal contamination in the Scheldt drainage network. J. Mar. Syst. 2013, 128, 77–88. [Google Scholar]
- Whitman, R.L.; Nevers, M.B. Summer E. coli patterns and responses along 23 Chicago beaches. Environ. Sci. Technol. 2008, 42, 9217–9224. [Google Scholar]
- De Marchis, M.; Freni, G.; Napoli, E. Modelling of E. coli distribution in coastal areas subjected to combined sewer overflows. Water Sci. Technol. 2013, 68, 1123–1136. [Google Scholar] [CrossRef] [PubMed]
- Davies, C.M.; Long, J.; Donald, M.; Ashbolt, N.J. Survival of fecal microorganisms in marine and freshwater sediments. Appl. Environ. Microbiol. 1995, 61, 1888–1896. [Google Scholar] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, G.; Falconer, R.A.; Lin, B. Integrated River and Coastal Flow, Sediment and Escherichia coli Modelling for Bathing Water Quality. Water 2015, 7, 4752-4777. https://doi.org/10.3390/w7094752
Huang G, Falconer RA, Lin B. Integrated River and Coastal Flow, Sediment and Escherichia coli Modelling for Bathing Water Quality. Water. 2015; 7(9):4752-4777. https://doi.org/10.3390/w7094752
Chicago/Turabian StyleHuang, Guoxian, Roger A. Falconer, and Binliang Lin. 2015. "Integrated River and Coastal Flow, Sediment and Escherichia coli Modelling for Bathing Water Quality" Water 7, no. 9: 4752-4777. https://doi.org/10.3390/w7094752
APA StyleHuang, G., Falconer, R. A., & Lin, B. (2015). Integrated River and Coastal Flow, Sediment and Escherichia coli Modelling for Bathing Water Quality. Water, 7(9), 4752-4777. https://doi.org/10.3390/w7094752