Model Spin-Up Behavior for Wet and Dry Basins: A Case Study Using the Xinanjiang Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
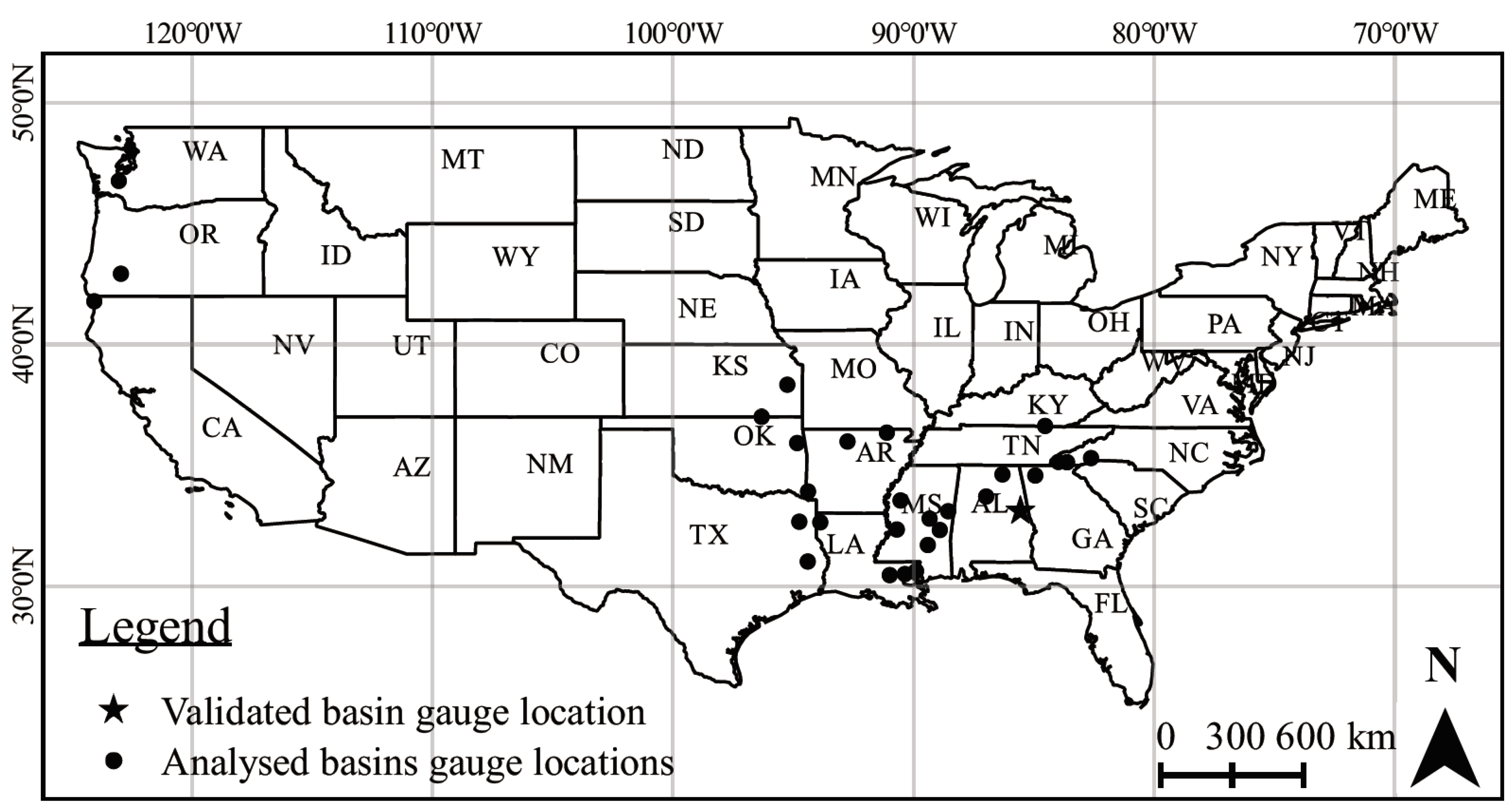
2.2. Data
| MOPEX ID | Location | Average Precipitation (mm/year) | Average Potential Evaporation (mm/year) | Average Snow-Days (day/year) | Average Total New Snow (mm/year) | Average Soil Moisture Saturation (%) | ||
|---|---|---|---|---|---|---|---|---|
| Longitude | Latitude | State | ||||||
| 11532500 | −124.05 | 41.79 | CA | 2687 | 740 | 0.00 | 0 | 82 |
| 12027500 | −123.03 | 46.78 | WA | 1599 | 579 | 3.00 | 127 | 75 |
| 03550000 | −83.98 | 35.14 | NC | 1846 | 771 | 3.90 | 193 | 75 |
| 03504000 | −83.62 | 35.13 | NC | 1893 | 762 | 3.90 | 193 | 90 |
| 03410500 | −84.53 | 36.63 | TN | 1389 | 817 | 6.20 | 160 | 74 |
| 02387500 | −84.94 | 34.58 | GA | 1480 | 901 | 0.70 | 18 | 73 |
| 03574500 | −86.31 | 34.62 | AL | 1467 | 941 | 0.80 | 41 | 74 |
| 14308000 | −122.95 | 42.93 | OR | 1347 | 805 | 2.20 | 76 | 62 |
| 07378500 | −90.99 | 30.46 | LA-MS | 1594 | 1077 | 0.60 | 23 | 63 |
| 07375500 | −90.36 | 30.51 | LA-MS | 1633 | 1074 | 0.60 | 23 | 64 |
| 02492000 | −89.90 | 30.63 | LA-MS | 1583 | 1071 | 0.60 | 23 | 47 |
| 02456500 | −86.98 | 33.71 | AL | 1425 | 982 | 0.80 | 41 | 66 |
| 02414500 * | −85.56 | 33.12 | AL | 1370 | 975 | 0.80 | 41 | 65 |
| 02472000 | −89.41 | 31.71 | MS | 1492 | 1060 | 0.60 | 23 | 64 |
| 02448000 | −88.56 | 33.10 | MS | 1421 | 1057 | 0.60 | 23 | 72 |
| 07290000 | −90.70 | 32.35 | MS | 1435 | 1073 | 0.60 | 23 | 57 |
| 07056000 | −92.75 | 35.98 | AR | 1180 | 916 | 3.80 | 132 | 68 |
| 07288500 | −90.54 | 33.55 | MS | 1381 | 1112 | 0.60 | 23 | 62 |
| 07340000 | −94.39 | 33.92 | OK | 1329 | 1156 | 5.60 | 198 | 70 |
| 07072000 | −91.11 | 36.35 | AR | 1114 | 964 | 3.80 | 132 | 62 |
| 07348000 | −93.88 | 32.65 | LA | 1173 | 1223 | 0.10 | 0 | 47 |
| 07346050 | −94.75 | 32.67 | TX | 1128 | 1246 | 1.3 | 4 | 53 |
| 06914000 | −95.25 | 38.33 | KS | 957 | 1206 | 10.00 | 373 | 61 |
2.3. Xinanjiang Model Parameters, Calibration and Validation
| Parameter | Physical Meaning | Range |
|---|---|---|
| Cp | Ratio of measured precipitation to actual precipitation | 0.8–1.2 |
| Cep | Ratio of potential evaporation to pan evaporation | 0–2.0 |
| b | Exponent of the tension water capacity curve | 0.1–0.3 |
| imp | Ratio of the impervious to the total area of the basin | 0–0.005 |
| WUM | Water capacity in the upper soil layer (mm) | 5–20 |
| WLM | Water capacity in the lower soil layer (mm) | 60–90 |
| WDM | Water capacity in the deeper soil layer (mm) | 10–100 |
| C | Coefficient of deep evaporation | 0.1–0.3 |
| SM | Areal mean free water capacity of the surface soil layer (mm) | 1–50 |
| EX | Exponent of the free water capacity curve | 0.5–2.5 |
| KI | Outflow coefficient of the free water storage to interflow | 0–0.7; KI + KG = 0.7 |
| KG | Outflow coefficient of the free water storage to groundwater | 0–0.7; KI + KG = 0.7 |
| cs | Recession constant for channel routing | 0.5–0.9 |
| ci | Recession constant for the lower interflow storage | 0.5–0.9 |
| cg | Daily recession constant of groundwater storage | 0.9835–0.998 |
2.4. Recursive Simulation Design
2.4.1. Preparation of Input Files
2.4.2. Initial Conditions
| Initial Condition | Physical Meaning |
|---|---|
| Saturated | 100% of the field capacity |
| Intermediate | 50% of the field capacity |
| Dry | Zero soil moisture |
| Climatology | Mean climatology initial condition |
2.4.3. Model Calibration
2.5. Definition of Model Spin-Up Time
2.6. Reporting of Model Spin-Up Time
2.7. Calculation of Basin Aridity Index and Soil Moisture Memory
3. Results and Discussion
3.1. Hydrograph, SMM Timescale and Aridity Index
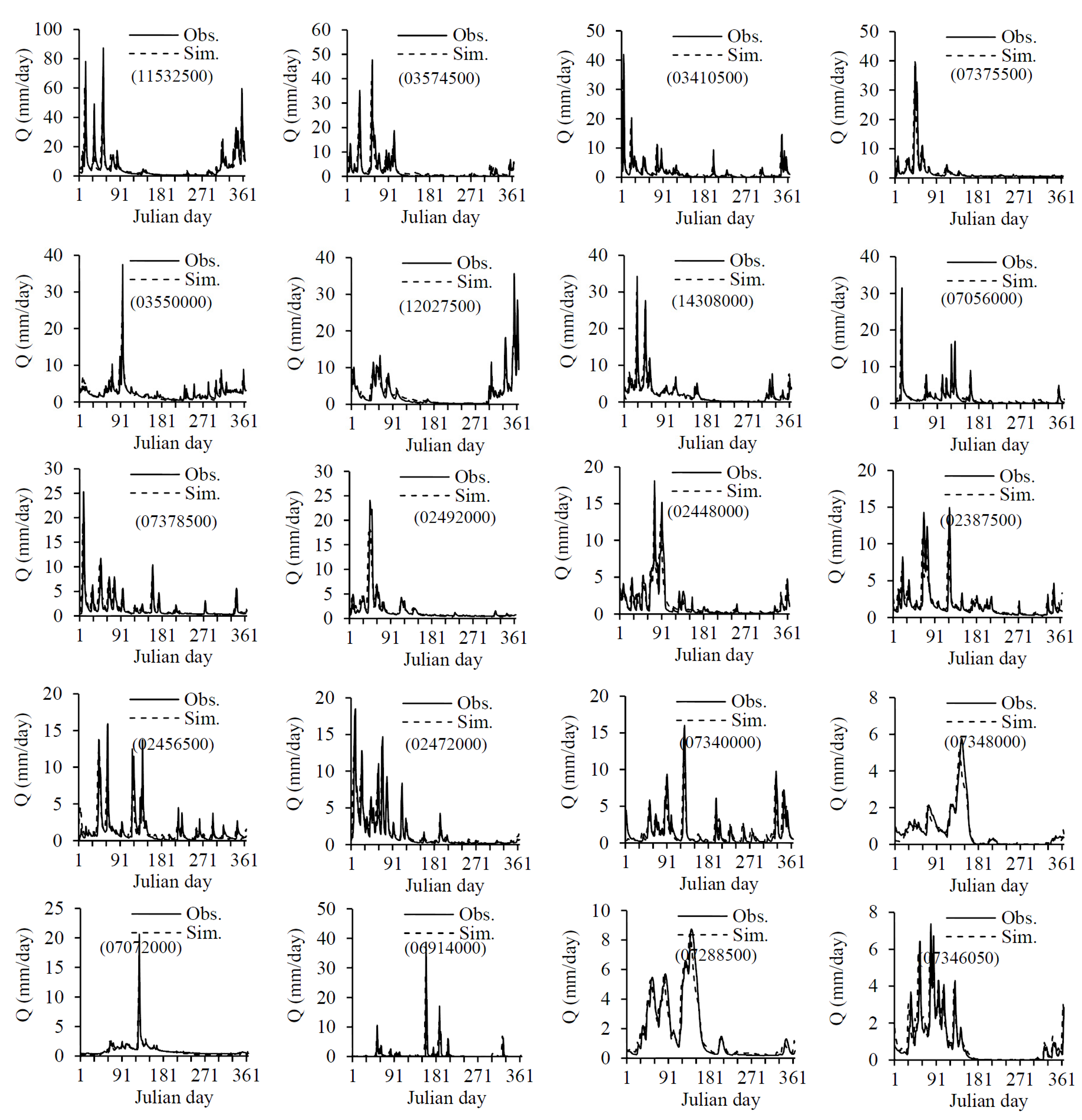
3.2. XAJ Model Spin-Up Time and SMM Timescale
| MOPEX ID | Area (sq.km) | Daily NASH | Aridity Index (ζ) | τSMM (day) | τXsp (day) |
|---|---|---|---|---|---|
| 11532500 | 1577 | 0.70–0.75 | 0.29 | 11 | 7 |
| 12027500 | 2318 | 0.71–0.73 | 0.39 | 16 | 3 |
| 03550000 | 269 | 0.58–0.72 | 0.40 | 16 | 2 |
| 03504000 | 135 | 0.70–0.77 | 0.40 | 16 | 9 |
| 03410500 | 2471 | 0.59–0.70 | 0.58 | 26 | 14 |
| 02387500 | 4144 | 0.67–0.72 | 0.61 | 28 | 18 |
| 03574500 | 829 | 0.72–0.82 | 0.64 | 30 | 23 |
| 14308000 | 1163 | 0.77–0.84 | 0.68 | 33 | 27 |
| 07378500 | 3315 | 0.43–0.61 | 0.70 | 35 | 43 |
| 07375500 | 1673 | 0.75–0.85 | 0.71 | 35 | 40 |
| 02492000 | 3142 | 0.77–0.82 | 0.71 | 36 | 24 |
| 02456500 | 2292 | 0.65–0.70 | 0.72 | 36 | 43 |
| 02414500 * | 2696 | 0.79 | 0.73 | 37 | 55 |
| 02472000 | 1924 | 0.48–0.79 | 0.76 | 39 | 40 |
| 02448000 | 1989 | 0.43–0.83 | 0.80 | 42 | 73 |
| 07290000 | 7283 | 0.54–0.61 | 0.80 | 43 | 131 |
| 07056000 | 2147 | 0.64–0.81 | 0.81 | 43 | 65 |
| 07288500 | 1987 | 0.75–0.84 | 0.86 | 48 | 68 |
| 07340000 | 6895 | 0.58–0.61 | 0.88 | 50 | 342 |
| 07072000 | 1134 | 0.61–0.87 | 0.90 | 52 | 192 |
| 07348000 | 8125 | 0.46–0.71 | 1.09 | 72 | 134 |
| 07346050 | 383 | 0.55–0.74 | 1.15 | 79 | 211 |
| 06914000 | 865 | 0.43–0.69 | 1.34 | 108 | 655 |
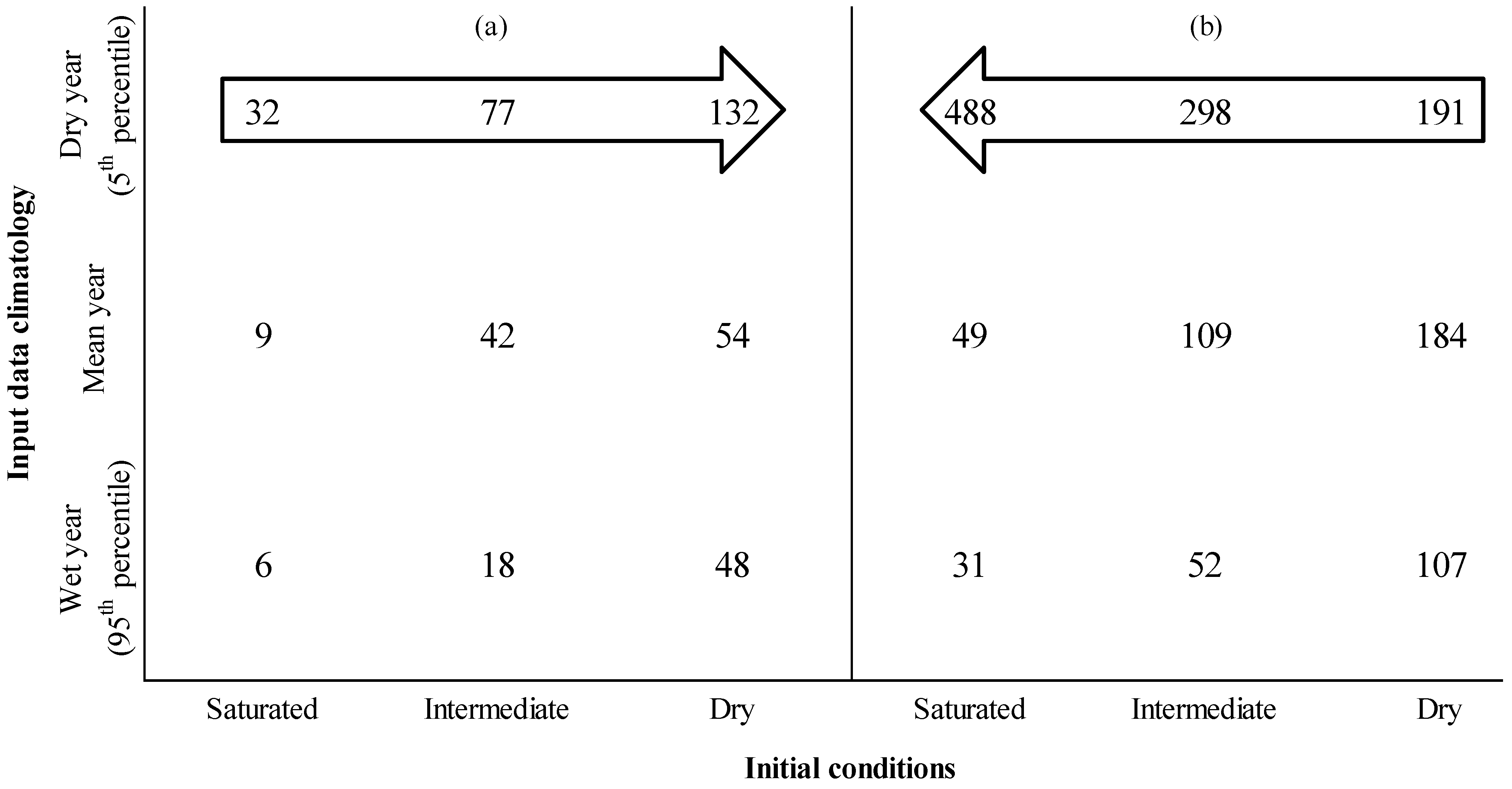
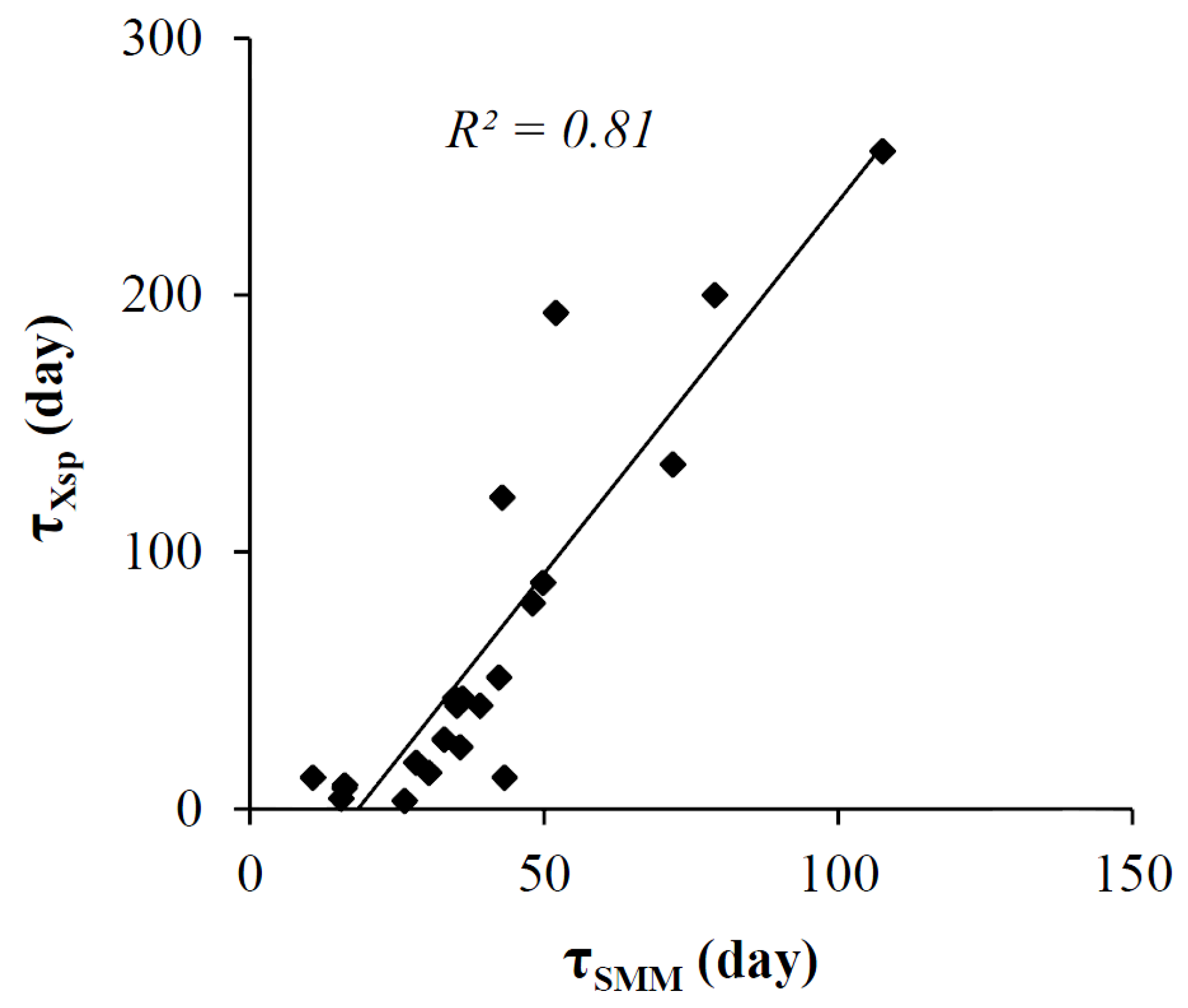
3.3. Predictability of XAJ Model Spin-Up Time from Basin Aridity Index
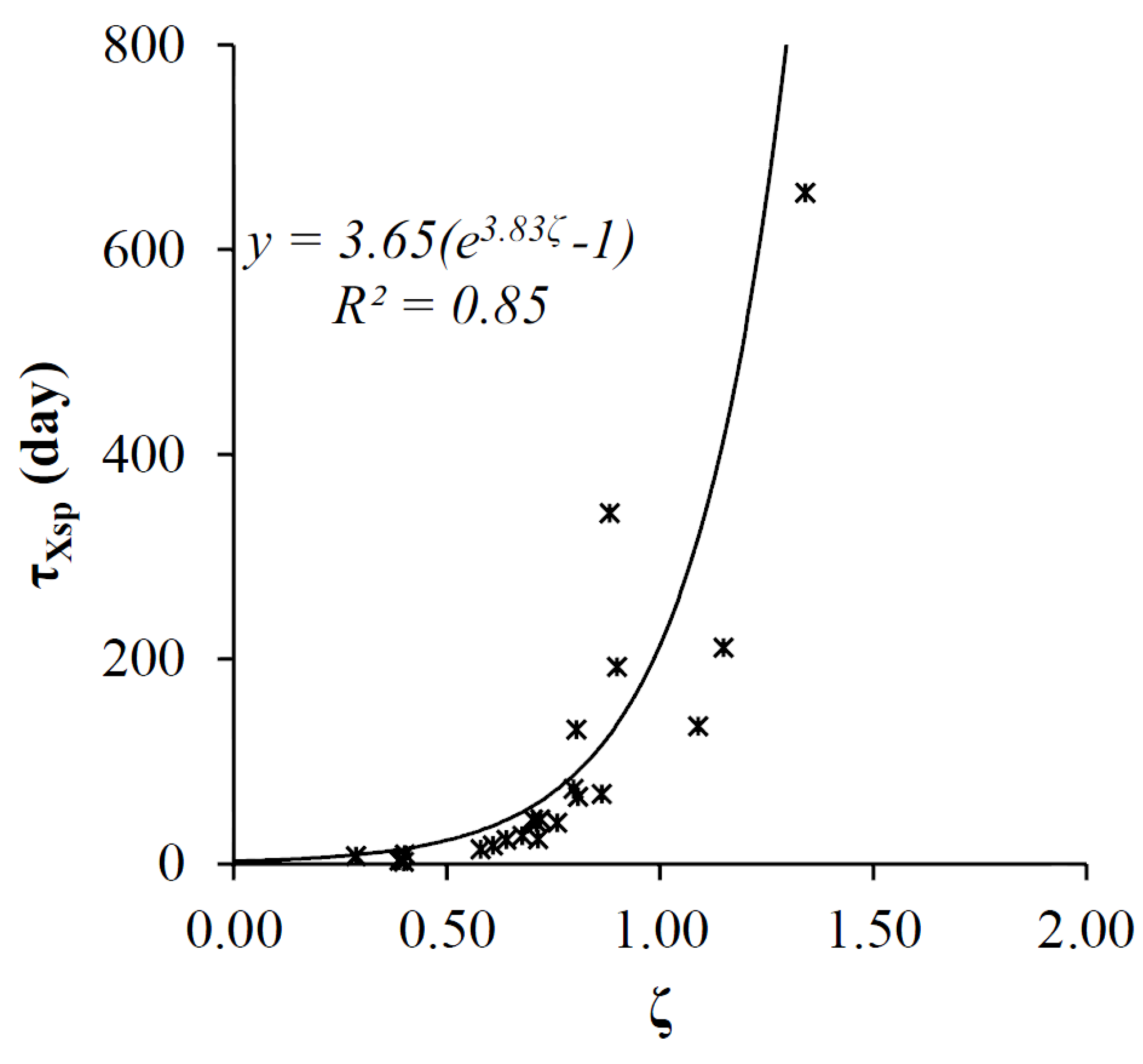
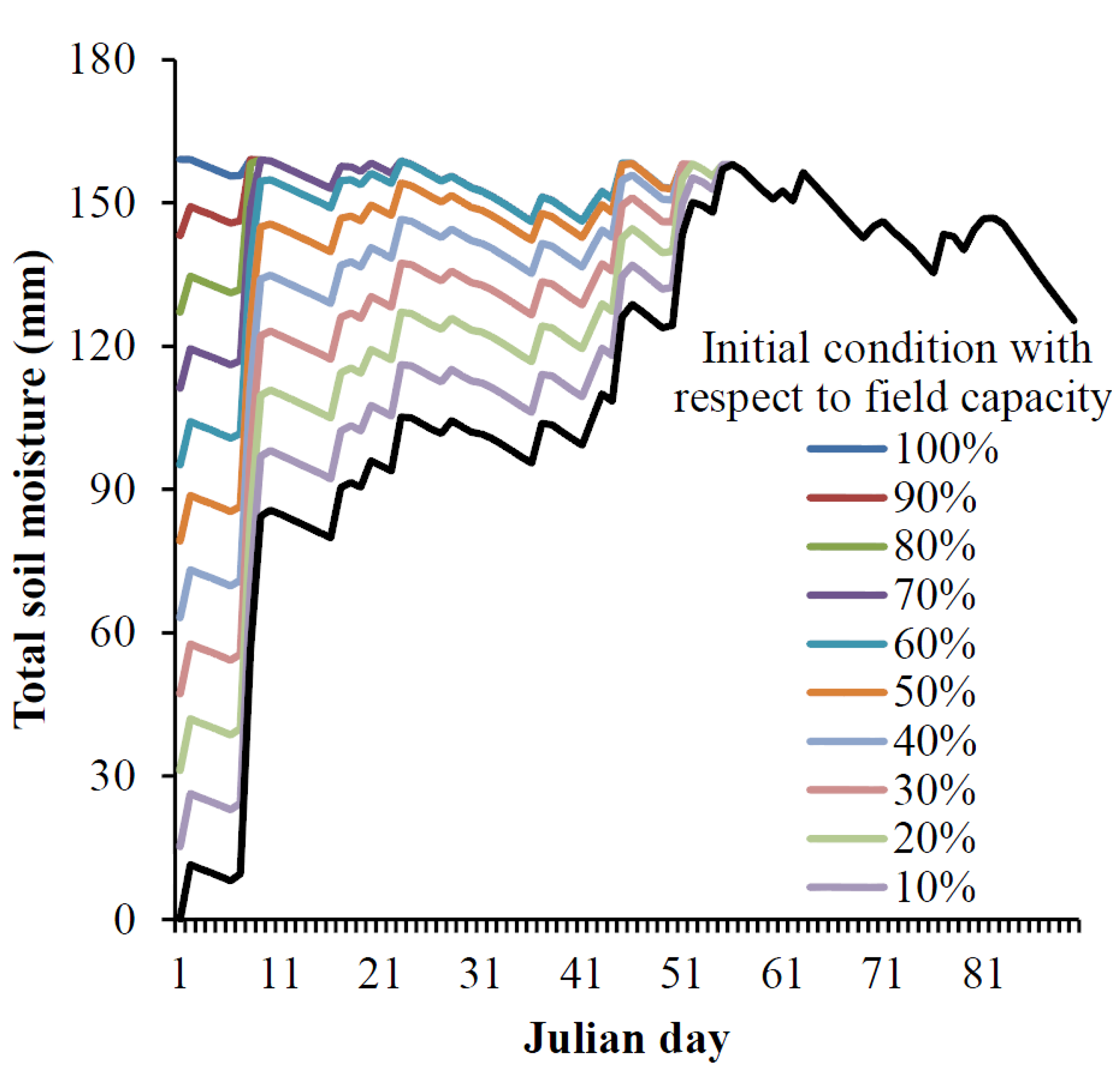
4. Conclusions
References
- Berthet, L.; Andréassian, V.; Perrin, C.; Javelle, P. How crucial is it to account for the antecedent moisture conditions in flood forecasting? Comparison of event-based and continuous approaches on 178 catchments. Hydrol. Earth Syst. Sci. 2009, 13, 819–831. [Google Scholar] [CrossRef]
- Castillo, V.; Gomez-Plaza, A.; Martinez-Mena, M. The role of antecedent soil water content in the runoff response of semiarid catchments: A simulation approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Goodrich, D.; Schmugge, T.; Jackson, T.; Unkrich, C.; Keefer, T.; Parry, R.; Bach, L.; Amer, S. Runoff simulation sensitivity to remotely sensed initial soil water content. Water Resour. Res. 1994, 30, 1393–1405. [Google Scholar] [CrossRef]
- Minet, J.; Laloy, E.; Lambot, S.; Vanclooster, M. Effect of high-resolution spatial soil moisture variability on simulated runoff response using a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2011, 15, 1323–1338. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M.; Vivoni, E.R.; Papadopoulos, A. Sensitivity of a mountain basin flash flood to initial wetness condition and rainfall variability. J. Hydrol. 2011, 402, 165–178. [Google Scholar] [CrossRef]
- Senarath, S.U.; Ogden, F.L.; Downer, C.W.; Sharif, H.O. On the calibration and verification of two-dimensional, distributed, Hortonian, continuous watershed models. Water Resour. Res. 2000, 36, 1495–1510. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, H.; Nearing, M. Effects of antecedent soil moisture on runoff modeling in small semiarid watersheds of southeastern Arizona. Hydrol. Earth Syst. Sci. 2011, 15, 3171–3179. [Google Scholar] [CrossRef]
- Yang, Z.L.; Dickinson, R.; Henderson-Sellers, A.; Pitman, A. Preliminary study of spin-up processes in land surface models with the first stage data of Project for Intercomparison of Land Surface Parameterization Schemes Phase 1 (a). J. Geophys. Res. Atmos. 1995, 100, 16553–16578. [Google Scholar] [CrossRef]
- De Goncalves, L.; Shuttleworth, W.J.; Burke, E.J.; Houser, P.; Toll, D.L.; Rodell, M.; Arsenault, K. Toward a South America Land Data Assimilation System: Aspects of land surface model spin-up using the Simplified Simple Biosphere. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K. Using the GEWEX/ISLSCP forcing data to simulate global soil moisture fields and hydrological cycle for 1987–1988. J. Meteorol. Soc. Japan 1999, 77, 167–182. [Google Scholar]
- Cosgrove, B.A.; Lohmann, D.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. Land surface model spin-up behaviour in the North American Land Data Assimilation System (NLDAS). J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Berg, A.; Famiglietti, J. Evaluation of 10 methods for initializing a land surface model. J. Hydrometeorol. 2005, 6, 146–155. [Google Scholar] [CrossRef]
- Seck, A.; Welty, C.; Maxwell, R.M. Spin-up behavior and effects of initial conditions for an integrated hydrologic model. Water Resour. Res. 2015, 15. [Google Scholar] [CrossRef]
- Ajami, H.; McCabe, M.F.; Evans, J.P.; Stisen, S. Assessing the impact of model spin-up on surface water-groundwater interactions using an integrated hydrologic model. Water Resour. Res. 2014, 50, 2636–2656. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lu, M.; Kyi, K.H. Variability of soil moisture memory for wet and dry basins. J. Hydrol. 2015, 523, 107–118. [Google Scholar] [CrossRef]
- Ajami, H.; Evans, J.; McCabe, M.; Stisen, S. Technical Note: Reducing the spin-up time of integrated surface water-groundwater models. Hydrol. Earth Syst. Sci. Discuss. 2014, 18, 5169–5179. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.P.; Liang, X.; Lohmann, D.; Boone, A.; Chang, S.; Chen, F.; Dai, Y.; Dickinson, R.E.; Duan, Q.; et al. The project for Intercomparison of Land-surface Parameterization Schemes (PILPS) phase 2 (c) Red-Arkansas River basin experiment: 1. Experiment description and summary intercomparisons. Glob. Planet. Chang. 1998, 19, 115–135. [Google Scholar] [CrossRef]
- Lim, Y.J.; Hong, J.; Lee, T.Y. Spin-up behaviour of soil moisture content over East Asia in a land surface model. Meteorol. Atmos. Phys. 2012, 118, 151–161. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Lu, M.; Li, X. Time scale dependent sensitivities of the Xinanjiang model parameters. Hydrol. Res. Lett. 2014, 8, 51–56. [Google Scholar] [CrossRef]
- Lin, C.A.; Wen, L.; Lu, G.; Wu, Z.; Zhang, J.; Yang, Y.; Zhu, Y.; Tong, L. Atmospheric-hydrological modeling of severe precipitation and floods in the Huaihe River Basin, China. J. Hydrol. 2006, 330, 249–259. [Google Scholar] [CrossRef]
- Lu, G.; Wu, Z.; Wen, L.; Lin, C.A.; Zhang, J.; Yang, Y. Real-time flood forecast and flood alert map over the Huaihe River Basin in China using a coupled hydro-meteorological modeling system. Sci. China Ser. E Technol. Sci. 2008, 51, 1049–1063. [Google Scholar] [CrossRef]
- National Climate Data Center. Available online: http://www.ncdc.noaa.gov/oa/climate/normals/usnormals.html (accessed on 13 November 2013).
- Schaake, J.; Cong, S.; Duan, Q. The US MOPEX Data Set. Publication number 307; International Association of Hydrological Sciences Publication: Oxfordshire, UK, 2006. [Google Scholar]
- Model Parameter Estimation Experiment. Available online: ftp://hydrology.nws.noaa.gov/pub/gcip/mopex/US_Data/ (accessed on 19 October 2013).
- Li, X.; Lu, M. Application of aridity index in estimation of data adjustment parameters in the Xinanjiang model. Annu. J. Hydraul. Eng. JSCE 2014, 58, 163–168. [Google Scholar] [CrossRef]
- Kyi, K.H. Development of a User Friendly Web-Based Xinanjiang Model with Calibration Support System. Master Thesis, Department of Civil and Environmental Engineering, Nagaoka University of Technology, Nagaoka, Japan, 2014. [Google Scholar]
- Laboratory of Hydrology and Meteorology. Available online: http://lmj.nagaokaut.ac.jp/~khin/ (accessed on 13 January 2015).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part-I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Schlosser, C.A.; Slater, A.G.; Robock, A.; Pitman, A.J.; Vinnikov, K.Y.; Henderson-Sellers, A.; Speranskaya, N.A.; Mitchell, K. Simulations of a boreal grassland hydrology at Valdai, Russia: PILPS Phase 2 (d). Mon. Weather Rev. 2000, 128, 301–321. [Google Scholar] [CrossRef]
- Delworth, T.L.; Manabe, S. The influence of potential evaporations on the variabilities of simulated soil wetness and climate. J. Clim. 1988, 1, 523–547. [Google Scholar] [CrossRef]
- Simmonds, I.; Lynch, A.H. The influence of pre-existing soil moisture content on Australian winter climate. Int. J. Clim. 1992, 12, 33–54. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; McGuffie, K.; Pitman, A. The project for inter-comparison of land-surface parametrization schemes (PILPS): 1992 to 1995. Clim. Dyn. 1996, 12, 849–859. [Google Scholar] [CrossRef]
- Chen, T.H.; Henderson-Sellers, A.; Milly, P.; Pitman, A.; Beljaars, A.; Polcher, J.; Abramopoulos, F.; Boone, A.; Chang, S.; Chen, F.; et al. Cabauw experimental results from the project for inter-comparison of land-surface parameterization schemes. J. Clim. 1997, 10, 1194–1215. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. Soil moisture memory in climate models. J. Hydrometeorol. 2001, 2, 558–570. [Google Scholar] [CrossRef]
- Vinnikov, K.Y.; Robock, A.; Speranskaya, N.A.; Schlosser, C.A. Scales of temporal and spatial variability of midlatitude soil moisture. J. Geophys. Res. Atmos. 1996, 101, 7163–7174. [Google Scholar] [CrossRef]
- Entin, J.K.; Robock, A.; Vinnikov, K.Y.; Hollinger, S.E.; Liu, S.; Namkhai, A. Temporal and spatial scales of observed soil moisture variations in the extratropics. J. Geophys. Res. Atmos. 2000, 105, 11865–11877. [Google Scholar] [CrossRef]
- Wu, W.; Dickinson, R.E. Time Scales of Layered Soil Moisture Memory in the Context of Land-Atmosphere Interaction. J. Clim. 2004, 17, 2752–2764. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. Modeling the land surface boundary in climate models as a composite of independent vegetation stands. J. Geophys. Res. Atmos. 1992, 97, 2697–2715. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; Lu, M. Model Spin-Up Behavior for Wet and Dry Basins: A Case Study Using the Xinanjiang Model. Water 2015, 7, 4256-4273. https://doi.org/10.3390/w7084256
Rahman MM, Lu M. Model Spin-Up Behavior for Wet and Dry Basins: A Case Study Using the Xinanjiang Model. Water. 2015; 7(8):4256-4273. https://doi.org/10.3390/w7084256
Chicago/Turabian StyleRahman, Mohammad Mahfuzur, and Minjiao Lu. 2015. "Model Spin-Up Behavior for Wet and Dry Basins: A Case Study Using the Xinanjiang Model" Water 7, no. 8: 4256-4273. https://doi.org/10.3390/w7084256
APA StyleRahman, M. M., & Lu, M. (2015). Model Spin-Up Behavior for Wet and Dry Basins: A Case Study Using the Xinanjiang Model. Water, 7(8), 4256-4273. https://doi.org/10.3390/w7084256





