Uncertainty Estimation and Evaluation of Shallow Aquifers’ Exploitability: The Case Study of the Adige Valley Aquifer (Italy)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
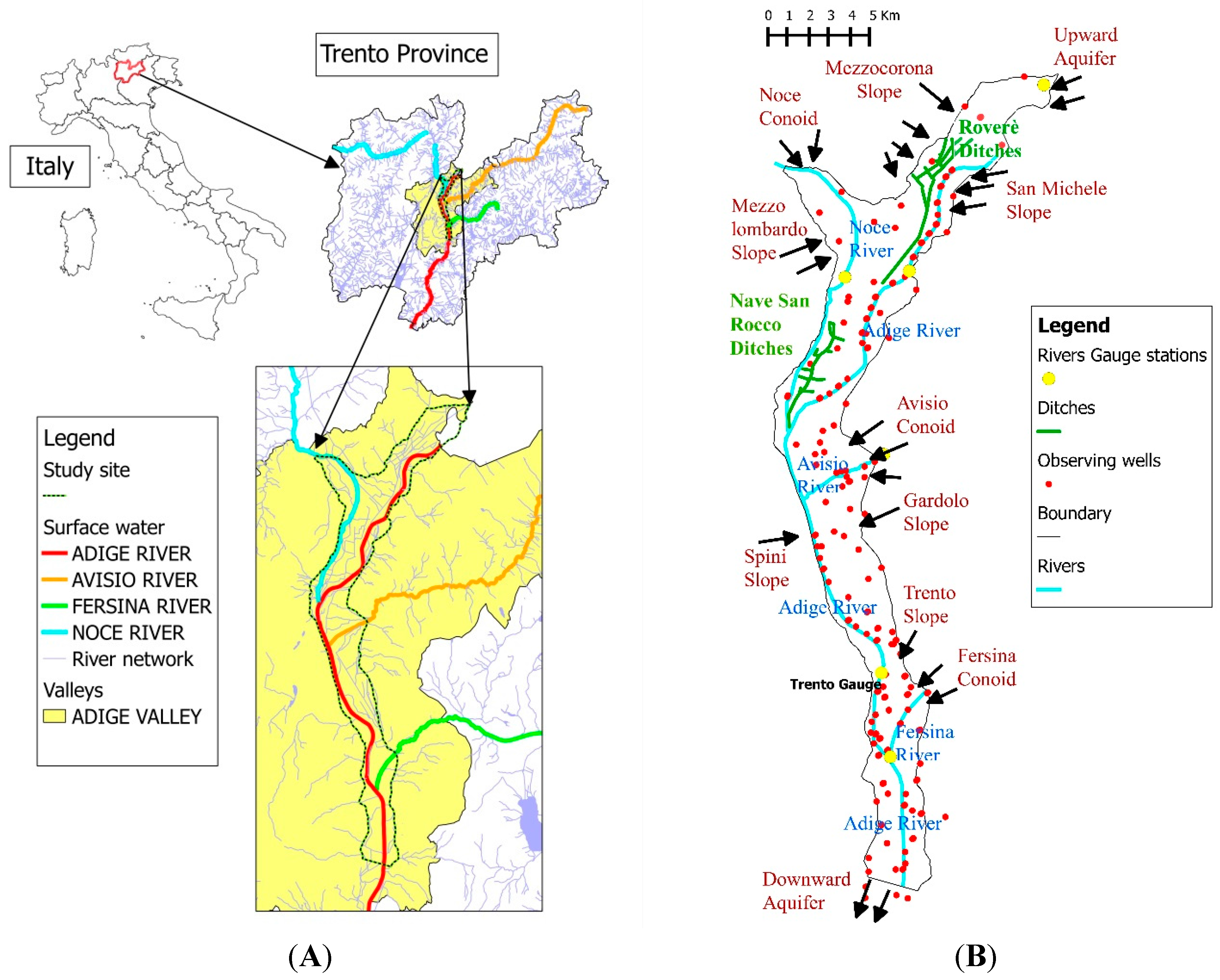
2.2. Assessment Criteria
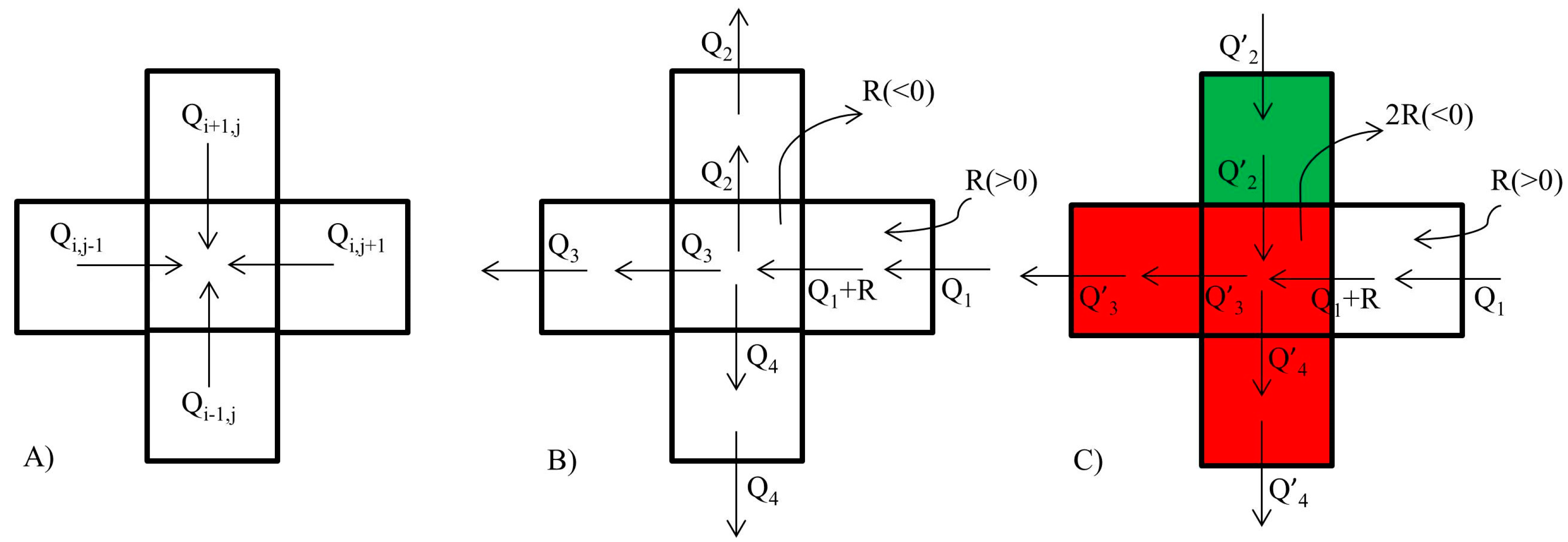
2.3. Physical Model for the Aquifer
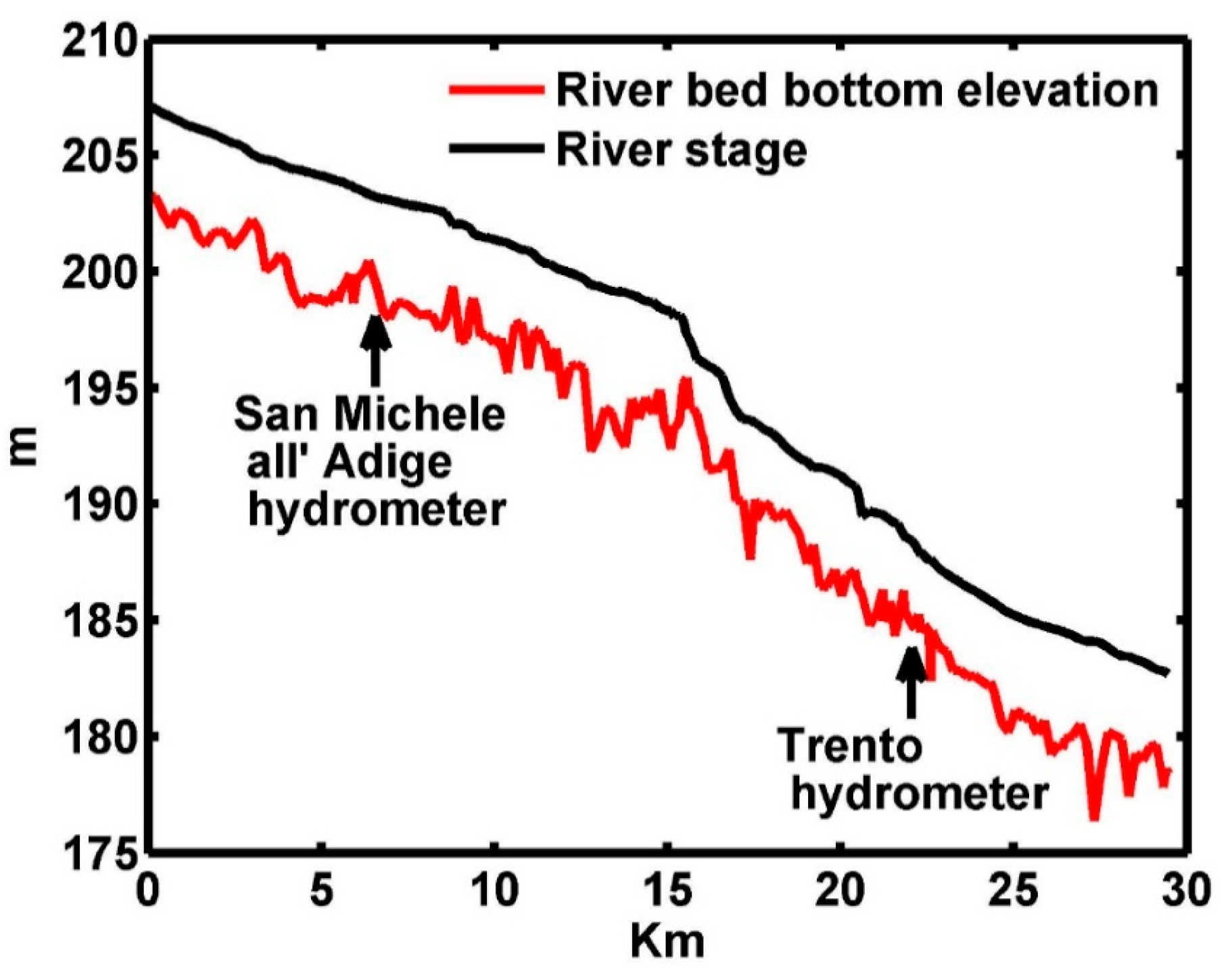
2.3.1. River–Aquifer Exchange Model
2.3.2. Ditches–Aquifer Exchange Model
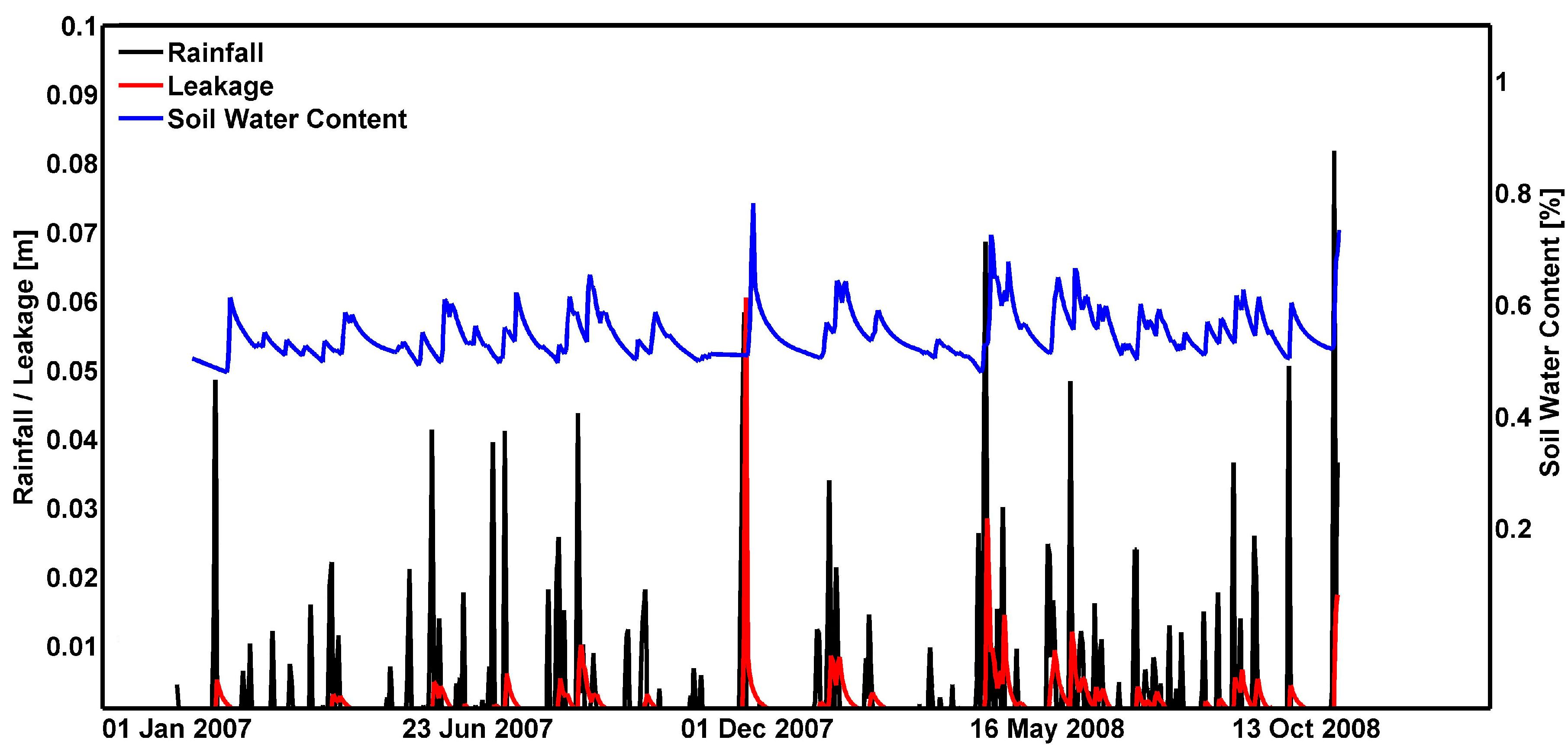
2.3.3. Leakage Model
| 12.7 | 1.0 | 0.0001 | 0.52 | 0.08 | 0.11 | 0.31 | 0.42 | 1.0 |
2.3.4. Heterogeneous Hydraulic Conductivity Fields
| Mean Length (m) | ||||
|---|---|---|---|---|
| Material | Volume Fraction (%) | X (strike) | Y (dip) | Z (vertical) |
| 1 | 30.0 | 100.0 | 510.0 | 6.02 |
| 2 | 39.0 | 41.3 | 55.0 | 3.4 |
| 3 | 20.0 | 63.2 | 63.0 | 3.11 |
| 4 | 11.0 | 58.0 | 58.0 | 3.87 |
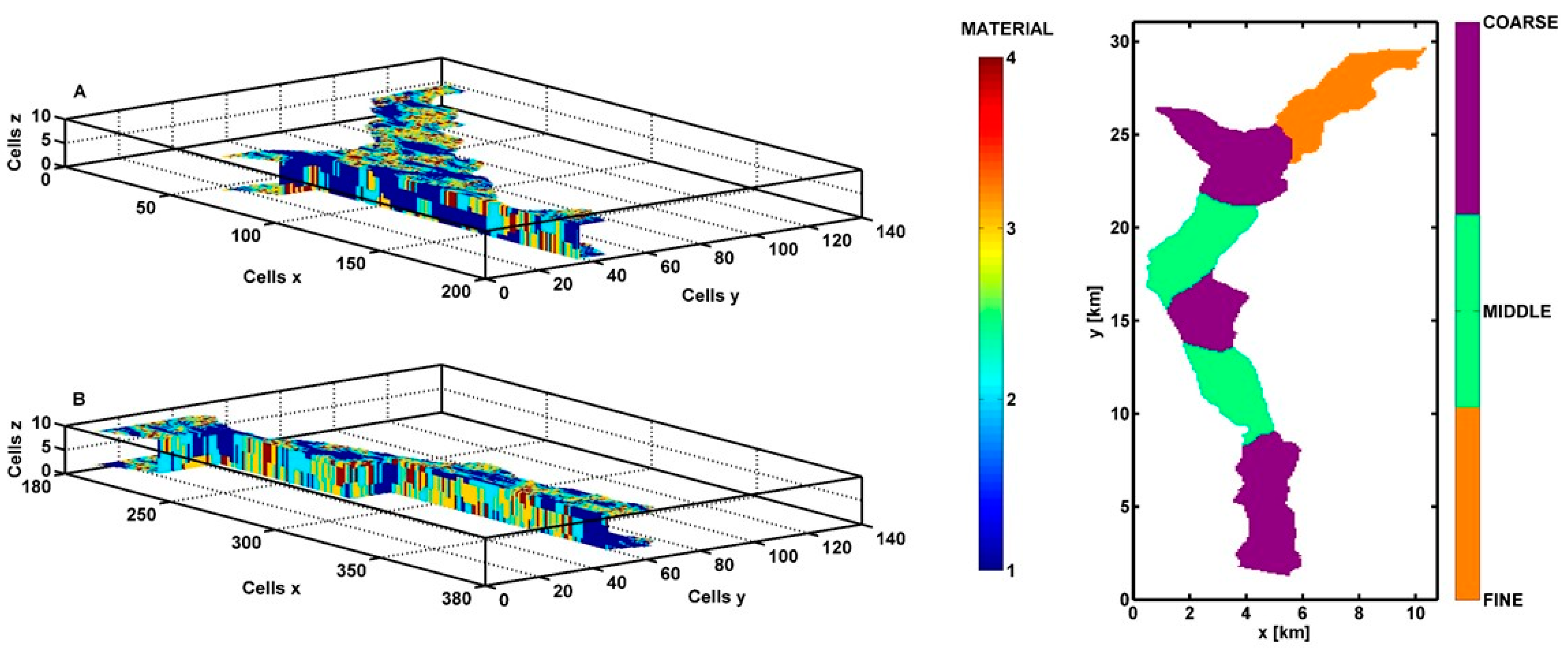
2.4. Parameter Estimation and Uncertainty of the Assessment Criteria
3. Results and Discussion
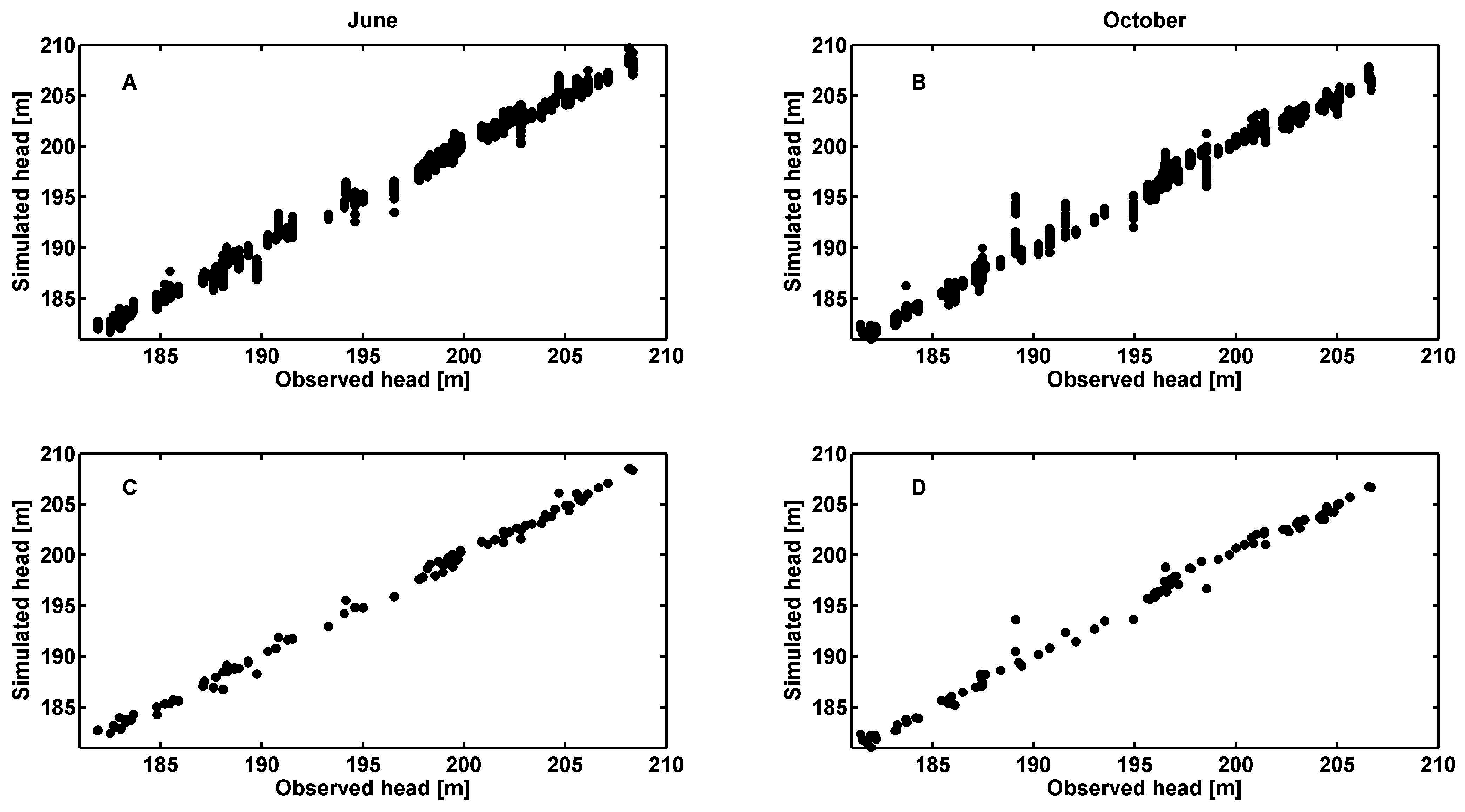
3.1. Calibration and Validation of the Numerical Model
3.2. Assessment Criteria Evaluation
| Name | Description |
|---|---|
| Base | CASE 1 (Calibrated shallow aquifer model for June 2008) |
| RS05 | CASE 1 with the rivers stage halved |
| PW2 | CASE 1 with the rate of each pumping well doubled and assuming that the ditches quickly drain the water from the aquifer |
| PW5A | CASE 1 with the rate of each pumping well quintupled and assuming that the ditches quickly drain the water from the aquifer |
| PW5B | CASE 1 with the rate of each pumping well quintupled and assuming that the ditches are able to store water and are refilled by surface water. |
3.2.1. Depth to Water
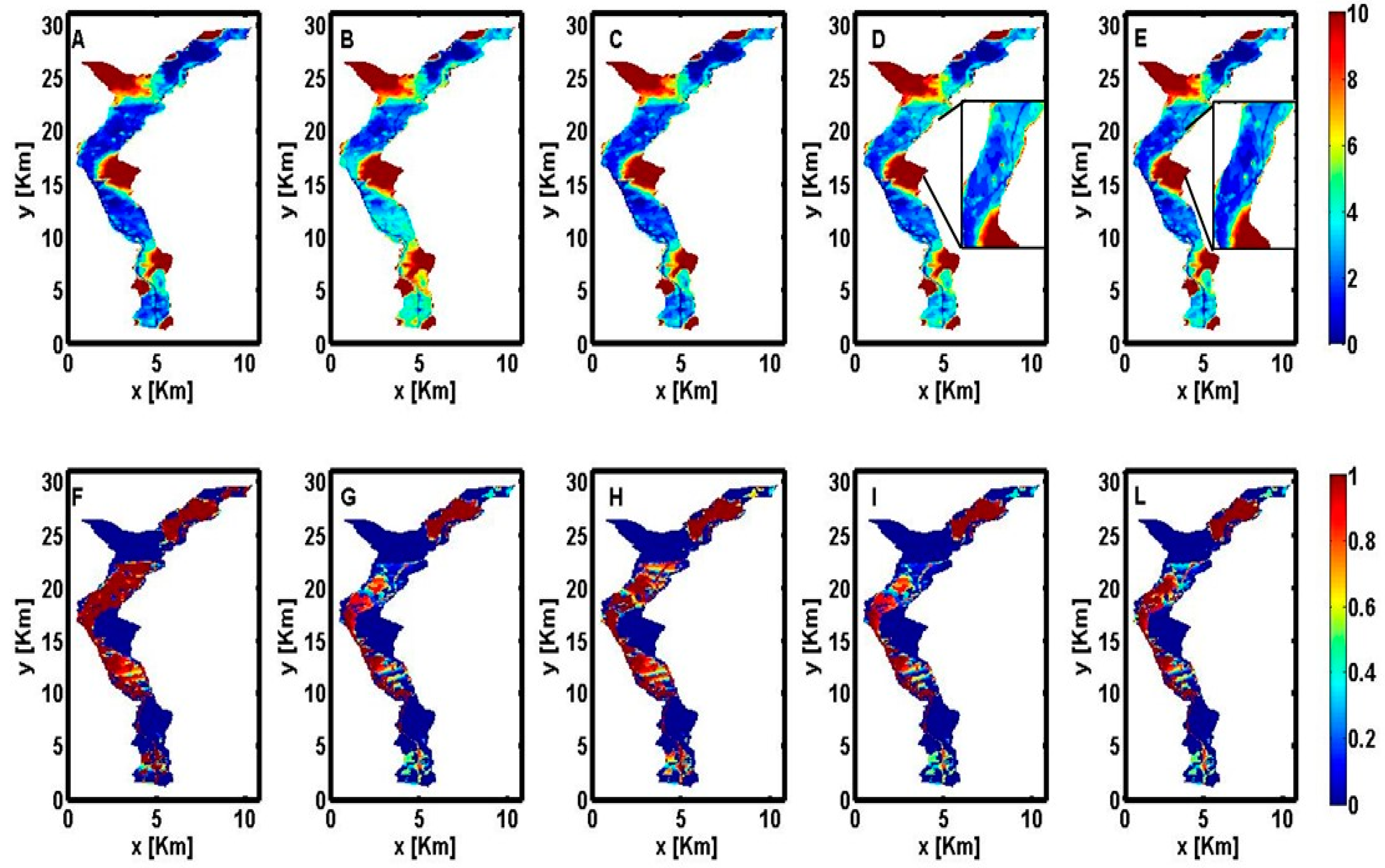
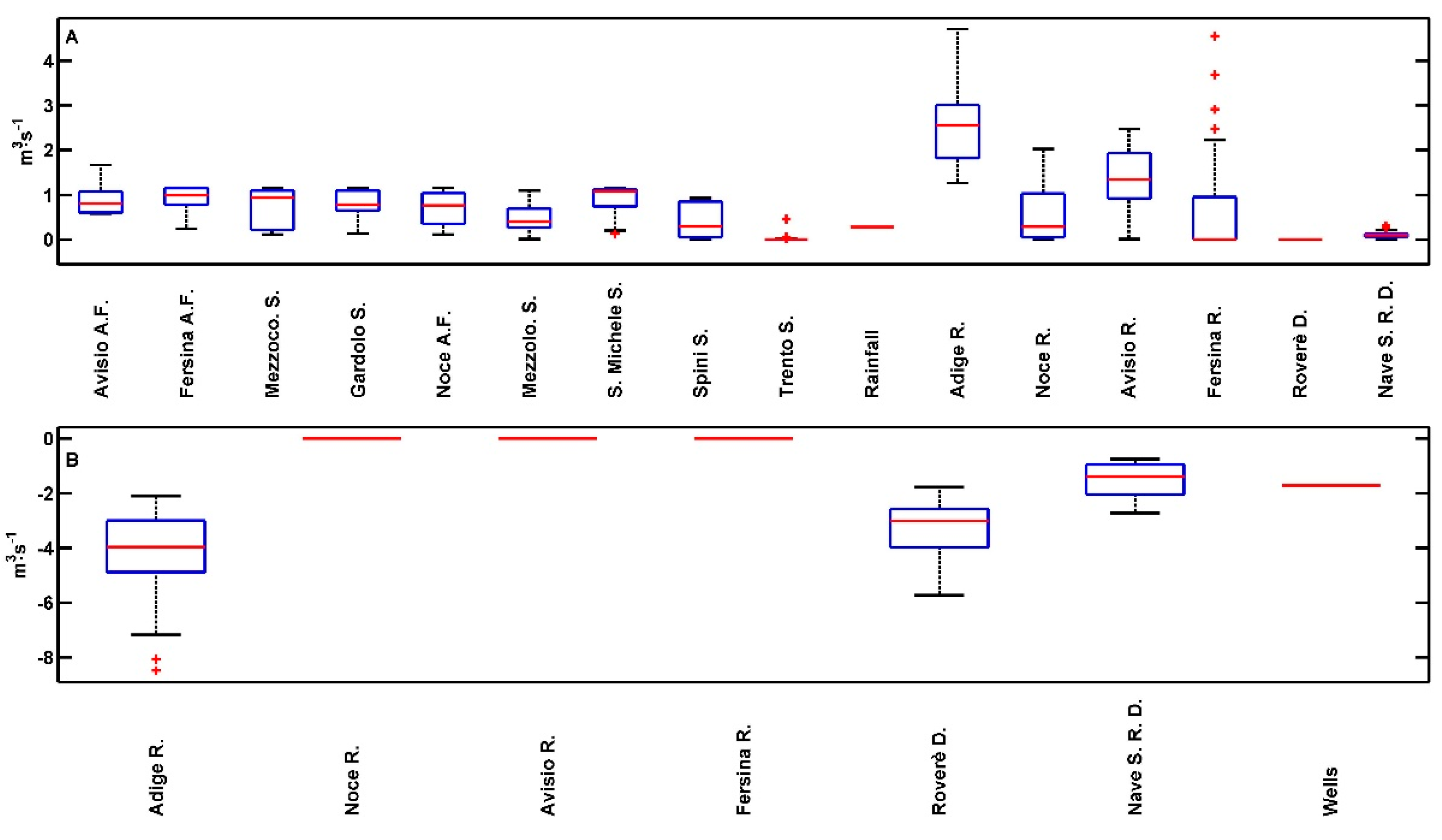
3.2.2. Recharge/Discharge Analysis
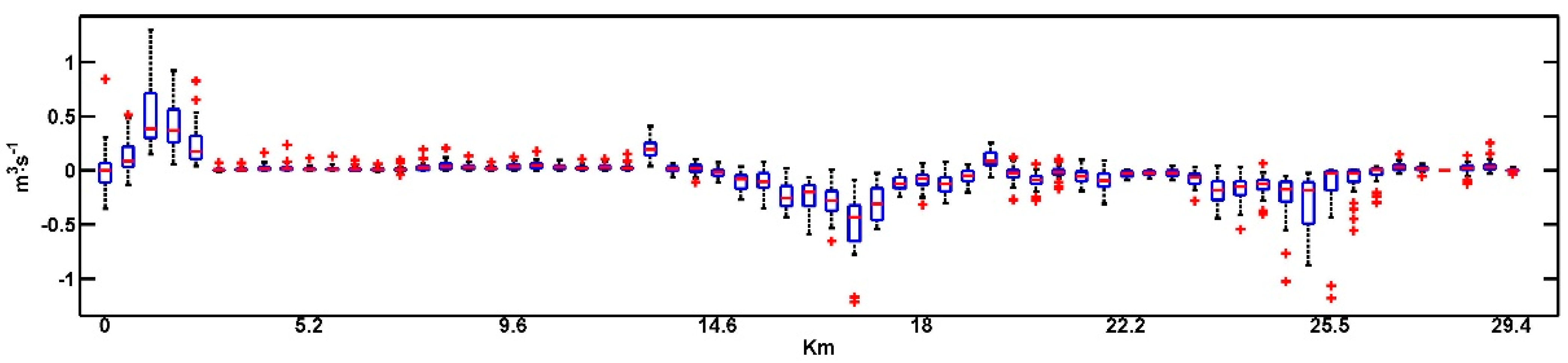
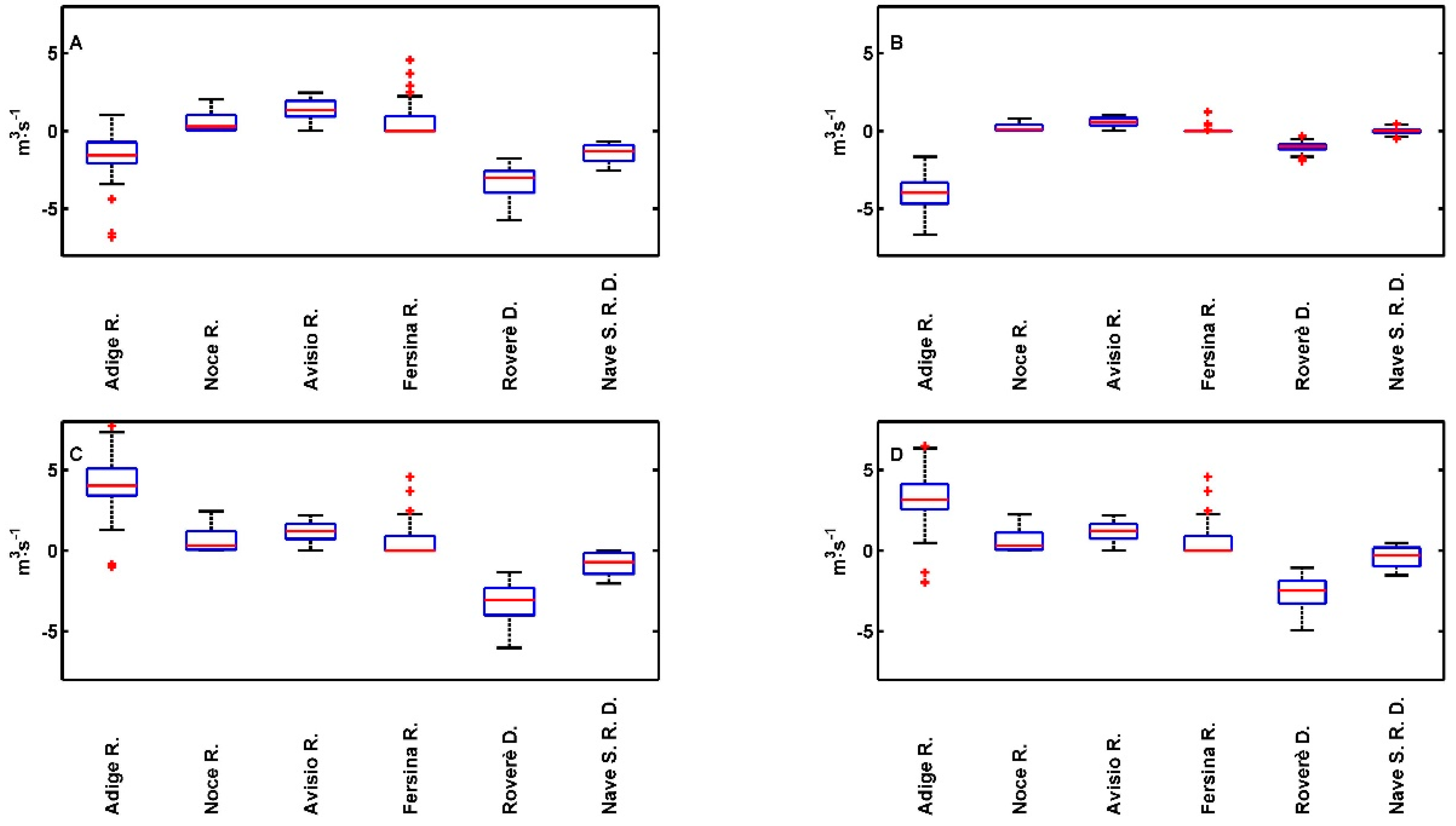
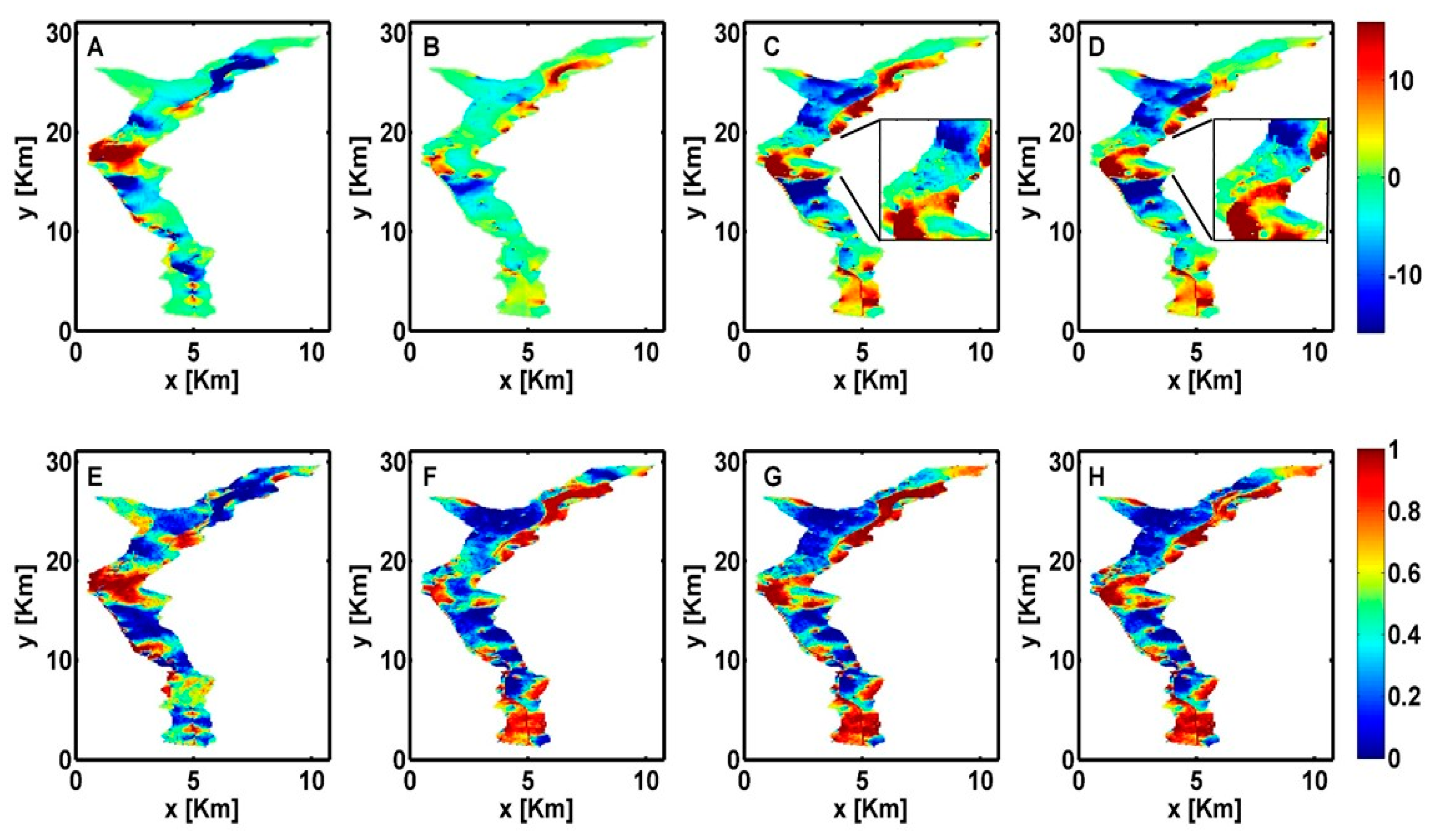
3.2.3. Sustainability of the Aquifer
4. Conclusions
- •
- The Adige River plays a fundamental role in aquifer behavior, and globally, in June 2008, the aquifer recharged the river. The actual equilibrium between surface and groundwater would be broken by increasing extractions from the wells.
- •
- DTW is generally affected by the river stage and by well extractions and locally also by the ditch management. In particular, the Adige River stage rules the aquifer DTW with a clear effect on the vulnerability of the aquifer, on the pumping costs and potentially on the ecological status of the aquifer. In the ditch areas, the increase in the DTW due to well extraction can be balanced by the recharge flow from the ditches under the hypothesis that they are refilled with external surface water.
- •
- The recharge/discharge pattern is chiefly affected by the Adige River stage and by the amount of water extracted from the wells. Increasing the recharge from the Adige River to aquifer may affect the vulnerability of the aquifer.
- •
- The S index shows heterogeneous patterns, highlighting areas with different recharge capacity, which should be evaluated in order to minimize the adverse effect of aquifer exploitation.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Qriv (L3/T) | Exchange flux between aquifer and river |
| Criv (L2/T) | Riverbed conductance of the river bed |
| Hriv (L) | River stage |
| Rbot (L) | Riverbed bottom elevation |
| i | Row position index of each numerical grid cell |
| j | Column position index of each numerical grid cell |
| k | Layer number of each numerical grid cell |
| hijk (L) | Hydraulic head computed at the numerical grid cell i,j,k |
| n | Soil porosity |
| Zr (L) | Soil thickness of the unsaturated zone |
| θ | Degree of saturation of the unsaturated zone |
| P (L/T) | Rainfall rate |
| Irr (L/T) | Irrigation rate |
| ET (L/T) | Evapotranspiration rate |
| L (L/T) | Aquifer recharge due to the leakage from the unsaturated soil |
| θh | Degree of saturation of the hygroscopic point |
| Θw | Degree of saturation of the wilting point |
| Ew (L/T) | Evapotranspiration loss at the wilting point |
| Emax (L/T) | Potential evapotranspiration |
| θ* | Soil moisture content under which the plants start to reduce transpiration to protect stomata |
| Ks (L/T) | Saturated hydraulic conductivity of the superficial soil |
| Θfc | Degree of saturation at the field capacity |
| β | Empirical parameters of the water-retention curve |
| tm1,m2 | Transition probability of the Markov chain method between material m1 and material m2 with reciprocal distance equal to d |
| T (dφ) | Transition probability matrix |
| Rφ | Transition rate matrix for each direction φ = x,y,z |
| Ll,φ (L) | Mean facies length along φ composed by the material l |
| DTW (L) | Depth to water index |
| Qi±1,j±1 (L3/T) | Volume exchange between the numerical grid cell i,j and the surrounding cells |
| Ri,j (L3/T) | Recharge/Discharge Index for the numerical grid cell identified by i,j |
| W (L3/T) | Total amount of water extracted from the aquifer in the Base scenario |
| ΔW (L3/T) | Total amount of extracted water in the over-exploited scenarios for the aquifer minus the total amount of water extracted from the aquifer in the Base scenario |
| Si,j (L3/T) | Sustainability Index for the numerical grid cell identified by i,j |
| s (L2/T) | Specific Sustainability Index for the numerical grid cell identified by i,j, computed as
, where
is the cell’s size |
| Qij°ut (L3/T) | Global flow exiting the vertical column i,j (from the position i,j to the surrounding vertical columns) |
| Z (L) | Head measurements collected in field in correspondence to the observing points |
| V | Assessment criteria |
| NV | Total number of assessment criteria |
| Z* (L) | Hydraulic heads simulated by the numerical model in correspondence to the observing points |
| Nobs | Number of observing points of the hydraulic heads |
| A | Unknown parameters of the numerical model utilized for reproducing the aquifer behavior and which are calibrated with the PSO |
| Na | Number of unknown parameters of the numerical model |
| Np | Number of particles utilized in the PSO algorithm |
| Ns | Number of iterations of the PSO algorithm |
| MC | Number of Monte Carlo simulations |
References
- European Commission (2008). Groundwater Protection in Europe–The New Groundwater Directive–Consolidating the EU Regulatory Framework. Available online: http://ec.europa.eu/environment/water/water-framework/groundwater/pdf/brochure/en.pdf (accessed on 23 June 2015).
- Custodio, E. Aquifer overexploitation: What does it mean? Hydrogeol. J. 2002, 10, 254–277. [Google Scholar] [CrossRef]
- Mattas, C.; Voudouris, K.S.; Panagopoulos, A. Integrated groundwater resources management using the DPSIR approach in a GIS environment context: A case study from the Gallikos river basin, Noth Greece. Water 2014, 6, 1043–1068. [Google Scholar] [CrossRef]
- Foster, S.; Garduno, H.; Evans, R.; Olson, D.; Tian, Y.; Zhang, W.; Han, Z. Quaternary aquifer of the North China Plain—Assessing and achieving groundwater resource sustainability. Hydrogeol. J. 2004, 12, 81–93. [Google Scholar] [CrossRef]
- Troldborg, M.; Lemming, G.; Binning, P.J.; Tuxen, N.; Bjerg, P.L. Risk assessment and prioritisation of contaminated sites on the catchment scale. J. Contam. Hydrol. 2008, 101, 14–28. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J.M.; Shamir, U.; Nemati, H.R. Groundwater quality management under uncertainty: Stochastic programming approaches and the value of information. Water Resour. Res. 1992, 28, 1233–1246. [Google Scholar] [CrossRef]
- Fienen, M.N.; Masterson, J.P.; Plant, N.G.; Gutierrez, B.T.; Thieler, E.R. Bridging groundwater models and decision support with a Bayesian network. Water Resour. Res. 2013, 49, 6459–6473. [Google Scholar] [CrossRef]
- Uddameri, V.; Singaraju, S.; Hernandez, E.A. Impacts of sea-level rise and urbanization on groundwater availability and sustainability of coastal communities in semi-arid South Texas. Environ. Earth Sci. 2014, 71, 2503–2515. [Google Scholar] [CrossRef]
- Durga Rao, H.; Korada, V. Spatial Optimisation Technique for planning groundwater supply schemes in a rapid growing urban environment. Water Resour. Manag. 2014, 28, 731–747. [Google Scholar]
- Lerma, N.; Paredes-Arquiola, J.; Molina, J.-L.; Andreu, J. Evolutionary network flow models for obtaining operation rules in multi-reservoir water systems. J. Hydroinform. 2014, 16, 33–49. [Google Scholar] [CrossRef]
- Pierce, S.A.; Sharp, J.M.; Guillaume, J.J.H.A.; Mace, R.E.; Eaton, D.J. Aquifer-Yield continuum as a guide and typology for science-based groundwater management. Hydrogeol. J. 2013, 21, 331–334. [Google Scholar] [CrossRef]
- Megdal, S.B.; Dillon, P. Policy and economics of managed aquifer recharge and water banking. Water 2015, 7, 592–598. [Google Scholar] [CrossRef]
- Morio, M.; Schädler, S.; Finkel, M. Applying a multi-criteria genetic algorithm framework for brownfield reuse optimization: Improving redevelopment options based on stakeholders preferences. J. Environ. Manag. 2013, 130, 331–346. [Google Scholar] [CrossRef] [PubMed]
- Portoghese, I.; D’Agostino, D.; Giordano, R.; Scardigno, A.; Apollonio, C.; Vurro, M. An integrated modelling tool to evaluate the acceptability of irrigation constraint measures for groundwater protection. Environ. Model. Softw. 2013, 46, 90–103. [Google Scholar] [CrossRef]
- Molina, J.-L.; Pulido-Velázquez, D.; García-Aróstegui, J.L.; Pulido-Velázquez, M. Dynamic Bayesian networks as a decision support tool for assessing climate change impacts on highly stressed groundwater systems. J. Hydrol. 2013, 479, 113–129. [Google Scholar] [CrossRef]
- Hadded, R.; Nouiri, I.; Alshihabi, O.; Maßmann, L.; Huber, M.; Laghouane, A.; Yahiaoui, H.; Tarhouni, J. A decision support system to manage the groundwater of the Zeuss Koutine Aquifer using the WEAP-MODFLOW framework. Water Resour. Manag. 2013, 27, 1981–2000. [Google Scholar] [CrossRef]
- Massuel, S.; George, B.A.; Venot, J.-P.; Bharati, L.; Acharya, S. Improving assessment of groundwater-resource sustainability with deterministic modelling: A case study of the semi-arid Musi sub-basin, South India. Hydrogeol. J. 2013, 21, 1567–1580. [Google Scholar] [CrossRef]
- Doherty, J.; Simmons, C.T. Groundwater modelling in decision support: Reflections on a unified conceptual framework. Hydrogeol. J. 2013, 21, 1531–1537. [Google Scholar] [CrossRef]
- Rojas, R.; Dassargues, A. Groundwater flow modelling of the regional aquifer of the Pampa del Tamarugal, Northern Chile. Hydrogeol. J. 2007, 15, 537–551. [Google Scholar] [CrossRef]
- El-Kadi, A.I.; Tillery, S.; Whittier, R.B.; Hagedorn, B.; Mair, A.; Ha, K.; Koh, G.-W. Assessing sustainability of groundwater resources on Jeju Island, South Korea, under climate change, drought, and increased usage. Hydrogeol. J. 2014, 22, 625–642. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Cooley, R.L. A Theory for Modeling Ground-Water Flow in Heterogeneous Media; U.S. Geological Survey: Reston, VA, USA, 2004. [Google Scholar]
- McLaughlin, D.; Townley, L.R. A reassessment of the groundwater inverse problem. Water Resour. Res. 1996, 32, 1131–1161. [Google Scholar] [CrossRef]
- Zhou, H.; Jaime Gomez-Hernandez, J.; Li, L. Inverse methods in hydrogeology: Evolution and recent trends. Adv. Water Resour. 2014, 63, 22–37. [Google Scholar] [CrossRef]
- Carrera, J.; Alcolea, A.; Medina, A.; Hidalgo, J.; Slooten, L.J. Inverse problem in hydrogeoloy. Hydrogeol. J. 2005, 13, 206–222. [Google Scholar] [CrossRef]
- Yeh, W.W.G. Review of Parameter identification procedures in groundwater hydrology–The inverse problem. Water Resour. Res. 1986, 22, 95–108. [Google Scholar] [CrossRef]
- Hill, M.C.H. The Practical Use of Simplicity in Developing Ground Water Models. Ground Water 2006, 44, 775–781. [Google Scholar] [CrossRef] [PubMed]
- Foglia, L.; Mehl, S.W.; Hill, M.C.; Perona, P.; Burlando, P. Testing alternative ground water models using cross—Validation and other methods. Ground Water 2007, 45, 627–641. [Google Scholar] [CrossRef] [PubMed]
- D’Agnese, F.A.; Faunt, C.C.; Hill, M.C.; Turner, A.K. Death valley regional ground-water flow model calibration using optimal parameter estimation methods and geoscientific information systems. Adv. Water Resour. 1999, 22, 777–790. [Google Scholar] [CrossRef]
- McKenna, S.A.; Poeter, E.P. Field example of data fusion in site characterization. Water Resour. Res. 1995, 31, 3229–3240. [Google Scholar] [CrossRef]
- Singh, A.; Minsker, B.S.; Valocchi, A.J. An interactive multi-objective optimization framework for groundwater inverse modeling. Adv. Water Resour. 2008, 31, 1269–1283. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Dassargues, A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Lee, J.; Kitanidis, P.K. Bayesian inversion with total variation prior for discrete geologic structure identification. Water Resour. Res. 2013, 49, 7658–7669. [Google Scholar] [CrossRef]
- Singh, A.; Walker, D.D.; Minsker, B.S.; Valocchi, A.J. Incorporating subjective and stochastic uncertainty in an interactive multi-objective groundwater calibration framework. Stoch. Environ. Res. Risk Assess. 2010, 24, 881–898. [Google Scholar] [CrossRef]
- Feyen, L; Caers, J. Quantifying geological uncertainty for flow and transport modeling in multi-modal heterogeneous formations. Adv. Water Resour. 2006, 29, 912–929. [Google Scholar]
- Jha, S.K.; Comunian, A.; Mariethoz, G.; Kelly, B.F.J. Parameterization of training images for aquifer 3-D facies modeling integrating geological interpretations and statistical inference. Water Resour. Res. 2014, 50, 7731–7749. [Google Scholar] [CrossRef]
- Guillaume, J.H.A.; Qureshi, M.E.; Jakeman, A.J. A structured analysis of uncertainty surrounding modeled impacts of groundwater-extraction rules. Hydrogeol. J. 2012, 20, 915–932. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- McKnight, U.S.; Finkel, M. A system dynamics model for the screening-level long-term assessment of human health risks at contaminated sites. Environ. Model. Softw. 2013, 40, 35–50. [Google Scholar] [CrossRef]
- Keating, E.H.; Doherty, J.; Vrugt, J.A.; Kang, Q. Optimization and uncertainty assessment of strongly nonlinear groundwater models with high parameter dimensionality. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Batelaan, O.; Dassargues, A. On the value of conditioning data to reduce conceptual model uncertainty in groundwater modeling. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Scott, A.C.; Bailey, C.J.; Marra, R.P.; Woods, G.J.; Ormerod, K.-J.; Lansey, K. Scenario planning to address critical uncertainties for robust and resilient water-wastewater infrastructures under conditions of water scarcity and rapid development. Water 2012, 4, 848–868. [Google Scholar] [CrossRef]
- Beretta, G.P. 2011: Progetto per la Definizione Strumenti Gestionali Delle Acque Sotterranee con L’ausilio di Modelli Idrogeologici; Provincia Autonoma di Trento: Trento, Italy, 2011. (In Italian) [Google Scholar]
- Carle, S.F. T-PROGS: Transition Probability Geostatistical Software, Users Manual version 2.1; University of California: Davis, CA, USA, 1999; p. 84. [Google Scholar]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Portale Geocartografico Trentino. Available online: http://www.territorio.provincia.tn.it/portal/server.pt/community/sondaggi/771/sondaggi/21171 (accessed on 23 June 2015). (In Italian)
- Chiogna, G.; Santoni, E.; Camin, F.; Tonon, A.; Majone, B.; Trenti, A.; Bellin, A. Stable isotope characterization of the Vermigliana catchment. J. Hydrol. 2014, 509, 295–305. [Google Scholar] [CrossRef]
- Navarro-Ortega, A.; Acuna, V.; Bellin, A.; Burek, P.; Cassiani, G.; Choukr-Allah, R.; Doledec, S.; Elosegi, A.; Ferrari, F.; Ginebreda, A.; et al. Managing the effects of multiple stressors on aquatic ecosystems under water scarcity. The GLOBAQUA project. Sci. Total Environ. 2015, 503, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Penna, D.; Engel, M.; Mao, L.; Dell’Agnese, A.; Bertoldi, G.; Comiti, F. Tracer-Based analysis of spatial and temporal variation of water sources in a glacierized catchment. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 4879–4924. [Google Scholar] [CrossRef]
- Zolezzi, G.; Siviglia, A.; Toffolon, M.; Maiolini, B. Thermopeaking in Alpine streams: Event characterization and time scales. Ecohydrology 2011, 4, 564–576. [Google Scholar] [CrossRef]
- Autorità di Bacino del Fiume Adige. Quaderno di Bilancio Idrico; Autorità di Bacino del Fiume Adige: Trento, Italy, 2008. [Google Scholar]
- Cargnelutti, M.; Quaranta, N. Application of MIKE SHE to the Alluvial aquifer of river Adige’s Valley. In Proceedings of the 3rd DHI Software Conference, Helsingor, Denmark, 7–11 June 1999.
- Bazzanella, F.; Bazzoli, G.; Vigna, I. Misure Freatimetriche nel Fondovalle Atesino. Relazione e Schede Monografiche; Provincia Autonoma di Trento: Trento, Italy, 2008. (In Italian) [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model–the Ground-Water Flow Process; U.S. Geological Survey (USGS) Techniques and Methods 6-A16; USGS: Reston, Virginia, 2005. [Google Scholar]
- Aller, L.; Bennett, Y.; Leht, J.H.; Petty, R.J.; Hackett, G. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings; U.S. Environmental Protection Agency: Washington, DC, USA, 1987. [Google Scholar]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Lin, Y.-F.; Anderson, M. A Digital procedure for groundwater Recharge and Discharge pattern recognition and rate estimation. Ground Water 2003, 41, 306–315. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.F.; Wang, J.; Valocchi, A.J. PRO-GRADE:GIS toolkits for ground water recharge and discharge estimation. Ground Water 2009, 47, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Stoertz, M.W.; Bradbury, K.R. Mapping recharge areas using a ground-water flow model: A case study. Ground Water 1989, 27, 220–228. [Google Scholar] [CrossRef]
- Uddameri, V.; Honnungar, V. Interpreting sustainable yield of an aquifer using a fuzzy Framework. Environ. Geol. 2007, 51, 911–919. [Google Scholar] [CrossRef]
- Regione Lombardia. ACQUE SOTTERRANEE IN LOMBARDIA Gestione Sostenibile di una Risorsa Strategica; Regione Lombardia: GiugnoMilano, Italy, 2001. (In Italian) [Google Scholar]
- Neff, B.P.; Pigott, A.R.; Sheets, R.A. Estimation of Shallow Ground-Water Recharge in the Great Lakes Basin; U.S. Department of the Interior U.S. Geological Survey: Reston, VA, USA, 2006. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process; U.S. Geological Survey Open-File Report 00–92; U.S. Geological Survey: Washington, DC, USA, 2000; p. 121. [Google Scholar]
- McDonald, M.G.; Harbaugh, A.W. Chapter A1: A modular three-dimensional finite-difference ground-water flow model. In Book 6: Modeling Techniques; US Geological Survey (USGS) Techniques of Water-Resources Investigations: Washington, DC, USA, 1988. [Google Scholar]
- Mehl, S.; Hill, M.C. Grid-Size dependence of Cauchy boundary conditions used to simulate stream–aquifer interactions. Adv. Water Resour. 2010, 33, 430–442. [Google Scholar] [CrossRef]
- Lackey, G.; Neupauer, R.M.; Pitlick, J. Effects of streambed conductance on stream depletion. Water 2015, 7, 271–287. [Google Scholar] [CrossRef]
- Manning, R. On the flow of Water in Open Channels and Pipes; Transactions Institute of Civil Engineers of Ireland: Dublin, Ireland, 1891; Volume 20, pp. 161–209. [Google Scholar]
- Bertolini, L. Raccolta Dati Idrogeologici del Bacino di Bonifica di Nave San Rocco. Master’s Thesis, Dipartimento di Ingegneria Civile Ambientale, University of Trento, Trento, Italy, 2004. [Google Scholar]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Toller, G. I Fabbisogni di Acqua Irrigua nel Trentino; Istituto Agrario San Michele all’ Adige: San Michele all’Adige, Italy, 2002. (In Italian) [Google Scholar]
- Rodriguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics (Paperback); Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Carle, S.F.; Fogg, G.E. Modeling spatial variability with one and multidimensional continuous-lag Markov chains. Math. Geol. 1997, 29, 891–918. [Google Scholar] [CrossRef]
- Clerc, M. Standard Particle Swarm Optimisation. Available online: http://clerc.maurice.free.fr/pso/SPSO_descriptions.pdf (accessed on 24 September 2012).
- Castagna, M.; Bellin, A. A Bayesian approach for inversion of hydraulic tomographic data. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Castagna, M.; Becker, M.W.; Bellin, A. Joint estimation of transmissivity and storativity in a bedrock fracture. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Castagna, M. SmartGeo: Software for the Generation of Heterogeneous Hydraulic Parameters for Groundwater Applications. Available online: http://www.smarthydrosol.com/SmartGEO.php?l=2 (accessed on 24 June 2015).
- Beven, K.J.; Binley, A.M. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Rubin, Y.; Chen, H.M.; Hahn, M. A Bayesian approach for inverse modeling, data assimilation, and conditional simulation of spatial random fields. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castagna, M.; Bellin, A.; Chiogna, G. Uncertainty Estimation and Evaluation of Shallow Aquifers’ Exploitability: The Case Study of the Adige Valley Aquifer (Italy). Water 2015, 7, 3367-3395. https://doi.org/10.3390/w7073367
Castagna M, Bellin A, Chiogna G. Uncertainty Estimation and Evaluation of Shallow Aquifers’ Exploitability: The Case Study of the Adige Valley Aquifer (Italy). Water. 2015; 7(7):3367-3395. https://doi.org/10.3390/w7073367
Chicago/Turabian StyleCastagna, Marta, Alberto Bellin, and Gabriele Chiogna. 2015. "Uncertainty Estimation and Evaluation of Shallow Aquifers’ Exploitability: The Case Study of the Adige Valley Aquifer (Italy)" Water 7, no. 7: 3367-3395. https://doi.org/10.3390/w7073367
APA StyleCastagna, M., Bellin, A., & Chiogna, G. (2015). Uncertainty Estimation and Evaluation of Shallow Aquifers’ Exploitability: The Case Study of the Adige Valley Aquifer (Italy). Water, 7(7), 3367-3395. https://doi.org/10.3390/w7073367






