Large-Scale Hydrological Modeling and Decision-Making for Agricultural Water Consumption and Allocation in the Main Stem Tarim River, China
Abstract
:1. Introduction
2. Hydrological Modeling
2.1. Study Area
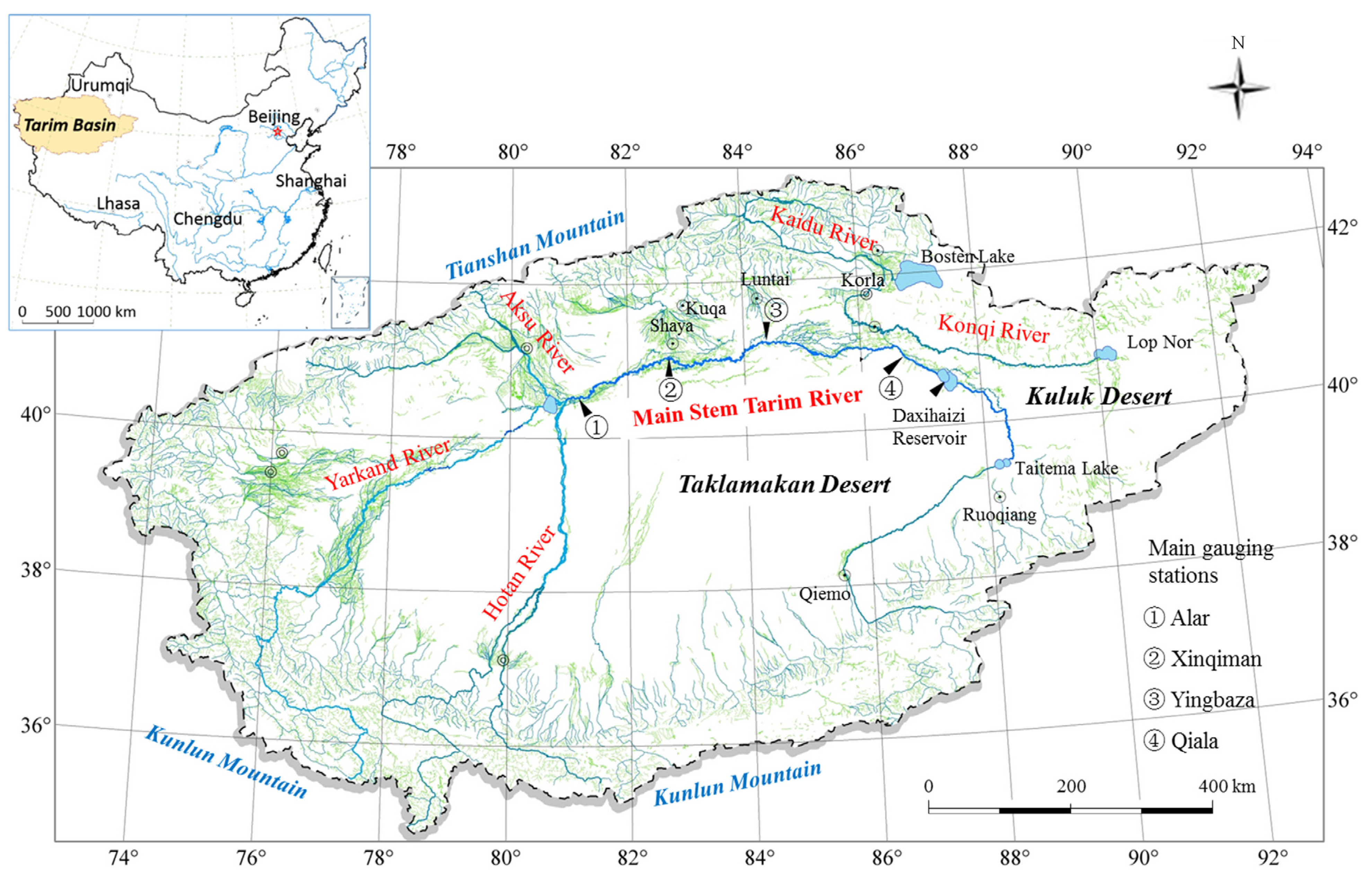
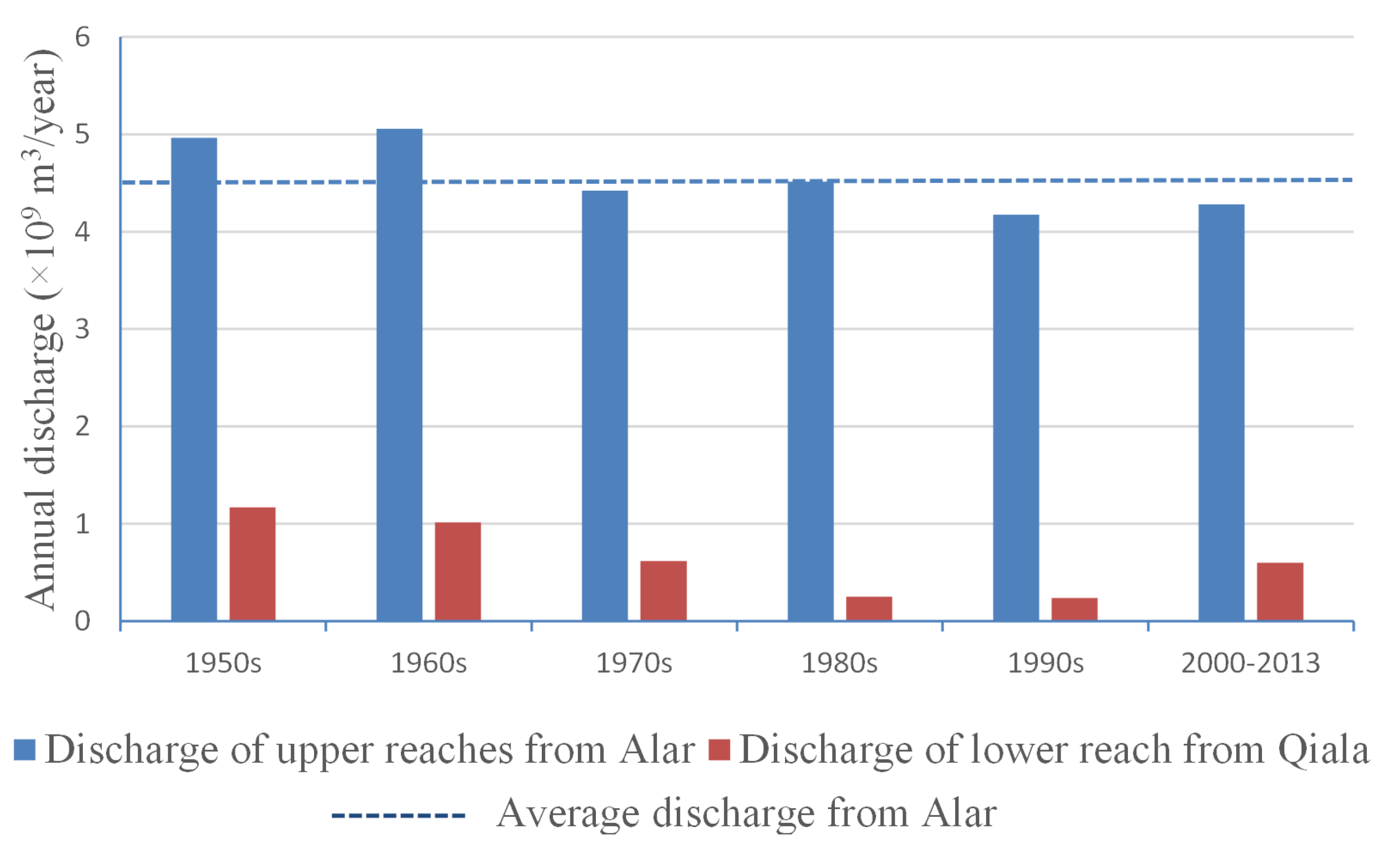
2.2. MIKE HYDRO Model Setup
2.2.1. Sub-Catchments and Data
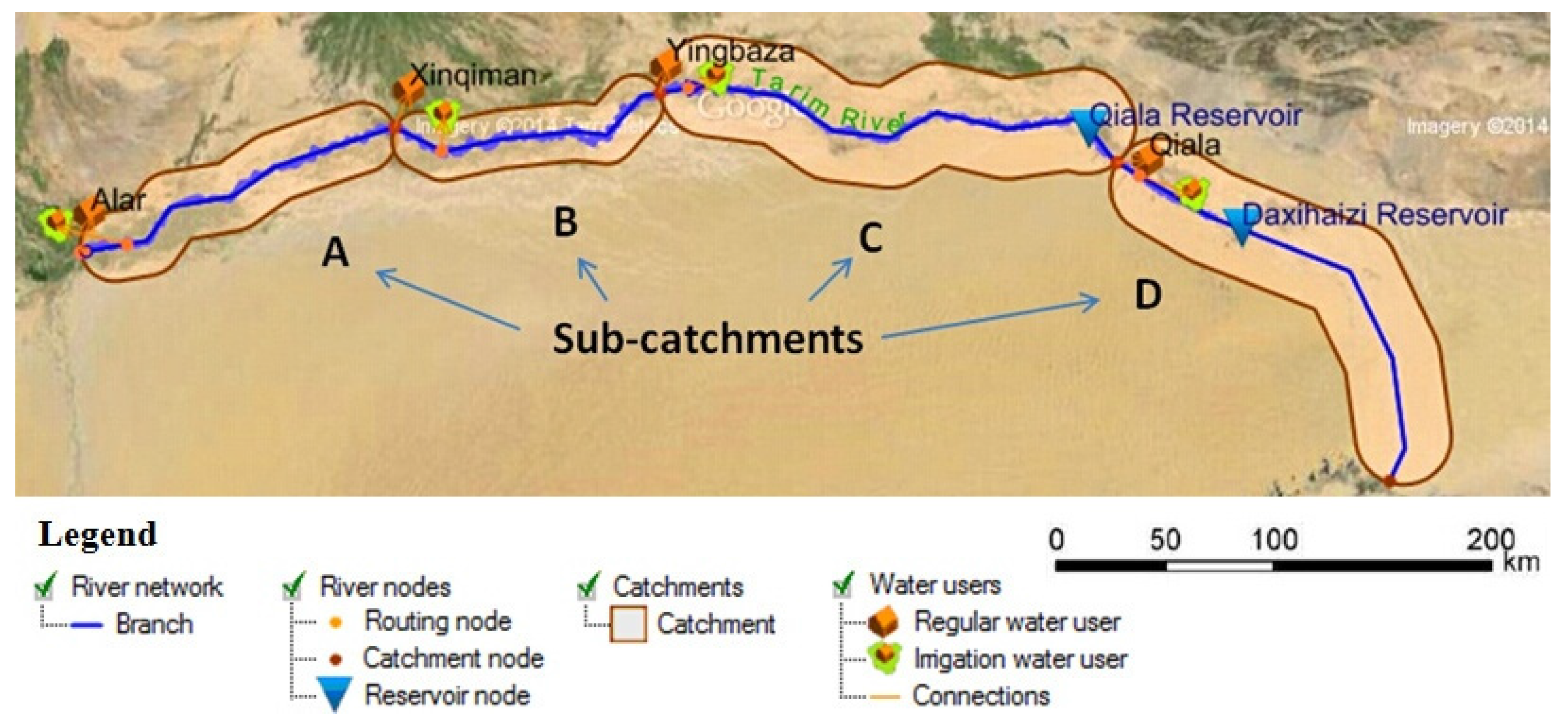
2.2.2. Muskingum Routing
| Muskingum Routing | Upper Reaches | Middle Reach | Lower Reach | |
|---|---|---|---|---|
| Sub-Catchment | A | B | C | D |
| River Length (km) | 189 | 258 | 398 | 428 |
| K (h) | 51 | 86 | 158 | 198 |
2.2.3. Crop Factors and Growth Stages
| Crops | Share (%) | Sowing Day | Length (Days) | RD (mm) | MH (m) | INI | Kcb | LAT | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| INI | DEV | MID | LAT | MID | |||||||
| Wheat | 2.7 | 03.21 | 15 | 25 | 40 | 20 | 1500 | 1 | 0.4 | 1.2 | 0.5 |
| Maize | 1.6 | 04.16 | 20 | 25 | 60 | 15 | 1700 | 2 | 0.4 | 1.2 | 0.7 |
| Sugarbeet | 5.1 | 03.26 | 25 | 35 | 60 | 45 | 1200 | 0.5 | 0.5 | 1.2 | 0.8 |
| Bean | 1.7 | 04.21 | 20 | 30 | 30 | 10 | 700 | 0.4 | 0.4 | 1.1 | 0.9 |
| Melon | 2.1 | 04.01 | 25 | 35 | 40 | 20 | 1500 | 0.4 | 0.5 | 1 | 0.8 |
| Cotton | 82.6 | 04.21 | 25 | 45 | 50 | 40 | 1700 | 1.5 | 0.5 | 1.2 | 0.8 |
| Tomato | 2.1 | 04.11 | 35 | 40 | 50 | 25 | 1500 | 0.6 | 0.5 | 1.2 | 0.8 |
2.3. Discharge and Calibration
| NAM Parameters | Parameter Descriptions | Units | Value Ranges | Calibrated Values |
|---|---|---|---|---|
| Umax | Maximum water content in surface storage | mm | 10–20 | 17.79 |
| Lmax | Maximum water content in root zone storage | mm | 100–300 | 166.25 |
| CQOF | Overland flow runoff coefficient | - | 0.1–1 | 0.51 |
| CKIF | Time constant for routing interflow | h | 200–1000 | 533.28 |
| CK1 | Time constant 1 for routing overland flow | h | 10–50 | 22.98 |
| CK2 | Time constant 2 for routing overland flow | h | 10–50 | 10 |
| TOF | Root zone threshold value for overland flow | - | 0–0.99 | 0.56 |
| TIF | Root zone threshold value for interflow | - | 0–0.99 | 0.53 |
| TG | Root zone threshold value for groundwater recharge | - | 0–0.99 | 0.03 |
| CKBF | Time constant for routing base flow | h | 1000–4000 | 2179.01 |
| CQLOW | Lower base flow, recharge to lower reservoir | percentage | 0–100 | 0 |
| CKLOW | Time constant for routing lower base flow | h | 1000–30,000 | 10,000 |
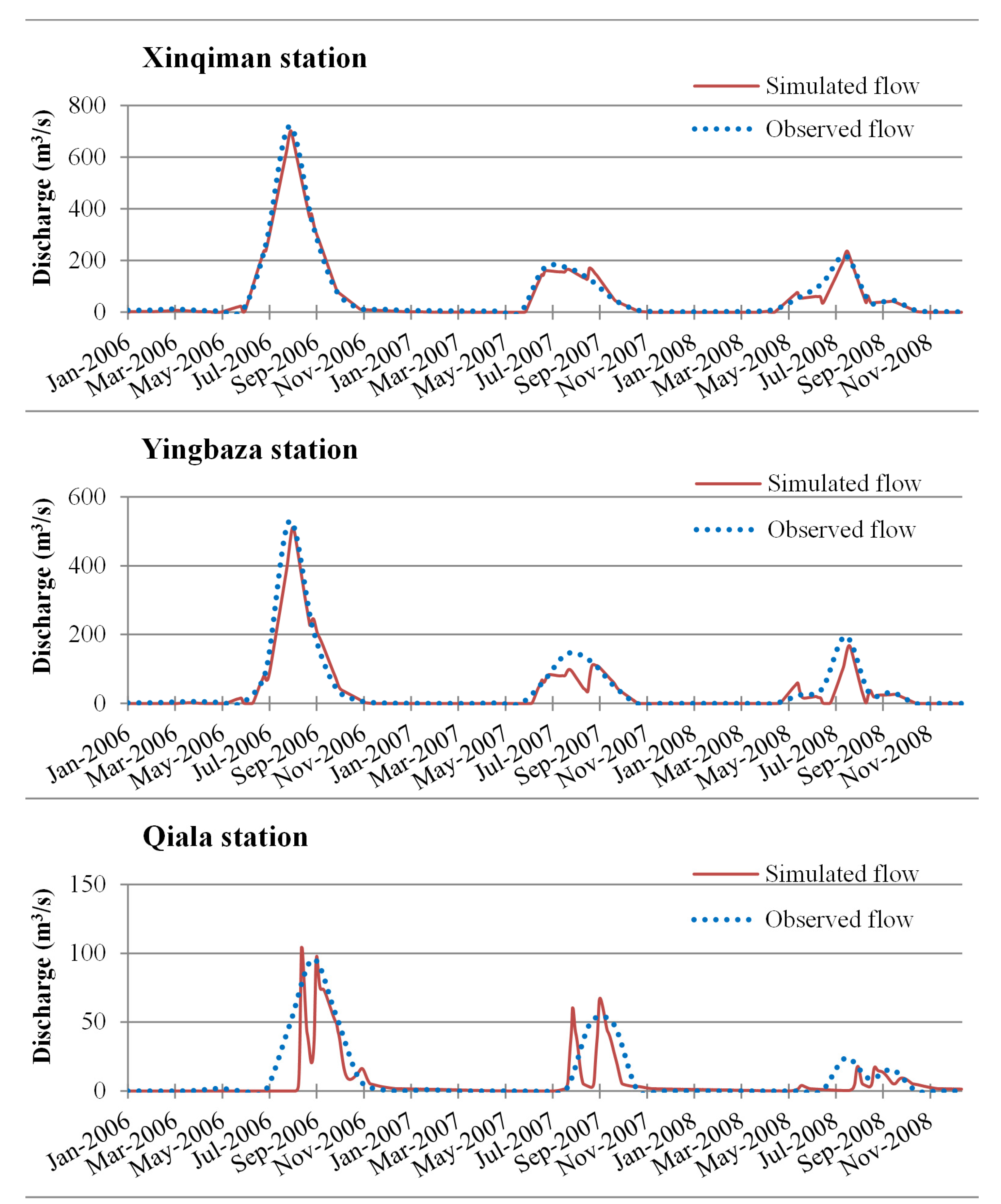
| Gauging Stations | NSE | RMSE (m3/s) | RSR | % Bias |
|---|---|---|---|---|
| Xinqiman | 0.88 | 14.7 | 0.11 | −2.41 |
| Yingbaza | 0.86 | 11.53 | 0.12 | −3.42 |
| Qiala | 0.92 | 3.58 | 0.10 | −8.24 |
3. Design of Scenarios
3.1. Irrigation Scenarios
3.1.1. Total Available Water (TAW) Scenarios
3.1.2. Water-Saving Irrigation Scenarios
3.2. Land Use Scenarios
4. Results and Discussion
4.1. Actual Crop Evapotranspiration (ETa) and Deep Percolation (DP)
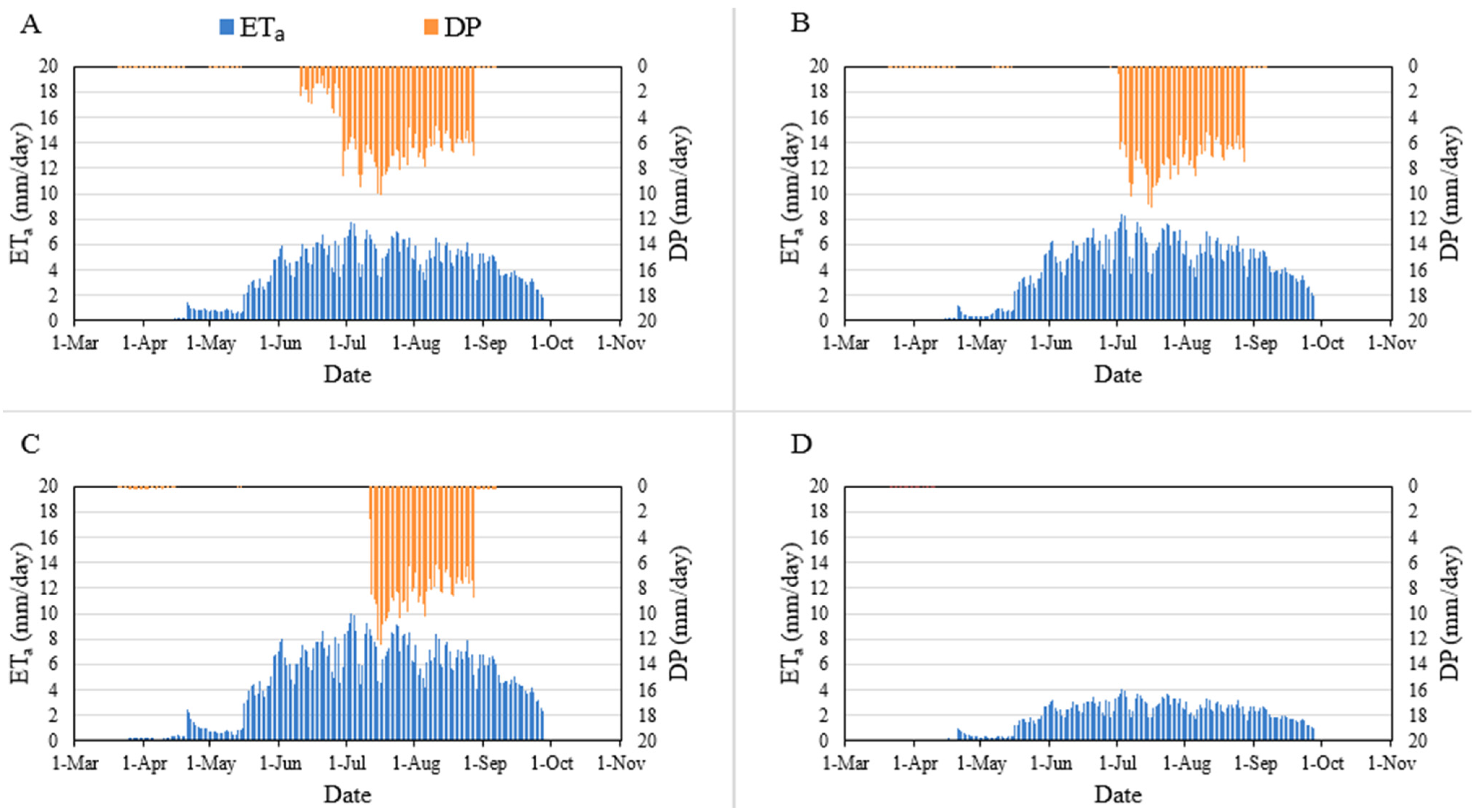
4.2. Effects of Scenarios
4.2.1. Irrigation Scenarios
Total Available Water (TAW) Scenarios
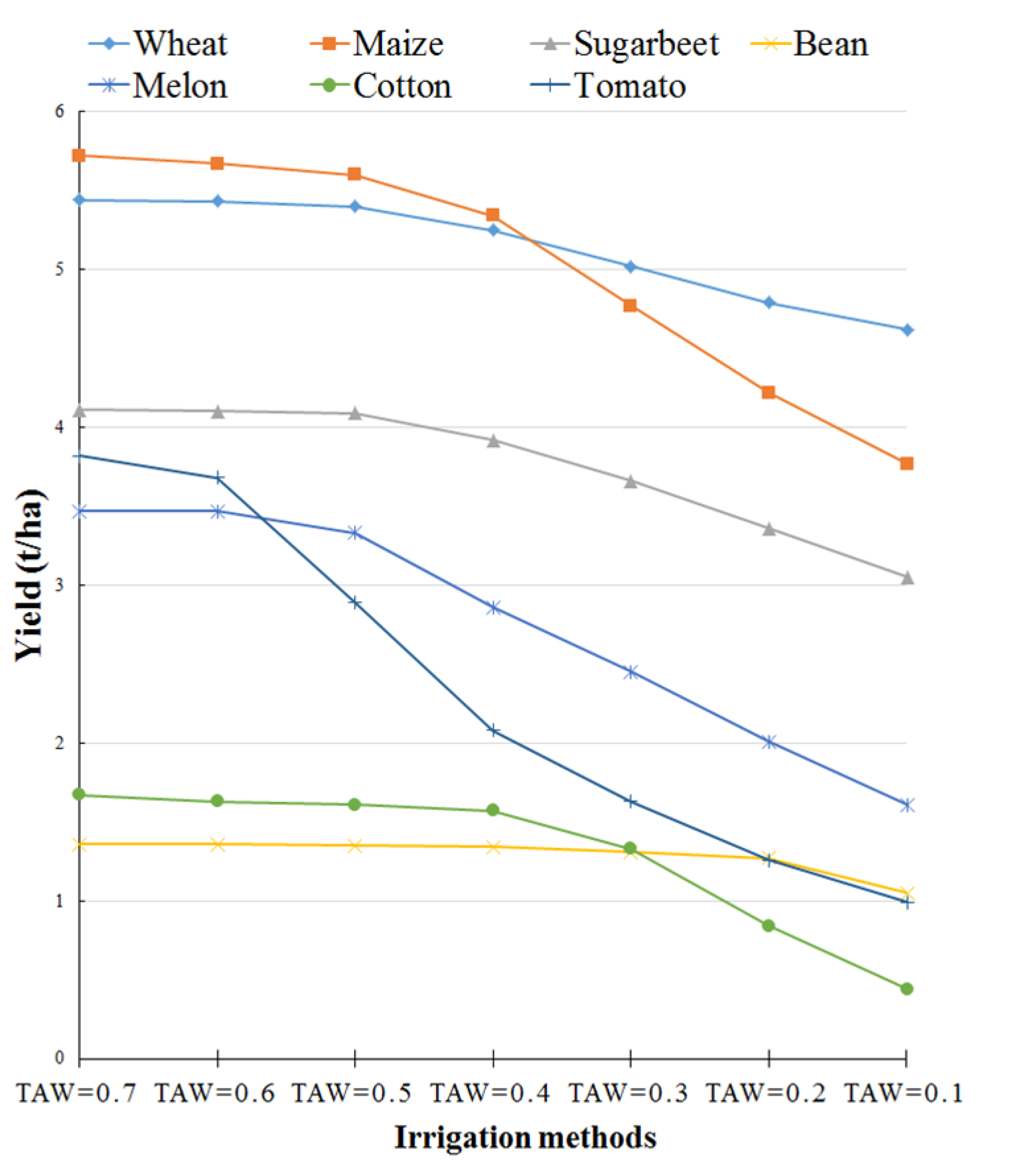
Water-Saving Irrigation Scenarios
| % DIUM | % SL | % WF | % WS | % RWDD |
|---|---|---|---|---|
| 10 | 46 | 91 | 6 | 5 |
| 30 | 38 | 73 | 17 | 12 |
| 50 | 30 | 55 | 25 | 16 |
| 70 | 22 | 37 | 32 | 22 |
| 100 | 10 | 10 | 40 | 30 |
4.2.2. Land Use Scenarios

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schmitz, C.; Lotze-Campen, H.; Gerten, D.; Dietrich, J.P.; Bodirsky, B.; Biewald, A.; Popp, A. Blue water scarcity and the economic impacts of future agricultural trade and demand. Water Resour. Res. 2013, 49, 3601–3617. [Google Scholar] [CrossRef]
- Cai, X.M.; Rosegrant, M.W. Optional water development strategies for the Yellow River Basin: Balancing agricultural and ecological water demands. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Z. Plausible impact of global climate change on water resources in the Tarim River Basin. Sci. China Ser. D Earth Sci. 2005, 48, 65–73. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Zhu, X.; Li, W.; Zhang, Y.; Xu, H. Analysis on the ecological benefits of the stream water conveyance to the dried-up river of the lower reaches of Tarim River, China. Sci. China Ser. D Earth Sci. 2004, 47, 1053–1064. [Google Scholar] [CrossRef]
- Thevs, N. Water scarcity and allocation in the Tarim Basin: Decision structures and adaptations on the local level. J. Curr. Chin. Aff. 2011, 40, 113–137. [Google Scholar]
- Chen, Y.N.; Takeuchi, K.; Xu, C.; Chen, Y.P.; Xu, Z.X. Regional climate change and its effects on river runoff in the Tarim Basin, China. Hydrol. Process. 2006, 20, 2207–2216. [Google Scholar] [CrossRef]
- Hao, X.M.; Chen, Y.; Xu, C.; Li, W. Impacts of climate change and human activities on the surface runoff in the Tarim River Basin over the last fifty years. Water Resour. Manag. 2008, 22, 1159–1171. [Google Scholar] [CrossRef]
- Ling, H.B.; Xu, H.L.; Fu, J.Y. High- and low-flow variations in annual runoff and their response to climate change in the headstreams of the Tarim River, Xinjiang, China. Hydrol. Process. 2013, 27, 975–988. [Google Scholar] [CrossRef]
- Feng, Q.; Endo, K.N.; Cheng, G.D. Towards sustainable development of the environmentally degraded arid rivers of China-a case study from Tarim River. Environ. Geol. 2001, 41, 229–238. [Google Scholar] [CrossRef]
- Qi, F.; Wei, L.; Jianhua, S.; Yonghong, S.; Yewu, Z.; Zongqiang, C.; Haiyang, X. Environmental effects of water resource development and use in the Tarim River basin of northwestern China. Environ. Geol. 2005, 48, 202–210. [Google Scholar] [CrossRef]
- Hao, X.; Chen, Y.; Li, W. The driving forces of environmental change during the last 50 years in the Tarim River Basin. Acta Geogr. Sin. 2006, 61, 262–272. [Google Scholar]
- Chen, Y.; Ye, Z.; Shen, Y. Desiccation of the Tarim River, Xinjiang, China, and mitigation strategy. Quat. Int. 2011, 244, 264–271. [Google Scholar] [CrossRef]
- Huang, S.; Krysanova, V.; Zhai, J.; Su, B. Impact of intensive irrigation activities on river discharge under agricultural scenarios in the semi-arid Aksu River basin, northwest China. Water Resour. Manag. 2015, 29, 945–959. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Biancamaria, S.; Bates, P.D.; Boone, A.; Mognard, N.M. Large-scale coupled hydrologic and hydraulic modeling of the Ob river in Siberia. J. Hydrol. 2009, 379, 136–150. [Google Scholar] [CrossRef]
- Paz, A.R.; Bravo, J.M.; Allasia, D.; Collischonn, W.; Tucci, C.E.M. Large-Scale hydrodynamic modeling of a complex river network and floodplains. J. Hydrol. Eng. 2010, 15, 152–165. [Google Scholar] [CrossRef]
- Gunduz, O. Coupled Flow and Contaminant Transport Modeling in Large Watersheds. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2004. [Google Scholar]
- Danish Hydraulic Institute (DHI). MIKE HYDRO User Manual; DHI: Hoersholm, Denmark, 2014. [Google Scholar]
- Chen, Y.N.; Xu, C.C.; Hao, X.M.; Li, W.H.; Chen, Y.P.; Zhu, C.G. Fifty-Year climate change and its effect on annual runoff in the Tarim River Basin, China. Quat. Int. 2009, 208, 53–61. [Google Scholar]
- Xu, H.; Ye, M.; Li, J. The water transfer effects on agricultural development in the lower Tarim River, Xinjiang of China. Agric. Water Manag. 2008, 95, 59–68. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Tata McGraw-Hill Education: New York, NY, USA, 1988; p. 572. [Google Scholar]
- Veissman, W.; Lewis, G.L. Introduction to Hydrology, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003; p. 612. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300. [Google Scholar]
- Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. Crop Yield Response to Water; FAO: Rome, Italy, 2012; pp. 17–40. [Google Scholar]
- Nash, J.; Sutcliffe, V. River flow forecasting through conceptual models, part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Girolamo, D.; Porto, L. Land use scenario development as a tool for watershed management within the Rio Mannu Basin. Land Use Policy 2012, 29, 691–701. [Google Scholar] [CrossRef]
- Molina-Navarro, E.; Trolle, D.; Martínez-Pérez, S.; Sastre-Merlín, A.; Jeppesen, E. Hydrological and water quality impact assessment of a Mediterranean limno-reservoir under climate change and land use management scenarios. J. Hydrol. 2014, 509, 354–366. [Google Scholar] [CrossRef]
- Stewart, J.I.; Hagan, R.M.; Pruitt, W.O.; Danielson, R.E.; Franklin, W.T.; Hanks, R.J.; Riley, J.P.; Jackson, E.B. Optimizing Crop Production through Control of Water and Salinity Levels in the Soil; Utah State University: Logan, UT, USA, 1977; p. 67. [Google Scholar]
- Doorenbos, J.; Kassam, A.H. Yield Response to Water; Irrigation and Drainage Paper; FAO: Rome, Italy, 1979; Volume 33, p. 257. [Google Scholar]
- Zia-Khan, S.; Spreer, W.; Pengnian, Y.; Zhao, X.; Othmanli, H.; He, X.; Müller, J. Effect of dust deposition on stomatal conductance and leaf temperature of cotton in northwest China. Water 2014, 7, 116–131. [Google Scholar] [CrossRef]
- Thevs, N.; Zerbe, S.; Kyosev, Y.; Rozi, A.; Tang, B.; Abdusalih, N.; Novitskiy, Z. Apocynum venetum L. and Apocynum pictum Schrenk (Apocynaceae) as multi-functional and multi-service plant species in Central Asia: A review on biology, ecology, and utilization. J. Appl. Bot. Food Qual. 2012, 85, 159–167. [Google Scholar]
- Ma, X.; Chen, Y.; Zhu, C.; Li, W. The variation in soil moisture and the appropriate groundwater table for desert riparian forest along the Lower Tarim River. J. Geogr. Sci. 2011, 21, 150–162. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, P.; Shao, M.A.; Luo, Y.; Zhu, X. Energy and water exchanges over a riparian Tamarix spp. stand in the lower Tarim River basin under a hyper-arid climate. Agric. For. Meteorol. 2014, 194, 144–154. [Google Scholar] [CrossRef]
- Stričevič, R.; Čaki, E. Relationships between available soil water and indicators of plant water status of sweet sorghum to be applied in irrigation scheduling. Irrig. Sci. 1997, 18, 17–21. [Google Scholar]
- Liu, Y.; Chen, Y. Impact of population growth and land-use change on water resources and ecosystems of the arid Tarim River basin in western China. Int. J. Sustain. Dev. World Ecol. 2006, 13, 295–305. [Google Scholar] [CrossRef]
- Hu, S.; Song, Y.; Zhou, H.; Tian, C. Experimental study on water use efficiency of cotton in the Tarim River Basin. Agric. Res. Arid Areas 2001, 20, 66–70. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Disse, M.; Yu, R.; Yu, G.; Sun, L.; Huttner, P.; Rumbaur, C. Large-Scale Hydrological Modeling and Decision-Making for Agricultural Water Consumption and Allocation in the Main Stem Tarim River, China. Water 2015, 7, 2821-2839. https://doi.org/10.3390/w7062821
Yu Y, Disse M, Yu R, Yu G, Sun L, Huttner P, Rumbaur C. Large-Scale Hydrological Modeling and Decision-Making for Agricultural Water Consumption and Allocation in the Main Stem Tarim River, China. Water. 2015; 7(6):2821-2839. https://doi.org/10.3390/w7062821
Chicago/Turabian StyleYu, Yang, Markus Disse, Ruide Yu, Guoan Yu, Lingxiao Sun, Philipp Huttner, and Christian Rumbaur. 2015. "Large-Scale Hydrological Modeling and Decision-Making for Agricultural Water Consumption and Allocation in the Main Stem Tarim River, China" Water 7, no. 6: 2821-2839. https://doi.org/10.3390/w7062821
APA StyleYu, Y., Disse, M., Yu, R., Yu, G., Sun, L., Huttner, P., & Rumbaur, C. (2015). Large-Scale Hydrological Modeling and Decision-Making for Agricultural Water Consumption and Allocation in the Main Stem Tarim River, China. Water, 7(6), 2821-2839. https://doi.org/10.3390/w7062821







